An inertial forward–backward splitting method for solving combination of equilibrium problems and inclusion problems

Abstract

In this paper, we prove a weak convergence theorem for finding a common solution of combination of equilibrium problems, infinite family of nonexpansive mappings, and the modified inclusion problems using inertial forward–backward algorithm. Further, we discuss some applications of our obtained results. Furthermore, we provide some numerical results to illustrate the convergence behavior of some of our results, and compare the convergence rate between the existing projection method and the proposed inertial forward–backward algorithm.

1 Introduction

Throughout the paper, unless otherwise stated, let H be a real Hilbert space. Inner product and induced norm are, respectively, denoted by the notations $\langle .,.\rangle$ and $\Vert .\Vert$. Weak convergence and strong convergence are denoted by $``\rightharpoonup$” and $``\rightarrow$”, respectively. Let C be a nonempty, closed, and convex subset of H. The fixed point problem for the mapping $T : C\rightarrow H$ is to find $x\in C$, such that $x = Tx$. We denote the fixed point set of a mapping T by $\mathrm{Fix}(T)$.

A mapping $T:C\rightarrow C$ is called nonexpansive if

$$\begin{aligned} \Vert Tx-Ty\Vert \le \Vert x-y\Vert , \quad \forall x,y\in C. \end{aligned}$$

T is called $\alpha$-inverse strongly monotone if there exists a positive real number $\alpha >0$, such that

$$\begin{aligned} \langle Tx-Ty, x-y\rangle \ge \alpha \Vert Tx-Ty\Vert ^2, \quad \forall x,y\in C. \end{aligned}$$

Let $F : C \times C\rightarrow {\mathbb {R}}$ be a bifunction; then, the classical equilibrium problem (for short, EP) is to find $x\in C$, such that

$$\begin{aligned} F(x, y)\ge 0, \quad \forall y\in C. \end{aligned}$$

(1.1)

The set of all solutions of the equilibrium problem $\mathrm{EP}$ (1.1) is denoted by $\mathrm{EP}(F)$, that is

$$\begin{aligned} \mathrm{EP}(F) = \{x\in C : F(x,y)\ge 0,~\forall y\in C\}. \end{aligned}$$

(1.2)

Equilibrium problem $\mathrm{EP}$ (1.1) introduced by Blum and Oettli (1994) in 1994 is the most intensively studied class of problems. This theory has helped in many ways of developing several thrust areas in physics, optimization, economics, and transportation problems. In recent past, various classes and forms of equilibrium problems and their applications have been studied, and as a result, various techniques and iterative schemes have been developed over the year to solve equilibrium problems; see (Blum and Oettli 1994; Combettes and Hirstoaga 2005; Farid et al. 2017; Khan and Chen 2015; Suwannaut and Kangtunyakarn 2014) and references therein.

Recently, Suwannaut and Kangtunyakarn (2014) proposed the following combination of equilibrium problems: for each $i=1,2,\ldots ,N$, let $F_i:C\times C\rightarrow {\mathbb {R}}$ be a bifunction and $a_i\in (0,1)$ with $\sum \nolimits _ {i=1}^N a_i=1$. The combination of equilibrium problems (for short, CEP) is to find $x\in C$, such that

$$\begin{aligned} \sum \limits _ {i=1}^N a_iF_i(x,y)\ge 0, \quad \forall y\in C. \end{aligned}$$

(1.3)

The set of all solutions of the combination of equilibrium problem $\mathrm{CEP}$ (1.3) is denoted by $\mathrm{EP}\big (\sum \nolimits _ {i=1}^N a_iF_i\big )$, that is

$$\begin{aligned} \mathrm{EP}\left( \sum \limits _ {i=1}^N a_iF_i\right) = \left\{ x\in C :\left( \sum \limits _ {i=1}^N a_iF_i\right) (x,y)\ge 0, \quad \forall y\in C\right\} . \end{aligned}$$

(1.4)

If $F_i=F,~\forall i=1,2,\ldots ,N$, then $\mathrm{CEP}$ (1.3) reduces to $\mathrm{EP}$ (1.1).

Let $A : H\rightarrow H$ is an operator and $B : H\rightarrow 2^H$ is a multi-valued operator. The variational inclusion problem (for short, VIP) is to find $x\in H$, such that

$$\begin{aligned} 0\in Ax+Bx. \end{aligned}$$

(1.5)

The set of the solution of VIP (1.5) is denoted by $(A+B)^{-1}(0)$. Variational inclusion problems are investigated and studied in minimization problem, complementarity problems, optimal control, convex programming, split feasibility problem, and variational inequalities.

An important method for solving problem VIP (1.5) is the forward–backward splitting method given by

$$\begin{aligned} x_{n+1} = (I + rB)^{-1}(x_n - rAx_n),\quad n \ge 1, \end{aligned}$$

(1.6)

where $J^B_r=(I + rB)^{-1}$ with $r > 0$. Forward–backward splitting methods are versatile in offering ways of exploiting the special structure of variational inequality problems. In this algorithm, $I -rA$ gives a forward step with step size r, whereas $(I +rB)^{-1}$ gives a backward step. Forward–backward splitting method is very useful and feasible, because computation of resolvent of $(I + rA)^{-1}$ and $(I + rB)^{-1}$ is much easier than computation of sum of resolvent the two operators $A+B$. This method provides a range of approaches to solve large-scale optimization problems and variational inequality problems; see (Bauschke and Combettes 2011; Cholamjiak 1994; Combettes and Wajs 2005; Lions and Mercier 1979; Lopez et al. 2012; Passty 1979; Tseng 2000 and reference therein. Forward–backward splitting method includes the proximal point algorithm and the gradient method as special cases; see (Alvarez 2004; Douglas and Rachford 1956; Lions and Mercier 1979; Peaceman and Rachford 1955) and references therein.

If $A=\bigtriangledown h$ and $B=\partial k$, where $\bigtriangledown h$ is the gradient of h and $\partial g$ is the subdifferential of k, then VIP (1.5) problem reduces to the following minimization problem:

$$\begin{aligned} \min \limits _{x\in H}h(x)+k(x), \end{aligned}$$

(1.7)

and solution (1.6) reduces to

$$\begin{aligned} x_{n+1} = \mathrm{prox}_{rk}(x_n - r\bigtriangledown h(x_n)),\quad n \ge 1, \end{aligned}$$

(1.8)

where $\mathrm{prox}_{rk}=(I + r\partial k)^{-1}$ is the proximity operator of k.

In 1964, Polyak (1964) introduced a two-step iterative method known as the heavy-ball method involving minimizing a smooth convex function h given by

$$\begin{aligned} \left\{ \begin{array}{ll} y_n=x_n+\theta _n (x_n-x_{n-1}) &{}\\ x_{n+1}= y_n-r\bigtriangledown h(x_n) ,~n\ge 1, \end{array} \right. \end{aligned}$$

(1.9)

where $\theta _n\in [0, 1)$ is an extrapolation factor with step size r that has to be chosen sufficiently small. Inspired by work of Polyak, in 2001, Alvarez and Attouch (2001) introduced an inertial forward–backward algorithm which was modification of the forward–backward splitting algorithm (1.9), and is given by

$$\begin{aligned} \left\{ \begin{array}{ll} y_n=x_n+\theta _n (x_n-x_{n-1}) &{}\\ x_{n+1}= (I + rB)^{-1}y_n,~n\ge 1. \end{array} \right. \end{aligned}$$

(1.10)

They proved the general convergence for monotone inclusion problems under the condition $\sum \nolimits _ {n=1}^\infty \theta _n\Vert x_n-x_{n-1}\Vert ^2<\infty$ with $\{\theta _n\}\subset [0, 1)$ in a Hilbert space setting. The term $\theta _n(x_n-x_{n-1})$ is known as inertia with an extrapolation factor $\theta _n$ which leads to faster convergence while keeping nature of each iteration basically unchanged; see (Alvarez 2004; Dang et al. 2017; Dong et al. 2017, 2018; Khan et al. 2018; Lorenz and Pock 2015; Nesterov 1983).

Recently, Moudafi and Oliny (2003) proposed the following inertial proximal point algorithm for solving the zero-finding problem of the sum of two monotone operators:

$$\begin{aligned} \left\{ \begin{array}{ll} y_n=x_n+\theta _n (x_n-x_{n-1}) &{}\\ x_{n+1}= (I + rB)^{-1}(y_n-r_nAx),~n\ge 1. \end{array} \right. \end{aligned}$$

(1.11)

They proved the weak convergence and computed the operator B as the inertial extrapolate $y_n$ under the condition $\sum \nolimits _ {n=1}^\infty \theta _n\Vert x_n-x_{n-1}\Vert ^2<\infty$.

Very recently, Khan et al. (2018) proposed inertial forward–backward splitting algorithm for solving the inclusion problems as follows:

$$\begin{aligned} \left\{ \begin{array}{ll} y_n=x_n+\theta _n (x_n-x_{n-1}) &{}\\ x_{n+1}= \alpha _nu+\beta _ny_n+\gamma _n(I + rB)^{-1}(y_n-s_nAx),~n\ge 1, \end{array} \right. \end{aligned}$$

(1.12)

and proved a strong convergence theorem of the sequence $\{x_n\}$ under suitable conditions of the parameters $\{\alpha _n\}, \{\beta _n\}, \{\gamma _n\}$ and $\{\theta _n\}$ in the setting of Hilbert space.

In 2014, Khuangsatung and Kangtunyakarn (2014) generalized variational inclusion problem (1.5) as follows: for $i =1,2,\ldots ,N$, let $A_i : H\rightarrow H$ be a single-valued mapping and let $B : H\rightarrow H$ be a multi-valued mapping. The combination of variational inclusion problem (for short, CVIP) is to find $x\in H$, such that

$$\begin{aligned} 0\in \sum \limits _ {i=1}^N b_iA_ix+Bx, \end{aligned}$$

(1.13)

for all $b_i\in (0,1)$ with $\sum \nolimits _ {i=1}^N b_i=1$. The set of all solutions of the combination of variational inclusion problem CVIP (1.13) is denoted by $\Big (\sum \nolimits _ {i=1}^N b_iA_i+B\Big )^{-1}(0)$. If $A_i=A,~\forall i=1,2,\ldots ,N$, then CVIP (1.13) reduces to VIP (1.5).

Motivated by the recent research works (Cholamjiak 1994; Dang et al. 2017; Dong et al. 2017, 2018; Khan et al. 2018; Khuangsatung and Kangtunyakarn 2014) going in this direction, we propose an iterative method of modified forward–backward algorithm involving the inertial technique for solving the combination of equilibrium problems, modified inclusion problems, and fixed point problems. Furthermore, we prove a weak convergence theorem for finding a common element of the combination of inclusion problems, fixed point sets of a infinite family of nonexpansive mappings, and the solution sets of a combination of equilibrium problems in the setting of Hilbert space. Furthermore, we utilize our main theorem to provide some applications in finding a common element of the set of fixed points of a finite family of k-strictly pseudo-contractive mappings and the set of solution of equilibrium problem in Hilbert space. Finally, we give some numerical examples to support and justify our results, which shows that our proposed inertial projection method has a better convergence rate than the standard projection method.

2 Preliminaries

To prove our main result, we recall some basic definitions and lemmas, which will be needed in the sequel.

Lemma 2.1

Takahashi (2000) Let H be a real Hilbert space. Then, the following holds:

• (i) $\Vert x+y\Vert ^2\le \Vert x\Vert ^2 + 2\langle y, x+y\rangle$, for all $x,y\in H$;

• (ii) $\Vert \alpha x+ \beta y+ \gamma z\Vert ^2 =\alpha \Vert x\Vert ^2 + \beta \Vert y\Vert ^2+ \gamma \Vert z\Vert ^2-\alpha \beta \Vert x-y\Vert -\beta \gamma \Vert y-z\Vert -\gamma \alpha \Vert z-x\Vert$, for all $\alpha , \beta , \gamma \in [0, 1]$ with $\alpha + \beta + \gamma = 1$ and $x,y,z\in H$.

A mapping $P_C:H\rightarrow C$ is said to be metric projection if, for every point $x\in H$, there exists a unique nearest point in C denoted by $P_C(x)$, such that

$$\begin{aligned} \Vert x-P_C(x)\Vert \le \Vert x-y\Vert , \quad \forall y\in C. \end{aligned}$$

It is well known that $P_C$ is nonexpansive and firmly nonexpansive, that is

$$\begin{aligned} \Vert P_C(x)-P_C(y)\Vert ^2\le \langle P_C(x)-P_C(y), x-y \rangle , \quad \forall x, y\in H. \end{aligned}$$

We also recall the following basic result in the setting of a real Hilbert space.

Lemma 2.2

Lopez et al. (2012) Let H be a Hilbert space. Let $A :H\rightarrow H$ be an $\alpha$-inverse strongly monotone and $B : H\rightarrow 2^H$ a maximal monotone operator. If $T^{A,B}_r:=J^{B}_r(I-rA)={(I+rB)}^{-1}(I-rA),~r>0$ , then the following holds:

• (i) for $r>0$, $\mathrm{Fix}(T^{A,B}_r)={(A+B)}^{-1}(0)$. Further, if $r\in (0,2\alpha ]$, then ${(A+B)}^{-1}(0)$ is a closed convex subset in H;

• (ii) for $0<s\le r$ and $x\in H,~\Vert x-T^{A,B}_sx\Vert \le 2\Vert x-T^{A,B}_rx\Vert$.

Lemma 2.3

Lopez et al. (2012) Let H be a Hilbert space. Let A is $\alpha$-inverse strongly monotone operator. Then, for given $r > 0$

$$\begin{aligned}&\Vert T^{A,B}_rx-T^{A,B}_ry\Vert ^2\le \Vert x-y\Vert ^2-r(2\alpha -r)\Vert Ax-Ay\Vert ^2\\&\quad -\Vert (I-J^B_r)(I-rA)x-(I-J^B_r)(I-rA)y\Vert , \end{aligned}$$

for all $x,y\in H$.

Lemma 2.4

Goebel and Kirk (1990) Let C be a nonempty closed convex subset of a uniformly convex space X and T a nonexpansive mapping with $\mathrm{Fix}(T)\ne \emptyset$. If $\{x_n\}$ is a sequence in C, such that $x_n\rightharpoonup x$ and $(I - T)x_n\rightarrow y$, then $(I - T)x = y$. In particular, if $y = 0$, then $x\in \mathrm{Fix}(T)$.

Lemma 2.5

Alvarez and Attouch (2001) Let $\{\psi _n\}, \{\delta _n\}$ and $\{\alpha _n\}$ be the sequences in $[0,+\infty )$, such that $\psi _{n+1}\le \psi _{n}+\alpha _n(\psi _{n}-\psi _{n-1})+\delta _n$ for all $n\ge 1,~\sum \nolimits _ {n=1}^\infty \delta _n<+\infty$, and there exists a real number $\alpha$ with $0\le \alpha _n\le \alpha <1$ for all $n\ge 1$. Then, the following holds:

• (i) $\sum \nolimits _{n\ge 1}[\psi _{n}-\psi _{n-1}]_+<+\infty$, where $[t]_+=\max \{t,0\}$;

• (ii) there exists $\psi ^*\in [0,+\infty )$, such that $\lim \nolimits _{n\rightarrow +\infty }\psi _n=\psi ^*$.

Lemma 2.6

Opial (1967) Each Hilbert space H satisfies the Opial’s condition that is, for any sequence $\{x_n\}$ with $x_n\rightharpoonup x$, the inequality

$$\begin{aligned} \lim \inf \limits _{n\rightarrow \infty }\Vert x_n-x\Vert <\lim \inf \limits _{n\rightarrow \infty }\Vert x_n-y\Vert \end{aligned}$$

holds for every $y\in H$ with $y\ne x$.

Definition 2.1

Kangtunyakarn (2011) Let C be a nonempty convex subset of a real Banach space X. Let $\{T_i\}^\infty _{i=1}$ be an infinite family of nonexpansive mappings of C into itself, and let $\lambda _1, \lambda _2, \ldots ,$ be real numbers in [0, 1]. Define the mapping $K_n : C\rightarrow C$ as follows:

$$\begin{aligned} U_{0}= & {} I,\\ U_{1}= & {} \lambda _1T_1U_{0}+(1-\lambda _1)U_{0},\\ U_{2}= & {} \lambda _2T_2U_{1}+(1-\lambda _2)U_{1},\\&\vdots&\\ U_{k}= & {} \lambda _kT_kU_{k-1}+(1-\lambda _k)U_{k-1},\\ U_{k+1}= & {} \lambda _{k+1}T_{k+1}U_{k}+(1-\lambda _{k+1})U_{k},\\ U_{N-1}= & {} \lambda _{N-1}T_{N-1}U_{N-2}+(1-\lambda _{N-1})U_{N-2},\\ K_n= & {} U_{N}=\lambda _{N}T_{N}U_{N-1}+(1-\lambda _{N})U_{N-1}. \end{aligned}$$

Such a mapping $K_n$ is called the K-mapping generated by $T_1, T_2, \ldots , T_N$ and $\lambda _1, \lambda _2, \ldots ,\lambda _N$.

Lemma 2.7

Kangtunyakarn (2011) Let C be a nonempty closed convex subset of a strictly convex Banach space. Let $\{T_i\}^\infty _{i=1}$ be an infinite family of nonexpansive mappings of C into itself with $\bigcap \nolimits _ {i=1}^\infty \mathrm{Fix}(T_i)\ne \emptyset$, and let $\lambda _1, \lambda _2, \ldots ,$ be real numbers, such that $0<\lambda _i < 1$ for every $i = 1, 2, \ldots ,$ with $\sum \nolimits _ {i=1}^\infty \lambda _i<\infty$. For every $n\in N$, let $K_n$ be the K-mapping generated by $T_1, T_2, \ldots , T_N$ and $\lambda _1, \lambda _2, \ldots ,\lambda _N$. Then, for every $x\in C$ and $k\in N, \lim \nolimits _{n\rightarrow \infty }K_nx$ exists.

For every $k\in N$ and $x\in C$, a mapping $K:C\rightarrow C$ is defined by $Kx=\lim \nolimits _{n\rightarrow \infty }K_nx$ is called K-mapping generated by $T_1, T_2, \ldots$ and $\lambda _1, \lambda _2, \ldots$.

Remark 2.1

Kangtunyakarn (2011) For every $n\in N, K_n$ is a nonexpansive mapping and $\lim \nolimits _{n\rightarrow \infty }\sup \nolimits _{x\in D}\Vert K_nx-Kx\Vert =0$, for every bounded subset D of C.

Lemma 2.8

Kangtunyakarn (2011) Let C be a nonempty closed convex subset of a strictly convex Banach space. Let $\{T_i\}^\infty _{i=1}$ be an infinite family of nonexpansive mappings of C into itself with $\bigcap \nolimits _ {i=1}^\infty \mathrm{Fix}(T_i)\ne \emptyset$, and let $\lambda _1, \lambda _2, \ldots ,$ be real numbers, such that $0<\lambda _i < 1$ for every $i = 1, 2, \ldots ,$ with $\sum \nolimits _ {i=1}^\infty \lambda _i<\infty$. For every $n\in N$, let $K_n$ be the K-mapping generated by $T_1, T_2, \ldots , T_N$ and $\lambda _1, \lambda _2, \ldots ,\lambda _N$, and let K be the K-mapping generated by $T_1, T_2, \ldots$ and $\lambda _1, \lambda _2, \ldots$. Then, $\mathrm{Fix}(K)=\bigcap \nolimits _ {i=1}^\infty \mathrm{Fix}(T_i)$.

Assumption 2.1

Blum and Oettli (1994) We assume that $F : C\times C \rightarrow {\mathbb {R}}$ satisfies the following conditions:

• (A1) $F(x, x) = 0,~\forall x\in C$;

• (A2) F is monotone, i.e., $F(x, y) + F(y, x)\le 0,~\forall x, y\in C$;

• (A3) F is upper hemicontinuous, i.e., for each $x, y, z\in C$,

  $$\begin{aligned} \limsup \limits _{t\rightarrow 0}F(tz + (1- t)x, y)\le F(x, y); \end{aligned}$$

• (A4) For each $x\in C$ fixed, the function $y\rightarrow F(x, y)$ is convex and lower semicontinuous;

• (A5) For fixed $r > 0$ and $z\in C$, there exists a nonempty compact convex subset K of H and $x\in C\cap K$, such that

  $$\begin{aligned} F(y,x) + {1\over r}\langle y-x, x-z\rangle < 0, \quad \forall y\in C\backslash K. \end{aligned}$$

Lemma 2.9

Combettes and Hirstoaga (2005) Assume that the bifunction $F: C\times C \rightarrow {\mathbb {R}}$ satisfies Assumption 2.1. For $r > 0$ and for all $x\in H$, define a mapping $T_{r}: H\rightarrow C$ as follows:

$$\begin{aligned} T_{r}(x)=\Big \{z\in C:~F(z,y) + {1\over r}\langle y- z, z-x\rangle \ge 0, \quad \forall y\in C\Big \}, \end{aligned}$$

for all $x\in H$. Then, the following holds:

• (i) $T_{r}$ is nonempty and single-valued.

• (ii) $T_{r}$ is firmly nonexpansive, i.e., for any $x,y\in H$,

  $$\begin{aligned} \Vert T_{r}x-T_{r}y\Vert ^2\le \langle T_{r}x-T_{r}y, x-y\rangle . \end{aligned}$$

• (iii) $\mathrm{Fix}(T_{r}) = \mathrm{EP}(F)$.

• (iv) $\mathrm{EP}(F)$ is closed and convex.

Lemma 2.10

Suwannaut and Kangtunyakarn (2014) Let C be a nonempty, closed, and convex subset of a real Hilbert space H. For each $i=1,2,\ldots ,N$, let $F_i:C\times C\rightarrow {\mathbb {R}}$ be a bifunction satisfying Assumption 2.1 with $\bigcap \nolimits _ {i=1}^N \mathrm{EP}(F_i)\ne \emptyset$. Then

$$\begin{aligned} \mathrm{EP}\left( \sum \limits _ {i=1}^N a_iF_i\right) =\bigcap \limits _ {i=1}^N \mathrm{EP}(F_i), \end{aligned}$$

where $a_i\in (0,1)$ for $i=1,2,\ldots ,N$ and $\sum \nolimits _ {i=1}^N a_i=1$.

Remark 2.2

Suwannaut and Kangtunyakarn (2014) From Lemma 2.10, it is easy to see that $\sum \nolimits _ {i=1}^N a_iF_i$ satisfies Assumption 2.1. Using Lemma 2.9, we obtain

$$\begin{aligned} \mathrm{Fix}(T^{\sum }_r)=\mathrm{EP}\left( \sum \limits _ {i=1}^N a_iF_i\right) =\bigcap \limits _ {i=1}^N \mathrm{EP}(F_i), \end{aligned}$$

where

$$\begin{aligned} T^{\sum }_r(x)=\left\{ z\in C:~\left( \sum \limits _ {i=1}^N a_iF_i\right) (z,y) + {1\over r}\langle y- z, z-x\rangle \ge 0,~ \forall y\in C\right\} , \end{aligned}$$

and $a_i\in (0,1)$, for each $i=1,2,\ldots ,N$ and $\sum \nolimits _ {i=1}^N a_i=1$.

Theorem 2.1

Khuangsatung and Kangtunyakarn (2014) Let H be a real Hilbert space and let $B:H\rightarrow 2^H$ be a maximal monotone mapping. For every $i=1,2,\ldots ,N$, let $A_i:H\rightarrow H$ be $\alpha _i$-inverse strongly monotone mapping with $\eta =\min _{i=1,\ldots ,N}\{\alpha _i\}$ and $\bigcap \nolimits _ {i=1}^N(A_i+B)^{-1}(0)\ne \emptyset$. Then

$$\begin{aligned} \left( \sum \limits _ {i=1}^N b_iA_i+B\right) ^{-1}(0)=\bigcap \limits _ {i=1}^N(A_i+B)^{-1}(0), \end{aligned}$$

where $\sum \nolimits _ {i=1}^N b_i=1$ and $b_i\in (0,1)$ for every $i=1,2,\ldots ,N$. Moreover, $J^{B}_s(I-s\sum \nolimits _ {i=1}^N b_iA_i)$ is a nonexpansive mapping for all $0<s<2\eta$.

Remark 2.3

From Lemma 2.2 and Theorem 2.1, we obtain

$$\begin{aligned} \mathrm{Fix}(T^{{\sum A},B}_r)=\left( \sum \limits _ {i=1}^N b_iA_i+B\right) ^{-1}(0)=\bigcap \limits _ {i=1}^N(A_i+B)^{-1}(0), \end{aligned}$$

where $T^{{\sum A},B}_r:=J^{B}_r(I-r\sum \nolimits _ {i=1}^N b_iA_i)={(I+rB)}^{-1}(I-r\sum \nolimits _ {i=1}^N b_iA_i),~r>0$.

Lemma 2.11

Xu (2003) Assume that $\{s\}$ is a sequence of nonnegative real numbers, such that

$$\begin{aligned} s_{n+1}\le (1-\alpha _n)s +\delta _n, \quad \forall n\ge 0, \end{aligned}$$

where $\{\alpha _n\}$ is a sequence in (0, 1) and $\{\delta _n\}$ is a sequence, such that

• (i) $\sum \nolimits _ {n=1}^\infty \alpha _n=\infty$;

• (ii) $\lim \sup \nolimits _ {n\rightarrow \infty }{\delta _n\over \alpha _n}\le 0$ or $\sum \nolimits _ {n=1}^\infty |\delta _n|<\infty$.

Then, $\lim \nolimits _ {n\rightarrow \infty }s=0$.

3 Main result

In this section, we prove a weak convergence theorem for finding a common element of the fixed point sets of a infinite family of nonexpansive mappings, the solution sets of a combination of equilibrium problems, and combination of inclusion problems

Theorem 3.1

Let C be a nonempty, closed, and convex subset of a real Hilbert space H. For each $i=1,2,\ldots ,N$, let $F_i:C\times C\rightarrow {\mathbb {R}}$ be a bifunction satisfying Assumption 2.1. Let $\{T_i\}^\infty _{i=1}$ be an infinite family of nonexpansive mappings of C into itself with $\bigcap \nolimits _ {i=1}^\infty \mathrm{Fix}(T_i)\ne \emptyset$ and let $\lambda _1, \lambda _2, \ldots ,$ be real numbers, such that $0<\lambda _i < 1$ for every $i = 1, 2, \ldots ,$ with $\sum \nolimits _ {i=1}^\infty \lambda _i<\infty$. For every $n\in N$, let $K_n$ be the K-mapping generated by $T_1, T_2, \ldots , T_N$ and $\lambda _1, \lambda _2, \ldots ,\lambda _N$, and let K be the K-mapping generated by $T_1, T_2, \ldots$ and $\lambda _1, \lambda _2, \ldots$ for every $x\in C$. For every $i=1,2,\ldots ,N$, let $A_i:H\rightarrow H$ be $\alpha _i$-inverse strongly monotone mapping with $\eta =\min _{i=1,\ldots ,N}\{\alpha _i\}$ and $B:H\rightarrow 2^H$ be a maximal monotone mapping. Assume that $\Omega :=\bigcap \nolimits _ {i=1}^N(A_i+B)^{-1}(0)\bigcap \bigcap \nolimits _ {i=1}^\infty \mathrm{Fix}(T_i)\bigcap \bigcap \nolimits _ {i=1}^N \mathrm{EP}(F_i)\ne \emptyset$. For given initial points $x_0, x_1\in H$, let the sequences $\{x_n\}, \{y_n\}$ and $\{u_n\}$ be generated by

$$\begin{aligned} \left\{ \begin{array}{ll} y_n=x_n+\theta _n (x_n-x_{n-1}) &{}\\ \sum _ {i=1}^N a_iF_i(u_n,y)+{1\over r_n}\langle y-u_n, u_n-y_n\rangle \ge 0,~~\forall y\in C, &{}\\ x_{n+1}=\alpha _nx_n + \beta _nK_nu_n + \gamma _nJ_{s}^B\left( I-s\sum _ {i=1}^N b_iA_i\right) u_n, \end{array} \right. \end{aligned}$$

(3.1)

where the sequences $\{\alpha _n\}, \{\beta _n\}$ and $\{\gamma _n\}\subset [0, 1]$ with $\alpha _n + \beta _n + \gamma _n=1$, for all $n\ge 1$ and $\{\theta _n\}\subset [0,\theta ], \theta \in [0,1],~\lim \inf \nolimits _ {n\rightarrow \infty }r_n>0~ and ~0<s<2\eta$, where $\eta =\min _{i=1,\ldots ,N}\{\alpha _i\}$. Suppose the following conditions hold:

• (i) $\sum \nolimits _ {n=1}^\infty \theta _n \Vert x_n-x_{n-1}\Vert <\infty$;

• (ii) $\sum \nolimits _ {n=1}^\infty \alpha _n<\infty ,~ \lim \nolimits _ {n\rightarrow \infty } \alpha _n=0$;

• (iii) $\sum \nolimits _ {n=1}^\infty |r_{n+1}-r_n|<\infty ,~\sum \nolimits _ {n=1}^\infty |\alpha _{n+1}-\alpha _n|<\infty ,~ \sum \nolimits _ {n=1}^\infty |\beta _{n+1}-\beta _n|<\infty , \sum \nolimits _ {n=1}^\infty |\gamma _{n+1}-\gamma _n|<\infty .$

Then, sequence $\{x_n\}$ converges weakly to $q\in \Omega$.

Proof

We divide the proof in the following steps.

Step 1. First, we show that $\{x_n\}$ is bounded.

Let $p\in \Omega$, and then, from Lemma 2.9, we have $u_n=T^{\sum }_{r_n}y_n$. We estimate that

$$\begin{aligned} \Vert u_n-p\Vert= & {} \left\| T^{\sum }_{r_n}y_n-T^{\sum }_{r_n}p \right\| \nonumber \\\le & {} \Vert y_n-p\Vert \nonumber \\\le & {} \Vert x_n-p\Vert +\theta _n \Vert x_n-x_{n-1}\Vert . \end{aligned}$$

(3.2)

From (3.2) and nonexpansiveness of $J_{s}^B(I-s\sum \nolimits _ {i=1}^N b_iA_i)$, we arrive that

$$\begin{aligned} \Vert x_{n+1}-p\Vert= & {} \left\| \alpha _nx_n+ \beta _nK_nu_n + \gamma _nJ_{s}^B\left( I-s\sum \limits _ {i=1}^N b_iA_i\right) u_n-p\right\| \nonumber \\\le & {} \alpha _n\left\| x_n-p\right\| + \beta _n\left\| K_nu_n-p\right\| + \gamma _n\left\| J_{s}^B\left( I-s\sum \limits _ {i=1}^N b_iA_i\right) u_n-p\right\| \nonumber \\\le & {} \alpha _n\left\| x_n-p\right\| + (1-\alpha _n)\left\| u_n-p\right\| \nonumber \\\le & {} \left\| x_n-p\right\| + (1-\alpha _n)\theta _n \left\| x_n-x_{n-1}\right\| . \end{aligned}$$

(3.3)

From Lemma 2.5 and condition (i), we obtain $\lim \nolimits _{n\rightarrow \infty }\Vert x_{n}-p\Vert$ exists and it follows that $\{x_n\}$ is bounded and also $\{y_n\}$ and $\{u_n\}$ are bounded.

Step 2. We will show that $\lim \nolimits _{n\rightarrow \infty }\Vert x_{n+1}-x_n\Vert =0.$

Let us take $J^{{\sum A},B}_s=J^{B}_s(I-s\sum \nolimits _ {i=1}^N b_iA_i)$. Then, we have

$$\begin{aligned}&\Vert x_{n+1}-x_n\Vert =\Vert \alpha _nx_n+ \beta _nK_nu_n + \gamma _nJ^{{\sum A},B}_su_n-\alpha _{n-1}x_{n-1}- \beta _{n-1}K_{n-1}u_{n-1}- \gamma _{n-1}J^{{\sum A},B}_su_{n-1}\nonumber \\&\quad \le \alpha _n\Vert x_n-x_{n-1}\Vert + |\alpha _n-\alpha _{n-1}|\Vert x_{n-1}\Vert +\beta _n\Vert K_nu_n-K_{n}u_{n-1}\Vert + \beta _n\Vert K_nu_{n-1}-K_{n-1}u_{n-1}\Vert \nonumber \\&\qquad + |\beta _n-\beta _{n-1}|\Vert K_{n-1}u_{n-1}\Vert + \gamma _n\Vert J^{{\sum A},B}_su_n-J^{{\sum A},B}_su_{n-1}\Vert + |\gamma _n-\gamma _{n-1}|\Vert J^{{\sum A},B}_su_{n-1}\Vert \nonumber \\&\quad \le \alpha _n\Vert x_n-x_{n-1}\Vert + |\alpha _n-\alpha _{n-1}|\Vert x_{n-1}\Vert +\beta _n\Vert u_n-u_{n-1}\Vert + \beta _n\Vert K_nu_{n-1}-K_{n-1}u_{n-1}\Vert \nonumber \\&\qquad + |\beta _n-\beta _{n-1}|\Vert K_{n-1}u_{n-1}\Vert + \gamma _n\Vert u_n-u_{n-1}\Vert + |\gamma _n-\gamma _{n-1}|\Vert J^{{\sum A},B}_su_{n-1}\Vert \nonumber \\&\quad \le \alpha _n\Vert x_n-x_{n-1}\Vert + (1-\alpha _n)\Vert u_n-u_{n-1}\Vert + |\alpha _n-\alpha _{n-1}|\Vert x_{n-1}\Vert + \beta _n\Vert K_nu_{n-1}-K_{n-1}u_{n-1}\Vert \nonumber \\&\qquad + |\beta _n-\beta _{n-1}|\Vert K_{n-1}u_{n-1}\Vert + |\gamma _n-\gamma _{n-1}|\Vert J^{{\sum A},B}_su_{n-1}\Vert . \end{aligned}$$

(3.4)

Since $u_n=T^{\sum }_{r_n}y_n$, therefore, using the definition of $T^{\sum }_{r_n}$, we have

$$\begin{aligned} \sum \limits _ {i=1}^N a_iF_i\left( T^{\sum }_{r_n}y_n,y\right) +{1\over r_n}\left\langle y-T^{\sum }_{r_n}y_n, T^{\sum }_{r_n}y_n-y_n\right\rangle \ge 0, \quad \forall y\in C, \end{aligned}$$

(3.5)

and

$$\begin{aligned} \sum \limits _ {i=1}^N a_iF_i\left( T^{\sum }_{r_{n+1}}y_{n+1},y\right) +{1\over r_{n+1}}\left\langle y-T^{\sum }_{r_{n+1}}y_{n+1}, T^{\sum }_{r_{n+1}}y_{n+1}-y_{n+1}\right\rangle \ge 0, \quad \forall y\in C. \end{aligned}$$

(3.6)

From (3.5) and (3.6), it follows that:

$$\begin{aligned} \sum \limits _ {i=1}^N a_iF_i\left( T^{\sum }_{r_n}y_n,T^{\sum }_{r_{n+1}}y_{n+1}\right) +{1\over r_n}\langle T^{\sum }_{r_{n+1}}y_{n+1}-T^{\sum }_{r_n}y_n, T^{\sum }_{r_n}y_n-y_n\rangle \ge 0, \quad \forall y\in C, \end{aligned}$$

(3.7)

and

$$\begin{aligned}&\sum \limits _ {i=1}^N a_iF_i\left( T^{\sum }_{r_{n+1}}y_{n+1},T^{\sum }_{r_n}y_n\right) \nonumber \\&\quad +{1\over r_{n+1}}\left\langle T^{\sum }_{r_n}y_n-T^{\sum }_{r_{n+1}}y_{n+1}, T^{\sum }_{r_{n+1}}y_{n+1}-y_{n+1}\right\rangle \ge 0, \quad \forall y\in C. \end{aligned}$$

(3.8)

From (3.7), (3.8), and monotonicity of $\sum \nolimits _ {i=1}^N a_iF_i$, we have

$$\begin{aligned} {1\over r_n}\Bigg \langle T^{\sum }_{r_{n+1}}y_{n+1}-T^{\sum }_{r_n}y_n, T^{\sum }_{r_n}y_n-y_n\Bigg \rangle +{1\over r_{n+1}}\Bigg \langle T^{\sum }_{r_n}y_n-T^{\sum }_{r_{n+1}}y_{n+1}, T^{\sum }_{r_{n+1}}y_{n+1}-y_{n+1}\Bigg \rangle \ge 0, \end{aligned}$$

which follows that

$$\begin{aligned} \left\langle T^{\sum }_{r_n}y_n-T^{\sum }_{r_{n+1}}y_{n+1},~ {T^{\sum }_{r_{n+1}}y_{n+1}-y_{n+1}\over r_{n+1}}-{T^{\sum }_{r_n}y_n-y_n\over r_n}\right\rangle \ge 0. \end{aligned}$$

It follows that

$$\begin{aligned} \left\langle T^{\sum }_{r_{n+1}}y_{n+1}-T^{\sum }_{r_n}y_n,~ T^{\sum }_{r_{n}}y_{n}-T^{\sum }_{r_{n+1}}y_{n+1} + T^{\sum }_{r_{n+1}}y_{n+1}-y_n -{r_n\over r_{n+1}}\big (T^{\sum }_{r_{n+1}}y_{n+1}-y_{n+1}\big )\right\rangle \ge 0. \end{aligned}$$

It follows that

$$\begin{aligned} \big \Vert T^{\sum }_{r_{n+1}}y_{n+1}-T^{\sum }_{r_n}y_n\big \Vert ^2\le & {} \Big \langle T^{\sum }_{r_{n+1}}y_{n+1}-T^{\sum }_{r_n}y_n,~ T^{\sum }_{r_{n+1}}y_{n+1}-y_n -{r_n\over r_{n+1}}\big (T^{\sum }_{r_{n+1}}y_{n+1}-y_{n+1}\big )\Big \rangle \\\le & {} \Big \langle T^{\sum }_{r_{n+1}}y_{n+1}-T^{\sum }_{r_n}y_n,~ y_{n+1}-y_n+\big (1-{r_n\over r_{n+1}}\big )\big (T^{\sum }_{r_{n+1}}y_{n+1}-y_{n+1}\big )\Big \rangle \\\le & {} \Big \Vert T^{\sum }_{r_{n+1}}y_{n+1}-T^{\sum }_{r_n}y_n\big \Vert \big \Vert y_{n+1}-y_n+\big (1-{r_n\over r_{n+1}}\big )\big (T^{\sum }_{r_{n+1}}y_{n+1}-y_{n+1}\big )\Big \Vert \\\le & {} \Big \Vert T^{\sum }_{r_{n+1}}y_{n+1}-T^{\sum }_{r_n}y_n\Big \Vert \Big \{\Vert y_{n+1}-y_n\Vert +\big |1-{r_n\over r_{n+1}}\big |\Vert T^{\sum }_{r_{n+1}}y_{n+1}-y_{n+1}\Vert \Big \}\\\le & {} \Big \Vert T^{\sum }_{r_{n+1}}y_{n+1}-T^{\sum }_{r_n}y_n\Big \Vert \Big \{\Vert y_{n+1}-y_n\Vert +{1\over r_{n+1}}|r_{n+1}-r_n|\Vert T^{\sum }_{r_{n+1}}y_{n+1}-y_{n+1}\Vert \Big \}\\\le & {} \Big \Vert T^{\sum }_{r_{n+1}}y_{n+1}-T^{\sum }_{r_n}y_n\Big \Vert \Big \{\Vert y_{n+1}-y_n\Vert +{1\over d}|r_{n+1}-r_n|\Vert T^{\sum }_{r_{n+1}}y_{n+1}-y_{n+1}\Vert \Big \}, \end{aligned}$$

which implies

$$\begin{aligned} \Bigg \Vert T^{\sum }_{r_{n+1}}y_{n+1}-T^{\sum }_{r_n}y_n\Bigg \Vert \le \Vert y_{n+1}-y_n\Vert +{1\over d}|r_{n+1}-r_n|\Vert T^{\sum }_{r_{n+1}}y_{n+1}-y_{n+1}\Vert , \end{aligned}$$

which follows that

$$\begin{aligned} \Vert u_{n+1}-u_n\Vert \le \Vert y_{n+1}-y_n\Vert +{1\over d}|r_{n+1}-r_n|\Vert u_{n+1}-y_{n+1}\Vert , \end{aligned}$$

Which implies that

$$\begin{aligned} \Vert u_n-u_{n-1}\Vert \le \Vert y_n-y_{n-1}\Vert +{1\over d}|r_{n}-r_{n-1}|\Vert u_n-y_n\Vert . \end{aligned}$$

(3.9)

From (3.1) and (3.9), we have

$$\begin{aligned} \Vert u_n-u_{n-1}\Vert\le & {} \Vert x_n-x_{n-1}\Vert +\theta _n\Vert x_n-x_{n-1}\Vert -\theta _{n-1}\Vert x_{n-1}-x_{n-2}\Vert \nonumber \\&+{1\over d}|r_{n}-r_{n-1}|\Vert u_n-y_n\Vert .\le (1+\theta _n)\Vert x_n-x_{n-1}\Vert +{1\over d}|r_{n}-r_{n-1}|\Vert u_n-y_n\Vert . \end{aligned}$$

(3.10)

Now, from (3.4) and (3.10), we have

$$\begin{aligned} \Vert x_{n+1}-x_n\Vert\le & {} (1-\alpha _n\theta _n)\Vert x_n-x_{n-1}\Vert + \theta _n\Vert x_n-x_{n-1}\Vert \nonumber \\&+ {{1-\alpha _n}\over d}|r_{n}-r_{n-1}|\Vert u_n-y_n\Vert +|\alpha _n-\alpha _{n-1}|\Vert x_{n-1}\Vert \nonumber \\&+ \beta _n\Vert K_nu_{n-1}-K_{n-1}u_{n-1}\Vert + |\beta _n-\beta _{n-1}|\Vert K_{n-1}u_{n-1}\Vert \nonumber \\&+ |\gamma _n-\gamma _{n-1}|\Vert J^{{\sum A},B}_su_{n-1}\Vert . \end{aligned}$$

(3.11)

Following the lines of Lemma 2.11 in Kangtunyakarn (2011), we have

$$\begin{aligned} K_nu_{n-1}-K_{n-1}u_{n-1}=\lambda _N\big (T_NK_{n-1}u_{n-1}-K_{n-1}u_{n-1}\big ). \end{aligned}$$

Since $\lambda _N\rightarrow 0$ as $n\rightarrow \infty$, we have

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }\Vert K_nu_{n-1}-K_{n-1}u_{n-1}\Vert =0. \end{aligned}$$

(3.12)

From (3.11), (3.12), Lemma 2.11, and conditions (i), (iii), we have

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }\Vert x_{n+1}-x_n\Vert =0. \end{aligned}$$

(3.13)

Step 3. We will show that $q\in \bigcap \nolimits _ {i=1}^N(A_i+B)^{-1}(0)$.

From Lemma 2.3, we have

$$\begin{aligned} \Vert x_{n+1}-p\Vert ^2= & {} \Vert \alpha _nx_n+ \beta _nK_nu_n + \gamma _nJ^{{\sum A},B}_su_n-p\Vert ^2\nonumber \\= & {} \Vert \alpha _n(x_n-p)+ \beta _n(K_nu_n-p) + \gamma _n(J^{{\sum A},B}_su_n-p)\Vert ^2\nonumber \\\le & {} \alpha _n\Vert x_n-p\Vert ^2+ \beta _n\Vert K_nu_n-p\Vert ^2 + \gamma _n\Vert J^{{\sum A},B}_su_n-p\Vert ^2\nonumber \\\le & {} \alpha _n\Vert x_n-p\Vert ^2+ \beta _n\Vert K_nu_n-p\Vert ^2 \nonumber \\&+ \gamma _n\left( \Vert u_n-p\Vert ^2-s\sum \limits _ {i=1}^N b_i(2\eta -s)\Vert A_iu_n-A_ip\Vert ^2\right. \nonumber \\&\left. -\Vert u_n-J^{{\sum A},B}_su_n+s\sum \limits _ {i=1}^N b_iA_ip-s\sum \limits _ {i=1}^N b_iA_iu_n\Vert \right) \nonumber \\\le & {} \alpha _n\Vert x_n-p\Vert ^2+ (1-\alpha _n)\Vert u_n-p\Vert ^2 -\gamma _ns\sum \limits _ {i=1}^N b_i(2\eta -s)\Vert A_iu_n-A_ip\Vert ^2\nonumber \\&-\gamma _n\Vert u_n-J^{{\sum A},B}_su_n+s\sum \limits _ {i=1}^N b_iA_ip-s\sum \limits _ {i=1}^N b_iA_iu_n\Vert \nonumber \\\le & {} \alpha _n\Vert x_n-p\Vert ^2+ (1-\alpha _n)(\Vert x_n-p\Vert + (1-\alpha _n)\theta _n \Vert x_n-x_{n-1}\Vert )^2\nonumber \\&-\gamma _ns\sum \limits _ {i=1}^N b_i(2\eta -s)\left\| A_iu_n-A_ip\right\| ^2\nonumber \\&-\gamma _n\left\| u_n-J^{{\sum A},B}_su_n+s\sum \limits _ {i=1}^N b_iA_ip-s\sum \limits _ {i=1}^N b_iA_iu_n\right\| \nonumber \\\le & {} \Vert x_n-p\Vert ^2+ 2(1-\alpha _n)^2\theta _n\langle x_n-x_{n-1}, y_n-p\rangle \nonumber \\&-\gamma _ns\sum \limits _ {i=1}^N b_i(2\eta -s)\Vert A_iu_n-A_ip\Vert ^2\nonumber \\&-\gamma _n\left\| u_n-J^{{\sum A},B}_su_n+s\sum \limits _ {i=1}^N b_iA_ip-s\sum \limits _ {i=1}^N b_iA_iu_n\right\| . \end{aligned}$$

(3.14)

Now, from (3.14), we obtain

$$\begin{aligned}&\gamma _ns\sum \limits _ {i=1}^N b_i(2\eta -s)\Vert A_iu_n-A_ip\Vert ^2\le \Vert x_{n+1}-x_n\Vert (\Vert x_{n}-p\Vert +\Vert x_{n+1}-p\Vert )\\&\qquad + 2(1-\alpha _n)^2\theta _n\langle x_n-x_{n-1}, y_n-p\rangle \\&\qquad -\gamma _n \left\| u_n-J^{{\sum A},B}_su_n+s\sum \limits _ {i=1}^N b_iA_ip-s\sum \limits _ {i=1}^N b_iA_iu_n\right\| .\\&\quad \le \Vert x_{n+1}-x_n\Vert (\Vert x_{n}-p\Vert +\Vert x_{n+1}-p\Vert )+ 2(1-\alpha _n)^2\theta _n\langle x_n-x_{n-1}, y_n-p\rangle . \end{aligned}$$

From condition (i) and (3.13), it follows that

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }\Vert A_iu_n-A_ip\Vert =0. \end{aligned}$$

(3.15)

By the following same line as above and using (3.15), we have

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }\Vert u_n-J^{{\sum A},B}_su_n\Vert =0. \end{aligned}$$

(3.16)

Since $p\in \Omega$ and $T^{\sum }_{r}$ is firmly nonexpansive, we have

$$\begin{aligned} \Vert u_n-p\Vert ^2= & {} \Vert T^{\sum }_{r_n}y_n-T^{\sum }_{r_n}p\Vert ^2\le \left\langle T^{\sum }_{r_n}y_n-T^{\sum }_{r_n}p, y_n -p\right\rangle \\= & {} \langle u_n-p, y_n-p\rangle \\= & {} {1\over 2}\big \{\Vert u_n-p\Vert ^2 +\Vert y_n-p\Vert ^2 -\Vert y_n-u_n\Vert ^2\big \}. \end{aligned}$$

Hence, it follows that

$$\begin{aligned} \Vert u_n-p\Vert ^2\le \Vert y_n-p\Vert ^2 -\Vert y_n-u_n\Vert ^2. \end{aligned}$$

(3.17)

Now, from (3.1), we have

$$\begin{aligned} \Vert x_{n+1}-p\Vert ^2= & {} \Vert \alpha _n(x_n-p)+ \beta _n(K_nu_n-p) + \gamma _n(J^{{\sum A},B}_su_n-p)\Vert ^2\\\le & {} \alpha _n\Vert x_n-p\Vert ^2+ \beta _n\Vert K_nu_n-p\Vert ^2 + \gamma _n\Vert J^{{\sum A},B}_su_n-p)\Vert ^2\\\le & {} \alpha _n\Vert x_n-p\Vert ^2+ (1-\alpha _n)\Vert u_n-p\Vert ^2. \end{aligned}$$

From (3.17) and (3.2), above inequality can be written as

$$\begin{aligned} \Vert x_{n+1}-p\Vert ^2\le & {} \alpha _n\Vert x_n-p\Vert ^2+ (1-\alpha _n)\Vert y_n-p\Vert ^2 -(1-\alpha _n)\Vert y_n-u_n\Vert ^2\nonumber \\\le & {} \alpha _n\Vert x_n-p\Vert ^2+ (1-\alpha _n)(\Vert x_n-p\Vert +\theta _n \Vert x_n-x_{n-1}\Vert )^2 -(1-\alpha _n)\Vert y_n-u_n\Vert ^2\nonumber \\\le & {} \Vert x_n-p\Vert ^2+ 2(1-\alpha _n)\theta _n\langle x_n-x_{n-1}, y_n-p\rangle -(1-\alpha _n)\Vert y_n-u_n\Vert ^2. \end{aligned}$$

(3.18)

From (3.13), (3.18), and condition (i), it follows that

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }\Vert y_n-u_n\Vert =0. \end{aligned}$$

(3.19)

From the definition of $y_n$ and condition (i), we have

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }\Vert y_n-x_n\Vert =\lim \limits _{n\rightarrow \infty }\theta _n\Vert x_n-x_{n-1}\Vert =0. \end{aligned}$$

(3.20)

From (3.19), we obtain

$$\begin{aligned} \Vert u_n-x_n\Vert \le \Vert u_n-y_n\Vert +\Vert y_n-x_n\Vert \rightarrow 0, \end{aligned}$$

(3.21)

as $n\rightarrow \infty$. From (3.13) and (3.21), it follows that

$$\begin{aligned} \Vert x_{n+1}-u_n\Vert \le \Vert x_{n+1}-x_n\Vert +\Vert x_{n}-u_n\Vert \rightarrow 0, \end{aligned}$$

(3.22)

as $n\rightarrow \infty$. Since $\{x_n\}$ is bounded and H is reflexive, $w_w(x_n) =\{x\in H : x_{n_i}\rightharpoonup x,~ \{x_{n_i}\}\subset \{x_n\}\}$ is nonempty. Let $q\in w_w(x_n)$ be an arbitrary element. Then, there exists a subsequence $\{x_{n_i}\}\subset \{x_n\}$ converging weakly to q. Let $p\in w_w(x_n)$ and $\{x_{n_m}\}\subset \{x_n\}$ be such that $x_{n_m}\rightharpoonup p$. From (3.21), we also have $u_{n_i}\rightharpoonup q$ and $u_{n_m}\rightharpoonup p$. Since $J^{{\sum A},B}_s$ is nonexpansive, by Lemma 2.4, we have $p,q\in \bigcap \nolimits _ {i=1}^N(A_i+B)^{-1}(0)$. Applying Lemma 2.6, we obtain $p = q$.

Step 4. We will show that $q\in \bigcap \nolimits _ {i=1}^\infty \mathrm{Fix} (T_i)=\mathrm{Fix}(K)$.

Now, from Lemma 2.1 and (3.18), we have

$$\begin{aligned} \Vert x_{n+1}-p\Vert ^2= & {} \Vert \alpha _n(x_n-p)+ \beta _n(K_nu_n-p) + \gamma _n(J^{{\sum A},B}_su_n-p)\Vert ^2\nonumber \\\le & {} \alpha _n\Vert x_n-p\Vert ^2+ \beta _n\Vert K_nu_n-p\Vert ^2 \nonumber \\&+ \gamma _n\Vert J^{{\sum A},B}_su_n-p\Vert ^2-\alpha _n\beta _n\Vert x_n-K_nu_n\Vert \nonumber \\&-\beta _n\gamma _n\Vert K_nu_n-J^{{\sum A},B}_su_n\Vert -\gamma _n\alpha _n\Vert J^{{\sum A},B}_su_n-x_n\Vert ^2\nonumber \\\le & {} \Vert x_n-p\Vert ^2+ 2(1-\alpha _n)\theta _n\langle x_n-x_{n-1}, y_n-p\rangle -\alpha _n\beta _n\Vert x_n-K_nu_n\Vert \nonumber \\&-\beta _n\gamma _n\Vert K_nu_n-J^{{\sum A},B}_su_n\Vert -\gamma _n\alpha _n\Vert J^{{\sum A},B}_su_n-x_n\Vert ^2. \end{aligned}$$

(3.23)

From (3.13), and conditions (i), (ii), we obtain

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }\Vert K_nu_n-J^{{\sum A},B}_su_n\Vert =0. \end{aligned}$$

(3.24)

From (3.11), we have

$$\begin{aligned} \Vert x_{n+1}-K_nu_n\Vert= & {} \left\| \alpha _nx_n+ \beta _nK_nu_n + \gamma _nJ^{{\sum A},B}_su_n-K_nu_n\right\| \\= & {} \left\| \alpha _n(x_n-K_nu_n)+ \gamma _n(J^{{\sum A},B}_su_n-K_nu_n)\right\| . \end{aligned}$$

In addition, we can estimate

$$\begin{aligned} \Vert K_nu_n-u_n\Vert\le & {} \Vert K_nu_n-x_{n+1}\Vert + \Vert x_{n+1}-x_n\Vert \nonumber \\\le & {} \alpha _n\Vert x_n-K_nu_n\Vert + \gamma _n\Vert J^{{\sum A},B}_su_n-K_nu_n\Vert + \Vert x_{n+1}-x_n\Vert . \end{aligned}$$

(3.25)

From (3.13), (3.24), (3.25), and condition (ii), we obtain

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }\Vert K_nu_n-u_n\Vert =0. \end{aligned}$$

(3.26)

Now, suppose to the contrary that $q\not \in \mathrm{Fix}(K)$, i.e., $Kq\ne q$ and by Lemma 2.6, we see that

$$\begin{aligned}&\lim \inf \limits _{i\rightarrow \infty }\Vert u_{n_i}-q\Vert <\lim \inf \limits _{i\rightarrow \infty }\Vert u_{n_i}-Kq\Vert \nonumber \\&\quad \le \lim \inf \limits _{i\rightarrow \infty }\{\Vert u_{n_i}-Ku_{n_i}\Vert +\Vert Ku_{n_i}-Kq\Vert \}\nonumber \\&\quad \le \lim \inf \limits _{i\rightarrow \infty }\{\Vert u_{n_i}-Ku_{n_i}\Vert +\Vert u_{n_i}-q\Vert \}. \end{aligned}$$

(3.27)

On the other hand, we have

$$\begin{aligned} \Vert Ku_n-u_n\Vert \le \Vert Ku_n-K_nu_n\Vert +\Vert K_nu_n-u_n\Vert \le \sup \limits _{y\in C} \Vert Ky-K_ny\Vert +\Vert K_nu_n-u_n\Vert . \end{aligned}$$

(3.28)

Using Remark 2.1 and (3.26), we obtain that $\lim \nolimits _{n\rightarrow \infty }\Vert Ku_n-u_n\Vert =0$. From (3.27), we obtain

$$\begin{aligned} \lim \inf \limits _{i\rightarrow \infty }\Vert u_{n_i}-q\Vert <\lim \inf \limits _{i\rightarrow \infty }\Vert u_{n_i}-q\Vert , \end{aligned}$$

which is a contradiction, so we have $q\in \mathrm{Fix}(K) =\bigcap \nolimits _ {i=1}^\infty \mathrm{Fix} (T_i)$.

Step 5. Show that $q\in \bigcap \nolimits _ {i=1}^N \mathrm{EP}(F_i)$.

Since $u_n=T^{\sum }_{r_n}y_n$, we have

$$\begin{aligned} \sum \limits _ {i=1}^N a_iF_i(u_n,y)+{1\over r_n}\langle y-u_n, u_n-y_n\rangle \ge 0,~~\forall y\in C. \end{aligned}$$

Since $\sum \nolimits _ {i=1}^N a_iF_i$ satisfies Assumption 2.1, so from monotonicity of $\sum \nolimits _ {i=1}^N a_iF_i$, we get

$$\begin{aligned} {1\over r_n}\langle y-u_n, u_n-y_n\rangle \ge \sum \limits _ {i=1}^N a_iF_i(y,u_n),\quad \forall y\in C. \end{aligned}$$

(3.29)

Since $\liminf \nolimits _{n\rightarrow \infty }r_n>0$ and from (3.19), it follows that

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }{ \Vert u_{n}-y_{n}\Vert \over r_{n}}=0. \end{aligned}$$

(3.30)

It follows from (3.29), (3.30), and (A4) that

$$\begin{aligned} \sum \limits _ {i=1}^N a_iF_i(y,q)\le 0, \quad \forall y\in C. \end{aligned}$$

For $t\in (0,1]$ and $y\in C$, let $y_t:=ty+(1-t)q$. Since $y\in C$, we have $y_t\in C$, and hence, $\sum \nolimits _ {i=1}^N a_iF_i(y_t,q)\le 0$. Therefore, we have

$$\begin{aligned} 0= & {} \sum \limits _ {i=1}^N a_iF_i(y_t,y_t)\\= & {} \sum \limits _ {i=1}^N a_iF_i(y_t,ty +(1-t)q)\\\le & {} t\sum \limits _ {i=1}^N a_iF_i(y_t,y) +(1-t)\sum \limits _ {i=1}^N a_iF_i(y_t,q))\\\le & {} t\sum \limits _ {i=1}^N a_iF_i(y_t,y). \end{aligned}$$

Dividing by t, we get

$$\begin{aligned} \sum \limits _ {i=1}^N a_iF_i(ty+(1-t)q,y)\ge 0 \quad \forall y\in C. \end{aligned}$$

Letting $t\downarrow 0$ and from (A3), we get

$$\begin{aligned} \sum \limits _ {i=1}^N a_iF_i(q,y)\ge 0 \quad \forall y\in C. \end{aligned}$$

Therefore, $q\in \mathrm{EP}(\sum \nolimits _ {i=1}^N a_iF_i)$. Hence, by Lemma 2.10, we obtain $q\in \bigcap \nolimits _ {i=1}^N \mathrm{EP}(F_i).$ Therefore, $q\in \Omega$. This completes the proof. $\square$

As direct consequences of Theorem 3.1, we have the following corollaries.

Corollary 3.1

Let C be a nonempty, closed, and convex subset of a real Hilbert space H. Let $F:C\times C\rightarrow {\mathbb {R}}$ be a bifunction satisfying Assumption 2.1. Let $\{T_i\}^\infty _{i=1}$ be an infinite family of nonexpansive mappings of C into itself with $\bigcap \nolimits _ {i=1}^\infty \mathrm{Fix}(T_i)\ne \emptyset$ and let $\lambda _1, \lambda _2, \ldots ,$ be real numbers, such that $0<\lambda _i < 1$ for every $i = 1, 2, \ldots ,$ with $\sum \nolimits _ {i=1}^\infty \lambda _i<\infty$. For every $n\in N$, let $K_n$ be the K-mapping generated by $T_1, T_2, \ldots , T_N$ and $\lambda _1, \lambda _2, \ldots ,\lambda _N$, and let K be the K-mapping generated by $T_1, T_2, \ldots$ and $\lambda _1, \lambda _2, \ldots$ for every $x\in C$. For every $i=1,2,\ldots ,N$, let $A:H\rightarrow H$ be $\alpha$-inverse strongly monotone mapping and $B:H\rightarrow 2^H$ be a maximal monotone mapping. Assume that $\Omega :=(A+B)^{-1}(0)\bigcap \bigcap \nolimits _ {i=1}^\infty \mathrm{Fix}(T_i)\bigcap \mathrm{EP}(F)\ne \emptyset$. For given initial points $x_0, x_1\in H$, let the sequences $\{x_n\}, \{y_n\}$ and $\{u_n\}$ be generated by

$$\begin{aligned} \left\{ \begin{array}{ll} y_n=x_n+\theta _n (x_n-x_{n-1}) &{}\\ F(u_n,y)+{1\over r_n}\langle y-u_n, u_n-y_n\rangle \ge 0, \quad \forall y\in C, &{}\\ x_{n+1}=\alpha _nx_n + \beta _nK_nu_n + \gamma _nJ_{s}^B(I-sA)u_n, \end{array} \right. \end{aligned}$$

where the sequences $\{\alpha _n\}, \{\beta _n\}$, and $\{\gamma _n\}\subset [0, 1]$ with $\alpha _n + \beta _n + \gamma _n=1$, for all $n\ge 1$ and $\{\theta _n\}\subset [0,\theta ], \theta \in [0,1],~\lim \inf \nolimits _ {n\rightarrow \infty }r_n>0~ and~0<s<2\alpha$. Suppose that the following conditions hold:

• (i) $\sum \nolimits _ {n=1}^\infty \theta _n \Vert x_n-x_{n-1}\Vert <\infty$;

• (ii) $\sum \nolimits _ {n=1}^\infty \alpha _n<\infty ,~ \lim \nolimits _ {n\rightarrow \infty } \alpha _n=0$;

• (iii) $\sum \nolimits _ {n=1}^\infty |r_{n+1}-r_n|<\infty ,\sum \nolimits _ {n=1}^\infty |\alpha _{n+1}-\alpha _n|<\infty , \sum \nolimits _ {n=1}^\infty |\beta _{n+1}-\beta _n|<\infty , \sum \nolimits _ {n=1}^\infty |\gamma _{n+1}-\gamma _n|<\infty .$

Then, sequence $\{x_n\}$ converges weakly to $q\in \Omega$.

Proof

By taking $F_i=F$ and $A_i=A,~\forall i=1,2,\ldots N$, in Theorem 3.1, the conclusion of Corollary 3.1 is followed. $\square$

Corollary 3.2

Let C be a nonempty, closed, and convex subset of a real Hilbert space H. Let $\{T_i\}^\infty _{i=1}$ be an infinite family of nonexpansive mappings of C into itself with $\bigcap \nolimits _ {i=1}^\infty \mathrm{Fix}(T_i)\ne \emptyset$, and let $\lambda _1, \lambda _2, \ldots ,$ be real numbers, such that $0<\lambda _i < 1$ for every $i = 1, 2, \ldots ,$ with $\sum \nolimits _ {i=1}^\infty \lambda _i<\infty$. For every $n\in N$, let $K_n$ be the K-mapping generated by $T_1, T_2, \ldots , T_N$ and $\lambda _1, \lambda _2, \ldots ,\lambda _N$, and let K be the K-mapping generated by $T_1, T_2, \ldots$ and $\lambda _1, \lambda _2, \ldots$ for every $x\in C$. For every $i=1,2,\ldots ,N$, let $A:H\rightarrow H$ be $\alpha$-inverse strongly monotone mapping and $B:H\rightarrow 2^H$ be a maximal monotone mapping. Assume that $\Omega :=(A+B)^{-1}(0)\bigcap \bigcap \nolimits _ {i=1}^\infty \mathrm{Fix}(T_i)\ne \emptyset$. For given initial points $x_0, x_1\in H$, let the sequences $\{x_n\}$ and $\{y_n\}$ be generated by

$$\begin{aligned} \left\{ \begin{array}{ll} y_n=x_n+\theta _n (x_n-x_{n-1}) &{}\\ x_{n+1}=\alpha _nx_n + \beta _nK_nu_n + \gamma _nJ_{s}^B(I-sA)u_n, \end{array} \right. \end{aligned}$$

where the sequences $\{\alpha _n\}, \{\beta _n\}$, and $\{\gamma _n\}\subset [0, 1]$ with $\alpha _n + \beta _n + \gamma _n=1$, for all $n\ge 1$ and $\{\theta _n\}\subset [0,\theta ], \theta \in [0,1],~0<s<2\alpha$. Suppose that the following conditions hold:

• (i) $\sum \nolimits _ {n=1}^\infty \theta _n \Vert x_n-x_{n-1}\Vert <\infty$;

• (ii) $\sum \nolimits _ {n=1}^\infty \alpha _n<\infty ,~ \lim \nolimits _ {n\rightarrow \infty } \alpha _n=0$;

• (iii) $\sum \nolimits _ {n=1}^\infty |\alpha _{n+1}-\alpha _n|<\infty ,~ \sum \nolimits _ {n=1}^\infty |\beta _{n+1}-\beta _n|<\infty , \sum \nolimits _ {n=1}^\infty |\gamma _{n+1}-\gamma _n|<\infty$.

Then, sequence $\{x_n\}$ converges weakly to $q\in \Omega$.

Proof

By taking $F_i\equiv 0$ and $A_i=A,~\forall i=1,2,\ldots N$, in Theorem 3.1, the conclusion of Corollary 3.2 is followed. $\square$

4 Applications

In this section, we discuss various applications of inertial forward–backward method to establish weak convergence result for finding a common element of the fixed point set of infinite family of nonexpansive mappings, solution sets of a combination of equilibrium problem, and k-strict pseudo-contraction mapping in the setting of Hilbert space. To prove these results, we need the following results.

Definition 4.1

A mapping $T : C\rightarrow C$ is said to be a k-strict pseudo-contraction mapping, if there exists $k\in [0,1)$, such that

$$\begin{aligned} \Vert Tx - Ty\Vert ^2\le \Vert x-y\Vert ^2+k\Vert (I-T)x-(I-T)y\Vert ^2~~\forall x,y\in C. \end{aligned}$$

Lemma 4.1

Zhou (2008) Let C be a nonempty closed convex subset of a real Hilbert space H and $T : C\rightarrow C$ a k-strict pseudo-contraction. Define $S : C\rightarrow C$ by $Sx = ax + (1 - a)Tx$, for each $x\in C$. Then, S is nonexpansive, such that $\mathrm{Fix}(S) = \mathrm{Fix}(T)$, for $a\in [k, 1)$.

Theorem 4.1

Let C be a nonempty, closed, and convex subset of a real Hilbert space H. For each $i=1,2,\ldots ,N$, let $F_i:C\times C\rightarrow {\mathbb {R}}$ be a bifunction satisfying Assumption 2.1. Let $\{T_i\}^\infty _{i=1}$ be an infinite family of $k_i$-strictly pseudo-contractive mappings of C into itself. Define a mapping $T_{k_i}$ by $T_{k_i}=k_ix+(1-k_i)T_ix,~\forall x\in C, i\in {\mathbb {N}}$ with $\bigcap \nolimits _ {i=1}^\infty \mathrm{Fix}(T_{k_i})\ne \emptyset$, and let $\lambda _1, \lambda _2, \ldots ,$ be real numbers, such that $0<\lambda _i < 1$ for every $i = 1, 2, . . . ,$ with $\sum \nolimits _ {i=1}^\infty \lambda _i<\infty$. For every $n\in {\mathbb {N}}$, let $K_n$ be the K-mapping generated by $T_{k_1}, T_{k_2}, \ldots , T_{k_n}$ and $\lambda _1, \lambda _2, \ldots ,\lambda _N$, and let K be the K-mapping generated by $T_{k_1}, T_{k_2}, \ldots$ and $\lambda _1, \lambda _2, \ldots$ for every $x\in C$. For every $i=1,2,\ldots ,N$, let $A_i:H\rightarrow H$ be $\alpha _i$-inverse strongly monotone mapping with $\eta =\min _{i=1,\ldots ,N}\{\alpha _i\}$ and $B:H\rightarrow 2^H$ be a maximal monotone mapping. Assume that $\Omega :=\bigcap \nolimits _ {i=1}^N(A_i+B)^{-1}(0)\bigcap \bigcap \nolimits _ {i=1}^\infty \mathrm{Fix}(T_i)\bigcap \bigcap \nolimits _ {i=1}^N \mathrm{EP}(F_i)\ne \emptyset$. For given initial points $x_0, x_1\in H$, let the sequences $\{x_n\}, \{y_n\}$ and $\{u_n\}$ be generated by

$$\begin{aligned} \left\{ \begin{array}{ll} y_n=x_n+\theta _n (x_n-x_{n-1}) &{}\\ \sum \nolimits _ {i=1}^N a_iF_i(u_n,y)+{1\over r_n}\langle y-u_n, u_n-y_n\rangle \ge 0,~~\forall y\in C, &{}\\ x_{n+1}=\alpha _nx_n + \beta _nK_nu_n + \gamma _nJ_{s}^B\left( I-s\sum \nolimits _ {i=1}^N b_iA_i\right) u_n, \end{array} \right. \end{aligned}$$

(4.1)

where the sequences $\{\alpha _n\}, \{\beta _n\}$, and $\{\gamma _n\}\subset [0, 1]$ with $\alpha _n + \beta _n + \gamma _n=1$, for all $n\ge 1$ and $\{\theta _n\}\subset [0,\theta ], \theta \in [0,1],~\lim \inf \nolimits _ {n\rightarrow \infty }r_n>0 ~and~0<s<2\eta$, where $\eta =\min _{i=1,\ldots ,N}\{\alpha _i\}$. Suppose that the following conditions hold:

• (i) $\sum \nolimits _ {n=1}^\infty \theta _n \Vert x_n-x_{n-1}\Vert <\infty$;

• (ii) $\sum \nolimits _ {n=1}^\infty \alpha _n<\infty ,~ \lim \nolimits _ {n\rightarrow \infty } \alpha _n=0$;

• (iii) $\sum \nolimits _ {n=1}^\infty |r_{n+1}-r_n|<\infty ,~\sum \nolimits _ {n=1}^\infty |\alpha _{n+1}-\alpha _n|<\infty ,~ \sum \nolimits _ {n=1}^\infty |\beta _{n+1}-\beta _n|<\infty , \sum \nolimits _ {n=1}^\infty |\gamma _{n+1}-\gamma _n|<\infty .$

Then, sequence $\{x_n\}$ converges weakly to $q\in \Omega$.

Proof

For every $i\in {\mathbb {N}}$, by Lemma 4.1, we have that $T_{k_i}$ is a nonexpansive mapping and $\bigcap \nolimits _ {i=1}^\infty \mathrm{Fix}(T_{k_i})=\bigcap \nolimits _ {i=1}^\infty \mathrm{Fix}(T_i)$. From Theorem 3.1 and Lemma 2.8, the conclusion of Theorem 4.1 is followed.

Now, we consider a property of finite family of strictly pseudo-contractive mappings in Hilbert space as follows: $\square$

Proposition 4.1

Fan et al. (2009) Let C be a nonempty closed convex subset of a real Hilbert space H.

• (i) For any integer $N\ge 1$, let, for each $1\le i\le N,~S_i:C\rightarrow H$ is $k_i$-strict pseudo-contraction for some $0\le k_i<1$. Let $\{b_i\}^ N_{i}$ is a positive sequence, such that $\sum \nolimits _ {i=1}^ N b_i=1$. Then, $\sum \nolimits _ {i=1}^ N b_iS_i$ is a k-strict pseudo-contraction, with $k=\max _{i=1,\ldots , N}\{k_i\}$;

• (ii) Let $\{S_i\}^ N_{i}$ and $\{b_i\}^ N_{i}$ be given as in (i) above. Suppose that $\{S_i\}^ N_{i}$ has a common fixed point. Then

  $$\begin{aligned} \mathrm{Fix}\left( \sum \limits _ {i=1}^N b_iS_i\right) =\bigcap \limits _ {i=1}^N \mathrm{Fix}(S_i). \end{aligned}$$

Theorem 4.2

Let C be a nonempty, closed, and convex subset of a real Hilbert space H. For each $i=1,2,\ldots ,N$, let $F_i:C\times C\rightarrow {\mathbb {R}}$ be a bifunction satisfying Assumption 2.1. Let $\{S_i\}^ N_{i=1}$ be an finite family of $k_i$-strictly pseudo-contractive mappings of C into itself with $k=\max _{i=1,\ldots ,{\mathbb {N}}}\{k_i\}$. Let $\{T_i\}^\infty _{i=1}$ be an infinite family of nonexpansive mappings with $\bigcap \nolimits _ {i=1}^\infty \mathrm{Fix}(T_{i})\ne \emptyset$, and let $\lambda _1, \lambda _2, \ldots ,$ be real numbers, such that $0<\lambda _i < 1$ for every $i = 1, 2, \ldots ,$ with $\sum \nolimits _ {i=1}^\infty \lambda _i<\infty$. For every $n\in {\mathbb {N}}$, let $K_n$ be the K-mapping generated by $T_{1}, T_{2}, \ldots , T_{n}$ and $\lambda _1, \lambda _2, \ldots ,\lambda _N$, and let K be the K-mapping generated by $T_{1}, T_{2}, \ldots$ and $\lambda _1, \lambda _2, \ldots$ for every $x\in C$. Assume that $\Omega :=\bigcap \nolimits _ {i=1}^N \mathrm{Fix}(S_i)\bigcap \bigcap \nolimits _ {i=1}^\infty \mathrm{Fix}(T_i)\bigcap \bigcap \nolimits _ {i=1}^N \mathrm{EP}(F_i)\ne \emptyset$. For given initial points $x_0, x_1\in H$, let the sequences $\{x_n\}, \{y_n\}$ and $\{u_n\}$ be generated by

$$\begin{aligned} \left\{ \begin{array}{ll} y_n=x_n+\theta _n (x_n-x_{n-1}) &{}\\ \sum \nolimits _ {i=1}^N a_iF_i(u_n,y)+{1\over r_n}\langle y-u_n, u_n-y_n\rangle \ge 0, \quad \forall y\in C, &{}\\ x_{n+1}=\alpha _nx_n + \beta _nK_nu_n + \gamma _n \left( (1-s)u_n+ s\sum \nolimits _ {i=1}^N b_iS_iu_n\right) , \end{array} \right. \end{aligned}$$

(4.2)

where the sequences $\{\alpha _n\}, \{\beta _n\}$, and $\{\gamma _n\}\subset [0, 1]$ with $\alpha _n + \beta _n + \gamma _n=1$, for all $n\ge 1$ and $\{\theta _n\}\subset [0,\theta ], \theta \in [0,1],~\lim \inf \limits _ {n\rightarrow \infty }r_n>0 and~0<s<1-k$. Suppose that the following conditions hold:

• (i) $\sum \nolimits _ {n=1}^\infty \theta _n \Vert x_n-x_{n-1}\Vert <\infty ;$

• (ii) $\sum \nolimits _ {n=1}^\infty \alpha _n<\infty ,~ \lim \nolimits _ {n\rightarrow \infty } \alpha _n=0;$

• (iii) $\sum \nolimits _ {n=1}^\infty |r_{n+1}-r_n|<\infty ,~\sum \nolimits _ {n=1}^\infty |\alpha _{n+1}-\alpha _n|<\infty ,~ \sum \nolimits _ {n=1}^\infty |\beta _{n+1}-\beta _n|<\infty , \sum \nolimits _ {n=1}^\infty |\gamma _{n+1}-\gamma _n|<\infty$.

Then, sequence $\{x_n\}$ converges weakly to $q\in \Omega$.

Proof

Let $A_i = I-S_i$ and $B = 0$ in Theorem 3.1, and then, we have that $A_i$ is $\alpha _i$-inverse strongly monotone with ${{1-k}\over 2}$ . Now, we show that $\bigcap \nolimits _ {i=1}^N(A_i+B)^{-1}(0)=\bigcap \nolimits _ {i=1}^N \mathrm{Fix}(S_i)$. Since $A_i = I-S_i$ and $B = 0$, therefore, using Theorem 2.1 and Proposition 4.1, we have

$$\begin{aligned}&x\in \bigcap \limits _ {i=1}^N(A_i+B)^{-1}(0)\Leftrightarrow x\in \left( \sum \limits _ {i=1}^N b_iA_i+B\right) ^{-1}(0)\Leftrightarrow 0\in \sum \limits _ {i=1}^N b_iA_ix+Bx\\&\quad \Leftrightarrow 0\in \sum \limits _ {i=1}^N b_iA_ix\Leftrightarrow 0\in \sum \limits _ {i=1}^N b_i(I-S_i)x\\&\quad \Leftrightarrow x= \sum \limits _ {i=1}^N b_iS_ix\Leftrightarrow x\in \mathrm{Fix}\left( \sum \limits _ {i=1}^N b_iS_ix\right) \Leftrightarrow x\in \bigcap \limits _ {i=1}^N \mathrm{Fix}(S_i). \end{aligned}$$

It follows that

$$\begin{aligned} \bigcap \limits _ {i=1}^N(A_i+B)^{-1}(0)=\bigcap \limits _ {i=1}^N \mathrm{Fix}(S_i). \end{aligned}$$

We know that $J_{s}^B(I-s\sum \nolimits _ {i=1}^N b_iA_i)u_n=(I+sB)^{-1}(I-s\sum \nolimits _ {i=1}^N b_iA_i)u_n$.

Since  $B=0,~\mathrm{we~ have}~~J_{s}^B\left( I-s\sum \nolimits _ {i=1}^N b_iA_i\right) u_n=u_n-s\sum \nolimits _ {i=1}^N b_iA_iu_n$

$$\begin{aligned}= & {} u_n-s\sum \limits _ {i=1}^N b_i(I-S_i)u_n\\= & {} (1-s)u_n+ s\sum \limits _ {i=1}^N b_iS_iu_n. \end{aligned}$$

Since $s\in (0,1-k)\subset (0, 1)$, then $(1-s)u_n+ s\sum \nolimits _ {i=1}^N b_iS_iu_n\in H$. Therefore, from Theorem 3.1, we obtain the desired result. $\square$

5 Example and numerical results

Finally, we give the following numerical example to illustrate Theorems 3.1 and 4.2.

Example 5.1

Let ${\mathbb {R}}$ be the set of real numbers. For each $i=1,2,\ldots ,N$, let $F_i:{\mathbb {R}}\times {\mathbb {R}}\rightarrow {\mathbb {R}}$ be defined by

$$\begin{aligned} F_i(x,y)=i(y^2-2x^2+xy+3x-3y). \end{aligned}$$

Furthermore, let $a_i={4\over 5^i}+{1\over N5^N}$, such that $\sum \nolimits _ {i=1}^N a_i=1$, for every $i=1,2,\ldots ,N$. Then, we have

$$\begin{aligned} \sum \limits _ {i=1}^N a_iF_i(x,y)= & {} \sum \limits _ {i=1}^N\Big ( {4\over 5^i}+{1\over N5^N}\Big )i(y^2-2x^2+xy+3x-3y)\\= & {} \Psi (y^2-2x^2+xy+3x-3y), \end{aligned}$$

where $\Psi =\sum \nolimits _ {i=1}^N \Big ({4\over 5^i}+{1\over N5^N}\Big )i$.

It is easy to check that $\sum \nolimits _ {i=1}^N a_iF_i$ satisfies all the conditions of Theorem 3.1 and $\mathrm{EP}\big (\sum \nolimits _ {i=1}^N a_iF_i\big )=\bigcap \nolimits _ {i=1}^N \mathrm{EP}(F_i)=\{1\}.$

For each $i=1,2,\ldots ,N$, let $A_i:{\mathbb {R}}\rightarrow {\mathbb {R}}$ be defined by $A_i(x)={x-(4i+1)\over i}$ and $B:{\mathbb {R}}\rightarrow 2^{\mathbb {R}}$ is defined by $B(x)=\{4x\}$.

It is easy to observe that $A_i$ is i-inverse strongly monotone mapping with $\eta =\min _{i=1,\ldots ,N}\{\ i\}=1$ and $\bigcap \nolimits _ {i=1}^N(A_i+B)^{-1}(0)=\{ 1\}$.

Further, let $b_i={3\over 4^i}+{1\over N4^N}$, such that $\sum \nolimits _ {i=1}^N b_i=1$, for every $i=1,2,\ldots ,N$. It is easy to check that $A_i$ and B satisfy all the conditions of Theorem 3.1 and $\Big (\sum \nolimits _ {i=1}^N b_iA_i+B\Big )^{-1}(0)=\bigcap \nolimits _ {i=1}^N(A_i+B)^{-1}(0)=\{ 1\}$.

Let the mapping $T_i:{\mathbb {R}}\rightarrow {\mathbb {R}}$ is defined by $T_i(x)={x+i\over i+1},~i=1,2,\ldots ,$. It is easy to check that $\{T_i\}^\infty _{i=1}$ is infinite family of nonexpansive mapping. For each i, let $\lambda _i={i\over i+1}$ be real numbers, such that $0<\lambda _i < 1$ for every $i = 1, 2, \ldots ,$ with $\sum \nolimits _ {i=1}^\infty \lambda _i<\infty$. Since $K_n$ is K-mapping generated by $T_1, T_2, \ldots ,$ and $\lambda _1, \lambda _2, \ldots$; therefore, we obtain

$$\begin{aligned} U_{0}u_n= & {} u_n,\\ U_{1}u_n= & {} {1\over 2}\left( {U_{0}u_n +1\over 2}\right) +{1\over 2}U_{0}u_n,\\ U_{2}u_n= & {} {2\over 3}\left( {U_{1}u_n +2\over 3}\right) +{1\over 3}U_{1}u_n,\\&\vdots&\\ K_nu_n= & {} U_{N}u_n={N\over N+1}\left( {U_{{N-1}}u_n +N\over N+1}\right) +{1\over N+1}U_{{N-1}}u_n. \end{aligned}$$

It is easy to see that $\bigcap \nolimits _ {i=1}^\infty \mathrm{Fix}(T_i)=\{1\}$. Therefore, it is easy to see that

$$\begin{aligned} \bigcap \limits _ {i=1}^N(A_i+B)^{-1}(0)\bigcap \bigcap \limits _ {i=1}^\infty \mathrm{Fix}(T_i)\bigcap \bigcap \limits _ {i=1}^N \mathrm{EP}(F_i)=\{ 1\}. \end{aligned}$$

By Lemma 2.9, we have that $T^{\sum }_{r_n}x$, is a single-valued mapping for each $x\in {\mathbb {R}}$. Hence, for $r_n > 0$, there exist sequences $\{x_n\}$ and $\{u_n\}$, such that

$$\begin{aligned} \sum \limits _ {i=1}^N a_iF_i(u_n, y) + {1\over r_n}\langle y -u_n, u_n -y_n\rangle \ge 0, \quad \forall y\in {\mathbb {R}}, \end{aligned}$$

which is equivalent to

$$\begin{aligned} P(y):=\Psi r_ny^2+(\Psi u_nr_n+u_n-y_n-3\Psi r_n)y+ 3\Psi r_nu_n-u^2_n-2\Psi r_nu^2_n +u_ny_n\ge 0. \end{aligned}$$

Since $P(y)=ay^2+by+c\ge 0,$ for all $y\in {\mathbb {R}}$, then $b^2-4ac=(u_n-3\Psi r_n+3\Psi r_nu_n-y_n)^2\le 0$, which yields $(u_n-3\Psi r_n+3\Psi r_nu_n-y_n)^2= 0$. Therefore, for each $r_n>0$, it implies that

$$\begin{aligned} u_n=T^{\sum }_{r_n}y_n={y_n+3\Psi r_n\over 1+3\Psi r_n}. \end{aligned}$$

(5.1)

By choosing $\alpha _n=r_n={1\over 6n}, \beta _n={18n-3\over 30n}, \gamma _n={12n-2\over 30n}$, $\theta _n={1\over 12}$ and $s=0.1$ as $0<s<2\eta$, where $\eta =\min _{i=1,\ldots ,N}\{\alpha _i\}=1$. It is clear that the sequences $\{\alpha _n\}, \{\beta _n\}$, $\{\gamma _n\}$ and $\{\theta _n\}$ for all $n\ge 1$ satisfy all the conditions of Theorem 3.1. For each $n\in {\mathbb {N}}$, using (5.1), algorithm (3.1) can be re-written as follows:

$$\begin{aligned} \left\{ \begin{array}{ll} y_n=x_n+{\theta _n}(x_n-x_{n-1}) &{}\\ u_n={y_n+3\Psi r_n\over 1+3\Psi r_n} &{}\\ x_{n+1}={1\over 6n}x_n + {18n-3\over 30n}K_nu_n + {12n-2\over 30n}\Big ({u_n-s\sum \nolimits _ {i=1}^N\Big ( {4(u_n-4i-1)\over i5^i}+{u_n-4i-1\over iN5^N}\Big )\over 1+4s}\Big ). \end{array} \right. \end{aligned}$$

(5.2)

By taking $x_0=2,~x_1=0$ with $N=2$ and $N=20$ for $n=25$ iterations in the algorithm (5.2), we have the numerical results in Table 1 and Fig. 1.

Table 1 Values of $\{x_{n}\}$ with initial values $x_{0} = 2$ and $x_{1} = 0$

Fig. 1

Convergence of ${x}_{{n}}$

We can conclude that the sequence $\{x_n\}$ converges to 1, as shown in Table 1 and Fig. 1. It can also be easily seen that sequence $\{x_n\}$ for $N=20$ converges more quickly than for $N=2$.

Fig. 2

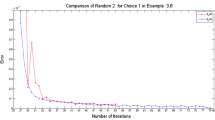
Error plot for Example 5.1

Figure 2 shows that the sequence generated by our proposed inertial forward–backward method proposed in Theorem 3.1 has a better convergence rate than standard forward–backward method (i.e., at $\theta _n=0)$.

Example 5.2

Let ${\mathbb {R}}$ be the set of real numbers. For each $i=1,2,\ldots ,N$, let $F_i:{\mathbb {R}}\times {\mathbb {R}}\rightarrow {\mathbb {R}}$ be defined by

$$\begin{aligned} F_i(x,y)=i(y^2-3x^2+2xy). \end{aligned}$$

Furthermore, let $a_i={4\over 5^i}+{1\over N5^N}$, such that $\sum \nolimits _ {i=1}^N a_i=1$, for every $i=1,2,\ldots ,N$. Then, it is easy to check that $\sum \nolimits _ {i=1}^N a_iF_i$ satisfies all the conditions of Theorem 3.1 and $\mathrm{EP}\big (\sum \nolimits _ {i=1}^N a_iF_i\big )=\bigcap \nolimits _ {i=1}^N \mathrm{EP}(F_i)=\{0\}.$

Let the mapping $T_i:{\mathbb {R}}\rightarrow {\mathbb {R}}$ is defined by $T_i(x)={ix\over i+1},~i=1,2,\ldots ,$. It is easy to check that $\{T_i\}^ \infty _{i=1}$ is infinite family of nonexpansive mapping. For each i, let $\lambda _i={i\over i+1}$ be real numbers, such that $0<\lambda _i < 1$ for every $i = 1, 2, \ldots ,$ with $\sum \nolimits _ {i=1}^\infty \lambda _i<\infty$. Since $K_n$ is K-mapping generated by $T_1, T_2, \ldots ,$ and $\lambda _1, \lambda _2, \ldots$; therefore, we obtain

$$\begin{aligned} U_{0}u_n= & {} u_n,\\ U_{1}u_n= & {} \Bigg ({1\over 2}\Bigg )^2U_{0}u_n+{1\over 2}U_{0}u_n,\\ U_{2}u_n= & {} \Bigg ({2\over 3}\Bigg )^2U_{1}u_n+{1\over 3}U_{1}u_n,\\&\vdots&\\ K_nu_n= & {} \Bigg ({N\over N+1}\Bigg )^2U_{N-1}u_n+{1\over N+1}U_{{N-1}}u_n. \end{aligned}$$

For each $i=1,2,\ldots ,N$, let a mapping $S_i:{\mathbb {R}}\rightarrow {\mathbb {R}}$ is defined by

$$\begin{aligned} S_i(x)=\left\{ \begin{array}{ll} -ix,~~~~~~~~~x\in [0,\infty )\\ &{}\\ x ,~~~~~~~~~x\in (-\infty ,0), &{}\\ \end{array} \right. \end{aligned}$$

be a finite family of ${i^2-1\over {(i+1)}^2}$-strictly pseudo-contractive mappings. Furthermore, let $b_i={7\over 8^i}+{1\over N8^N}$, such that $\sum \nolimits _ {i=1}^N b_i=1$, for every $i=1,2,\ldots ,N$. It is easy to see that $\bigcap \nolimits _ {i=1}^N \mathrm{Fix}(S_i)=\{0\}$. Therefore, it is easy to see that

$$\begin{aligned} \bigcap \limits _ {i=1}^N \mathrm{Fix}(S_i)\bigcap \bigcap \limits _ {i=1}^\infty \mathrm{Fix}(T_i)\bigcap \bigcap \limits _ {i=1}^N \mathrm{EP}(F_i)=\{ 0\}. \end{aligned}$$

By Lemma 2.9, for each $x\in {\mathbb {R}}$, a single-valued mapping $T^{\sum }_{r_n}x$ as Example 5.1, can be computed as

$$\begin{aligned} u_n=T^{\sum }_{r_n}y_n={y_n\over 1+4S_1 r_n}, \end{aligned}$$

(5.3)

where $S_1=\sum \nolimits _ {i=1}^N({4\over 5^i}+{1\over N5^N})i$. By choosing $\alpha _n=r_n={1\over 6n}, \beta _n={18n-3\over 30n}, \gamma _n={12n-2\over 30n}$, $\theta _n={1\over 20}$, and $s=0.1$ as $0<s<2\eta$, where $\eta =\min _{i=1,\ldots ,N}\{\alpha _i\}=1$. It is clear that the sequences $\{\alpha _n\}, \{\beta _n\}$, $\{\gamma _n\}$ and $\{\theta _n\}$ for all $n\ge 1$ satisfy all the conditions of Theorem 4.2 For each $n\in {\mathbb {N}}$, using (5.3), algorithm (4.2) can be re-written as follows:

$$\begin{aligned} \left\{ \begin{array}{ll} y_n=x_n+{\theta _n}(x_n-x_{n-1}) &{}\\ u_n={y_n\over 1+4S_1 r_n} &{}\\ x_{n+1}={1\over 6n}x_n + {18n-3\over 30n}K_nu_n + {12n-2\over 30n}\big ((1-s)u_n-s\sum \nolimits _ {i=1}^N\big ( {7\over 8^i}+{1\over N8^N}\big )S_iu_n\big ). \end{array} \right. \end{aligned}$$

(5.4)

By taking $x_0=4,~x_1=4.5$ with $N=4$ and $N=20$ for $n=25$ iterations in the algorithm (5.4), we have the numerical results in Table 2 and Fig. 3.

Table 2 Values of $\{x_{n}\}$ with initial values $x_{0} = 4$ and $x_{1} = 4.5$

Fig. 3

Convergence of ${x}_{{n}}$

We can conclude that the sequence $\{x_n\}$ converges to 0, as shown in Table 2 and Fig. 3. It can also be easily seen that sequence $\{x_n\}$ for $N=20$ converges more quickly than for $N=4$.

Fig. 4

Error plot for Example 5.2

Figure 4, shows that the sequence generated by our proposed inertial forward–backward method proposed in Theorem 4.2 has a better convergence rate than forward–backward method (i.e., at $\theta _n=0)$.

6 Conclusion

In this work, we established weak convergence result for finding a common element of the fixed point sets of a infinite family of nonexpansive mappings and the solution sets of a combination of equilibrium problems and combination of inclusion problems. It has been illustrated by an example with different choices that our proposed method involving the inertial term converges faster than usual projection method. Finally, we discussed some applications of modified inclusion problems in finding a common element of the set of fixed points of a infinite family of strictly pseudo-contractive mappings and the set of solution of equilibrium problem supported by numerical result. The method and results presented in this paper generalize and unify the corresponding known results in this area (see Cholamjiak 1994; Dong et al. 2017; Khan et al. 2018; Khuangsatung and Kangtunyakarn 2014).