A modified inertial shrinking projection method for solving inclusion problems and quasi-nonexpansive multivalued mappings

Abstract

In this work, we propose a modified inertial and forward–backward splitting method for solving the fixed point problem of a quasi-nonexpansive multivalued mapping and the inclusion problem. Then, we establish the weak convergence theorem of the proposed method. The strongly convergent theorem is also established under suitable assumptions in Hilbert spaces using the shrinking projection method. Some preliminary numerical experiments are tested to illustrate the advantage performance of our methods.

1 Introduction

Let H be a real Hilbert space with inner product $\langle \cdot ,\cdot \rangle$ and norm $\Vert \cdot \Vert$, respectively. Let CB(H) and K(H) denote the families of nonempty closed bounded subsets and nonempty compact subsets of H, respectively. The Hausdorff metric on CB(H) is defined by the following:

$$\begin{aligned} H(A,B)=\max \left\{ \sup _{x\in A}d(x,B), \ \sup _{y\in B}d(y,A)\right\} \end{aligned}$$

for all $A,B \in CB(H)$, where $d(x,B)=\inf _{b\in B}\Vert x-b\Vert$. A single-valued mapping $T:H\rightarrow H$ is said to be nonexpansive if

$$\begin{aligned} \Vert Tx-Ty\Vert \le \Vert x-y\Vert \end{aligned}$$

for all $x,y\in H$. A multivalued mapping $T:H\rightarrow CB(H)$ is said to be nonexpansive if

$$\begin{aligned} H(Tx,Ty)\le \Vert x-y\Vert \end{aligned}$$

for all $x,y\in H$. An element $z\in H$ is called a fixed point of $T:H\rightarrow H$ (resp., $T:H \rightarrow CB(H)$) if $z=Tz$ (resp., $z\in Tz$). The fixed point set of T is denoted by F(T). If $F(T)\ne \emptyset$ and

$$\begin{aligned} H(Tx,Tp)\le \Vert x-p\Vert \end{aligned}$$

for all $x\in H$ and $p\in F(T)$, then T is said to be quasi-nonexpansive. We write ${{x}_{n}}\rightharpoonup x$ to indicate that the sequence $\left\{ {{x}_{n}} \right\}$ converges weakly to x and ${{x}_{n}}\rightarrow x$ implies that $\left\{ {{x}_{n}} \right\}$ converges strongly to x.

For solving the fixed point problem of a single-valued nonlinear mapping, the Noor iteration [see Noor (2000)] is defined by $x_1\in H$ and

$$\begin{aligned} \left\{ \begin{array}{llll} y_n =\gamma _n x_n+(1-\gamma _n)Tx_n\\ z_n=\beta _nx_n+(1-\beta _n)Ty_n\\ x_{n+1} =\alpha _nx_n+(1-\alpha _n)Tz_n, \end{array} \right. \end{aligned}$$

(1.1)

for all $n\ge 1$, where $\{\alpha _n\}$, $\{\beta _n\}$, $\{\gamma _n\}$ are sequences in [0,1]. The iterative process Eq. (1.1) is generalized form of the Mann(one-step) iterative process by Mann (1953) and the Ishikawa (two-step) iterative process by Ishikawa (1974). Phuengrattana and Suantai (2011), in 2011, introduced the new process using the concept of the Noor iteration and it is called the SP iteration. These iteration is generated by $x_1\in H$ and

$$\begin{aligned} \left\{ \begin{array}{lll} y_n =\gamma _n x_n+(1-\gamma _n)Tx_n\\ z_n=\beta _ny_n+(1-\beta _n)Ty_n\\ x_{n+1} =\alpha _nz_n+(1-\alpha _n)Tz_n, \end{array} \right. \end{aligned}$$

(1.2)

for all $n\ge 1$, where $\{\alpha _n\}$, $\{\beta _n\}$, $\{\gamma _n\}$ are sequences in [0,1]. They compared the convergence speed of Mann, Ishikawa, Noor, and SP iteration, and obtained the SP iteration converges faster than the others for the class of continuous and nondecreasing functions. However, the Noor iteration and the SP iteration have only weak convergence even in a Hilbert space.

Let $T:H\rightarrow CB(H)$ be a multivalued mapping, $I-T$ (I is an identity mapping) is said to be demiclosed at $y\in H$ if $\{x_{n}\}_{n=1}^{\infty }\subset H$, such that $x_{n}\rightharpoonup x$ and $\{x_n-z_n\}\rightarrow y$, where $z_n\in Tx_n$ imply $x-y\in Tx$.

Since 1969, fixed point theorems and the existence of fixed points of multivalued mappings have been intensively studied and considered by many authors (see, for examples, Assad and Kirk 1972; Nadler 1969; Pietramala 1991; Song and Wang 2009; Shahzad and Zegeye 2009). The study multivalued mapping is much more complicated and difficult more than single-valued mapping. Many of the results have found nontrivial applications in pure and applied science. Examples of such applications are in control theory, convex optimization, differential inclusions, game theory, and economics. For the early results involving fixed points of multivalued mappings and their applications, see Assad and Kirk (1972), Brouwer (1912), Chidume et al. (2013), Daffer and Kaneko (1995), Deimling (1992), Dominguez Benavides and Gavira (2007), Downing and Kirk (1977), Feng and Liu (2006), Geanakoplos (2003), Goebel and Reich (1984), Jung (2007), Kakutani (1941), Khan et al. (2011), Liu (2013), Reich (1978), Reich and Zaslavski (2002), Song and Cho (2011), Turkoglu and Altun (2007), and references therein.

In 2008, Kohsaka and Takahashi (2008a, b) presented a new mapping which is called a nonspreading mapping and obtained fixed point theorems for a single nonspreading mapping and also a common fixed point theorems for a commutative family of nonspreading mapping in Banach spaces. Let H be a Hilbert space. A mapping $T : H\rightarrow H$ is said to be nonspreading if

$$\begin{aligned} 2\Vert Tx-Ty\Vert ^2 \le \Vert x-Ty\Vert ^2+\Vert y-Tx\Vert ^2 \end{aligned}$$

for all $x,y\in H$. Recently, Iemoto and Takahashi (2009) showed that $T : H\rightarrow H$ is nonspreading if and only if

$$\begin{aligned} \Vert Tx-Ty\Vert ^2 \le \Vert x-y\Vert ^2+2\langle x-Ty, y-Ty\rangle \ \forall x,y \in H. \end{aligned}$$

Furthermore, Takahashi (2010) defined a class of nonlinear mappings which is called hybrid as follows:

$$\begin{aligned} \Vert Tx-Ty\Vert ^{2}\le \Vert x-y\Vert ^{2}+\langle x-Tx, y-Ty\rangle \end{aligned}$$

for all $x, y\in H$. It was shown that a mapping $T:H \rightarrow H$ is hybrid if and only if

$$\begin{aligned} 3\Vert Tx-Ty\Vert ^{2}\le \Vert x-y\Vert ^{2}+\Vert y-Tx\Vert ^{2}+\Vert x-Ty\Vert ^{2} \end{aligned}$$

for all $x, y\in H$.

In addition, recently, in 2013, Liu (2013) introduced the following class of multivalued mappings: A mapping $T:H\rightarrow CB(H)$ is said to be nonspreading if

$$\begin{aligned} 2\Vert u_{x}-u_{y}\Vert ^{2}\le \Vert u_{x}-y\Vert ^{2}+\Vert u_{y}-x\Vert ^{2} \end{aligned}$$

for $u_{x}\in Tx$ and $u_{y}\in Ty$ for all $x,y\in H$. In addition, he obtained a weak convergence theorem for finding a common fixed point of a finite family of nonspreading and nonexpansive multivalued mappings.

Very recently, Cholamjiak and Cholamjiak (2016) introduced a new concept of multivalued mappings in Hilbert spaces using Hausdorff metric. A multivalued mapping $T:H \rightarrow CB(H)$ is said to be hybrid if

$$\begin{aligned} 3H(Tx,Ty)^{2}\le \Vert x-y\Vert ^{2}+d( y,Tx)^{2}+d(x,Ty)^{2} \end{aligned}$$

for all $x, y\in H$. They showed that if T is hybrid and $F(T)\ne \emptyset$, then T is quasi-nonexpansive. Moreover, they gave an example of a hybrid multivalued mapping which is not nonexpansive (see Cholamjiak and Cholamjiak (2016)) and proved some properties and the existence of fixed points of these mappings. Furthermore, they also proved weak and strong convergence theorems for a finite family of hybrid multivalued mappings.

Moreover, we study the following inclusion problem: find $\hat{x}\in H$, such that

$$\begin{aligned} 0\in A\hat{x}+B\hat{x}, \end{aligned}$$

(1.3)

where $A:H\rightarrow H$ is an operator and $B:H\rightarrow 2^{H}$ is a multivalued operator. We denote the solution set of Eq. (1.3) by $(A+B)^{-1}(0)$. This problem has received much attention due to its applications in large variety of problems arising in convex programming, variational inequalities, split feasibility problem, and minimization problem. To be more precise, some concrete problems in machine learning, image processing, and linear inverse problem can be modeled mathematically as this formulation.

For solving the problem (1.3), the forward–backward splitting method (Bauschke and Combettes 2011; Cholamjiak 1994; Combettes and Wajs 2005; López et al. 2012; Lorenz and Pock 2015; Passty 1979; Tseng 2000) is usually employed and is defined by the following manner: $x_{1}\in H$ and

$$\begin{aligned} x_{n+1}=(I+rB)^{-1}(x_{n}-rAx_{n}),\ n\ge 1, \end{aligned}$$

(1.4)

where $r>0$. In this case, each step of iterates involves only with A as the forward step and B as the backward step, but not the sum of operators. This method includes, as special cases, the proximal point algorithm (Rockafellar 1976) and the gradient method. In Lions and Mercier (1979), Lions and Mercier introduced the following splitting iterative methods in a real Hilbert space:

$$\begin{aligned} x_{n+1}=(2J^{A}_{r}-I)(2J^{B}_{r}-I)x_{n},\ n\ge 1 \end{aligned}$$

(1.5)

and

$$\begin{aligned} x_{n+1}=J^{A}_{r}(2J^{B}_{r}-I)x_{n}+(I-J^{B}_{r})x_{n},\ n\ge 1, \end{aligned}$$

(1.6)

where $J^{T}_{r}=(I+rT)^{-1}$ with $r > 0$. The first one is often called Peaceman–Rachford algorithm (Peaceman and Rachford 1955) and the second one is called Douglas–Rachford algorithm (Douglas and Rachford 1956). We note that both algorithms are weakly convergent in general (Bauschke and Combettes 2001; Lions and Mercier 1979).

Many problems can be formulated as a problem of from Eq. (1.3). For instance, a stationary solution to the initial valued problem of the evolution equation:

$$\begin{aligned} 0\in \frac{\partial u}{\partial t}-Fu, \ \ u(0)=u_0 \end{aligned}$$

(1.7)

can be recast as Eq. (1.3) when the governing maximal monotone F is of the form $F=A+B$ (Lions and Mercier 1979). In optimization, it often needs (Combettes and Wajs 2005) to solve a minimization problem of the form:

$$\begin{aligned} \min _{x\in H}f(x)+g(x), \end{aligned}$$

(1.8)

where f and g are proper and lower semicontinuous convex functions from $H_1$ to the extended real line $\bar{\mathbb {R}}=(-\infty ,\infty ]$, such that f is differentiable with L-Lipschitz continuous gradient, and the proximal mapping of g is as follows:

$$\begin{aligned} x\mapsto \arg \min _{y\in H}g(y)+\frac{\Vert x-y\Vert ^2}{2r}. \end{aligned}$$

(1.9)

In particular, if $A:=\nabla f$ and $B:=\partial g$, where $\nabla f$ is the gradient of f and $\partial g$ is the subdifferential of g which is defined by $\partial g (x) := \big \{ s\in H : g(y) \ge g(x) + \langle s, y-x \rangle , \ \ \forall y\in H \big \}$, then problem (1.3) becomes Eqs. (1.4) and (1.8) also becomes

$$\begin{aligned} x_{n+1}=\mathrm{prox}_{rg}(x_n-r \nabla f(x_n)), n\ge 1, \end{aligned}$$

(1.10)

where $r > 0$ is the stepsize and $\mathrm{prox}_{rg}=(I+r\partial g)^{-1}$ is the proximity operator of g.

In 2001, Alvarez and Attouch (2001) employed the heavy ball method which was studied in Polyak (1987, 1964) for maximal monotone operators by the proximal point algorithm. This algorithm is called the inertial proximal point algorithm and it is of the following form:

$$\begin{aligned} \left\{ \begin{array}{l} y_n = x_n+\theta _n(x_n-x_{n-1})\\ x_{n+1} = (I+r_nB)^{-1}y_n,~~n \ge 1. \end{array} \right. \end{aligned}$$

(1.11)

It was proved that if $\{r_{n}\}$ is nondecreasing and $\{\theta _{n}\}\subset [0,1)$ with

$$\begin{aligned} \sum _{n=1}^{\infty } \theta _n\Vert x_n-x_{n-1}\Vert ^2<\infty , \end{aligned}$$

(1.12)

then algorithm (1.11) converges weakly to a zero of B. In particular, Condition (1.12) is true for $\theta _{n}<1/3$. Here, $\theta _{n}$ is an extrapolation factor and the inertia is represented by the term $\theta _n(x_{n}-x_{n-1})$. It is remarkable that the inertial terminology greatly improves the performance of the algorithm and has a nice convergence properties (Alvarez 2004; Dang et al. 2017; Dong et al. 2018; Nesterov 1983).

Recently, Moudafi and Oliny (2003) proposed the following inertial proximal point algorithm for solving the zero-finding problem of the sum of two monotone operators:

$$\begin{aligned} \left\{ \begin{array}{llll} y_n = x_n+\theta _n(x_n-x_{n-1})\\ x_{n+1} =(I+r_nB)^{-1}(y_n-r_nAx_n),~~n \ge 1, \end{array} \right. \end{aligned}$$

(1.13)

where $A:H\rightarrow H$ and $B:H\rightarrow 2^{H}$. They obtained the weak convergence theorem provided $r_{n}<2/L$ with L the Lipschitz constant of A and the condition (1.12) holds. It is observed that, for $\theta _n>0$, the algorithm (1.13) does not take the form of a forward–backward splitting algorithm, since operator A is still evaluated at the point $x_n$.

Recently, Lorenz and Pock (2015) proposed the following inertial forward–backward algorithm for monotone operators:

$$\begin{aligned} \left\{ \begin{array}{l} y_n = x_n+\theta _n(x_n-x_{n-1}) \quad \\ x_{n+1} =(I+r_nB)^{-1}(y_n-r_nAy_n), \quad n \ge 1, \end{array} \right. \end{aligned}$$

(1.14)

where $\{r_{n}\}$ is a positive real sequence. It is observed that algorithm (1.14) differs from that of Moudafi and Oliny insofar that they evaluated the operator B as the inertial extrapolate $y_{n}$. The algorithms involving the inertial term mentioned above have weak convergence, and however, in some applied disciplines, the norm convergence is more desirable that the weak convergence (Bauschke and Combettes 2001).

In this work, we introduce a new algorithm combining the SP iteration with the inertial technical term for approximating common elements of the set of solutions of fixed point problems for a quasi-nonexpansive mapping and the set of solutions of inclusion problems. We prove some weak convergence theorems of the sequences generated by our iterative process under appropriate additional assumptions in Hilbert spaces. We aim to introduce an algorithm that ensures the strong convergence. To this end, using the idea of Takahashi et al. (2008), we employ the following projection method which is defined by: For $C_{1}=C$, $x_{1}=P_{C_{1}}x_{0}$ and

$$\begin{aligned} \left\{ \begin{array}{l} y_{n}=\alpha _{n}x_{n}+(1-\alpha _{n})Tx_{n},\\ C_{n+1}=\{z\in C_{n}:\Vert y_{n}-z\Vert \le \Vert x_{n}-z\Vert \},\\ x_{n+1}=P_{C_{n+1}}x_{0}, \quad \forall n\in {\mathbb {N}}, \end{array} \right. \end{aligned}$$

(1.15)

where $0\le \alpha _{n}\le a<1$ for all $n\in {\mathbb {N}}$. It was proved that the sequence $\{x_n\}$ generated by (1.15) converges strongly to a fixed point of a nonexpansive mapping T. This method is usually called the shrinking projection method [see also Nakajo and Takahashi (2003)]. Furthermore, we then establish the strong convergence result under some suitable conditions. Finally, we test some numerical experiments for supporting our main results and give a comparison between our inertial projection method and the standard projection method. It is remarkable that the convergence behavior of our method has a good convergence rate.

2 Preliminaries and lemmas

Let C be a nonempty, closed, and convex subset of a Hilbert space H. The nearest point projection of H onto C is denoted by $P_{C}$, that is, $\Vert x-P_{C}x\Vert \le \Vert x-y\Vert$ for all $x\in H$ and $y\in C$. Such $P_{C}$ is called the metric projection of H onto C. We know that the metric projection $P_{C}$ is firmly nonexpansive, that is

$$\begin{aligned} \Vert P_{C}x-P_{C}y\Vert ^{2}\le \langle P_{C}x-P_{C}y,x-y\rangle \end{aligned}$$

for all $x,y\in H$. Furthermore, $\langle x-P_{C}x,y-P_{C}x\rangle \le 0$ holds for all $x\in H$ and $y\in C$; see (Takahashi 2000).

Lemma 2.1

(Takahashi 2000) Let H be a real Hilbert space. Then, the following equations hold:

• (1)   $\Vert x-y\Vert ^{2}=\Vert x\Vert ^{2}-\Vert y\Vert ^{2}-2\langle x-y,y\rangle$ for all $x,y \in H$.

• (2)   $\Vert x+y\Vert ^{2}\le \Vert x\Vert ^{2}+2\langle y,x+y\rangle$ for all $x,y \in H$.

• (3)   $\Vert tx+(1-t)y\Vert ^{2}=t\Vert x\Vert ^{2}+(1-t)\Vert y\Vert ^{2}-t(1-t)\Vert x-y\Vert ^{2}$ for all $t\in [0,1]$ and $x,y \in H$.

Lemma 2.2

(Martinez-Yanes and Xu 2006) Let C be a nonempty closed and convex subset of a real Hilbert space $H_1$. For each x, y $\in$ $H_1$, and $a \in {\mathbb {R}}$, the set

$$\begin{aligned} D=\{v \in C : \Vert y-v\Vert ^{2}\le \Vert x-v\Vert ^{2}+\langle z,v \rangle +a\} \end{aligned}$$

is closed and convex.

In what follows, we shall use the following notation:

$$\begin{aligned} T_r^{A,B}=J_r^B(I-rA)=(I+rB)^{-1}(I-rA), \ \ r>0. \end{aligned}$$

(2.1)

Lemma 2.3

(López et al. 2012) Let X be a Banach space. Let $A:X\rightarrow X$ be an $\alpha$-inverse strongly accretive of order q and $B:X\rightarrow 2^X$ an m-accretive operator. Then, we have

• (i) For $r>0$, $F(T_r^{A,B})=(A+B)^{-1}(0)$.

• (ii) For $0<s\le r$ and $x\in X, \Vert x-T_s^{A,B}x\Vert \le 2\Vert x-T_r^{A,B}x\Vert$.

Lemma 2.4

(López et al. 2012) Let X be a uniformly convex and q-uniformly smooth Banach space for some $q\in (0,2]$. Assume that A is a single-valued $\alpha$-inverse strongly accretive of order q in X. Then, given $r>0$, there exists a continuous, strictly increasing, and convex function $\phi _q:{\mathbb {R}}^+\rightarrow {\mathbb {R}}^+$ with $\phi _q(0)=0$, such that, for all $x,y\in B_r$,

$$\begin{aligned} \Vert T^{A,B}_rx-T^{A,B}_ry\Vert ^q\le & {} \Vert x-y\Vert ^q-r(\alpha q-r^{q-1}k_q)\Vert Ax-Ay\Vert ^q\\&-\phi _q(\Vert (I-J_r^B)(I-rA)x-(I-J_r^B)(I-rA)y\Vert ), \end{aligned}$$

where $k_q$ is the q-uniform smoothness coefficient of X.

Lemma 2.5

(Alvarez and Attouch 2001) Let $\{\psi _n\}$, $\{\delta _n\}$, and $\{\alpha _n\}$ be the sequences in $[0,+\infty )$, such that $\psi _{n+1}\le \psi _n+\alpha _n(\psi _n-\psi _{n-1})+\delta _n$ for all $n\ge 1$, $\sum _{n=1}^\infty \delta _n<+\infty$ and there exists a real number $\alpha$ with $0\le \alpha _n\le \alpha <1$ for all $n\ge 1$. Then, the followings hold:

• (i) $\Sigma _{n\ge 1}[\psi _n-\psi _{n-1}]_+<+\infty$, where $[t]_+=\max \{t,0\}$;

• (ii) there exists $\psi ^*\in [0,+\infty )$, such that $\lim _{n\rightarrow +\infty }\psi _n=\psi ^*$.

Lemma 2.6

(Browder 1965) Let C be a nonempty closed convex subset of a uniformly convex space X and T a nonexpansive mapping with $F(T)\ne \emptyset$. If $\{x_n\}$ is a sequence in C, such that $x_n\rightharpoonup x$ and $(I-T)x_n\rightarrow y$, then $(I-T)x=y$. In particular, if $y=0$, then $x\in F(T)$.

Lemma 2.7

(Suantai 2005) Let X be a Banach space satisfying Opial’s condition and let $\{x_{n}\}$ be a sequence in X. Let u, v $\in$ X be such that

$\lim _{n \rightarrow \infty }\Vert x_{n}-u\Vert$   and   $\lim _{n \rightarrow \infty }\Vert x_{n}-v\Vert$ exist.

If $\{x_{n_{k}}\}$ and $\{x_{m_{k}}\}$ are subsequences of $\{x_{n}\}$ which converge weakly to u and v, respectively, then $u=v$.

Proposition 2.8

(Cholamjiak 1994) Let $q>1$ and let X be a real smooth Banach space with the generalized duality mapping $j_q$. Let $m\in {\mathbb {N}}$ be fixed. Let $\{x_i\}_{i=1}^m\subset X$ and $t_i\ge 0$ for all $i=1,2,\ldots ,m$ with $\sum _{i=1}^mt_i\le 1$. Then, we have

$$\begin{aligned} \left\| \sum _{i=1}^mt_ix_i\right\| ^q\le \frac{\sum _{i=1}^mt_i\Vert x_i\Vert ^q}{q- (q-1)\left( \sum _{i=1}^mt_i \right) }. \end{aligned}$$

Condition (A) Let H be a Hilbert space. A multivalued mapping $T:H\rightarrow CB(H)$ is said to satisfy Condition (A) if $\Vert x-p\Vert =d(x,Tp)$ for all $x\in H$ and $p\in F(T)$.

Lemma 2.9

(Cholamjiak and Cholamjiak 2016) Let H be a real Hilbert space. Let $T:H\rightarrow K(H)$ be a hybrid multivalued mapping. If $F(T)\ne \emptyset$, then T is quasi-nonexpansive multivalued mapping.

Lemma 2.10

(Cholamjiak and Cholamjiak 2016) Let H be a real Hilbert space. Let $T:H\rightarrow K(H)$ be a hybrid multivalued mapping with $F(T)\ne \emptyset$. Then, F(T) is closed.

Lemma 2.11

Cholamjiak and Cholamjiak (2016) Let H be a real Hilbert space. Let $T:H\rightarrow K(H)$ be a hybrid multivalued mapping with $F(T)\ne \emptyset$. If T satisfies Condition (A), then F(T) is convex.

Lemma 2.12

Cholamjiak and Cholamjiak (2016) Let H be a real Hilbert space. Let $T:H\rightarrow K(H)$ be a hybrid multivalued mapping. Let $\{x_{n}\}$ be a sequence in H, such that $x_{n}\rightharpoonup p$ and $\lim _{n\rightarrow \infty }\Vert x_{n}-y_{n}\Vert =0$ for some $y_{n}\in Tx_{n}$. Then, $p\in Tp$.

3 Main results

In this section, we aim to introduce and prove the strong convergence of an inertial method with a forward–backward method for solving inclusion problems and fixed point problems of quasi-nonexpansive mapping in Hilbert spaces. To this end, we need the following crucial results.

Lemma 3.1

Let H be a real Hilbert space. Let $T:H\rightarrow CB(H)$ be a quasi-nonexpansive mapping with $F(T)\ne \emptyset$. Then, F(T) is closed.

Proof

If $F(T)=\emptyset$, then it is closed. Assume that $F(T)\ne \emptyset$. Let $\{x_{n}\}$ be a sequence in F(T), such that $x_{n}\rightarrow x$ as $n\rightarrow \infty$. We have

$$\begin{aligned} d(x,Tx)\le & {} \Vert x-x_{n}\Vert +d(x_{n},Tx) \\\le & {} \Vert x-x_{n}\Vert +H(Tx_{n},Tx)\\\le & {} 2\Vert x-x_{n}\Vert . \end{aligned}$$

It follows that $d(x,Tx)=0$. Hence, $x\in F(T)$. We conclude that F(T) is closed. $\square$

Lemma 3.2

Let C be a closed convex subset of a real Hilbert space H. Let $T:H\rightarrow CB(H)$ be a quasi-nonexpansive mapping with $F(T)\ne \emptyset$. If T satisfies Condition (A), then F(T) is convex.

Proof

Let $p=tp_{1}+(1-t)p_{2}$, where $p_{1},p_{2}\in F(T)$ and $t\in (0,1)$. Let $z\in Tp$. It follows from Lemma 2.1 that

$$\begin{aligned} \Vert p-z\Vert ^{2}= & {} \Vert t(z-p_{1})+(1-t)(z-p_{2})\Vert ^{2}\\= & {} t\Vert z-p_{1}\Vert ^{2}+(1-t)\Vert z-p_{2}\Vert ^{2}-t(1-t)\Vert p_{1}-p_{2}\Vert ^{2}\\= & {} t d(z,Tp_{1})^{2}+(1-t)d(z,Tp_{2})^{2}-t(1-t)\Vert p_{1}-p_{2}\Vert ^{2}\\\le & {} t H(Tp,Tp_{1})^{2}+(1-t)H(Tp,Tp_{2})^{2}-t(1-t)\Vert p_{1}-p_{2}\Vert ^{2}\\\le & {} t\Vert p-p_{1}\Vert ^{2}+(1-t)\Vert p-p_{2}\Vert ^{2}-t(1-t)\Vert p_{1}-p_{2}\Vert ^{2}\\= & {} t(1-t)^{2}\Vert p_{1}-p_{2}\Vert ^{2}+(1-t)t^{2}\Vert p_{1}-p_{2}\Vert ^{2}-t(1-t)\Vert p_{1}-p_{2}\Vert ^{2}\\= & {} 0, \end{aligned}$$

and hence, $p=z$. Therefore, $p\in F(T)$. This completes the proof.

Theorem 3.3

Let H be a real Hilbert space and $T:H\rightarrow CB(H)$ be a quasi-nonexpansive mapping satisfying Condition (A). Let $A:H\rightarrow H$ be an $\alpha$-inverse strongly monotone operator and $B:H\rightarrow 2^{H}$ a maximal monotone operator. Assume that $S=(A+B)^{-1}(0)\cap F(T)\ne \emptyset$ and $I-T$ is demiclosed at 0 . Let $\{x_{n}\}, \{y_{n}\}$ and $\{z_n\}$ be sequences generated by $x_{0},x_{1}\in H$ and

$$\begin{aligned} \left\{ \begin{array}{l} y_{n}=x_n+\theta _n(x_n-x_{n-1})\\ z_n\in \alpha _ny_{n}+(1-\alpha _n)Ty_{n},\\ x_{n+1}=\beta _nz_n+(1-\beta _{n})J^{B}_{r_{n}}(I-r_{n}A)z_{n},\ \ \ n\ge 1, \end{array} \right. \end{aligned}$$

(3.1)

where $J^{B}_{r_{n}}=(I+r_{n}B)^{-1}$, $\{r_{n}\}\subset (0, 2\alpha )$, $\{\theta _{n}\}\subset [0,\theta ]$ for some $\theta \in [0,1)$ and $\{\alpha _{n}\}$ and $\{\beta _{n}\}$ are sequences in [0, 1]. Assume that the following conditions hold:

• (i) $\sum _{n=1}^{\infty }\theta _{n}\Vert x_{n}-x_{n-1}\Vert <\infty$.

• (ii) $0<\liminf _{n\rightarrow \infty }\alpha _n\le \limsup _ {n\rightarrow \infty }\alpha _n<1$.

• (iii) $\limsup _{n\rightarrow \infty }\beta _{n}<1$;

• (iv) $0<\liminf _{n\rightarrow \infty }r_{n}\le \limsup _{n\rightarrow \infty }r_{n}<2\alpha$.

  Then, the sequence $\{x_{n}\}$ converges weakly to $q\in S$.

Proof

Write $J_n=(I+r_nB)^{-1}(I-r_nA)$. Notice that we can write

$$\begin{aligned} x_{n+1}=\beta _nz_n+(1-\beta _n)J_nz_n. \end{aligned}$$

(3.2)

Let $p\in S$ and T satisfies Condition (A). For $w_n\in Ty_n$, such that

$$\begin{aligned} z_{n}=\alpha _ny_n+(1-\alpha _n)w_n, \end{aligned}$$

(3.3)

we have

$$\begin{aligned} \Vert z_n-p\Vert\le & {} \alpha _n\Vert y_n-p\Vert +(1-\alpha _n)\Vert w_n-p\Vert \nonumber \\= & {} \alpha _n\Vert y_n-p\Vert +(1-\alpha _n)d(w_n,Tp)\nonumber \\\le & {} \alpha _n\Vert y_n-p\Vert +(1-\alpha _n)H(Ty_n,Tp)\nonumber \\\le & {} \Vert y_n-p\Vert \nonumber \\\le & {} \Vert x_n-p\Vert +\theta _n\Vert x_n-x_{n-1}\Vert . \end{aligned}$$

(3.4)

By Lemma 2.4 and Eq. (3.4), we have

$$\begin{aligned} \Vert x_{n+1}-p\Vert\le & {} \beta _n\Vert z_n-p\Vert +(1-\beta _n)\Vert J_nz_n-p\Vert \nonumber \\\le & {} \Vert z_n-p\Vert \nonumber \\\le & {} \Vert x_n-p\Vert +\theta _n\Vert x_n-x_{n-1}\Vert . \end{aligned}$$

(3.5)

From Lemma 2.5 and the assumption (i), we obtain $\lim _{n\rightarrow \infty }\Vert x_n-p\Vert$ exists, in particular, $\{x_n\}$ is bounded and also are $\{y_n\}$ and $\{z_n\}$. We next show that $x_n\rightharpoonup q\in (A+B)^{-1}(0)$. By Lemmas 2.1, 2.4, and T which satisfies Condition (A), we have

$$\begin{aligned} \Vert x_{n+1}-p\Vert ^2= & {} \Vert \beta _n(z_n-p)+(1-\beta _n)(J_nz_n-p)\Vert ^2\nonumber \\\le & {} \beta _n\Vert z_n-p\Vert ^2+(1-\beta _n)\Vert J_nz_n-p\Vert ^2\nonumber \\\le & {} \Vert z_n-p\Vert ^2-(1-\beta _n)\big (r_n(2\alpha -r_n)\Vert Az_n-Ap\Vert ^2\nonumber \\&-\Vert z_ n-r_nAz_n-J_nz_n+r_nAp\Vert \big )\nonumber \\\le & {} \alpha _n\Vert y_n-p\Vert ^2+(1-\alpha _n)\Vert w_n-p\Vert ^2\nonumber \\&-(1-\beta _n)\big (r_n(2\alpha -r_n)\Vert Az_n-Ap\Vert ^2\nonumber \\&-\Vert z_n-r_nAz_n-J_nz_n+r_nAp\Vert \big )\nonumber \\= & {} \alpha _n\Vert y_n-p\Vert ^2+(1-\alpha _n)d(w_n,Tp)^2\nonumber \\&-(1-\beta _n)\big (r_n( 2\alpha -r_n)\Vert Az_n-Ap\Vert ^2\nonumber \\&-\Vert z_n-r_nAz_n-J_nz_n+r_nAp\Vert \big )\nonumber \\\le & {} \alpha _n\Vert y_n-p\Vert ^2+(1-\alpha _n)H(Ty_n,Tp)^2\nonumber \\&-(1-\beta _n) \big (r_n(2\alpha -r_n)\Vert Az_n-Ap\Vert ^2\nonumber \\&-\Vert z_n-r_nAz_n-J_nz_n+r_nAp\Vert \big )\nonumber \\\le & {} \Vert y_n-p\Vert ^2-(1-\beta _n)\big (r_n(2\alpha -r_n)\Vert Az_n-Ap\Vert ^2\nonumber \\&-\Vert z_n -r_nAz_n-J_nz_n+r_nAp\Vert \big )\nonumber \\\le & {} \Vert x_n-p\Vert ^2+2\theta _n\langle x_n-x_{n-1},y_n-p\rangle \nonumber \\&-(1-\beta _n)\big (r_n(2\alpha -r_n)\Vert Az_n- Ap\Vert ^2\nonumber \\&-\Vert z_n-r_nAz_n-J_nz_n+r_nAp\Vert \big ). \end{aligned}$$

(3.6)

Since $\lim _{n\rightarrow \infty }\Vert x_n-p\Vert$ exists, it follows, from Eq. (3.6), the assumptions (i), (iii), and (iv) that:

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert Az_n-Ap\Vert =\lim _{n\rightarrow \infty }\Vert z_n -r_nAz_n-J_nz_n+r_nAp\Vert =0. \end{aligned}$$

(3.7)

This give, by the triangle inequality, that

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert J_nz_n-z_n\Vert =0. \end{aligned}$$

(3.8)

Since $\liminf _{n\rightarrow \infty }r_n>0$, there is $r>0$, such that $r_n\ge r$ for all $n\ge 1$. Lemma 2.3 (ii) yields that

$$\begin{aligned} \Vert T_r^{A,B}z_n-z_n\Vert \le 2\Vert J_nz_n-z_n\Vert . \end{aligned}$$

(3.9)

Then, by Eqs. (3.8) and (3.9), we obtain

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert T_r^{A,B}z_n-z_n\Vert =0. \end{aligned}$$

(3.10)

From Eq. (3.8), we have

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert x_{n+1}-z_n\Vert =\lim _{n\rightarrow \infty } (1-\beta _n)\Vert J_nz_n-z_n\Vert =0. \end{aligned}$$

(3.11)

Again by Lemmas 2.1, 2.4, and T satisfies Condition (A), we have

$$\begin{aligned} \Vert x_{n+1}-p\Vert ^2\le & {} \beta _n\Vert z_n-p\Vert ^2+(1-\beta _n)\Vert J_nz_n-p\Vert ^2\nonumber \\\le & {} \Vert z_n-p\Vert ^2\nonumber \\\le & {} \alpha _n\Vert y_n-p\Vert ^2+(1-\alpha _n)\Vert w_n-p\Vert ^2-\alpha _n(1- \alpha _n)\Vert w_n-y_n\Vert ^2\nonumber \\= & {} \alpha _n\Vert y_n-p\Vert ^2+(1-\alpha _n)d(w_n,Tp)^2-\alpha _n(1-\alpha _n) \Vert w_n-y_n\Vert ^2\nonumber \\\le & {} \alpha _n\Vert y_n-p\Vert ^2+(1-\alpha _n)H(Ty_n,Tp)^2-\alpha _n(1 -\alpha _n)\Vert w_n-y_n\Vert ^2\nonumber \\\le & {} \Vert y_n-p\Vert ^2-\alpha _n(1-\alpha _n)\Vert w_n-y_n\Vert ^2\nonumber \\\le & {} \Vert x_n-p\Vert ^2+2\theta _n\langle x_n-x_{n-1},y_n-p\rangle -\alpha _n(1-\alpha _n)\Vert w_n-y_n\Vert ^2.\qquad \qquad \end{aligned}$$

(3.12)

Since $\lim _{n\rightarrow \infty }\Vert x_n-p\Vert$ exists and the Assumption (i) and (ii), it follows from Eq. (3.12) that

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert w_n-y_n\Vert =0. \end{aligned}$$

(3.13)

This implies that

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert z_n-y_n\Vert =\lim _{n\rightarrow \infty }(1 -\alpha _n)\Vert w_n-y_n\Vert =0. \end{aligned}$$

(3.14)

From the definition of $\{y_n\}$ and the Assumption (i), we have

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert y_n-x_n\Vert =\lim _{n\rightarrow \infty }\theta _ n\Vert x_n-x_{n-1}\Vert =0. \end{aligned}$$

(3.15)

It follows from Eqs. (3.11), (3.14), and (3.15) that

$$\begin{aligned} \Vert x_{n+1}-x_n\Vert \le \Vert x_{n+1}-z_n\Vert +\Vert z_n-y_n\Vert +\Vert y_n-x_n\Vert \rightarrow 0 \end{aligned}$$

(3.16)

as $n\rightarrow \infty$. From Eqs. (3.11) and (3.16), we obtain

$$\begin{aligned} \Vert z_n-x_n\Vert \le \Vert z_n-x_{n+1}\Vert +\Vert x_{n+1}-x_n\Vert \rightarrow 0 \end{aligned}$$

(3.17)

as $n\rightarrow \infty$. Since $\{x_n\}$ is bounded and H is reflexive, $\omega _w(x_n)=\{x\in H:x_{n_i}\rightharpoonup x, \{x_{n_i}\}\subset \{x_n\}\}$ is nonempty. Let $q\in \omega _w(x_n)$ be an arbitrary element. Then, there exists a subsequence $\{x_{n_i}\}\subset \{x_n\}$ converging weakly to q. Let $p\in \omega _w(x_n)$ and $\{x_{n_m}\}\subset \{x_n\}$ be such that $x_{n_m}\rightharpoonup p$. From Eq. (3.17), we also have $z_{n_i}\rightharpoonup q$ and $z_{n_m}\rightharpoonup p$. Since $T_r^{A,B}$ is nonexpansive, by Lemma 2.6 and Eq. (3.9), we have $p,q\in (A+B)^{-1}(0)$. From Eq. (3.15), we obtain $y_{n_i}\rightharpoonup q$ and $y_{n_m}\rightharpoonup p$. Since $I-T$ is demiclosed at 0 and Eq. (3.13), we have $p,q\in F(T)$. Applying Lemma 2.7, we obtain $p=q$. $\square$

Theorem 3.4

Let H be a real Hilbert space and $T:H\rightarrow CB(H)$ be a quasi-nonexpansive mapping satisfying Condition (A). Let $A:H\rightarrow H$ be an $\alpha$-inverse strongly monotone operator and $B:H\rightarrow 2^{H}$ a maximal monotone operator. Assume that $S=(A+B)^{-1}(0)\cap F(T)\ne \emptyset$ and $I-T$ is demiclosed at 0 . Let $\{x_{n}\}, \{y_{n}\}$, $\{z_n\}$ and $\{v_n\}$ be sequences generated by $x_{0},x_{1}\in H$ and

$$\begin{aligned} \left\{ \begin{array}{l} y_{n}=x_n+\theta _n(x_n-x_{n-1})\\ z_n\in \alpha _ny_{n}+(1-\alpha _n)Ty_{n},\\ v_{n}=\beta _nz_n+(1-\beta _{n})J^{B}_{r_{n}}(I-r_{n}A)z_{n},\\ C_{n+1}=\{z\in C_n:\Vert v_n-z\Vert ^2\le \Vert x_n-z\Vert ^2+2\theta _n^2\Vert x_n-x_{n-1} \Vert ^2-2\theta _n\langle x_n-z,x_{n-1}-x_n\rangle \},\\ x_{n+1}=P_{C_{n+1}}x_1,\ \ \ n\ge 1, \end{array} \right. \end{aligned}$$

(3.18)

where $J^{B}_{r_{n}}=(I+r_{n}B)^{-1}$, $\{r_{n}\}\subset (0, 2\alpha )$, $\{\theta _{n}\}\subset [0,\theta ]$ for some $\theta \in [0,1)$, and $\{\alpha _{n}\}$ and $\{\beta _{n}\}$ are sequences in [0, 1]. Assume that the following conditions hold:

• (i) $\sum _{n=1}^{\infty }\theta _{n}\Vert x_{n}-x_{n-1}\Vert <\infty$.

• (ii) $0<\liminf _{n\rightarrow \infty }\alpha _n\le \limsup _ {n\rightarrow \infty }\alpha _n<1$.

• (iii) $\limsup _{n\rightarrow \infty }\beta _{n}<1$.

• (iv) $0<\liminf _{n\rightarrow \infty }r_{n}\le \limsup _ {n\rightarrow \infty }r_{n}<2\alpha$.

  Then, the sequence $\{x_{n}\}$ converges strongly to $q=P_{S}x_1$.

Proof

We split the proof into five steps.

Step 1 Show that $P_{C_{n+1}}x_1$ is well defined for every $x\in H$. We know that $(A+B)^{-1}(0)$ is closed and convex by Lemma 2.3. Since T satisfies Condition (A), F(T) is closed and convex by Lemmas 3.1 and 3.2. From the definition of $C_{n+1}$ and Lemma 2.9, $C_{n+1}$ is closed and convex for each $n\ge 1$. For each $n\in {\mathbb {N}}$, we put $J_n=(I+r_nB)^{-1}(I-r_nA)$ and let $p\in S$. Since $J_n$ is nonexpansive, we have

$$\begin{aligned} \Vert v_{n}-p\Vert ^2\le & {} \beta _n\Vert z_n-p\Vert ^2+(1-\beta _n)\Vert J_nz_n-p\Vert ^2\nonumber \\\le & {} \Vert z_n-p\Vert ^2\nonumber \\\le & {} \alpha _n\Vert y_n-p\Vert ^2+(1-\alpha _n)\Vert w_n-p\Vert ^2\nonumber \\= & {} \alpha _n\Vert y_n-p\Vert ^2+(1-\alpha _n)d(w_n,Tp)^2\nonumber \\\le & {} \alpha _n\Vert y_n-p\Vert ^2+(1-\alpha _n)H(Ty_n,Tp)^2\nonumber \\\le & {} \Vert y_n-p\Vert ^2\nonumber \\\le & {} \Vert x_n-p\Vert ^2+2\theta _n \langle x_n-x_{n-1},y_n-p\rangle \nonumber \\\le & {} \Vert x_n-p\Vert ^2+2\theta _n^2\Vert x_n-x_{n-1}\Vert ^2-2\theta _n\langle x_n-p,x_{n-1}-x_{n}\rangle . \end{aligned}$$

(3.19)

Therefore, we have $p\in C_{n+1}$, and thus, $S\subset C_{n+1}$. Therefore, $P_{C_{n+1}}x_1$ is well defined.

Step 2 Show that $\lim _{n\rightarrow \infty }\Vert x_n-x_1\Vert$ exists. Since S is nonempty, closed, and convex subset of H, there exists a unique $v\in S$, such that

$$\begin{aligned} v=P_Sx_1. \end{aligned}$$

(3.20)

From $x_n=P_{C_n}x_1$, $C_{n+1}\subset C_n$, and $x_{n+1}\in C_{n+1}$, $\forall n\ge 1$, we get

$$\begin{aligned} \Vert x_n-x_1\Vert \le \Vert x_{n+1}-x_1\Vert , \ \ \forall n\ge 1. \end{aligned}$$

(3.21)

On the other hand, as $S\subset C_n$, we obtain

$$\begin{aligned} \Vert x_n-x_1\Vert \le \Vert v-x_1\Vert , \ \ \forall n\ge 1. \end{aligned}$$

(3.22)

It follows that the sequence $\{x_n\}$ is bounded and nondecreasing. Therefore, $\lim _{n\rightarrow \infty }\Vert x_n-x_1\Vert$ exists.

Step 3 Show that $x_{n}\rightarrow q\in C$ as $n\rightarrow \infty$. For $m>n$, by the definition of $C_{n}$, we have $x_{m}=P_{{C}_{m}}x_{1}\in C_{m}\subseteq C_{n}$. By Lemma 2.9, we obtain that

$$\begin{aligned} \Vert x_{m}-x_{n}\Vert ^2\le & {} \Vert x_{m}-x_{1}\Vert ^2-\Vert x_{n}-x_{1}\Vert ^2. \end{aligned}$$

(3.23)

Since $\lim _{n\rightarrow \infty }\Vert x_{n}-x_{1}\Vert$ exists, it follows from Eq. (3.23) that $\lim _{n\rightarrow \infty }\Vert x_{m}-x_{n}\Vert =0$. Hence, $\{x_{n}\}$ is Cauchy sequence in C and so $x_{n}\rightarrow q\in C$ as $n\rightarrow \infty$.

Step 4 Show that $q\in S$. From Step 3, we have that $\lim _{n\rightarrow \infty }\Vert x_{n+1}-x_n\Vert =0$. Since $x_{n+1}\in C_n$, we have

$$\begin{aligned} \Vert v_{n}-x_{n}\Vert\le & {} \Vert v_{n}-x_{n+1}\Vert +\Vert x_{n+1}-x_{n}\Vert \nonumber \\\le & {} \sqrt{\Vert x_n-x_{n+1}\Vert ^2+2\theta _n^2\Vert x_n-x_{n-1}\Vert ^2-2\theta _n\langle x_n-x_{n+1},x_{n-1}-x_{n}\rangle }\nonumber \\&+\Vert x_{n+1}-x_{n}\Vert . \end{aligned}$$

(3.24)

By the Assumption (i) and Eq. (3.24), we obtain

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert v_{n}-x_{n}\Vert =0. \end{aligned}$$

(3.25)

Since $J_n$ is nonexpansive and T satisfies Condition (A), by Lemma 2.1, we have

$$\begin{aligned} \Vert v_{n}-p\Vert ^2= & {} \Vert \beta _n(z_n-p)+(1-\beta _n)(J_nz_n-p)\Vert ^2\nonumber \\\le & {} \beta _n\Vert z_n-p\Vert ^2+(1-\beta _n)\Vert J_nz_n-p\Vert ^2\nonumber \\\le & {} \Vert z_n-p\Vert ^2-(1-\beta _n)\big (r_n(2\alpha -r_n)\Vert Az_n-Ap\Vert ^2\nonumber \\&-\Vert z_n-r_nAz_n-J_nz_n+r_nAp\Vert \big )\nonumber \\\le & {} \alpha _n\Vert y_n-p\Vert ^2+(1-\alpha _n)\Vert w_n-p\Vert ^2-(1-\beta _n)\big (r_n(2\alpha -r_n)\Vert Az_n-Ap\Vert ^2\nonumber \\&-\Vert z_n-r_nAz_n-J_nz_n+r_nAp\Vert \big )\nonumber \\= & {} \alpha _n\Vert y_n-p\Vert ^2+(1-\alpha _n)d(w_n,Tp)^2-(1-\beta _n)\big (r_n(2\alpha -r_n)\Vert Az_n-Ap\Vert ^2\nonumber \\&-\Vert z_n-r_nAz_n-J_nz_n+r_nAp\Vert \big )\nonumber \\\le & {} \alpha _n\Vert y_n-p\Vert ^2+(1-\alpha _n)H(Ty_n,Tp)^2-(1-\beta _n)\big (r_n(2\alpha -r_n)\Vert Az_n-Ap\Vert ^2\nonumber \\&-\Vert z_n-r_nAz_n-J_nz_n+r_nAp\Vert \big )\nonumber \\\le & {} \Vert y_n-p\Vert ^2-(1-\beta _n)\big (r_n(2\alpha -r_n)\Vert Az_n-Ap\Vert ^2\nonumber \\&-\Vert z_n -r_nAz_n-J_nz_n+r_nAp\Vert \big )\nonumber \\\le & {} \Vert x_n-p\Vert ^2+2\theta _n\langle x_n-x_{n-1},y_n-p\rangle -(1-\beta _n) \big (r_n(2\alpha -r_n)\Vert Az_n-Ap\Vert ^2\nonumber \\&-\Vert z_n-r_nAz_n-J_nz_n+r_nAp\Vert \big ). \end{aligned}$$

(3.26)

It follows from Eq. (3.26), the Assumptions (i), (iii), and (iv) that

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert Az_n-Ap\Vert =\lim _{n\rightarrow \infty }\Vert z_n-r_nAz_n-J_nz_n+r_nAp\Vert =0. \end{aligned}$$

(3.27)

This give, by the triangle inequality, that

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert J_nz_n-z_n\Vert =0. \end{aligned}$$

(3.28)

Since $\liminf _{n\rightarrow \infty }r_n>0$, there is $r>0$, such that $r_n\ge r$ for all $n\ge 1$. Lemma 2.3 (ii) yields that

$$\begin{aligned} \Vert T_r^{A,B}z_n-z_n\Vert \le 2\Vert J_nz_n-z_n\Vert . \end{aligned}$$

(3.29)

Then, by Eqs. (3.28) and (3.29), we obtain

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert T_r^{A,B}z_n-z_n\Vert =0. \end{aligned}$$

(3.30)

From Eq. (3.29), we have

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert v_n-z_n\Vert =\lim _{n\rightarrow \infty }(1 -\beta _n)\Vert J_nz_n-z_n\Vert =0. \end{aligned}$$

(3.31)

It follows from Eqs. (3.25) and (3.31) that

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert z_n-x_n\Vert =0. \end{aligned}$$

(3.32)

By the definition of $\{y_n\}$ and the Assumption (i), we obtain

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert y_n-x_n\Vert =0. \end{aligned}$$

(3.33)

It follows from Eqs. (3.25) and (3.33) that

$$\begin{aligned} \Vert v_n-y_n\Vert \le \Vert v_n-x_n\Vert +\Vert x_n-y_n\Vert \rightarrow 0 \end{aligned}$$

(3.34)

as $n\rightarrow \infty$. Since $\{x_n\}$ is bounded and H is reflexive, $\omega _w(x_n)=\{x\in H:x_{n_i}\rightharpoonup x, \{x_{n_i}\}\subset \{x_n\}\}$ is nonempty. Let $q\in \omega _w(x_n)$ be an arbitrary element. Then, there exists a subsequence $\{x_{n_i}\}\subset \{x_n\}$ converging weakly to q. Let $p\in \omega _w(x_n)$ and $\{x_{n_m}\}\subset \{x_n\}$ be such that $x_{n_m}\rightharpoonup p$. From Eq. (3.32), we also have $z_{n_i}\rightharpoonup q$ and $z_{n_m}\rightharpoonup p$. Since $T_r^{A,B}$ is nonexpansive, by Lemma 2.6 and Eq. (3.30), we have $p,q\in (A+B)^{-1}(0)$. From Eq. (3.33), we obtain $y_{n_i}\rightharpoonup q$ and $y_{n_m}\rightharpoonup p$. Since $I-T$ is demiclosed at 0 and Eq. (3.34), we have $p,q\in F(T)$. Applying Lemma 2.7, we obtain $p=q$.

Step 5 Show that $q=P_{S}x_1$. Since $x_n=P_{C_n}x_1$ and $S\subset C_n$, we obtain

$$\begin{aligned} \langle x_1-x_n,x_n-z\rangle \ge 0, \ \forall z\in S. \end{aligned}$$

(3.35)

By taking the limit in Eq. (3.35), we obtain

$$\begin{aligned} \langle x_1-q,q-z\rangle \ge 0, \ \forall z\in S. \end{aligned}$$

(3.36)

This shows that $q=P_{S}x_1$.

By Lemmas 2.9–2.11, we know that if $F(T)\ne \emptyset$, then a hybrid multivalued mapping $T:H\rightarrow K(H)$ is quasi-nonexpansive and F(T) is closed and convex. We also know that $I-T$ is demiclosed at 0 by Lemma 2.12. We then obtain the following results.

Theorem 3.5

Let H be a real Hilbert space and $T:H\rightarrow K(H)$ be a hybrid multivalued mapping satisfying Condition (A). Let $A:H\rightarrow H$ be an $\alpha$-inverse strongly monotone operator and $B:H\rightarrow 2^{H}$ a maximal monotone operator. Assume that $S=(A+B)^{-1}(0)\cap F(T)\ne \emptyset$. Let $\{x_{n}\}, \{y_{n}\}$ and $\{z_n\}$ be sequences generated by $x_{0},x_{1}\in H$ and

$$\begin{aligned} \left\{ \begin{array}{l} y_{n}=x_n+\theta _n(x_n-x_{n-1})\\ z_n\in \alpha _ny_{n}+(1-\alpha _n)Ty_{n},\\ x_{n+1}=\beta _nz_n+(1-\beta _{n})J^{B}_{r_{n}}(I-r_{n}A)z_{n}, \quad n\ge 1, \end{array} \right. \end{aligned}$$

(3.37)

where $J^{B}_{r_{n}}=(I+r_{n}B)^{-1}$, $\{r_{n}\}\subset (0, 2\alpha )$, $\{\theta _{n}\}\subset [0,\theta ]$ for some $\theta \in [0,1)$ and $\{\alpha _{n}\}$ and $\{\beta _{n}\}$ are sequences in [0, 1]. Assume that the following conditions hold:

• (i) $\sum _{n=1}^{\infty }\theta _{n}\Vert x_{n}-x_{n-1}\Vert <\infty$.

• (ii) $0<\liminf _{n\rightarrow \infty }\alpha _n\le \limsup _ {n\rightarrow \infty }\alpha _n<1$.

• (iii) $\limsup _{n\rightarrow \infty }\beta _{n}<1$.

• (iv) $0<\liminf _{n\rightarrow \infty }r_{n}\le \limsup _ {n\rightarrow \infty }r_{n}<2\alpha$.

  Then, the sequence $\{x_{n}\}$ converges weakly to $q\in S$.

Theorem 3.6

Let H be a real Hilbert space and $T:H\rightarrow CB(H)$ be a hybrid multivalued mapping satisfying Condition (A). Let $A:H\rightarrow H$ be an $\alpha$-inverse strongly monotone operator and $B:H\rightarrow 2^{H}$ a maximal monotone operator. Assume that $S=(A+B)^{-1}(0)\cap F(T)\ne \emptyset$. Let $\{x_{n}\}, \{y_{n}\}$, $\{z_n\}$, and $\{v_n\}$ be sequences generated by $x_{0},x_{1}\in H$ and

$$\begin{aligned} \left\{ \begin{array}{ll} y_{n}=x_n+\theta _n(x_n-x_{n-1})\\ z_n\in \alpha _ny_{n}+(1-\alpha _n)Ty_{n},\\ v_{n}=\beta _nz_n+(1-\beta _{n})J^{B}_{r_{n}}(I-r_{n}A)z_{n},\\ C_{n+1}=\{z\in C_n:\Vert v_n-z\Vert ^2\le \Vert x_n-z\Vert ^2+2\theta _n^2\Vert x_n-x_ {n-1}\Vert ^2-2\theta _n\langle x_n-z,x_{n-1}-x_n\rangle \},\\ x_{n+1}=P_{C_{n+1}}x_1,\ \ \ n\ge 1, \end{array} \right. \end{aligned}$$

(3.38)

where $J^{B}_{r_{n}}=(I+r_{n}B)^{-1}$, $\{r_{n}\}\subset (0, 2\alpha )$, and $\{\theta _{n}\}\subset [0,\theta ]$ for some $\theta \in [0,1)$, and $\{\alpha _{n}\}$ and $\{\beta _{n}\}$ are sequences in [0, 1]. Assume that the following conditions hold:

• (i) $\sum _{n=1}^{\infty }\theta _{n}\Vert x_{n}-x_{n-1}\Vert <\infty$.

• (ii) $0<\liminf _{n\rightarrow \infty }\alpha _n\le \limsup _{n\rightarrow \infty }\alpha _n<1$.

• (iii) $\limsup _{n\rightarrow \infty }\beta _{n}<1$.

• (iv) $0<\liminf _{n\rightarrow \infty }r_{n} \le \limsup _{n\rightarrow \infty }r_{n}<2\alpha$.

  Then, the sequence $\{x_{n}\}$ converges strongly to $q=P_{S}x_1$.

Remark 3.7

We remark here that the condition (i) is easily implemented in numerical computation, since the value of $\Vert x_n-x_{n-1}\Vert$ is known before choosing $\theta _{n}$. Indeed, the parameter $\theta _{n}$ can be chosen, such that $0\le \theta _n\le \bar{\theta }_{n}$, where

$$\begin{aligned} \bar{\theta }_{n}= \left\{ \begin{array}{ll} \min \left\{ \frac{\omega _n}{\Vert x_n-x_{n-1}\Vert }, \theta \right\} &{} \qquad {\text{ if }} \ x_n\ne x_{n-1},\\ \theta &{} \qquad {\text{ otherwise }}, \end{array} \right. \end{aligned}$$

where $\{\omega _n\}$ is a positive sequence, such that $\sum _{n=1}^{\infty } \omega _n<\infty$.

We now give an example in Euclidean space ${\mathbb {R}}^3$ to support the main theorem.

Example 3.8

Let $H={\mathbb {R}}^3$ and $C=\{x\in {\mathbb {R}}^3:\Vert x\Vert \le 2\}$, and let $T:{\mathbb {R}}^3\rightarrow CB({\mathbb {R}}^3)$ be defined by

$$\begin{aligned} Tx= \left\{ \begin{array}{ll} \{(0,0,0)\} &{}\qquad {\text {if}} \ x \in C; \\ \{y\in {\mathbb {R}}^3:\Vert y\Vert \le \frac{1}{\Vert x\Vert }\} &{} \qquad {\text{ otherwise }}, \end{array} \right. \end{aligned}$$

where $x=(x_1,x_2,x_3)\in {\mathbb {R}}^3$. We see that T is a quasi-nonexpansive multivalued mapping. Let $A:{\mathbb {R}}^3\rightarrow {\mathbb {R}}^3$ be defined by $Ax=3x+(1,2,1)$ and let $B:{\mathbb {R}}^3\rightarrow {\mathbb {R}}^3$ be defined by $Bx=4x$, where $x=(x_1,x_2,x_3)\in {\mathbb {R}}^3$. We see that A is 1/3-inverse strongly monotone and B is maximal monotone. Moreover, by a direct calculation, we have for $r_n>0$

$$\begin{aligned} J_{r_n}^B(x-r_nAx)= & {} (I+r_nB)^{-1}(x-r_nAx)\nonumber \\= & {} \frac{1-3r_n}{1+4r_n}x-\frac{r_n}{1+4r_n}(1,2,1), \end{aligned}$$

(3.39)

where $x=(x_1,x_2,x_3)\in {\mathbb {R}}^3$. Since $\alpha =1/3$, we can choose $r_n=0.1$ for all $n\in {\mathbb {N}}$. Let $\alpha _n=\beta _n=\frac{n}{100n+1}$ and

$$\begin{aligned}\theta _{n}= \left\{ \begin{array}{ll} \min \left\{ \frac{1}{n^{2}\Vert x_n-x_{n-1}\Vert }, 0.5\right\} &{} \quad {\text{ if }} \ x_n\ne x_{n-1},\\ 0.5 &{} \quad {\text{ otherwise }}. \end{array} \right. \end{aligned}$$

We provide a numerical test of a comparison between our inertial forward–backward method defined in Theorem 3.4 and a standard forward–backward method (i.e., $\theta _n=0$). The stoping criterion is defined by $E_n=\Vert x_{n+1}-x_n\Vert <10^{-9}$.

The different choices of $x_0$ and $x_1$ are given as follows:

• Choice 1: $x_0=(-2,8,-5)$ and $x_{1}=(-3,-5,8)$.

• Choice 2: $x_0=(-1,7,6)$ and $x_{1}=(-3,1,-1)$.

• Choice 3: $x_0=(-2.34,3.29,-4.56)$ and $x_{1}=(6.13,-5.24,-1.19)$.

Fig. 1

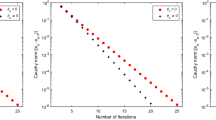
Error plotting $E_n$ of $\theta _{n}\ne 0$ and $\theta _{n}=0$ for each of the randoms of choice 1 in Table 1 is shown in the following figures, respectively

Fig. 2

Error plotting of $E_n$ of $\theta _{n}\ne 0$ and $\theta _{n}=0$ for each of the randoms of choice 2 in Table 1 is shown in the following figures, respectively

Fig. 3

Error plotting of $E_n$ of $\theta _{n}\ne 0$ and $\theta _{n}=0$ for each of the randoms of choice 3 in Table 1 is shown in the following figures, respectively

Remark 3.9

From Figs. 1, 2, and 3, it is shown that our forward–backward method with the inertial technical term has a good convergence speed and requires small number of iterations than the standard forward–backward method for each of the randoms.

4 Applications and numerical experiments

In this section, we discuss various applications in the variational inequality problem and the convex minimization problem.

4.1 Variational inequality problem

The variational inequality problem (VIP) is to find a point $\hat{x}\in C$, such that

$$\begin{aligned} \langle A\hat{x},x-\hat{x}\rangle \ge 0, \ \ \forall x\in C, \end{aligned}$$

(4.1)

where $A:C\rightarrow H$ is a nonlinear monotone operator. The solution set of Eq. (4.1) will be denoted by S. The extragradient method is used to solve the VIP (4.1). It is also known that the VIP is a special case of the problem of finding zeros of the sum of two monotone operators. Indeed, the resolvent of the normal cone is nothing but the projection operator. Therefore, we obtain immediately the following results.

Theorem 4.1

Let H be a real Hilbert space and $T:H\rightarrow CB(H)$ be a quasi-nonexpansive mapping satisfying Condition (A). Let $A:H\rightarrow H$ be an $\alpha$-inverse strongly monotone operator and C be a nonempty closed convex subset of H. Assume that $S\cap F(T)\ne \emptyset$ and $I-T$ is demiclosed at 0. Let $\{x_{n}\}, \{y_{n}\}$, $\{z_n\}$, and $\{v_n\}$ be sequences generated by $x_{0},x_{1}\in H$ and

$$\begin{aligned} \left\{ \begin{array}{ll} y_{n}=x_n+\theta _n(x_n-x_{n-1})\\ z_n\in \alpha _ny_{n}+(1-\alpha _n)Ty_{n},\\ v_{n}=\beta _nz_n+(1-\beta _{n})P_C(z_n-r_nAz_n),\\ C_{n+1}=\{z\in C_n:\Vert v_n-z\Vert ^2\le \Vert x_n-z\Vert ^2+2\theta _n^2\Vert x_n-x_{n-1}\Vert ^2-2\theta _n\langle x_n-z,x_{n-1}-x_n\rangle \},\\ x_{n+1}=P_{C_{n+1}}x_1,\ \ \ n\ge 1, \end{array} \right. \end{aligned}$$

(4.2)

where $\{r_{n}\}\subset (0, 2\alpha )$, $\{\theta _{n}\}\subset [0,\theta ]$ for some $\theta \in [0,1)$, and $\{\alpha _{n}\}$ and $\{\beta _{n}\}$ are sequences in [0, 1]. Assume that the following conditions hold:

• (i) $\sum _{n=1}^{\infty }\theta _{n}\Vert x_{n}-x_{n-1}\Vert <\infty$.

• (ii) $0<\liminf _{n\rightarrow \infty }\alpha _n\le \limsup _ {n\rightarrow \infty }\alpha _n<1$.

• (iii) $\limsup _{n\rightarrow \infty }\beta _{n}<1$.

• (iv) $0<\liminf _{n\rightarrow \infty }r_{n}\le \limsup _{n\rightarrow \infty } r_{n}<2\alpha$.

  Then, the sequence $\{x_{n}\}$ converges strongly to $q=P_{S\cap F(T)}x_1$.

Example 4.2

Let $H={\mathbb {R}}^3$ and $C=\{(x_1,x_2,x_3)\in {\mathbb {R}}^3| \langle a,x\rangle \ge b\}$, where $a=(2,1,-3)$ and $b=2$, and let $A={{\left( \begin{array}{ccc} 1 &{} -1 &{} 5 \\ 0 &{} 1 &{} 3 \\ 0 &{} 0 &{} 2 \\ \end{array} \right) }}$.

We see that A is 1 / 2-inverse strongly monotone. Therefore, we can choose $r_n=0.1$ for all $n\in {\mathbb {N}}$. Let $\alpha _n$, $\beta _n$, and $\theta _n$ be as in Example 3.8. The stoping criterion is defined by $E_n=\Vert x_{n+1}-x_n\Vert <10^{-9}$. Starting $x_0=(0,2,1)$, $x_1=(1,-2,1)$ and computing iteratively algorithm in Theorem 3.4. The different choices of $x_0$ and $x_1$ are given as follows:

• Choice 1: $x_0=(1,-3,7)^T$ and $x_{1}=(9,2,-1)^T$.

• Choice 2: $x_0=(-3,1,4)^T$ and $x_{1}=(2,-8,1)^T$.

Table 1 Comparison of $\theta _{n}\ne 0$ and $\theta _{n}=0$ in Example 3.8

Table 2 Comparison of $\theta _{n}\ne 0$ and $\theta _{n}=0$ in Example 4.2

Table 3 Comparison of $\theta _{n}\ne 0$ and $\theta _{n}=0$ in Example 4.4

Fig. 4

Error plotting $E_n$ of $\theta _{n}\ne 0$ and $\theta _{n}=0$ for each of the randoms of choice 1 in Table 2 is shown in the following figures, respectively

Fig. 5

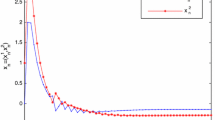
Error plotting $E_n$ of $\theta _{n}\ne 0$ and $\theta _{n}=0$ for each of the randoms of choice 2 in Table 2 is shown in the following figures, respectively

Fig. 6

Error plotting $E_n$ of $\theta _{n}\ne 0$ and $\theta _{n}=0$ for each of the randoms of choice 1 in Table 3 is shown in the following figures, respectively

Fig. 7

Error plotting $E_n$ of $\theta _{n}\ne 0$ and $\theta _{n}=0$ for each of the randoms of choice 2 in Table 3 is shown in the following figures, respectively

4.2 Convex minimization problem

Let $F:H\rightarrow {\mathbb {R}}$ be a convex smooth function and $G:H\rightarrow {\mathbb {R}}$ be a convex, lower semicontinuous, and nonsmooth function. We consider the problem of finding $\hat{x}\in H$, such that

$$\begin{aligned} F(\hat{x})+G(\hat{x})\le F(x)+G(x) \end{aligned}$$

(4.3)

for all $x\in H$. This problem (4.3) is equivalent, by Fermat’s rule, to the problem of finding $\hat{x}\in H$, such that

$$\begin{aligned} 0\in \nabla F(\hat{x})+\partial G(\hat{x}), \end{aligned}$$

(4.4)

where $\nabla F$ is a gradient of F and $\partial G$ is a subdifferential of G. The minimizer of $F+G$ will be denoted by S. We know that if $\nabla F$ is $\frac{1}{L}$-Lipschitz continuous, then it is L-inverse strongly monotone (Baillon and Haddad 1977, Corollary 10). Moreover, $\partial G$ is maximal monotone (Rockafellar 1970, Theorem A). If we set $A=\nabla F$ and $B=\partial G$ in Theorem 3.3, then we obtain the following result.

Theorem 4.3

Let H be a real Hilbert space and $T:H\rightarrow CB(H)$ be a quasi-nonexpansive mapping satisfying Condition (A). Let $F:H\rightarrow {\mathbb {R}}$ be a convex and differentiable function with $\frac{1}{L}$-Lipschitz continuous gradient $\nabla F$ and $G:H\rightarrow {\mathbb {R}}$ be a convex and lower semicontinuous function which $F+G$ attains a minimizer. Assume that $S\cap F(T)\ne \emptyset$ and $I-T$ is demiclosed at 0 . Let $\{x_{n}\}, \{y_{n}\}$, $\{z_n\}$, and $\{v_n\}$ be sequences generated by $x_{0},x_{1}\in H$ and

$$\begin{aligned} \left\{ \begin{array}{l} y_{n}=x_n+\theta _n(x_n-x_{n-1})\\ z_n\in \alpha _ny_{n}+(1-\alpha _n)Ty_{n},\\ v_{n}=\beta _nz_n+(1-\beta _{n})J_{r_n}^{\partial G}(z_n-r_n\nabla F(z_n)),\\ C_{n+1}=\{z\in C_n:\Vert v_n-z\Vert ^2\le \Vert x_n-z\Vert ^2+2\theta _n^2\Vert x_n-x_{n-1}\Vert ^2-2\theta _n\langle x_n-z,x_{n-1}-x_n\rangle \},\\ x_{n+1}=P_{C_{n+1}}x_1,\ \ \ n\ge 1, \end{array} \right. \end{aligned}$$

(4.5)

where $J_{r_n}^{\partial G}=(I+r_n\partial G)^{-1}$, $\{r_{n}\}\subset (0, 2/L)$, and $\{\theta _{n}\}\subset [0,\theta ]$ for some $\theta \in [0,1)$, and $\{\alpha _{n}\}$ and $\{\beta _{n}\}$ are sequences in [0, 1]. Assume that the following conditions hold:

• (i) $\sum _{n=1}^{\infty }\theta _{n}\Vert x_{n}-x_{n-1}\Vert <\infty$.

• (ii) $0<\liminf _{n\rightarrow \infty }\alpha _n\le \limsup _ {n\rightarrow \infty }\alpha _n<1$.

• (iii) $\limsup _{n\rightarrow \infty }\beta _{n}<1$.

• (iv) $0<\liminf _{n\rightarrow \infty }r_{n}\le \limsup _ {n\rightarrow \infty }r_{n}<2/L$.

  Then, the sequence $\{x_{n}\}$ converges strongly to $q=P_{S\cap F(T)}x_1$.

Example 4.4

Solve the following minimization problem:

$$\begin{aligned} \min _{x\in {\mathbb {R}}^3}\Vert x\Vert ^2_2+(3,5,-1)x+\Vert x\Vert _1, \end{aligned}$$

(4.6)

where $x=(x_1,x_2,x_3)\in {\mathbb {R}}^3$.

Set $F(x)=\Vert x\Vert ^2_2+(3,5,-1)x$ and $G(x)=\Vert x\Vert _1$ for all $x\in {\mathbb {R}}^3$. We have for $x\in {\mathbb {R}}^3$ and $r>0$, $\nabla F=2x+(3,5,-1)$ and

$$\begin{aligned} J^{\partial G}_{r}(x)=(\max \{|x_1|-r,0\}sign(x_1),\max \{|x_2|-r,0\} sign(x_2),\max \{|x_3|-r,0\}sign(x_3)). \end{aligned}$$

We see that $\nabla F$ is 2-Lipschitz continuous; consequently, it is 1 / 2-inverse strongly monotone. Choose $r_n=0.1$ for all $n\in {\mathbb {N}}$. Let $\alpha _n$, $\beta _n$, $\gamma _n$, and $\theta _n$ be as in Example 3.8. The stoping criterion is defined by $\Vert x_{n+1}-x_n\Vert <10^{-9}$. The different choices of $x_0$ and $x_1$ are given as follows:

• Choice 1: $x_0=(-2,-1,-1)^T$ and $x_{1}=(3,6,7)^T$.

• Choice 2: $x_0=(-5,-6,-3)^T$ and $x_{1}=(-3,4,-5)^T$.

From above preliminary numerical results, we see that the inertial forward–backward method with the inertial technical term has a good convergence speed than the standard forward–backward method for each of the randoms.

5 Conclusion

In this paper, we present a new modified inertial forward–backward splitting method combining the SP iteration for solving the fixed point problem of a quasi-nonexpansive multivalued mapping and the inclusion problem. The weak convergence theorem is established under some suitable conditions in Hilbert space. we then use the shrinking projection method for obtaining the strong convergence theorem and apply our result to solve the variational inequality problem and the convex minimization problem. Some numerical experiments show that our inertial forward–backward method have a competitive advantage over the standard forward–backward method (see in Tables 1, 2, 3, and Figs. 1, 2, 3, 4, 5, 6, and 7).