Generalized Jacobi–Galerkin method for nonlinear fractional differential algebraic equations

Abstract

In this paper, we provide an approximate approach based on the Galerkin method to solve a class of nonlinear fractional differential algebraic equations. The fractional derivative operator in the Caputo sense is utilized and the generalized Jacobi functions are employed as trial functions. The existence and uniqueness theorem as well as the asymptotic behavior of the exact solution are provided. It is shown that some derivatives of the solutions typically have singularity at origin dependence on the order of the fractional derivative. The influence of the perturbed data on the exact solutions along with the convergence analysis of the proposed scheme is also established. Some illustrative examples provided to demonstrate that this novel scheme is computationally efficient and accurate.

1 Introduction

Fractional differential algebraic equations have recently verified to be a useful devise in the modeling of the various physical problems such as electrochemical processes, non-integer order optimal controller design, complex biochemical (Damarla and Kundu 2015) and etc. Recently, providing the various numerical methods for solving the functional differential equations with fractional order have been receiving more attentions by many authors (Babaei and Banihashemi 2017; Bhrawy and Zaky 2016a, b; Dabiri and Butcher 2016, 2017a, b; Dabiri et al. 2016, 2018; Ghoreishi and Mokhtary 2014; Keshi 2018; Mokhtary 2016a; Mokhtary and Ghoreishi 2014a; Mokhtary 2015, 2016b, 2017; Mokhtary and Ghoreishi 2011, 2014b; Mokhtary et al. 2016; Moghaddam and Aghili 2012; Moghaddam and Machado 2017a, b; Moghaddam et al. 2017a, b; Pedas et al. 2016; Taghavi et al. 2017; Zaky 2017). Significantly less attention has been paid for the fractional differential algebraic equations (Damarla and Kundu 2015; Ding and Jiang 2014; İbis et al. 2011; İbis and Bayram 2011; Jaradat et al. 2014; Zurigat et al. 2010). In particular, very little has been focused on some crucial items such as the analysis of the asymptotic behavior and smoothness degree of the exact solutions, introducing an easy way to implement numerical technique with powerful convergence properties. These failures motivate us in the presented paper to develop and analyze an effective numerical method for solving the fractional differential algebraic equations

$$\begin{aligned} \left\{ \begin{array}{l} ^C_0D_t^{\alpha }x(t)=f(t,x(t),y(t)) , \\ 0=g(t,x(t),y(t)),\\ x(0)=y(0)=0,~~\alpha \in (0,1],~t \in I=[0,1], \end{array}\right. \end{aligned}$$

(1)

where $f, g: I \times \mathbb {R}\times \mathbb {R} \rightarrow \mathbb {R}$ are given continuous functions and x(t), y(t) are the exact solutions of the problem. The fractional derivative operator $^C_0D_t^\alpha$ is used in the left Caputo sense and defined by Diethelm (2010), and Podlubny (1999)

$$\begin{aligned} ^C_0D_t^\alpha x(t)=~_0I_t^{1-\alpha }(x'), \end{aligned}$$

where

$$\begin{aligned} _0I_t^{1-\alpha } x(t)=\frac{1}{\Gamma {(1-\alpha )}}\int \limits _{0}^{t}{(t-s)^{-\alpha } x(s)\mathrm{d}s}, \end{aligned}$$

is the left fractional integral operator of order $1-\alpha$. Here, $\mathbb R$ and $\Gamma {(.)}$ are the set of all real numbers and the Gamma function respectively. Properties of the operators $^C_0D_t^\alpha$ and $_0I_t^\alpha$ can be found in Diethelm (2010), and Podlubny (1999). Also we recall the following relations

$$\begin{aligned} _0I_t^\alpha \left( ^C_0D_t^\alpha x(t)\right) =x(t)-x(0), \end{aligned}$$

(2)

$$\begin{aligned} ^C_0D_t^{\alpha }t^k=\left\{ \begin{array}{ll} \frac{k!}{\Gamma (k-\alpha +1)}t^{k-\alpha }, &{}\quad k\ge 1, \\ \\ 0, &{}\quad k=0. \end{array}\right. \end{aligned}$$

(3)

In this paper, we design our methodology based on the Galerkin method which represents the approximate solutions of (1) by means of a truncated series expansion such that the residual function minimized in a certain way (Canuto et al. 2006; Hesthaven et al. 2007; Shen et al. 2006). Moreover, we discuss about existence, uniqueness, smoothness and wellposedness properties of the solutions of (1). We prove that some derivatives of the exact solutions typically suffer from discontinuity at origin and thereby representation of the Galerkin solution of (1) as a linear combination of the smooth basis functions leads to a numerical method with poor convergence results. To avoid this drawback, we employ generalized Jacobi functions which were introduced by Chen et al. (2016) as trial functions. These functions are orthogonal with respect to a suitable weight function and enable us to produce a Galerkin approximation with the same asymptotic performance with the exact solution which is a essential item in providing a high accuracy.

The organization of the article is as follows: The next section is devoted to some preliminaries and definitions that are used in the sequel. In Sect. 3, the existence and uniqueness theorem for (1) as well as its regularity and well-posedness properties are discussed. In Sect. 4, we explain the numerical treatment of the problem. Convergence analysis of the proposed scheme is established in Sect. 5. In Sect. 6, we illustrate the obtained numerical results to confirm the effectiveness of the proposed scheme and finally in Sect. 7 we give our concluded remarks.

2 Preliminaries

In this section, we review the basic definitions and properties that are required in the rest of the paper. Throughout the paper C and $C_i$ are generic positive constants independent of the approximation degree N. First we define the shifted generalized Jacobi functions on I that will be used as the basis functions in the Galerkin solution of (1). To this end, we denote the shifted generalized Jacobi functions on I by $P^{\delta ,-\beta }_{n}(t),~n \ge 0$ and define

$$\begin{aligned} P^{\delta ,-\beta }_n(t)=(2t)^{\beta }J_n^{\delta ,\beta }(t),\quad \text {for }\delta \in \mathbb R,~~\beta >-1, \end{aligned}$$

(4)

where $J_{n}^{\delta ,\beta }(t)$ is the shifted Jacobi polynomials on I with real parameters (Chen et al. 2016). It can be verified that $\{P_n^{\delta ,-\beta }(t)\}_{n \ge 0}$ are orthogonal for $\delta , \beta >-1$ in the following sense

$$\begin{aligned} \left( P_n^{\delta ,-\beta },P_m^{\delta ,-\beta } \right) _{\delta ,-\beta }:=\int \limits _{I}{P_n^{\delta ,-\beta }(t)P_m^{\delta ,-\beta }(t)w^{\delta ,-\beta }(t)\mathrm{d}t}=0,\quad n \ne m, \end{aligned}$$

where $w^{\delta ,-\beta }(t)=2^{\delta -\beta }(1-t)^{\delta } t^{-\beta }$ is the shifted weight function on I (Chen et al. 2016).

Now, let $\mathcal {F}_{N}^{\delta ,-\beta }(I)$ be the finite-dimensional space

$$\begin{aligned} \mathcal {F}_{N}^{\delta ,-\beta }(I)=\text {Span}\left\{ P_{n}^{\delta ,-\beta }(t):~ 0\le n\le N\right\} , \end{aligned}$$

and define the orthogonal projection $\Pi _N^{\delta ,-\beta }u \in \mathcal {F}_N^{\delta ,-\beta }(I)$ for $\beta>0,~\delta >-1$ as

$$\begin{aligned} \left( \Pi _{N}^{\delta ,-\beta }u-u,v_N\right) _{\delta ,-\beta }=0,\quad \forall ~ v_N\in \mathcal {F}_N^{\delta ,-\beta }(I), \end{aligned}$$

which can be represented by

$$\begin{aligned} \Pi _N^{\delta ,-\beta }u=\sum \limits _{n=0}^{N}{u_n^{\delta ,-\beta } P_n^{\delta ,-\beta }(t)},~~\quad u_n^{\delta ,-\beta }=\frac{\left( u,P_n^{\delta ,-\beta } \right) _{\delta ,-\beta }}{\Vert P_n^{\delta ,-\beta }\Vert _{\delta ,-\beta }^2}, \end{aligned}$$

(5)

with $\Vert P_n^{\delta ,-\beta }\Vert _{\delta ,-\beta }^2:=\big (P_n^{\delta ,-\beta },P_n^{\delta ,-\beta }\big )_{\delta ,-\beta }$ as the weighted $L_{\delta ,-\beta }^2$-norm of $P_n^{\delta ,-\beta }(t)$ on I. To simplicity we use the symbol $(L^2(I),\Vert .\Vert )$ when $\delta =\beta =0$. To characterize the truncation error bound of $\Pi _N^{\delta ,-\beta }u$ we introduce the weighted space (Chen et al. 2016)

$$\begin{aligned} B_{\delta ,\beta }^m(I):=\{u \in L_{\delta ,-\beta }^2(I);~~^C_0D_t^{\beta +l}u \in L_{\delta +\beta +l,l}^2(I),~~\text {for}~~0\le l \le m\},~~ m \in \mathbb N_0:=\mathbb N \cup \{0\}, \end{aligned}$$

and give the following lemma.

Lemma 2.1

(Chen et al. 2016) Assume that for $\delta>-1,~\beta >0$ and a fixed number $m \in \mathbb N_0$ we have $u \in B_{\delta ,\beta }^{m}(I)$. Then

$$\begin{aligned} \Vert \Pi _N^{\delta ,-\beta }u-u\Vert _{\delta ,-\beta } \le C N^{-(\beta +m)}\Vert ^C_0D_t^{\beta +m}u\Vert _{\delta +\beta +m,m}. \end{aligned}$$

Note that in view of $P_n^{\delta ,-\beta }(0)=0$ for $\delta>-1,~\beta >0$, the functions $\{P_n^{\delta , -\beta }(t);~~n \ge 0\}$ are suitable basis functions for the Galerkin solution of functional equations with homogeneous initial conditions.

We also recall the Legendre Gauss interpolation operator $I_N^t$ for any function u(t), defined on I as

$$\begin{aligned} I_N^t u(t)=\sum \limits _{n=0}^{N}{\frac{\big (u,L_n\big )_N}{\Vert L_n\Vert _{0,0}^2} L_n(t)}, \end{aligned}$$

where $\{L_n(t)\}_{n \ge 0}$ are the shifted Legendre polynomials on I and $\big (u,L_n\big )_N$ is the discrete Legendre Gauss inner product defines by

$$\begin{aligned} (u,L_n)_{N}=\sum _{i=0}^{N}{u(t_i)L_n(t_i)w_i}, \end{aligned}$$

(6)

where $\{t_i,w_i\}_{i=0}^{N}$ are the shifted Legendre Gauss nodal points and corresponding weights over I, respectively (Canuto et al. 2006; Hesthaven et al. 2007; Shen et al. 2006). To provide an error estimation of the interpolation approximation of the function u(t), we define the non-uniformly sobolev space $W^m(I)$ by Mokhtary (2015) and Shen et al. (2006)

$$\begin{aligned} W^m(I):=\{u \in L^2(I);~~ u^{(l)} \in L_{l,l}^2(I),~~\text {for}~~0\le l \le N\}, \end{aligned}$$

and give the following lemma.

Lemma 2.2

(Mokhtary 2015; Shen et al. 2006) Assume that $I_N^t(u)$ is the Legendre Gauss interpolation approximation of the function u(t). Then for any $u(t) \in W^{m}(I)$ with $m \ge 1$ we have

$$\begin{aligned} \Vert u-I_N^{t}(u)\Vert \le C N^{-m} \Vert u^{(m)}\Vert _{m,m}. \end{aligned}$$

3 Existence and uniqueness theorem and influence of perturbed data

In this section, we provide an existence and uniqueness theorem for the exact solution of (1) and give its regularity properties. We also discuss about the behavior of the solution under perturbations in the given data. First we give two theorems which will be used in our analysis.

Theorem 3.1

(Zhang and Ge 2011) Assume that $H:I \times \mathbb {R} \times \mathbb {R} \rightarrow \mathbb {R}$ is continuously differentiable and there exists a positive constant d such that $\big |\frac{\partial }{\partial y}H(t,x,y)\big |>d>0$ for all $(t,x,y) \in I \times \mathbb R \times \mathbb R$. Then there exists a unique continuously differentiable function $h:I \times \mathbb R \rightarrow \mathbb R$ such that $H(t,x,h(t,x))=0$.

Theorem 3.2

(Diethelm 2010) Let the function $F:I \times \mathbb {R} \rightarrow \mathbb {R}$ be continuous and satisfies in a Lipschitz condition with respect to its second variable, i.e., we have

$$\begin{aligned} |F(t,u(t))-F(t,v(t))| \le C |u(t)-v(t)|, \end{aligned}$$

for all real value functions u(t) and v(t) on I. Then, the fractional differential equation

$$\begin{aligned} \left\{ \begin{array}{l} ^C_0D_t^{\alpha }u(t)=F(t,u(t)),\\ u(0)=d_0,\quad t\in I,~ \alpha \in (0,1),~d_0 \in \mathbb R, \end{array}\right. \end{aligned}$$

has a unique continuous solution. Moreover, if $F \in C^v(I\times \mathbb {R})$ for $v\ge 0$, we have $u(t) \in C^{v}(0,1]\cap C(I)$ with $u'(t)=O(t^{\alpha -1})$ as $t\rightarrow 0^+$. Here, C(I) is the space of all continuous functions on I and $C^v(I):=\{u(t)|~u^{(v)} \in C(I),~~v \ge 0\}$.

Now, we are ready to prove the existence and uniqueness theorem of the solution of (1).

Theorem 3.3

Assume that the functions $f, g:I \times \mathbb {R} \times \mathbb {R} \rightarrow \mathbb {R}$ are given such that the function f is continuous and satisfies in a Lipschitz condition with respect to its second and third variables, i.e., we have

$$\begin{aligned} |f(t,x,y)-f(t,z,u)| \le C_1 |x-z|+ C_2 |y-u|, \end{aligned}$$

and g is a continuously differentiable function and there exists a positive constant d such that $\big |\frac{\partial }{\partial y}g(t,x,y)\big |>d>0$ for all $(t,x,y) \in I \times \mathbb R \times \mathbb R$. Then the fractional differential algebraic equation (1) has a unique continuous solution. In addition, if $f,g \in C^v(I\times \mathbb {R}\times \mathbb {R})$ for $v\ge 0$, we have

$$\begin{aligned}&x(t)\in C^v(0,1]\cap C(I),~~ \text {with}~~ |x'(t)| \le C_{\alpha } t^{\alpha -1},\\ \\&y(t)\in C^{v}(0,1]\cap C^{\tilde{v}}(I),~~ \text {with}~~ ~|y^{(\tilde{v}+1)}(t)|\le C_{\alpha }t^{\alpha -1},~~ \tilde{v} \ge 0, \end{aligned}$$

where the value of $\tilde{v}$ depends on the smoothness of the function g and $C_\alpha$ is a generic positive constant dependent on $\alpha$.

Proof

Theorem 3.1, concludes that there exists a smooth function $G:I \times \mathbb R \rightarrow \mathbb R$ such that $y(t)=G(t,x(t))$ and thereby its substituting in (1) yields

$$\begin{aligned} ^C_0D_t^{\alpha }x(t)=f(t,x(t),G(t,x(t))):=F(t,x(t)), \end{aligned}$$

(7)

with $x(0)=0$ as the initial condition. Now we show that the function F(t, x(t)) defined in (7) has a Lipschitz property with respect to its second variable. To this end, we can write

$$\begin{aligned} |F(t,x(t))-F(t,z(t))|= & {} |f(t,x(t),G(t,x(t))-f(t,z(t),G(t,z(t))|\nonumber \\\le & {} C_1 |x(t)-z(t)|+C_2 |G(t,x(t))-G(t,z(t))|, \end{aligned}$$

(8)

in view of the Lipschitz assumption on f(t, x(t), y(t)). Moreover, since G(t, x(t)) is continuously differentiable then it also satisfies in a Lipschitz condition with respect to its second variable and this indicates that F(t, x(t)) satisfies in a Lipschitz condition with respect to its second component. Consequently the desired result can be obtained by applying Theorem 3.2 on (7). $\square$

After providing principles for the existence and uniqueness of solutions of (1) as well as its regularity properties, we now investigate the dependence of the exact solution to some small perturbations in the given data. This is clearly an important factor in the numerical solution of (1) because the influence of perturbations in the discretized equation is of fundamental importance in the analysis of convergence and determining the roundoff errors.

Theorem 3.4

Consider the Eq. (1) and suppose all conditions of Theorem 3.3 are satisfied. Let us now consider the perturbed equation

$$\begin{aligned} \left\{ \begin{array}{l} ^C_0D_t^{\alpha }\tilde{x}(t)=f(t,\tilde{x}(t),\tilde{y}(t))+\delta _1(t) ,\\ 0=g(t,\tilde{x}(t),\tilde{y}(t))+\delta _2(t),\\ \tilde{x}(0)=\varepsilon _0,\tilde{y}(0)=\varepsilon _1,~~\alpha \in (0,1],~t \in I, \end{array}\right. \end{aligned}$$

(9)

with small perturbations $\delta _1, \delta _2, \varepsilon _0, \varepsilon _1$ and the perturbed solutions $\tilde{x}, \tilde{y}$. Then we have

$$\begin{aligned} \Vert x-\tilde{x}\Vert \le C_1\left( |\varepsilon _0|+\Vert \delta _1\Vert +\Vert \delta _2\Vert \right) , \end{aligned}$$

(10)

$$\begin{aligned} \Vert y-\tilde{y}\Vert \le C_2\left( \Vert x-\tilde{x}\Vert +\Vert \delta _2\Vert \right) , \end{aligned}$$

(11)

Proof

Using Theorem 3.1, y and $\tilde{y}$ can be extracted from the algebraic constraints of (1) and (9) respectively as $y=G(t,x)$ and $\tilde{y}=G(t,\tilde{x})+\delta _2(t)$. Then we can write

$$\begin{aligned} \tilde{y}(t)-y(t)=G(t,\tilde{x})-G(t,x)+\delta _2(t). \end{aligned}$$

Since G is a continuously differentiable function then it satisfies in a Lipschitz condition with respect to its second variable and this implies the following inequality

$$\begin{aligned} \Vert y-\tilde{y}\Vert \le C_2\left( \Vert x-\tilde{x}\Vert +\Vert \delta _2\Vert \right) , \end{aligned}$$

(12)

which implies (11). Now, we subtract the first equations of (9) and (1) each other and obtain

$$\begin{aligned} ^C_0D_t^\alpha (\tilde{x}-x)=f(t,\tilde{x},\tilde{y})-f(t,x,y)+\delta _1(t). \end{aligned}$$

(13)

Applying the fractional integral operator $_0I_t^\alpha$ on both sides of (13) and using Lipschitz assumption for f yield

$$\begin{aligned} |\tilde{x}-x|\le & {} |\tilde{x}(0)-x(0)|+~_0I_t^\alpha \left( C_1|\tilde{x}-x|+C_3|\tilde{y}-y| \right) +~_0I_t^\alpha \left( |\delta _1| \right) \nonumber \\\le & {} |\varepsilon _0|+~_0I_t^\alpha \left( C_4(|\tilde{x}-x|+|\delta _2|) \right) +~_0I_t^\alpha \left( |\delta _1| \right) , \end{aligned}$$

(14)

in view of (2) and (12). Gronwall’s inequality (Mokhtary and Ghoreishi 2014a; Mokhtary 2016b) concludes

$$\begin{aligned} \Vert \tilde{x}-x\Vert \le C_5\left( |\varepsilon _0|+\Vert \delta _2\Vert +\Vert \delta _1\Vert \right) , \end{aligned}$$

due to boundedness of operator $_0I_t^\alpha$ (Mokhtary 2016a) which is the desired result (10). $\square$

Theorem 3.4, indicates that the Eq. (1) has perturbation index one along the solutions x(t) and y(t) which studied the effect of small perturbations and classified the complexities in the numerical solution of (1) (Gear 1990; Hairer et al. 1989). Moreover, Theorem 3.4 indicates the well-posedness of the considered problem (1) in the sense that small perturbations in the input data leads to a small changes in the exact solution. More precisely, the occurrence of small perturbations in the right hand sides of the inequalities (10) and (11) will translate in the numerical solution into a small discrete perturbations due to roundoff errors and wellposedness property does not allow a meaningful effect on the accuracy of the approximate solution.

4 Numerical approach

In this section, we introduce the generalized Jacobi Galerkin method for the numerical solution of (1). As we can see from Theorem 3.3, some derivatives of the exact solution of (1) have singularity at $t=0^+$. Then, representation of the Galerkin solution of (1) by a linear combination of classical orthogonal polynomials leads to a loss in the global convergence order. To solve this difficulty, we should employ suitable basis functions which produce an approximate solution with the same asymptotic performance of the exact solution. From the definition of the shifted generalized Jacobi functions on I it can be easily seen that by representing the Galerkin solution of (1) as

$$\begin{aligned} x_N(t)= & {} \sum \limits _{i=0}^{N}{a_i P_i^{0,-\alpha }(t)}=\underline{a}\overline{P}=\underline{a}P \underline{T},\nonumber \\ y_N(t)= & {} \sum \limits _{i=0}^{N}{b_i P_i^{0,-\alpha }(t)}=\underline{b}\overline{P}=\underline{b}P \underline{T}, \end{aligned}$$

(15)

we can produce a numerical solution for (1) that is matched with the singularity of the exact solution. Here $\underline{a}=[a_0, a_1,\ldots , a_N],~\underline{b}=[b_0, b_1,\ldots , b_N]$ are the unknown vectors and $\overline{P}=[P_{0}^{0,-\alpha }(t), P_1^{0,-\alpha }(t),\ldots ,P_N^{0,-\alpha }(t)]^{T}$ is the shifted generalized Jacobi function basis in I. P is a non-singular lower triangular coefficient matrix of order $N+1$ and $\underline{T}=[t^{\alpha },t^{\alpha +1},t^{\alpha +2},\ldots ,t^{\alpha +N}]^T$.

Inserting (15) into (1) we obtain

$$\begin{aligned} \left\{ \begin{array}{l} \underline{a} P ~^C_0D_t^\alpha \underline{T}=f(t,\underline{a}\overline{P}, \underline{b}\overline{P})\\ 0=g(t,\underline{a}\overline{P}, \underline{b}\overline{P}). \end{array}\right. \end{aligned}$$

(16)

Applying (3) we can write

$$\begin{aligned} ^C_0D_t^{\alpha } \underline{T}= & {} \left[ ~^C_0D_t^{\alpha }(t^\alpha ),~^C_0D_t^{\alpha }(t^{\alpha +1}),\ldots ,~^C_0D_t^{\alpha } (t^{\alpha +N}) \right] ^T\nonumber \\= & {} \left[ \frac{\alpha !}{0!}\ t^0, \frac{(\alpha +1)!}{1!}\ t,\ldots , \frac{(\alpha +N)!}{N!}\ t^{N}\right] ^T:=\underline{T}^\alpha . \end{aligned}$$

(17)

Substituting (17) into (16) we have

$$\begin{aligned} \left\{ \begin{array}{l} \underline{a} P \underline{T}^\alpha =f(t,\underline{a}\overline{P}, \underline{b}\overline{P})\\ 0=g(t,\underline{a}\overline{P}, \underline{b}\overline{P}). \end{array}\right. \end{aligned}$$

(18)

In the Galerkin method, the unknown vectors $\underline{a}, \underline{b}$ are computed in such a way that (18) is orthogonal to the finite dimensional space $\mathcal F_N^{0,-\alpha }(I)$. Thus the unknown vectors $\underline{a}, \underline{b}$ must satisfy in the following algebraic system

$$\begin{aligned} \left\{ \begin{array}{l} \underline{a} P \left( \underline{T}^\alpha ,P_j^{0,-\alpha }(t) \right) _{0,-\alpha }=\left( f(t,\underline{a}\overline{P}, \underline{b}\overline{P}),P_j^{0,-\alpha }(t) \right) _{0,-\alpha }\\ \\ 0= \left( g(t,\underline{a}\overline{P}, \underline{b}\overline{P}),P_j^{0,-\alpha }(t) \right) _{0,-\alpha }, \end{array}\right. \end{aligned}$$

(19)

for $0 \le j \le N$. Using the relations (4), (6) and (17), we have

$$\begin{aligned} \left( \underline{T}^\alpha , P_j^{0,-\alpha }(t) \right) _{0,-\alpha }= & {} \int \limits _{I}{\underline{T}^\alpha P_j^{0,-\alpha }(t)(2t)^{-\alpha }\mathrm{d}t}=\int \limits _{I}{\underline{T}^\alpha J_j^{0,\alpha }(t)\mathrm{d}t}\nonumber \\= & {} \left[ \frac{(\alpha +s)!}{s!}\int \limits _I{t^s J_j^{0,\alpha }(t)\mathrm{d}t} \right] _{s=0}^N\nonumber \\= & {} \left[ \frac{(\alpha +s)!}{s!} \left( t^s,J_j^{0,\alpha } \right) _N \right] _{s=0}^N:=\underline{\tilde{T}}^{\alpha ,j}, \end{aligned}$$

(20)

in view of the exactness of Legendre Gauss quadrature for all polynomials with degree at most $2N+1$ (Canuto et al. 2006; Hesthaven et al. 2007; Shen et al. 2006).

In the implementation process, we approximate the integrals of the right hand side of (19) using the shifted Legendre Gauss quadrature formula over I as follows

$$\begin{aligned} \left( f(t,\underline{a}\overline{P}, \underline{b}\overline{P}),P_j^{0,-\alpha }(t) \right) _{0,-\alpha }= & {} \int \limits _I{f(t,\underline{a}\overline{P}, \underline{b}\overline{P})P_j^{0,-\alpha }(t)(2t)^{-\alpha }\mathrm{d}t}\nonumber \\= & {} \int \limits _I{f(t,\underline{a}\overline{P}, \underline{b}\overline{P})J_j^{0,\alpha }(t)\mathrm{d}t}\simeq \left( f(t,\underline{a}\overline{P}, \underline{b}\overline{P}),J_j^{0,\alpha } \right) _N,\nonumber \\ \end{aligned}$$

(21)

$$\begin{aligned} \left( g(t,\underline{a}\overline{P}, \underline{b}\overline{P}),P_j^{0,-\alpha }(t) \right) _{0,-\alpha }= & {} \int \limits _I{g(t,\underline{a}\overline{P}, \underline{b}\overline{P})P_j^{0,-\alpha }(t)(2t)^{-\alpha }\mathrm{d}t}\nonumber \\= & {} \int \limits _I{g(t,\underline{a}\overline{P}, \underline{b}\overline{P})J_j^{0,\alpha }(t)\mathrm{d}t}\simeq \left( g(t,\underline{a}\overline{P}, \underline{b}\overline{P}),J_j^{0,\alpha } \right) _N.\nonumber \\ \end{aligned}$$

(22)

Substituting (20), (21) and (22) into (19), we have the following $2N+2$ nonlinear algebraic system of equations

$$\begin{aligned} \left\{ \begin{array}{l} \underline{a} P \underline{\tilde{T}}^{\alpha ,j}=\left( f(t,\underline{a}\overline{P}, \underline{b}\overline{P}),J_j^{0,\alpha } \right) _{N}\\ 0= \left( g(t,\underline{a}\overline{P}, \underline{b}\overline{P}),J_j^{0,\alpha } \right) _{N},\quad 0 \le j \le N \end{array}\right. \end{aligned}$$

(23)

which when solved gives us the unknown vectors $\underline{a}$ and $\underline{b}$.

5 Convergence analysis

In this section, we provide an error analysis to justify the convergence of the generalized Jacobi Galerkin approximation of (1).

Theorem 5.1

Assume that the conditions of Theorem 3.3 are satisfied and $x_N(t), y_N(t)$ are the generalized Jacobi Galerkin approximations of (1) with the exact solutions x(t), y(t). If the following conditions are satisfied

• $f \in W^{m_1}(I) \cap B_{0,-\alpha }^{m_3}(I),\quad m_1 \ge 1,~ m_3 \ge 0,$

• $g \in W^{m_2}(I) \cap B_{0,-\alpha }^{m_4}(I),\quad m_2 \ge 1,~ m_4 \ge 0,$

• $^C_0D_t^{\alpha }x \in B_{0,-\alpha }^{m_5}(I),\quad m_5 \ge 0$,

then for sufficiently large N we have

$$\begin{aligned} \Vert e_N\Vert\le & {} C \left[ N^{-m_1}\Vert f^{(m_1)}\Vert _{m_1,m_1}+N^{-m_2}\Vert g^{(m_2)}\Vert _{m_2,m_2}+N^{-(\alpha +m_3)}\Vert ^C_0D_t^{\alpha +m_3}f\Vert _{\alpha +m_3,m_3}\right. \nonumber \\&\left. +\, N^{-(\alpha +m_4)}\Vert ^C_0D_t^{\alpha +m_4}g\Vert _{\alpha +m_4,m_4}+N^{-(\alpha +m_5)}\Vert ^C_0D_t^{\alpha +m_5}(^C_0D_t^\alpha x)\Vert _{\alpha +m_5,m_5}\right] \end{aligned}$$

(24)

$$\begin{aligned} \Vert \varepsilon _N\Vert\le & {} C \left[ N^{-m_2}\Vert g^{(m_2)}\Vert _{m_2,m_2}+N^{-(\alpha +m_4)}\Vert ^C_0D_t^{\alpha +m_4}g\Vert _{\alpha +m_4,m_4}+\Vert e_N\Vert \right] , \end{aligned}$$

(25)

where $e_N(t)=x(t)-x_N(t)$ and $\varepsilon _N(t)=y(t)-y_N(t)$ are the error functions.

Proof

According to the proposed numerical scheme in the previous section, we have

$$\begin{aligned} \left\{ \begin{array}{l} \left( ~^C_0D_t^{\alpha }x_N, P_j^{0,-\alpha } \right) _{0,-\alpha }=\left( f(t,x_N(t),y_N(t)),J_j^{0,\alpha } \right) _{N},\\ 0= \left( g(t,x_N(t),y_N(t)),J_j^{0,\alpha } \right) _{N}, \end{array}\right. \end{aligned}$$

(26)

for $0 \le j \le N$. Furthermore, we can write

$$\begin{aligned} \left( f(t,x_N(t),y_N(t)),J_j^{0,\alpha } \right) _N= & {} \sum \limits _{i=0}^{N}{f(t_i,x_N(t_i),y_N(t_i))J_j^{0,\alpha }(t_i)w_i}\nonumber \\= & {} \sum \limits _{i=0}^{N}{I_N^t f(t,x_N(t),y_N(t))\Big |_{t=t_i} J_j^{0,\alpha }(t_i)w_i}\nonumber \\= & {} \int \limits _I{I_N^t f(t,x_N(t),y_N(t)) J_j^{0,\alpha }(t)\mathrm{d}t}\nonumber \\= & {} \left( I_N^t f(t,x_N(t),y_N(t)),P_j^{0,-\alpha } \right) _{0,-\alpha }, \end{aligned}$$

(27)

and similarly we have

$$\begin{aligned} \left( g(t,x_N(t),y_N(t)),J_j^{0,\alpha } \right) _N= \left( I_N^t g(t,x_N(t),y_N(t)),P_j^{0,-\alpha } \right) _{0,-\alpha }, \end{aligned}$$

(28)

in view of the exactness of the Legendre Gauss quadrature for all polynomials with degree at most $2N+1$. Inserting (27) and (28) into (26) we conclude

$$\begin{aligned} \left\{ \begin{array}{l} \left( ~^C_0D_t^{\alpha }x_N, P_j^{0,-\alpha } \right) _{0,-\alpha }=\left( I_N^t f(t,x_N(t),y_N(t)),P_j^{0,-\alpha } \right) _{0,-\alpha },\\ 0= \left( I_N^t g(t,x_N(t),y_N(t)),P_j^{0,-\alpha } \right) _{0,-\alpha }. \end{array}\right. \end{aligned}$$

(29)

Considering (5), multiplying both sides of (29) by $\frac{P_{i}^{0,-\alpha }(t)}{\Vert P_{i}^{0,-\alpha }\Vert _{0,-\alpha }^2}$ and summing up from 0 to N we obtain

$$\begin{aligned} \left\{ \begin{array}{l} \Pi _{N}^{0,-\alpha }(^C_0D_t^{\alpha }x_N) =\Pi _{N}^{0,-\alpha }(I_N^t \widetilde{f}),\\ 0=\Pi _{N}^{0,-\alpha }(I_N^t\widetilde{g}), \end{array}\right. \end{aligned}$$

(30)

where $\tilde{f}=f(t,x_N(t),y_N(t))$ and $\tilde{g}=g(t,x_N(t),y_N(t))$. Now, we subtract (1) from (30) and achieve

$$\begin{aligned} \left\{ \begin{array}{l} ^C_0D_t^\alpha x(t)-\Pi _{N}^{0,-\alpha }(^C_0D_t^{\alpha }x_N) =f(t,x(t),y(t))-\Pi _{N}^{0,-\alpha }(I_N^t \widetilde{f}), \\ 0=g(t,x(t),y(t))-\Pi _{N}^{0,-\alpha }(I_N^t \widetilde{g}), \end{array}\right. \end{aligned}$$

(31)

which can be rewritten as

$$\begin{aligned} \left\{ \begin{array}{l} ^C_0D_t^{\alpha } e_N + e_{\Pi _{N}^{0,-\alpha }}(^C_0D_t^{\alpha }x_N) = f-\widetilde{f}+ e_{\Pi _{N}^{0,-\alpha }} (\widetilde{f}) +\Pi _{N}^{0,-\alpha }( e_{I_N^t}\widetilde{f}),\\ 0=g-\widetilde{g}+e_{\Pi _{N}^{0,-\alpha }}(\widetilde{g})+\Pi _{N}^{0,-\alpha }( e_{I_N^t}\widetilde{g}), \end{array}\right. \end{aligned}$$

(32)

with

$$\begin{aligned} e_{\Pi _{N}^{0,-\alpha }}(u)=u - \Pi _{N}^{0,-\alpha } (u) ,\ \ \ e_{I_N^t} (u)=u - I_N^t (u). \end{aligned}$$

Applying Taylor expansion formula for g(t, x, y) in some open neighborhood around $(x_N,y_N)$, we can write

$$\begin{aligned} g-\tilde{g}=g(t,x(t),y(t))-g(t,x_N(t),y_N(t))\simeq e_N(t) \frac{\partial g(\xi )}{\partial x}+\varepsilon _N(t)\frac{\partial g(\xi )}{\partial y}, \end{aligned}$$

(33)

where $\xi =(t,\xi _1,\xi _2)$ which $\xi _1$ lies between x(t) and $x_N(t)$ and $\xi _2$ lies between y(t) and $y_N(t)$.

Thus using (33) and the second relation of (32) we obtain

$$\begin{aligned} \varepsilon _N(t) \simeq \frac{1}{\frac{\partial g(\xi )}{\partial y}}\left( e_{\Pi _{N}^{0,-\alpha }}(\widetilde{g})+\Pi _{N}^{0,-\alpha }(e_{I_N^t} (\widetilde{g}))-\frac{\partial g(\xi )}{\partial x} e_N \right) , \end{aligned}$$

(34)

in view of $\frac{\partial g}{\partial y}\ne 0$. Now, applying the left fractional Riemann–Liouville integral operator $_0I_t^{\alpha }$ on the both sides of the first equation (32) and using (2) concludes

$$\begin{aligned} |e_N| \le ~_0I_t^{\alpha }(|f-\widetilde{f}|)+\left| ~_0I_t^{\alpha } \left[ e_{\Pi _{N}^{0,-\alpha }}(^C_0D_t^{\alpha }x_N)+e_{\Pi _{N}^{0,-\alpha }} (\widetilde{f})+\Pi _{N}^{0,-\alpha }(e_{I_N^t}\widetilde{f}) \right] \right| , \end{aligned}$$

which can be rewritten as

$$\begin{aligned} |e_N| \le ~ _0I_t^{\alpha }(C_1|e_N|+C_2|\varepsilon _N|)+\left| ~_0I_t^{\alpha } \left[ e_{\Pi _{N}^{0,-\alpha }}(^C_0D_t^{\alpha }x_N)+e_{\Pi _{N}^{0,-\alpha }} (\widetilde{f})+\Pi _{N}^{0,-\alpha }(e_{I_N^t}\widetilde{f}) \right] \right| , \end{aligned}$$

in view of the Lipschitz assumption on f. Inserting (34) into the above inequality we obtain to the following inequality

$$\begin{aligned}&|e_N| \le ~_0I_t^{\alpha }\left( \left[ C_1-C_2\frac{\frac{\partial g(\xi )}{\partial x}}{\frac{\partial g(\xi )}{\partial y}}\right] |e_N|\right) \nonumber \\&+ \left| ~_0I_t^{\alpha } \left[ e_{\Pi _{N}^{0,-\alpha }}\left( ^C_0D_t^{\alpha }x_N\right) +e_{\Pi _{N}^{0,-\alpha }} (\widetilde{f})+\Pi _{N}^{0,-\alpha }\left( e_{I_N^t}\widetilde{f}\right) \right. \right. \nonumber \\&\left. \left. +\frac{1}{\frac{\partial g(\xi )}{\partial y}}\left( e_{\Pi _{N}^{0,-\alpha }}(\widetilde{g})+\Pi _{N}^{0,-\alpha }\left( e_{I_N^t} (\widetilde{g})\right) \right) \right] \right| . \end{aligned}$$

(35)

Applying the Gronwall’s inequality (Mokhtary and Ghoreishi 2014a; Mokhtary 2016b), in (35) we get

$$\begin{aligned} \Vert e_N\Vert\le & {} \left\| ~_0I_t^{\alpha } \left[ e_{\Pi _{N}^{0,-\alpha }}\left( ^C_0D_t^{\alpha }x_N\right) +e_{\Pi _{N}^{0,-\alpha }} (\widetilde{f})+\Pi _{N}^{0,-\alpha }\left( e_{I_N^t}\widetilde{f}\right) \right. \right. \\&\left. \left. +\frac{1}{\frac{\partial g(\xi )}{\partial y}}\left( e_{\Pi _{N}^{0,-\alpha }}(\widetilde{g})+\Pi _{N}^{0,-\alpha }\left( e_{I_N^t} (\widetilde{g})\right) \right) \right] \right\| . \end{aligned}$$

Due to boundedness of the operator $_0I_t^\alpha$ (Mokhtary 2016a), and the orthogonal projection operator norm $\Vert \Pi _N^{0,-\alpha }\Vert _{0,-\alpha }=1$ (Atkinson and Han 2009), the inequality above can be written as follows

$$\begin{aligned} \Vert e_N\Vert\le & {} C_3 \left( \Vert e_{\Pi _{N}^{0,-\alpha }}(^C_0D_t^{\alpha }x_N)\Vert +\Vert e_{\Pi _{N}^{0,-\alpha }} (\widetilde{f})\Vert +\Vert e_{I_N^t}\widetilde{f}\Vert +\Vert e_{\Pi _{N}^{0,-\alpha }}(\widetilde{g})\Vert +\Vert e_{I_N^t} (\widetilde{g})\Vert \right) \nonumber \\\le & {} C_4 \left( \Vert e_{\Pi _{N}^{0,-\alpha }}(^C_0D_t^{\alpha }x_N)\Vert _{0,-\alpha }+\Vert e_{\Pi _{N}^{0,-\alpha }} (\widetilde{f})\Vert _{0,-\alpha }\right. \nonumber \\&\left. +\,\Vert e_{I_N^t}\widetilde{f}\Vert +\Vert e_{\Pi _{N}^{0,-\alpha }}(\widetilde{g})\Vert _{0,-\alpha }+\Vert e_{I_N^t} (\widetilde{g})\Vert \right) . \end{aligned}$$

(36)

From Lemma 2.2, we have

$$\begin{aligned}&\Vert e_{I_N^t}\widetilde{f}\Vert \le C_5 N^{-m_1}\Vert \tilde{f}^{(m_1)}\Vert _{m_1,m_1} \simeq C_6 N^{-m_1} \left( \Vert f^{(m_1)} \Vert _{m_1,m_1}+\Vert e_N\Vert _{m_1,m_1}+\Vert \varepsilon _N\Vert _{m_1,m_1} \right) ,\nonumber \\&\Vert e_{I_N^t}\widetilde{g}\Vert \le C_7 N^{-m_2} \Vert \tilde{g}^{(m_2)}\Vert _{m_2,m_2} \simeq C_8 N^{-m_2} \left( \Vert g^{(m_2)} \Vert _{m_2,m_2}+\Vert e_N\Vert _{m_2,m_2}+\Vert \varepsilon _N\Vert _{m_2,m_2} \right) ,\nonumber \\ \end{aligned}$$

(37)

and from Lemma 2.1, the following inequalities hold

$$\begin{aligned} \Vert e_{\Pi _{N}^{0,-\alpha }} (\widetilde{f})\Vert _{0,-\alpha }\le & {} C_9 N^{-(\alpha +m_3)} \Vert ^C_0D_t^{m_3+\alpha }\tilde{f}\Vert _{\alpha +m_3,m_3}\nonumber \\\simeq & {} C_9 N^{-(\alpha +m_3)} \Vert ^C_0D_t^{m_3+\alpha }(f+e_N \frac{\partial f}{\partial x}+\varepsilon _N \frac{\partial f}{\partial y})\Vert _{\alpha +m_3,m_3}, \end{aligned}$$

(38)

$$\begin{aligned} \Vert e_{\Pi _{N}^{0,-\alpha }} (\widetilde{g})\Vert _{0,-\alpha }\le & {} C_{10} N^{-(\alpha +m_4)} \Vert ~^C_0D_t^{m_4+\alpha }\tilde{g}\Vert _{\alpha +m_4,m_4}\nonumber \\\simeq & {} C_{10} N^{-(\alpha +m_4)} \Vert ~^C_0D_t^{m_4+\alpha }(g+e_N \frac{\partial g}{\partial x}+\varepsilon _N \frac{\partial g}{\partial y})\Vert _{\alpha +m_4,m_4}, \end{aligned}$$

(39)

$$\begin{aligned} \Vert e_{\Pi _{N}^{0,-\alpha }}(~^C_0D_t^{\alpha }x_N)\Vert _{0,-\alpha }\le & {} C_{11} N^{-(\alpha +m_5)} \Vert ~^C_0D_t^{m_5+\alpha }(~^C_0D_t^\alpha x_N)\Vert _{\alpha +m_5,m_5}\nonumber \\\simeq & {} C_{11} N^{-(\alpha +m_5)}\Vert ~^C_0D_t^{m_5+\alpha }\left( ~^C_0D_t^\alpha x+~^C_0D_t^\alpha e_N \right) \Vert _{\alpha +m_5,m_5}.\nonumber \\ \end{aligned}$$

(40)

Substituting the relations (37)–(40) into (36) the desired error estimation (24) can be obtained by ignoring some unnecessary terms for sufficiently large values of N. In addition, from (34) we can write

$$\begin{aligned} \Vert \varepsilon _N\Vert\le & {} C_{12}\left( \Vert e_{\Pi _{N}^{0,-\alpha }}(\widetilde{g})\Vert +\Vert \Pi _{N}^{0,-\alpha }(e_{I_N^t} (\widetilde{g}))\Vert +\Vert e_N\Vert \right) \\\le & {} C_{13}\left( \Vert e_{\Pi _{N}^{0,-\alpha }}(\widetilde{g})\Vert _{0,-\alpha }+\Vert \Pi _{N}^{0,-\alpha }(e_{I_N^t} (\widetilde{g}))\Vert _{0,-\alpha }+\Vert e_N\Vert \right) \\\le & {} C_{14}\left( \Vert e_{\Pi _{N}^{0,-\alpha }}(\widetilde{g})\Vert _{0,-\alpha }+\Vert e_{I_N^t} (\widetilde{g})\Vert +\Vert e_N\Vert \right) . \end{aligned}$$

Trivially, the second desired estimation (25) can be concluded by applying the relations (37) and (39) into the equation above and ignoring some unnecessary terms for sufficiently large values of N. $\square$

6 Numerical results

In this section, we illustrate the generalized Jacobi Galerkin method for the Eq. (1) in the context of some test problems in order to confirm the computational efficiency of the scheme. All the calculations were supported by the Mathematica$^\circledR$ software and all obtained nonlinear algebraic systems were solved by employing the well known iterative quasi Newton method (Fletcher 1987). The numerical errors reported in tables are calculated by $L^2$-norm of the error function.

Example 6.1

Consider the fractional differential algebraic equation

$$\begin{aligned} \left\{ \begin{array}{ll} ^C_0D_t^{\frac{1}{2}}{x(t)}=\left( 1-e^{y(t)} \right) x(t)+\frac{\sqrt{\pi }}{2}-\sqrt{t}(1-e^{t \sqrt{t}}),\\ 0=y(t)-sin \big (x(t)\big )-t \sqrt{t}+\sin {\sqrt{t}},\\ \end{array}\right. \end{aligned}$$

(41)

with the initial conditions $x(0)=y(0)=0$. The exact solution is

$$\begin{aligned} x(t)=\sqrt{t},\quad y(t)=t\sqrt{t}. \end{aligned}$$

To show the efficiency of the proposed scheme in approximating (1), we implement the generalized Jacobi Galerkin method for the numerical solution of (6.1) with approximation degree $N=1$ and consider

$$\begin{aligned} \nonumber x_1(t)= & {} \underline{a}P\underline{T}=[a_0, a_1]\left[ \begin{array}{ll} \sqrt{2} &{}\quad 0 \\ -\frac{3}{\sqrt{2}} &{}\quad \frac{5}{\sqrt{2}} \\ \end{array} \right] \left[ \begin{array}{l} \sqrt{t} \\ t \sqrt{t} \\ \end{array} \right] =\sqrt{2t}\left( a_0+\frac{a_1}{2}(5t-3)\right) ,\\ y_1(t)= & {} \underline{b}P\underline{T}=[b_0, b_1]\left[ \begin{array}{ll} \sqrt{2} &{}\quad 0 \\ -\frac{3}{\sqrt{2}} &{}\quad \frac{5}{\sqrt{2}} \\ \end{array} \right] \left[ \begin{array}{l} \sqrt{t} \\ t \sqrt{t} \\ \end{array} \right] =\sqrt{2t}\left( b_0+\frac{b_1}{2}(5t-3) \right) , \end{aligned}$$

(42)

as approximate solutions of (41). Substituting (42) into (41) and using the described technique in the Sect. 4, we obtain the following nonlinear algebraic system

$$\begin{aligned} 0= & {} 0.30 x_0+0.49 x_1 + (0.33 x_0-0.32 x_1) e^{0.65 y_0-0.63 y_1}\\&+\,(0.63 x_0-0.30 x_1) e^{1.26 y_0-0.59 y_1}-1.36, \\ 0= & {} -0.29 x_0 + 0.42 x_1 + (-0.32 x_0 + 0.31 x_1)e^{0.65 y_0-0.63 y_1}\\&+\,(0.30 x_0 + 0.14 x_1) e^{1.26 y_0 - 0.59 y_1}+0.03, \\ 0= & {} - 0.5 \sin {(0.65 x_0 - 0.63 x_1)} -0.5 \sin {(1.26 x_0+0.59 x_1)} +\, 0.95 y_0 -0.02 y_1 +0.21, \\ 0= & {} 0.49 \sin {(0.65 x_0 - 0.63 x_1)} -0.24 \sin {(1.26 x_0+0.59 x_1)}-0.20 y_0 +0.45 y_1 - 0.15, \end{aligned}$$

with the following solution

$$\begin{aligned} a_0= & {} 0.7071,\quad a_1=1.2505e-16,\nonumber \\ b_0= & {} 0.4243, \quad b_1=0.2828. \end{aligned}$$

(43)

Replacing (43) into (42) we obtain

$$\begin{aligned} x_1(t)=\sqrt{t}+(4.4210e-16)t\sqrt{t},~~ y_1(t)=(-4.4409e-16)\sqrt{t}+t\sqrt{t}, \end{aligned}$$

with the errors

$$\begin{aligned} \Vert e_1\Vert= & {} \Vert x(t)-x_1(t)\Vert =\left( \int _{I}{(x(t)-x_1(t))^2 \mathrm{d}t} \right) ^{\frac{1}{2}}=\left( \int _{I}{((4.4210e-16)t\sqrt{t})^2 \mathrm{d}t} \right) ^{\frac{1}{2}}\\= & {} 2.1395e-16,\\ \Vert \varepsilon _1\Vert= & {} \Vert y(t)-y_1(t)\Vert =\left( \int _{I}{(y(t)-y_1(t))^2 \mathrm{d}t} \right) ^{\frac{1}{2}}\\= & {} \left( \int _{I}{((4.4409e-16)\sqrt{t})^2 \mathrm{d}t} \right) ^{\frac{1}{2}}=1.4987e-16, \end{aligned}$$

which proves the high accuracy of the approximate solutions (42).

Example 6.2

Consider the following fractional differential algebraic equation

$$\begin{aligned} \left\{ \begin{array}{ll} ^C_0D_t^{\frac{1}{2}}{x(t)}=x(t)-x(t)y(t)+q_1(t),\\ ^C_0D_t^{\frac{1}{2}}{y(t)}=y(t)-x^2(t)+z(t)+q_2(t),\\ 0=z(t)-x^2(t)+q_3(t), \\ \end{array}\right. \end{aligned}$$

(44)

with the initial conditions $x(0)=y(0)=z(0)=0$. The functions $q_1(t), q_2(t) , q_3(t)$ are chosen such that the exact solution of the problem is $x(t)=\sin {(\sqrt{t})}, y(t)=e^{t \sqrt{t}}-1, z(t)=t \tan (\sqrt{t})$.

In this example, we make a comparison between our scheme and the variational iteration method (VIM) proposed in İbis and Bayram (2011) to show the efficiency of our described approach. To this end, we first implement the proposed method and the following VIM’s convergent iterations

$$\begin{aligned} \left\{ \begin{array}{l} \bar{x}_0(t)=\bar{y}_0(t)=\bar{z}_0(t)=0,\\ \bar{z}_{k+1}(t)=(\bar{x}_k(t))^2-q_3(t),\\ \bar{y}_{k+1}(t)=\bar{y}_k(t)-I^\alpha \left( ~^C_0D_t^\alpha (\bar{y}_k(t))-\bar{y}_k(t)+(\bar{x}_k(t))^2-\bar{z}_{k+1}(t)-q_2(t) \right) ,\\ \bar{x}_{k+1}(t)=\bar{x}_k(t)-I^\alpha \left( ~^C_0D_t^\alpha (\bar{x}_k(t))-\bar{x}_k(t)+\bar{x}_k(t)\bar{y}_{k+1}(t)-q_1(t) \right) , \end{array}\right. \end{aligned}$$

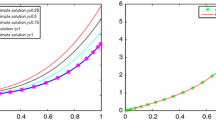
and give the obtained results in Table 1 and Fig.1. The reported $L^2$-norm errors show a significant superiority of our scheme over VIM such that it produces a lower errors with less values of N in compared with the VIM.

Table 1 Comparison of the numerical errors of our method and VIM with different values of N for Example 6.2

Fig. 1

Comparison of the obtained errors between our method (solid lines) and VIM (dashed lines) with different values of N for Example 6.2

Example 6.3

(Ding and Jiang 2014) Consider the following fractional differential algebraic equation

$$\begin{aligned} \left\{ \begin{array}{ll} ^C_0D_t^{\frac{1}{2}}{x(t)}=z(t)-x(t) y(t) +q_1(t),\\ ^C_0D_t^{\frac{1}{2}}{y(t)}=\frac{\Gamma (5)}{\Gamma (\frac{9}{2})} \sqrt{t}x(t)-2 y(t)-x(t) z(t)+q_2(t),\\ 0=t^2 y(t)-x^2(t)-z(t)+q_3(t), \end{array}\right. \end{aligned}$$

with the initial conditions $x(0)=y(0)=0, z(0)=1$. The functions $q_1(t), q_2(t) , q_3(t)$ are chosen such that the exact solution of the problem is $x(t)=t^3,~~ y(t)=2t +t^4,~~z(t)=e^t+t \sin {(t)}$.

Table 2 The numerical errors with different values of N for Example 6.3

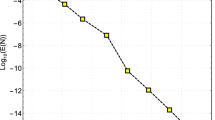
In order to obtain the homogeneous initial conditions, we apply the transformation $w(t)=z(t)-1$ and solve the new equation using the proposed approach. The obtained numerical results are listed in Table 2 and Fig. 2. This example was also solved in Ding and Jiang (2014) by employing the waveform relaxation method and reported the following numerical errors

$$\begin{aligned} \Vert x(t)-x_N(t)\Vert ,~\Vert y(t)-y_N(t)\Vert \simeq 10^{-3},~~\text {and}~~\Vert z(t)-z_N(t)\Vert \simeq 10^{-4}, \end{aligned}$$

(45)

with 16 iterations. Comparing our reported results with those obtained in (45) approves the superiority and reliability of the proposed scheme over the method presented in Ding and Jiang (2014).

Fig. 2

The numerical errors with different values of N for Example 6.3

In the next example, we illustrate a problem when we do not have access to exact solution.

Example 6.4

(İbis and Bayram 2011) Consider the following fractional differential algebraic equation

$$\begin{aligned} \left\{ \begin{array}{ll} ^C_0D_t^{\alpha }{x(t)}=y(t)-x(t)-\sin {t},\\ x(t)+y(t)=e^{-t}+\sin {t}, \end{array}\right. \end{aligned}$$

(46)

with the initial conditions $x(0)=1, y(0)=0$.

Since a generally applicable method to determine the analytical solutions of (46) is not readily available, we have to return to some convergent numerically computed solutions. To this end, we can use the Adomian decomposition method (İbis and Bayram 2011) which represents the exact solutions x(t) and y(t) by the following convergent infinite series

$$\begin{aligned} x(t)=\sum \limits _{k=0}^{\infty }{\tilde{x}_k(t)},\quad y(t)=\sum \limits _{k=0}^{\infty }{\tilde{y}_k(t)}, \end{aligned}$$

(47)

where the iterates $x_k(t)$ and $y_k(t)$ are determined in the following recursive way

$$\begin{aligned} \left\{ \begin{array}{l} \tilde{x}_0(t)=1,~~\tilde{y}_0(t)=0,\\ \\ \tilde{y}_1(t)=-\tilde{x}_0(t)+\tilde{g}_1(t),~~ \tilde{x}_1(t)=~_0I_t^\alpha \left( -\tilde{x}_0(t)+\tilde{y}_0(t)-\tilde{g}_2 \right) ,\\ \\ \tilde{y}_{k+1}(t)=-\tilde{x}_k(t),~~\tilde{x}_{k+1}(t)=~_0I_t^\alpha \left( -\tilde{x}_k(t)+\tilde{y}_k(t) \right) , \end{array}\right. \end{aligned}$$

such that $\tilde{g}_1(t), \tilde{g}_2(t)$ are Taylor series of $e^{-t}+\sin {t}$ and $\sin {t}$, respectively. In view of (47), we may be assured that the following source solutions

$$\begin{aligned} \tilde{x}(t)=\sum \limits _{k=0}^{L}{\tilde{x}_k(t)},\quad \tilde{y}(t)=\sum \limits _{k=0}^{L}{\tilde{y}_k(t)}, \end{aligned}$$

(48)

for sufficiently large values of L, shows a qualitatively correct picture of the exact solutions x(t) and y(t) in evaluating the precision of the proposed generalized Jacobi Galerkin method. Here we have chosen $L=100$.

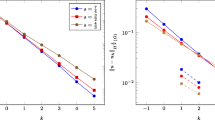
We solve (46) using the method described in Sect. 4 with $N=15, \alpha =0.5$ and compare the obtained results with those obtained by reference solutions (48) in Table 3 and Fig. 3. The reported results approve that our approach produces the approximate solutions which are in a good agreement with source ones.

Table 3 The values of the approximate solutions at some selected grid points with $N=15, L=100$ and $\alpha =0.5$ for Example 6.4

Fig. 3

Plots of the generalized Jacobi Galerkin approximations (dashed lines) and the reference solutions (rectangle markers) of x(t) (left hand side) and y(t) (right hand side) for Example 6.4

Example 6.5

In this example, we consider a practical application of differential algebraic equations in modeling of the following simple RLC circuit with a voltage source V(t), inductance L, a resistor with conductance R and a capacitor with capacitance $C>0$ (Fig. 4):

Fig. 4

A simple RLC circuit for Example 6.5

Table 4 The numerical errors with different values of N and $\alpha =1$ for Example 6.5

To this end, applying Kirchhoff’s voltage and current laws yield

• Conservation of current: $i_E = i_R,~ i_R = i_C,~ i_C = i_L,$

• Conservation of energy: $V_R + V_L + V_C + V_E = 0,$

• Ohm’s Laws: $C V'_C = i_C; ~ L V'_L = i_L; ~ V_R = R i_R.$

After replacing $i_R$ with $i_E$ and $i_C$ with $i_L$, we get the following differential algebraic equation

$$\begin{aligned} \left\{ \begin{array}{cc} ^C_0D_t^{\alpha }{X(t)}=A X(t),\\ B X(t)+ G V_E=0, \end{array}\right. \end{aligned}$$

(49)

where $\alpha =1, X=\big (V_C(t),V_L(t),V_R(t),i_L(t),i_E(t)\big )^T$ and

$$\begin{aligned} A=\left( \begin{array}{ccccc} 0 &{}\quad 0 &{}\quad 0 &{}\quad \frac{1}{C} &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad \frac{1}{L} &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ \end{array} \right) , \quad B= \left( \begin{array}{ccccc} 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad R \\ 1 &{}\quad 1 &{}\quad 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad -1 \\ \end{array} \right) , \quad G=\left( \begin{array}{c} 0 \\ 1 \\ 0 \\ \end{array} \right) . \end{aligned}$$

Clearly, for homogeneous initial conditions, $\alpha =1$ and current $i_L=\sin {t}$, we have the exact solutions $V_C= \frac{1}{C}(1-\cos {t}),~V_L= \frac{1}{L}(1-\cos {t}),~V_R=-R \sin {t}, i_L=\sin {t}$ and $V_E=\Big (\frac{1}{C}+\frac{1}{L}\Big ) (\cos {t}-1)+R \sin {t}$.

Fig. 5

The approximate solutions with different values of $\alpha$ and $N=10$ for Example 6.5

Now we consider (49) with input data $R=4, L=0.4, C=2$ and implement the proposed scheme for various $\alpha$ and report the obtained numerical results in Table 4 and Fig. 5. In Table 4, we have listed the obtained numerical errors with various values of N and $\alpha =1$. In Fig. 5, we plot the approximate solutions for different values of $\alpha$. In overall, the reported results indicate that as $\alpha$ tends to 1, the approximate solutions tend to the exact solution of (49) with $\alpha =1$. This confirms the effectiveness and reliability of the proposed generalized Jacobi Galerkin method in approximating the practical models of fractional differential algebraic equations.

7 Conclusion

In this article, we developed and analyzed the generalized Jacobi Galerkin method for the numerical solution of a class of the nonlinear fractional differential algebraic equation. First, we investigated the existence and uniqueness theorem along with the regularity and well-posedness properties of the exact solution and proved that some derivatives of the exact solution have singularity at the origin. To obtain a numerical solution with good convergence properties we considered the Galerkin solution of the problem by a linear combination of the recently defined generalized Jacobi functions which matched with the singularity of the exact solution. We also estimated the numerical errors obtained from implementation of the presented method. Finally, we confirmed the effectiveness of the numerical scheme by illustrating some numerical examples.