Jacobi spectral Galerkin methods for fractional integro-differential equations

Abstract

We propose general spectral and pseudo-spectral Jacobi–Galerkin methods for fractional order integro-differential equations of Volterra type. The fractional derivative is described in the Caputo sense. We provide rigorous error analysis for spectral and pseudo-spectral Jacobi–Galerkin methods, which show that the errors of the approximate solution decay exponentially in $L^\infty$ norm and weighted $L^2$-norm. The numerical examples are given to illustrate the theoretical results.

1 Introduction

Many phenomena in engineering, physics, chemistry, and other sciences can be described very successfully by models using mathematical tools from fractional calculus, i.e., the theory of derivatives and integrals of fractional order. This allows one to describe physical phenomena more accurately. Moreover, fractional calculus was applied to model the frequency dependent damping behavior of many viscoelastic materials, economics and dynamics of interfaces between nanoparticles and substrates. Recently, several numerical methods to solve fractional differential equations (FDEs) and fractional integro-differential equations (FIDEs) have been proposed.

In this article, we are concerned with the numerical study of the following fractional integro-differential equation:

$$\begin{aligned} D^\gamma y(t)&= y(t) +\int ^{t}_0{K}(t,{\tau })y({\tau })d{\tau }+f(t), \quad 0<\gamma \le 1,\quad {t}\in [0,T],\nonumber \\ y(0)&= y_0, \end{aligned}$$

(1.1)

where source function $f$ and the kernel function ${{K}}$ are given, the function $y(t)$ is the unknown function and $y(0)\in R$. Here, the given functions $f$, ${{ K}}$ are assumed to be sufficiently smooth on their respective domains $[0,T]$ and $0\le \tau \le t\le T$, i.e. $f(t)\in C^m([0,T])$, ${{ K}}(t,{\tau })\in C^m(\Omega )$, $m \ge 1$, $\Omega =:\{(t,\tau ):0\le \tau \le t\le T\}$. Such kind of equations arises in the mathematical modeling of various physical phenomena, such as heat conduction in materials with memory [1]. In recent years, the analytic results on existence and uniqueness of solutions to fractional integro-differential equations have been investigated by many authors [12].

In Eq. (1.1), $D^\gamma$ denotes the Caputo fractional derivative of order $\gamma$. When $\gamma =1$, (1.1) is the classical integro-differential equation:

$$\begin{aligned}&y'(t)=y(t) +\int ^{t}_0{K}(t,{\tau })y({\tau })d{\tau }+f(t) , \quad {t}\in [0,T],\nonumber \\&y(0)=y_0. \end{aligned}$$

(1.2)

Let $\Gamma (\cdot )$ denote the Gamma function. For any positive integer $n$ and $n-1<\gamma <n$, the Caputo derivative is defined as follows:

$$\begin{aligned} D^\gamma f(t)=\frac{1}{\Gamma (n-\gamma )}\int ^t_a\frac{f^{(n)}(\tau )}{(t-\tau )^{(\gamma -n+1)}}d\tau ,\quad t\in [a,b], \end{aligned}$$

(1.3)

Here $I^\gamma$ denotes the Riemann–Liouville fractional integral of order $\gamma$ and is defined as

$$\begin{aligned} I^\gamma f(t)=\frac{1}{\Gamma (\gamma )}\int ^t_a(t-\tau )^{\gamma -1}f(\tau )d\tau . \end{aligned}$$

(1.4)

We note that

$$\begin{aligned} I^\gamma (D^\gamma f(t))=f(t)-\sum ^{n-1}_{k=0}f^{(k)}(a)\frac{t^k}{k!}. \end{aligned}$$

(1.5)

In order to simplify the notations and without lose of generality, we consider the case $y(0)=0$ in the scheme construction and its numerical analysis. From (1.5), fractional integro-differential equation (1.1) can be described as

$$\begin{aligned} D^\gamma y(t)&= y(t) +\int ^{t}_0{{K}}(t,{\tau })y({\tau })d{\tau }+f(t) , \quad 0<\gamma \le 1,\quad {t}\in [0,T],\nonumber \\ y(t)&= z\frac{1}{\Gamma (\gamma )}\int ^t_{0} (t-\tau )^{\gamma -1} D^\gamma y(\tau )d\tau . \end{aligned}$$

(1.6)

Spectral methods have been proposed to solve fractional differential equations, such as the Legendre collocation method [9], tau and pseudo-spectral methods[7], shifted Legendre spectral methods [3], shifted Chebyshev operational matrix [2]. However, very few theoretical results were provided to justify the high accuracy numerically obtained. Chen and Tang [5] developed a novel spectral spectral Jacobi-collocation method to solve second kind Volterra integral equations with a weakly singular kernel and provided a rigorous error analysis which theoretically justifies the spectral rate of convergence, Recently, in [16, 17], the authors provided general spectral and pseudo-spectral Jacobi–Petrov–Galerkin approaches for the second kind Volterra integro-differential equations. Inspired by the work of [16], we extend the approach to fractional order integro-differential equations and provide a rigorous convergence analysis for the spectral and pseudo-spectral Jacobi–Galerkin methods, which indicates that the proposed methods converge exponentially provided that the data in the given fractional integro-differential equation is smooth.

This paper is organized as follows. In Sect. 2, we demonstrate the implementation of the spectral and pseudo-spectral Galerkin approaches for fractional order integro-differential equation. Some lemmas useful for establishing the convergence result will be provided in Sect. 3. The convergence analysis for both spectral and pseudo-spectral Jacobi–Galerkin methods will be given in Sect. 4. Numerical results will be carried out in Sect. 5, which will be used to verify the theoretical results.

2 Spectral and pseudo-spectral Galerkin methods

For the sake of applying the theory of orthogonal polynomials, we use the change of variable

$$\begin{aligned} t=\frac{1}{2}T(1+x),\quad x=\frac{2t}{T}-1,\quad \tau =\frac{1}{2}T(1+s),\quad s=\frac{2\tau }{T}-1, \end{aligned}$$

and let

$$\begin{aligned} u(x)&= y\left( \frac{1}{2}T(1+x)\right) ,\quad D^\gamma u(x)=D^\gamma y\left( \frac{1}{2}T(1+x)\right) ,\\ g(x)&= f\left( \frac{1}{2}T(1+x)\right) ,\\ k(x,s)&= \frac{T}{2}{{K}}\left( \frac{1}{2}T(1+x),\frac{1}{2}T(1+s)\right) . \end{aligned}$$

The fractional integro-differential equation in one dimension (1.6) is of the form

$$\begin{aligned} D^\gamma u(x)&= u(x)+\int ^x_{-1}k(x,s)u(s)ds+g(x), \quad 0<\gamma \le 1,\quad x\in \Lambda :=[-1,1],\nonumber \\ u(x)&= \frac{1}{\Gamma (\gamma )}\left( \frac{T}{2}\right) ^\gamma \int ^x_{-1} (x-s)^{-\mu } D^\gamma u(s)ds, \end{aligned}$$

(2.1)

with $-\mu =\gamma -1\in (-1,0)$.

To propose the Jacobi-spectral Galerkin scheme and investigate the global convergence properties for the problem (2.1), we first define a linear integral operator $G: C(\Lambda )\rightarrow C(\Lambda )$ by

$$\begin{aligned} (G\phi )(x)&:= \int _{-1}^xk(x,s)\phi (s)ds,\\ (G'\phi )(x)&:= \frac{1}{\Gamma (\gamma )}\left( \frac{T}{2}\right) ^\gamma \int ^x_{-1} (x-s)^{-\mu } \phi (s)ds. \end{aligned}$$

Then, the problem (2.1) reads: find $u=u(x)$ and $D^\gamma u=D^\gamma u(x)$ such that

$$\begin{aligned} D^\gamma u(x)&= u(x)+(Gu)(x)+g(x),\quad x\in \Lambda ,\nonumber \\ u(x)&= (G'D^\gamma u)(x), \end{aligned}$$

(2.2)

and its weak form is to find $u\in L^2(\Lambda )$ such that

$$\begin{aligned} (D^\gamma u,v)&= (u,v)+(Gu,v)+(g,v),\quad \forall \quad v \in L^2(\Lambda ),\nonumber \\ (u,v)&= (G'D^\gamma u,v), \end{aligned}$$

(2.3)

where $(\cdot ,\cdot )$ denotes the usual inner product in the $L^2$-space.

Firstly, let us demonstrate the numerical implementation of the spectral Jacobi–Galerkin approach . Denote by ${\mathbb {N}}$ the set of all nonnegative integers. For any $N\in \mathbb {N}$, ${{P}}_N$ denotes the set of all algebraic polynomials of degree at most $N$ in $\Lambda$, $\phi _j (x)$ is the $j$-th Jacobi polynomial corresponding to the weight function $\omega ^{\alpha ,\beta }(x)=(1-x)^\alpha (1+x)^\beta$. As a result,

$$\begin{aligned} P_N=\text {span}\{\phi _0(x),\phi _1(x),\ldots ,\phi _N(x)\}. \end{aligned}$$

Our spectral Jacobi–Galerkin approximation of (2.2) is now defined as: Find $u_N\in {{P}}_N$ and $u^\gamma _N\in {{P}}_N$ such that

$$\begin{aligned} (u^{\gamma }_N,v_N)_{\omega ^{\alpha ,\beta }}&= (u_N,v_N)_{\omega ^{\alpha ,\beta }}+ (Gu_N,v_N)_{\omega ^{\alpha ,\beta }}+(g,v_N)_{\omega ^{\alpha ,\beta }},\quad \forall v_N\in {{P}}_N,\nonumber \\ (u_N,v_N)_{\omega ^{\alpha ,\beta }}&= (G'u^\gamma _N,v_N)_{\omega ^{\alpha ,\beta }}, \end{aligned}$$

(2.4)

where

$$\begin{aligned} (u,v)_{\omega ^{\alpha ,\beta }}= \int ^1_{-1} u(x)v(x)\omega ^{\alpha ,\beta }(x)dx \end{aligned}$$

is the continuous inner product. Set $u_N(x) = \sum ^N_{ j=0} \xi _j\phi _j (x)$ and $u^\gamma _N(x) = \sum ^N_{ j=0} \xi ^\gamma _j\phi _j (x)$. Substituting it into (2.4) and taking $v_N = \phi _i(x)$, we obtain

$$\begin{aligned}&\sum ^N_{ j=0}\xi ^\gamma _j(\phi _i,\phi _j)_{\omega ^{\alpha ,\beta }}= \sum ^N_{ j=0}\xi _j(\phi _i,\phi _j)_{\omega ^{\alpha ,\beta }}+\sum ^N_{ j=0}\xi _j(\phi _i,G\phi _j)_{\omega ^{\alpha ,\beta }} + (\phi _i,g)_{\omega ^{\alpha ,\beta }},\nonumber \\&\sum ^N_{ j=0}\xi _j(\phi _i,\phi _j)_{\omega ^{\alpha ,\beta }}= \sum ^N_{ j=0}\xi ^\gamma _j(\phi _i,G'\phi _j)_{\omega ^{\alpha ,\beta }}, \end{aligned}$$

(2.5)

which leads to quations of the matrix form

$$\begin{aligned}&A\xi ^\gamma =(A+B)\xi +G^N,\nonumber \\&A\xi =C\xi ^\gamma , \end{aligned}$$

(2.6)

where

$$\begin{aligned}&\xi =[\xi _0,\xi _1,\ldots ,\xi _N]^T,\quad \xi ^\gamma =[\xi ^\gamma _0,\xi ^\gamma _1,\ldots ,\xi ^\gamma _N]^T, \quad A_{i,j}=(\phi _i,\phi _j)_{\omega ^{\alpha ,\beta }},\\&B_{i,j}=(\phi _i,G\phi _j)_{\omega ^{\alpha ,\beta }},\quad C_{i,j}=(\phi _i,G'\phi _j)_{\omega ^{\alpha ,\beta }},\quad G^N_i=(\phi _i,g)_{\omega ^{\alpha ,\beta }}. \end{aligned}$$

Now we turn to describe the pseudo-spectral Jacobi–Galerkin method. Set

$$\begin{aligned} s(x,\theta )=\frac{1+x}{2}\theta +\frac{x-1}{2},\quad -1\le \theta \le 1, \end{aligned}$$

it is clear that

$$\begin{aligned} Gu(x)=&\int ^x_{-1}k(x,s)u(s)ds= \int ^1_{-1}\tilde{k}(x,s(x,\theta ))u(s(x,\theta ))d\theta ,\nonumber \\ G'D^\gamma u(x)=&\frac{1}{\Gamma (\gamma )}\left( \frac{T(1+x)}{4}\right) ^\gamma \int ^1_{-1}(1-\theta )^{-\mu }D^\gamma u(s(x,\theta ))d\theta , \end{aligned}$$

(2.7)

with $\tilde{k}(x,s(x,\theta ))=\frac{1+x}{2}{k}(x,s(x,\theta ))$. Using $(N +1)$-point Gauss quadrature formula to approximation (2.7) yields

$$\begin{aligned} Gu(x)\approx G_N u(x)&:= \sum ^N_{k=0}\tilde{k}(x,s(x,\theta _k)) u(s(x,\theta _k))\omega _k^{0,0},\end{aligned}$$

(2.8)

$$\begin{aligned} G'D^\gamma u(x)\approx G'_N D^\gamma u(x)&:= \frac{1}{\Gamma (\gamma )}\left( \frac{T(1+x)}{4}\right) ^\gamma \sum ^N_{k=0}D^\gamma u(s(x,\theta '_k))\omega ^{-\mu ,0}_k,\qquad \quad \end{aligned}$$

(2.9)

where $\{\theta _k\}^N_{ k=0}$ and $\{{\theta }'_k\}^N_{k=0}$ are the $(N + 1)$-degree Jacobi–Gauss points corresponding to the weights $\{\omega _k^{0,0}\}^N_{ k=0}$ and $\{\omega ^{-\mu ,0}_k\}^N_{k=0}$, respectively.

On the other hand, instead of the continuous inner product, the discrete inner product will be implemented in (2.4) and (2.5), i.e.

$$\begin{aligned} (u,v)_{\omega ^{\alpha ,\beta }}\approx (u,v)_{\omega ^{\alpha ,\beta },N} =\sum ^N_{k=0}u(x_k)v(x_k)\omega _k^{\alpha ,\beta }(x_k), \end{aligned}$$

(2.10)

where $\{x_k\}^N _{k=0}$ and $\{\omega _k^{\alpha ,\beta }\}^N _{k=0}$are the $(N + 1)$-degree Jacobi–Gauss points and their corresponding Jacobi weights, respectively. As a result,

$$\begin{aligned} (u,v)_{\omega ^{\alpha ,\beta }}=(u,v)_{\omega ^{\alpha ,\beta },N},\quad \text {if }uv\in P_{2N+1}. \end{aligned}$$

Substitute (2.8), (2.9), and (2.10) into (2.4), the pseudo-spectral Jacobi–Galerkin method is to find

$$\begin{aligned} \bar{u}_N(x) = \sum ^N_{ j=0} \bar{\xi }_j\phi _j (x),\quad \bar{u}^\gamma _N(x) = \sum ^N_{ j=0} \bar{\xi }^\gamma _j\phi _j (x) \end{aligned}$$

such that

$$\begin{aligned}&(\bar{u}^\gamma _N,v_N)_{\omega ^{\alpha ,\beta },N}= (\bar{u}_N,v_N)_{\omega ^{\alpha ,\beta },N}\!+\!(G_N\bar{u}_N,v_N)_{\omega ^{\alpha ,\beta },N}\!+\!(g,v_N)_{\omega ^{\alpha ,\beta },N},\quad \forall v_N\!\in \! {{P}}_N,\nonumber \\&(\bar{u}_N,v_N)_{\omega ^{\alpha ,\beta },N}=(G'_N\bar{u}^\gamma _N,v_N)_{\omega ^{\alpha ,\beta },N}, \end{aligned}$$

(2.11)

where $\{\bar{\xi }_j\}^N_{j=0}$ are determined by

$$\begin{aligned}&\sum ^N_{ j=0}\bar{\xi }^\gamma _j(\phi _i,\phi _j)_{\omega ^{\alpha ,\beta },N}= \sum ^N_{ j=0}\bar{\xi }_j(\phi _i,\phi _j)_{\omega ^{\alpha ,\beta },N}\nonumber \\&\quad +\sum ^N_{ j=0}\bar{\xi }_j(\phi _i,G_N\phi _j)_{\omega ^{\alpha ,\beta },N} + (\phi _i,g)_{\omega ^{\alpha ,\beta },N},\nonumber \\&\sum ^N_{ j=0}\bar{\xi }_j(\phi _i,\phi _j)_{\omega ^{\alpha ,\beta },N}= \sum ^N_{ j=0}\bar{\xi }^\gamma _j(\phi _i,G'_N\phi _j)_{\omega ^{\alpha ,\beta },N}, \end{aligned}$$

(2.12)

which can be written in the following matrix form

$$\begin{aligned}&\bar{A}\xi ^\gamma =(\bar{A}+\bar{B})\xi +\bar{G}^N,\nonumber \\&\bar{A}\xi =\bar{C}\xi ^\gamma , \end{aligned}$$

(2.13)

with

$$\begin{aligned}&\bar{\xi }=[\bar{\xi }_0,\bar{\xi }_1,\ldots ,\bar{\xi }_N]^T, \quad \bar{\xi }^\gamma =[\bar{\xi }^\gamma _0,\bar{\xi }^\gamma _1,\ldots ,\bar{\xi }^\gamma _N]^T,\quad \bar{A}_{i,j}=(\phi _i,\phi _j)_{\omega ^{\alpha ,\beta },N},\\&\bar{B}_{i,j}=(\phi _i,G\phi _j)_{\omega ^{\alpha ,\beta },N},\quad \bar{C}_{i,j}=(\phi _i,G'\phi _j)_{\omega ^{\alpha ,\beta },N},\quad \bar{G}^N_i=(\phi _i,g)_{\omega ^{\alpha ,\beta },N}. \end{aligned}$$

3 Some useful lemmas

In this section, we will provide some elementary lemmas, which are important for the derivation of the main results in the subsequent section.

First we define the Jacobi orthogonal projection operator $\Pi _N:L^2_{\omega }\rightarrow P_N$ which satisfies

$$\begin{aligned}&(\Pi _N u,v_N)_{\omega ^{\alpha ,\beta }} =(u,v_N)_{\omega ^{\alpha ,\beta }},\quad \forall u\in L^2_{\omega ^{\alpha ,\beta }}, v_N\in P_N,\nonumber \\&L^2_{\omega ^{\alpha ,\beta }}(\Lambda )=\{u,u \text { is measurable and } \Vert u\Vert _{\omega ^{\alpha ,\beta }}<\infty \},\nonumber \\&\Vert u\Vert _{\omega ^{\alpha ,\beta }}=\left( \int _{-1}^{1} u^2(x)\omega ^{\alpha ,\beta }dx\right) ^{\frac{1}{2}}. \end{aligned}$$

(3.1)

Furthermore, we define

$$\begin{aligned} H^m_{\omega ^{\alpha ,\beta }}(\Lambda )=\{u:D^ku\in L^2_{\omega ^{\alpha ,\beta }}(\Lambda ),0\le k\le m\}, \end{aligned}$$

equipped with the norm

$$\begin{aligned} \Vert u\Vert _{H^m_{\omega ^{\alpha ,\beta }}(\Lambda )} =\left( \sum ^m_{k=0}\left\| \frac{d^ku}{dx^k} \right\| ^2_{\omega ^{\alpha ,\beta }}\right) ^{\frac{1}{2}}. \end{aligned}$$

Lemma 3.1

(see [16]) Suppose that $u \in H^m_{\omega ^{\alpha ,\beta }}(\Lambda )$ and $m\le 1$, then

$$\begin{aligned}&\Vert u-\Pi _N u\Vert _{\omega ^{\alpha ,\beta }}\le CN^{-m}|u|_{H^{m;N}_{\omega ^{\alpha ,\beta }}(\Lambda )},\end{aligned}$$

(3.2)

$$\begin{aligned}&\Vert u-\Pi _N u\Vert _{\infty }\le CN^{\frac{3}{4}-m}|u|_{H^{m;N}_{\omega ^{\alpha ,\beta }}(\Lambda )}, \end{aligned}$$

(3.3)

where $|u|_{H^{m;N}_{\omega ^{\alpha ,\beta }}(\Lambda )}$ denotes the seminorm defined by

$$\begin{aligned} |u|_{H^{m;N}_{\omega ^{\alpha ,\beta }}(\Lambda )}=\left( \sum _{k=\min (m,N+1)}^m \left\| \frac{d^ku}{dx^k} \right\| ^2_{\omega ^{\alpha ,\beta }}\right) ^{1/2}. \end{aligned}$$

Lemma 3.2

(see [8]) Suppose that $u \in L^2_{\omega ^{\alpha ,\beta }}(\Lambda )$, then

$$\begin{aligned} \Vert \Pi _N u\Vert _{\omega ^{\alpha ,\beta }}\le C\Vert u\Vert _{\omega ^{\alpha ,\beta }},\quad \Vert \Pi _N u\Vert _\infty \le C\Vert u\Vert _\infty . \end{aligned}$$

Lemma 3.3

(see [4]) Assume that an $(N + 1)$-point Gauss quadrature formula relative to the Jacobi weight is used to integrate the product $u\varphi$, where $u \in H^m(I)$ for some $m\ge 1$ and $\varphi \in {\mathcal {P}}_N$. Then there exists a constant $C$ independent of $N$ such that

$$\begin{aligned} \left| \int ^1_{-1}u(x)\varphi (x)\omega ^{\alpha ,\beta }(x)dx-(u,\varphi )_{\omega ^{\alpha ,\beta },N}\right| \le CN^{-m}|u|_{{H}^{m,N}_{\omega ^{\alpha ,\beta }}(\Lambda )}\Vert \varphi \Vert _{{\omega ^{\alpha ,\beta }}}. \end{aligned}$$

(3.4)

Lemma 3.4

(see [4]) Assume that $u \in H^m_{\omega ^{\alpha ,\beta }}(\Lambda )$, $m\ge 1$, $I^{\alpha ,\beta }_Nu$ denotes the interpolation operator of $u$ based on $(N + 1)$-degree Jacobi–Gauss points corresponding to the weight function $\omega ^{\alpha ,\beta }(x)$ with $-1<\alpha ,\beta <1$, then

$$\begin{aligned}&\Vert u-I^{\alpha ,\beta }_Nu\Vert _{{\omega ^{\alpha ,\beta }}}\le CN^{-m}|u|_{{H}^{m,N}_{\omega ^{\alpha ,\beta }}(\Lambda )}, \end{aligned}$$

(3.5a)

$$\begin{aligned}&\Vert u-I^{\alpha ,\beta }_Nu\Vert _{\infty }\le {\left\{ \begin{array}{ll} CN^{\frac{1}{2}-m}\log N|u|_{{H}^{m,N}_{\omega ^{c}}(\Lambda )},\quad &{}-1\le \alpha ,\beta < -\frac{1}{2},\\ CN^{\nu +1-m}|u|_{{H}^{m,N}_{\omega ^{c}}(\Lambda )},\quad &{}\text {otherwise}, \nu =\max (\alpha ,\beta ), \end{array}\right. } \end{aligned}$$

(3.5b)

where $\omega ^c=\omega ^{-\frac{1}{2},-\frac{1}{2}}$ denotes the Chebyshev weight function.

Lemma 3.5

(see [11]) For every bounded function $u$, there exists a constant $C$, independent of $u$ such that

$$\begin{aligned} \Vert I_N^{\alpha ,\beta }u(x_j)\Vert _{\omega ^{\alpha ,\beta }}\le C\Vert u\Vert _\infty , \end{aligned}$$

where $I_N^{\alpha ,\beta }u(x)=\sum ^N_{j=0}u(x_j)F_j(x)$ is the Lagrange interpolation basis function associated with $(N + 1)$-degree Jabobi-Gauss points corresponding to the weight function $\omega ^{\alpha ,\beta }(x)$.

Lemma 3.6

(see [11]) Assume that $\{F_j(x)\}^N_{j=0}$ are the $j-th$ degree Lagrange basis polynomials associated with the Gauss points of the Jacobi polynomials. Then,

$$\begin{aligned} \Vert I^{\alpha ,\beta }_N\Vert _{\infty }\le \max _{x\in [-1,1]}\sum ^N_{j=0}\mid F_j(x)\mid = {\left\{ \begin{array}{ll} \mathcal {O}(\log N),&{}\quad -1<\alpha ,\beta \le -\frac{1}{2},\\ \mathcal {O}(N^{\nu +\frac{1}{2}}),&{}\quad \nu =\max (\alpha ,\beta ),\text { otherwise}. \end{array}\right. }\nonumber \\ \end{aligned}$$

(3.6)

Lemma 3.7

(see [14]) For a nonnegative integer $r$ and $\kappa \in (0, 1)$, there exists a constant $C_{r,\kappa } > 0$ such that for any function $v\in C^{r,\kappa }([-1, 1])$, there exists a polynomial function $\mathcal {T}_Nv \in \mathcal {P}_N$ such that

$$\begin{aligned} \Vert v-\mathcal {T}_Nv\Vert _{\infty }\le C_{r,\kappa }N^{-(r+\kappa )}\Vert v\Vert _{r,\kappa }, \end{aligned}$$

(3.7)

where $\Vert \cdot \Vert _{r,\kappa }$ is the standard norm in $C^{r,\kappa }([-1, 1])$, $\mathcal {T}_N$ is a linear operator from $C^{r,\kappa }([-1, 1])$ into $\mathcal {P}_N$, as stated in [14, 15].

Lemma 3.8

(see [6]) Let $\kappa \in (0, 1)$ and let $\mathcal {M}$ be defined by

$$\begin{aligned} (\mathcal {M}v)(x)=\int ^x_{-1}(x-\tau )^{-\mu }K(x,\tau )v(\tau )d\tau . \end{aligned}$$

Then, for any function $v \in C([-1, 1])$, there exists a positive constant $C$ such that

$$\begin{aligned} \frac{|\mathcal {M}v(x')-\mathcal {M}v(x'')|}{|x'-x''|}\le C\max _{x\in [-1,1]}|v(x)|, \end{aligned}$$

under the assumption that $0 < \kappa < 1 -\mu$, for any $x', x'' \in [-1, 1]$ and $x'\ne x''$. This implies that

$$\begin{aligned} \parallel \mathcal {M}v\parallel _{0,\kappa }\le C\max _{x\in [-1,1]}|v(x)|,\quad 0<\kappa <1-\mu . \end{aligned}$$

Here and below, $C$ denotes a positive constant which is independent of $N$, and whose particular meaning will become clear by the context in which it arises.

4 Convergence analysis for spectral and pseudo-spectral Jacobi–Galerkin method

According to (2.4) and the definition of the projection operator $\Pi _N$, the spectral Legendre-Galerkin solution $u_N$ and $u^\gamma _N$ satisfies

$$\begin{aligned}&u^\gamma _N=u_N+\Pi _NG u_N+\Pi _Ng,\nonumber \\&u_N=\Pi _NG' u^\gamma _N \end{aligned}$$

(4.1)

Theorem 4.1

Suppose that $u_N$ is the spectral Jacobi–Galerkin solution determined by (2.4), if the solution $u$ of (2.1) satisfies $u\in {H}^{m,N}_{\omega ^{\alpha ,\beta }}(\Lambda )$, then we have the following error estimates

$$\begin{aligned}&\Vert u-u_N\Vert _{\infty }\le CN^{\frac{3}{4}-m}V_1,\nonumber \\&\Vert D^\gamma u-u^\gamma _N\Vert _{\infty }\le CN^{\frac{3}{4}-m}V_1,\nonumber \\&\Vert u-u_N\Vert _{\omega ^{\alpha ,\beta }}\le CN^{-m}\left( CN^{\frac{3}{4}-\kappa }+1\right) V_1,\quad \kappa \in (0,\gamma ),\nonumber \\&\Vert D^\gamma u-u^\gamma _N\Vert _{\omega ^{\alpha ,\beta }}\le CN^{-m}\left( CN^{\frac{3}{4}-\kappa }+1\right) V_1,\quad \kappa \in (0,\gamma ) , \end{aligned}$$

(4.2)

where $V_1=|u|_{{H}^{m,N}_{\omega ^{\alpha ,\beta }}(\Lambda )}+|D^\gamma u|_{{H}^{m,N}_{\omega ^{\alpha ,\beta }}(\Lambda )}$.

Proof

Subtracting (4.1) from (2.2), yields

$$\begin{aligned}&D^\gamma u-u^\gamma _N=u-u_N+Gu-\Pi _NG u_N+g-\Pi _Ng,\nonumber \\&u-u_N=G'D^\gamma u-\Pi _NG'u^\gamma _N. \end{aligned}$$

(4.3)

Set $e=u-u_N$, $e^\gamma =D^\gamma u-u^\gamma _N$. Direct computation shows that

$$\begin{aligned}&Gu-\Pi _NG u_N\nonumber \\&\quad =Gu-\Pi _NG u+\Pi _NG(u-u_N)\nonumber \\&\quad =Gu-\Pi _NG u+G(u-u_N)-[G(u-u_N)-\Pi _NG(u-u_N)]\nonumber \\&\quad =(D^\gamma u-u-g)-\Pi _N(D^\gamma u-u-g)+G(u-u_N)\nonumber \\&\qquad -[G(u-u_N)-\Pi _NG(u-u_N)]\nonumber \\&\quad =(D^\gamma u-u-g)-\Pi _N(D^\gamma u-u-g)+Ge-[Ge-\Pi _NGe]. \end{aligned}$$

(4.4)

Similarly,

$$\begin{aligned} G'D^\gamma u-\Pi _NG'u^\gamma _N=u-\Pi _Nu+G'e^\gamma -[G'e^\gamma -\Pi _NG'e^\gamma ]. \end{aligned}$$

(4.5)

The insertion of (4.4) and (4.5) into (4.3) yields

$$\begin{aligned} e^\gamma (x)&= e(x)+\int ^x_{-1}k(x,s)e(s)ds+D^\gamma u-\Pi _ND^\gamma u+ u-\Pi _Nu+[\Pi _NGe-Ge]\nonumber \\&= e(x)+\int ^x_{-1}k(x,s)e(s)ds+I_1+ I_2+I_3,\nonumber \\ e(x)&= \frac{1}{\Gamma (\gamma )}\left( \frac{T(1+x)}{4}\right) ^\gamma \int ^x_{-1} (x-s)^{\gamma -1} e^\gamma (s)ds+I_2+I_4, \end{aligned}$$

(4.6)

where

$$\begin{aligned} I_1\!=\!D^\gamma u-\Pi _ND^\gamma u,\quad I_2\!=\!u\!-\!\Pi _Nu,\quad I_3\!=\! \Pi _NGe\!-\!Ge,\quad I_4\!=\!\Pi _NG'e^\gamma \!-\!G'e^\gamma . \end{aligned}$$

Using the Dirichlet’s formula which states that

$$\begin{aligned} \int ^x_{-1}\int ^\tau _{-1}\Phi (\tau ,s)dsd\tau =\int ^x_{-1}\int ^x_s\Phi (\tau ,s)d\tau ds, \end{aligned}$$

(4.7)

provided the integral exists, we obtain

$$\begin{aligned} e^\gamma (x)&=e(x)+\int ^{x}_{-1}\left( \int ^{x}_{\tau }\frac{1}{\Gamma (\gamma )}{k}(x,s)ds\right) (x-\tau )^{-\mu }e^\gamma (\tau )d\tau \nonumber \\&\quad \ +\,\int ^{x}_{-1}{k}(x,s)\left( I_2(s)+I_4(s)\right) ds+I_1(x)+I_2(x)+I_3(x)\nonumber \\&\le |e(x)|+C\int ^{x}_{-1}(x-\tau )^{-\mu }|e^\gamma |(\tau )d\tau +|I_1(x)|+|I_2(x)|\nonumber \\&\quad \ +C|I_3(x)| +C|I_4(x)|. \end{aligned}$$

(4.8)

It follows from the Gronwall inequality that

$$\begin{aligned} \parallel e^\gamma (x) \parallel _{\infty }\le C\left( \parallel e(x)\parallel _{\infty } +\sum ^4_{i=1}\parallel I_i\parallel _{\infty }\right) ,\\ \parallel e(x) \parallel _{\infty }\le C\left( \parallel e^\gamma (x)\parallel _{\infty }+\sum ^4_{i=1}\parallel I_i\parallel _{\infty }\right) , \end{aligned}$$

then we have

$$\begin{aligned} \parallel e^\gamma (x) \parallel _{\infty }\le C\sum ^4_{i=1}\parallel I_i\parallel _{\infty },\nonumber \\ \parallel e(x) \parallel _{\infty }\le C\sum ^4_{i=1}\parallel I_i\parallel _{\infty }. \end{aligned}$$

(4.9)

By Lemma 3.1,

$$\begin{aligned} \Vert I_1\Vert _{\infty }&\le CN^{\frac{3}{4}-m}|D^\gamma u|_{H^{m;N}_{\omega ^{\alpha ,\beta }}(\Lambda )},\nonumber \\ \Vert I_2\Vert _{\infty }&\le CN^{\frac{3}{4}-m}| u|_{H^{m;N}_{\omega ^{\alpha ,\beta }}(\Lambda )},\end{aligned}$$

(4.10)

$$\begin{aligned} \Vert I_3\Vert _{\infty }&\le CN^{-\frac{1}{4}}\left| \int ^x_{-1}K(x,s)e(s)ds\right| _{H^{1;N}_{\omega ^{\alpha ,\beta }}(\Lambda )} \le CN^{-\frac{1}{4}} \left\| e\right\| _{\infty }. \end{aligned}$$

(4.11)

In the virtue of Lemmas 3.2, 3.7 and 3.8,

$$\begin{aligned} \parallel I_4\parallel _{\infty }=&\,\parallel (\Pi _N-I)\mathcal {M} e^\gamma \parallel _{ \infty }\nonumber \\ =&\,\parallel (\Pi _N-I)(\mathcal {M} e^\gamma -\mathcal {T}_N\mathcal {M}e^\gamma )\parallel _{ \infty } \nonumber \\ \le&\, \parallel \Pi _N(\mathcal {M} e^\gamma -\mathcal {T}_N\mathcal {M}e^\gamma )\parallel _{ \infty }+\parallel \mathcal {M} e^\gamma -\mathcal {T}_N\mathcal {M}e^\gamma \parallel _{ \infty }\nonumber \\ \le&\,C\parallel \mathcal {M} e^\gamma -\mathcal {T}_N\mathcal {M}e^\gamma \parallel _{ \infty }\nonumber \\ \le&\, CN^{-\kappa }\parallel \mathcal {M} e^\gamma \parallel _{0,\kappa }\quad \kappa \in (0,1-\mu )=(0,\gamma )\nonumber \\ \le&\, CN^{-\kappa }\parallel e^\gamma \parallel _{ \infty }. \end{aligned}$$

(4.12)

Combining (4.9), (4.10), (4.11), and (4.12), when $N$ is large enough, we obtain

$$\begin{aligned}&\Vert u-u_N\Vert _{\infty }\le CN^{\frac{3}{4}-m}\left( |u|_{H^{m;N}_{\omega ^{\alpha ,\beta }}(\Lambda )}+|D^\gamma u|_{H^{m;N}_{\omega ^{\alpha ,\beta }}(\Lambda )}\right) ,\\&\Vert D^\gamma u-u^\gamma _N\Vert _{\infty }\le CN^{\frac{3}{4}-m}\left( |u|_{H^{m;N}_{\omega ^{\alpha ,\beta }}(\Lambda )}+|D^\gamma u|_{H^{m;N}_{\omega ^{\alpha ,\beta }}(\Lambda )}\right) . \end{aligned}$$

Now we investigate the $\Vert \cdot \Vert _{\omega ^{\alpha ,\beta }}$-error estimates. It follows from (4.8) and Gronwall inequality that

$$\begin{aligned}&\parallel e^\gamma (x) \parallel _{\omega ^{\alpha ,\beta }}\le C\sum ^4_{i=1}\parallel I_i\parallel _{\omega ^{\alpha ,\beta }},\nonumber \\&\parallel e(x) \parallel _{\omega ^{\alpha ,\beta }}\le C\sum ^4_{i=1}\parallel I_i\parallel _{\omega ^{\alpha ,\beta }}. \end{aligned}$$

(4.13)

Due to Lemma 3.1, we have

$$\begin{aligned} \Vert I_1\Vert _{\omega ^{\alpha ,\beta }}&\le CN^{-m}|u|_{{H}^{m,N}_{\omega ^{\alpha ,\beta }}(\Lambda )},\nonumber \\ \Vert I_2\Vert _{\omega ^{\alpha ,\beta }}&\le CN^{-m}|D^\gamma u|_{{H}^{m,N}_{\omega ^{\alpha ,\beta }}(\Lambda )},\end{aligned}$$

(4.14)

$$\begin{aligned} \Vert I_3\Vert _{\omega ^{\alpha ,\beta }}&\le CN^{-1}\left| \int ^x_{-1}K(x,s)e(x)\right| _{H^{1;N}_{\omega ^{\alpha ,\beta }}(\Lambda )} \le CN^{-1} \left\| e\right\| _{\infty }. \end{aligned}$$

(4.15)

It follows from Lemmas 3.2, 3.7 and 3.8 that

$$\begin{aligned} \parallel I_4\parallel _{ \omega ^{\alpha ,\beta }}&= \parallel (\Pi _N-I)\mathcal {M} e^\gamma \parallel _{ \omega } =\parallel (\Pi _N-I)(\mathcal {M} e^\gamma -\mathcal {T}_N\mathcal {M}e^\gamma )\parallel _{ \omega } \nonumber \\&\le \parallel \Pi _N(\mathcal {M} e^\gamma -\mathcal {T}_N\mathcal {M}e^\gamma )\parallel _{ \omega }+\parallel \mathcal {M} e^\gamma -\mathcal {T}_N\mathcal {M}e^\gamma \parallel _{ \omega }\nonumber \\&\le C\parallel \mathcal {M} e^\gamma -\mathcal {T}_N\mathcal {M}e^\gamma \parallel _{ \infty }\nonumber \\&\le CN^{-\kappa }\parallel \mathcal {M} e^\gamma \parallel _{0,\kappa } \le CN^{-\kappa }\parallel e^\gamma \parallel _{ \infty },\quad \kappa \in (0,1-\mu )=(0,\gamma ).\nonumber \\ \end{aligned}$$

(4.16)

The combination of (4.13), (4.14), (4.15), and (4.16) yields,

$$\begin{aligned} \Vert u-u_N\Vert _{\omega ^{\alpha ,\beta }}\le CN^{-m}\left( 1+N^{\frac{3}{4}-\kappa }\right) V_1 ,\\ \Vert D^\gamma u-u^\gamma _N\Vert _{\omega ^{\alpha ,\beta }}\le CN^{-m}\left( 1+N^{\frac{3}{4}-\kappa }\right) V_1, \end{aligned}$$

provided $N$ is large enough. Hence, the theorem is proved. $\square$

As $I^{\alpha ,\beta }_N$ is the interpolation operator which is based on the $(N+1)$-degree Jacobi–Guass points, in terms of (2.11), the pseudo-spectral Galerkin solution $\bar{u}_N$ satisfies

$$\begin{aligned}&(\bar{u}^\gamma _N,v_N)_{\omega ^{\alpha ,\beta }}= (\bar{u}_N,v_N)_{\omega ^{\alpha ,\beta }}+(I_N^{\alpha ,\beta }G_N\bar{u}_N,v_N)_{\omega ^{\alpha ,\beta }}+(I_N^{\alpha ,\beta }g,v_N)_{\omega ^{\alpha ,\beta }},\nonumber \\&(\bar{u}_N,v_N)_{\omega ^{\alpha ,\beta }}=(I_N^{\alpha ,\beta }G'\bar{u}^\gamma _N,v_N)_{\omega ^{\alpha ,\beta }},\quad \forall v_N\in {{P}}_N. \end{aligned}$$

(4.17)

Let

$$\begin{aligned} I(x)&= G\bar{u}_N-G_N\bar{u}_N\nonumber \\&= \int ^1_{-1}\tilde{k}(x,s(x,\theta ))u(s(x,\theta ))d\theta -\sum ^N_{k=0}\tilde{k}(x,s(x,\theta _k))u(s(x,\theta _k))\omega _k^{0,0}.\qquad \qquad \end{aligned}$$

(4.18)

Note that $\bar{u}^\gamma _N(x)\in P_N$,

$$\begin{aligned} (1,u^\gamma _N(s(x,\theta )))_{\omega ^{-\mu ,0}} =&\int ^1_{-1}(1-\theta )^{-\mu }u^\gamma _N(s(x,\theta ))d\theta =\sum ^N_{k=0}D^\gamma u(s(x,\theta '_k))\omega ^{-\mu ,0}_k\\ =&(1,u^\gamma _N(s(x,\theta )))_{\omega ^{-\mu ,0},N}, \end{aligned}$$

so we have

$$\begin{aligned} G'_Nu^\gamma _N=G'u^\gamma _N. \end{aligned}$$

Combing (4.17) and (4.18), yields

$$\begin{aligned}&(\bar{u}^\gamma _N,v_N)_{\omega ^{\alpha ,\beta }}= (\bar{u}_N,v_N)_{\omega ^{\alpha ,\beta }}+(I_N^{\alpha ,\beta }G\bar{u}_N-I_N^{\alpha ,\beta }I(x),v_N)_{\omega ^{\alpha ,\beta }}+(I_N^{\alpha ,\beta }g,v_N)_{\omega ^{\alpha ,\beta }},\nonumber \\&(\bar{u}_N,v_N)_{\omega ^{\alpha ,\beta }}=(I_N^{\alpha ,\beta }G'\bar{u}^\gamma _N,v_N)_{\omega ^{\alpha ,\beta }},\quad \forall v_N\in {{P}}_N. \end{aligned}$$

(4.19)

which gives rise to

$$\begin{aligned}&\bar{u}^\gamma _N=\bar{u}^N+I_N^{\alpha ,\beta }G\bar{u}^N -I_N^{\alpha ,\beta }I(x)+I_N^{\alpha ,\beta }g,\nonumber \\&\bar{u}^N=I_N^{\alpha ,\beta }G'u^\gamma _N. \end{aligned}$$

(4.20)

We first consider an auxiliary problem, i.e., find $\hat{u}^N\in P_N$, such that

$$\begin{aligned}&(\hat{u}^\gamma _N,v_N)_{\omega ^{\alpha ,\beta },N}= (\hat{u}_N,v_N)_{\omega ^{\alpha ,\beta },N}+(G\hat{u}_N,v_N)_{\omega ^{\alpha ,\beta },N}+(g,v_N)_{\omega ^{\alpha ,\beta },N},\quad \forall v_N\!\in \! {{P}}_N,\nonumber \\&(\hat{u}_N,v_N)_{\omega ^{\alpha ,\beta },N}=(G'\hat{u}^\gamma _N,v_N)_{\omega ^{\alpha ,\beta },N}. \end{aligned}$$

(4.21)

In terms of the definition of $I_N^{\alpha ,\beta }$, (4.21) can be written as

$$\begin{aligned}&(\hat{u}^\gamma _N,v_N)_{\omega ^{\alpha ,\beta }}= (\hat{u}_N,v_N)_{\omega ^{\alpha ,\beta }}+(I_N^{\alpha ,\beta }G\hat{u}_N,v_N)_{\omega ^{\alpha ,\beta }} +(I_N^{\alpha ,\beta }g,v_N)_{\omega ^{\alpha ,\beta }},\nonumber \\&(\hat{u}_N,v_N)_{\omega ^{\alpha ,\beta }}= (I_N^{\alpha ,\beta }G'\hat{u}^\gamma _N,v_N)_{\omega ^{\alpha ,\beta }},\quad \forall v_N\in {{P}}_N, \end{aligned}$$

(4.22)

which is equivalent to

$$\begin{aligned}&\hat{u}^\gamma _N=\hat{u}_N+I_N^{\alpha ,\beta }G\hat{u}_N+I_N^{\alpha ,\beta }g,\nonumber \\&\hat{u}_N=I_N^{\alpha ,\beta }G'\hat{u}^\gamma _N. \end{aligned}$$

(4.23)

Lemma 4.9

Suppose $\hat{u}^N$ is determined by (4.23), $-1\le \nu =\max (\alpha ,\beta )\le \min (0,\gamma -\frac{1}{2})$ and $0<\kappa <\gamma$, if the solution $u$ of (2.1) satisfies $u\in {H}^{m,N}_{\omega ^{\alpha ,\beta }}(\Lambda )$, we have

$$\begin{aligned} \Vert u-\hat{u}_N\Vert _{\infty }&\le {\left\{ \begin{array}{ll} CN^{\frac{1}{2}-m}\log NV_2,\quad &{}-1\le \nu < -\frac{1}{2},\\ CN^{\nu +1-m}V_2,\quad &{}\text {otherwise}, \end{array}\right. }\nonumber \\ \Vert D^\gamma u-\hat{u}^\gamma _N\Vert _{\infty }&\le {\left\{ \begin{array}{ll} CN^{\frac{1}{2}-m}\log NV_2,\quad &{}-1\le \nu < -\frac{1}{2},\\ CN^{\nu +1-m}V_2,\quad &{}\text {otherwise}, \end{array}\right. }\nonumber \\ \Vert u-\hat{u}_N\Vert _{\omega ^{\alpha ,\beta }}&\le {\left\{ \begin{array}{ll} CN^{-m}\left( V_1+\log N N^{\frac{1}{2}-\kappa }V_2\right) ,\quad &{}-1\le \nu < -\frac{1}{2},\\ CN^{-m}\left( V_1+N^{\nu +1-\kappa }V_2\right) ,\quad &{}\text {otherwise}, \end{array}\right. }\nonumber \\ \Vert D^\gamma u-\hat{u}^\gamma _N\Vert _{\omega ^{\alpha ,\beta }}&\le {\left\{ \begin{array}{ll} CN^{-m}\left( V_1+\log NN^{\frac{1}{2}-\kappa }V_2\right) ,\quad &{}-1\le \nu < -\frac{1}{2},\\ CN^{-m}\left( V_1+N^{\nu +1-\kappa }V_2\right) ,\quad &{}\text {otherwise}, \end{array}\right. }\qquad \quad \end{aligned}$$

(4.24)

where $V_2=|u|_{{H}^{m,N}_{\omega ^{c}}(\Lambda )}+|D^\gamma u|_{{H}^{m,N}_{\omega ^{c}}(\Lambda )}$.

Proof

Subtracting (4.23) from (2.2), yields

$$\begin{aligned}&D^\gamma u-\hat{u}^\gamma _N=u-\hat{u}_N+Gu-I_N^{\alpha ,\beta }G u^N+g-I_N^{\alpha ,\beta }g,\nonumber \\&u-\hat{u}_N=G'D^\gamma u-I_N^{\alpha ,\beta }G'u^\gamma _N. \end{aligned}$$

(4.25)

Set $\varepsilon =u-\hat{u}^N$, $\varepsilon ^\gamma =D^\gamma u-\hat{u}^\gamma _N$. Direct computation shows that

$$\begin{aligned}&Gu-I_N^{\alpha ,\beta }G \hat{u}^N\nonumber \\&\quad =Gu-I_N^{\alpha ,\beta }G u+(Gu-G\hat{u}^N)-\left[ (Gu-G\hat{u}^N)-I_N^{\alpha ,\beta }(Gu-G\hat{u}^N)\right] \nonumber \\&\quad =(D^\gamma u-u-g)-I_N^{\alpha ,\beta }(D^\gamma u-u-g)+G\varepsilon -[G\varepsilon -I_N^{\alpha ,\beta }G\varepsilon ]\nonumber \\&\quad =D^\gamma u-I_N^{\alpha ,\beta }D^\gamma u+I_N^{\alpha ,\beta }u-u+I_N^{\alpha ,\beta }g-g+G\varepsilon -[G\varepsilon -I_N^{\alpha ,\beta }G\varepsilon ]\end{aligned}$$

(4.26)

$$\begin{aligned}&G'D^\gamma u-I_N^{\alpha ,\beta }G'u^\gamma _N=u-I_N^{\alpha ,\beta }u+G'\varepsilon ^\gamma -[G'\varepsilon ^\gamma -I_N^{\alpha ,\beta }G'\varepsilon ^\gamma ]. \end{aligned}$$

(4.27)

The insertion of (4.26) and (4.27) into (4.25) yields

$$\begin{aligned}&\varepsilon ^\gamma =\varepsilon +\int ^x_{-1}k(x,s)\varepsilon (s)ds+J_1+J_2+J_3,\nonumber \\&\varepsilon =\frac{1}{\Gamma (\gamma )}\left( \frac{T}{2}\right) ^\gamma \int ^x_{-1} (x-s)^{\gamma -1}\varepsilon ^\gamma (s)ds+J_1+J_4, \end{aligned}$$

(4.28)

where

$$\begin{aligned} J_1&= u-I_N^{\alpha ,\beta }{u},\quad J_2=D^\gamma u-I_N^{\alpha ,\beta }D^\gamma u,\quad J_3=I_N^{\alpha ,\beta }G\varepsilon -G\varepsilon ,\\ J_4&= I_N^{\alpha ,\beta }G'\varepsilon ^\gamma -G'\varepsilon ^\gamma . \end{aligned}$$

A similar procedure of (4.6)–(4.8) in Theorem 4.1, and using the Dirichlet’s formula (4.7), we have

$$\begin{aligned} \varepsilon ^\gamma \le \varepsilon +C\int ^x_{-1} (x-s)^{\gamma -1}\varepsilon ^\gamma (s)ds+J_1+J_2+J_3+J_4, \end{aligned}$$

(4.29)

it follows from Gronwall inequality that

$$\begin{aligned}&\Vert \varepsilon ^\gamma (x)\Vert _{\infty }\le C\left( \Vert J_1\Vert _{\infty }+\Vert J_2\Vert _{\infty }+\Vert J_3\Vert _{\infty }+\Vert J_4\Vert _{\infty }\right) ,\nonumber \\&\Vert \varepsilon (x)\Vert _{\infty }\le C\left( \Vert J_1\Vert _{\infty }+\Vert J_2\Vert _{\infty }+\Vert J_4\Vert _{\infty }+\Vert J_4\Vert _{\infty }\right) . \end{aligned}$$

(4.30)

Due to Lemma 3.4,

$$\begin{aligned} \Vert J_1\Vert _{\infty }&= \Vert u-I_N^{\alpha ,\beta }{u}\Vert _{\infty }\le {\left\{ \begin{array}{ll} CN^{\frac{1}{2}-m}\log N|u|_{{H}^{m,N}_{\omega ^{c}}(\Lambda )},\quad &{}-1\le \nu < -\frac{1}{2},\\ CN^{\nu +1-m}|u|_{{H}^{m,N}_{\omega ^{c}}(\Lambda )},\quad &{}-\frac{1}{2}\le \nu <0, \end{array}\right. },\nonumber \\ \Vert J_2\Vert _{\infty }&= \Vert D^\gamma u-I_N^{\alpha ,\beta }{D^\gamma u}\Vert _{\infty }\le {\left\{ \begin{array}{ll} CN^{\frac{1}{2}-m}\log N|D^\gamma u|_{{H}^{m,N}_{\omega ^{c}}(\Lambda )},\quad &{}-1\le \nu < -\frac{1}{2},\\ CN^{\nu +1-m}|D^\gamma u|_{{H}^{m,N}_{\omega ^{c}}(\Lambda )},\quad &{}-\frac{1}{2}\le \nu <0. \end{array}\right. }\nonumber \\ \end{aligned}$$

(4.31)

By virtue of Lemma 3.4 with $m = 1$, we obtain

$$\begin{aligned} \Vert J_3\Vert _{\infty }&= \Vert I_N^{\alpha ,\beta }G\varepsilon -G\varepsilon \Vert _{\infty }\nonumber \\&\le \!\!{\left\{ \begin{array}{ll} CN^{-\frac{1}{2}}\log N\Vert G\varepsilon \Vert _{H^{1;N}_{\omega ^c}},\quad &{}-1\le \nu < -\frac{1}{2},\\ CN^{\nu }\Vert G\varepsilon \Vert _{H^{1;N}_{\omega ^c}},\quad &{}-\frac{1}{2}\le \nu <0, \end{array}\right. } \nonumber \\&\le \!\!{\left\{ \begin{array}{ll} CN^{-\frac{1}{2}}\log N\Vert \varepsilon (x)\Vert _{\infty },\quad &{}-1\le \nu < -\frac{1}{2},\\ CN^{\nu }\Vert \varepsilon (x)\Vert _{\infty },\quad &{}-\frac{1}{2}\le \nu <0. \end{array}\right. } \end{aligned}$$

(4.32)

It follows from Lemmas 3.7, 3.8 and 3.6 that

$$\begin{aligned} \parallel J_4\parallel _{ \infty }=&\parallel (I_N^{\alpha ,\beta }-I)\mathcal {M} \varepsilon ^\gamma \parallel _{ \infty }\nonumber \\ =&\parallel (I_N^{\alpha ,\beta }-I)(\mathcal {M} \varepsilon ^\gamma -\mathcal {T}_N\mathcal {M}\varepsilon ^\gamma )\parallel _{ \infty } \nonumber \\ \le&\parallel I_N^{\alpha ,\beta }(\mathcal {M} \varepsilon ^\gamma -\mathcal {T}_N\mathcal {M}\varepsilon ^\gamma )\parallel _\infty +\parallel \mathcal {M} \varepsilon ^\gamma -\mathcal {T}_N\mathcal {M}\varepsilon ^\gamma \parallel _{ \infty }\nonumber \\ \le&{\left\{ \begin{array}{ll} \mathcal {O}(\log N)\parallel \mathcal {M} \varepsilon ^\gamma -\mathcal {T}_N\mathcal {M}e^\gamma \parallel _{ \infty },&{}\quad -1<\nu \le -\frac{1}{2},\\ \mathcal {O}(N^{\nu +\frac{1}{2}})\parallel \mathcal {M} \varepsilon ^\gamma -\mathcal {T}_N\mathcal {M}\varepsilon ^\gamma \parallel _{ \infty },&{}\quad -\frac{1}{2}\le \nu <\min (0,\gamma -\frac{1}{2}), \end{array}\right. }\nonumber \\ \le&{\left\{ \begin{array}{ll} C\log NN^{-\kappa }\parallel \mathcal {M}\varepsilon ^\gamma \parallel _{0,\kappa },&{}\quad -1<\nu \le -\frac{1}{2},\\ CN^{\nu +\frac{1}{2}-\kappa }\parallel \mathcal {M} \varepsilon ^\gamma \parallel _{0,\kappa },&{}\quad -\frac{1}{2}\le \nu <\min (0,\gamma -\frac{1}{2}), \end{array}\right. } 0<\kappa <\gamma ,\nonumber \\ \le&{\left\{ \begin{array}{ll} C\log NN^{-\kappa }\parallel \varepsilon ^\gamma \parallel _{\infty },&{}\quad -1<\nu \le -\frac{1}{2},\\ CN^{\nu +\frac{1}{2}-\kappa }\parallel \varepsilon ^\gamma \parallel _{\infty },&{}\quad -\frac{1}{2}\le \nu <\min (0,\gamma -\frac{1}{2}), \end{array}\right. } 0<\kappa <\gamma ,\nonumber \\ \le&{\left\{ \begin{array}{ll} C\log NN^{-\kappa }\left( \Vert J_1\Vert _{\infty }+\Vert J_2\Vert _{\infty }+\Vert J_4\Vert _{\infty }+\Vert J_4\Vert _{\infty }\right) ,\\ CN^{\nu +\frac{1}{2}-\kappa }\left( \Vert J_1\Vert _{\infty }+\Vert J_2\Vert _{\infty }+\Vert J_4\Vert _{\infty }+\Vert J_4\Vert _{\infty }\right) . \end{array}\right. } \end{aligned}$$

(4.33)

Combining (4.30), (4.31), (4.32) and (4.33), when $N$ is large enough, we obtain

$$\begin{aligned} \Vert u-\hat{u}_N\Vert _{\infty }\le {\left\{ \begin{array}{ll} CN^{\frac{1}{2}-m}\log N\left( |u|_{{H}^{m,N}_{\omega ^{c}}(\Lambda )}+|D^\gamma u|_{{H}^{m,N}_{\omega ^{c}}(\Lambda )}\right) , &{}-1\le \nu < -\frac{1}{2},\\ CN^{\nu +1-m}\left( |u|_{{H}^{m,N}_{\omega ^{c}}(\Lambda )}+|D^\gamma u|_{{H}^{m,N}_{\omega ^{c}}(\Lambda )}\right) , &{}-\frac{1}{2}\le \nu <\min (0,\gamma -\frac{1}{2}), \end{array}\right. }\\ \Vert D^\gamma u-\hat{u}^\gamma _N\Vert _{\infty }\le {\left\{ \begin{array}{ll} CN^{\frac{1}{2}-m}\log N\left( |u|_{{H}^{m,N}_{\omega ^{c}}(\Lambda )}+|D^\gamma u|_{{H}^{m,N}_{\omega ^{c}}(\Lambda )}\right) , &{}-1\le \nu < -\frac{1}{2},\\ CN^{\nu +1-m}\left( |u|_{{H}^{m,N}_{\omega ^{c}}(\Lambda )}+|D^\gamma u|_{{H}^{m,N}_{\omega ^{c}}(\Lambda )}\right) , &{}-\frac{1}{2}\le \nu <\min (0,\gamma -\frac{1}{2}). \end{array}\right. } \end{aligned}$$

Now we investigate the $\Vert \cdot \Vert _{\omega ^{\alpha ,\beta }}$-error estimate. It follows from (4.28), (4.29) and the Gronwall inequality that

$$\begin{aligned}&\Vert \varepsilon ^\gamma (x)\Vert _{\omega ^{\alpha ,\beta }}\le C\left( \Vert J_1\Vert _{\omega ^{\alpha ,\beta }}+\Vert J_2\Vert _{\omega ^{\alpha ,\beta }}+\Vert J_3\Vert _{\omega ^{\alpha ,\beta }}+\Vert J_4\Vert _{\omega ^{\alpha ,\beta }}\right) ,\nonumber \\&\Vert \varepsilon (x)\Vert _{\omega ^{\alpha ,\beta }}\le C\left( \Vert J_1\Vert _{\omega ^{\alpha ,\beta }}+\Vert J_2\Vert _{\omega ^{\alpha ,\beta }}+\Vert J_3\Vert _{\omega ^{\alpha ,\beta }}+\Vert J_4\Vert _{\omega ^{\alpha ,\beta }}\right) . \end{aligned}$$

(4.34)

By Lemma 3.4, we have

$$\begin{aligned} \Vert J_1\Vert _{\omega ^{\alpha ,\beta }}&= \Vert u-I_N^{\alpha ,\beta }{u}\Vert _{\omega ^{\alpha ,\beta }}\le CN^{-m}|u|_{H^{m;N}_{\omega ^{\alpha ,\beta }}},\nonumber \\ \Vert J_2\Vert _{\omega ^{\alpha ,\beta }}&= \Vert D^\gamma u-I_N^{\alpha ,\beta }{D^\gamma u}\Vert _{\omega ^{\alpha ,\beta }}\le CN^{-m}|D^\gamma u|_{H^{m;N}_{\omega ^{\alpha ,\beta }}}. \end{aligned}$$

(4.35)

By virtue of Lemma 3.4 with $m = 1$, we obtain

$$\begin{aligned} \Vert J_3\Vert _{\omega ^{\alpha ,\beta }}=&\Vert I_N^{\alpha ,\beta }G\varepsilon -G\varepsilon \Vert _{\omega ^{\alpha ,\beta }} \le CN^{-1}\Vert G\varepsilon \Vert _{H^{1;N}_{\omega ^{\alpha ,\beta }}}\nonumber \\ =&CN^{-1}\left\| \int ^x_1k(x,t)\varepsilon (s)ds\right\| _{H^{1;N}_{\omega ^{\alpha ,\beta }}} \le CN^{-1}\Vert \varepsilon (x)\Vert _{\omega ^{\alpha ,\beta }}. \end{aligned}$$

(4.36)

It follows from Lemmas 3.5, 3.7 and 3.8 that

$$\begin{aligned} \parallel J_4\parallel _{ \omega ^{\alpha ,\beta }}=&\parallel (I_N^{\alpha ,\beta }-I)\mathcal {M} \varepsilon ^\gamma \parallel _{ \omega ^{\alpha ,\beta }} =\parallel (I_N^{\alpha ,\beta }-I)(\mathcal {M} \varepsilon ^\gamma -\mathcal {T}_N\mathcal {M}\varepsilon ^\gamma )\parallel _{ \omega ^{\alpha ,\beta }} \nonumber \\ \le&\parallel I_N^{\alpha ,\beta }(\mathcal {M} \varepsilon ^\gamma -\mathcal {T}_N\mathcal {M}\varepsilon ^\gamma )\parallel _{ \omega ^{\alpha ,\beta }}+\parallel \mathcal {M} \varepsilon ^\gamma -\mathcal {T}_N\mathcal {M}\varepsilon ^\gamma \parallel _{ \omega ^{\alpha ,\beta }}\nonumber \\ \le&\,\, C\parallel \mathcal {M} \varepsilon ^\gamma -\mathcal {T}_N\mathcal {M}\varepsilon ^\gamma \parallel _{ \infty } \le C N^{-\kappa }\parallel \varepsilon ^\gamma \parallel _{\infty }. \end{aligned}$$

(4.37)

Combining (4.34), (4.35), (4.36), and (4.37) we obtain, when $N$ is large enough,

$$\begin{aligned}&\Vert u-\hat{u}_N\Vert _{\omega ^{\alpha ,\beta }}\le {\left\{ \begin{array}{ll} CN^{-m}\left( V_1+\log N N^{\frac{1}{2}-\kappa }V_2\right) ,\quad &{}-1\le \nu < -\frac{1}{2},\\ CN^{-m}\left( V_1+N^{\nu +1-\kappa }V_2\right) ,\quad &{}-\frac{1}{2}\le \nu <\min (0,\gamma -\frac{1}{2}), \end{array}\right. }\\&\Vert D^\gamma u-\hat{u}^\gamma _N\Vert _{\omega ^{\alpha ,\beta }}\le {\left\{ \begin{array}{ll} CN^{-m}\left( V_1+\log NN^{\frac{1}{2}-\kappa }V_2\right) ,\quad &{}-1\le \nu < -\frac{1}{2},\\ CN^{-m}\left( V_1+N^{\nu +1-\kappa }V_2\right) ,\quad &{}-\frac{1}{2}\le \nu <\min (0,\gamma -\frac{1}{2}). \end{array}\right. } \end{aligned}$$

This completes the proof of the lemma. $\square$

Theorem 4.2

Suppose that the solution $u$ of (2.1) satisfies $u\in {H}^{m,N}_{\omega ^{\alpha ,\beta }}(\Lambda )$, $-1\le \nu =\max (\alpha ,\beta )\le \min (0,\gamma -\frac{1}{2})$ and $0<\kappa <\gamma$, for the pseudo spectral Jacobi–Galerkin solution $\bar{u}_N$, such that (2.11) holds, we have

$$\begin{aligned}&\Vert u-\bar{u}_N\Vert _\infty \nonumber \\&\quad \le {\left\{ \begin{array}{ll} CN^{-m} \left[ \log NK^*\Vert u\Vert _{\omega ^{0,0}}+\log N N^{\frac{1}{2}} V_2 \right] , &{}-1\le \nu < -\frac{1}{2},\\ CN^{-m}\left[ N^{\nu +\frac{1}{2}}K^*\Vert u\Vert _{\omega ^{0,0}}+N^{\nu +1}V_2\right] , &{}\text {otherwise}, \end{array}\right. }\nonumber \\&\Vert D^\gamma u-\bar{u}^\gamma _N\Vert _{\infty }\nonumber \\&\quad \le {\left\{ \begin{array}{ll} CN^{-m}\left[ \log NK^*\Vert u\Vert _{\omega ^{0,0}}+\log N N^{\frac{1}{2}} V_2\right] , &{}-1\le \nu < -\frac{1}{2},\\ CN^{-m}\left[ N^{\nu +\frac{1}{2}}K^*\Vert u\Vert _{\omega ^{0,0}}+N^{\nu +1}V_2\right] , &{}\text {otherwise}, \end{array}\right. }\nonumber \\&\Vert u-\bar{u}_N\Vert _{\omega ^{\alpha ,\beta }}\nonumber \\&\quad \le {\left\{ \begin{array}{ll} CN^{-m} \left[ \left( 1+\log NN^{-\kappa }\right) K^*\Vert u\Vert _{\omega ^{0,0}}+V_1+\log N N^{\frac{1}{2}-\kappa }V_2 \right] , &{}-1\le \nu < -\frac{1}{2},\\ CN^{-m}\left[ \left( 1+N^{\nu +\frac{1}{2}-\kappa }\right) K^*\Vert u\Vert _{\omega ^{0,0}}+V_1+N^{\nu +1-\kappa }V_2\right] , &{}\text {otherwise}, \end{array}\right. }\nonumber \\&\Vert D^\gamma u-\bar{u}^\gamma _N\Vert _{\omega ^{\alpha ,\beta }}\nonumber \\&\quad \le {\left\{ \begin{array}{ll} CN^{-m}\left[ \left( 1+\log NN^{-\kappa }\right) K^*\Vert u\Vert _{\omega ^{0,0}}+V_1+\log N N^{\frac{1}{2}-\kappa }V_2\right] , &{}-1\le \nu < -\frac{1}{2},\\ CN^{-m}\left[ \left( 1+N^{\nu +\frac{1}{2}-\kappa }\right) K^*\Vert u\Vert _{\omega ^{0,0}}+V_1+N^{\nu +1-\kappa }V_2\right] , &{}\text {otherwise}, \end{array}\right. } \end{aligned}$$

(4.38)

where $K^*=\max _{x\in (-1,1)}|k(x,s(x,\cdot ))|_{H^{m;N}_{\omega ^{0,0}}}$.

Proof

Now subtracting (4.20) from (4.23) leads to

$$\begin{aligned}&\bar{u}^\gamma _N-\hat{u}^\gamma _N=\bar{u}_N-\hat{u}_N+I^{\alpha ,\beta }_N(G\bar{u}^N-G\hat{u}^N) -I^{\alpha ,\beta }_NI(x),\nonumber \\&\bar{u}_N-\hat{u}_N=I^{\alpha ,\beta }_N(G'\bar{u}^\gamma _ N-G'\hat{u}^\gamma _N) , \end{aligned}$$

(4.39)

by setting $E=\bar{u}_N-\hat{u}^N$, $E^\gamma =\bar{u}^\gamma _N-\hat{u}^\gamma _N$

$$\begin{aligned} E^\gamma&= E+I^{\alpha ,\beta }_NGE -I^{\alpha ,\beta }_NI(x) =E+GE-GE+I^{\alpha ,\beta }_NGE -I^{\alpha ,\beta }_NI(x)\nonumber \\&= E+GE+Q_1 -I^{\alpha ,\beta }_NI(x),\nonumber \\ E&= I^{\alpha ,\beta }_NG'E^\gamma =G'E^\gamma -G'E^\gamma + I^{\alpha ,\beta }_NG'E^\gamma =G'E^\gamma +Q_2, \end{aligned}$$

(4.40)

which yields

$$\begin{aligned} E^\gamma =G'E^\gamma +Q_2+G(G'E^\gamma +Q_2)+Q_1 -I^{\alpha ,\beta }_NI(x), \end{aligned}$$

(4.41)

with $Q_1=I^{\alpha ,\beta }_NGE-GE$, $Q_2= I^{\alpha ,\beta }_NG'E^\gamma -G'E^\gamma$. It follows from a similar procedure of (4.6)–(4.8) in Theorem 4.1, the Dirichlet’s formula (4.7) and the Gronwall inequality that

$$\begin{aligned}&\Vert E^\gamma \Vert _\infty =\Vert Q_1\Vert _\infty +\Vert Q_2\Vert _\infty +\Vert I^{\alpha ,\beta }_NI(x)\Vert _\infty ,\nonumber \\&\Vert E\Vert _\infty =\Vert Q_1\Vert _\infty +\Vert Q_2\Vert _\infty +\Vert I^{\alpha ,\beta }_NI(x)\Vert _\infty . \end{aligned}$$

(4.42)

By virtue of Lemma 3.4 with $m = 1$,

$$\begin{aligned} \Vert Q_1\Vert _\infty =\Vert I^{\alpha ,\beta }_NGE-GE\Vert _\infty \le {\left\{ \begin{array}{ll} CN^{-\frac{1}{2}}\log N\Vert E\Vert _\infty ,\quad &{}-1\le \nu < -\frac{1}{2},\\ CN^{\nu }\Vert E\Vert _\infty ,\quad &{}-\frac{1}{2}\le \nu <0. \end{array}\right. } \end{aligned}$$

Similarly to (4.33), we have

$$\begin{aligned} \Vert Q_2\Vert _\infty =\Vert I^{\alpha ,\beta }_NG'E^\gamma -G'E^\gamma \Vert _\infty \le {\left\{ \begin{array}{ll} CN^{-\kappa }\log N\Vert E^\gamma \Vert _\infty ,\quad &{}-1\le \mu < -\frac{1}{2},\\ CN^{\nu +\frac{1}{2}-\kappa }\Vert E^\gamma \Vert _\infty ,\quad &{}-\frac{1}{2}\le \nu <\min (0,\gamma -\frac{1}{2}). \end{array}\right. } \end{aligned}$$

Using Lemmas 3.3 and 3.6, we have

$$\begin{aligned}&\!\!\Vert I^{\alpha ,\beta }_NI(x)\Vert _\infty \le {\left\{ \begin{array}{ll} C\log N\max _{x\in (-1,1)}{I(x)},\quad -1\le \nu <-\frac{1}{2},\\ C N^{\nu +\frac{1}{2}}\max _{x\in (-1,1)}{I(x)},\quad -\frac{1}{2}\le \nu <0, \end{array}\right. }\\&\!\!\quad \le {\left\{ \begin{array}{ll} CN^{-m}\log N\max _{x\in (-1,1)}|k(x,s(x,\cdot ))|_{H^{m;N}_{\omega ^{0,0}}}\Vert \bar{u}_N\Vert _{\omega ^{0,0}},\quad -1\le \nu <-\frac{1}{2},\\ CN^{-m} N^{\nu +\frac{1}{2}}\max _{x\in (-1,1)}|k(x,s(x,\cdot ))|_{H^{m;N}_{\omega ^{0,0}}}\Vert \bar{u}_N\Vert _{\omega ^{0,0}},\quad -\frac{1}{2}\le \nu <0, \end{array}\right. }\\&\!\!\quad \le {\left\{ \begin{array}{ll} CN^{-m}\log N\max _{x\in (-1,1)}|k(x,s(x,\cdot ))|_{H^{m;N}_{\omega ^{0,0}}}\left( \Vert u\Vert _{\omega ^{0,0}}+\Vert E\Vert _{\infty }\right) ,\quad -1\le \nu <-\frac{1}{2},\\ CN^{-m} N^{\nu +\frac{1}{2}}\max _{x\in (-1,1)}|k(x,s(x,\cdot ))|_{H^{m;N}_{\omega ^{0,0}}}\left( \Vert u\Vert _{\omega ^{0,0}}+\Vert E\Vert _{\infty }\right) ,\quad -\frac{1}{2}\le \nu <0. \end{array}\right. } \end{aligned}$$

Set $K^*=\max _{x\in (-1,1)}|k(x,s(x,\cdot ))|_{H^{m;N}_{\omega ^{0,0}}}$, we now obtain the estimate $E$ by using (4.42)

$$\begin{aligned}&\Vert E\Vert _\infty \le {\left\{ \begin{array}{ll} CN^{-m}\log NK^*\Vert u\Vert _{\omega ^{0,0}},\quad &{}-1\le \nu < -\frac{1}{2},\\ CN^{\nu +\frac{1}{2}-m}K^*\Vert u\Vert _{\omega ^{0,0}},\quad &{}-\frac{1}{2}\le \nu <\min (0,\gamma -\frac{1}{2}), \end{array}\right. }\nonumber \\&\Vert E^\gamma \Vert _\infty \le {\left\{ \begin{array}{ll} CN^{-m}\log NK^*\Vert u\Vert _{\omega ^{0,0}},\quad &{}-1\le \nu < -\frac{1}{2},\\ CN^{\nu +\frac{1}{2}-m}K^*\Vert u\Vert _{\omega ^{0,0}},\quad &{}-\frac{1}{2}\le \nu <\min (0,\gamma -\frac{1}{2}). \end{array}\right. } \end{aligned}$$

(4.43)

Next, we will give the error estimation in $\Vert \cdot \Vert _{\omega ^{\alpha ,\beta }}$. It follows from (4.41) and the Gronwall inequality that

$$\begin{aligned}&\Vert E^\gamma \Vert _{\omega ^{\alpha ,\beta }}=\Vert Q_1\Vert _{\omega ^{\alpha ,\beta }} +\Vert Q_2\Vert _{\omega ^{\alpha ,\beta }}+\Vert I^{\alpha ,\beta }_NI(x)\Vert _{\omega ^{\alpha ,\beta }},\nonumber \\&\Vert E\Vert _{\omega ^{\alpha ,\beta }}=\Vert Q_1\Vert _{\omega ^{\alpha ,\beta }} +\Vert Q_2\Vert _{\omega ^{\alpha ,\beta }}+\Vert I^{\alpha ,\beta }_NI(x)\Vert _{\omega ^{\alpha ,\beta }}. \end{aligned}$$

(4.44)

Due to Lemma 3.4,

$$\begin{aligned} \Vert Q_1\Vert _{\omega ^{\alpha ,\beta }}=\Vert I^{\alpha ,\beta }_NGE-GE\Vert _{\omega ^{\alpha ,\beta }}\le CN^{-1}\Vert E\Vert _{\omega ^{\alpha ,\beta }}. \end{aligned}$$

$\Vert Q_2\Vert _{\omega ^{\alpha ,\beta }}$ can be established in a similar way as (4.37),

$$\begin{aligned} \Vert Q_2\Vert _{\omega ^{\alpha ,\beta }}=\Vert I^{\alpha ,\beta }_NG'E^\gamma -G'E^\gamma \Vert _{\omega ^{\alpha ,\beta }}\le CN^{-\kappa }\Vert E^\gamma \Vert _{\omega ^{\alpha ,\beta }}. \end{aligned}$$

Using Lemmas 3.3 and 3.5, we have

$$\begin{aligned}&\Vert I^{\alpha ,\beta }_NI(x)\Vert _{\omega ^{\alpha ,\beta }}\le C\Vert I(x)\Vert _{\omega ^{\alpha ,\beta }} \le CN^{-m}K^*\left( \Vert u\Vert _{\omega ^{0,0}}+\Vert E\Vert _\infty \right) . \end{aligned}$$

We obtain

$$\begin{aligned}&\Vert E\Vert _{\omega ^{\alpha ,\beta }}\le {\left\{ \begin{array}{ll}CN^{-m} \left( 1+\log NN^{-\kappa }\right) K^*\Vert u\Vert _{\omega ^{0,0}},\quad &{}-1\le \nu < -\frac{1}{2},\\ CN^{-m}\left( 1+N^{\nu +\frac{1}{2}-\kappa }\right) K^*\Vert u\Vert _{\omega ^{0,0}},\quad &{}-\frac{1}{2}\le \nu <0, \end{array}\right. }\nonumber \\&\Vert E^\gamma \Vert _{\omega ^{\alpha ,\beta }}\le {\left\{ \begin{array}{ll} CN^{-m}\left( 1+\log NN^{-\kappa }\right) K^*\Vert u\Vert _{\omega ^{0,0}},\quad &{}-1\le \nu < -\frac{1}{2},\\ CN^{-m}\left( 1+N^{\nu +\frac{1}{2}-\kappa }\right) K^*\Vert u\Vert _{\omega ^{0,0}},\quad &{}-\frac{1}{2}\le \nu <0. \end{array}\right. }\qquad \end{aligned}$$

(4.45)

when $N$ is large enough.

Finally, it follows from triangular inequality, Lemma 4.9, (4.43) and (4.45), that

$$\begin{aligned}&\Vert u-\bar{u}_N\Vert _\infty \\&\quad \le \Vert u-\hat{u}_N\Vert _\infty +\Vert \hat{u}_N-\bar{u}_N\Vert _\infty \\&\quad \le {\left\{ \begin{array}{ll}CN^{-m} \left[ \log NK^*\Vert u\Vert _{\omega ^{0,0}}+\log N N^{\frac{1}{2}} V_2 \right] , &{}-1\le \nu < -\frac{1}{2},\\ CN^{-m}\left[ N^{\nu +\frac{1}{2}}K^*\Vert u\Vert _{\omega ^{0,0}}+N^{\nu +1}V_2\right] , &{}-\frac{1}{2}\le \nu <\min (0,\gamma -\frac{1}{2}), \end{array}\right. }\\&\Vert D^\gamma u-\bar{u}^\gamma _N\Vert _{\infty }\\&\quad \le \Vert D^\gamma u-\hat{u}^\gamma _N\Vert _{\infty }+\Vert \hat{u}^\gamma _N-\bar{u}^\gamma _N\Vert _{\infty }\\&\quad \le {\left\{ \begin{array}{ll} CN^{-m}\left[ \log NK^*\Vert u\Vert _{\omega ^{0,0}}+\log N N^{\frac{1}{2}} V_2\right] , &{}-1\le \nu < -\frac{1}{2},\\ CN^{-m}\left[ N^{\nu +\frac{1}{2}}K^*\Vert u\Vert _{\omega ^{0,0}}+N^{\nu +1}V_2\right] , &{}-\frac{1}{2}\le \nu <\min (0,\gamma -\frac{1}{2}). \end{array}\right. } \end{aligned}$$

$$\begin{aligned}&\Vert u-\bar{u}_N\Vert _{\omega ^{\alpha ,\beta }} \le \Vert u-\hat{u}_N\Vert _{\omega ^{\alpha ,\beta }}+\Vert \hat{u}_N-\bar{u}_N\Vert _{\omega ^{\alpha ,\beta }}\\&\quad \le {\left\{ \begin{array}{ll} CN^{-m} \left[ \left( 1+\log NN^{-\kappa }\right) K^*\Vert u\Vert _{\omega ^{0,0}}+V_1+\log N N^{\frac{1}{2}-\kappa }V_2 \right] , &{}-1\le \nu < -\frac{1}{2},\\ CN^{-m}\left[ \left( 1+N^{\nu +\frac{1}{2}-\kappa }\right) K^*\Vert u\Vert _{\omega ^{0,0}}+V_1+N^{\nu +1-\kappa }V_2\right] , &{}-\frac{1}{2}\le \nu <\min (0,\gamma -\frac{1}{2}), \end{array}\right. }\\&\Vert D^\gamma u-\bar{u}^\gamma _N\Vert _{\omega ^{\alpha ,\beta }} \le \Vert D^\gamma u-\hat{u}^\gamma _N\Vert _{\omega ^{\alpha ,\beta }}+\Vert \hat{u}^\gamma _N-\bar{u}^\gamma _N\Vert _{\omega ^{\alpha ,\beta }}\\&\quad \le {\left\{ \begin{array}{ll} CN^{-m}\left[ \left( 1+\log NN^{-\kappa }\right) K^*\Vert u\Vert _{\omega ^{0,0}}+V_1+\log N N^{\frac{1}{2}-\kappa }V_2\right] , &{}-1\le \nu < -\frac{1}{2},\\ CN^{-m}\left[ \left( 1+N^{\nu +\frac{1}{2}-\kappa }\right) K^*\Vert u\Vert _{\omega ^{0,0}}+V_1+N^{\nu +1-\kappa }V_2\right] , &{}-\frac{1}{2}\le \nu <\min (0,\gamma -\frac{1}{2}). \end{array}\right. } \end{aligned}$$

We obtain the desired estimated (4.38). $\square$

5 Numerical experiments

We give some numerical examples to confirm our analysis. To examine the accuracy of the results, $\Vert \cdot \Vert _\infty$ and $\Vert \cdot \Vert _{\omega ^{\alpha ,\beta }}$ errors are employed to assess the efficiency of the method. All the calculations are supported by Matlab.

Example 5.1

Consider the following fractional integro-differential equation

$$\begin{aligned}&D^{\gamma }y(t)=1+2t-y(t)+t(1+2t)\int ^t_0e^{\tau (t-\tau )}y(\tau )d\tau ,\nonumber \\&y(0) = 1 \end{aligned}$$

(5.1)

when $\gamma =1$, the exact solution of (5.1) is $y(t) = e^{t^2}$ (the only case for which we know the exact solution).

We have reported the obtained numerical results of spectral Jacobi–Galerkin method for $N = 20$ and $\gamma = 0.25, 0.5, 0.75$ and $1$ in Fig. 1(left). We can see that, as $\gamma$ approaches $1$, the numerical solutions converges to the exact solution $y(t) = e^{t^2}$, i.e. in the limit, the solution of fractional integro-differential equations approaches to that of the integer order integro-differential equations. When $\gamma =1$, (5.1) is an integro-differential equation, $y'(t)=2te^{t^2}$, Fig. 1(right) illustrates the numerical result of spectral Jacobi–Galerkin approximation solution for $N = 20$ and exact solution of $y'(t)$.

Fig. 1

Example 5.1: Approximation solutions of spectral Jacobi–Galerkin method with different $\gamma$ and exact solution of $y(t)$ with $\gamma =1$(left). Comparison between approximate solution of spectral Jacobi–Galerkin method and exact solution of $y'(t)$(right)

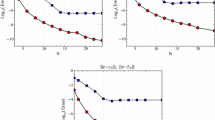
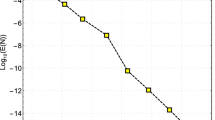
For $\gamma =1$, we adopt the spectral and pseudo-spectral Jacobi–Galerkin methods with Jacobi weight $\omega ^{\gamma -1,\gamma -1}(x)=\omega ^{0,0}(x)$. First we implement the numerical scheme (2.4) based on the spectral Jacobi–Galerkin method to solve this example. Figure 2(left) illustrates $\Vert \cdot \Vert _\infty$ and $\Vert \cdot \Vert _{\omega ^{\alpha ,\beta }}$ errors of spectral Jacobi–Galerkin method versus the number $N$ of the steps. Next the $\Vert \cdot \Vert _\infty$ and $\Vert \cdot \Vert _{\omega ^{\alpha ,\beta }}$ errors of the pseudo-spectral Jacobi–Galerkin method are demonstrated in Fig. 2(right). Clearly, these figures show the exponential rate of convergence predicted by the proposed method.

Fig. 2

Example 5.1: $L^\infty$ and $L^2_{\omega }$ errors of spectral Jacobi–Galerkin method versus $N$(left). $L^\infty$ and $L^2_{\omega }$ norms errors of pseudo-spectral Jacobi–Galerkin method versus $N$ (right)

In practice, many Volterra equations are usually nonlinear. However, the nonlinearity adds rather little to the difficulty of obtaining a numerical solution. The methods described above remain applicable. Below we will provide a numerical example using the spectral technique proposed in this work.

Example 5.2

Our second example is about a nonlinear problem in one-dimension. Consider the following fractional integro-differential equation,

$$\begin{aligned} D^{0.5}y(t)&= f(t)y(t)+g(t)+\sqrt{t}\int ^t_0y^2(\tau )d\tau ,\nonumber \\ y(0)&= 0 \end{aligned}$$

(5.2)

with

$$\begin{aligned} f(t)=2\sqrt{t}+2t^{\frac{3}{2}}-\left( \sqrt{t}+t^{\frac{3}{2}}\right) \ln (1+t), \quad g(t)=\frac{2{\arcsin \text {h}}(\sqrt{t})}{\sqrt{\pi (1+t)}}-2t^{\frac{3}{2}}. \end{aligned}$$

The exact solution is $y(t) = \ln (1 + t)$.

This is a nonlinear problem. The numerical scheme leads to a nonlinear system, and a proper solver for the nonlinear system (e.g., Newton method) should be used. Figure 3 presents the approximate and exact solution, which are found in excellent agreement. Next, Fig. 4(left) illustrates the $L^\infty$ and $L^2_{\omega }$ errors of the spectral Jacobi–Galerkin method, Fig. 4(right) illustrates the $L^\infty$ and $L^2_{\omega }$ errors of the pseudo-spectral-Galerkin method. These results indicate that the spectral accuracy is obtained for this problem, although the given functions $f (t)$ and $g(t)$ are not very smooth.

Fig. 3

Example 5.2: Comparison between approximate solution and exact solution of $y(t)$

Fig. 4

Example 5.2: $L^\infty$ and $L^2_{\omega }$ errors of spectral Jacobi–Galerkin method versus $N$. $L^\infty$ and $L^2_{\omega }$ norms errors of pseudo-spectral Jacobi–Galerkin method versus $N$

Example 5.3

Following Odibat and Momani [13], we consider fractional Riccati equation

$$\begin{aligned} D^\alpha y(t)=2y(t)-y(t)^2+1,\quad 0<\alpha \le 1,\quad 0\le t<2 \end{aligned}$$

(5.3)

subject to the initial state $y(0)=0$, which is studied by Odibat [13] by using the modified homotopy perturbation method and Li [10] by using the Chebyshev wavelet operational matrices method. Here we use pseudo-spectral Galerkin method to solve it.

This is a nonlinear system of algebraic equations. The numerical solution, for $N=20$, is shown in Fig. 5. The exact solution of this problem, when $\alpha =1$, is

$$\begin{aligned} y(t)=1+\sqrt{2}tanh\left( \sqrt{2}t+\frac{1}{2}ln\left( \frac{\sqrt{2}-1}{\sqrt{2}+1}\right) \right) \end{aligned}$$

and we can observe that, as $t\rightarrow \infty$, $y(t)\rightarrow 1+\sqrt{2}$. Figure 5 shows that our numerical solution is very good agreement with the exact solution when $\alpha = 1$. When $\alpha = 0.5$ and $\alpha = 0.75$, the numerical solution is very good agreement with the result in [10]. Therefore, we hold that the solution for $\alpha = 0.5$ and $\alpha = 0.75$ is also credible.

Fig. 5

The behavior of the exact and approximate solution of example with $N=20$ of Example 5.3

Table 1 shows the comparison of the numerical approximations of [10, 13] and this paper on the discrete points in $[0,1]$. We think our results are better than that in [13] for $\alpha =0.5$ and $\alpha =0.75$, because in [13] only the fourth-order term of the homotopy perturbation solution were used in evaluating the approximate solutions. While the Chebyshev wavelet operational matrices method in [10] used 192 degrees of freedom, our method reached the same accuracy with only 20 degrees of freedom.

Table 1 Numerical results with comparison to Refs.  [10] and [13] for Example 5.3

6 Conclusions and future work

The fractional derivatives are global dependence problems, they are definite by the integral in [0, T], from this point, the global methods spectral methods is more suit to solve the FIDEs than the local method, such as finite difference methods. This work has been concerned with the spectral and pseudo-spectral Jacobi–Galerkin analysis of the fractional order integro-differential equations of Volterra type with Caputo derivatives. The most important contribution of this work is that we are able to demonstrate rigorously that the errors of spectral approximations decay exponentially in both infinity and weighted norms, which is a desired feature for a spectral method.

Although in this work our convergence theory does not cover the nonlinear case, the methods described above remain applicable, it will be possible to extend the results of this paper to nonlinear case which will be the subject of our future work. We only investigated the fractional derivatives are described in the Caputo sense, in our future work, the case other definitions of fractional derivatives (Riemann–Liouville, Riesz, Grnwald–Letnikov), the spectral Jacobi–Galerkin methods will be studied.