Supermemory gradient methods for monotone nonlinear equations with convex constraints

Abstract

This paper presents two new supermemory gradient algorithms for solving convex-constrained nonlinear monotone equations, which combine the idea of supermemory gradient method with the projection method. The feature of these proposed methods is that at each iteration, they do not require the Jacobian information and solve any subproblem, even if they do not store any matrix. Thus, they are suitable for solving large-scale equations. Under mild conditions, the proposed methods are shown to be globally convergent. Preliminary numerical results show that the proposed methods are efficient and can be applied to solve large-scale nonsmooth equations.

1 Introduction

In this paper, we consider the following problem: finding a vector $x\in R^n$ such that

$$\begin{aligned} F(x)=0, \quad x\in X, \end{aligned}$$

(1.1)

where $F: R^n\rightarrow R^n$ is continuous and monotone mapping, i.e.,

$$\begin{aligned} (F(x)-F(y))^T(x-y)\ge 0, \quad \forall x, y\in R^n, \end{aligned}$$

(1.2)

$X\subset R^n$ is a nonempty closed convex set, and sometimes an $n$-dimensional box, i.e., $X=\{x\in R^n: \ l\le x\le u\}$. Throughout the paper, $\Vert \cdot \Vert$ denotes the Euclidean norm on $R^{n}$, and $F_k$ denotes $F(x_k)$.

Systems of monotone equations commonly arise in many applications, for instance, they are used as subproblems of the generalized proximal algorithms with Bregman distance (Iusem and Solodov 1997). Some monotone variational inequality problems can be converted into systems of nonlinear monotone equations (Zhao and Li 2001). Moreover, the equations with convex constraints come from the problems such as the power flow equations and the $l_1$-norm regularized optimization problems in compressive sensing, see Refs. Wood and Wollenberg (1996) and Figueiredo (2007) for instance.

In recent years, this special class of optimization problem (1.1) has been studied extensively and there are already many numerical methods for solving it, such as Newton-based methods, Levenberg–Marquardt method, trust region method and projection method, see Refs. Tong and Zhou (2005), Fan (2013), Jia and Zhu (2011) and Wang (2007) for instance. However, these methods need to solve a linear system of equations or a trust region subproblem at each iteration using the Jacobian matrix or an approximation of it, thus they are only suitable for small-scale problems. More recently, large-scale nonlinear constrained equations have been attracting more and more attention from researchers, and some efficient methods have been proposed, which mainly include the spectral gradient method and conjugate gradient method, see Refs. Yu et al. (2009) and Xiao and Zhu (2013) for instance. The main feature of these methods is that at each iteration, the search direction can be obtained without using the Jacobian information and storing any matrix. The drawback of these methods is that they use the previous one-step iterative information at best to generate the search direction at each iteration. It is worth mentioning that the derivative-free methods for problem (1.1) with $X=R^n$ also belong to the conjugate gradient scheme, see Refs. Yan et al. (2010), Li and Li (2011) and Ahookhosh et al. (2013) for instance.

Similar methods to the conjugate gradient methods for unconstrained optimization [see Ref. Hager and Zhang 2006 for details] are the memory gradient (MG) method and the supermemory gradient (SMG) method (Shi and Shen 2005). Not only is their basic idea simple but also they avoid the computation and the storage of some matrices so that they are also suitable to solve large-scale optimization problems. Compared with CG methods, however, the main difference is that MG and SMG methods can sufficiently use the previous multi-step iterative information to generate a new iterate at each iteration, and hence it is more helpful to design algorithms with fast convergence rate, see Refs. Shi and Shen (2005), Narushima and Yabe (2006), Ou and Wang (2012), Ou and Liu (2014) and Sun and Ba (2011) for instance.

Motivated by the supermemory gradient method (Ou and Liu 2014) and the projection strategy (Wang 2007), we propose two new supermemory gradient methods for solving the nonlinear monotone equations (1.1). The main properties of the proposed methods are that we establish the global convergence without using any merit function and making the differentiability assumption on $F$. Furthermore, these methods do not solve any subproblem and store any matrix. Thus, they can be applied to solve large-scale nonlinear equations. Preliminary numerical results are reported to show that the proposed methods are efficient and stable.

The rest of the paper is organized as follows. In Sect. 2, the detailed algorithm is outlined and then some of its properties are given. Section 3 is devoted to analyze the global convergence property of our algorithm under some mild conditions. In Sect. 4, further discussion on the choice of search direction is given. In Sect. 5, numerical results and comparison are reported to show the efficiency of the proposed methods. Some conclusions are summarized in the final section.

2 Supermemory gradient algorithm

This section is devoted to constructing a new supermemory gradient method for solving problem (1.1), then giving some properties of the proposed method.

We first recall the iterative scheme of supermemory gradient method (Ou and Liu 2014) for solving the unconstrained optimization problem:

$$\begin{aligned} \min _{x\in R^n} f(x), \end{aligned}$$

(2.1)

where $f: R^n\rightarrow R$ is a continuously differentiable function whose gradient at $x_k$ is denoted by $g_k:=\nabla f(x_k)$. Given any starting point $x_0\in R^n$, the algorithm in Ou and Liu (2014) is to generate a sequence $\{x_k\}$ which satisfies the following recursive form

$$\begin{aligned} x_{k+1}=x_k+\alpha _kd_k, \quad k=0, 1, 2, \ldots , \end{aligned}$$

(2.2)

where $\alpha _k$ is a stepsize, and $d_k$ is a descent direction of $f(x)$ at $x_k$ defined by

$$\begin{aligned} d_k=\left\{ \begin{array}{l@{\quad }l} -g_k, &{} k\le m,\\ -g_k+\sum _{i=1}^{m}\beta _k^id_{k-i},&{} k\ge m+1, \end{array} \right. \end{aligned}$$

(2.3)

where $m$ denotes the number of the past iterations remembered, and

$$\begin{aligned} \beta _k^i=\frac{\rho \Vert g_k\Vert }{\Vert d_{k-i}\Vert } \end{aligned}$$

(2.4)

with $\rho \in (0, \frac{1}{m})$. For details, see Ref. Ou and Liu (2014).

Based on the above scheme (2.3)–(2.4), here we define $d_k$ as

$$\begin{aligned} d_k=\left\{ \begin{array}{l@{\quad }l} -F_k, &{} \; k\le m,\\ -F_k+\sum _{i=1}^{m}\beta _k^id_{k-i},&{} \; k\ge m+1, \end{array} \right. \end{aligned}$$

(2.5)

where

$$\begin{aligned} \beta _k^i=\frac{\rho \Vert F_k\Vert }{\sum _{i=1}^{m}\Vert d_{k-i}\Vert } \end{aligned}$$

(2.6)

with $\rho \in (0, \frac{1}{2})$.

To describe our algorithm, we introduce the definition of projection operator $P_{\varOmega } [\cdot ]$ which is defined as a mapping from $R^n$ to a nonempty closed convex subset $\varOmega$:

$$\begin{aligned} P_{\varOmega } [x]=\text{ arg }\min _{y\in \varOmega }\{\Vert y-x\Vert \}, \quad \forall x\in R^n. \end{aligned}$$

(2.7)

A well-known property of this operator is that it is nonexpansive [see Wang (2007)], namely,

$$\begin{aligned} \Vert P_{\varOmega } [x]-P_{\varOmega } [y]\Vert \le \Vert x-y\Vert , \quad \forall x, y\in R^n. \end{aligned}$$

(2.8)

We now formally state the steps of the supermemory gradient algorithm for solving problem (1.1) as follows.

Algorithm 2.1

• Step 0 Given an initial point $x_0\in X$, $\epsilon \ge 0$, $\sigma \in (0, 1)$, $\rho \in (0, \frac{1}{2})$, an integer $m>0$, and $\beta \in (0, 1)$. Set $k:= 0$.

• Step 1 Compute $F_k$. If $\Vert F_k\Vert \le \epsilon$, then stop.

• Step 2 Construct a memory search direction $d_k$ using (2.5)–(2.6).

• Step 3 Compute the trial point $z_k=x_k+\alpha _k d_k$, where $\alpha _k=\beta ^{l_k}$ with $l_k$ being the smallest nonnegative integer $l$ such that

  $$\begin{aligned} -F(x_k+\beta ^l d_k)^{T} d_k\ge \sigma \beta ^l\Vert F(x_k+\beta ^l d_k)\Vert \Vert d_k\Vert ^2. \end{aligned}$$

  (2.9)

• Step 4 Compute the new iterate $x_{k+1}$ by

  $$\begin{aligned} x_{k+1}=P_X \left[ x_k-\frac{(x_k-z_k)^TF(z_k)}{\Vert F(z_k)\Vert ^2}F(z_k)\right] . \end{aligned}$$

  (2.10)

• Step 5 Set $k:=k+1$, and go to Step 1.

Remark 2.1

The line search scheme (2.9) is similar to that in Refs. Yan et al. (2010), Li and Li (2011) and Ahookhosh et al. (2013). Because it does not include any matrix and gradient information, it can be used to devise efficient methods for solving large-scale nonlinear equations. From Lemma 3.1 below, it follows that the line search scheme (2.9) is well defined, namely, it terminates in a finite number of steps.

It should be pointed out that there are two distinct differences between the proposed algorithm and the algorithms in Refs. Yu et al. (2009) and Xiao and Zhu (2013), that is, the construction of search direction $d_k$ and the line search scheme, see Refs. Yu et al. (2009) and Xiao and Zhu (2013) for details.

Remark 2.2

Step 4 has a nice geometric interpretation as follows: suppose $x_k$ is not a solution to problem (1.1). Then, using the line search scheme (2.9), the trial point $z_k$ is obtained to satisfy

$$\begin{aligned} F(z_k)^T(z_k-x_k)<0. \end{aligned}$$

(2.11)

On the other hand, using the monotonicity property of $F(x)$, for any $\bar{x}$ such that $F(\bar{x})=0$, we conclude that

$$\begin{aligned} F(z_k)^T(z_k-\bar{x})\ge 0, \end{aligned}$$

(2.12)

which, together with (2.11), implies that the hyperplane

$$\begin{aligned} H_k=\{x\in R^n|F(z_k)^T(x-z_k)=0\} \end{aligned}$$

(2.13)

strictly separates the current iterate $x_k$ from the solution set of problem (1.1). Based on this fact, we can see that the next iterate $x_{k+1}$ is computed by projecting $x_k$ onto the intersection of the feasible set X with the halfspace $H_k^{-}=\{x\in R^n|F(z_k)^T(x-z_k)\le 0\}$.

Obviously, the search direction $d_k$ defined by (2.5) and (2.6) satisfies the following properties:

$$\begin{aligned} F_k^Td_k\le -(1-\rho )\Vert F_k\Vert ^2, \quad \forall k, \end{aligned}$$

(2.14)

and

$$\begin{aligned} \Vert d_k\Vert \le (1+\rho )\Vert F_k\Vert , \quad \forall k. \end{aligned}$$

(2.15)

3 Convergence analysis

In this section, we analyze the global convergence property of Algorithm 2.1 when it is applied to problem (1.1). For this purpose, we first make the following assumptions.

• A1 The solution set $X^{*}$ of problem (1.1) is nonempty.

• A2 The mapping $F$ is Lipschitz continuous on the nonempty closed convex set $X$, namely, there exists a constant $L>0$ such that

  $$\begin{aligned} \Vert F(x)-F(y)\Vert \le L\Vert x-y\Vert , \quad \forall x, y\in X. \end{aligned}$$

  (3.1)

In what follows we assume that $F_k\ne 0$ for all $k$, namely, Algorithm 2.1 generates an infinite sequence $\{x_k\}$. Otherwise, we obtain a solution of problem (1.1).

The following lemma shows that Algorithm 2.1 is well defined.

Lemma 3.1

Algorithm 2.1 is well defined, namely, there exists a nonnegative number $l_k$ satisfying the line search scheme (2.9) for all $k$.

Proof

By contradiction, suppose that there exists $k_0\ge 0$ such that (2.9) fails to hold for any nonnegative number $l$, namely

$$\begin{aligned} -F(x_{k_0}+\beta ^l d_{k_0})^{T} d_{k_0}< \sigma \beta ^l\Vert F(x_{k_0}+\beta ^l d_{k_0})\Vert \Vert d_{k_0}\Vert ^2, \quad \forall l\ge 0. \end{aligned}$$

(3.2)

Taking $l\rightarrow +\infty$ on both sides of (3.2) and using the continuity of $F$, we have

$$\begin{aligned} -F(x_{k_0})^T d_{k_0}\le 0 \end{aligned}$$

which contracts this fact that $-F_k^Td_k\ge (1-\rho )\Vert F_k\Vert ^2 >0$ for all $k$.

Lemma 3.2

Let $x^{*}\in X^{*}$ and the sequences $\{x_k\}$ and $\{z_k\}$ be generated by Algorithm 2.1. Then we have

$$\begin{aligned} \Vert x_{k+1}-x^{*}\Vert ^2\le \Vert x_k-x^{*}\Vert ^2-\sigma ^2\Vert x_k-z_k\Vert ^4, \end{aligned}$$

(3.3)

and

$$\begin{aligned} \lim _{k\rightarrow +\infty }\Vert x_k-z_k\Vert = \lim _{k\rightarrow +\infty } \alpha _k \Vert d_k\Vert =0. \end{aligned}$$

(3.4)

Proof

From the line search scheme (2.9), it follows that

$$\begin{aligned} F(z_k)^T(x_k-z_k)=-\alpha _k F(z_k)^Td_k\ge \sigma \alpha _k^2\Vert F(z_k)\Vert \Vert d_k\Vert ^2, \end{aligned}$$

(3.5)

which implies that

$$\begin{aligned} \frac{F(z_k)^T(x_k-z_k)}{\Vert F(z_k)\Vert }\ge \sigma \alpha _k^2 \Vert d_k\Vert ^2=\sigma \Vert x_k-z_k\Vert ^2. \end{aligned}$$

(3.6)

Using the monotonicity of mapping $F$ and $F(x^*)=0$, we have

$$\begin{aligned} F(z_k)^T(z_k-x^*)\ge F(x^*)^T(z_k-x^*)=0. \end{aligned}$$

(3.7)

This together with (3.5) implies that

$$\begin{aligned} F(z_k)^T(x_k-x^*)\ge F(z_k)^T(x_k-z_k)\ge 0. \end{aligned}$$

(3.8)

Combining this inequality with (2.8) and (3.6) gives

$$\begin{aligned} \Vert x_{k+1}-x^{*}\Vert ^2= & {} \Vert P_X [x_k-\frac{(x_k-z_k)^TF(z_k)}{\Vert F(z_k)\Vert ^2}F(z_k)] -P_X[x^*]\Vert ^2\nonumber \\\le & {} \Vert x_k-\frac{(x_k-z_k)^TF(z_k)}{\Vert F(z_k)\Vert ^2}F(z_k)-x^*\Vert ^2\nonumber \\\le & {} \Vert x_k-x^{*}\Vert ^2-\frac{[F(z_k)^T(x_k-z_k)]^2}{\Vert F(z_k)\Vert ^2}\nonumber \\\le & {} \Vert x_k-x^{*}\Vert ^2-\sigma ^2\Vert x_k-z_k\Vert ^4. \end{aligned}$$

(3.9)

Thus, this inequality (3.3) holds true. Furthermore, it follows directly from (3.3) that the sequence $\{\Vert x_k-x^*\Vert \}$ is decreasing monotonically and convergent. Taking $k\rightarrow +\infty$ on both sides of (3.3) yields (3.4). This completes the proof. $\Vert$

Corollary 3.3

Let the sequence $\{x_k\}$ be generated by Algorithm 2.1. If Assumptions A1 and A2 hold, then there exists a constant $M>0$ such that

$$\begin{aligned} \Vert F_k\Vert \le M, \quad \forall k, \end{aligned}$$

(3.10)

and

$$\begin{aligned} \Vert F(x_k+\alpha _k\beta ^{-1}d_k)\Vert \le M, \quad \forall k. \end{aligned}$$

(3.11)

Proof

Let $x^{*}\in X^{*}$. It follows from A2 and (3.3) that

$$\begin{aligned} \Vert F_k\Vert =\Vert F_k-F(x^*)\Vert \le L\Vert x_k-x^*\Vert \le L\Vert x_{k-1}-x^*\Vert \le \cdots \le L\Vert x_0-x^*\Vert . \end{aligned}$$

(3.12)

By (3.4), we can deduce that there exists a constant $M_0>0$ such that

$$\begin{aligned} \alpha _k\Vert d_k\Vert \le M_0, \quad \forall k. \end{aligned}$$

(3.13)

Combining (3.13) with (3.3) gives

$$\begin{aligned} \Vert F(x_k+\alpha _k\beta ^{-1}d_k)\Vert= & {} \Vert F(x_k+\alpha _k\beta ^{-1}d_k)-F(x^*)\Vert \nonumber \\\le & {} L\Vert x_k+\alpha _k\beta ^{-1}d_k-x^*\Vert \nonumber \\\le & {} L\Vert x_k-x^{*}\Vert +L\beta ^{-1}\alpha _k\Vert d_k\Vert \nonumber \\\le & {} L\Vert x_0-x^*\Vert +L\beta ^{-1}M_0, \ \forall k. \end{aligned}$$

(3.14)

Let $M=L\Vert x_0-x^*\Vert +L\beta ^{-1}M_0$. Then the conclusions (3.10) and (3.11) follow directly from the above inequalities (3.12) and (3.14). This completes the proof. $\Vert$

Lemma 3.4

Suppose that Assumptions A1 and A2 hold. Then there exists a constant $\gamma >0$ such that the stepsize $\alpha _k$ involved in Step 3 of Algorithm 2.1 satisfies

$$\begin{aligned} \alpha _k\ge \min \left\{ 1, \; \gamma \frac{\Vert F_k\Vert ^2}{\Vert d_k\Vert ^2}\right\} . \end{aligned}$$

(3.15)

Proof

If $\alpha _k\ne 1$, then it follows from the acceptance rule of stepsize $\alpha _k$ in Step 3 of Algorithm 2.1 that $\alpha _k'=\frac{\alpha _k}{\beta }$ does not satisfy (2.9), namely

$$\begin{aligned} -F(x_{k}+\alpha _k' d_{k})^{T} d_{k}< \sigma \alpha _k'\Vert F(x_{k}+\alpha _k'd_{k})\Vert \Vert d_{k}\Vert ^2. \end{aligned}$$

(3.16)

This together with (2.14) and (3.11) implies that

$$\begin{aligned} (1-\rho )\Vert F_k\Vert ^2\le & {} -F_k^Td_k\nonumber \\= & {} [F(x_k+\alpha _k'd_k)-F_k]^Td_k-F(x_k+\alpha _k'd_k)^Td_k\nonumber \\\le & {} \alpha _k'L\Vert d_k\Vert ^2+\sigma \alpha _k' \Vert F(x_{k}+\alpha _k'd_{k})\Vert \Vert d_{k}\Vert ^2\nonumber \\\le & {} \alpha _k'(L+\sigma M)\Vert d_{k}\Vert ^2. \end{aligned}$$

(3.17)

Obviously, if $\Vert d_k\Vert \ne 0$, then (3.15) follows directly from (3.17), where $\gamma =\frac{\beta (1-\rho )}{L+\sigma M}$.

In what follows, we verify the validity of the assertion $\Vert d_k\Vert \ne 0$ for all $k$. In fact, it follows from (2.14) that

$$\begin{aligned} \Vert d_{k}\Vert ^2= & {} \Vert d_{k}+F_k\Vert ^2+\Vert F_{k}\Vert ^2-2F_k^T(F_k+d_k)\nonumber \\\ge & {} \Vert F_{k}\Vert ^2-2F_k^T(F_k+d_k)\nonumber \\\ge & {} 2(1-\rho )\Vert F_k\Vert ^2-\Vert F_{k}\Vert ^2\nonumber \\= & {} (1-2\rho )\Vert F_{k}\Vert ^2, \quad \forall k, \end{aligned}$$

(3.18)

which implies that $\Vert d_k\Vert \ne 0$ for all $k$, due to $\rho \in (0, \frac{1}{2})$ and $|F_{k}\Vert \ne 0$ for all $k$. This completes the proof. $\Vert$

Using these lemmas mentioned above, we obtain the global convergence of Algorithm 2.1 as follows.

Theorem 3.5

Suppose that Assumptions A1 and A2 hold. Then we have

$$\begin{aligned} \lim _{k\rightarrow +\infty }\inf \Vert F_k\Vert =0. \end{aligned}$$

(3.19)

Furthermore, the sequence $\{x_k\}$ generated by Algorithm 2.1 converges to a solution of (1.1).

Proof

Suppose on the contrary that there exists $\delta >0$ such that

$$\begin{aligned} \Vert F_k\Vert \ge \delta , \quad \forall k. \end{aligned}$$

(3.20)

From Corollary 3.3 and (2.15), it follows that there exists a constant $M>0$ such that

$$\begin{aligned} \Vert d_k\Vert \le (1+\rho )\Vert F_k\Vert \le (1+\rho )M. \end{aligned}$$

(3.21)

On the other hand, using (3.18) and (3.20), we have

$$\begin{aligned} \Vert d_k\Vert \ge \sqrt{1-2\rho } \ \Vert F_k\Vert \ge \sqrt{1-2\rho } \ \delta . \end{aligned}$$

(3.22)

Combining (3.15) with (3.20)–(3.22) gives

$$\begin{aligned} \alpha _k\Vert d_k\Vert \ge \min \left\{ 1, \; \gamma \frac{\Vert F_k\Vert ^2}{\Vert d_k\Vert ^2}\right\} \Vert d_k\Vert \ge \min \left\{ \sqrt{1-2\rho } \ \delta , \; \frac{\gamma \delta ^2}{(1+\rho )M}\right\} . \end{aligned}$$

This yields a contradiction with (3.4). Thus, the assertion (3.19) holds true.

Now, we will prove the second assertion. By the continuity of $F$ and the boundedness of $\{x_k\}$ due to (3.3), it is clear that the sequence $\{x_k\}$ exists an accumulation point $\bar{x}$ such that $F(\bar{x})=0$ due to (3.19). Taking $x^*=\bar{x}$ in (3.3), we further deduce that the sequence $\{\Vert x_k-\bar{x}\Vert \}$ is convergent, and thus the sequence $\{x_k\}$ converges globally to $\bar{x}$. The proof is completed. $\Vert$

At the end of this section, we must point out that the requirement (1.2) of monotonicity on $F$ seems to be strong for the purpose of ensuring the global convergence property. Actually, if the mapping $F$ has the following property:

$$\begin{aligned} F(x)^T(x-x^*)\ge 0, \quad \forall x\in R^n, \quad x^*\in X^*, \end{aligned}$$

(3.23)

then it can be easily verified that all the preceding conclusions still hold true, provided that a little modification is made in the proof process of Lemma 3.2. Note that the property (3.23) is satisfied if $F$ is monotone or pseudomonotone, but not vice versa, see Ref. Solodov and Svaiter (1999) for instance. Therefore, our convergence results can be restated under the assumption (3.23), which is considerably weaker than the assumption (1.2) of monotonicity on $F$. We omit them here.

4 Further discussion

From Step 2 of Algorithm 2.1, we can see that the search direction $d_k$ plays a key role in designing a method for solving problem (1.1). In fact, there are some other possible choices of $d_k$. For example, we may choose

$$\begin{aligned} d_k=\left\{ \begin{array}{l@{\quad }l} -F_k, &{} \text{ if } \; k\le m,\\ -\lambda _{k}^{(k)}F_k-\sum _{i=1}^{m}\lambda _{k-i}^{(k)}d_{k-i}, &{} \text{ if } \; k\ge m+1 \end{array} \right. \end{aligned}$$

(4.1)

with

$$\begin{aligned} \lambda _{k}^{(k)}=1-\sum _{i=1}^{m}|\lambda _{k-i}^{(k)}|, \; \lambda _{k-i}^{(k)}=\left\{ \begin{array}{l@{\quad }l} \frac{\rho }{m}\cdot \frac{\Vert F_k\Vert ^2}{\Vert F_k\Vert ^2+|F_k^Td_{k-i}|}, &{} \text{ if } \; F_k^Td_{k-i}\ge 0,\\ -\frac{\rho }{m} \cdot \frac{\Vert F_k\Vert ^2}{\Vert F_k\Vert ^2+|F_k^Td_{k-i}|}, &{} \text{ if } \; F_k^Td_{k-i}< 0, \end{array} \right. \end{aligned}$$

($i=1, 2, \ldots , m$) and $0<\rho <1$.

Remark 4.1

Based on the direction $d_k$ defined as (4.1), we can construct a new algorithm denoted by Algorithm 4.1, which is similar to Algorithm 2.1 except that the direction $d_k$ in Step 2 is replaced by (4.1), we omit it here.

In what follows, we discuss the global convergence of Algorithm 4.1. To this end, we give two properties as follows.

Lemma 4.1

For any $k\ge 0$, we have

$$\begin{aligned} F_k^Td_k\le -(1-\rho )\Vert F_k\Vert ^2. \end{aligned}$$

(4.2)

Proof

If $k\le m$, then (4.2) is obvious. If $k\ge m+1$, then we have

$$\begin{aligned} |\lambda _{k-i}^{(k)}|= & {} \frac{\rho }{m}\cdot \frac{\Vert F_k\Vert ^2}{\Vert F_k\Vert ^2+|F_k^Td_{k-i}|},\\ |\lambda _{k-i}^{(k)}F_k^Td_{k-i}|= & {} \lambda _{k-i}^{(k)}F_k^Td_{k-i}, \quad i=1, 2, \ldots , m, \end{aligned}$$

which, together with (4.1), implies that

$$\begin{aligned} -F_k^Td_k= & {} \lambda _k^{(k)}\Vert F_k\Vert ^2+ \sum _{i=1}^{m}\lambda _{k-i}^{(k)}F_k^Td_{k-i} \\= & {} \left( 1-\sum _{i=1}^{m}|\lambda _{k-i}^{(k)}|\right) \Vert F_k\Vert ^2+ \sum _{i=1}^{m}\lambda _{k-i}^{(k)}F_k^Td_{k-i} \\= & {} \Vert F_k\Vert ^2-\sum _{i=1}^{m}|\lambda _{k-i}^{(k)}|(\Vert F_k\Vert ^2 -|F_k^Td_{k-i}|)\\\ge & {} \Vert F_k\Vert ^2-\sum _{i=1}^{m}|\lambda _{k-i}^{(k)}|(\Vert F_k\Vert ^2 +|F_k^Td_{k-i}|)\\= & {} (1-\rho )\Vert F_k\Vert ^2. \end{aligned}$$

This completes this proof. $\Vert$

Lemma 4.2

• 1. For any $k\ge m$, we have

  $$\begin{aligned} \Vert d_k\Vert \le \max _{1\le i\le m} \{\Vert F_k\Vert , \; \Vert d_{k-i}\Vert \}. \end{aligned}$$

  (4.3)

• 2. For any $k\ge 0$, we have

  $$\begin{aligned} \Vert d_k\Vert \le \max _{0\le i\le k}\Vert F_{i}\Vert . \end{aligned}$$

  (4.4)

Proof

If $k\le m$, then (4.3) is obvious. We now show that (4.3) holds for $k\ge m+1$. Clearly, $\lambda _{k}^{(k)}\le 1$ and

$$\begin{aligned} \lambda _{k}^{(k)}= & {} 1-\sum _{i=1}^{m}|\lambda _{k-i}^{(k)}|\\= & {} 1-\frac{\rho }{m}\sum _{i=1}^{m} \frac{\Vert F_k\Vert ^2}{\Vert F_k\Vert ^2+|F_k^Td_{k-i}|}\\\ge & {} 1-\frac{\rho }{m}\cdot m\\= & {} 1-\rho >0 \end{aligned}$$

This implies that

$$\begin{aligned} \sum _{i=0}^{m}|\lambda _{k-i}^{(k)}|=1. \end{aligned}$$

(4.5)

Hence, it follows from (4.1) and (4.5) that

$$\begin{aligned} \Vert d_k\Vert\le & {} \left( 1-\sum _{i=1}^{m}|\lambda _{k-i}^{(k)}|\right) \Vert F_k\Vert + \sum _{i=1}^{m}|\lambda _{k-i}^{(k)}| \cdot \Vert d_{k-i}\Vert \\\le & {} \max _{1\le i\le m} \{\Vert F_k\Vert , \; \Vert d_{k-i}\Vert \}, \end{aligned}$$

which implies that this inequality (4.3) holds true.

Using induction process, we can deduce directly from (4.3) and (4.1) that this inequality (4.4) also holds true. This completes this proof. $\Vert$

Using Lemmas 4.1 and 4.2, we can easily establish the global convergence of Algorithm 4.1, whose proof is the same as that of Theorem 3.5 and thus is omitted.

Theorem 4.3

Suppose that Assumptions A1 and A2 hold. Then we have

$$\begin{aligned} \lim _{k\rightarrow +\infty }\inf \Vert F_k\Vert =0. \end{aligned}$$

Furthermore, the sequence $\{x_k\}$ generated by Algorithm 4.1 converges to a solution of (1.1).

5 Numerical tests

In this section, we present some numerical experiments to evaluate the performance of the proposed methods on two sets of test problems. At the same time, we give some comparisons with the related algorithms, including the performance profiles of Dolan and More (2002).

We first present some numerical experiments for Algorithms 2.1 and 4.1 on three constrained monotone testing problems, which are chosen from Refs. Yu et al. (2009) and Yan et al. (2010).

Problem 1

The elements of function $F$ are given by

$$\begin{aligned} F_i(x)=\exp (x_i)-1, \quad i=1, 2, \ldots , n, \quad \mathrm{and}\quad X=\{x\in R^n| x_i\ge 0, \quad i=1, 2, \ldots , n\}. \end{aligned}$$

Problem 2

The elements of function $F$ are given by

$$\begin{aligned}&F_i(x)=x_i-\sin (|x_i-1|), \quad i=1, 2, \ldots , n, \quad \mathrm{and}\quad \\&\quad X=\left\{ x\in R^n| \sum _{i=1}^{n}x_i\le n, x_i\ge 0, \quad i=1, 2, \ldots , n\right\} . \end{aligned}$$

Obviously, this problem is nonsmooth at point $(1, 1, \ldots , 1)^T \in R^n$.

Problem 3

The elements of function $F$ are given by

$$\begin{aligned} F_1(x)= & {} x_1-\exp \left( \cos \left( \frac{x_1+x_2}{n+1}\right) \right) ,\\ F_i(x)= & {} x_i-\exp \left( \cos \left( \frac{x_{i-1}+x_{i}+x_{i+1}}{n+1}\right) \right) , \quad i=2, 3, \ldots , n-1,\\ F_n(x)= & {} x_n-\exp \left( \cos \left( \frac{x_{n-1}+x_{n}}{n+1}\right) \right) , \end{aligned}$$

and $X=\{x\in R^n| x_i\ge 0, \ i=1, 2, \ldots , n\}$.

To validate Algorithms 2.1 and 4.1 from a computational point of view, we compare them with the algorithm in Ref. Yu et al. (2009) (abbreviated Algorithm Yu) and the algorithm in Ref. Xiao and Zhu (2013) (abbreviated Algorithm Xiao) for the same problems mentioned above, where the latter two algorithms were also devised especially for the monotone case.

We implemented all the algorithms with the codes written in Matlab 7.12. The testing is performed on a PC computer with HPdx2810SE Pentium(R) Dual-Core CPU E5300 @ 2.60 GHZ 2.00 GB. Throughout the computational experiments, the parameters used in Algorithms 2.1 and 4.1 are chosen as follows: $\rho =0.0001, \ \sigma =0.0001, \ \beta =0.9, \ m=5$; the parameters used in Algorithm Yu are chosen as follows: $\beta =0.5, \ \sigma =0.01, \ r=0.01$, while the parameters used in Algorithm Xiao are chosen as follows: $\xi =1, \ \rho =0.5, \ \sigma =0.0001$.

All testing examples start at six initial points listed as follows:

$$\begin{aligned} X1= & {} (10, 10, \ldots , 10)^T, \quad X2=(1, 1, \ldots , 1)^T, \quad X3=\left( 1, \frac{1}{2}, \ldots , \frac{1}{n}\right) , \\ X4= & {} (0.1, 0.1,\ldots , 0.1)^T, \quad X5=\left( \frac{1}{n}, \frac{2}{n}, \ldots , 1\right) ^T,\quad X6=\left( 1-\frac{1}{n}, 1-\frac{2}{n}, \ldots , 0\right) ^T, \end{aligned}$$

and the stopping condition for each algorithm is

$$\begin{aligned} \Vert F_k\Vert \le 10^{-5}. \end{aligned}$$

(5.1)

The numerical results are reported in Tables 1, 2 and 3, where the number $n$ refers to the dimension of variables. The numerical results are given in the form of $It/NF/T/FN$, where $It$, $NF$, $T$ and $FN$ denote the number of iterations, the number of function evaluations, the CPU time in seconds and the final norm of $F$, respectively. If a method does not find a solution, but terminates by exceeding 300 s, or presets iteration limit $k=5000$, we denote it by the word F.

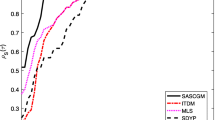
We use the performance profile proposed by Dolan and More (2002) to display the performance of each implementation on the set of test problems. That is, for each method, we plot the fraction $P$ of problems for which the method is within a factor $\tau$ of the smallest number of iterations/function evaluations/CPU times. Clearly, the left side of the figure gives the percentage of the test problems for which a method is the best one according to the number of iterations/function evaluations/CPU times, while the right side of the figure gives the percentage of the test problems that is successfully solved by these algorithms. For more details about the performance profile, please see Ref. Dolan and More (2002). Based on the testing results in Tables 1, 2 and 3, we give the performance profiles in Figs. 1, 2 and 3.

From Figs. 1, 2 and 3, we observe the following facts:

• In terms of the number of iterations, Algorithm 4.1 performs best, and Algorithm 2.1 performs roughly the same as Algorithm Yu, while Algorithm Xiao performs worst.

• In terms of the number of function evaluations, Algorithm 4.1 performs roughly the same as Algorithm Yu and Algorithm 2.1, but does better than Algorithm Xiao.

• In terms of the CPU time, Algorithm 4.1 performs roughly the same as Algorithm Yu, but both of them do better than Algorithm 2.1, while Algorithm Xiao performs worst.

• For the test problems, Algorithms 2.1 and 4.1 are competitive with the other two methods, in terms of the accuracy of approximate solutions obtained.

Therefore, we could say that Algorithms 2.1 and 4.1 are competitive to Algorithms Yu and Xiao, in terms of the computational effort and accuracy.

Table 1 Numerical results for Problem 1

Table 2 Numerical results for Problem 2

Table 3 Numerical results for Problem 3

Fig. 1

Performance profile for the number of iterations

Fig. 2

Performance profile for the number of function evaluations

Fig. 3

Performance profile for the CPU time

To examine Algorithm 2.1’s sensitivity to the choices of the parameters $m$ and $\rho$, we also do some preliminary numerical experiments with varying values of them, and then give the performance profiles in Figs. 4 and 5. From Figs. 4 and 5, we can observe the following facts:

• The choice of $\rho$ has little impact on Algorithm 2.1 if $\gamma \in (0, 0.001]$ and the other parameters keep the same as the initial values, i.e., $\sigma =0.0001$, $\beta =0.9$, $m=5$.

• The choice of $m$ has little impact on Algorithm 2.1 if $3\le m\le 6$ and the other parameters keep the same as the initial values, i.e., $\rho =0.0001$, $\sigma =0.0001$, $\beta =0.9$.

Similarly, it has been observed that Algorithm 4.1 is also not very sensitive to the choices of the parameters $m$ and $\rho$.

Fig. 4

Performance profile for CPU with varying values of $\rho$

Fig. 5

Performance profile for CPU with varying values of $m$

According to an anonymous referee’s suggestion, in the second set of numerical experiments, we compare the performance of Algorithms 2.1 and 4.1 with two typical gradient-based methods for solving large-scale unconstrained optimization problems: L-BFGS method with the Wolfe line search (see Ref. Nocedal and Wright 1999 for details) and CG-HZ method with the Wolfe line search (Hager and Zhang 2005). The test problems are listed as follows (Li and Li 2011):

Problem 4

The elements of function $F$ are given by

$$\begin{aligned} F_i(x)=2x_i-\sin (x_i), \quad i=1, 2, \ldots , n, \quad \mathrm{and}\quad X=R^n. \end{aligned}$$

Problem 5

The elements of function $F$ are given by

$$\begin{aligned} F_i(x)=\ln (x_i+1)-\frac{x_i}{n}, \quad i=1, 2, \ldots , n,\quad \mathrm{and}\quad X=R^n. \end{aligned}$$

These testing problems start at six initial points listed as follows:

$$\begin{aligned} X7= & {} (10, 10, \ldots , 10)^T, \quad X8=(1, 1, \ldots , 1)^T, \quad X9=\left( 1, \frac{1}{2}, \ldots , \frac{1}{n}\right) ,\\ X10= & {} (0.1, 0.1, \ldots , 0.1)^T, \quad X11=-X10, \quad X12=\left( \frac{1}{n}, \frac{1}{n}, \ldots , \frac{1}{n}\right) ^T. \end{aligned}$$

Throughout the computational experiments, the L-BFGS method and the CG-HZ method implement the Wolfe line search conditions (Nocedal and Wright 1999) with $c_1=0.01$ and $c_2=0.9$. In addition, the merit function $f(x)=\sum _{i=1}^{n}F_i^2(x)$ is used in implementing the L-BFGS method and the CG-HZ method. Each method is stopped if the condition (5.1) is satisfied.

Tables 4 and 5 show the test results, where $M$ is the number of limited memory corrections stored, and the numerical results are given in the form of $T/FN$, while other meanings are the same as those in Table 1. Based on the test results in Tables 4 and 5, we also give the performance profiles in Fig. 6.

Table 4 Numerical results for Problem 4

Table 5 Numerical results for Problem 5

From Fig. 6, we can see that for the test problems, the proposed algorithms are competitive to the L-BFGS and CG-HZ methods for large-scale problems, in terms of the CPU times and robustness, while the latter two methods perform slightly better than the former in terms of the accuracy of approximate solutions obtained.

Fig. 6

Performance profile for the CPU time

While it would be unwise to draw any firm conclusions from the limited numerical results and comparisons, they indicate some promise for the new approaches proposed in this paper, compared with the related methods mentioned above. Further improvement is expected from more suitable implementation.

6 Conclusion

In this paper, we propose two new supermemory gradient methods for convex-constrained nonlinear monotone equations. The main properties of the proposed methods are that we establish the global convergence without using any merit function and making the differentiability assumption. Furthermore, these methods do not solve any subproblem and store any matrix. Thus, they can be applied to solve large-scale nonlinear equations. Preliminary numerical results are reported to show that the proposed methods are efficient.

Since the most computational cost of each algorithm for problem (1.1) is to determine the search direction $d_k$ and find the stepsize $\alpha _k$ in line search, we will study some more effective methods for constructing a descent direction $d_k$ and an inexpensive line search in our future research. Furthermore, we should proceed to make some numerical comparisons of the performance between our proposed methods and some popular algorithms for nonsmooth problems in the future research work.