Introduction

In this paper, we focus on solving large-scale nonlinear system of equations

$$\begin{array}{*{20}l} F(x) = 0, \end{array} $$
(1)

where \(F:\mathbb {R}^{n}\rightarrow \mathbb {R}^{n}\) is continuous and monotone. A function F is monotone if it satisfies the monotonicity condition

$$\begin{array}{*{20}l} (F(x)-F(y))^{T}(x-y) \geq 0, \quad \forall x,y\in\mathbb{R}^{n}. \end{array} $$
(2)

Nonlinear monotone equations arise in many practical applications, for example, chemical equilibrium systems [1], economic equilibrium problems [2], and some monotone variational inequality problems [3]. A number of computational methods have been proposed to solve nonlinear equations. Among them, Newton’s method, quasi-Newton method, Gauss-Newton method, and their variants are very popular due to their local superlinear convergence property (see, for example, [4–9]). However, they are not suitable for large-scale nonlinear monotone equations as they need to solve a linear system of equations using the second derivative information (Jacobian matrix or an approximation of it).

Due to their modest memory requirements, conjugate gradient-based projection methods are suitable for solving large-scale nonlinear monotone equations (1). Conjugate gradient-based projection methods generate a sequence {xk} by exploring the monotonicity of the function F. Let zk=xk+αkdk, where αk>0 is the step length that is determined by some line search and

$$d_{k}=\left\{\begin{array}{ll}-F_{k},& k=0,\\ -F_{k} + \beta_{k}d_{k-1},& k\geq 1,\end{array}\right.$$

Fk=F(xk) and βk is a parameter, is the search direction. Then by monotonicity of F, the hyperplane

$$\begin{array}{*{20}l} H_{k}=\{x\in\mathbb{R}^{n}|F(z_{k})^{T}(x-z_{k})=0\} \end{array} $$

strictly separates the current iterate xk from the solution set of (1). Projecting xk on this hyperplane generates the next iterate xk+1 as

$$\begin{array}{*{20}l} x_{k+1}=x_{k}-\frac{F(z_{k})^{T}(x_{k}-z_{k})}{\|F(z_{k})\|^{2}}F(z_{k}). \end{array} $$
(3)

This projection concept on the hyperplane Hk was first presented by Solodov and Svaiter [10].

Following Solodov and Svaiter [10], a lot of work has been done, and continues to be done, to come up with a number of conjugate gradient-based projection methods for nonlinear monotone equations. For example, Hu and Wei [11] proposed a conjugate gradient-based projection method for nonlinear monotone equations (1) where the search direction dk is given as

$$\begin{array}{*{20}l} d_{k}=\left\{\begin{array}{ll} -F_{k}, & k=0, \\ -F_{k}+\frac{F_{k}^{T}y_{k-1}d_{k-1}-d_{k-1}^{T}F_{k}y_{k-1}} {\max\left(\gamma\|d_{k-1}\|\|y_{k-1}\|,d_{k-1}^{T}y_{k-1},-d_{k-1}^{T}F_{k-1}\right)}, & k\geq 1, \end{array}\right. \end{array} $$

yk−1=Fk−Fk−1 and γ>0. This method was shown to perform well numerically and its global convergence was established using the line search

$$\begin{array}{*{20}l} -F(z_{k})^{T}d_{k}\geq\sigma\alpha_{k}\|F(z_{k})\|\| d_{k}\|^{2}, \end{array} $$
(4)

with σ>0 being a constant.

Recently, three term conjugate gradient-based projection methods have also been presented. One such method is that by Feng et al. [12] who presented their direction as

$$d_{k}=\left\{\begin{array}{ll}-F_{k},&k=0,\\ -\left(1+\beta_{k}\frac{F_{k}^{T}d_{k-1}}{\|F_{k}\|^{2}}\right)F_{k}+\beta_{k}d_{k-1},&k\geq 1,\end{array}\right.$$

where \(|\beta _{k}|\leq t\frac {\|F_{k}\|}{\|d_{k-1}\|},\,\, \forall k\geq 1\), and t>0 is a constant. The global convergence of this method was also established using the line search (4). For other conjugate gradient-based projection methods, the reader is referred to [13–27].

In this paper, following the work of Abubakar and Kumam [21], Hu and Wei [11] and that of Liu and Li [22], we propose a self adaptive spectral conjugate gradient-based projection method for solving systems of nonlinear monotone Eq. (1). This method is presented in the next section and the rest of the paper is organized as follows. In “Convergence analysis” section, we show that the proposed method satisfies the descent property \(F_{k}^{T}d_{k}\leq -c\|F_{k}\|^{2}, c>0\), and also establish its global convergence. In “Numerical experiments” section, we present the numerical results and lastly, conclusion is presented in “Conclusion” section.

Algorithm

In this section, we give the details of the proposed method. We start by briefly reviewing the work of Abubakar and Kumam [21] and that of Liu and Li [22].

Most recently, Abubakar and Kumam [21] proposed the direction

$$\begin{array}{*{20}l} d_{k}=\left\{\begin{array}{ll} -F_{k}, & k=0, \\ -F_{k}+\frac{F_{k}^{T}w_{k-1}d_{k-1}-F_{k}^{T}d_{k-1}w_{k-1}}{\max\left(\mu\|d_{k-1}\|\|w_{k-1}\|,w_{k}^{T}d_{k-1}\right)}, & k\geq 1, \end{array}\right. \end{array} $$

where μ is a positive constant and

$$w_{k-1}=y_{k-1}+t\|F_{k}\|s_{k-1},\,\,\, t=1+\|F_{k}\|^{-1}\max\left(0,-\frac{y_{k-1}^{T}s_{k-1}}{\|s_{k-1}\|^{2}}\right)$$

and sk−1=zk−1−xk−1=αk−1dk−1. This method was shown to perform well numerically and its global convergence was established using line search (4). In 2015, Liu and Li [22] proposed a spectral DY-type projection method for nonlinear monotone system of Eq. (1) with the search direction dk as

$$\begin{array}{*{20}l} d_{k}=\left\{\begin{array}{ll} -F_{k}, & k=0,\\ -\lambda_{k} F_{k}+\beta_{k}^{DY}d_{k-1}, & k\geq 1, \end{array}\right. \end{array} $$

where\(\beta _{k}^{DY}=\frac {\|F_{k}\|^{2}}{d_{k-1}^{T}u_{k-1}}\), uk−1=yk−1+tdk−1, \(t=1+\max \left \{0,-\frac {d_{k-1}^{T}y_{k-1}}{d_{k-1}^{T}d_{k-1}}\right \}\), yk−1=Fk−Fk−1+rsk−1 with sk−1=xk−xk−1, r>0 being a constant and \(\lambda _{k}=\frac {s_{k-1}^{T}s_{k-1}}{s_{k-1}^{T}y_{k-1}}\). The global convergence of this method was established using the line search

$$\begin{array}{*{20}l} -F(z_{k})^{T}d_{k}\geq\sigma\alpha_{k}\| d_{k}\|^{2}. \end{array} $$
(5)

Motivated by the work of Abubakar and Kumam [21], Hu and Wei [11] and that of Liu and Li [22], in this paper we present our direction as

$$\begin{array}{*{20}l} d_{k}=\left\{\begin{array}{ll} -F_{k}, & k=0,\\ -\lambda_{k}^{*} F_{k}+\beta_{k}^{MP}d_{k-1}-\delta_{k}^{MP}y_{k-1}, & k\geq 1, \end{array}\right. \end{array} $$
(6)

where

$$\begin{array}{*{20}l} \beta_{k}^{MP}=\frac{F_{k}^{T}y_{k-1}}{\max\{\mu_{k}d_{k-1}^{T}y_{k-1},-\eta F_{k-1}^{T}d_{k-1}+\mu_{k}\|d_{k-1}\|\|y_{k-1}\|\}} \end{array} $$
(7)

and

$$\begin{array}{*{20}l} \delta_{k}^{MP}=\frac{F_{k}^{T}d_{k-1}}{\max\{\mu_{k}d_{k-1}^{T}y_{k-1},-\eta F_{k-1}^{T}d_{k-1}+\mu_{k}\|d_{k-1}\|\|y_{k-1}\|\}} \end{array} $$
(8)

with η>0 being a constant and the parameters \(\lambda _{k}^{*}=\frac {s_{k-1}^{T}y_{k-1}}{s_{k-1}^{T}s_{k-1}}\) and \(\mu _{k}>\frac {1}{\lambda _{k}^{*}}\) where sk−1=xk−xk−1 and yk−1=Fk−Fk−1+rsk−1, r∈(0,1). With dk defined by (6), (7), and (8), we now present our algorithm.

Throughout this paper, we assume that the following assumption holds.

Assumption 1

(i) The function F(·) is monotone on \(\mathbb {R}^{n}\), i.e. \((F(x)-F(y))^{T}(x-y) \geq 0, \forall x,y\in \mathbb {R}^{n}\). (ii) The solution set of (1) is nonempty. (iii) The function F(·) is Lipschitz continuous on \(\mathbb {R}^{n}\), i.e. there exists a positive constant L such that

$$\begin{array}{*{20}l} \parallel F(x)-F(y)\parallel \, \leq L\parallel x-y\parallel, \quad \forall\, x,y\in\mathbb{R}^{n}. \end{array} $$
(9)

Convergence analysis

In this section we present the descent property and global convergence of the proposed method.

Lemma 1

For all k≥0, we have

$$\begin{array}{*{20}l} r\leq\,\lambda_{k}^{*}\leq\,L+r. \end{array} $$
(10)

Proof

From the definition of yk−1, we get that

$$\begin{array}{*{20}l} s_{k-1}^{T}y_{k-1}=(F_{k}-F_{k-1})^{T}(x_{k}-x_{k-1})+r\|s_{k-1}\|^{2}, \end{array} $$

which using the monotonicity of F it follows that

$$\begin{array}{*{20}l} s_{k-1}^{T}y_{k-1}\geq\,r\|s_{k-1}\|^{2}. \end{array} $$
(11)

Also, from the Lipschitz continuity we obtain that

$$\begin{array}{*{20}l} s_{k-1}^{T}y_{k-1}\,\leq\,(L+r)\|s_{k-1}\|^{2}. \end{array} $$
(12)

Combining (11) and (12) we get the inequality (10). This, therefore, means that \(\lambda _{k}^{*}\) is well defined.

Lemma 2

Suppose that Assumption 1 holds. Let the sequence {xk} be generated by Algorithm 1. Then the search direction dk satisfies the descent condition

$$\begin{array}{*{20}l} F_{k}^{T}d_{k}\,\leq\,-r\|F_{k}\|^{2}, \quad \forall\,k\geq0. \end{array} $$
(13)

Proof

Since d0=−F0, we have \(F_{0}^{T}d_{0}=-\|F_{0}\|^{2}\), which satisfies (13). For k≥ 1, we have from (6) that

$$\begin{array}{*{20}l} F_{k}^{T}d_{k}=-\lambda_{k}^{*}\|F_{k}\|^{2}+\beta_{k}^{MP}F_{k}^{T}d_{k-1}-\delta_{k}^{MP}F_{k}^{T}y_{k-1}. \end{array} $$
(14)

Using (7) and (8) we obtain

$$\begin{array}{*{20}l} F_{k}^{T}d_{k}&=-\lambda_{k}^{*}\|F_{k}\|^{2}+\frac{\left(F_{k}^{T}y_{k-1}\right)\left(F_{k}^{T}d_{k-1}\right)}{\max\left\{\mu_{k}d_{k-1}^{T}y_{k-1},-\eta F_{k-1}^{T}d_{k-1}+\mu_{k}\|d_{k-1}\|\|y_{k-1}\|\right\}}\\ &\quad\, -\frac{\left(F_{k}^{T}d_{k-1}\right)\left(F_{k}^{T}y_{k-1}\right)}{\max\left\{\mu_{k}d_{k-1}^{T}y_{k-1},-\eta F_{k-1}^{T}d_{k-1}+\mu_{k}\|d_{k-1}\|\|y_{k-1}\|\right\}}\\ &=-\lambda_{k}^{*}\|F_{k}\|^{2}\\ &\leq -r\|F_{k}\|^{2}. \end{array} $$

Lemma 3

For all k≥0, we have

$$\begin{array}{*{20}l} r\|F_{k}\|\leq\|d_{k}\|\leq\,3(L+r)\|F_{k}\|. \end{array} $$
(15)

Proof

From (13) and Cauchy-Schwarz inequality, we have

$$\begin{array}{*{20}l} \|d_{k}\|\geq\,r\|F_{k}\|. \end{array} $$
(16)

Also, we have that

$$\begin{array}{*{20}l} {}\max\left\{\mu_{k}d_{k-1}^{T}y_{k-1},-\eta F_{k-1}^{T}d_{k-1}+\mu_{k}\|d_{k-1}\|\|y_{k-1}\|\right\}\!\geq\!-\eta F_{k-1}^{T}d_{k-1}\,+\,\mu_{k}\|d_{k-1}\|\|y_{k-1}\|. \end{array} $$

It then follows from (6), (7), and (8) that

$$\begin{array}{*{20}l} \|d_{k}\|&\leq\,\lambda_{k}^{*}\|F_{k}\|+|\beta_{k}|\|d_{k-1}\|+|\delta_{k}|\|y_{k-1}\|\\ &\leq\,\lambda_{k}^{*}\|F_{k}\|+\frac{\|F_{k}\|\|y_{k-1}\|}{\mu_{k}\|d_{k-1}\|\|y_{k-1}\|}\|d_{k-1}\|+\frac{\|F_{k}\|\|d_{k-1}\|}{\mu_{k}\|d_{k-1}\|\|y_{k-1}\|}\|y_{k-1}\|\\ &=\lambda_{k}^{*}\|F_{k}\|+\frac{2}{\mu_{k}}\|F_{k}\|\\ &\leq\,3\lambda_{k}^{*}\|F_{k}\|\\ &\leq\,3(L+r)\|F_{k}\|. \end{array} $$

Lemma 4

Suppose Assumption 1 holds and let {xk} be generated by Algorithm 1. Then the steplength αk is well defined and satisfies the inequality

$$\begin{array}{*{20}l} \alpha_{k}\,\geq\,\min\left\{\kappa,\frac{\rho r}{9(L+\sigma)(L+r)^{2}}\right\}. \end{array} $$
(17)

Proof

Suppose that, at kth iteration, xk is not a solution, that is, Fk≠0, and for all i=0,1,2,..., inequality (5) fails to hold, that is

$$\begin{array}{*{20}l} -F(x_{k}+\kappa\rho^{i} d_{k})^{T}d_{k}<\sigma\kappa\rho^{i}\parallel d_{k}\parallel^{2}. \end{array} $$
(18)

Since F is continuous, taking limits as i→∞ on both sides of (18) yields

$$\begin{array}{*{20}l} -F(x_{k})^{T}d_{k}\leq\,0, \end{array} $$
(19)

which contradicts Lemma 2. So, the steplength αk is well defined and can be determined within a finite number of trials. Now, we prove inequality (17). If αk≠κ, then \(\alpha '_{k}=\frac {\alpha _{k}}{\rho }\) does not satisfy (5), that is

$$\begin{array}{*{20}l} -F(x_{k}+\alpha'_{k}d_{k})^{T}d_{k}<\sigma\alpha'_{k}\parallel d_{k}\parallel^{2}. \end{array} $$

Using (9), (13) and (15) we have that

$$\begin{array}{*{20}l} r\|F_{k}\|^{2}&\,\leq\,-F_{k}^{T}d_{k}\\ &=\left(F\left(x_{k}+\alpha'_{k}d_{k}\right)-F_{k}\right)^{T}d_{k}-F\left(x_{k}+\alpha'_{k}d_{k}\right)^{T}d_{k}\\ &\leq\, L\alpha'_{k}\|d_{k}\|^{2}+\sigma\alpha'_{k}\|d_{k}\|^{2}\\ &=(L+\sigma)\alpha_{k}\rho^{-1}\|d_{k}\|^{2}\\ &\leq (L+\sigma)\alpha_{k}\rho^{-1}\left(3(L+r)\|F_{k}\|\right)^{2}. \end{array} $$

Thus

$$\begin{array}{*{20}l} \alpha_{k}\,\geq\,\min\left\{\kappa,\frac{\rho r}{9(L+\sigma)(L+r)^{2}}\right\}. \end{array} $$

The following lemma shows that if the sequence {xk} is generated by Algorithm 1, and x∗ is a solution of (1), i.e. F(x∗)=0, then the sequence {∥xk−x∗∥} is decreasing and convergent. Thus, the sequence {xk} is bounded.

Lemma 5

Suppose Assumption 1 holds and the sequence {xk} is generated by Algorithm 1. For any x∗ such that F(x∗)=0, we have that

$$\begin{array}{*{20}l} \|x_{k+1}-x^{*}\|^{2}\leq\|x_{k}-x^{*}\|^{2}-\|x_{k+1}-x_{k}\|^{2} \end{array} $$
(20)

and the sequence {xk} is bounded. Furthermore, either {xk} is finite and the last iterate is a solution of (1), or {xk} is infinite and

$$\begin{array}{*{20}l} \sum_{k=0}^{\infty}\|x_{k+1}-x_{k}\|^{2}<\infty, \end{array} $$

which means

$$\begin{array}{*{20}l} {\lim}_{k\rightarrow\infty}\|x_{k+1}-x_{k}\| = 0. \end{array} $$
(21)

Proof

The conclusion follows from Theorem 2.1 in [10].

Theorem 1

Let {xk} be the sequence generated by Algorithm 1. Then

$$\begin{array}{*{20}l} {\lim}_{k\rightarrow\infty}\inf\| F_{k}\| = 0. \end{array} $$
(22)

Proof

Suppose that the inequality (22) is not true. Then there exists a constant ε1>0 such that

$$\begin{array}{*{20}l} \|F_{k}\|\,\geq\,\epsilon_{1}, \quad\,\forall\,k\,\geq\,0. \end{array} $$

This together with (13) implies that

$$\begin{array}{*{20}l} \|d_{k}\|\,\geq\,r\|F_{k}\|\,\geq\,r\epsilon_{1} >0, \quad \quad \forall\,k\,\geq\,0. \end{array} $$
(23)

This and (21) gives that

$$\begin{array}{*{20}l} {\lim}_{k\rightarrow\infty}\alpha_{k} = 0. \end{array} $$
(24)

On the other hand, Lemma 5 implies that

$$\begin{array}{*{20}l} \alpha_{k}\,\geq\,\min\left\{\kappa,\frac{\rho r}{9(L+\sigma)(L+r)^{2}}\right\}>0, \end{array} $$

which contradicts (24). Therefore (22) is true.

Numerical experiments

In this section, results of our proposed method SASCGM are presented together with those of improved three-term derivative-free method (ITDM) [21], the modified Liu-Storey conjugate gradient projection (MLS) method [11], and the spectral DY-type projection method (SDYP) [22]. All algorithms are coded in MATLAB R2016a. In our experiments, we set ε=10−4, i.e., the algorithms are stopped whenever the inequality ∥Fk∥≤10−4 is satisfied, or the total number of iterations exceeds 1000. The method SASCGM is implemented with the parameters σ=10−4, ρ=0.5, r=10−3, \(\mu _{k}=\frac {1}{\lambda _{k}^{*}}+0.1\) and κ=1, while parameters for algorithms ITDM, MLS, and SDYP are set as in respective papers.

The methods are compared using number of iterations, number of function evaluations and CPU time taken for each method to reach the optimal value or termination. We test the algorithms on ten (10) test problems with their dimensions varied from 5000 to 20000, and with four (4) different starting points \(x_{0}=\left (\frac {1}{n},\frac {1}{n},\ldots,\frac {1}{n}\right)^{T}\), x1=(−1,−1,…,−1)T, x2=(0.5,0.5,…,0.5)T and x3=(−0.5,−0.5,…,−0.5)T. The test functions are listed as follows:

Problem 1. Sun and Liu [19] The mapping F is given by

$$\begin{array}{*{20}l} F(x) = Ax+g(x), \end{array} $$

where

$$\begin{array}{*{20}l} A=\left(\begin{array}{ccccc} 2 & -1 & & & \\ -1 & 2 & -1 & & \\ & \ddots & \ddots & \ddots & \\ & & \ddots & \ddots & -1 \\ & & & -1 & 2 \end{array} \right) \end{array} $$

and \(\phantom {\dot {i}\!}g(x)=(2e^{x_{1}}-1, 3e^{x_{2}}-1,\ldots,3e^{x_{n-1}}-1, 2e^{x_{n}}-1)^{T}\).

Problem 2. Liu and Li [22] Let F be defined by

$$\begin{array}{*{20}l} F(x) = Ax+g(x), \end{array} $$

where \(\phantom {\dot {i}\!}g(x)=(e^{x_{1}}-1, e^{x_{2}}-1,\ldots,e^{x_{n}}-1)^{T}\) and

$$\begin{array}{*{20}l} A=\left(\begin{array}{ccccc} 2 & -1 & & & \\ -1 & 2 & -1 & & \\ & \ddots & \ddots & \ddots & \\ & & \ddots & \ddots & -1 \\ & & & -1 & 2 \end{array} \right). \end{array} $$

Problem 3. Liu and Feng [18] The mapping F is given by

$$\begin{array}{*{20}l} F_{1}(x) = & 3x_{1}^{3}+2x_{2}-5+\sin(x_{1}-x_{2})\sin(x_{1}+x_{2}),\\ F_{i}(x) = & -x_{i-1}e^{(x_{i-1}-x_{i})}+x_{i}(4+3x_{i}^{2})+2x_{i+1}\\ &+\sin(x_{i}-x_{i+1})\sin(x_{i}+x_{i+1})-8,\,\,\,\, i = 2,3,\ldots,n-1,\\ F_{n}(x) = & -x_{n-1}e^{(x_{n-1}-x_{n})}+4x_{n}-3. \end{array} $$

Problem 4. Liu and Li [20] The mapping F is given by

$$\begin{array}{*{20}l} F_{1}(x) &= 2x_{1}-x_{2}+e^{x_{1}}-1,\\ F_{i}(x) &= -x_{i-1}+2x_{i}-x_{i+1}+e^{x_{i}}-1, \,\,\,\, i=2, 3,\ldots, n-1,\\ F_{n}(x) &= -x_{n-1}+2x_{n}+e^{x_{n}}-1. \end{array} $$

Problem 5. Abubakar and Kumam [21] The mapping F is given by

$$\begin{array}{*{20}l} F_{i}(x) = e^{x_{i}} - 1, \,\,\,\, i=1,2,3,\ldots,n. \end{array} $$

Problem 6. Hu and Wei [11] The mapping F is given by

$$\begin{array}{*{20}l} F_{1}(x) &= 2.5x_{1}+x_{2}-1,\\ F_{i}(x) &= x_{i-1}+2.5x_{i}+x_{i+1}-1, \,\,\,\, i=2, 3,\ldots, n-1,\\ F_{n}(x) &= x_{n-1}+2.5x_{n}-1. \end{array} $$

Problem 7. Hu and Wei [11] The mapping F is given by

$$\begin{array}{*{20}l} F_{1}(x) &= 2x_{1}+0.5h^{2}(x_{1}+h)^{3}-x_{2},\\ F_{i}(x) &= 2x_{i}+0.5h^{2}(x_{i}+hi)^{3}-x_{i-1}+x_{i+1},\,\,\,\,i=2,3,...,n-1,\\ F_{n}(x) &= 2x_{n}+0.5h^{2}(x_{n}+hn)^{3}-x_{n-1}, \end{array} $$

where \(h=\frac {1}{n+1}\).

Problem 8. Wang and Guan [25] The mapping F is given by

$$\begin{array}{*{20}l} F_{i}(x) &= 2x_{i}-\sin|x_{i}-1|, \,\,\,\, i=1,2,3,...,n. \end{array} $$

Problem 9. Wang and Guan [25] The mapping F is given by

$$\begin{array}{*{20}l} F_{i}(x) = e^{x_{i}} - 2, \,\,\,\, i=1,2,3,...,n. \end{array} $$

Problem 10. Gao and He [24] The mapping F is given by

$$\begin{array}{*{20}l} F_{i}(x) &= x_{i}-\sin(|x_{i}|-1), \,\,\,\, i=1,2,3,...,n. \end{array} $$

The numerical results are reported in Tables 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10, where “SP” represents the starting point (initial point), “DIM” denotes the dimension of the problem, “NI” refers to the number of iterations, “NFE” stands for the number of function evaluations, and “CPU” is the CPU time in seconds. In Table 3, “*” indicates that the algorithm did not converge within the maximum number of iterations. From the tables, we observe that the proposed method performs better than the other methods in Problems 2, 3, 4, 6, 9, and 10. The proposed method performs slightly lower in Problems 1, 5, 7, and 8. However, overall, the proposed method shows that it is very competitive with the other methods and can be a good addition to the existing methods in the literature.

Table 1 Numerical results of Problem 1
Full size table
Table 2 Numerical results of Problem 2
Full size table
Table 3 Numerical results of Problem 3
Full size table
Table 4 Numerical results of Problem 4
Full size table
Table 5 Numerical results of Problem 5
Full size table
Table 6 Numerical results of Problem 6
Full size table
Table 7 Numerical results of Problem 7
Full size table
Table 8 Numerical results of Problem 8
Full size table
Table 9 Numerical results of Problem 9
Full size table
Table 10 Numerical results of Problem 10
Full size table

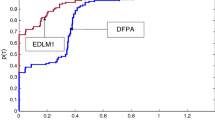
The performance of the three methods is further presented graphically in Figs. 1, 2, and 3 based on the number of iterations (NI), number of function evaluations (NFE), and the CPU time, respectively, using the performance profile of Dolan and Mor\(\acute {e}\) [28]. That is, we plot the probability ρS(τ) of the test problems for which each of the three methods was within a factor τ. Figures 1, 2, and 3 clearly show the efficiency of the proposed SASCGM method as compared to the other three methods.

Fig. 1
figure 1

Iterations performance profile

Full size image
Fig. 2
figure 2

Function evaluations performance profile

Full size image
Fig. 3
figure 3

Cpu time performance profile

Full size image

Conclusion

In this paper, we proposed a self adaptive spectral conjugate gradient-based projection (SASCGM) method for solving systems of large-scale nonlinear monotone equations. The proposed method is free from derivative evaluations and also satisfies the descent condition \(F_{k}^{T}d_{k}\leq -c\|F_{k}\|^{2}, c>0\), independent of any line search. The global convergence of the proposed method was also established. The proposed algorithm was tested on some benchmark problems with different initial points and different dimensions and the numerical results show that the method is competitive.