Global stability for a tuberculosis model with isolation and incomplete treatment

Abstract

This paper deals with the global analysis of a dynamical model for the spread of tuberculosis with isolation and incomplete treatment. The model exhibits the traditional threshold behavior. We prove that when the basic reproductive number is less than unity, the disease-free equilibrium is globally asymptotically stable. When the basic reproductive number is greater than unity, the disease-free equilibrium is unstable and a unique endemic equilibrium exists which is locally asymptotically stable and globally asymptotically stable when the disease-induced death rate is equal to zero. The stability of disease-free equilibrium is derived by using Lyapunov stability theory and LaSalle’s invariant set theorem. The global stability of endemic equilibrium is proved by generalized Dulac–Bendixson criterion when the disease-induced death rate is equal to zero. Numerical simulations support our analytical results.

1 Introduction

Tuberculosis (TB) is a disease caused by infection with Mycobacterium tuberculosis, which most frequently affects the lungs (pulmonary TB). It is one of the most common infectious diseases with about 2 billion people (one-third of the world’s population) currently infected. About 9 million new cases of active disease develop each year, resulting in two million deaths, mostly in developing countries. There were an estimated 8.7 million incident cases of TB globally in 2011 (World Health Organization 2012). TB infection remains a serious public health challenge in China. According to the WHO estimates, China has the world’s second largest TB epidemic accounting for 12 % of global cases, only after India, with more than 1.3 million new cases of TB being reported every year. From the website of National Health and Family Planning Commission of the PRC (2001–2013), we know that over the period 2003–2013 TB was the second largest cause of death among China’s 39 notifiable communicable diseases, after HIV/AIDS (National Health and Family Planning Commission of the PRC 2003–2014).

Fortunately, TB is treatable and curable. TB patients can be treated and can recover using antibiotics, though TB requires much longer periods of treatment than many other diseases (typically 6–9 months) for complete removal of the causative bacteria (Palomino et al. 2009). The treatment is usually divided into two stages: the first 2 months and subsequent 4 months or more. If treatment compliance is maintained and the Mycobacterium strain is drug sensitive, 85 % of patients convert from sputum positive to sputum negative, becoming noninfectious within the first 2 months (American Thoracic Society 1994). Nearly 95 % of patients convert to sputum negative on completion of treatment (American Thoracic Society 1994; Kirschner 1999). The vast majority of TB cases can be cured when medicines are provided and taken properly (World Health Organization 2014). In this case, the individuals recover and become susceptible after being treated (they may be infected again if they come in contact with other infectious persons). On the other hand, within weeks following treatment initiation, the majority of bacteria are removed and patients begin to see resolution of symptoms. Due to these and other reasons, treatment is often interrupted or ceased (Mittal and Gupta 2011). If treatment is interrupted, a fraction of the bacterial population (termed persisters) remains in the body, and in this case the individuals after being treated may still be TB carriers and become latent.

Mathematical models can provide a useful tool to analyze the spread and control of infectious diseases (Anderson and May 1991; Hetcote 2000). Mathematical models for tuberculosis are especially useful tools in assessing the epidemiological consequences of medical or behavioral interventions (which may cause many direct and indirect effects), because they contain explicit mechanisms that link individuals with a population-level outcome such as incidence or prevalence. Different mathematical models for tuberculosis have been formulated and studied (see e.g., Blower et al. 1995, 1996; Castillo and Feng 1997; Connell and Driessche 2004; Castillo and Song 2004; Yang et al. 2010; Liu and Zhang 2011; Feng et al. 2000, 2002; Yang et al. 2012 and references therein).

In (Yang et al. 2010, 2012), incomplete treatment and self-cure are incorporated in mathematics models. In (Castillo and Feng 1997; Feng et al. 2000, 2002), it is assumed that the treated individuals have temporary immunity and can be infected through contacts with other infectious individuals. In this paper, incomplete treatment and isolation are incorporated in our model. We assume that the individuals become susceptible when received complete treatment or become latent individuals when received incomplete treatment. It is assumed that the treated individuals are isolated, and they are not able to infect others and cannot be infected during the treatment period. Restricted by the levels of economic and social development, especially in developing countries, we assume that the period of isolation is 1–2 months, not the entire treatment period. In addition, we assume that the treated individuals cannot be infected by the infectious individual before they finish their treatment, and not only the isolation period.

The rest of the paper is organized as follows: Sect. 2 presents a TB model with isolation and incomplete treatment. In Sect. 3, we present the global properties of the proposed model. The basic reproductive number of infection is obtained and used to determine conditions for the existence and uniqueness of endemic equilibrium. Lyapunov function is constructed to prove the global asymptotic stability of the disease-free equilibrium. The global stability of the endemic equilibrium is proved by generalized Dulac–Bendixson criterion with disease-induced death rate $d=0$. In Sect. 4, numerical simulations were given to support the analytical results. Some discussions have been given in Sect. 5.

2 Model construction

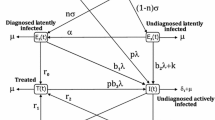
In this section, we formulate a model for the spread of tuberculosis in the human population. Figure 1 shows the model diagram. The total population at time t denoted by $N(t)$ is divided into four classes: susceptible ($S$), latent ($E$, infected but not infectious), infectious ($I$) and treated individuals ($T$). All recruitment is into the susceptible class and occurs at a constant rate $\Lambda$. We assume that an individual may be infected only through contacts with infectious individuals. The natural death rate is $\mu$. The infectious class has an additional death rate due to the disease with constant rate $d$. $k$ is the rate coefficient at which an individual leaves the latent class and becomes infectious. Infectious individuals are treated with constant rate $r$, entering the treatment class. $\delta$ is the rate coefficient at which a treated individual leaves compartment $T$. The leaving treated individuals enter into the latent class with a fraction $q$ and into the susceptible class with a fraction $1-q$. Susceptible individuals acquire TB infection from individuals with active TB at rate $\beta S\frac{I}{N}$ where $\beta$ is the disease transmission coefficient. A fraction $c$ of newly infected individuals moves to the latent TB class ($E$), and the remaining fraction $1-c$ moves to the active TB class ($I$). It is assumed that individuals in the latent class do not transmit infection. Combining all the aforementioned assumptions, the model for the transmission dynamics of TB is given by the following system of differential equations:

$$\begin{aligned} \left\{ \begin{array}{l} \dfrac{\text {d}S}{\text {d}t}=\Lambda -\beta S \dfrac{I}{N}-\mu S+(1-q)\delta T,\\ \dfrac{\text {d}E}{\text {d}t}=c\beta S \dfrac{I}{N}+q \delta T-(\mu +k)E,\\ \dfrac{\text {d}I}{\text {d}t}=(1-c) \beta S\dfrac{I}{N}+kE-(\mu +r+d)I,\\ \dfrac{\text {d}T}{\text {d}t}=rI-(\mu +\delta )T. \end{array} \right. \end{aligned}$$

(1)

Fig. 1

The transfer diagram for system (1)

By adding all Eq. (1), the dynamics of the total population $N(t)$ is given by:

$$\begin{aligned} \text {d}N/\text {d}t=\Lambda -\mu N-\text {d}I. \end{aligned}$$

(2)

Since $\text {d}N/\text {d}t<0$ for $N>\Lambda /\mu$, then, without loss of generality, we can only consider solutions of (1) in the following positively subset of ${\varvec{R}}^4$:

$$\begin{aligned} \Omega _\varepsilon = \left\{ (S,E,I,T)|S,E,I,T\ge 0,S+E+I+T\le \frac{\Lambda }{\mu } \right\} . \end{aligned}$$

With respect to system (1), we have the following result.

Proposition 2.1

The compact set $\Omega _\varepsilon$ is a positively invariant and absorbing set that attracts all solutions of Eq. (1) in ${\varvec{R}}^4$.

Proof

Define a Lyapunov function as $W(t)=S(t)+E(t)+I(t)+T(t)$, then we have:

$$\begin{aligned} \frac{\text {d}W(t)}{\text {d}t}=\Lambda -\mu W-\text {d}I\le \Lambda -\mu W. \end{aligned}$$

(3)

Hence, that $\frac{\text {d}W}{\text {d}t}\le 0$ for $W>\frac{\Lambda }{\mu }$. $\Omega _\varepsilon$ is a positively invariant set. On the other hand, solving the differential inequality Eq. (3) yields:

$$\begin{aligned} 0<W(t)<\frac{\Lambda }{\mu }+W(0)\text {e}^{-\mu t}. \end{aligned}$$

where $W(0)$ is the initial condition of $W(t)$. Thus, as $t\rightarrow \infty$, one has that $0\le W(t)\le \frac{\Lambda }{\mu }$.

3 Mathematical analysis

In this section, the model is analyzed to obtain the basic reproductive number, conditions for the existence and uniqueness of endemic equilibria and asymptotic stabilities of equilibria.

3.1 Basic reproductive number

The disease-free equilibrium of system (1) is $X_0=(S_0,0,0,0)$ with $S_0 = \Lambda /\mu$. To compute the basic reproductive number, it is important to distinguish new infections from all other class transitions in the population. The infected classes are $E$, $I$ and $T$. Following Van den Driessche and Watmough (2002), we can rewrite system (1) as

$$\begin{aligned} \dot{x}=f(x)=\fancyscript{F}(x)-\fancyscript{V}(x)=\fancyscript{F}(x)-(\fancyscript{V^-}(x)-\fancyscript{V^+}(x)). \end{aligned}$$

where $x=(E,I,T,S)$, $\fancyscript{F}$ is the rate of appearance of new infections in each class, $\fancyscript{V^+}$ is the rate of transfer into each class by all other means and $\fancyscript{V^-}$ is the rate of transfer out of each class. Hence,

$$\begin{aligned} \fancyscript{F}(x)= \left( \beta c S \frac{I}{N},(1-c)\beta S \frac{I}{N},0,0 \right) ^\mathrm{T}. \end{aligned}$$

and

$$\begin{aligned} \fancyscript{V}(x)=\left( \begin{array}{c} (\mu +K)E-q\delta T \\ (\mu +r+d)I-kE \\ (\mu +\delta )T-rI\\ \mu S+\beta S \frac{I}{N}-(1-q)\delta T-\Lambda \end{array} \right) . \end{aligned}$$

The Jacobian matrices of $\fancyscript{F}$ and $\fancyscript{V}$ at the disease-free equilibrium $X_0=(0, 0, 0,\Lambda /\mu )$ can be partitioned as

$$\begin{aligned} D\fancyscript{F}(X_0)=\left( \begin{array}{l@{\quad }l} F &{} 0\\ 0 &{} 0\\ \end{array} \right) \, \, \, \hbox {and} \, \, \, D\fancyscript{V}(X_0)=\left( \begin{array}{l@{\quad }l} V &{} 0 \\ J_1 &{} J_2 \\ \end{array} \right) , \end{aligned}$$

where $F$ and $V$ correspond to the derivatives of $\fancyscript{F}$ and $\fancyscript{V}$ with respect to the infected classes:

$$\begin{aligned} F=\left( \begin{array}{lll} o &{} \quad \beta c &{}\quad 0\\ 0 &{} \quad (1-c)\beta &{}\quad 0\\ 0 &{} \quad 0 &{} \quad 0 \\ \end{array} \right) \, \, \, \hbox {and} \, \, \, V=\left( \begin{array}{lll} \mu +k &{}\quad 0 &{}\quad -q\delta \\ -k &{}\quad \mu +r+d &{}\quad 0\\ 0 &{}\quad -r &{} \quad \mu +\delta \\ \end{array} \right) . \end{aligned}$$

The basic reproductive number is defined, following Van den Driessche and Watmough (2002), as the spectral radius of the next generation matrix, $FV^{-1}$:

$$\begin{aligned} R_0=\frac{\beta (\mu +\delta )[k+(1-c)\mu ]}{(\mu +\delta )(\mu +k)(\mu +r+d)-krq\delta }. \end{aligned}$$

3.2 Stability of the disease-free equilibrium

We have the following result about the global stability of the disease-free equilibrium.

Theorem 3.1

When $R_0>1$, the disease-free equilibrium $X_0$ is unstable. When $R_0\le 1$, the disease-free equilibrium $X_0$ is globally asymptotically stable in $\Omega _\varepsilon$; this implies the global asymptotic stability of the disease-free equilibrium on the nonnegative orthant ${\varvec{R}}^4$. This means that the disease naturally dies out.

Proof

The Jacobian matrix of (1) at $X_0$ is

$$\begin{aligned} J(X_0)=\left( \begin{array}{llll} -\mu &{}\quad 0 &{}\quad -\beta &{}\quad (1-q)\delta \\ 0 &{}\quad -(\mu +k) &{}\quad \beta c &{}\quad q\delta \\ 0 &{}\quad k &{}\quad -(\mu +r+d)+(1-c)\beta &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad r &{}\quad -(\mu +\delta ) \end{array} \right) , \end{aligned}$$

and the characteristic equation is

$$\begin{aligned} f(\lambda )=(\lambda +\mu )(\lambda ^3+a\lambda ^2+b\lambda +e)=0 \end{aligned}$$

where

$$\begin{aligned}&a=3\mu +k+r+d+\delta -(1-c)\beta ,\\&b=(\mu +\delta )(2\mu +k+r+d)+(\mu +k)(\mu +r+d)-(2\mu +k+\delta )(1-c)\beta -\beta c k,\\&e=\beta (\mu +\delta )[k+(1-c)\mu ] \left( \frac{1}{R_0}-1 \right) . \end{aligned}$$

When $R_0>1$, we have $e<0$; thus $f(0)=\mu e<0$ and $f(\lambda )\rightarrow \infty$ as $\lambda \rightarrow \infty$. It follows that $f(\lambda ^*)=0$ for some $\lambda ^*>0$. Therefore $J$ has a positive eigenvalue, and $X_0$ is unstable.

We define the following Lyapunov–LaSalle function

$$\begin{aligned} V(t)=E+\frac{\mu +k}{k}I+\frac{q\delta }{\mu +\delta }T. \end{aligned}$$

Its time derivative along the trajectories of system (1) satisfies

$$\begin{aligned} \dot{V}&= \dot{E}+\frac{\mu +k}{k}\dot{I}+\frac{q\delta }{\mu +\delta }\dot{T}\\&= \beta c S \frac{I}{N}+q\delta T-(\mu +k)E+\frac{\mu +k}{k}(1-c)\beta S \frac{I}{N}+(\mu +k)E\\&-\frac{\mu +k}{k}(\mu +r+d)I+\frac{q\delta r}{\mu +\delta }I-q \delta T\\&= \frac{k+(1-c)\mu }{k}\cdot \beta S\frac{I}{N}-\frac{(\mu +k)(\mu +r+d)}{k}I+\frac{q\delta r}{\mu +\delta }I\\&= \frac{\beta [k+(1-c)\mu ]I}{k} \left[ \frac{S}{N}-\frac{1}{R_0} \right] \\&\le \frac{\beta [k+(1-c)\mu ]I}{k} \left( 1-\frac{1}{R_0} \right) . \end{aligned}$$

$R_0\le 1$ implies that $\dot{V}\le 0$. By LaSalle’s invariance principle, the largest invariant set in $\Omega _\varepsilon$ contained in $\{(S,E,I,T)\in \Omega _\varepsilon ,\dot{V}=0\}$ is reduced to the disease-free equilibrium $X_0$. This proves the global asymptotic stability of $X_0$ on $\Omega _\varepsilon$ (Bhatia and Szegö 1970). Since $\Omega _\varepsilon$ is absorbing, this proves the global asymptotic stability on the nonnegative octant for $R_0\le 1$. It should be stressed that we need to consider a positively invariant compact set to establish the stability of $X_0$ since $V$ is not positive definite. Generally, the LaSalle’s invariance principle only proves the attractivity of the equilibrium. Considering $\Omega _\varepsilon$ permits to conclude for the stability (LaSalle 1976, 1968; Bhatia and Szegö 1970). This achieves the proof.

3.3 Existence and uniqueness of endemic equilibrium

To find an endemic equilibrium $(S^*,E^*,I^*,T^*)$ of system (1) with $I^*>0,$ we let $x=I^*/N^*$. Then,

$$\begin{aligned} I^*=\frac{\Lambda }{\mu +dx}x,\ \ S^*=\frac{\Lambda }{\mu +\beta x}+\frac{(1-q)\delta }{\mu +\beta x}\frac{r}{\mu +\delta }\frac{\Lambda }{\mu +dx}x,\ T^*=\frac{r}{\mu +\delta }\frac{\Lambda }{\mu +dx}x,\\ E^*=\frac{\mu +r+d}{k}\frac{\Lambda }{\mu +dx}x-\frac{(1-c)\beta x}{k}\frac{\Lambda }{\mu +\beta x}-\frac{(1-c)\beta x}{k}\frac{(1-q)\delta }{\mu +\beta x}\frac{r}{\mu +\delta }\frac{\Lambda }{\mu +dx}x. \end{aligned}$$

Using $S^*+E^*+I^*+T^*=N^*=\Lambda /(\mu +d x)$ and the definition of $R_0,$ we get

$$\begin{aligned} x(mx-n)=0. \end{aligned}$$

with

$$\begin{aligned} m&= \beta [(\mu +k)(\mu +\delta +r)+\delta r(c+q)+cd(\mu +\delta )-cq\delta r],\\ n&= [(\mu +\delta )(\mu +k)(\mu +r+d)-krq \delta ](R_0-1). \end{aligned}$$

Then, one can observe that the above equation has two solutions: $x=0$ which corresponds to the disease-free equilibrium and $x=\frac{n}{m}$. Thus, when $R_0>1,n>0$ and $x=\frac{n}{m}>0$. The endemic equilibrium is defined by

$$\begin{aligned}&S^*=\frac{\Lambda m[(\mu +\delta )(\mu m+dn)+(1-q)\delta rn]}{(\mu +\delta )(\mu m+\beta n)(\mu m+d n)},I^*=\frac{\Lambda n}{\mu m+dn},T^*=\frac{r\Lambda n}{(\mu +\delta )(\mu m+dn)},\nonumber \\&E^*=\frac{\Lambda n[(\mu +r+d)-(1-c)\beta n]}{k(\mu m+dn)}-\frac{(1-c)(1-q)\beta \delta r\Lambda n^2}{k(\mu +\delta )(\mu m+\beta n)(\mu m+d n)}. \end{aligned}$$

(4)

Then we have the following result:

Theorem 3.2

When $R_0>1$, there exists a unique endemic equilibrium $X^*\!=\!(S^*,E^*,I^*,T^*)$ for the system (1) where $S^*,E^*,I^*$ and $T^*$ are defined as in Eq. (4) which is in the nonnegative octant $R^4_+$.

3.4 Stability of endemic equilibrium

Theorem 3.3

If $R_0>1$, the unique endemic equilibrium $X^*$ of the system (1) is locally asymptotically stable.

Proof

Since the total population $N(t)=S(t)+E(t)+I(t)+T(t)$ satisfies $\text {d}N/\text {d}t=\Lambda -\mu N-\text {d}I$, we can replace $E(t)$ by $E(t)=N(t)-S(t)-I(t)-T(t)$. Then the system (1) is equivalent to the following system, and the endemic equilibrium becomes $X^{*'}=(S^*,I^*,T^*,N^*)$.

$$\begin{aligned} \left\{ \begin{array}{l} \dfrac{\text {d}S}{\text {d}t}=\Lambda -\beta S \dfrac{I}{N}-\mu S+(1-q)\delta T,\\ \dfrac{\text {d}I}{\text {d}t}=(1-c) \beta S\dfrac{I}{N}+kE-(\mu +r+d)I,\\ \dfrac{\text {d}T}{\text {d}t}=rI-(\mu +\delta )T,\\ \dfrac{\text {d}N}{\text {d}t}=\Lambda -\mu N-\text {d}I \end{array} \right. \end{aligned}$$

(5)

The Jacobian matrix of the system (5) at the endemic equilibrium $X^{*'}=(S^*,I^*,T^*,N^*)$ is

$$\begin{aligned} J(X^{*'})=\left( \begin{array}{llll} -\mu -\frac{\beta I^*}{N^*} &{}\quad -\frac{\beta S^*}{N^*} &{}\quad (1-q)\delta &{}\quad \frac{\beta S^* I^*}{N^{*2}}\\ \frac{(1-c)\beta I^*}{N^*}-k &{}\quad -(\mu +r+d+k)+\frac{(1-c)\beta S^*}{N^*} &{}\quad -k &{}\quad k-\frac{(1-c)\beta S^*I^*}{N^{*2}} \\ 0 &{}\quad r &{}\quad -(\mu +\delta ) &{}\quad 0 \\ 0 &{}\quad -d &{}\quad 0 &{}\quad -\mu \\ \end{array} \right) \end{aligned}$$

and the characteristic equation is

$$\begin{aligned} \lambda ^4+m_3\lambda ^3+m_2\lambda ^2+m_1\lambda +m_0=0 \end{aligned}$$

where

$$\begin{aligned} m_0=&\,\,d(\mu +\delta ) \left( \mu +\frac{\beta I^*}{N^*} \right) \left( k-\frac{(1-c)\beta S^*I^*}{N^{*2}} \right) +d(\mu +\delta )\frac{\beta S^*I^*}{N^{*2}} \left( \frac{(1-c)\beta I^*}{N^*}-k \right) \\&+ \; \mu r k \left( \mu +\frac{\beta I^*}{N^*} \right) \\&+\; \mu (\mu +\delta ) \left( \mu +\frac{\beta I^*}{N^*}\right) \left( \mu +r+d+k-\frac{(1-c)\beta S^*}{N^*}\right) \\&+ \; \mu (\mu +\delta )\frac{\beta S^*}{N^*} \left( k-\frac{(1-c)\beta S^*I^*}{N^*}\right) \\&- \; \mu r\delta (1-q) \left( \frac{(1-c)\beta I^*}{N^*}-k \right) \\ =&\,\, d(\mu +\delta )(\mu +k) \left( \frac{\beta I^*}{N^*}-\frac{\beta S^* I^*}{N^{*2}}\right) +dc\mu (\mu +\delta )\frac{\beta S^* I^*}{N^{*2}}\\&+ \; [\mu (\mu +k)(\mu +r+\delta )+c\mu r\delta +\mu \delta r q(1-c)]\frac{\beta I^*}{N^*}>0,\\ m_1=&\,\,d \left( k-\frac{(1-c)\beta S^*I^*}{N^{*2}} \right) \left( 2\mu +\delta +\frac{\beta I^*}{N^*} \right) +d\frac{\beta S^* I^*}{N^{*2}} \left( \frac{(1-c)\beta I^*}{N^{*}}-k \right) \\&+ \; (2\mu +\delta )\frac{(1-c)\beta ^2 S^*I^*}{N^{*2}}\\&+ \; \mu (\mu +\delta ) \left( 2\mu +r+d+k-\frac{(1-c)\beta S^*}{N^*}\right) \\&+ \; \left( \mu +\frac{\beta I^*}{N^*} \right) \left( \mu +r+d+k-\frac{(1-c)\beta S^*}{N^*}\right) (2\mu +\delta )\\&- \; (1-q)\delta r \left( \frac{(1-c)\beta I^*}{N^{*}}-k \right) +kr \left( 2\mu +\frac{\beta I^*}{N^*}\right) \\&+ \; (2\mu +\delta )\frac{\beta S^*}{N^*} \left( \frac{(1-c)\beta I^*}{N^*}-k\right) -k(2\mu +\delta )\frac{\beta S^*}{N^{*}}\\ =&\,\, d(2\mu +\delta +k) \left( \frac{\beta I^*}{N^*}-\frac{\beta S^* I^*}{N^{*2}} \right) +\mu (\mu +\delta )\frac{k E^*}{I^*}+\mu (\mu +\delta )(\mu +k)+\frac{q\delta r k \mu }{\mu +\delta }\\&+\; dc(2\mu +\delta )\frac{\beta S^* I^*}{N^{*2}}+[\mu (\mu +\delta )+2\mu (\mu +r+k)+\delta (\mu +k)+kr\\&+ \; \delta r(c+q-qc)]\frac{\beta I^*}{N^*}>0,\\ m_2=&\,\,d \left( k\!-\!\frac{(1-c)\beta S^*I^*}{N^{*2}} \right) \!+\!\mu (\mu +\delta )\!+\! \left( \mu \!+\!\frac{\beta I^*}{N^*} \right) \left( \mu +r+d+k-\frac{(1-c)\beta S^*}{N^*} \right) \\&+ \left( \mu +\frac{\beta I^*}{N^*} \right) (\mu +\delta )\!+\!\mu \left( \mu +\frac{\beta I^*}{N^*} \right) \!+\!(\mu +\delta ) \left( \mu +r+d+k\!-\!\frac{(1-c)\beta S^*}{N^*} \right) \\&+ kr +\mu \left( \mu +r+d+k-\frac{(1-c)\beta S^*}{N^*} \right) +\frac{\beta S^*}{N^*} \left( \frac{(1-c)\beta I^*}{N^*}-k \right) \\ =&\,\,d \left( \frac{\beta I^*}{N^*}-\frac{\beta S^* I^*}{N^{*2}} \right) +(2\mu +\delta )\frac{k E^*}{I^*}+(3\mu +\delta +r+k)\frac{\beta I^*}{N^*}+(2\mu +k)(\mu +\delta )\\&+ \; \mu ^2+\frac{kq \delta r}{\mu +\delta }+dc\frac{\beta S^* I^*}{N^{*2}}>0,\\ m_3=&\,\,\mu +\frac{\beta I^*}{N^{*}}+\mu +r+d+k-\frac{(1-c)\beta S^*}{N^{*}}+\mu +\delta +\mu \\ =&\,\,3\mu +\delta +k+\frac{\beta I^*}{N^{*}}+\frac{kE^*}{I^*}>0. \end{aligned}$$

We can calculate easily $m_1m_2-m_0m_3>0,m_1m_2m_3-m_0m_3^2-m_1^2>0$. According to Hurwitz criterion, the endemic equilibrium $X^{*'}$ is locally asymptotically stable, i.e., the endemic equilibrium $X^*$ is locally asymptotically stable.

To prove the following theorem, we first give a lemma: generalized Dulac–Bendixson criterion.

Lemma 3.4

(Busenberg and Driessche 1990) Let ${\varvec{f}}: R^3\rightarrow R^3$ be a Lipschitz continuous vector field and let $\Gamma (t)$ be a closed, piecewise smooth, curve which is the boundary of an orientable smooth surface $\mathbf S \subset R^3$. Suppose that ${{\varvec{g}}}: R^3\rightarrow R^3$ is defined and piecewise smooth in a neighborhood of $S$ and that is satisfies:

$$\begin{aligned} {{\varvec{g}}}(\Gamma (t))\cdot {{\varvec{f}}}(\Gamma (t))\le 0\ \ \ (\text {or} \ge 0) \ \ \text {for all} \ \ t \end{aligned}$$

and

$$\begin{aligned} (Curl {{\varvec{g}}})\cdot {{\varvec{n}}}\ge 0 (\le 0)\ \ \text {on} \ \ \mathbf S , \ \ \mathrm{and} \ \ (Curl {{\varvec{g}}})\cdot {{\varvec{n}}}> 0 (< 0) \ \ \text {for some point on}\ \ \mathbf S \end{aligned}$$

where ${{\varvec{n}}}$ is the unit normal to $\mathbf S$. Then, $\Gamma (t)$ is not the finite union of solution trajectories of

$$\begin{aligned} {{\varvec{x}}}'={{\varvec{f}}}({{\varvec{x}}}). \end{aligned}$$

which are traversed in the positive sense relation to the direction of ${{\varvec{n}}}$.

Theorem 3.5

If $R_0>1$ and $d=0$, the unique endemic equilibrium $X^*$ of the system (1) is globally asymptotically stable.

Proof

When $d=0$, from Eq. (2) we have

$$\begin{aligned} N(t)=\frac{\Lambda }{\mu }+ \left( N(0)-\frac{\Lambda }{\mu } \right) \mathrm{e}^{-\mu t}. \end{aligned}$$

We only need to analyze the limiting system where $N$ is replaced by its equilibrium value [the dynamics of the resulting limiting system is qualitatively equivalent to that of the original system (1) (Castillo and Thieme 1995; Castillo et al. 1996, 1999)]. Furthermore, it is convenient to transform system (1) into proportions (using the change of variables $x=\frac{S}{N},y=\frac{E}{N},z=\frac{I}{N},w=\frac{T}{N}$ and $N=\frac{\Lambda }{\mu }$) and also to use the relation $x+y+z+w=1$ to eliminate the variable $w$. Performing the above manipulations gives

$$\begin{aligned} \left\{ \begin{array}{l} \frac{\text {d}x}{\text {d}t}=\mu -\beta xz-\mu x+(1-q)\delta (1-x-y-z),\\ \frac{\text {d}y}{\text {d}t}=c\beta x z+q \delta (1-x-y-z)-(\mu +k)y,\\ \frac{\text {d}z}{\text {d}t}=(1-c) \beta x z+ky-(\mu +r)z.\\ \end{array} \right. \end{aligned}$$

(6)

We only need to prove the global stability of $P(x^*,y^*,z^*)$ of system (6) on the invariant set $\Omega ^*=\{(x,y,z):x\ge 0,y\ge 0,z\ge 0,x+y+z\le 1\}$. Obviously, the solutions of system (6) are bounded, and the endemic equilibrium $P(x^*,y^*,z^*)$ is locally asymptotically stable. It is only necessary to prove that system (6) has no periodic solution in the invariant domain $\Omega ^*$.

Obviously, the boundary curve of the domain $\Omega ^*$ cannot form the periodic solution of system (6). We consider the following in the interior of $\Omega ^*$.

Assuming that system (6) has a periodic solution $\phi (t) = \{x(t), y(t), z(t)\}$, the image $\Gamma$ of $\phi (t)$ is the boundary of a plane domain $\Pi$ which is in the interior of domain $\Omega ^*$.

Let ${{\varvec{f}}}=(f_1,f_2,f_3)^\mathrm{T}$ (T denotes transpose) and ${{\varvec{g}}}(x,y,z)=\frac{1}{xyz}\cdot {{\varvec{r}}}\times {{\varvec{f}}}$, (where ${{\varvec{r}}}=(x,y,z)^\mathrm{T}$), then

$$\begin{aligned} {{\varvec{g}}}\cdot {{\varvec{f}}}=\mathbf 0 . \end{aligned}$$

Let ${{\varvec{g}}}=(g_1,g_2,g_3)$ and $\text {Curl}{{\varvec{g}}}=(\frac{\partial g_3}{\partial y}-\frac{\partial g_2}{\partial z},\frac{\partial g_1}{\partial z}-\frac{\partial g_3}{\partial x},\frac{\partial g_2}{\partial x}-\frac{\partial g_1}{\partial y})$. By calculating straightforwardly, we get in the interior of domain $\Omega ^*$

$$\begin{aligned} (\text {Curl}{{\varvec{g}}})\cdot (1,1,1)^\mathrm{T}&= -\frac{q\delta (1\!-\!x\!-\!y\!-\!z)}{y^2} \left( \frac{1}{x}\!+\!\frac{1}{z} \right) -\frac{(1-q)\delta (1-x-y-z)}{x^2} \left( \frac{1}{y}+\frac{1}{z} \right) \\&- k \left( \frac{1}{z^2}+\frac{1}{xz}+\frac{y}{xz^2} \right) -\frac{\mu }{x^2} \left( \frac{1}{y}+\frac{1}{z} \right) -c \beta \left( \frac{1}{y}+\frac{x}{y^2}+\frac{z}{y^2} \right) <0. \end{aligned}$$

If we choose the direction of plane domain $\Pi$ upward, the direction of the image $\Gamma$ conforms to the right-hand rule with the direction of plane domain $\Pi$. Vector $(1,1,1)$ is the normal vector of plane domain $\Pi$, then we get by Stokers theorem:

$$\begin{aligned} \frac{1}{\sqrt{3}}\int \int _{\Pi } \text {Curl}{{\varvec{ g}}}\cdot (1,1,1)^\mathrm{T} \mathrm{d}S=\oint _{\Gamma }\frac{{{\varvec{g}}}\cdot {{\varvec{f}}}}{\mid {{\varvec{f}}}\mid } \mathrm{d}S. \end{aligned}$$

This is in contradiction with the calculation above. The Theorem is proved.

4 Numerical results

In this section we will study the system (1) numerically to support our analytical results. Our numerical simulations support that the result of Theorem 3.5 is also established when $d>0$.

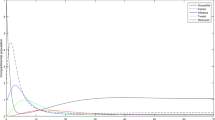
• 1. Choosing the following parameters: $\Lambda =600$, $\beta =0.055$, $k=0.00527$, $\mu =1/70$, $d=0.02$, $r=1/6$, $q=0.1$, $\delta =0.01$, $c=0.7$, we can get $R_0=0.7214<1$. Hence, the condition of Theorem 3.1 is satisfied. System (1) has a disease-free equilibrium and it is globally asymptotically stable (Fig. 2).

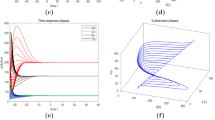
• 2. Choosing the following parameters: $\Lambda =1{,}000$, $\beta =1.2$, $k=0.00527$, $\mu =1/70$, $d=0.02$, $r=1/6$, $q=0.4$, $\delta =0.5$, $c=0.95$, we can get $R_0=2.0013>1$. Hence, the conditions of Theorem 3.2 and Theorem 3.5 are satisfied. System (1) has a endemic equilibrium and it is globally asymptotically stable with different initial values (Fig. 3).

• 3. Choosing the following parameters: $\Lambda =1{,}000$, $k=0.00527$, $\mu =1/70$, $d=0.02$, $q=0.4$, $\delta =0.5$, $c=0.95$ and with the values of $\beta$ and $r$ being variable. We can get the relation between the number of infectious individuals $I(t)$ and the parameters $\beta , r$ (Fig. 4).

• 4. Choosing the following parameters: $\Lambda =1{,}000$, $\beta =1.2$, $k=0.00527$, $\mu =1/70$, $d=0.02$, $r=1/6$, $c=0.95$ and with the values of $\delta$ and $q$ being variable. We can get the relation between the number of infectious individuals $I(t)$ and the parameters $\delta , q$ (Fig. 5).

Fig. 2

Trajectories of system (1) when $\Lambda =600$, $\beta =0.055$, $k=0.00527$, $\mu =1/70$, $d=0.02$, $r=1/6$, $q=0.1$, $\delta =0.01$, $c=0.7$, so that $R_0=0.7214<1$. It shows that the disease-free equilibrium $X_0$ is globally asymptotically stable

Fig. 3

Trajectories of system (1) when $\Lambda =1{,}000$, $\beta =1.2$, $k=0.00527$, $\mu =1/70$, $d=0.02$, $r=1/6$, $q=0.4$, $\delta =0.5$, $c=0.95$, so that $R_0=2.0013>1$. It shows that the endemic equilibrium $X^*$ is globally asymptotically stable

Fig. 4

Left effect of $\beta$ on the number of infectious individuals $I(t)$ where all other parameters are same as described in Fig. 3; right effect of $r$ on the number of infectious individuals $I(t)$ where all other parameters are same as described in Fig. 3

Fig. 5

Left effect of $\delta$ on the number of infectious individuals $I(t)$ where all other parameters are same as described in Fig. 3; right effect of $q$ on the number of infectious individuals $I(t)$ where all other parameters are same as described in Fig. 3

5 Discussion

In this paper, we have studied a tuberculosis model with isolation and incomplete treatment. By using the Lyapunov stability theory, LaSalle’s invariant set theorem and generalized Dulac–Bendixson criterion, we have proved the global stabilities of disease-free equilibrium and endemic equilibrium when the disease-induced death rate is equal to zero of the proposed model. The basic reproductive number $R_0$ provided the threshold condition which determines the rate of spread of tuberculosis. When $R_0<1$, the disease-free equilibrium $X_0$ is globally asymptotically stable and the disease will die out (Fig. 2). When $R_0>1$, a unique endemic equilibrium $X^*$ exists and is globally asymptotically stable when $d=0$. Numerical simulations support our analytical results and we get the global stability of the endemic equilibrium when $d\ne 0$ (Fig. 3). The effect of parameters $\beta$ and $r$ are shown in Fig. 4. The effect of parameters $\delta$ and $q$ are shown in Fig. 5.

To control the epidemic of TB is to eliminate the disease or to control the number of infectious individuals. Figure 4 indicates that the number of infectious individuals decreases as the value of $\beta$ decreases and the value of $r$ increases. Figure 5 indicates that the number of infectious individuals decreases as the values of $\delta$ and $q$ decrease. Therefore, there are four control strategies to control the number of infectious individuals. The first strategy is decreasing the value of transmission rate $\beta$. It is the most effective measure to decrease the value of transmission rate $\beta$ by isolating the infectious individuals. But, this is not feasible because of the long-term treatment and high cost. Another measure to decrease the value of transmission rate $\beta$ is increasing case detection. Much transmission occurs before patients seek treatment; therefore more case detection can help more infectious individuals to seek treatment and decrease the transmission rate. The second strategy is increasing the treatment rate. To increase the treatment rate, the most effective measure is reducing treatment costs so that more infectious individuals can get appropriate treatment. The third strategy is decreasing the leaving rate $\delta$ from the treatment class. This is also not feasible. The fourth strategy is decreasing the fraction leaving treated individuals enter into latent class $q$. Decreasing the value of $q$ can increase the treatment success rate such as taking care of patients until complete treatment. The above discussions show that effective and feasible strategies can be achieved by virtue of increasing case detection and treatment success rate and reducing treatment costs.