1 Introduction

Unmanned aerial vehicles (UAVs) have attracted the attention of the scientific community from multiple disciplines due to their numerous applications. Their popularity has increased worldwide, including helicopters, which is mainly due to their ability to hover and maneuver in tight and dangerous places (Castaneda et al. 2016; Liu et al. 2013; Marantos et al. 2017). In these kinds of applications, a robust controller is required to cope with various uncertainties like changes in gravity, mass, inertia, and other unpredictable factors. Similar to aircrafts, helicopter motion also consists of controlling the pitch, roll, and yaw axis with only two rotors. However, the unique body structure of helicopters makes the pitch, roll, and yaw dynamics strongly coupled (Castaneda et al. 2016). Therefore, controlling them is not trivial. Unlike conventional helicopters that use a single main rotor, the three-degree-of-freedom (3-DOF) helicopter uses two rotors and a suspending mass making it more fault tolerant. However, stabilizing the 3-DOF helicopter is not an easy task to undertake. It exhibits a complex nonlinear and unstable open-loop dynamics. The severe nonlinearities, coupling, varying operating conditions, structured and unstructured uncertainties, and external disturbances are among the typical challenges to be faced.

Various control approaches have been proposed for helicopters (Castaneda et al. 2016; Liu et al. 2013; Li et al. 2015b; Xian et al. 2015), including classical, robust, and adaptive control laws. Among popular methods, input–output linearization and back-stepping are used for their simplicity. However, linearization does not guarantee the stability in all operating conditions. Moreover, they suffer from sensitivity to parameter variations. The presence of high, particularly unstructured, uncertainties such as nonlinearities significantly changes the system’s dynamics (Chaoui and Sicard 2012b). So, modeling the system’s dynamics based on presumably accurate mathematical models cannot be applied efficiently in this case. This raises the urgency to consider alternative approaches for the control of this type of systems to keep up with their increasingly demanding design requirements. In Dube and Patel (2016), the translation dynamics of 3-DOF helicopter is discussed with the design of adaptive control system design. The proposed control scheme is validated experimentally. In Coza and Macnab (2006), a robust adaptive fuzzy control is used for a quadrotor. A real-time stabilization control of tri-rotor with non-cyclic propellers is proposed in Cruz et al. (2008). In Tanaka et al. (2004), a robust stabilization controller is designed for RC helicopters that guarantees robust stability, good speed response, and avoidance of actuators’ saturation. An adaptive fuzzy-based back-stepping control is proposed for a 3-DOF helicopter testbed with dead zone in Li et al. (2017), where fuzzy logic is used to approximate the model uncertainty and external disturbances.

A lot of research has been done on helicopters and UAVs and is still ongoing. Different control strategies are used to control helicopters. In Castaneda et al. (2016), a continuous differentiator based on adaptive second-order sliding-mode control is proposed for helicopter control. The proposed scheme combines a continuous differentiator with adaptive super twisting controllers. In Liu et al. (2013), a robust linear quadratic regulator (LQR) is used to control the altitude of a 3-DOF helicopter. In this approach, a feedback control is used for linearized approximation and a robust controller is designed to cope with uncertainties, disturbances, and other nonlinear properties. In Boby et al. (2014), a robust adaptive linear quadratic regulator (LQR) controller is designed for a 3-DOF helicopter. Results show that the integral action can eliminate the tracking errors and that the adaptive controller estimates and compensates for the uncertainty in the system. In Veeraboina and Ordonez (2018), a comparison of four different control scheme is carried out with input and output feedback linearizing (IOFL)-, direct adaptive fuzzy controller (DAC)-, linear quadratic regulator (LQR)-, and proportional integral derivative (PID)-based LQR control design. Comparison results of all four control schemes are provided. A nonlinear robust tracking control of a helicopter is proposed in Li et al. (2015b). The controller also includes a second-order auxiliary system to generate filtered error signals along with an estimator of uncertainties and disturbances. In Marantos et al. (2017), a robust control strategy is proposed to track the trajectory for small-scale unmanned helicopters. The control scheme does not depend on the explicit knowledge of the model’s parameters, and each model guarantees trajectory tracking with prescribed transient and steady-state response in the presence of external disturbances. An adaptive output feedback control is used for a helicopter in Kutay et al. (2005). The adaptive control achieves adaptation to both parametric uncertainty and unmodeled dynamics and incorporates a novel approach that adapts to known actuator characteristics. In Fradkov et al. (2010), an estimator and a controller are designed for a helicopter developed at the Laboratory for Analysis and Architecture of Systems (LAAS). In here, a hybrid continuous–discrete observation procedure is proposed for transmission of the measured data over the limited band communication channel with adaptive tuning of the coder range parameters. An adaptive back-stepping tracking control of a 6-DOF helicopter is proposed in Xian et al. (2015), where the proposed controller combines the back-stepping method with online parameters update law to achieve the control objective. In Gao and Fang (2012), another adaptive integral back-stepping control strategy proposed for a 3-DOF helicopter, the controller is capable of approximating model uncertainties online and improve the robustness of the model. Machine learning and artificial intelligence were also used to control the helicopters. In Zou and Zheng (2015), a robust adaptive radial basis function neural network is used to control the helicopter with back-stepping as the main control framework, which is amplified by radial basis function neural networks (RBFNNs) to approximate the unmodeled dynamics. An adaptive neural fault-tolerant controller of a 3-DOF helicopter is proposed in Chen et al. (2016) to cope with uncertainty and nonlinear actuator faults. A neural network disturbances observer is developed based on a radial basis function neural network, and a different nonlinear observer is also designed for the unknown external disturbances. A neural network tracking control of the 3-DOF helicopter is designed in Guo et al. (2016), with time-varying disturbances and input saturation. In Du et al. (2014), a frequency-domain system identification of an unmanned helicopter is designed based on an adaptive genetic algorithm. The model is identified based on the inputs and outputs, and then, a control compensator is designed based on the identified model. A decentralized robust second-order consensus tracking control of multiple 3-DOF helicopters using output feedback is done in Li et al. (2015a). The controller can drive the system to achieve second-order consensus tracking without measuring the velocity, so that the velocity sensor can be avoided. In Zheng and Zhong (2011), a robust attitude regulator is designed for a 3-DOF helicopter, where a linear-invariant robust controller is used to improve tracking performance. The results are validated through experiments. In Kocagil et al. (2018), a model reference adaptive control (MRAC) is designed using state-dependent Riccati equation (SDRE) for a 3-DOF helicopter.

Fig. 1
figure 1

3-DOF helicopter

Full size image

Studies have shown that the design of robust controllers for mathematically ill-defined systems that may be subjected to structured and unstructured uncertainties is made possible with computational intelligence tools, such as artificial neural networks and fuzzy logic systems (Efe 2011; Pedro and Kala 2015; Khayamy et al. 2016). The approximation capabilities have been the main driving force behind the increasing popularity of such methods as they are theoretically capable of uniformly approximating any continuous real function to any degree of accuracy (Chaoui and Sicard 2012a). This has led to the recent advances in the area of intelligent control (Chaoui and Gueaieb 2008; Chaoui and Sicard 2012b). Satisfactory performance is achieved with various neural network models for complex control systems (Coza and Macnab 2006; Dierks and Jagannathan 2010).

Adaptive control offers good performance in the presence of structured (parametric) uncertainties, but it falls short in the presence of unstructured uncertainties, such as disturbances. Henceforth, the contribution of this paper is to achieve motion tracking for a 3-DOF helicopter in the presence of both structured and unstructured uncertainties. The proposed control scheme combines the power of adaptive control theory against parameters variation and a reference model to cope with time-varying modeling and disturbance uncertainties. As stated earlier, conventional adaptive controllers fail to achieve robustness against both parameter uncertainties and disturbances. Thus far, very few nonlinear controllers have been proposed for the 3-DOF helicopter. Unlike many controllers, the closed-loop control scheme’s stability is guaranteed by Lyapunov direct method. Furthermore, convergence analysis is also provided. The rest of the paper is organized as follows: Sect. 2 outlines the dynamic model of the helicopter. Then, the proposed adaptive control methodology is outlined in Sect. 3. In Sect. 4, numerical results are presented and discussed. Finally, we conclude with a few remarks and suggestions.

2 System Description

2.1 Dynamics

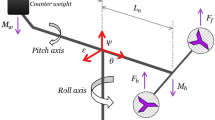
The helicopter consists of a 3-DOF rotational motion body actuated by two propellers (Rajappa et al. 2013). The two rotors provide upwards propulsion as well as direction control. The model of the system is shown in Fig. 1, which depicts the body/global coordinate systems and forces exerted on the helicopter by the counterweight and motors. The dynamic mathematical model based on Euler–Lagrange formulation is described by the following equations (Castaneda et al. 2016):

$$\begin{aligned} J_\epsilon \ddot{\epsilon }&= G \cos \epsilon + L_\mathrm{a} \cos \theta u_1 \end{aligned}$$
(1a)
$$\begin{aligned} J_\psi \ddot{\psi }&= L_\mathrm{a} \cos \epsilon \sin \theta u_1 \end{aligned}$$
(1b)
$$\begin{aligned} J_\theta \ddot{\theta }&= L_\mathrm{h} u_2 \end{aligned}$$
(1c)
Fig. 2
figure 2

Autopilot scheme

Full size image

with \(u_1 = F_\mathrm{f} + F_\mathrm{b}\), \(u_2 = F_\mathrm{f} - F_\mathrm{b}\) , \(G = g (M_\mathrm{h} L_\mathrm{a} - M_\mathrm{w} L_\mathrm{w})\), where

  • \(M_\mathrm{h} \in {\mathbb {R}}\): mass of the helicopter

  • \(M_\mathrm{w} \in {\mathbb {R}}\): mass of the counterweight

  • \(L_\mathrm{a} \in {\mathbb {R}}\): length from the rotors to the center of mass

  • \(L_\mathrm{w} \in {\mathbb {R}}\): length from the tail to the center of mass

  • \(L_\mathrm{h} \in {\mathbb {R}}\): length between the rotors

  • \(g \in {\mathbb {R}}\): gravitational constant

  • \(\epsilon \in {\mathbb {R}}\): roll angle of the helicopter

  • \(\psi \in {\mathbb {R}}\): yaw angle of the helicopter

  • \(\theta \in {\mathbb {R}}\): pitch angle of the helicopter

  • \(u \in {\mathbb {R}}^2\): control input vector

  • \(J_\epsilon \in {\mathbb {R}}\): moment of inertia about roll

  • \(J_\psi \in {\mathbb {R}}\): moment of inertia about yaw

  • \(J_\theta \in {\mathbb {R}}\): moment of inertia about pitch

  • \(F_\mathrm{f}\): front motor force

  • \(F_\mathrm{b}\): back motor force

Before we proceed further, let us introduce the following assumptions (Castaneda et al. 2016):

Assumption 1

The yaw and roll axes are perpendicular.

Assumption 2

All the axes intersect in the same point, which is considered as the origin of the global coordinate frame.

Assumption 3

The helicopter frame and counterweight mass centers are collinear with respect to the pitch axis.

Assumption 4

The Joint friction, air resistance, and centrifugal forces are neglected.

Assumption 5

The thrust force is proportional to the motor voltage, and motors/propellers dynamics are neglected.

Remark 1

It is noteworthy that this system is underactuated, i.e., two input forces to control three states (the yaw angle \(\psi \), the roll angle \(\epsilon \), and the pitch angle \(\theta \)).

2.2 Adaptive Autopilot Control Structure

Since the 3-DOF helicopter is underactuated, the motion along the roll and yaw axes has to be controlled simultaneously by one single input. The adaptive autopilot control structure, depicted in Fig 2, considers that the control input \(u_1\) controls both roll and yaw dynamics, while the control input \(u_2\) controls the pitch dynamics. Thus, it is necessary to design a control strategy to control the attitude of the system with only two control inputs. To achieve this, the roll and yaw trajectories are defined as a user defined input. The pitch trajectory is affected by both yaw and roll dynamics, and the desired trajectory for the pitch is calculated based on an internal loop. Define the virtual inputs \(v_1\) and \(v_2\) as Castaneda et al. (2016),

$$\begin{aligned} v_1&= \cos \theta u_1 \end{aligned}$$
(2a)
$$\begin{aligned} v_2&= \cos \epsilon \sin \theta u_1 \end{aligned}$$
(2b)

which makes the dynamic equations (1) as,

$$\begin{aligned} J_\epsilon \ddot{\epsilon }&= G \cos \epsilon + L_\mathrm{a} v_1 \end{aligned}$$
(3a)
$$\begin{aligned} J_\psi \ddot{\psi }&= L_\mathrm{a} v_2 \end{aligned}$$
(3b)
$$\begin{aligned} J_\theta \ddot{\theta }&= L_\mathrm{h} u_2 \end{aligned}$$
(3c)

Using (2), the input \(u_1\) can be written as Castaneda et al. (2016),

$$\begin{aligned} u_1^2 = v_1^2 + \frac{v_2^2}{\cos ^2\epsilon } \end{aligned}$$
(4)

The proposed autopilot is based on this fact: The decoupling can be carried out provided that the virtual inputs \(v_1\) and \(v_2\) given in (2) are satisfied. Then, the control \(u_1\) can be expressed as,

$$\begin{aligned} u_1 = S \cdot \sqrt{v_1^2 + \frac{v_2^2}{\cos ^2\epsilon }} \end{aligned}$$
(5)

where

$$\begin{aligned} S= {\left\{ \begin{array}{ll} \hbox {sgn}(v_1), &{}\quad \text {if}\;v_1 \ne 0\\ 0, &{} \quad \text {if}\;v_1 = 0 \end{array}\right. } \end{aligned}$$

Then, a way to decouple the system consists in forcing the angle \(\theta \), by the control input \(u_2\), to track the following desired trajectory,

$$\begin{aligned} \theta ^*(t) = \tan ^{-1}{\frac{v_2}{\cos \epsilon {v_1}}} \end{aligned}$$
(6)

The control objective is to design a control law \(v_1\), \(v_2\), and \(u_2\) to make the system’s states \(\epsilon \), \(\psi \), and \(\theta \) track their respective pre-defined time-dependent reference trajectories \(\epsilon ^*\), \(\psi ^*\), and \(\theta ^*\) under the assumption of unknown parameters. In this paper, all parameters, \(M_\mathrm{h}, M_\mathrm{w}, L_\mathrm{a}, L_\mathrm{w}, L_\mathrm{h}, g, J_\epsilon , J_\psi \), and \(J_\theta \) are assumed to be unknown.

3 Adaptive Control Strategy

The control approach is based on a feedforward adaptive controller and a stabilizing feedback loop. The feedforward is designed to learn online the helicopter’s inverse dynamics through first-order reference models that define the desired errors dynamics. Due to the nature and high complexity order of the helicopter’s dynamical model, the adaptive controller may take a relatively long time to converge which may lead to an unstable or unsatisfactory performance. Therefore, a stabilizing feedback loop is designed to guarantee the system’s stability. The feedback loop can be viewed as a proportional-derivative compensator that stabilizes the system at start-up while the adaptive parameters are being updated. Additionally, it adds a disturbance rejection property to classical adaptive control that is known to suffer from unstructured uncertainties. Let \(e_\epsilon = \epsilon - \epsilon ^*\), \(e_\psi = \psi - \psi ^*\), and \(e_\theta = \theta - \theta ^*\) denote the system’s tracking errors. The control objective is to track these errors to zero. For that, let us define the following reference model:

$$\begin{aligned} s_\epsilon&= {\dot{e}}_\epsilon + \eta _\epsilon ~e_\epsilon = {\dot{\epsilon }} - {\dot{\epsilon }}_r \end{aligned}$$
(7a)
$$\begin{aligned} s_\psi&= {\dot{e}}_\psi + \eta _\psi ~e_\psi = {\dot{\psi }} - {\dot{\psi }}_r \end{aligned}$$
(7b)
$$\begin{aligned} s_\theta&= {\dot{e}}_\theta + \eta _\theta ~e_\theta = {\dot{\theta }} - {\dot{\theta }}_r \end{aligned}$$
(7c)

with \({\dot{\bullet }}_r = {\dot{\bullet }}^* - \eta _\bullet ~e_\bullet \) and \(\eta _\bullet \) being a positive constant that defines the desired bandwidth of the closed-loop system. The symbol \(\bullet \) can be \(\epsilon \), \(\psi \), or \(\theta \). Formulation (3) can also be expressed as:

$$\begin{aligned} v_1&= \frac{1}{L_\mathrm{a}} \left( J_\epsilon \ddot{\epsilon } - G \cos \epsilon \right) \end{aligned}$$
(8a)
$$\begin{aligned} v_2&= \frac{1}{L_\mathrm{a}} J_\psi \ddot{\psi } \end{aligned}$$
(8b)
$$\begin{aligned} u_2&= \frac{1}{L_\mathrm{h}} J_\theta \ddot{\theta } \end{aligned}$$
(8c)

Therefore, the desired dynamics can be expressed by the following helicopter’s inverse dynamics regression model:

$$\begin{aligned}&\frac{1}{L_\mathrm{a}} \left( J_\epsilon \ddot{\epsilon }_r - G \cos \epsilon \right) = \varUpsilon ^{T}_\epsilon P_\epsilon \end{aligned}$$
(9a)
$$\begin{aligned}&\frac{1}{L_\mathrm{a}} J_\psi \ddot{\psi }_r = \varUpsilon ^{T}_\psi P_\psi \end{aligned}$$
(9b)
$$\begin{aligned}&\frac{1}{L_\mathrm{h}} J_\theta \ddot{\theta }_r = \varUpsilon ^{T}_\theta P_\theta \end{aligned}$$
(9c)

where \(\varUpsilon _\bullet \) is a vector of known functions (regressor) and \(P_\bullet \) is a vector of unknown parameters defined as,

$$\begin{aligned}&P_\epsilon = \left[ \frac{J_\epsilon }{L_\mathrm{a}}~~~\frac{G}{L_\mathrm{a}} \right] \end{aligned}$$
(10a)
$$\begin{aligned}&P_\psi = \frac{J_\psi }{L_\mathrm{a}} \end{aligned}$$
(10b)
$$\begin{aligned}&P_\theta = \frac{J_\theta }{L_\mathrm{h}} \end{aligned}$$
(10c)
Table 1 Physical parameters of the helicopter
Full size table
Fig. 3
figure 3

Desired trajectory for all angles

Full size image
Fig. 4
figure 4

Nominal case: a tracking errors; b yaw; c pitch; d roll; and e control signals

Full size image

Therefore, the control law is defined as,

$$\begin{aligned} v_1&= \varUpsilon ^{T}_\epsilon {\hat{P}}_\epsilon - K_\epsilon s_\epsilon \end{aligned}$$
(11a)
$$\begin{aligned} v_2&= \varUpsilon ^{T}_\psi {\hat{P}}_\psi - K_\psi s_\psi \end{aligned}$$
(11b)
$$\begin{aligned} u_2&= \varUpsilon ^{T}_\theta {\hat{P}}_\theta - K_\theta s_\theta \end{aligned}$$
(11c)

where \(K_\bullet \) is a positive constant gain. The symbol \({\hat{\bullet }}\) denotes the estimate vector.

Theorem 1

Consider a nonlinear system in the form (1) with slowly time-varying parameters. Using the control law (11), the closed-loop system’s stability is guaranteed with the following adaptation law:

$$\begin{aligned} \dot{{\hat{P}}}_\epsilon&= -\varGamma _\epsilon \varUpsilon _\epsilon s_\epsilon \end{aligned}$$
(12a)
$$\begin{aligned} \dot{{\hat{P}}}_\psi&= -\varGamma _\psi \varUpsilon _\psi s_\psi \end{aligned}$$
(12b)
$$\begin{aligned} \dot{{\hat{P}}}_\theta&= -\varGamma _\theta \varUpsilon _\theta s_\theta \end{aligned}$$
(12c)

where \(\varGamma =[\gamma _1,\gamma _2,\ldots ,\gamma _m]^\mathrm{T}\) and \(\gamma _{i}\) is a positive constant gain, \({{i}={1},\ldots ,{m}}\).

Proof

Taking the time derivative of (7) yields,

$$\begin{aligned} {\dot{s}}_\epsilon&= \ddot{\epsilon } - \ddot{\epsilon }_r \end{aligned}$$
(13a)
$$\begin{aligned} {\dot{s}}_\psi&= \ddot{\psi } - \ddot{\psi }_r \end{aligned}$$
(13b)
$$\begin{aligned} {\dot{s}}_\theta&= \ddot{\theta } - \ddot{\theta }_r \end{aligned}$$
(13c)

Using (3) and the regression model (9) leads to,

$$\begin{aligned} {\dot{s}}_\epsilon&= v_1 - \varUpsilon ^{T}_\epsilon P_\epsilon \end{aligned}$$
(14a)
$$\begin{aligned} {\dot{s}}_\psi&= v_2 - \varUpsilon ^{T}_\psi P_\psi \end{aligned}$$
(14b)
$$\begin{aligned} {\dot{s}}_\theta&= u_2 - \varUpsilon ^{T}_\theta P_\theta \end{aligned}$$
(14c)
Fig. 5
figure 5

Parameter estimation: a\({\hat{P}}_\epsilon \); b\({\hat{P}}_\theta \); and c\({\hat{P}}_\psi \)

Full size image
Fig. 6
figure 6

Disturbances added: a tracking errors; b yaw; c pitch; d roll; and e control signals

Full size image

Consider a Lyapunov candidate as follows:

$$\begin{aligned} V&= \frac{1}{2} \{ s_\epsilon ^2 + s_\psi ^2 + s_\theta ^2 + {\tilde{P}}_\epsilon ^T \varGamma _\epsilon ^{-1} {\tilde{P}}_\epsilon \\&\quad + {\tilde{P}}_\psi ^T \varGamma _\psi ^{-1} {\tilde{P}}_\psi + {\tilde{P}}_\theta ^T \varGamma _\theta ^{-1} {\tilde{P}}_\theta \} \end{aligned}$$

Take the time derivative of V:

$$\begin{aligned} {\dot{V}}&= {\dot{s}}_\epsilon s_\epsilon + {\dot{s}}_\psi s_\psi + {\dot{s}}_\theta s_\theta \\&\quad + {\tilde{P}}_\epsilon ^T \varGamma _\epsilon ^{-1} \dot{{\hat{P}}}_\epsilon + {\tilde{P}}_\psi ^T \varGamma _\psi ^{-1} \dot{{\hat{P}}}_\psi + {\tilde{P}}_\theta ^T \varGamma _\theta ^{-1} \dot{{\hat{P}}}_\theta \end{aligned}$$

The variation of parameters \(P_\bullet \) is assumed to be negligible compared to the system’s time constants, i.e., \(\dot{{\tilde{P}}}_\bullet = \dot{{\hat{P}}}_\bullet \). Substitute \({\dot{s}}_\epsilon \), \({\dot{s}}_\psi \), and \({\dot{s}}_\theta \) from (14):

$$\begin{aligned} {\dot{V}}&= \{v_1 - \varUpsilon ^{T}_\epsilon P_\epsilon \} s_\epsilon + \{v_2 - \varUpsilon ^{T}_\psi P_\psi \} s_\psi + \{u_2 - \varUpsilon ^{T}_\theta P_\theta \} s_\theta \\&\quad + {\tilde{P}}_\epsilon ^T \varGamma _\epsilon ^{-1} \dot{{\hat{P}}}_\epsilon + {\tilde{P}}_\psi ^T \varGamma _\psi ^{-1} \dot{{\hat{P}}}_\psi + {\tilde{P}}_\theta ^T \varGamma _\theta ^{-1} \dot{{\hat{P}}}_\theta \end{aligned}$$

Setting the control law as in (11) leads to,

$$\begin{aligned} {\dot{V}}&= \varUpsilon ^{T}_\epsilon {\tilde{P}}_\epsilon s_\epsilon + \varUpsilon ^{T}_\psi {\tilde{P}}_\psi s_\psi + \varUpsilon ^{T}_\theta {\tilde{P}}_\theta s_\theta \\&\quad + {\tilde{P}}_\epsilon ^T \varGamma _\epsilon ^{-1} \dot{{\hat{P}}}_\epsilon + {\tilde{P}}_\psi ^T \varGamma _\psi ^{-1} \dot{{\hat{P}}}_\psi + {\tilde{P}}_\theta ^T \varGamma _\theta ^{-1} \dot{{\hat{P}}}_\theta \\&\quad - K_\epsilon s_\epsilon ^2 - K_\psi s_\psi ^2 - K_\theta s_\theta ^2 \end{aligned}$$

where \({\tilde{P}}_\bullet = {\hat{P}}_\bullet - P_\bullet \). Setting the adaptation law as in (12) implies that,

$$\begin{aligned} {\dot{V}} = - K_\epsilon s_\epsilon ^2 - K_\psi s_\psi ^2 - K_\theta s_\theta ^2 < 0\quad \forall K_\bullet > 0 \end{aligned}$$

Setting \(K_\bullet > 0\) yields \({\dot{V}} < 0\), \(\forall ~s_\bullet \ne 0\) so that \(s_\bullet = 0\) is a globally asymptotically stable equilibrium point. A positive Lyapunov function V, which is decreasing \(({\dot{V}} < 0)\), must converge to a finite limit. Therefore, the system is asymptotically stable in the sense of Lyapunov. Hence, signals \(s_\bullet \), \({\tilde{P}}_\bullet \), and \({\hat{P}}_\bullet \) are also bounded and converge to finite values. It follows from (7) that \(e_\bullet \) and \({\dot{e}}_\bullet \) are bounded, which implies from (14) that \({\dot{s}}_\bullet \) is also bounded. \(\square \)

For non-autonomous systems, finding a Lyapunov function V with a negative definite derivative (\({\dot{V}} < 0\)) does not lead to a conclusion about the asymptotic stability. Therefore, Barbalat’s lemma is applied for the time-varying system in hand to prove its asymptotic stability and convergence.

Lemma 1

(Barbalat) If the differentiable function V(t) has a finite limit as \(t \rightarrow \infty \), and if \({\dot{V}}(t)\) is uniformly continuous, then \({\dot{V}}(t) \rightarrow 0\) as \(t \rightarrow \infty \).

Taking the derivative of \({\dot{V}}\) yields,

$$\begin{aligned} {\ddot{V}} = - 2 (K_\epsilon {\dot{s}}_\epsilon s_\epsilon + K_\psi {\dot{s}}_\psi s_\psi + K_\theta {\dot{s}}_\theta s_\theta ) \end{aligned}$$

Therefore, \({\ddot{V}}\) is also bounded.

Fig. 7
figure 7

Tracking errors under parameters change: a doubled mass; b half mass; c control signals for doubled mass; and d control signals for half mass

Full size image
Fig. 8
figure 8

Nonzero initial conditions: a tracking errors; b yaw; c pitch; and d roll; e control signals

Full size image

From Lemma 1, V has a finite limit as \(t \rightarrow \infty \) and \({\dot{V}}\) is uniformly continuous. Therefore, \(\lim _{t \rightarrow \infty } {\dot{V}} = 0\), and hence, \(\lim _{t \rightarrow \infty } s_\bullet = 0\). Therefore, \(\lim _{t \rightarrow \infty } e_\bullet = 0\) and \(\lim _{t \rightarrow \infty } {\dot{e}}_\bullet = 0\).

4 Results and Discussion

4.1 Setup

Different tests are performed to show the effectiveness of the proposed scheme. Table 1 summarizes the physical parameters of the helicopter along with their respective values. The control coefficients are set to \(\eta _\epsilon = 40\), \(\eta _\psi = 12\), \(\eta _\theta = 16\), \(K_\epsilon = 25\), \(K_\psi = 2.5\), \(K_\theta = 3\), \(\varGamma _\epsilon = [4.5 \times 10^{-2}, 0.3]^\mathrm{T}\), \(\varGamma _\psi = 8 \times 10^{-3}\), \(\varGamma _\theta = 5 \times 10^{-2}\), and the gravitational constant is set to \(g=9.8~\hbox {m}/\hbox {s}^2\). The controller is set to operate at a sampling frequency of 100 Hz. The desired position reference trajectory is considered as a sequence of step responses of a critically damped second-order system with a natural frequency \(w_\mathrm{n} = 2\) rad/s, as illustrated in Fig. 3. The system’s response is studied taking into account the helicopter’s angles. To better show the convergence properties of the adaptive controller, all adaptive parameters \({\hat{P}}_\bullet \) are initially set to zero. It is important to note that the desired values of \({\hat{P}}_\bullet \) are calculated using (10) and the physical parameters of the helicopter in Table 1.

4.2 Results

4.2.1 Nominal Case

The system’s response is studied taking into account the helicopter’s tracking errors \(e_\bullet \) and the adaptive parameters \({\hat{P}}_\bullet \), and the control signals \(v_1\), \(v_2\), and \(u_2\). First, the proposed adaptive control scheme is tested on the helicopter in the nominal case. Results are shown in Fig. 4. As it is shown, the motion tracking errors converge gradually to zero after each reference trajectory change. On the other hand, parameter estimation performance is depicted in Fig. 5. The adaptive parameters show good convergence to their nominal values. The ability of the proposed controller in dealing with parametric uncertainties is clearly demonstrated.

Fig. 9
figure 9

Comparison: a adaptive SMC; b PID control; and c adaptive control

Full size image

4.2.2 Effect of Disturbances

To show the robustness of the controller against unstructured uncertainties, unexpected sudden step disturbances are introduced to the system. For that, a step disturbance of 1 rad is added to the yaw, pitch, and roll axes at time 4 s, 9 s, and 14 s, respectively. Results reported in Fig. 6 show that even under the disturbances the controller is efficient in decaying the errors to approximately zero without significant overshoot or oscillations. It is noteworthy the saturation of control signals at \(\pm \,20\) as shown in Fig. 6e. The advantage behind the use of such controller is revealed by this test.

4.2.3 Effect of Parameter Variations

To further show the effectiveness of the controller under the parametric uncertainties, the mass of the system is changed by a factor of two and in another case by half. Similar to the nominal case, the tracking errors depicted in Fig. 7 show that controller is able to get the tracking errors to converge to zero even in the presence of parametric uncertainties. This is expected since no a priori parameters knowledge is required by the controller even in the nominal case. Thus, the proposed controller is instrumental in achieving the needed robustness against parametric uncertainties.

4.2.4 Effect of Nonzero Initial Conditions

To study the effect of initial conditions on the proposed controller, an initial condition of (\(\epsilon = \psi = \theta = 0.25\)) rad is introduced. Results, depicted in Fig. 8, are shown for 3s to better show the convergence properties of the system. The controller provides a satisfactory transient response. All angles converge quickly to their desired trajectories. Figure 8e shows control signals raising saturation and decreasing gradually as the initial tracking errors are minimized.

Table 2 Performance comparison
Full size table
Fig. 10
figure 10

Sine-wave trajectory: a tracking errors; b yaw; c pitch; d roll; and e control signals

Full size image

4.2.5 Comparison Against Other Control Methods

The proposed adaptive control scheme is compared against a conventional PID controller and the adaptive sliding-mode controller (SMC) presented in Li et al. (2015b). The tracking errors are shown in Fig. 9. It is clearly shown that unlike sliding-mode control, the proposed adaptive controller is able to bring the tracking errors to zero over time. In principle, sliding mode is achieved by discontinuous control and switching at infinite frequency. However, switching frequency is limited in real-life applications and results in discretization chattering problem as it is illustrated in Fig. 9. To overcome this problem, the boundary solution can be used to replace the discontinuous control by a saturation function that approximates the sign function in a boundary layer of sliding-mode manifold. This solution preserves partially the invariance property of sliding mode where states are confined to a small vicinity of the manifold, and convergence to zero cannot be guaranteed because robustness to parameter variations and uncertain disturbances is obtained only when sliding mode truly occurs. Similarly, the PID controller is able to decay the tracking errors to a magnitude within the range obtained by the adaptive SMC. It is important to note that tracking errors under PID control and the proposed control scheme have a similar initial magnitude; but, only the adaptive controller is able to decrease the magnitude of these errors further as parameters converge to their desired values.

To quantitatively adjudge the trajectory tracking performance, two performance metrics are introduced. First, the integral of the tracking error \(\sigma _\mathrm{e}\) is calculated over a single run. The second performance index \(\sigma _\mathrm{c}\) consists of the integral of the control signals. These metrics are calculated as follows:

$$\begin{aligned} \sigma _\mathrm{e}&= \int _{t_0}^{t_f} (e_{\epsilon }^2+e_{\psi }^2+e_{\theta }^2)~\hbox {d}t \end{aligned}$$
(15a)
$$\begin{aligned} \sigma _\mathrm{c}&= \int _{t_0}^{t_f} (v_{1}^2+v_{2}^2+u_{2}^2)~\hbox {d}t \end{aligned}$$
(15b)

where \(t_0\) and \(t_\mathrm{f}\) are initial and final time instants, respectively. The obtained numerical values for both performance metrics are displayed in Table 2. The proposed adaptive control method yields the lowest tracking performance index with a control effort equal to that of the PID controller. The adaptive SMC achieves the highest tracking performance index and control effort.

4.2.6 Effect of Other Reference Trajectories

Finally, the proposed adaptive controller is validated using different reference trajectories. For that, a 0.33 rad/s and 0.5 rad/s sine-wave trajectories are, respectively, set to the yaw and roll. Results are depicted in Fig. 10. Regardless of the trajectory, the proposed controller tracks all trajectories with high precision.

5 Conclusion

In this paper, a Lyapunov-based adaptive controller is proposed for high-performance control of a 3-DOF helicopter. The controller learns over time the system’s inverse model while also coping with unstructured uncertainties. As such, the control scheme achieves asymptotic convergence and tracking by a Lyapunov-based adaptation law in the presence of both structured and unstructured uncertainties. Unlike other controllers, no a priori parameters knowledge is required and the system’s closed-loop stability is guaranteed by Lyapunov direct method. The controller is tested under different conditions to evaluate its robustness properties in the presence of various uncertainties. Results show that the helicopter’s motion can be tracked with high accuracy. Henceforth, the adaptive control approach can be extended to improve static and dynamic performance of high-performance motion systems. As a future work, a comparative study against various advanced control schemes can be envisioned along with physical implementation.