1 Introduction

Helicopters and other aerial vehicles have been of significant research interest over the past few decades due to their multi-disciplinary applications. Their commercial demand has expanded globally because of their flexible nature to reach remote destinations [1]. Therefore, it is essential that the helicopter is equipped with a robust controller to deal with unprecedented circumstances like natural and human induced disturbances, changes in mass, friction, parameter variation [2]. The helicopter control dynamics primarily involve the control of the roll, yaw, and pitch, which is very similar to the airplanes with two rotors [3]. However, due to the distinctive skeletal structure of the helicopter, the three control parameters are strongly coupled with each other. The primary difference between a conventional helicopter and a 3-DOF helicopter lies in the number of rotors used [4]. While a conventional helicopter uses a single rotor, a 3-DOF helicopter is equipped to handle two rotors which makes it more fault resistant [2]. Nevertheless, the main challenge lies in stabilizing the 3-DOF helicopter because of its highly non-linear nature, open-loop dynamics, and structured and unstructured uncertainties which the helicopter might face.

Numerous control techniques like robust, classical, and adaptive control techniques have been proposed for the control of a 3-DOF helicopter [5]. Techniques like back-stepping and input-output linearization are some of the well known classical methods as they are relatively easy to deal with, but sheer linearization does not assure stability under all operating circumstances, and they can also be victims to parameter fluctuations [6]. They also have system dynamics that are prone to modification because of the presence of uncertainties, and so, solely relying on classical methods does not guarantee the best results [7]. Hence, there is a need to resort to an alternative approach of control to keep up with the highly sophisticated design requirements. An adaptive control system technique is used in [8], in which the translation dynamics of a 3-DOF helicopter are presented. Using the state-dependent Riccati equation, a model reference adaptive control for a 3-DOF helicopter is mentioned in [9]. Based on the adaptive genetic algorithm in [8], frequency-domain system identifications are used for aerial vehicles.

Fig. 1
figure 1

3-DOF Helicopter

Full size image

In [10], a continuous differentiator-based adaptive second-order control strategy that integrates twisting controllers with a continuous differentiator is proposed to control the 3-DOF helicopter. The control strategy mentioned in [4] controls the attitude of the helicopter using the Linear Quadratic Regulator (LQR) method. Here, feedback linearization is achieved, and the controller is incorporated to take into account unpredictable events. Using integral action, tracking error is minimized in [11], in which an adaptive LQR is developed and provides a solution for the unknown faults in the system. In [12], a non-linear control of a second-order auxiliary system is implemented to filter the error signals while estimating some disturbances and uncertainties. To track the trajectory of small helicopters in [3], a robust control algorithm is implemented. This control method does not rely on the system’s model parameters. In [13], a control strategy involving an adaptive back-stepping tracker for a 6-DOF helicopter is implemented where the controller juxtaposes the proposed parameters with the online parameters. A similar control technique for a 3-DOF helicopter involving back-stepping is mentioned in [14], where the controller is equipped with the ability to approximate model uncertainties and accelerate the performance of the model. In [15], to deal with non-linear actuator faults and other uncertainties, an adaptive neural-fault controller is proposed.

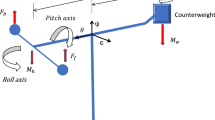
The main challenge in designing a controller for a 3-DOF helicopter is stabilizing the 3-DOF helicopter system as it is non-linear and has unstable dynamics. The motion of a 3-DOF helicopter is dictated by the three axes of rotation shown in Fig. 1. These axes, the roll, yaw, and pitch, are non-linear and coupled, which complicates the controller design. A 3-DOF helicopter system is an underactuated system, as three degrees of freedom (yaw, roll, and pitch) are present while there are only two controlling forces available. Therefore, for optimal results and tracking, these three non-linear parameters must be modeled as state-space equations, and then necessary control techniques are executed on these parameters. This paper aims at motion tracking for a 3-DOF helicopter using the LQR control technique in the presence of both structured and unstructured uncertainties. The objective is to ensure that the three parameters (roll, yaw, and pitch) operate at their desired value and that in the event of uncertainties, the LQR control strategy brings the three parameters back to their original position. In this control system, once the non-linear parameters are linearized, the PI controller-based technique is employed. LQR control method has an upper hand over the conventional control methods involving PI or PID controllers.

An adaptive control strategy was implemented in coping with structured and unstructured uncertainties in [16], and in that paper, the derivative of the error, which is noisy and thereby limits the system’s performance, is used in achieving disturbance rejection. Authors in [17] addressed this shortcoming by using an advanced control method to cope with unstructured uncertainties (like external disturbance). Nevertheless, the strategy introduced in [17] contains a lot of complexity and is almost overkill. Unlike [16], and [17], the Linear Quadratic Regulator control strategy proposed in this paper is an optimal tracking controller that achieves similar performance to [17] but with much more simplicity. Not only does this paper introduce a simple strategy, but it is also one of the first attempts, to the best of the author’s knowledge, to implement an LQR strategy in coping with a 3-DOF helicopter. An LQR strategy has been used to control 2-DOF helicopters, but the work presented in this paper has novelty in its use on the 3-DOF helicopter. This paper is divided into the following sections: Sect. 2 explains the mathematical model and system dynamics on the 3-DOF helicopter, and the equivalent state-space model is derived. Section 3 demonstrates the design of the LQR feedback controller, which is integrated with a PI-based controller plant model. The performance of the LQR controller under structured and unstructured uncertainties is validated in Sect. 4, and finally, Sect. 5 expresses the conclusion with remarks and suggestions for future works.

2 Operating principle of the 3-DOF helicopter

2.1 System model

The 3-DOF helicopter shown in Fig. 1 is used as a benchmark to validate the effectiveness of various control strategies. This benchmark model has features like nonlinear model dynamics, uncertain characteristics, and a dual-motor cross coupling system, like a real 3-DOF helicopter [18]. The system was designed by Quanser to provide researcher with a platform to test different control strategies [19]. Such system can also be used for other educational purposes, and real applications of 3-DOF flight control dynamics [20]. At the centre of gravity of the 3-DOF helicopter, we can define a three-dimensional coordinate system of movement with three axes. These axes are called roll (\(\epsilon \)), pitch (\(\theta \)), and yaw (\(\psi \)). The roll axis revolves around the longitudinal axis that extends from the nose to the tail of the helicopter system. A helicopter’s rolling motion is an up and down movement of its wing tips [21]. The pitch axis is parallel to the plane of the helicopter’s wings, and it extends from the left wing tip to the right wing tip. A helicopter’s pitch motion is an up and down movement of its nose or tail [21]. The yaw axis is perpendicular to the plane of the helicopter’s wings and directed towards the bottom of the aircraft. A helicopter’s yawing motion is the movement of its nose or tail from side to side [21]. The dynamics of the propeller motion of the 3-DOF helicopter are highly non-linear and interlinked, which makes the helicopter unstable [18].

The mathematical model for the system is developed using Fig. 1 and the Euler-Lagrange equation. The forces acting on the helicopter by the DC motor and the counter mass are also considered. The mathematical model is given by the following equations [16]:

$$\begin{aligned} J_\epsilon \ddot{\epsilon }&= G \cos \epsilon + L_a \cos \theta u_1 \end{aligned}$$
(1a)
$$\begin{aligned} J_\psi \ddot{\psi }&= L_a \cos \epsilon \sin \theta u_1 \end{aligned}$$
(1b)
$$\begin{aligned} J_\theta \ddot{\theta }&= L_h u_2 \end{aligned}$$
(1c)

with, \(u_1 = F_f + F_b\), \(u_2 = F_f - F_b\) , \(G = g (M_h L_a - M_w L_w)\), where, \(\ddot{\epsilon }\), \(\ddot{\theta }\), and \(\ddot{\psi }\) are the double derivatives of the roll, pitch and yaw axes respectively, and,

$$\begin{aligned}&M_h : \hbox {mass of the helicopter}\\&M_w :\hbox {mass of the counterweight}\\&L_a :\hbox {length from the rotors to the center of mass}\\&L_w :\hbox {length from the tail to the center of mass}\\&L_h :\hbox {length between the rotors}\\&g :\hbox {gravitational constant} \\&\epsilon :\hbox {roll angle of the helicopter}\\&\psi :\hbox {yaw angle of the helicopter}\\&\theta :\hbox {pitch angle of the helicopter}\\&u_1:\hbox {control input vector} \\&u_2:\hbox {control input vector} \\&J_\epsilon :\hbox {moment of inertia about roll}\\&J_\psi :\hbox {moment of inertia about yaw}\\&J_\theta :\hbox {moment of inertia about pitch}\\&F_f:\hbox {front motor force}\\&F_b:\hbox {back motor force}\\ \end{aligned}$$

Before we derive the state-space model of the 3-DOF helicopter, let us introduce some properties of the helicopter system [16]:

Property 1::

The roll and axes are perpendicular to one another.

Property 2::

The three axes intersect at the same point; this point is the origin of the global coordinate frame.

Property 3::

The helicopter frame and counterweight mass are parallel to the pitch axis.

Property 4::

The system’s centrifugal forces, joint friction, and air resistance are ignored.

Property 5::

The thrust force is correlative to the motor voltage, and the dynamics of the motors/propeller are ignored.

It is important to note that the 3-DOF helicopter is underactuated. This means that the system has only two input forces/actuators to control three degrees of freedom (roll (\(\epsilon \)), pitch (\(\theta \)), and yaw (\(\psi \))) [22].

2.2 State space model

The state-space model for the 3-DOF helicopter is derived based on the following assumptions:

  • The roll and yaw axis are orthogonal to each other

  • The helicopter rectangular frame bed and the counterweight are in the same line with reference to the pitch axis

  • Air resistance, centrifugal forces, and joint friction are neglected

  • The thrust force generated is proportional to the DC motor voltage, and the dynamics of the propeller is neglected

The 3-DOF helicopter has three parameters: the roll, yaw, and pitch. These parameters are the state variables of the system which need to be controlled. There are also only two control inputs available, and they are:

$$\begin{aligned} u_1&= F_f + F_b, ~\text {and,} \end{aligned}$$
(2a)
$$\begin{aligned} u_2&= F_f - F_b \end{aligned}$$
(2b)

Equations (1a), (1b), and (1c) are used in deriving the state-space model of the 3-DOF helicopter. It is clear that Eq. 1a is a non-linear equation so before proceeding with the state-space derivation, Eq. 1a is linearized around an equilibrium point. Since three variables must be controlled, two fictitious inputs are intentionally introduced and they are denoted as:

$$\begin{aligned} v_1&= u_1 \cos \theta \end{aligned}$$
(3a)
$$\begin{aligned} v_2&= u_1 \cos \epsilon \sin \theta \end{aligned}$$
(3b)

which re-defines Eqs. (1a), (1b), and (1c) as,

$$\begin{aligned} J_\epsilon \ddot{\epsilon }&= G \cos \epsilon + L_a v_1 \end{aligned}$$
(4a)
$$\begin{aligned} J_\psi \ddot{\psi }&= L_a v_2 \end{aligned}$$
(4b)
$$\begin{aligned} J_\theta \ddot{\theta }&= L_h u_2 \end{aligned}$$
(4c)

Equation (4a) is still non-linear and needs to be linearized even further before the state-space model is derived.

Let us consider an equilibrium point \(\epsilon _0\) around which the equation would be linearized. Re-arranging Eq. (4a) gives,

$$\begin{aligned} \ddot{\epsilon }&= \frac{1}{J_\epsilon } \left( L_a v_1 + G \cos \epsilon \right) = y = f(\epsilon ) \end{aligned}$$
(5a)

Applying Taylor series expansion on the above equation and using first order expansion,

$$\begin{aligned} y = y \epsilon _0 + \frac{dy}{d\epsilon _0} \left( \epsilon - \epsilon _0 \right) \end{aligned}$$
(6a)

Taking the partial derivative of Eq. (6a),

$$\begin{aligned} \frac{dy}{d\epsilon }|_{\epsilon =\epsilon _0}= \frac{G}{J\epsilon } \left( -sin \epsilon _0 \right) \left( \epsilon _0 \right) \end{aligned}$$
(7a)

and using,

$$\begin{aligned} \epsilon _0 = \frac{\pi }{2}, \end{aligned}$$

the Taylor series expansion becomes,

$$\begin{aligned} y= \frac{G}{J\epsilon } \cos \frac{\pi }{2} +\left( \frac{1}{J\epsilon } L_a v_1 \right) -\left( \frac{G \epsilon }{J\epsilon } \sin {\frac{\pi }{2}} \right) \end{aligned}$$
(8a)

which is reduced to,

$$\begin{aligned} \ddot{\epsilon }= y= - \frac{G \epsilon }{J_\epsilon } + \left( \frac{L_a v_1}{J_\epsilon } \right) \end{aligned}$$
(9a)

Now the system has three linear equations given by,

$$\begin{aligned} \ddot{\epsilon }&= - \frac{G \epsilon }{J_\epsilon } + \left( \frac{L_a v_1}{J_\epsilon } \right) \end{aligned}$$
(10a)
$$\begin{aligned} \ddot{\psi }&= \frac{L_a v_2}{J_\psi } \end{aligned}$$
(10b)
$$\begin{aligned} \ddot{\theta }= \frac{L_h u_2}{J_\theta } \end{aligned}$$
(10c)

The actual and desired position and velocity coordinates are denoted as, \(x_1,x_1^d ,x_2,x_2^d ,x_3,x_3^d ,x_4,x_4^d ,x_5,x_5^d ,x_6,x_6^d\).

Fig. 2
figure 2

Block diagram of optimal control tracking system for a 3-DOF helicopter

Full size image

The desired velocity of the propeller is assumed to be zero, so the error between the actual and the desired coordinates is defined as:

$$\begin{aligned} e_1&= x_1 - x_1^d\end{aligned}$$
(11a)
$$\begin{aligned} e_2&= x_2 - x_2^d\end{aligned}$$
(11b)
$$\begin{aligned} e_3&= x_3 - x_3^d\end{aligned}$$
(11c)
$$\begin{aligned} e_4&= x_4 - x_4^d\end{aligned}$$
(11d)
$$\begin{aligned} e_5&= x_5 - x_5^d\end{aligned}$$
(11e)
$$\begin{aligned} e_6&= x_6 - x_6^d \end{aligned}$$
(11f)

To obtain minimum error,

$$\begin{aligned} \begin{aligned} x_1 = x_1^d \end{aligned} \end{aligned}$$
(12)

The state variables are defined in terms of the error variables as:

$$\begin{aligned}&\dot{e}_1= e_2 = {{\dot{\epsilon }}}\end{aligned}$$
(13a)
$$\begin{aligned}&\dot{e}_2 =\ddot{\epsilon }= - \frac{G e_1}{J_\epsilon } + \left( \frac{L_a v_1}{J_\epsilon } \right) \end{aligned}$$
(13b)
$$\begin{aligned}&\dot{e}_1 = e_2 = {{\dot{\psi }}}\end{aligned}$$
(13c)
$$\begin{aligned}&\ddot{\psi }= \frac{L_a v_2}{J_\psi }\end{aligned}$$
(13d)
$$\begin{aligned}&\dot{e}_1 = e_2 = {{\dot{\theta }}}\end{aligned}$$
(13e)
$$\begin{aligned}&\ddot{\theta }= \frac{L_h u_2}{J_\theta } \end{aligned}$$
(13f)

The state equations in the matrix form is given as:

$$\begin{aligned} \dot{x}&= A x + B u \end{aligned}$$
(14a)
$$\begin{aligned} y&= C x + D u \end{aligned}$$
(14b)

Using Eqs. (13a), (13b), (13c), (13d), (13e), and (13f) the state-space matrices are represented as:

$$\begin{aligned} \begin{bmatrix} \dot{e}_1\\ \dot{e}_2\\ \dot{e}_3\\ \dot{e}_4\\ \dot{e}_5\\ \dot{e}_6 \end{bmatrix}&= \begin{bmatrix} 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ -\frac{G}{J_\epsilon } &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \end{bmatrix} \begin{bmatrix} e_1\\ e_2\\ e_3\\ e_4\\ e_5\\ e_6 \end{bmatrix}\nonumber \\&\quad + \begin{bmatrix} 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad \frac{L_a}{J_\epsilon } &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad \frac{L_a}{J_\psi }\\ 0 &{}\quad 0 &{}\quad 0\\ \frac{L_h}{J_\theta } &{}\quad 0 &{}\quad 0 \end{bmatrix} \begin{bmatrix} u_2\\ v_1\\ v_2\\ \end{bmatrix} \end{aligned}$$
(15a)
$$\begin{aligned} \begin{bmatrix} e_1\\ e_2\\ e_3\\ e_4\\ e_5\\ e_6 \end{bmatrix}&= \begin{bmatrix} 1 &{}\quad 0 &{}\quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0\\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 \end{bmatrix} \begin{bmatrix} e_1\\ e_2\\ e_3\\ e_4\\ e_5\\ e_6 \end{bmatrix}\nonumber \\&\quad + \begin{bmatrix} 0 &{}0 &{}0\\ 0 &{}0 &{}0\\ 0 &{}0 &{}0\\ \frac{L_h}{J_\theta } &{}0 &{}0 \end{bmatrix} \begin{bmatrix} u_2 v_1 v_2 \end{bmatrix} \end{aligned}$$
(15b)

and matrices A and B are given as,

$$\begin{aligned} \mathbf{A} = \begin{bmatrix} 0 &{} \quad 1 &{} \quad 0 &{} \quad 0 &{} \quad 0 &{} \quad 0\\ -\frac{G}{J_\epsilon } &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \end{bmatrix} \mathbf{B} = \begin{bmatrix} 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad \frac{L_a}{J_\epsilon } &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad \frac{L_a}{J_\psi }\\ 0 &{}\quad 0 &{}\quad 0\\ \frac{L_h}{J_\theta } &{}\quad 0 &{}\quad 0 \end{bmatrix} \end{aligned}$$
(16)

3 Optimal tracking controller

The Linear Quadratic Regulator is a widely used method that gives optimally controlled feedback gains to enable the stability, and high performance of systems [23]. The LQR control technique employed to track the three state variables is used to improve the system performance and obtain satisfactory results. The feedback gain \(\tilde{{\mathbf {K}}}\) consists of the difference between the feedback gain \({\mathbf {K}}\) and the integral gain \({\mathbf {K}}_i\) and is used to minimize the cost value of J, the performance index. There are already pre-set values for roll, yaw, and pitch, and the purpose of the LQR is to ensure that the actual values remain close to the predefined values and the error obtained is as minimum as possible. Essentially, the LQR algorithm is an automated way of finding a suitable state-feedback controller for the 3-DOF helicopter system [24]. The system’s state-space equations can be written as,

$$\begin{aligned} \dot{{\mathbf {x}}}(t)&= {\mathbf {A}}{\mathbf {x}}(t) + {\mathbf {B}}{\mathbf {u}}(t) \end{aligned}$$
(17a)
$$\begin{aligned} {\mathbf {y}}(t)&= {\mathbf {C}}{\mathbf {x}}(t) \end{aligned}$$
(17b)

where y(t) is,

$$\begin{aligned} y(t)=\begin{bmatrix} \epsilon (t)\\ \psi (t)\\ \theta (t) \end{bmatrix} \end{aligned}$$
(18)

and the output matrix C is,

$$\begin{aligned} C=\begin{bmatrix} 1 &{}0 &{}0 &{}0 &{}0 &{}0\\ 0 &{}0 &{}1 &{}0 &{}0 &{}0\\ 0 &{}0 &{}0 &{}0 &{}0 &{}0\\ \end{bmatrix} \end{aligned}$$
(19)

The reference signal is denoted as r(t), and the reference to be tracked is given by,

$$\begin{aligned} y(t)=\begin{bmatrix} \epsilon ^d(t) \psi ^d(t) \theta ^d(t) \end{bmatrix} \end{aligned}$$
(20)

Here the optimum input voltage is tracked so that given an initial state \(x_0\) at \(t=0\), the output y(t) tracks the reference values. The main goal is to reduce the error, and since the state model is obtained in terms of the error variables, the augmented state and matrices are defined by,

$$\begin{aligned} \dot{{\mathbf {e}}}(t) = \tilde{{\mathbf {A}}}{\mathbf {e}}(t) + \tilde{{\mathbf {B}}}{\mathbf {u}}^*(t),~~\text {where,} \end{aligned}$$
(21)

the augmented state and matrices are defined as:

$$\begin{aligned}&{\tilde{A}}=\begin{bmatrix} A_{6X6} &{} 0_{6X3} \\ -C_{3X6} &{} 0_{3X3} \end{bmatrix}_{9X9} \end{aligned}$$
(22)
$$\begin{aligned}&{\tilde{B}} =\begin{bmatrix} B_{6X3} \\ 0_{3X3} \end{bmatrix}_{9X9} \end{aligned}$$
(23)

The augmented performance index J is defined,

$$\begin{aligned} J(\tilde{{\mathbf {u}}}) = \frac{1}{2}\int _0^{\infty }\left[ {\mathbf {e}}^T(t) \tilde{{\mathbf {Q}}}{\mathbf {e}}(t) + {\mathbf {u}}^T(t) \tilde{{\mathbf {R}}}{\mathbf {u}}(t)\right] \mathrm {dt}, \end{aligned}$$
(24)

where \({\tilde{Q}}\) is a \(9 \times 9\) positive definite matrix and \({\tilde{R}}\) is a \(3 \times 3\) positive definite matrix. These two matrices are also called the weighting matrices. The feedback gain matrix \({\tilde{K}}\) which gives us u(t) to minimize the performance index is given by,

$$\begin{aligned} \tilde{{\mathbf {K}}} = \tilde{{\mathbf {R}}}^{-1}\tilde{{\mathbf {B}}}^T\tilde{{\mathbf {P}}}, \end{aligned}$$
(25)

and \({\tilde{P}}\) is evaluated by,

$$\begin{aligned} \tilde{{\mathbf {A}}}^T \tilde{{\mathbf {P}}} + \tilde{{\mathbf {P}}}\tilde{{\mathbf {A}}} - \tilde{{\mathbf {P}}}\tilde{{\mathbf {R}}}^{-1}\tilde{{\mathbf {B}}}^T\tilde{{\mathbf {P}}} + \tilde{{\mathbf {Q}}} = {\mathbf {0}}. \end{aligned}$$
(26)

Note that the feedback gain \(\tilde{{\mathbf {K}}}\) is composed of the state-feedback gain \({\mathbf {K}}\) and the integral gain \({\mathbf {K}}_i,\) i.e. \(\tilde{{\mathbf {K}}} = [{\mathbf {K}}~~-{\mathbf {K}}_i].\) The key steps to implementing the proposed optimal tracking controller are summarized below.

Step 1::

Define the reference (pitch, roll and yaw angles) signal \({\mathbf {r}}(t).\)

Step 2::

Implement the model parameters of the 3-DOF helicopter system in determining the matrices \({\mathbf {A}},\) \({\mathbf {B}},\) and \({\mathbf {C}}\)

Step 3::

Calculate the augmented matrices \(\tilde{{\mathbf {A}}}\) and \(\tilde{{\mathbf {B}}}\) for Eq. (21)

Step 4::

Define the weighting matrices \(\tilde{{\mathbf {Q}}}\) and \(\tilde{{\mathbf {R}}},\)

Step 5::

Solve the optimal feedback gain matrix \(\tilde{{\mathbf {K}}}\) using Eqs. (25) and (26)

Step 6::

Separate the optimal feedback gain matrix \(\tilde{{\mathbf {K}}}\) from \({\mathbf {K}}\) and \({\mathbf {K}}_i\)

Step 7::

Run the optimal tracking control system shown in Fig. 2.

Table 1 Physical parameters of the helicopter
Full size table

The simplicity of the algorithms and key steps listed above reiterates our claim that the LQR control strategy is simpler than other control strategies proposed for the 3-DOF helicopter system.

4 Results and discussion

In this section, various computer experiments are carried out on the performance of the 3-DOF helicopter. Table 1 shows the physical parameters of the helicopter. To better show how robust the LQR controller is, the controller is implemented on the 3-DOF helicopter system, and the results are simulated in MATLAB/Simulink. The controller is put under several tests to validate our claim that it performs optimally even under structured and unstructured uncertainties. The desired position reference trajectory, p(t), is a step response of a first-order system with an initial value of 0 and a final value of 1, for \(\epsilon (t)\), \(\theta (t)\), and \(\psi (t)\), where \(t \in [0, 50]\) [s].

Fig. 3
figure 3

Nonzero initial condition, nominal case, disturbances a roll; b yaw; c pitch; d tracking errors; and e control signals

Full size image
Fig. 4
figure 4

PID controller: a roll; b yaw; c pitch; d tracking errors; and e control signals

Full size image
Table 2 Trajectory performance comparison
Full size table
Fig. 5
figure 5

Parameter variations: tracking errors with a halved parameters; b doubled parameters; and control signals with c halved parameters; d doubled parameters

Full size image

The system’s response is analyzed under various operating conditions using the helicopter’s pitch, roll, and yaw angles along with their respective tracking errors and control signals \(v_1, v_2,\) and \(u_2\). The proposed LQR control strategy is initially tested on the 3-DOF helicopter under a non-zero initial condition. For that, the initial position of the three axes is set to 0.5 [rad]. Once the system is stabilized, the pitch, roll, and yaw angle trajectories are subjected to a step change at different times, i.e., 25 s, 15 s, and 20 s, respectively. Finally, the 3-DOF helicopter undergoes an external disturbance on all angles at time 40 s. In here, the goal is to assess the control performance under three different operating conditions, i.e., non-zero initial condition, nominal case, and disturbance. Results are shown in Fig. 3. As it can be seen, the first 10 s of each graph in Fig. 3 shows the system under nonzero initial conditions, and in Fig. 3a–c, the system’s transient response starts at the nonzero initial condition values but still converges to the desired reference trajectory. The controller also maintains the stability of the system by bringing the control signals back to their desire state and converging the tracking errors to zero even with nonzero initial conditions. These show that with this controller, nonzero initial conditions have little to no influence on the 3-DOF helicopter system. Then, the system’s response under nominal conditions is shown from 10 s to 40 s. From these results, we can see that the controller’s tracking errors follow the reference trajectory, and with each change in the trajectory path, the tracking errors gradually converge to zero. The pitch, roll, and yaw angles which have a step time of 25 s, 15 s, and 20, s respectively, also closely follow the desired trajectory path. In Fig. 3e, despite the slight overshoot at 15 s, 20 s, and 25 s, the controller still maintains the system’s stability and brings the control signals back to their desired state. Finally, the system’s ability to cope with unexpected step disturbances of 1 [rad] is shown at time 40 s. Again, the controller decays all errors to zero without significant oscillation and significant overshoot (evident in Fig. 3e). On each graph in Fig. 3, the system’s performance under the presence of external disturbances is shown at time 40 s. The pitch, yaw, and roll angles experience a slight overshoot and then converge to the desired trajectory path. The control signals, \(u_1,\) \(v_2,\) and \(u_2,\) also successfully converge to zero, and the controller is able to maintain the system’s stability.

Next, a PID controller is tested on the 3-DOF helicopter system using the same operating conditions and the results are compared against the results obtained from the proposed LQR control strategy. The PID controller is used for comparison because it is a control solution that is as simple as the proposed control strategy. The results of this comparison are shown in Fig. 4, and the results contain the performance of the system under nonzero initial conditions [0 s to 5 s], nominal scenario [5 s to 40 s] and external disturbances [40 s to 50 s]. From these results, we see that the PID controller has more oscillations and does not converge to zero as easily as the LQR controller. The PID controller operates under the same circumstances as the proposed controller but takes more time to decay the tracking errors to zero. The graphs of the pitch, roll, and yaw angles for the PID controller also have sudden unexpected oscillations in the nominal scenario which are reflected in the tracking errors. Two performance metrics are also introduced to adjudge the trajectory tracking performance of the two controllers. The first metric, \(\sigma _e,\) is the integral of the tracking error (the integral of the pitch, roll, and yaw errors), and the second metric, \(\sigma _c,\) is the integral of the control signals. The expression for these metrics are shown below:

$$\begin{aligned} \sigma _e= & {} \int _{t_0}^{t_f}({\epsilon }^2+{\psi }^2+{\theta }^2){dt} \end{aligned}$$
(27)
$$\begin{aligned} \sigma _c= & {} \int _{t_0}^{t_f}({v_1}^2+{v_2}^2+{u_2}^2){dt} \end{aligned}$$
(28)

where \(t_0\) and \(t_f\) are the initial and final time instants. The numerical results obtained using Eqs. (27) and (28) are shown in Table 2. The results show that the proposed control strategy attains the lowest tracking index with the lowest control effort. A low tracking index indicates high tracking accuracy, so it is safe to say the proposed strategy achieved the highest tracking accuracy with the lowest control effort, thus demonstrating its superiority over the PID controller.

To test the effects of parametric uncertainties on our controller, the constant G is varied by a factor of 2 and then by a factor of 0.5. The constant \(G = g (M_h L_a - M_w L_w),\) so by keeping \(g, L_a, L_w\) constant and varying G,  the mass of the helicopter, \(M_h,\) and the mass of the counterweight, \(M_w,\) are varied. Figure 5 shows the results of the tracking errors and the control signals when these parameters are changed. From the results, we can see that even with parameter variations, the controller maintains the stability of the system. The tracking errors experience little to no change with the variation in parameter values, and the control signals experience a slight change, but these signals successfully return to their desired path. It is important to note that the control design is based on the system’s linearization around an operation point. Henceforth, a proper selection of such operation point is crucial to guarantee good performance. Future work envisions an experimental analysis to investigate any limitation such linearization might have on the physical system. Also, a comparison against more advanced control strategies can be carried out.

5 Conclusion

In this paper, an optimal tracking LQR control strategy is proposed for a high-performance 3-DOF helicopter system. The state-space model of the system and the mathematical model of the LQR control strategy are calculated. Despite the underactuated non-linear nature of the helicopter system, a successful linearization of the system’ is achieved. To test the robustness and effectiveness of the controller, numerical experiments are carried out and simulated using MATLAB/Simulink. External disturbances, parameter variation, non-zero initial conditions, e.t.c., are added to the system, and in all these cases, the controller is successful in maintaining the stability of the 3-DOF helicopter system. The LQR control strategy is also compared to the PID control strategy for the same 3-DOF helicopter system, and the LQR controller displays superiority in performance and robustness by achieving a higher tracking accuracy with a lower control effort. Future work could focus on a comparative study of other linear control strategies and their effects on a 3-DOF helicopter.