Application of a Basic Variable Neighborhood Search Algorithm in the Coordinated Tuning of PSS and POD Controllers

Abstract

This paper proposes the application of a Basic Variable Neighborhood Search algorithm in the coordinated and simultaneous tuning of the parameters of damping controllers known as power system stabilizer and thyristor-controlled series capacitor–power oscillation damping. The controllers are inserted into the multi-machine power system New England (10 generators, 39 buses and 46 transmission lines) in order to guarantee its small-signal stability. A current injection model for the thyristor-controlled series capacitor is presented and incorporated into the current sensitivity model, which is used to represent the electric power system and its components. The performance of the method proposed in this work is compared to three other methods found in the literature: local search, iterated local search and particle swarm optimization. The results show that, of the techniques analyzed, the Basic Variable Neighborhood Search is the most efficient for this type of problem, presenting high convergence rates and the shortest processing times with robust solutions considering different scenarios with load variations.

1 Introduction

The development of new technologies and their incorporation into the users lives makes society extensively dependent on the use of electric energy. In order for consumers to be able to use their equipment, electrical quantities such as voltage and frequency must meet certain standards, and disruptions in power supply should be avoided, i.e., the electric power system (EPS) must operate in a safe and reliable manner.

In view of this, interconnections of EPSs increase reliability, meeting the energy demand using different sources and improving energy use according to the needs of different interconnected regions. However, often the EPS interconnections are achieved by the installation of long transmission lines with high inductances. This factor linked to an operation with high loads and automatic voltage regulators (AVRs) with high gains and low time constants, favors the emergence of low-frequency electromechanical oscillations that may result in instability of the EPSs (Anderson and Fouad 2003).

Stability can be defined as the ability of an EPS that functions stably under normal operating conditions, to recover its state of equilibrium after being subjected to a perturbation (Kundur et al. 2004). Small-signal stability, the subject of this work, considers small load variations in the system and includes the study of electromechanical oscillatory modes that can be identified according to their natural undamped frequencies (Milano 2010). The most common electromechanical oscillatory modes are classified as local (0.7–2.0 Hz) or inter-area (0.1–0.8 Hz) (Klein et al. 1991).

In order to introduce additional damping to the oscillatory modes inherent to the EPSs, power system stabilizers (PSSs) are often coupled to the control loop of the excitation system of the synchronous generators (Demello and Concordia 1969; Talaq 2012). With tuned parameters, the PSS is able to introduce additional damping mainly to local modes. However, in some cases, its influence on the damping of inter-area modes may be insufficient (Cai and Erlich 2005).

The use of flexible AC transmission systems (FACTS) can optimize the performance of the EPS by controlling and directing power flow (Zhang et al. 2006). Studies show that when a power oscillation damping (POD) controller is coupled to a FACTS device, the FACTS–POD set is able to efficiently provide additional damping to inter-area modes (Cai and Erlich 2005; Simoes et al. 2009; Menezes et al. 2016).

In this work, the FACTS device used is a series compensator comprising a fixed capacitance in parallel with a controlled reactor by thyristor called a thyristor-controlled series capacitor (TCSC) (Del Rosso et al. 2003).

The damping controllers must be correctly tuned in order to provide desired damping to the oscillatory modes. Some classical techniques described in the literature have disadvantages such as the residue method (Yang et al. 1998; Valle and Araujo 2015), which does not provide coordinated tuning thus inhibiting its application in complex systems and the decentralized modal control (DMC) (Araujo and Zaneta 2001; Valle and Araujo 2015) which requires an auxiliary method to provide a quality starting point to achieve convergence.

Stochastic methods such as metaheuristics are of note in the coordinated tuning of supplementary damping controllers, as they are able to find feasible solutions without previous knowledge of the problem and independent of the number of controllers or the complexity of the system with reasonable computational times. Among the metaheuristics applied to this type of problem are the particle swarm optimization algorithm (Shayeghi et al. 2010; Menezes et al. 2016; Hasanvand et al. 2016), Bacterial Foraging Optimization Algorithm (BFOA) (Abd-Elazim and Ali 2012), Simulated Annealing (Abido 2000), in addition to methods based on Genetic Algorithms (GAs) (Hassan et al. 2014; Fortes et al. 2016).

In this article, a method based on the metaheuristic Basic Variable Neighborhood Search (BVNS) is proposed to perform the coordinated tuning of the PSS and TCSC–POD controllers. Variable neighborhood search algorithms are methods that systematically explore exchanges in neighborhood structures linked to a local search (Mladenović and Hansen 1997). The original BVNS is adapted to work with continuous coding, neighborhood structures based on position exchanges and a local search stage using the concept of sensitivity.

In order to evaluate the quality of the proposed method, comparisons are performed considering algorithms described in the literature: local search (LS) (Glover and Kochenberger 2003) and iterated local search (ILS) (Lourenço et al. 2010) that are local search algorithms, in addition to the PSO which is a populational and bio-inspired algorithm extensively used in several types of problems (Kennedy and Eberhart 1995).

In this work, simulations are performed using a test system known as New England (Araujo and Zaneta 2001). The EPS is represented by the Current Sensitivity Model (CSM) (Pádua Júnior et al. 2013). Finally, a model by current injection is presented for the TCSC device, which is incorporated into the representation of the EPS by the CSM.

Considering the above, the main contributions of this article are: (1) The implementation and analysis of the efficiency of the BVNS algorithm proposed in the coordinated and simultaneous tuning of the parameters of PSS and POD controllers, taking into account different damping levels and load variations; (2) modeling of the TCSC device by current injection for its incorporation into the CSM.

2 Current Sensitivity Model

The CSM is based on Kirchhoff’s current law with the current balance equations being the algebraic equations of the model. The balance expressed in Eqs. (1) and (2) must be met in all system buses and at all times during any dynamic process.

In Eqs. (1)–(2), $\Delta I_{gk}$ is the terminal current of the generator connected to bus k, $\Delta I_{ki}$ is the current flowing through the transmission line from bus k to bus i with $\varOmega _k$ being the set of buses connected directly to k by means of a transmission line and $\Delta I_{lk}$ is the current drained by the load connected to bus k. The currents are linearized, and the real (r) and imaginary (m) components are considered.

$$\begin{aligned} 0= & {} \Delta I_{gk_{r}} - \sum _{i\in \varOmega _k} \Delta I_{ki_{r}} - \Delta I_{lk_{r}} \end{aligned}$$

(1)

$$\begin{aligned} 0= & {} \Delta I_{gk_{m}} - \sum _{i\in \varOmega _k} \Delta I_{ki_{m}} - \Delta I_{lk_{m}} \end{aligned}$$

(2)

The representation in the time domain for a multi-machine system modeled by the CSM, consisting of nb buses and ng generators, is expressed in Eqs. (3)−(6) (Pádua Júnior et al. 2013; Fortes et al. 2016).

$$\begin{aligned}&\left[ \begin{array}{c} \Delta {\dot{x}}\\ 0 \end{array} \right] = \left[ \begin{array}{ll} J1 &{}\quad J2\\ J3 &{}\quad J4 \end{array} \right] \left[ \begin{array}{c} \Delta x \\ \Delta z \end{array} \right] + \left[ \begin{array}{c} B1 \\ B2 \end{array} \right] \left[ \begin{array}{c} \Delta u \end{array} \right] \end{aligned}$$

(3)

$$\begin{aligned}&\begin{aligned} \Delta x&= \left[ \left[ \Delta \omega _{1\cdots ng} \right] \left[ \Delta \delta _{1 \cdots ng}\right] \left[ \Delta E'_{q,1 \cdots ng} \right] \right. \\&\quad \,\,\left. \left[ \Delta E_{fd,1 \cdots ng} \right] \right] ^\mathrm{T} \end{aligned}\end{aligned}$$

(4)

$$\begin{aligned}&\begin{aligned}\Delta u&= \left[ \left[ \Delta P_{m,1 \cdots ng} \right] \left[ \Delta V_\mathrm{ref,1 \cdots ng} \right] \left[ \Delta P_{l,1 \cdots nb} \right] \right. \\&\quad \,\,\left. \left[ \Delta Q_{l,1 \cdots nb} \right] \right] ^\mathrm{T} \end{aligned} \end{aligned}$$

(5)

$$\begin{aligned}&\Delta z = \left[ \left[ \Delta \theta _{1 \cdots nb}\right] \left[ \Delta V_{1 \cdots nb} \right] \right] ^\mathrm{T} \end{aligned}$$

(6)

In Eqs. (3)−(6), $\Delta x$ is the vector of state variables consisting of $\Delta \omega$ (variations in the angular velocity of the generator rotor), $\Delta \delta$ (variations in the internal angle of the generator rotor), $\Delta E'_{q}$ and $\Delta E_\mathrm{fd}$ (variations in the internal voltage of the quadrature axis and in the field voltage). The variables $\Delta \theta$ and $\Delta V$ (variations in the angles and in the magnitudes of the EPS buses voltages) form the algebraic variables $\Delta z$. The vector of the input variables is $\Delta u$ formed by $\Delta P_m$ (variations in the mechanical input power of the generator), $\Delta V_\mathrm{ref}$ (variations in the reference voltage of the AVRs), $\Delta P_{l}$ and $\Delta Q_{l}$ (variations in the active and reactive power of the loads).

The representation in the space of states is obtained by eliminating the vector of algebraic variables according to Eq. (7). The ways of obtaining the states matrix A and the matrix of inputs B are presented in Eqs. (8) and (9).

$$\begin{aligned}&\Delta {\dot{x}} = A \Delta x + B \Delta u \end{aligned}$$

(7)

$$\begin{aligned}&A = J1-J2 J4^{-1}J3 \end{aligned}$$

(8)

$$\begin{aligned}&B = B1-J2 J4^{-1}B2 \end{aligned}$$

(9)

3 Thyristor-Controlled Series Capacitor

The FACTS TCSC device is a series compensator composed of a capacitance $( C)$ in parallel with a reactor $( L)$ controlled by thyristors associated in antiparallel as shown in Fig. 1. With the TCSC installed, it is possible to achieve different levels of compensation of the transmission line reactance from the firing angle of the thyristors.

Fig. 1

EPS buses with the TCSC installed

3.1 Current Injection Model for the TCSC

Among the models used to study stability, those based on current injection generally present higher convergence speeds for the power flow, some of these models can be found in Freitas and Morelato (2001). Furthermore, the TCSC modeling by current injection facilitates its inclusion in the CSM, justifying the adoption of this method. The model used in this work is based on the current injection model presented in Shayeghi et al. (2010). The diagram in Fig. 2 is used to deduce the model, and the TCSC is represented by a capacitive reactance $x_\mathrm{tcsc}$ installed between buses k and i connected by a transmission line with impedance ${\bar{Z}}_{ki}$ expressed in Eq. (10).

Fig. 2

EPS buses with the TCSC represented by an equivalent reactance

The circulation of the current $\bar{I}_{ki}$ expressed in Eq. (11) by the capacitive reactance causes a voltage drop that can be represented by a voltage source $\bar{V}_\mathrm{tcsc}$ as presented in Eq. (12). The transformation of the voltage source into a current source $\bar{I}_\mathrm{tcsc}$ gives Eq. (13). Finally, the currents $\bar{I}_\mathrm{tcsc_{k}}$ and $\bar{I}_\mathrm{tcsc_{i}}$ are injected into buses k and i as shown in Fig. 3 and expressed in Eqs. (14) and (15).

$$\begin{aligned}&\bar{Z}_{ki}= r_{ki} + jx_{ki} \end{aligned}$$

(10)

$$\begin{aligned}&\bar{I}_{ki}= \frac{\bar{V}_{k} - \bar{V}_{i} }{r_{ki} + j(x_{ki}-x_\mathrm{tcsc})} \end{aligned}$$

(11)

$$\begin{aligned}&\bar{V}_\mathrm{tcsc}= -jx_\mathrm{tcsc}\bar{I}_{ki} \end{aligned}$$

(12)

$$\begin{aligned}&\bar{I}_\mathrm{tcsc}= - j\frac{{x}_\mathrm{tcsc}}{r_{ki} + jx_{ki}} \,\frac{\bar{V}_{k} - \bar{V}_{i} }{r_{ki} + j(x_{ki}-x_\mathrm{tcsc})} \end{aligned}$$

(13)

$$\begin{aligned}&\bar{I}_\mathrm{tcsc_{k}}= \bar{I}_\mathrm{tcsc} \end{aligned}$$

(14)

$$\begin{aligned}&\bar{I}_\mathrm{tcsc_{i}}= -\bar{I}_\mathrm{tcsc} \end{aligned}$$

(15)

Fig. 3

Current injection by the TCSC

The current injections are linearized around an operating point, and the TCSC is incorporated into the CSM considering these injections in the currents balance for buses k and i (Fig. 4) that are connected by a transmission line with the TCSC installed, that is, in the algebraic equations of the model.

Fig. 4

Currents balance in the buses common to the TCSC installation

From Fig. 4, it is possible to deduce Eqs. (16)−(19) that represent the algebraic equations for the real (r) and imaginary (m) components, which are to be incorporated into the CSM for buses k and i common to the TCSC installation.

$$\begin{aligned} 0= & {} \Delta I_{gk_{r}} + \Delta I_\mathrm{tcsc_{ k,r}} - \sum _{i\in \varOmega _k} \Delta I_{ki_{r}} - \Delta I_{lk_{r}} \end{aligned}$$

(16)

$$\begin{aligned} 0= & {} \Delta I_{gk_{m}} + \Delta I_\mathrm{tcsc_{ k,m}} - \sum _{i\in \varOmega _k} \Delta I_{ki_{m}} - \Delta I_{lk_{m}} \end{aligned}$$

(17)

$$\begin{aligned} 0= & {} \Delta I_\mathrm{tcsc_{ i,r}} - \sum _{k\in \varOmega _i} \Delta I_{ik_{r}} - \Delta I_{li_{r}} \end{aligned}$$

(18)

$$\begin{aligned} 0= & {} \Delta I_\mathrm{tcsc_{ i,m}} - \sum _{k\in \varOmega _i} \Delta I_{ik_{m}} - \Delta I_{li_{m}} \end{aligned}$$

(19)

4 Power System Stabilizer and Power Oscillation Damping

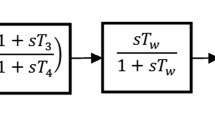
The PSS and POD controllers can be introduced to the system to insert additional damping to the EPS. The structures of these two controllers are similar; both have a gain, an input washout filter and two lead-lag compensator blocks. The generic structure of the PSS and POD is shown in Fig. 5.

Fig. 5

Block diagram: generic structure of PSS and POD controllers

In Fig. 5, $\Delta V_\mathrm{in}$ and $\Delta V_\mathrm{out}$ are the input and output signals, respectively. The gain K acts on the amplification or attenuation of the processed signal. The washout filter, formed by the time constant $T_{\omega }$, has the function of attenuating the variation of the input signal and zeroing the controller response in steady state. The lead-lag compensator blocks are responsible for phase compensation of the oscillatory mode of interest using the time constants $T_1, T_2, T_3$ and $T_4$.

The difference between the controllers is in the operating mode and the input and output signals. In this work, the PSS uses variations of the rotor angular velocity ($\Delta \omega _k$) as its input signal because it is an easily obtainable local signal. The controller inserts the output signal ($\Delta V_\mathrm{pss_k}$) into the AVR control loop of the generator in which it is installed, as shown in Fig. 6a, where $K_{a_k}$ is the gain and $T_{a_k}$ is the time constant of the AVR. $\Delta E_{f_{d_k}}, \Delta V_{\mathrm{ref}_k}$ and $\Delta V_k$ represent the field, reference and terminal voltages of the generator k, respectively.

Fig. 6

Block diagrams: control loop of the AVRs (a) and the TCSC (b)

The POD controller inserts an output stabilizing signal ($\Delta X_\mathrm{pod}$) into the control loop of the FACTS. In this work, the POD uses the variation of the active power of the transmission line ($\Delta P_{km}$) in which the TCSC is installed as the input signal, and this was chosen as it is a local signal and so avoids the use of an auxiliary communication system, in addition to have a high observability. It is also considered a first-order model for the FACTS. The TCSC–POD output stage is shown in Fig. 6b, where $\Delta X_\mathrm{ref}$ and $\Delta X_\mathrm{tcsc}$ represent the reference and TCSC reactances, and $T_\mathrm{tcsc}$ is the time constant of the FACTS device.

On analyzing the block diagrams in Figs. 5 and 6, it is possible to deduce the equations representing the dynamic behavior of the controllers, which can also be found in Fortes et al. (2016). With the modeling presented, the inclusion of the PSS controller introduces three new state variables into the model, which are expressed in Eqs. (20)−(22). The output modulated by the PSS with respect to the field voltage of the synchronous generator is shown in Eq. (23). The dynamic behavior of the POD controller is expressed in Eqs. (24)−(26), the inserted stabilizer signal in Eq. (27) and the state variable relating to the output signal in Eq. (28).

$$\begin{aligned}&\Delta {\dot{V}}_{1_k} = \Delta \dot{\omega }_k K_\mathrm{pss_{ i}} - \frac{1}{T_{\omega }}\Delta V_{1_k} \end{aligned}$$

(20)

$$\begin{aligned}&\Delta {\dot{V}}_{2_k} = \frac{1}{T_{2_i}} \Delta V_{1_k} + \frac{T_{1_i}}{T_{2_i}} \Delta {\dot{V}}_{1_k} - \frac{1}{T_{2_i}} \Delta V_{2_k} \end{aligned}$$

(21)

$$\begin{aligned}&\Delta {\dot{V}}_\mathrm{pss_{ k}} = \frac{1}{T_{4_i}} \Delta V_{2_k} + \frac{T_{3_i}}{T_{4_i}} \Delta {\dot{V}}_{2_k} - \frac{1}{T_{4_i}} \Delta V_\mathrm{pss_{ k}} \end{aligned}$$

(22)

$$\begin{aligned}&\Delta {\dot{E}}_{{fd}_k} = \frac{K_{a_k}}{T_{a_k}} \left( \Delta V_\mathrm{pss_{ k}} + \Delta V_{\mathrm{ref}_k} - \Delta V_{k}\right) - \frac{1}{T_{a_k}} \Delta E_{{fd}_k} \nonumber \\\end{aligned}$$

(23)

$$\begin{aligned}&\Delta {\dot{X}}_1 = \frac{1}{T_{\omega _p}}\left( K_\mathrm{pod}\Delta P_{km} - \Delta X_1\right) \end{aligned}$$

(24)

$$\begin{aligned}&\Delta {\dot{X}}_2 = \frac{1}{T_{2_p}} \left[ \left( 1-\frac{T_{1_p}}{T_{2_p}}\right) \left( K_\mathrm{pod}\Delta P_{km} - \Delta X_1\right) \right. \left. - \Delta X_2\right] \nonumber \\ \end{aligned}$$

(25)

$$\begin{aligned} \Delta \dot{X}_3= & {} \frac{1}{T_{4_p}} \left\{ \left[ \Delta X_2 + \frac{T_{1_p}}{T_{2_p}} \left( K_{\mathrm{{pod}}}\Delta P_{km} - \Delta X_1 \right) \right] \right. \nonumber \\&\left. \left( 1 - \frac{T_{3_p}}{T_{4_p}} \right) - \Delta X_3 \right\} \end{aligned}$$

(26)

$$\begin{aligned}&\Delta X_\mathrm{pod} = \Delta X_3 + \frac{T_{3_p}}{T_{4_p}} \left[ \Delta X_2 + \frac{T_{1_p}}{T_{2_p}}\right. \left. \left( K_\mathrm{pod}\Delta P_{km} - \Delta X_1\right) \right] \nonumber \\\end{aligned}$$

(27)

$$\begin{aligned}&\Delta {\dot{X}}_\mathrm{tcsc} = \frac{1}{T_\mathrm{tcsc}} (\Delta X_\mathrm{pod}+\Delta X_\mathrm{ref}-\Delta {X}_\mathrm{tcsc}) \end{aligned}$$

(28)

The parameters to be tuned by the optimization method are the time constants $T_{1_i} - T_{4_i}, T_{1_p} - T_{4_p}$ and the gains $K_\mathrm{pss}$ and $K_\mathrm{pod}$. However, it is usual to consider the same time constants for both compensator blocks, i.e., $T_{1_i} = T_{3_i}$ and $T_{2_i} = T_{4_i}$, with the same relation being true for the time constants of the POD.

5 Coordinated Tuning Method for the PSS and POD Controllers

In order for controllers to provide damping to the system efficiently, ensuring small-signal stability and the desired damping levels, their parameters must be tuned accordingly. In this section, the optimization problem is defined and the proposed tuning method based on the metaheuristic BVNS is presented.

5.1 Definition of the Optimization Problem

The tuning of the PSS and POD controllers occurs with the resolution of a constraint satisfaction problem, that is, act on their parameters to obtain predetermined damping levels, always taking into account the limits of the variables involved.

In this work, the optimization problem is formulated as shown in Eqs. (29)−(37), which is a modified version of the objective function presented in Do Bomfim et al. (2000). The objective function in Eq. (29) seeks to reduce the difference between the desired damping ($\xi _{i}^{\mathrm{{des}}}$) and the calculated damping ($\xi _{i}^{\mathrm{{calc}}}$) for all the m oscillatory modes of interest as shown in Eq. (36), considering the limits of the set of constraints expressed in Eqs. (30)−(35).

$$\begin{aligned} \min F_1(x)=\displaystyle \sum _{i=1}^{m} G_i \end{aligned}$$

(29)

$$\begin{aligned} s.t. T_{1}^{\mathrm{{min}}} \le T_{1_i} \le T_{1}^{\mathrm{{max}}} \end{aligned}$$

(30)

$$\begin{aligned} T_{2}^{\mathrm{{min}}} \le T_{2_i} \le T_{2}^{\mathrm{{max}}} \end{aligned}$$

(31)

$$\begin{aligned} T_{1_p}^{\mathrm{{min}}} \le T_{1_p}\le T_{1_p}^{\mathrm{{max}}} \end{aligned}$$

(32)

$$\begin{aligned} T_{2_p}^{\mathrm{{min}}} \le T_{2_p}\le T_{2_p}^{\mathrm{{max}}} \end{aligned}$$

(33)

$$\begin{aligned} K_{\mathrm{{pss}}}^{\mathrm{{min}}} \le K_{{pss}_{i}}\le K_{\mathrm{{pss}}}^{\mathrm{{max}}} \end{aligned}$$

(34)

$$\begin{aligned} K_{\mathrm{{pod}}}^{\mathrm{{min}}} \le K_{pod}\le K_{\mathrm{{pod}}}^{\mathrm{{max}}} \end{aligned}$$

(35)

$$\begin{aligned} G_i = \left\{ \begin{array}{r@{\quad }l@{\quad }l} 0 &{} \hbox {if} &{} \xi _{i}^{\mathrm{{des}}} \le \xi _{i}^{\mathrm{{calc}}} \\ \xi _{i}^{\mathrm{{des}}} - \xi _{i}^{\mathrm{{calc}}} &{} \hbox {if} &{} \xi _{i}^{\mathrm{{des}}} > \xi _{i}^{\mathrm{{calc}}} \\ \end{array}\right.&\end{aligned}$$

(36)

A sophisticated version of the objective function $F_1(x)$ is presented in Eq. (37); the objective function $F_2(x)$ considers additionally n scenarios of load variations for the EPS, thus assigning a relative robustness to the tuning obtained.

$$\begin{aligned} F_2(x)=\displaystyle \sum _{j=1}^{n} \sum _{i=1}^{m} G_{i,j} \end{aligned}$$

(37)

Equations (38) and (39) can be used to obtain the calculated damping ($\xi _{i}^\mathrm{calc}$), where $\lambda _i$ is the mode of interest i obtained by calculating the eigenvalues of the state matrix A expressed in Eq. (8), and $\sigma _i$ and $\omega _{d_i}$ represent the real part and the natural damped frequency of this oscillatory mode, respectively.

$$\begin{aligned}&\lambda _i=\sigma _i \pm j\omega _{d_i} \end{aligned}$$

(38)

$$\begin{aligned}&\xi _i^\mathrm{calc} = - \frac{\sigma _i}{\left| \lambda _i\right| } \end{aligned}$$

(39)

A graphical interpretation of the formulated problem is shown in Fig. 7. Note that in obtaining the minimum value of the objective function $F_1(x)$ or $F_2(x)$, which in the proposed formulation is zero, it is expected that the eigenvalues of interest have moved to a predefined region from the choice of the desired damping ($\xi _{i}^\mathrm{des}$).

Fig. 7

Desired displacement for the eigenvalues of interest

5.2 Basic Variable Neighborhood Search

Variable neighborhood search algorithms are simple methods that efficiently exploit the search space through systematic exchanges in the neighborhood structures linked to a local search stage, thus making it possible to obtain optimal solutions, while maintaining the ability to avoid stagnation at a local optimum (Mladenović and Hansen 1997). In this work, a method is proposed to tune the PSS and POD based on a BVNS algorithm. Figure 8 shows the algorithm pseudocode. Adaptations for the proposed problem include a continuous coding between 0 and 1, neighborhood structures based on the exchange of the values stored in the solution vector and a local search using the concept of sensitivity.

5.2.1 Continuous Coding

The controllers parameters are continuous variables formed of time constants (seconds) and gains (pu). Thus, it is interesting to perform a parameterization so that the variables in the coding can be treated as dimensionless and in the same range of magnitude (between 0 and 1); hence, a greater number of possible neighborhood structures can be explored, expanding the search capability of the method to different regions. The proposed coding is obtained with Eqs. (40) and (41).

$$\begin{aligned} \mu ^n= & {} x^n_\mathrm{max} - x^n_\mathrm{min} \end{aligned}$$

(40)

$$\begin{aligned} x_i^n= & {} x_\mathrm{min}^n + \alpha _i \mu ^n \end{aligned}$$

(41)

In Eqs. (40) and (41), $\mu ^n$ is the scaling factor for the difference between the maximum ($x^n_\mathrm{max}$) and minimum ($x^n_\mathrm{min}$) limits of any parameter n of the controllers, $\alpha _i$ is a dimensionless continuous variable between 0 and 1 that occupies the position i of the solution vector used internally by the BVNS. Finally, $x_i^n$ is the value of the n parameter in the i-th position of the solution vector as it returns to its original dimension.

Fig. 8

Pseudocode of Basic Variable Neighborhood Search

In other words, the BVNS works with an internal coding ($\alpha _i$); however when it is necessary to calculate the objective function for decision making, the method uses Eq. (41) to return to the original dimensions (seconds and pu). A further advantage of the proposed coding is that by ensuring that $\alpha _i$ is always between 0 and 1, it also guarantees that the parameters of the controllers will always be within their limits, thus eliminating the need to penalize the objective function to deal with infeasible solutions or even multi-objective optimization.

5.2.2 Neighborhood Structures

A relevant task is to select the set $N_k$ of neighborhood structures to be explored, where $k = 1,2,\ldots ,k_\mathrm{final}$. With the proposed coding, it is possible to use neighborhood structures based on position exchanges as shown in Fig. 9.

Fig. 9

Neighborhood structure: exchange in two (a); three (b) positions

Fig. 10

Local search pseudocode

The neighborhood structures perform exchanges between two or more positions (stored values) of the solution vector with these positions being defined randomly after choosing between two sets. The first set is formed by the time constants and the second set by the gains of the controllers. The sets are defined so that it is possible to maintain the physical meaning. The neighborhood structure selects one of the sets and defines the positions in this set that will have the values changed.

Fig. 11

Variation of a parameter in the local search

Fig. 12

Proposed solution vector for the optimization methods

Fig. 13

One-line diagram of the New England system

The greater the number of exchanges to generate a neighboring solution, the greater the possibility of leaving a local optimum and exploring other regions; hence, the BVNS starts with simple structures and evolves to more complex ones.

5.2.3 Local Search

The implemented LS is based on the concept of sensitivity and considers small variations in the values stored in the solution vector, and the LS pseudocode is shown in Fig. 10. Initially, a parameter is randomly chosen to suffer change, then a positive variation is applied and the objective function is evaluated. If there is an improvement in the objective function, another positive variation is applied and the process continues until there is no improvement or the limit for the parameter is reached. The successive variations must also cease if the limit of variations $n_v$ for the same parameter is reached; this limit is defined in order to avoid parameters migrating excessively to their extremes causing cycling during the process.

When, on applying a positive variation, the objective function of the generated solution is worse than the original, the variation to be applied must be negative and the process works in a similar manner to that described for positive variations. The variations consider $n_s$ search parameters randomly selected during the LS. The variation in a parameter i is expressed in Eq. (42), where $x'$ is the original solution, $\Delta x$ is the small variation and z is the solution vector after the variation. Figure  11 shows the possible variations in a parameter.

$$\begin{aligned} z(i) = x'(i) \pm \Delta x \end{aligned}$$

(42)

5.3 Coding of the Optimization Methods

The solution vector is shown in Fig. 12, where each controller has three parameters to be tuned (two time constants and one gain). The first positions are occupied by the time constants followed by the gains, thus dividing into two sets.

6 Simulations and Results

The methods used to tune the parameters of the controllers were implemented using MATLAB software and a computer with an Intel Core I7 6700 processor and 16 GB of RAM.

The simulations were performed in a test system known as New England that has 10 generators, 39 buses and 46 transmission lines. The single-line diagram of the test system is shown in Fig. 13, where Area 1 is compactly represented by the equivalent generator G10 (New York system) and Area 2 by the other generators (New England system); its complete description can be found in Araujo and Zaneta (2001). The initial conditions for the simulated scenarios are obtained by calculating the power flow with the Newton–Raphson method.

6.1 Dynamic Analysis of the Test System

The calculation of the initial conditions makes it possible to obtain the state matrix. The dominant eigenvalues of the state matrix, as well as the natural undamped frequencies ($\omega _{n}= \frac{\left| \lambda _i\right| }{2\pi }$) and the damping rates ($\xi$) are given in Table 1.

Table 1 Dominant eigenvalues of the New England system

There are nine oscillatory modes, eight local ($\lambda _{L_1}-\lambda _{L_8}$) and one inter-area ($\lambda _I$), and this conclusion is based on the analysis of the natural undamped frequencies and the participation factors (Kundur 1994). On analyzing Table 1, it is possible to conclude that the system at this point of operation is unstable, since the inter-area mode and three local modes ($\lambda _{L_1}, \lambda _{L_4}$ e $\lambda _{L_8}$) have positive real parts. Moreover, the stable modes are weakly damped. Thus, the installation of three PSSs controllers and one TCSC–POD should lead the system to stability; however, in this configuration, the controllers are not able to increase the damping levels of all oscillatory modes to desired levels, as presented in Menezes et al. (2016). Based on this, it is proposed to install a controller for each oscillatory mode, eight PSSs (local modes) and one TCSC–POD (inter-area mode) with the aim of ensuring small-signal stability and increasing the damping of all modes to desired levels.

Simulations not presented in this work were performed to determine the best location for the controllers, and it was considered the participation factors for the PSSs (Kundur 1994) and the open-loop transfer function (OLTF) for the POD (Moura et al. 2012). Generators G1, G2, G3, G4, G5, G7, G8 and G9 were identified as the best locations to install the PSSs. As for the POD, the OLTF shows that the transmission line between buses 30 and 31 has a large distance between the pole of interest and its respective zero, justifying its installation in this transmission line. The compensation applied by the TCSC is set at 10% and the time constant $T_\mathrm{tcsc}$ at 0.005 s.

6.2 Simulated Scenarios and Parameters of the Methods

The BVNS proposed for the coordinated tuning of the PSS and POD controllers is compared with three methods: LS, ILS and PSO. For each method, 200 tests were performed in each of the three simulated scenarios: $\xi _i^\mathrm{des} \ge 10\%$ and $\xi _i^\mathrm{des} \ge 15\%$ using the objective function $F_1(x)$ from Eq. (29) and $\xi _i^\mathrm{des} \ge 15\%$ with the objective function $F_2(x)$ from Eq. (37).

The objective function $F_1(x)$ considers only the loading of the Base Case. The objective function $F_2(x)$ considers n load variations in the system around the Base Case, as follows:

• Base case ($n=1$): load conditions considered as given in Araujo and Zaneta (2001);

• Case 1 ($n=2$): an increase of 5% in reactive loads;

• Case 2 ($n=3$): a 5% decrease in reactive loads;

• Case 3 ($n=4$): a 5% decrease in active and reactive loads;

• Case 4 ($n=5$): a 5% decrease in active loads;

• Case 5 ($n=6$): a 5% decrease in active loads and a 5% increase in reactive loads;

• Case 6 ($n=7$): a 5% increase in active and reactive loads;

• Case 7 ($n=8$): a 5% increase in active loads;

• Case 8 ($n=9$): a 5% increase in active loads and a 5% decrease in reactive loads.

The stop criterion for the methods is the limit of objective function evaluations (2500) or obtaining the minimum damping for all the oscillatory modes in the scenario under analysis, while meeting the restrictions shown in Eqs. (30)−(35). The limits of the time constants (seconds) and gains (pu) are defined in Table 2; these limits are based on values found in the literature as in Abido (2000) and Fortes et al. (2016).

Table 2 Limits of the parameters of the PSS and POD controllers

Table 3 Performance of the optimization methods in the coordinated tuning of PSS and POD controllers

The BVNS parameters were defined from a series of preliminary tests considering the New England system with 27 parameters to be tuned (TCSC–POD and 8 PSSs). From the tests it is possible to conclude that the value of $n_s$ should not be close to the number of positions of the solution vector ($n_s\ge 20$); in this case the BVNS works basically as a local search, which can stagnate the evolution of the method when finding a local optimum. However, the value of $n_s$ should not be too small ($n_s\le 5$), since the local search would have few possibilities to find better solutions. The maximum variation in the local search should not be large ($n_v \Delta x \le 0.25$), in order to avoid the variables migrating excessively to their extremes. In addition, the variation $\Delta x$ should be small ($\Delta x\le 0.05$) so that quality solutions are not ignored when applying variations. The set of neighborhood structures should generate solutions that are capable of leaving a local optimum without restarting the process, i.e., the number of exchange positions should be much smaller than the total number of positions.

Considering the above, the BVNS parameters were defined based on the best performance obtained: $n_s=10, n_v=5$ and $\Delta x=0.04$. The set of neighborhood structures $N_k$ is formed by:

• ($k=1$): 2 positions of the solution vector are changed;

• ($k=2$): 3 positions of the solution vector are changed;

• ($k=3$): 4 positions of the solution vector are changed;

• ($k=k_\mathrm{final}$): 8 positions of the solution vector are changed;

The pseudocode and parameters used by the LS are similar to the local search stage of the BVNS. The difference is in the random generation of the initial solution (in the BVNS, it comes from the neighborhood structure) and that there is no stop condition to limit the search parameters ($n_s$), and the method ends when the objective or the limit of evaluations is reached.

The ILS method generates the initial solution and goes through a perturbation stage ($x'(i)=|x(i)-1|$), where two of the solution vector parameters are randomly selected and their values are replaced by the difference in modulus between their current values x(i) and 1, thus taking on new values $x'(i)$. The local search stage is the same used by BVNS. The acceptance criterion considers the best solutions found.

Finally, the PSO has the following parameters: The population size is 30 particles, the acceleration constants $c_1$ and $c_2$ are set at 2.15 and the inertia factor decays linearly with the number of iterations ($W \in [0.3, 1.5]$). More details on the methods presented in this section can be found in Kennedy and Eberhart (1995), Mladenović and Hansen (1997), Glover and Kochenberger (2003) and Lourenço et al. (2010).

6.3 Performance Evaluation of the Optimization Methods

Table 3 presents the performance of the optimization methods showing the convergence rates, the processing times and the number of evaluations of the objective function required for convergence. In this work, convergence is considered as obtaining a feasible solution that meets the objective of the scenario, within the limit of 2500 evaluations.

On analyzing Table 3, it can be concluded that all methods were able to achieve 100% convergence for the simplest scenario ($F_1 - \xi _i\ge 10\%$), where the BVNS and LS methods required the shortest processing times on average.

On making the optimization problem more complex by increasing the desired damping and adding different load conditions, the success rate of the methods decreased; for example, the PSO was successful in only 37% of the tests for the most complex scenario. Again, the BVNS stood out with convergence rates close to 100% and with the shortest average processing times, it was 25.39 and 21.70% faster than the ILS (the second best method in this regard) for the intermediate and most complex scenarios, respectively.

Although a simple method, the LS was superior to the others with respect to the minimum processing time in almost all scenarios. This is justified because it is a method dependent on the initial solution and is most effective when the desired solution is near to the start solution. The excellent performance of the BVNS is based on the ability of the local search to find optimal solutions, but it still has the capacity to leave a local optimum and explore different regions with changes in neighborhood structure; hence, the method is able to achieve a better performance.

The results presented in this section show that of the tested methods, the BVNS is the best adapted for the problem. Thus, the BVNS is used to tune the controllers in the test system. Figure  14 shows the lowest and the highest damping among the modes of interest for each evaluation of the objective function, as well as the steps of the BVNS until convergence considering a test performed for the $F_1 - \xi _i^\mathrm{des}\ge 10\%$ scenario.

Fig. 14

Dynamics of the processing of the BVNS to tune the controllers

6.4 Small-Signal Stability with PSS and POD Included

In this section, the analysis of small-signal stability considers only the most complex scenario ($F_2 - \xi _i^\mathrm{des}\ge 15\%$), since an adjustment that solves this scenario is also valid for the others. Table 4 shows a tuning found by BVNS, which was randomly selected from all the tests performed. The time constant of the washout filter ($T_w$) is set previously and is not tuned by the method. Table 5 shows the eigenvalues of the test system with the inclusion of the damping controllers tuned according to the data shown in Table 4.

Table 4 Gains (pu) and time constants (seconds) of the PSS and POD

Table 5 Dominant eigenvalues with PSS and POD installed

The inclusion of the PSS and TCSC–POD properly tuned made the test system stable, since all the oscillatory modes of interest have a real negative part and present adequate damping levels, guaranteeing good functioning of the EPS from the point of view of the small-signal stability.

To better understand the stability analysis in the frequency domain, the displacement of the eigenvalues in the complex plane for the Base Case after inclusion of the PSS and POD is shown in Fig. 15.

Fig. 15

Displacement of the eigenvalues of interest

Fig. 16

Variation of the angular speed of generator G9 of the test system

Fig. 17

Damping rates of the oscillatory modes considering load variations in the New England system

On analyzing Fig. 15, it can be concluded that all eigenvalues have been shifted to the predefined region as desired. It would be possible to further shift the eigenvalues to the left side of the complex plane, but it would require a greater effort from the controllers (higher gains). Furthermore, if the limits of the controllers parameters and the limit of 2500 evaluations were maintained, the complexity of the optimization problem would increase considerably by requiring a higher damping of the oscillatory modes, which would lead to a decrease in the convergence rates and a small increase in the processing times for the optimization methods. However, the damping levels required in this work provide a safety margin in the operation of the SEP with respect to small-signal stability, as shown in Fig. 15.

For the analysis of the stability in the time domain, a 5% step-like perturbation in the mechanical power of generator G2 (system reference) is considered. The variation in the angular velocity of generator G9 after the perturbation is shown in Fig. 16, considering the scenarios without and with the inclusion of the PSSs and the TCSC–POD controllers.

The curve of the system without the inclusion of the controllers is characteristic of an unstable system, since it is composed of oscillations of increasing amplitudes. With the inclusion of the controllers, the system is stable as the curve related to this scenario is composed of oscillations of decreasing amplitude with the final value tending to zero.

Finally, the damping coefficients of the modes of interest with the n load variations considered in the last scenario are shown in Fig. 17. The tuning ensures damping ($\xi$) of at least 15% for all modes, regardless of variations (active or reactive) of up to 5% that occur in the load conditions of the EPS.

7 Conclusions

In this work, a BVNS algorithm was proposed to perform the coordinated and simultaneous tuning of the parameters of PSS and TCSC–POD damping controllers. The objective was to introduce additional damping to low-frequency electromechanical oscillations, and thus ensure the small-signal stability of the New England test system. For this, modeling of the TCSC by current injection was presented, which allowed its inclusion in the CSM used to represent the EPS.

The proposed BVNS method obtained high convergence rates for the simulated scenarios, as well as low processing times compared to other three methods used in this work (LS, ILS and PSO). The dynamic analysis of the system was performed considering the inclusion of the PSS and POD tuned by the BVNS, and the system became stable with desired damping levels regardless of load variations of up to 5%, which shows the robustness of the solutions found by the method.

In view of the above, the BVNS is accredited as a quality tool in the coordinated tuning of damping controllers, being possible the exploration of the method in other important applications in the analysis of the small-signal stability. A feature of the BVNS that should be explored in future works is the ability to find an optimal solution quickly, especially when the initial solution is close to the desired solution or if the search space is not very wide. However, it should be noted that the method may require higher processing times when the search space is very wide, in this case, a possible solution would be the discretization of the entire search space, thus reducing the number of possible solutions for exploration.