1 Introduction

Low-frequency electromechanical oscillations may seriously affect the angular stability and the transmission lines capability of large interconnected power systems (Kundur 1994). Interconnection of power systems pursues important benefits including higher reliability and security, economy in the power generation costs, flexible operation and stability improvement. However, other problems may arise due to interconnection such as necessity of an adequate interarea control (automatic generation control), tuning of controllers of synchronous generators, operation and control of flexible AC transmission system (FACTS) devices, interchange scheduling.

The use of damping sources is required to guarantee the power system dynamic security against low-frequency oscillations. Power system stabilizers (PSS) are the most used controllers in the electricity industry for damping these oscillations. The main function of PSS is to provide damping torque through an additional stabilizing signal to the automatic voltage regulator (AVR) of the generator.

The basic structure of a conventional PSS includes a gain, a washout filter, two blocks of phase compensation and an output limiter (Kundur 1994). The gain and phase-compensation blocks are used to compensate the system phase in the frequency interval of interest. The washout block is used to attenuate the stabilizing signal for low frequencies. If the PSS parameters are adequately tuned, the power system will benefit from a large damping torque and will be able to support a bigger number of disturbances for several operation conditions (Kundur 1994; Rogers 2000).

Despite the fact that power system stabilizers are able to damp local mode oscillations, their contribution for damping interarea modes of interconnected power systems is not entirely satisfactory (Deng et al. 2015). One solution for this problem is the deployment of FACTS devices (Simões et al. 2009) which give more flexibility for system operation. FACTS most used in actual electrical power systems is the static var compensator (SVC) and the thyristor-controlled series compensator (TCSC). Inserting well-tuned (in a robust way with several operating conditions) power oscillation damping (POD) controllers to the FACTS may guarantee the necessary damping for local and interarea oscillation modes. The interarea modes are strongly influenced by the interaction between the mechanical parts of the generators and the electrical part of the power system and also by the interactions between controllers, for example, PSSs and FACTS-PODs, PSSs and governors. However, the damping of power system oscillations is affected by setting the parameters of PSSs and FACTS-PODs, and consequently, a coordinated design among these stabilizers should be considered when a combination of devices is involved (Hassan et al. 2014).

The structure of a FACTS-POD is similar to the conventional PSS, but differs in its operation and its input signal (Menezes et al. 2016; Cai and Erlich 2005). A fundamental issue concerning the design of an effective and robust POD is the selection of an appropriate input signal. A local signal can be used to avoid the use of an auxiliary communication system (Gamino and Araujo 2017), but remote signals (or global signals) contain information about overall network dynamics as opposed to a local signal, which lack adequate observability of some of the significant interarea modes (Chaudhuri and Pal 2004). However, the use of remote signals creates new challenges, such as a time delay caused from the transmission of said remote signal. Time delays of remote signals are one of the key factors influencing the stability of the whole system and damping performance as well. Therefore, considering the delay of time is a necessary requirement during the controller design process (Shakarami and Davoudkhani 2016; Yao et al. 2011).

An efficient damping of both local and interarea oscillation modes may be obtained through the coordinated and simultaneous tuning of PSSs and FACTS-PODs, thus avoiding possible adverse interactions among the parameters of these controllers (Cai and Erlich 2005). Several techniques, both deterministic and stochastic, have been proposed for tuning PSSs and FACTS-PODs in order to maximize the system damping. For example, sequential quadratic programming (SQP) is proposed in (Cai and Erlich 2005; Ke et al. 2011) for tuning PSSs and TCSC; linear programming is used for tuning PSSs and SVC in (Pourbeik and Gibbard 1998); nonlinear programming is used for coordinated tuning of PSSs, SVC and TCSC in (Lei and Povh 2001); sequential conic programming for tuning several TCSC, thyristor-controlled phase shifter (TCPS) and SVC (Simfukwe et al. 2012). However, the need for a good initial guess represents a major disadvantage to these techniques (Werner et al. 2003). Artificial intelligence (AI) techniques have also been applied more recently for tuning PSSs and FACTS-PODs, such as: bacteria swarm optimization (Ali and Abd-Elazim 2012), seeker optimization (Afzalan and Joorabian 2013), particle swarm optimization (PSO) (Shayeghi et al. 2010; Menezes et al. 2016), artificial immune algorithm (Khaleghi et al. 2011), genetic algorithms (GA) (Hassan et al. 2014; Fortes et al. 2016), the artificial bee colony (ABC) algorithm (Martins et al. 2017) and the basic variable neighborhood search (VSA) algorithm (Gamino and Araujo 2017; Fortes et al. 2018). But, these works do not consider the use of remote signals.

Recently, a new AI technique called the ant lion optimizer (ALO) has been developed, which was inspired by the phenomenon of antlions hunting ants in nature. ALO is a population-based algorithm similar to GA and PSO, but the number of parameters to be tuned is less than GA and PSO. ALO has been confirmed to be better in solving various mathematical optimization functions compared to some well-known metaheuristics (Mirjalili 2015). The results, presented in (Mirjalili 2015), show that the ALO algorithm is able to solve real problems with unknown search spaces as well. Therefore, a main contribution of this article is the implementation and analysis of the ALO algorithm in the coordinated and simultaneous tuning of the parameters of PSSs and PODs controllers in multimachine power systems, which feature signal transmission delay.

2 Problem Formulation

The small-signal angular stability problem of a multimachine electric power system may be formulated as a set of linear differential equations. It follows the power system model, the structure of controllers, mathematical model of time delay and the optimization problem formulation for coordinated tuning of PSSs and FACTS-PODs.

2.1 Power System Model

The dynamics of the power system submitted to small disturbances is modeled by the linearization of the nonlinear differential equations of the system, representing the state variables by Δx and the algebraic variables by Δr, as shown in matrix form by Eq. (1) and in expanded form by Eq. (2).

$$ \left[ {\begin{array}{*{20}c} {\Delta^{.} x} \\ 0 \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} {J_{1} } \hfill & {J_{2} } \hfill \\ {J_{3} } \hfill & {J_{4} } \hfill \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\Delta x} \\ {\Delta r} \\ \end{array} } \right] $$
(1)
$$ \Delta^{.} x = \left( {J_{1} - J_{2} J_{4}^{ - 1} J_{3} } \right)\Delta x = \varvec{A}\Delta x $$
(2)

Dimension of the state matrix A is NxN, in which N is the number of state variables. The power system angular small-signal stability is assessed using the first stability criterion of Lyapunov through the analysis of eigenvalues of the state matrix. Modes of electromechanical oscillations are characterized by conjugate complex eigenvalue in the form: λi= σi± jωi. The real part σi is related to the exponential growth of response, while the imaginary part ωi represents the frequency of the respective ith oscillation mode (Kundur 1994).

2.2 Modeling of PSS and FACTS-POD

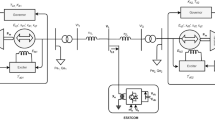
Several structures for power system stabilizers have been proposed in (Kamwa et al. 2005). In this study, the conventional PSS composed of four blocks is used. This model is shown in Fig. 1 where VPSS is the output signal of PSS, KPSS is the gain of stabilizer, Tw is the time constant of the washout block, T1–T4 are the time constants of two phase-compensation blocks, and Δωi is the angular speed deviation of the corresponding synchronous machine i.

Fig. 1
figure 1

Structure of PSS and POD

Full size image

The installation locations of FACTS devices generally are defined during planning studies of a power system for some objectives such as voltage control, increase power transmission capability, damping of low-frequency oscillations.

In this work the damping of interarea oscillations will be performed mainly through two FACTS: the SVC and TCSC, both equipped with PODs and considering remote transmission signal delay. The input signals to the FACTS devices may be selected by residues. Damping of local oscillations is solved with conventional stabilizers.

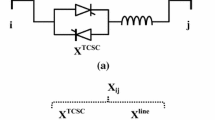
The dynamic linearized models of SVC and TCSC are represented in Fig. 2a and b, respectively. In this simplified model of SVC the time constant TSVC is the response time of the thyristor control circuitry, Tm is the time constant involved with the voltage measurement hardware, and Tv1 and Tv2 are the time constants of the voltage regulator block (Chaudhuri et al. 2004). Time constant TTCSC of the dynamic model of TCSC corresponds to the firing circuit delay (Deng et al. 2015). The POD controller used in this research has a similar structure to a conventional PSS (Fig. 1). Input signal of POD may, for example, be active power, reactive power, current magnitude, voltage magnitude or angular deviation of synchronous generators. In this study, the active power flow Pkm of branch k–m has been adopted as an input signal of POD due to its proven efficiency for damping low-frequency electromechanical oscillations (Yang et al. 1998).

Fig. 2
figure 2

FACTS block diagram: SVC (a) and TCSC (b)

Full size image

2.3 Mathematical Model of Time Delay

The Padé approximation method can be used to study the effect of time delay. The Padé approximation is based on the following property of the Laplace transforms shown in Eq. (3) (Milano 2016):

$$ {\mathcal{L}}\left\{ {f\left( {t - \tau } \right)u\left( {t - \tau } \right)} \right\} = e^{ - s\tau } F\left( s \right) $$
(3)

where \( s \) is the variable of the Laplace transform \( {\mathcal{L}} \), \( u\left( t \right) \) is the unit step function, \( F\left( s \right) \) is the Laplace transform of the function \( f\left( t \right) \), and τ is time delay.

Padé approximants are based on the Taylor’s expansion of \( e^{ - s\tau } \). The Padé approximants are expressed as Eq. (4).

$$ e^{ - s\tau } \approx \frac{{1 - K_{1} s + K_{2} s^{2} + \cdots \pm K_{n} s^{n} }}{{1 + K_{1} s + K_{2} s^{2} + \cdots \pm K_{n} s^{n} }} $$
(4)

where \( n \) is the order of approximation and \( K_{1} \), \( K_{2} \), \( \ldots \), \( K_{n} \) are constant coefficients (Shakarami and Davoudkhani 2016).

In this work the first-order Padé approximation is used with coefficients \( K_{1} = \tau /2 \) and \( K_{2} \), \( \cdots \), \( K_{n} = 0 \).

2.4 Objective Function

The coordinated tuning of PSSs and FACTS-PODs is formulated as an optimization problem based on the damping ratio \( \zeta_{i} \) (see Eq. 5), and the nonlinear objective function is the minimum of F as defined in Eq. (6), subject to a set of constraints of parameters of PSSs and FACTS-PODs given by (7). The objective is to shift all eigenvalues of state matrix into a left-side region limited by a pre-defined damping ratio.

$$ \zeta_{i} = \frac{{ - \sigma_{i} }}{{\sqrt {\sigma_{i}^{2} + \omega_{i}^{2} } }} $$
(5)

where i =1, 2,…, N, in which N is the total of state variables.

The coordinated tuning of power system stabilizers and power oscillation damping controllers consists of minimizing F in order to obtain the optimal or near-optimal set of PSSs and PODs parameters {KPSSj T1j T2j T3j T4j KPODk T1k; T2k T3k T4k, j =1, 2, …, NPSS; k =1, 2, …, NPOD}. Constraints are given by (7).

$$ \hbox{min} F = \left( {100 - \zeta_{ \hbox{min} } } \right)^{2} $$
(6)

Subject to,

$$ \begin{aligned} & {\text{lb}}_{i} = \left[ {K^{ \hbox{min} } T_{1}^{ \hbox{min} } T_{2}^{ \hbox{min} } T_{3}^{ \hbox{min} } T_{4}^{ \hbox{min} } } \right] \\ & {\text{ub}}_{i} = \left[ {K^{ \hbox{max} } T_{1}^{ \hbox{max} } T_{2}^{ \hbox{max} } T_{3}^{ \hbox{max} } T_{4}^{ \hbox{max} } } \right] \\ & {\text{lb}}_{i} \le x_{i} \le {\text{ub}}_{i} \\ & \zeta_{0} \le \zeta_{\hbox{min} } \\ \end{aligned} $$
(7)

where \( \zeta_{\hbox{min} } = \min_{{1 \le y \le n_{y} }} \left( {\min_{1 \le q \le N} \zeta_{q} } \right) \), \( \zeta_{q} \) is the damping ratio of the qth eigenvalue, \( n_{y} \) is the number of operating conditions, \( \zeta_{0} \) (positive value) is a constant value of the expected damping ratio defined by the user for PSSs and PODs design, \( x_{i} \) is a decision variable, and \( {\text{ub}}_{i} \) and \( {\text{lb}}_{i} \) are the upper and lower bounds on the parameters of the PSSs and PODs.

For solving the robust and coordinated tuning of PSSs and PODs of interconnected systems the ant lion optimizer has been selected because it is a recent metaheuristics with potential to solve efficiently complex and large-scale engineering problems. Some merits of ALO algorithm are, for example, an enhanced exploration of the solution space, local optima avoidance, exploitation and quick convergence, reduced number of variables.

3 The Ant Lion Optimizer

This section will describe the ant lion as a predator and the algorithm emulating the way it traps its prey.

3.1 The Ant Lion Insect

The ant lion (also ant-lion or antlion) is a group of species of insects in the family Myrmeleontidae and is most applied to the larval form, often called the doodlebug. Adult ant lions are winged insects that resemble dragonflies. The ant lion larvae construct small cones or funnel-shaped pits in fine, dry soil to trap its prey which are, primarily, ants. The average size of a trap is 5 cm deep and 7.5 cm wide at the edge. To avoid crater avalanches, ant lions construct pits with optimal slope considering the critical angle of repose of the sand (Fertin and Casas 2007; Guillete et al. 2009).

After the pit is complete, the ant lion patiently awaits its prey to fall into the bottom of its trap. When an inattentive ant or other small arthropod steps inside the rim of the trap, it falls to the bottom and will be captured by the ant lion. If the prey attempts to climb up the walls of the pit, it is brought down by a storm of loose sand grains which are thrown at it from the bottom of the trap by the ant lion (Guillette et al. 2009).

3.2 Basics of Ant Lion Optimizer

A strategy for simplifying nonlinear optimization problems based on the ant lion method was proposed earlier in (Stillinger and Weber 1988). More recently, the bio-inspired artificial intelligence technique, ant lion optimizer or ALO, was developed by Mirjalili (2015) to solve optimization problems based on the predatory behavior of ant lion larva.

The mathematical model of ALO is able to reproduce the interaction between the ant lions and the ants, their favorite prey (Fertin and Casas 2007). The bidimensional positions of ant lions and ants are stored in matrices which are started randomly. At any iteration the position of every ant related to the position the ant lion is obtained and updated using roulette-wheel selection and elitism. If the fitness of an ant is better than the respective ant lion, it means that the ant lion captured its prey and assumes this position. At any iteration the best fitness of ant lions is compared to the previous one and is updated if there was an improvement. The ant lion optimizer makes an adequate exploration and exploitation of search space, which, consequently, is able to approximate the global optimum of optimization problems.

3.3 Antlion: Features

There are four steps to hunting prey: the entrapment of ants in traps, the random walk of ants, elitism and catching preys/re-building traps (Mirjalili 2015; Chen et al. 2017).

3.3.1 The Entrapment of Ants in Traps

For mathematically modeling the behavior of entrapment of ants in traps, the following Eqs. (8) and (9) are proposed:

$$ c^{t} = \frac{{c^{t} }}{I},\quad d^{t} = \frac{{d^{t} }}{I} $$
(8)

In Eq. (8), \( I = 10^{w} \frac{t}{T} \), \( t \) is current iteration, \( T \) is the maximum number of iterations, and \( w \) is a constant that depends on current iteration whose values are given by Eq. (9).

$$ w = \left\{ {\begin{array}{*{20}l} {2\quad {\text{if}}\; t > 0.1T} \hfill \\ {3 \quad {\text{if}} \;t > 0.5T} \hfill \\ { 4 \quad {\text{if}} \;t > 0.75T} \hfill \\ {5 \quad {\text{if}} \;t > 0.9T} \hfill \\ { 6 \quad {\text{if}} \;t > 0.95T} \hfill \\ \end{array} } \right. $$
(9)

3.3.2 Random Walks of Ants

Ants generally walk randomly in nature when searching for food; hence, their walk is supposed to be stochastic in behavior. This behavior is expressed mathematically by the following equations (Chen et al. 2017):

$$ X\left( t \right) = \left[ {0, c\_s\left( {2r\left( {t_{1} } \right) - 1} \right), \ldots , c\_s\left( {2r\left( {t_{{t{ \hbox{max} }}} } \right) - 1} \right)} \right] $$
(10)

where \( c\_s \) denotes cumulative sum, tmax is the maximum number of iterations, t shows the iterations of random walk, and \( r\left( t \right) \) is a stochastic function defined by (11).

$$ r\left( t \right) = \left\{ {\begin{array}{*{20}l} {1,\quad {\text{if}}\; {\text{rand}} > 0.5} \hfill \\ {0, \quad {\text{if}}\; {\text{rand}} \le 0.5} \hfill \\ \end{array} } \right. $$
(11)

Here rand represents a uniformly distributed random number between 0 and 1.

In order to keep the random walks inside the search space, they are normalized using (12).

$$ X_{i}^{t + 1} = \frac{{\left( {X_{i}^{t} - a_{i} } \right)\left( {d_{i}^{t} - c_{i}^{t} } \right)}}{{b_{i} - a_{i} }} + c_{i}^{t} $$
(12)

In Eq. (12), \( a_{i} \) and \( b_{i} \) are the minimum and maximum of random walks of the \( i{\text{th}} \) variable, and \( c_{i}^{t} \) and \( d_{i}^{t} \) are the minimum and maximum of \( i{\text{th}} \) variable at \( t{\text{th}} \) iteration, which is defined as:

$$ c_{i}^{t} = {\text{Antlion}}_{j}^{t} + c^{t} ,\quad d_{i}^{t} = {\text{Antlion}}_{j}^{t} + d^{t} $$
(13)

where \( c^{t} \) indicates the vectors including the minimum of all variables at \( t{\text{th}} \) iteration, \( d^{t} \) indicates the vectors including the maximum of all variables at \( t{\text{th}} \) iteration, and \( {\text{Antlion}}_{j}^{t} \) shows the position of the selected \( j{\text{th}} \) ant lion at \( t{\text{th}} \) iteration.

3.3.3 Elitism Operation

Elitism is one of the most important characteristics of evolutionary algorithms. In the ALO algorithm, at any iteration the best ant lion obtained (solution of problem) is saved as an elite. Since the elite one is the fittest ant lion, it should be able to affect the movements of all the ants during iterations. In addition to this, the ants are not only designed to roam around the roulette wheel selected ant lion; rather, they are also allowed to move randomly around the elite ant lion simultaneously. For simplicity, the average of both random walks is considered to generate the new positions of the ant. The description of this operation is presented as (Mirjalili 2015):

$$ {\text{Ant}}_{i}^{t} = \frac{{\left( {R_{\text{A}}^{t} + R_{\text{E}}^{t} } \right)}}{2} $$
(14)

where \( R_{\text{A}}^{t} \) and \( R_{\text{E}}^{t} \) are the random walks around the roulette wheel selected antlion, and the elite at \( t{\text{th}} \) iteration, and \( {\text{Ant}}_{i}^{t} \) indicates the position of \( i{\text{th}} \) ant at \( t{\text{th}} \) iteration.

3.3.4 Catching Preys/Re-building Traps

The final stage of the hunt is when an ant reaches the bottom of the pit and is caught in the ant lion’s jaw. After this stage, the ant lion pulls the ant inside the sand and consumes its body. For mimicking this process, it is assumed that catching prey occurs when ants become fitter (goes inside the sand) than its corresponding ant lion. An ant lion is then required to update its position to the latest position of the hunted ant to enhance its chance of catching new prey. The following equation represents this concept (Mirjalili 2015).

$$ {\text{Antlion}}_{j}^{t} = {\text{Ant}}_{i}^{t} \quad {\text{if}} \quad f\left( {{\text{Ant}}_{i}^{t} } \right) < f\left( {{\text{Antlion}}_{j}^{t} } \right) $$
(15)

where \( {\text{Ant}}_{i}^{t} \) indicates the position of \( i{\text{th}} \) ant at \( t{\text{th}} \) iteration and \( f\left( \oplus \right) \) denotes the fitness function.

3.4 Pseudo-code ALO Applied to Design PSS and POD

ALO-based algorithm begins with input data of the power system for all operating conditions. Positions of ant lions and ants are initialized randomly and saved in matrix \( M_{{t_{\text{al}} }} \), an element of this matrix contains one parameter of PSS or POD, and the ith row contains all parameters of PSSs and PODs to be optimized. Then the initial condition (power flow problem solution) of the system for all scenarios is calculated with software ANAREDE (2015) and saved. The system state-space matrix A is obtained and saved for all operating conditions. Eigenvalues are computed with PacDyn (2011) and saved. The operation of ALO may be summarized to the pseudo-code, as presented in Algorithm 1 (see Fig. 3). ALO is used for robust tuning of the parameters of PSSs and PODs. First row of \( M_{{t_{\text{al}} }} \) will contain the best optimized parameters of PSSs and FACTS-PODs.

Fig. 3
figure 3

Pseudo-code of ant lion optimizer

Full size image

4 Simulations and Results

Two test systems are used for the application of the ant lion optimizer algorithm for robust design of PSSs and PODs. The first one is the New England–New York interconnected system (Pal and Chaudhuri 2005), composed of 16 generators and 68 buses, which is used for tuning 12 PSS, 1 TCSC and 1 SVC. The second system is a Brazilian equivalent, modeled with 24 synchronous machines and 107 buses (Alves 2007), where the objective is to tune 16 PSS, 1 TCSC and 1 SVC in three loading scenarios, while maximizing the damping process. In the present paper, the eigenvalues were calculated by using the MATLAB© platform routines. All test systems used in the paper will be freely available by e-mail to anyone who requests them.

The time washout constant Tw of all stabilizers and PODs was defined as being 10 s. The time delay is considered to be 300 ms. Table 1 shows the bounds of controller parameters used in both test systems. These bounds have been defined from typical values recommended in the literature about application of conventional PSSs to multimachine power systems.

Table 1 Parameter bounds
Full size table

The computer simulations were performed using a PC Intel (R) core (TM) i3, 3.30 GHz, with 8 GB of RAM.

4.1 68-Bus System (NETS-NYPS)

4.1.1 System Description

This is a 68-bus, 16-machine system, shown in Fig. 4. The detailed network parameters and the dynamic characteristics can be found in (Rogers 2000). The synchronous generators are represented by the fifth-order model, representing transient and subtransient effects in d and q axes, and do not consider the variation of the machine parameters and voltages with frequency. The stator dynamics are also neglected (PacDyn 2011). All generators are equipped with automatic voltage regulators-type IEEE standard DC exciter (DC4B), except generators 13–16, since they are equivalent areas. There are three transfer corridors between NETS and NYPS connecting buses 60–61, 53–54 and 27–53. Each of the corridors has a double-circuit tie-line. Based on that information, ten operating conditions were considered, which are detailed in Table 2 (CI—constant impedance, CC—constant current and CP—constant power) (Jabr et al. 2010). Through the modal analysis, it was verified that the system presents unstable local and interarea modes. Interarea modes area is shown in Table 3 and has a frequency within the range of 0.8–0.4 Hz.

Fig. 4
figure 4

Single-line diagram of NETS-NYPS system

Full size image
Table 2 Operating conditions used for 68-bus system
Full size table
Table 3 Interarea oscillation modes for 68-bus system
Full size table

4.1.2 Installation Location of the FACTS and Feedback Signal Selection of the POD

In order to enhance the interconnected ability, one SVC is installed on bus 40, and one TCSC is installed between bus 50 and bus 18. PSSs installed on generators 1–12 should dampen local modes. In contrast, the TCSC and SVC controllers should dampen the interarea modes, these FACTS being equipped with POD. The SVC-POD should be designed to dampen interarea 4 and 2 modes, as these modes are more correlated with areas 1 and 2. Furthermore, the POD of the TCSC should dampen modes 3 and 1, as they are more correlated with areas 3, 4 and 5 (Deng et al. 2015). From the residue values, feedback signals for SVC and TCSC damping controllers have active power flow on Line 13–17 and Line 16–18—in other words, P13–17 e P16–18, respectively. These signals are remote, so there is a time delay. The state-space representation of the closed-loop system has 215 state variables.

4.1.3 Tuning of Controllers

For the tuning of the PSSs and PODs it was specified in the design that all modes of oscillation must have a damping coefficient above 10%. The parameters obtained through the proposed methodology considering the ten cases of contingencies are presented in Table 4. The coordinated design of the PSS and POD applying the ALO algorithm proved to be effective in shifting all modes of oscillation into the desired region, according to Fig. 5b, which presents a comparison between the open-loop and closed-loop pole locations.

Table 4 Optimized parameters of PSSs and PODs for 68-bus system
Full size table
Fig. 5
figure 5

Open-loop poles map (a) and closed-loop poles map (b) considering the ten operating conditions of NETS-NYPS system

Full size image

4.2 Brazilian Equivalent System

4.2.1 System Description

The 107-bus test system has 24 bus generation and 230 circuits. Details of the data are given in (Alves 2007), and a simplified single-line diagram is shown in Fig. 6. Each of the machines is assumed to be equipped with a static excitation system having a time constant \( T_{a} = 0,05 s \) and a moderate gain given by \( T_{d0}^{'} /2T_{a} \), where \( T_{d0}^{'} \) is the generator d-axis open-circuit transient constant (Jabr et al. 2010). Besides AVR, the speed governors are represented in detail.

Fig. 6
figure 6

Single-line diagram of Brazilian 107-bus system

Full size image

For this system, heavy (base case—scenario 1), average (load—15% of base case—scenario 2) and light (load—25% of base case—scenario 3) loading conditions were considered during the tuning process. Figure 7a shows the mapping of the open-loop poles for three operating conditions. For these conditions, there are two interarea modes and several local modes. The frequencies and damping ratio of the interarea modes are exposed in Table 5.

Fig. 7
figure 7

Open-loop poles map (a) and closed-loop poles map (b) considering the three operating conditions of Brazilian 107-bus system

Full size image
Table 5 Interarea oscillation modes for 107-bus system
Full size table

4.2.2 Installation Location of the FACTS and Feedback Signal Selection of the POD

The local modes will be damped by the PSS, while the interarea modes by the FACTS. Based on participation factors, 16 PSSs were installed in the system under study. Based on the analysis of the shape modes, it was observed that interarea mode 1 involves the machines of the Mato Grosso and Southeast Area against the South Area. In contrast, interarea mode 2 involves the machines of the Mato Grosso Area against the machines of the Southeast Area. In this way, two FACTS controllers were installed in the system. A TCSC was installed in the line between buses #122 and #895 that interconnect the Southeast and South Areas in order to damp interarea mode 1, and a SVC was in bus 231 in order to damp interarea mode 2. The input signals of the corresponding PODs were obtained from the residue analysis, which are shown in Fig. 8. For mode 1, which will be damped by the POD corresponding to the TCSC, the input signal will be the active power flow on Line 995–904. In the case of interarea mode 2, whose damping will be provided by the POD of the SVC, the input signal will be the active power flow on Line 4533–4596.

Fig. 8
figure 8

Modal residues of Brazilian 107-bus system: mode 1 (a) and mode 2 (b)

Full size image

4.2.3 Tuning of Controllers

The state-space representation of the closed-loop system has 326 state variables. For the tuning of the PSSs and PODs it was specified in design that all modes of oscillation must have a damping coefficient above 5%. Figure 7b shows the closed-loop eigenvalues after tuning 16 PSSs and 2 PODs. Note that the system becomes stable with a minimum damping ratio greater than 5% for all three operating points.

4.3 Transient Stability Analysis

In practice, any stabilizer design needs to be checked for robustness under different operating conditions using a transient stability simulation (Jabr et al. 2010). Time-domain simulations use the ANATEM software (2010). Limit inputs of AVR and PSS were defined by the intervals [− 10, 10] and [− 0.1, 0.15], respectively. Two cases were considered for each test system and are presented in Table 6.

Table 6 Data of nonlinear simulations
Full size table

Figures 9 and 10 illustrate the behavior of the rotor angle of generators 13 (Fig. 9a) and 15 (Fig. 9b) with respect to the generator 16 and the speed deviation of generators 12 (Fig. 10a) and 3 (Fig. 10b), respectively, for the simulations performed in the 68-bus system. The legend “Classic” used in Figs. 9 and 10 means that the PSSs parameters used in these simulations were extracted from (Rogers 2000). In both cases, the power system, with the inclusion of PSSs and FACTS-PODs tuned by the ALO algorithm, stabilizes around 12 s. In addition, Figs. 11 and 12 show the active power flow behavior between one of the tie-lines 231–225 and the rotor angles of all machines relative to the machine 18, respectively. In Fig. 11, increasing oscillations of the active power flow are observed before inclusion of PSSs and FACTS-PODs. With the installation and tuning of these controllers, the oscillations were damped and the damping coefficients are higher than the minimum required. Note in Fig. 12a that the amplitudes of the rotor angles grow over time, so the system is unstable without installation of PSSs and FACTS-PODs. However, it can be seen clearly in Fig. 12b the rapid damping of the oscillations of the rotor angles and the recovery of the stability of the system due to insertion of PSSs and FACTS-PODs. The results demonstrate that the parameters obtained through the ALO technique are robust for nonlinear simulations of transient stability.

Fig. 9
figure 9

System responses with case 1: 68-bus system

Full size image
Fig. 10
figure 10

System responses with case 2: 68-bus system

Full size image
Fig. 11
figure 11

System responses with case 1: 107-bus system

Full size image
Fig. 12
figure 12

System responses with case 2: 107-bus system

Full size image

Two performance indices that reflect the settling time (PL1) and overshoots (PL2) as a function of the machine speed deviation are defined in Eqs. (16) and (17), where \( N_{\text{ger}} \) is the number of machines, and \( t_{\text{sim}} \) is the simulation time (Abido and Abdel-Magid 2002). Results are presented in Table 7, where the symbol * indicates that for the 68-bus system, the parameters used for the PSSs are in accordance with reference (Rogers 2000). In contrast, for the 107-bus system, it is equivalent to the system without PSS and FACTS-POD.

Table 7 Performance indices
Full size table
$$ {\text{PL}}_{1} = \mathop \sum \limits_{k = 1}^{{N_{\text{ger}} }} \mathop \smallint \limits_{t = 0}^{{t = t_{\text{sim}} }} \left[ {t\Delta \omega_{k} \left( t \right)} \right]^{2} {\text{d}}t $$
(16)
$$ {\text{PL}}_{2} = \mathop \sum \limits_{k = 1}^{{N_{\text{ger}} }} \mathop \smallint \limits_{t = 0}^{{t = t_{\text{sim}} }} \left[ {\Delta \omega_{k} \left( t \right)} \right]^{2} {\text{d}}t $$
(17)

4.4 Comparison with Other Techniques

Exploration (global search) and exploitation (local search) are characteristics of the ant lion optimizer to efficiently approximate the global optimum of constrained optimization problems such as robust tuning of PSSs and PODs.

Application results of ALO to test systems 68 bus and 107 bus demonstrate that robust tuning of PSSs and FACTS-PODs led to obtain damping values that may be competitive or even higher than other ones calculated with conventional optimization methods and AI-based techniques. A routine for constrained nonlinear optimization based on sequential quadratic programming, available in the MATLAB and algorithm PSO, was used for comparison with the algorithm ALO. Three cases were simulated, changing only the initial values of the decision variables. The results are shown in Table 8, where the symbol * means \( \zeta_{ \hbox{min} } < 0 \). Table 8 indicates that the SQP technique is very dependent on the initial estimate of solution. In contrast, ALO presented the best values, on average, for the two test systems.

Table 8 Minimum damping ratio (%)
Full size table

5 Conclusions

In this work, a methodology based on the ant lion optimizer for robust tuning of PSSs and FACTS-PODs of interconnected multimachine power systems has been proposed.

The model of the robust tuning process corresponds to a nonlinear optimization problem with an objective function for maximizing the minimum damping of the closed-loop system under multiple operating conditions.

The application results of ALO-based methodology demonstrated an efficient damping of local and interarea oscillations of two interconnected test systems. For the NETS-NYPS test system, the best minimum damping calculated with ALO is greater than most results reported in respective literature. For the 107-bus test system, results of robust tuning of PSSs and FACTS-PODs using ALO ensured damping ratios greater than typical values obtained with other conventional and AI-based methods.

Nonlinear time-domain simulations validated the robust tuning of PSSs and FACTS-PODs using ALO, and all results have shown that the optimized parameters of those controllers guaranteed the stability of the test systems.

Thus, the ALO-based methodology has demonstrated to be an efficient alternative to solve the robust tuning of PSSs and FACTS-PODs of multimachine power systems.