1 Introduction

It is known that different control policies are useful to control the queue size and effectively reduce the customers’ waiting time. If the number of arrivals during the server vacation is too large, system congestion may occur, which will degrade the quality of service and the customers’ satisfaction. In addition, a queueing system without a control policy will generate a large amount of switching costs if the system frequently switches its state for a long time. Therefore, in order to effectively control the queue size and overcome the cost problem caused by the frequent switching, the investigation concerning the queueing system with a control policy is worth doing. The earliest works on the control policy of queueing systems were the N-policy proposed by Yadin and Naor [1], the T-policy presented by Heyman [2], and the D-policy developed by Balachandran [3, 4]. In some M/G/1 queues, the N-policy and D-policy operate according to exhaustive service rule, i.e., the server is turned off when the system becomes empty. The N-policy means that the server resumes its service when there are N customers present in the system. In contrast, under the conventional D-policy, the server starts to serve only when the sum of the service times of all waiting customers firstly exceeds a predetermined threshold \(D(D\geqslant 0)\). We know that the stochastic decomposition property proposed in reference [5] cannot be applied to the classical D-policy queue. Thus, the research on D-policy queue has always been a very challenging task in queueing theory. Authors like Dashalalow [6], Artalejo [7, 8] and Lee et al. [9, 10] did some pioneering works in studying the queues with the conventional D-policy. On the other hand, the absence of the server or non-availability of the service in the system can be termed as vacation. Queues with vacations have been extensively investigated by many researchers. Doshi [11] provided an exhaustive survey of such work through 1985. Here, we refer the readers to the monograph by Tian [12] for more details. In the study of vacation models, most works were concentrated on the study of models with multiple vacations and single vacation. However, the randomized multiple vacation policy (also called multiple adaptive vacation policy, first proposed by Tian [13]) is more general than multiple and single vacation policies.

From the engineering point of view, employing a control involves installing some instruments, including precision counting and scanning gauges. When the manufacturing environment changes and the system owner wants to switch to another control policy, it is impossible, in many cases, to discard the existing hardware system. Therefore, with the fast development of the information era, there has been an increasing interest in investigating some queueing systems with the joint control policy. For example, Lee and Seo [14] studied about the M/G/1 queue with the dyadic Min(N, D)-policy in which the idle server resumes its service if either N customers accumulate in the system or the sum of the service times of the waiting customers exceeds D, whichever occurs first. Lee et al. [15] extended it to the MAP/G/1 queueing system. Until now, an enormous number of works on the joint control policy and vacation queues have been published. Some more extensive and extended research works on continuous-time and discrete-time queues with the threshold policies and vacation mechanism can refer to the references [16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31].

On the one hand, the meaning of the conventional D-policy above is “the server resumes its service when the cumulative service times of the waiting customers firstly reach or exceed D". However, in many practical applications, it is very difficult for the server to run D-policy designed according to the cumulative service times of the waiting customers in the system, because before each customer’s service is completed, the service time of the customer is randomly unknown. On the other hand, there are many queueing systems with vacation policies, the server cannot leave for vacation immediately after the service is completed and the system becomes empty, he/she has to go through a period of delayed time to prepare for the vacation. Sometimes this delayed period is very necessary, such as bank staff need to sort out accounts before going off work or leaving. In addition, the length of the server’s vacation time depends not only on the amount of auxiliary works which the server is engaged in during the vacation, but also on the constraints of the customers’ arrival process. Consequently, the number of consecutive vacations is often uncertain. Multiple adaptive vacation schedule is a more flexible vacation policy and is more general than most classical vacation policies in the sense that the well known multiple vacation policy and single vacation policy become two special cases of this policy. Under this framework, we can investigate many different vacation policies between these two extreme cases for the purpose of better allocation of the server’s time to perform primary jobs (serving queue) and to do secondary jobs (vacations). Thus, inspired by the facts mentioned above, we will propose a new continuous-time M/G/1 queueing model with delayed randomized multiple vacations under the modified Min(N, D)-policy, in which the idle server resumes its service if either N customers accumulate in the system or the accumulative workload (not the cumulative service times) of the waiting customers in the system exceeds D, whichever occurs first. In our model, the states of the server can be in the working state, the idle state (on duty) and the vacation state (off duty). Utilizing the stochastic decomposition theorem of the steady-state queue size in [5, 12], we present the stochastic decomposition structure of steady-state queue size. Moreover, the explicit expressions of the expected queue length and the additional queue-length distribution are derived. By numerical examples, we investigate the long-run expected cost per unit time of the system and discuss the optimal Min(N, D)-policy, the optimal N-policy and the optimal D-policy, respectively. The comparison of the minimum costs and the optimal threshold values for three different policies is presented. When the number of consecutive vacations is a fixed positive integer J, the optimal three-dimensional control policy (\(N^*, D^*, J^*\)) is also given.

The remainder of this paper is organized as follows. In Sect. 2, the details assumptions of the model are given. In Sect. 3, we firstly introduce several definitions and lemmas, and then obtain the probability generating function of the steady-state queue-length distribution by applying the well-known stochastic decomposition property of the steady-state queue size [5, 12]. Moreover, the explicit expressions of the expected queue size and the additional queue-length distribution are derived by some algebraic manipulations. Section 4 is devoted to obtain a long-run expected cost function to discuss a cost optimization problem, and numerically find the optimal control policy for economizing the system cost. At last, the conclusions are presented in Sect. 5.

2 Model Formulation

Considering a continuous-time M/G/1 queueing model with delayed randomized multiple vacations under the modified Min(N, D)-policy, the detailed assumptions of the model are given as follows:

  1. (1)

    The inter-arrival time \(\tau _n(n\geqslant 1)\) is exponentially distributed with cumulative distribution function \(F(t)=1-\mathrm{e}^{-\lambda t},~t\geqslant 0, \lambda >0\).

  2. (2)

    The workload of the server for the nth customer, denoted by \(W_n(n\geqslant 1),\) refers to the quantity of events included in the completed service items required by the customer and follows an arbitrary distribution \(W(x),x\geqslant 0\).

  3. (3)

    The service time required to complete the workload \(W_n\), that is, the service time of the nth customer, denoted by \(\chi _n(n\geqslant 1)\), is arbitrarily distributed with G(t) which is supposed to have finite mean \(1/\mu \).

  4. (4)

    The queueing system operates under the modified Min(N, D)-policy based on delayed randomized multiple vacations, that is, once the system becomes empty, the server goes through a delayed period Y with arbitrary distribution Y(t) before taking vacation. During the delayed period Y, if there are customers arriving in the system, the server starts its service at once until the system becomes empty and the server restarts a delayed period Y. Otherwise, the server immediately takes a vacation with a random length V which obeys arbitrary distribution V(t). Limited by the amount of current auxiliary work, the server is required to take a random maximum number of vacations ( denoted by H) after the system becomes empty, and H obeys a generally discrete distribution with

    $$\begin{aligned} P\{H=l\}=h_l,l=1,2,3,\cdots \end{aligned}$$

    and probability generating function (p.g.f) \(H(z)=\sum \nolimits _{l=1}^{\infty }h_lz^l,|z|<1\). In addition, for a certain positive integer \(k(1 \leqslant k \leqslant H)\), due to the vacation interruption mechanism, if the number of customers arriving in the system reaches \(N (N \geqslant 1)\) or the total workload of the server for all the waiting customers is not less than a given threshold \(D(D \geqslant 0)\), whichever occurs first, the server immediately interrupts the vacation and returns to system to serve. During the kth vacation, if there are less than N customers in the system as well as the total workload of the server for all the waiting customers is less than D, the server remains vacation state until the kth vacation ends and begins to serve at once. If no customer arrives in the system during the kth vacation, the server will prepare for \((k + 1)\)th vacation. This pattern repeats until the Hth vacation expires. If the total H vacations have been finished, the server will go back to system to stay idle and wait for the next arrival. Briefly speaking, there are four cases of starting a new server busy period after the system becomes empty:

    1. (a)

      Starting a new server busy period during a delayed period (arrival occurs during a delayed period);

    2. (b)

      Starting a new server busy period during a vacation (arrival occurs during vacation period and the queue size reaches N or the total workload of the server for all the waiting customers is not less than a given threshold D);

    3. (c)

      Starting a new server busy period at the completion instant of a vacation (arrival occurs during vacation period);

    4. (d)

      Starting a new server busy period during idle period (no arrival occurs during the given H vacations).

  5. (5)

    The inter-arrival time \(\tau \), the workload W of the server for each customer, the service time \(\chi \), the server’s continuous vacation number H, the delayed period Y and the server vacation time V are all independent of each other.

Remarks

  1. (1)

    The workload of the server for each customer refers to the quantity of events included in the completed service items required by the customer. The unit of measurement for the workload may be a counting unit, a weight unit, etc. For example, if a customer needs a certain factory to process 100 products, the workload of this factory for this customer is 100 products. If a truck arrives at a warehouse to load 3 000 kg(3 tons) of materials, the workload of the server for the truck is 3 000 kg(3 tons).

  2. (2)

    In practical applications, the modified D-policy proposed in this paper is very easy for the server to run the D-policy designed by the cumulative workload of the server for the waiting customers in the system, because before starting the service, the server can easily know the workload of the server for the waiting customers in the system according to the customers’ service items.

  3. (3)

    The queueing model studied in this paper generalizes the queueing models that have been studied in references [13, 17,18,19, 27]. For example, when \(P\{Y=\infty \}=1\), the queueing model considered in this paper is equivalent to the classic queueing model studied in [32]. When \(P\{Y=0\}=1\) and \(N=1\), it is equivalent to the queueing model considered in [12, 13]. When \(P\{Y=0\}=1\) and \(D\rightarrow \infty \), the considered queueing model in this paper can be reduced to the queueing model investigated in [27].

  4. (4)

    For later use, the following notations are adopted throughout this paper: \(g^*(s)=\int _{0}^{\infty }\mathrm{e}^{-st}G(t)\mathrm{d}t \) denotes the Laplace transform of the corresponding distribution G(t), \(g(s)=\int _{0}^{\infty }\mathrm{e}^{-st}\mathrm{d}G(t)\) denotes the Laplace–Stieltjes transform of the corresponding distribution G(t), \(G^{(k)}(t)\) denotes the k-fold convolution of G(t), i.e., \(G^{(k)}(t)=\int _{0}^{t}G^{(k-1)}(t-x)\mathrm{d}G(x),k\geqslant 1\) and \(G^{(0)}(t)=1,\rho =\lambda /\mu \) denotes the traffic intensity of the system, \(\Re (s)\) denotes the real part of the complex variable s.

3 The Stochastic Decomposition of the Stationary Queue Size

In this section, applying the well-known stochastic decomposition property of the steady-state queue size [5, 12], the probability generating function of the steady-state queue-length distribution is obtained. Moreover, the explicit expressions of the expected queue size and the additional queue-length distribution are derived by some algebraic manipulations. For later discussions, some definitions and lemmas will be presented as follows.

Definition 1

(Server busy period) It is the time interval when the server starts to serve customers until the system becomes empty again. Thus, the server busy period here is equivalent to the system busy period of the standard M/G/1 queueing system in [32].

Denote by b, the length of the server busy period that starts from only one customer, and let \(B(t)=P\{b\leqslant t\}, t\geqslant 0, \ b(s)=\int _{0}^{\infty }\mathrm{e}^{-st}\mathrm{d}B(t)\), we have the following lemma.

Lemma 1

(see [32]) For \(\Re (s)>0\), b(s) is the unique solution of the equation \(z=g(s+\lambda -\lambda z)\) in \(|z|<1\), and B(t) can be expressed as:

$$\begin{aligned} B(t)=\sum _{k=1}^{\infty }\int _{0}^{t}\frac{(\lambda x)^{k-1}}{k!} \mathrm{e}^{-\lambda x}\mathrm{d}G^{(k)}(x),\quad t\geqslant 0, \end{aligned}$$

and

$$\begin{aligned}&\lim _{t\rightarrow \infty }B(t)=\lim _{s\rightarrow 0^{+}}b(s)=\left\{ \begin{array}{cc} 1, &{} \rho \leqslant 1 \\ \omega , &{} \rho >1 \end{array}, \right. \ \ E[b]=\left\{ \begin{array}{cc} \frac{\rho }{\lambda (1-\rho )}, &{} \rho < 1, \\ \infty , &{} \rho \geqslant 1, \end{array} \right. \end{aligned}$$

where \(\omega (0<\omega <1)\) is the root of the equation \(z=g(\lambda -\lambda z)\) in (0,1).

Let \(b^{<i>}\) be the length of the server busy period evoked by \(i(i\geqslant 1)\) customers. Because the arrival process is a Poisson process, the probability distribution function of \(b^{<i>}\) is given by

$$\begin{aligned} P\{b^{<i>}\leqslant t\}=B^{(i)}(t),\ t\geqslant 0, \ i\geqslant 1. \end{aligned}$$

Definition 2

(Server non-busy period) It is the time period from the moment that the system just becomes empty until the moment when the server returns to the system after vacation and starts to serve customers.

Definition 3

(System idle period) It is a period of time during which the system is continuously idle (no customers). Obviously, the system idle period is the remaining time of an arrival interval. Let \({\hat{\tau }}_j\) represent the length of the jth system idle period, then \(\{{\hat{\tau }}_j, j\geqslant 1\}\) are independent identically distributed random variables each with distribution \(F(t)=1-\mathrm{e}^{-\lambda t},~t\geqslant 0\).

Definition 4

(System busy period) It is the time interval that starts at the instant at which the first customer arriving at the idle system and ends at the instant when the system becomes empty again.

Definition 5

(Busy cycle) It is the time interval that from the moment that the server non-busy period just begins until the moment that the next server busy period ends.

Theorem 1

Let P(z) be the p.g.f. of steady-state queue-length distribution for the queueing system studied in this paper, then for \(\rho < 1\) and \(|z|<1\), we have the stochastic decomposition of the steady-state queue-length as follows:

$$\begin{aligned} P(z)= & {} \frac{(1-\rho )(1-z)g(\lambda (1-z))}{g(\lambda (1-z))-z}\nonumber \\&\quad \cdot \frac{1-v(\lambda )+y(\lambda )[1-H(v(\lambda ))] \sum \limits _{k=1}^{N-1}z^{k}\int _{0}^{\infty }W^{(k)}(D)F^{(k+1)}(t)\mathrm{d}V(t)}{[1-v(\lambda )][1-y(\lambda )+y(\lambda )H(v(\lambda ))] +y(\lambda )[1-H(v(\lambda ))]\triangle _{N}},\qquad \end{aligned}$$
(1)

and the average steady-state queue size, denoted by E[L], is presented by

$$\begin{aligned} E[L]= & {} \rho +\frac{\lambda ^{2}E[\chi ^{2}]}{2(1-\rho )}\nonumber \\&+ \frac{y(\lambda )[1-H(v(\lambda ))] \sum \limits _{k=1}^{N-1}k\int _{0}^{\infty }W^{(k)}(D)F^{(k+1)}(t)\mathrm{d}V(t)}{[1-v(\lambda )][1-y(\lambda )+y(\lambda )H(v(\lambda ))] +y(\lambda )[1-H(v(\lambda ))]\triangle _{N}}, \end{aligned}$$
(2)

where \(\triangle _{N}=\sum \limits _{m=1}^{N}W^{(m-1)}(D)\int _{0}^{\infty }F^{(m)}(t)\mathrm{d}V(t), E[\chi ^2]=\int _0^\infty t^2 \mathrm{d}G(t).\)

Proof

See Appendix A.

Theorem 2

For \(\rho <1\), the probability distribution of the additional queue size \(L_1\) is presented by

$$\begin{aligned} P\{L_1=0\}= & {} {\frac{1-v(\lambda )}{[1-v(\lambda )][1-y(\lambda )+y(\lambda )H(v(\lambda ))] +y(\lambda )[1-H(v(\lambda ))]\triangle _N},}\quad \quad \end{aligned}$$
(3)
$$\begin{aligned} P\{L_1=j\}= & {} \frac{y(\lambda )[1-H(v(\lambda ))]\int _{0}^{\infty }W^{(j)}(D)F^{(j+1)}(t)\mathrm{d}V(t)}{[1-v(\lambda )][1-y(\lambda )+y(\lambda )H(v(\lambda ))] +y(\lambda )[1-H(v(\lambda ))]\triangle _N},\nonumber \\&\qquad \qquad \qquad \qquad \quad j=1,2,\cdots ,N-1. \end{aligned}$$
(4)

Proof

Let \({I(z)=1-v(\lambda )+y(\lambda )[1-H(v(\lambda ))]\sum \nolimits _{k=1}^{N-1}z^k \int _{0}^{\infty }W^{(k)}(D)F^{(k+1)}(t)} \mathrm{d}V(t)\), then the p.g.f. of the additional queue size distribution can be rewritten as:

$$\begin{aligned}&P_{L_1}(z)= \frac{I(z)}{[1-v(\lambda )][1-y(\lambda )+y(\lambda )H(v(\lambda ))] +y(\lambda )[1-H(v(\lambda ))]\triangle _N}.\quad \quad \end{aligned}$$

Through a simple calculation, we can obtain the following results:

$$\begin{aligned}&I^{(0)}(0)=1-v(\lambda ),\\&I^{(j)}(0)=(j!)y(\lambda )[1-H(v(\lambda ))]\int _{0}^{\infty }W^{(j)}(D) F^{(j+1)}(t)\mathrm{d}V(t),\\&\qquad \qquad \qquad \qquad \quad j=1,2,\cdots ,N-1. \end{aligned}$$

Thus, employing \(P\{L_1=j\}= \frac{1}{j!}\cdot \frac{\mathrm{d}^j}{\mathrm{d}z^j}[P_{L_1}(z)]|_{z=0}\), we can get Eqs. (3)–(4).

4 The Optimal Control Policy Under the Cost Model

In practice, the operating cost of system is closely related to the system benefit. Therefore, from the perspective of economic profit, taking optimal control of operating cost into account is very needed. In this section, in order to discuss the cost optimization problem, the cost structure model is first established as follows:

  1. (1)

    \(r\equiv \) fixed setup cost for per busy cycle (this cost is due to the server being turned on each time);

  2. (2)

    \(h\equiv \) fixed holding cost per unit time for each customer present in the system (this cost originates from the customer’s sojourn time that consists of waiting time and service time).

Let F(N, D) be the long-run expected cost per unit time of the system. Applying the renewal of reward process theorem for a busy cycle that is defined as the Definition 5 above, it leads to

$$\begin{aligned} F(N,D)=h\cdot E[L]+\frac{r}{E[U]}, \end{aligned}$$
(5)

where E[L] denotes the average steady-state queue size, and U denotes a busy cycle that consists of a server non-busy period (see Definition 2 above) and a server busy period (see Definition 1 above), denoted by I and B, respectively.

Next, we will find the expression of the expected busy cycle E[U] in the objective function. Clearly, based on Lemma 1, we obtain the average length of the server busy period as follows:

$$\begin{aligned} E[B]=E[b]\cdot E[L_2]=\frac{\rho }{\lambda (1-\rho )}\cdot E[L_2], \end{aligned}$$

where \(E[L_2]\) is given by Eq. (A7) in appendix.

We note that the number of customers in the system at the beginning of a server busy period is equal to the number of customers who arrived during the server non-busy period, and the arrival process is a Poisson process with rate \(\lambda \), then the expected length of the server non-busy period is given by

$$\begin{aligned} E[I]=\frac{E[L_2]}{\lambda }. \end{aligned}$$

Therefore, we can obtain the expected length of the busy cycle as follows:

$$\begin{aligned} E[U]=E[I]+E[B]=\frac{E[L_2]}{\lambda (1-\rho )}. \end{aligned}$$
(6)

Substituting Eqs. (2), (A7) and (6) into Eq. (5), we have

$$\begin{aligned} F{(N,D)}= & {} h\bigg \{\rho +\frac{{{\lambda }^{2}}E[{{\chi }^{2}}]}{2(1-\rho )}\nonumber \\&+\frac{y(\lambda )[1-H(v(\lambda ))] \sum \limits _{m=1}^{N-1}m{{W}^{(m)}}(D)\int _{0}^{\infty }{{{F}^{(m+1)}}}(t)\mathrm{d}V(t)}{[1-v(\lambda )][1-y(\lambda )+y(\lambda )H(v(\lambda ))]+y(\lambda )[1-H(v(\lambda ))] \triangle _N}\bigg \}\nonumber \\&+\frac{r\lambda (1-\rho )[1-v(\lambda )]}{[1-v(\lambda )][1-y(\lambda )+y(\lambda )H(v(\lambda ))]+y(\lambda )[1-H(v(\lambda ))] \triangle _N},\qquad \end{aligned}$$
(7)

where \(\triangle _N\) is determined in Theorem 1.

It is observed from Eq. (7) that the cost function F(N, D) is extremely complex and nonlinear with respect to the decision variables N and D, which poses a hard task to find the analytic results for the optimum values \(N^*\) and \(D^*\) directly. From Eq. (5), we see that the total cost consists of two parts, one part is the cost incurred by customers waiting in the system, which is determined by hE[L]. The other part is the setup cost per unit time, denoted by \(\frac{r}{E[U]}\). The dyadic \(\min (N, D)\) policy reduces the setup cost caused by frequently on/off a queueing system, but it also increases the cost of the customer’s waiting time. Therefore, the total cost function is a convex function of two variables N and D, and then, we can choose optimal values \((N^*, D^*)\) for the optimization problem. In order to solve the optimization problem in Eq. (7), numerical calculation examples are provided to demonstrate how to search the optimal values \(N^*\) and \(D^*\).

Numerical Example 1 To demonstrate the model’s application, we consider a practical situation related to a production system. In order to effectively use the remaining productivity of the production system, the manager decided to accept some outside production tasks to increase the revenue of the system. Therefore, the manager designs a strategy: When the system does not has orders to be produced which belong to the normal production task, the factory begins to prepare to undertake the accepted outside task. But it will take a random period Y to do this preparation. That is, the factory goes through a delayed period Y before undertaking the accepted outside task. During the delayed period Y, if there are normal orders that need to be processed arrive in the system, the factory starts its production at once until the system becomes empty and the factory restarts a delayed period Y. Otherwise, the factory immediately undertakes the production of accepted outside tasks for a random length V. In order to control the queue size of normal orders during the random length V and reduce the cost that the system frequently switches its state for a long time, the system operates under the above modified Min(N, D)-policy based on delayed randomized multiple vacations. In this case, the specific meaning of each cost above is stated in more detail as follows.

\(r\equiv \) fixed setup cost for each production normal order during per busy cycle;

\(h\equiv \) fixed holding cost per unit time for each normal order present in the system (this cost originates from the order’s sojourn time that consists of waiting time and production time).

Suppose that the inter-arrival time \(\tau \) of normal orders, the production time \(\chi \) of each normal order, the delayed period Y, and the time V for the factory to continuously undertake the accepted outside task follow exponential distribution with parameters \(\lambda \), \(\mu \), \(\beta \) and \(\theta \), respectively. Besides, we also assume that the number H of consecutive times that the factory undertakes the production of accepted outside tasks each with a random length V is geometrically distributed with parameter \(\alpha (0<\alpha <1)\), and the production workload W of the factory for each normal order follows the distribution \(W(x)=1-\mathrm{e}^{-\varepsilon x}\). Under these specific distributions and the above cost model, the expression of the cost function F(N, D) above can be rewritten as:

$$\begin{aligned} F(N,D)= & {} h\bigg \{ \frac{\lambda }{\mu -\lambda }\nonumber \\&+\frac{\lambda \beta \sum \limits _{m=1}^{N-1 }{m{{\left( \frac{\lambda }{\lambda +\theta } \right) }^{m}}\cdot \left[ 1-{{\mathrm{e}}^{-\varepsilon D}}\sum \limits _{i=0}^{m-1}{\frac{{{(\varepsilon D)}^{i}}}{i!}} \right] }}{( \lambda +\beta )( \lambda +\alpha \theta )+\lambda \beta \sum \limits _{m=1}^{N-1 }{{{\left( \frac{\lambda }{\lambda +\theta } \right) }^{m}}\cdot \left[ 1-{{\mathrm{e}}^{-\varepsilon D}}\sum \limits _{i=0}^{m-1}{\frac{{{(\varepsilon D)}^{i}}}{i!}} \right] }} \bigg \}\nonumber \\&+\frac{r\lambda \left( 1-\frac{\lambda }{\mu }\right) \cdot (\lambda +\beta )(\lambda +\alpha \theta )}{(\lambda +\beta )(\lambda +\alpha \theta ) +\lambda \beta \sum \limits _{m=1}^{N-1}{{{\left( \frac{\lambda }{\lambda +\theta } \right) }^{m}}\cdot \left[ 1-{{\mathrm{e}}^{-\varepsilon D}}\sum \limits _{i=0}^{m-1}{\frac{{{(\varepsilon D)}^{i}}}{i!}} \right] }}. \end{aligned}$$
(8)

Setting \(\lambda =1,\mu =2,\varepsilon =4,\theta =0.1,\beta =0.5,\alpha =0.2,r=100,h=2\), and putting them into Eq. (8), we have

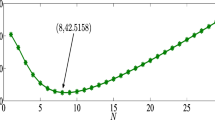
$$\begin{aligned} F(N,D)= & {} 2\bigg \{ 1 +\frac{5 \sum \nolimits _{m=1}^{N-1 }{m{{\left( \frac{10 }{11 } \right) }^{m}}\cdot \left[ 1-{{\mathrm{e}}^{-4 D}}\sum \nolimits _{i=0}^{m-1}{\frac{{{(4 D)}^{i}}}{i!}} \right] }}{ \frac{153}{10}+5 \sum \limits _{m=1}^{N-1 }{{{{\left( \frac{10 }{11 } \right) }^{m}}\cdot \left[ 1-{{\mathrm{e}}^{-4 D}}\sum \nolimits _{i=0}^{m-1}{\frac{{{(4 D)}^{i}}}{i!}} \right] } }} \bigg \}\nonumber \\&\quad +\frac{765}{ \frac{153}{10}+5 \sum \nolimits _{m=1}^{N-1 }{{{{\left( \frac{10 }{11 } \right) }^{m}}\cdot \left[ 1-{\mathrm{e}^{-4 D}}\sum \nolimits _{i=0}^{m-1}{\frac{{{(4 D)}^{i}}}{i!}}\right] } }}. \end{aligned}$$
(9)

Since the decision variable N is a discrete variable, the decision variable D is a continuous variable, for a fixed \(N(N=1,2,3,\cdots )\), we can find the corresponding optimum solution \(D_N^*\) by \(\frac{\partial F(N,D)}{\partial D}=0\). All the calculations have been done on the MATLAB software package. The numerical results are displayed in Table 1 and Fig. 1.

Table 1 The optimal threshold values and the minimum costs for different values of N
Full size table
Fig. 1
figure 1

The changes of F(N, D) with different values of N and D

Full size image
Table 2 Comparison of the minimum costs and the optimal threshold values for three different policies
Full size table

It can be seen from Table 1 and Fig. 1 that the optimal control threshold value (\(N^*,D^*)=(12, 7.45)\) and the corresponding minimum cost \(F(N^*,D^*) =24.897\,0\).

Table 2 shows the optimal values and the minimum costs for three policies under the cost function 8 when \(\mu =2,\varepsilon =4,\theta =0.1,\beta =0.5,\alpha =0.2,r=100,h=2\), with different inter-arrival rate.

Numerical Example 2 Based on Numerical Example 1 mentioned above, if the number H of consecutive times that the factory undertakes the production of accepted outside tasks is a fixed positive integer J, that is, \(P\{H=J\}=1\). Then, the expression of the cost function F(N, D) can be simplified as:

$$\begin{aligned}&F(N,D,J)=h\bigg \{ \frac{\lambda }{\mu -\lambda } \nonumber \\&\quad \quad \quad +\frac{ \beta \left[ 1- \left( \frac{\theta }{\lambda +\theta } \right) ^{J} \right] \sum \limits _{m=1}^{N-1 }{m{{\left( \frac{\lambda }{\lambda +\theta } \right) }^{m}}\cdot \left[ 1-{{\mathrm{e}}^{-\varepsilon D}}\sum \limits _{i=0}^{m-1}{\frac{{{(\varepsilon D)}^{i}}}{i!}} \right] }}{ \lambda +\beta + \beta \left[ 1- \left( \frac{\theta }{\lambda +\theta } \right) ^{J} \right] \sum \limits _{m=1}^{N-1 }{{{\left( \frac{\lambda }{\lambda +\theta } \right) }^{m}}\cdot \left[ 1-{{\mathrm{e}}^{-\varepsilon D}}\sum \limits _{i=0}^{m-1}{\frac{{{(\varepsilon D)}^{i}}}{i!}} \right] }} \bigg \}\nonumber \\&\quad \quad \quad +\frac{r\lambda \left( 1-\frac{\lambda }{\mu }\right) \cdot (\lambda +\beta )}{\lambda +\beta +\beta \left[ 1- \left( \frac{\theta }{\lambda +\theta } \right) ^{J} \right] \sum \limits _{m=1}^{N-1}{{{\left( \frac{\lambda }{\lambda +\theta } \right) }^{m}}\cdot \left[ 1-{{\mathrm{e}}^{-\varepsilon D}}\sum \limits _{i=0}^{m-1}{\frac{{{(\varepsilon D)}^{i}}}{i!}} \right] }}.\quad \end{aligned}$$
(10)

Setting \(\lambda =1.8,\mu =2,\varepsilon =1,\theta =0.1,\beta =4,r=100,h=4\), and putting them into Eq. (10), we have

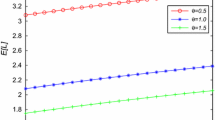
$$\begin{aligned} F(N,D,J)= & {} 4\bigg \{ 9+ \frac{20\left[ 1-\left( \frac{1}{19}\right) ^J\right] \sum \limits _{m=1}^{N-1}m \left( \frac{18}{19}\right) ^m \left( 1-\mathrm{e}^{-D} \sum \limits _{i=0}^{m-1}\frac{D^i}{i!} \right) }{29+20\left[ 1-\left( \frac{1}{19}\right) ^J\right] \sum \limits _{m=1}^{N-1} \left( \frac{18}{19}\right) ^m \left( 1-\mathrm{e}^{-D} \sum \limits _{i=0}^{m-1}\frac{D^i}{i!} \right) } \bigg \}\nonumber \\&+\frac{522}{29+20\left[ 1-\left( \frac{1}{19}\right) ^J\right] \sum \limits _{m=1}^{N-1} \left( \frac{18}{19}\right) ^m \left( 1-\mathrm{e}^{-D} \sum \limits _{i=0}^{m-1}\frac{D^i}{i!} \right) }. \end{aligned}$$
(11)

Since N and J are discrete variables, the variable D can be consecutively taken, we first take the fixed N to find minimum cost \(F(N,D_N^*,J_N^*)\) and the corresponding values of variables D and J. Then, by comparing the minimum values of \(F(N,D_N^*,J_N^*)\) at different values of N, the three-dimensional optimal control policy \((N^*,D^*,J^*)\) and the corresponding minimum cost \(F(N^*,D^*,J^*)\) are determined.

Obviously, Table 3 and Fig. 2 show that the cost F(N, D, J) keep decreasing until a minimum and then increase as N grows. We observe that the minimum operating cost is 47.250 7 under \(N^*= 3, D^* = \)12.27\(, J^* = 4\).

Table 3 The optimal threshold values and the minimum costs for different values of N
Full size table
Fig. 2
figure 2

The changes of F(N, D, 4) for different values of N and D

Full size image

5 Conclusions

In this paper, we proposed the modified Min(N, D)-policy based on the customers’ number and server’s workload, and studied an M/G/1 queueing model with delayed randomized multiple vacations under the control of the modified Min(N, D)-policy. The well-known stochastic decomposition property of the steady-state queue size was used to obtain the probability generating function of the steady-state queue-length distribution. Also, the explicit expressions of the expected queue size and the additional queue-length distribution were derived by directly algebraic manipulations. To demonstrate the model’s application, we further discussed the operating cost of system. Several numerical examples were provided to determine the optimal control policy for economizing the system cost. Thus, the analysis of this paper will provide a potentially practical application for system managers and decision makers in related application areas such as flexible manufacturing systems.