1 Introduction

The purpose of studying the queueing system is to adjust and control the system so that it operates optimally. It is well known that in some practical systems, there is a significant setup cost for each busy period. Reducing setup frequency has an economic benefit. Thus, finding the cost-minimization control policy and vacation policy is a typical control problem in queueing theory. The N-policy (Yadin and Naor 1963), T-policy (Heyman 1977), and D-policy (Balachandran 1973) were the earliest contributions to the control strategies of queueing systems. In the last two decades, there has been an increasing interest in investigating some related queueing systems with joint control policies or unreliable servers. Until now, an enormous number of works on threshold policies and vacation queues have been published. For example, Wang et al. (2006) and Sethi et al. (2020) studied the unreliable queues under N-policy control. Artalejo (2002) discussed the optimality of the N-policy and D-policy for the M/G/1 queue. Hur et al. (2003) studied an M/G/1 queue with N-policy and T-policy. Kuang et al. (2022) proposed an M/G/1 queue with bi-level randomized (p, N1, N2)-policy. Readers interested in joint control policies can refer to relevant literature (e.g., Lee and Seo et al. 2008; Lee et al. 2010; Wei et al. 2020).

Many scholars have studied the single and multiple vacation models as two essential generalizations of the classical M/G/1 queue. Some excellent studies on vacation models have been reported (e.g., Levy and Yechiali 1975; Doshi 1986; Tian and Zhang 2008). Utilizing the supplement variable technique, Lee et al. (1994a) considered an \({M}^{x}/G/1\) queueing model with N-policy and single vacation related to a manufacturing system. Kella (1989) first studied an M/G/1 queue by combining multiple vacation and N-policy. Lee et al. (1994b) further studied an \({M}^{x}/G/1\) queue N-policy and multiple vacation, in which multiple vacation mean that as soon as the system empties, the server leaves for a vacation of random length. If the server returns and finds the queue size is not less than the threshold N, the server immediately begins to serve the waiting customers. Otherwise, the server leaves for another vacation, and so on, until he finally finds at least N customers.

Also worth mentioning is that the above models with multiple vacation and N-policy are different from the models with multiple vacation and min(N, V)-policy (e.g., Wu et al. 2014; Lan and Tang 2019; Luo et al. 2023), i.e., the above multiple vacation cannot be interrupted immediately after the threshold is reached, whereas vacations are interrupted in the queueing model with min(N, V) policy. In some real-world scenarios, the auxiliary work of the server cannot be interrupted immediately. Customers must wait for the server to complete the auxiliary work before restarting the service. In the past two decades, queueing models with N-policy and uninterrupted vacations have also received much attention. Baba (2004) analyzed a GI/M/1 queue with multiple working vacations. Ayyappan and Nirmala (2020) consider a repairable queue with N-policy and multiple vacation. More literature on uninterrupted vacations can be found in references like Agarwal and Dshalalow (2005), Li and Tian (2010), Luo et al. (2013) and Ayyappan and Karpagam (2019).

In the previously studied models with uninterrupted multiple vacation, the server takes another vacation if the number of waiting customers does not reach N. In contrast to these existing literature, this paper will propose a new uninterrupted multiple vacation mechanism, i.e., when less than N customers are waiting for service in the system, the server waits for the number of customers to reach N and then provides service immediately instead of taking another vacation. When the vacation time is too long, or the arrival rate is too high, this flexible vacation mechanism can reduce the waiting time for existing customers and improve customer satisfaction. Additionally, the server cannot go on vacation immediately after the system is empty. He/She has to experience a delay before going on vacation, similar to a bank employee needs to sort out accounts before leaving work. Readers interested in delayed vacations can refer to papers by Tang et al. (2008) and Luo et al. (2023).

The prime objective of our research is to achieve cost minimization by determining the control threshold and adjusting vacation time. This paper will provide a reference and theoretical basis for decision-makers to manage such systems. Using an analysis technique different from the traditional analysis methods (e.g., embedded Markov chain and supplementary variable technique), we perform transient and steady-state analysis on the queue size employing the renewal process theory, total probability decomposition technique and Laplace transform. Furthermore, to minimize customer waiting times and trade off costs between customers and system managers, the cost optimization problems with and without the mean waiting time constraint are studied when the random variables obey different PH distributions.

The remainder of this paper is organized as follows. The next section describes the mathematical model under consideration and some notations adopted in this paper. Section 3 provides two lemmas and then presents the expressions of the Laplace transform of the transient queue size distribution concerning time t. Section 4 states some important queueing performance indices when the system is in equilibrium. Section 5 offers four numerical examples to determine the optimal control policy \({{N}^{*}}\) and the optimal two-dimensional control policy \(({{N}^{*}},{{T}^{*}})\) for minimizing the system cost. At last, Section 6 draws conclusions and puts forward some ideas for future work.

2 Model Description and Related Preparation

The queueing system with delayed uninterrupted multiple vacation and N-policy considered in this paper is described as follows:

  1. 1.

    The inter-arrival times \(\tau _{n},n\ge 1\) are independent identically distributed random variables each with distribution \({F}_{\tau }(t)=1-{{e}^{-\lambda t}}\), \(t\ge 0\), \(\lambda >0.\) The service times \(\chi _{n},n\ge 1\) are independent identically distributed random variables each with distribution \({F}_{\chi }(t),t\ge 0\), which is supposed to have a finite mean \(E[\chi ]\).

  2. 2.

    When the system becomes empty, the server experiences a delay period Y with an arbitrary distribution \({F}_{Y}(t)\) before taking a vacation. Once a customer arrives at the system within Y, the server starts serving the customer until the system becomes empty again and Y is restarted. If no customer arrives during Y, the server takes a vacation with a random length V that obeys an arbitrary distribution \({F}_{V}(t)\). After returning from vacation, the server will respond in three different ways depending on the state of the system: (i)If the number of customers in the system is greater than or equal to the control threshold value \(N\left( \ge 1 \right) \) which is set before, the server starts its service immediately; (ii)If there are less than N customers but at least one customer in the system, the server stays idle until there are N customers and starts its service at once; (iii)If no customers are waiting to be served, the server immediately goes on another vacation.

  3. 3.

    The inter-arrival time \({\tau }\), the service time \(\chi \), the delay period Y, and the vacation time V are mutually independent. In addition, if j \((\ge 1)\) customers are waiting at the initial time \(t=0\), the service begins at once. If the system is empty at \(t=0\), the server keeps idle until the next customer arrives and provides service immediately.

Remark 1

In our model formulation, to minimize waiting times for customers who are sensitive to delays, we assume that if the number of customers is less than N but there is at least one customer in the system, the server will stay idle until N customers are present, at which point the service will commence immediately. The assumptions here are quite different from those in existing literature (e.g., Kella 1989; Lee et al. (1994a, 1994b); Ayyappan and Karpagam 2019; Ayyappan and Nirmala 2020), which assumes that the server remains on vacation if there are fewer than N customers in the waiting line. The above assumption will undoubtedly increase the customer’s waiting time because the server’s vacation is still ongoing when N customers are accumulated in the system. At the same time, as we mentioned in the introduction, the multiple vacation model we present in this paper can reduce waiting time for existing customers. When the vacation time is too long or the arrival rate is too high, this vacation mechanism can increase customer satisfaction.

Remark 2

The queueing model considered in this paper extends previous models studied by other authors as shown below.

  • When \(P\left\{ Y=\infty \right\} =1\), the queueing model considered in this paper is equivalent to the classic M/G/1 queueing model that has been investigated (see e.g., Cohen 1982).

  • When \(P\left\{ Y=0 \right\} =1\) and \(N=1\), the queueing model considered in this paper can be simplified to the standard multiple vacation queueing model that has been studied (see e.g., Tian and Zhang 2008).

Remark 3

The notations used throughout this paper are listed as follow for reference.

  • N(t): The number of customers at time t;

  • \({{f}}_{\tau }(s)\): Laplace-Stieltjes transform for \({F}_{\tau }(t)\), i.e., \(f_{\tau }\left( s \right) =\int _{0}^{\infty }{{{e}^{-st}}dF_{\tau }(t)};\)

  • \(f_{\tau }^{*}(s)\): Laplace transform for \({F}_{\tau }(t)\), i.e., \(f_{\tau }^{*}(s)=\int _{0}^{\infty }{{{e}^{-st}}F_{\tau }(t)dt}\);

  • \(F_{\chi }^{(k)}(t)\): k-fold convolution of \(F_{\chi }(t)\), i.e., \(F_{\chi }^{(k)}(t)=\int _{0}^{t}{{F_{\chi }^{(k-1)}}(t-x)dF_{\chi }(x)}\), \(k\ge 1\), and \(F_{\chi }^{(0)}(t)=1\);

  • \(F_{\tau }(t)*F_{\chi }(t)\): \(F_{\tau }(t)*F_{\chi }(t)=\int _{0}^{t}{F_{\tau }\left( t-x \right) }dF_{\chi }(x)=\int _{0}^{t}{F_{\chi }\left( t-x \right) }dF_{\tau }(x)\);

  • \(\bar{F}_{\chi }(t),\bar{f}_{\chi }(s)\): \(\bar{F}_{\chi }(t)=1-F_{\chi }(t)\) and \(\bar{f}_{\chi }(s)=1-f_{\chi }(s)\);

  • \(E[\chi ],E[{{{\chi }}^{2}}]\): First two moments of \({\chi }\);

  • \(\rho =\lambda E[\chi ]\): Traffic intensity of the system;

  • \(\Re (s)\): Real part of the complex variable s;

  • \({{v}_{m}}\): Probability of m customers arriving at the system during vacation time, i.e., \({{v}_{m}}=\int _{0}^{\infty }{\frac{{{\left( \lambda t \right) }^{m}}}{m!}{{e}^{-\lambda t}}dF_{V}(t)},m\ge 0\);

  • \({{y}_{n}}\): Probability of n customers arriving at the system during delay period, i.e., \({{y}_{n}}=\int _{0}^{\infty }{\frac{{{\left( \lambda t \right) }^{n}}}{n!}{{e}^{-\lambda t}}dF_{Y}(t)},n\ge 0\).

3 The Transient Queue Length Distribution and its Laplace Transform Expression

Firstly, the definition of the server’s busy period and two lemmas are introduced as follows.

Server’s busy period: It is the period from when the server begins to provide service until the end of all services. As a result, the server’s busy period here is identical to the system busy period of the classic M/G/1 queueing system.

Let b denote the duration of the server’s busy period which begins with just one customer, and \(F_{B}(t)=P\{b\le t\},t\ge 0\), \(f_{B}(s)=\int _{0}^{\infty }{{{e}^{-st}}dF_{B}(t)}\). Similar to the discussing in Cohen (1982), we have the following Lemma 1.

Lemma 1

For \(\Re (s)>0\), \(f_{B}(s)\) is the unique solution of the equation \(z={{f}_{\chi }}(s+\lambda (1-z))=\int _{0}^{\infty }{{{e}^{-(s+\lambda (1-z))}}}d{{F}_{\chi }}(t)\) in \(|z|<1\), and \(F_{B}(t)\) is given by

$$\begin{aligned} F_{B}\left( t \right) =\underset{k=1}{\overset{\infty }{\mathop \sum }}\,\int _{0}^{t}{\frac{{{\left( \lambda x \right) }^{k-1}}}{k!}{{e}^{-\lambda x}}d{F_{\chi }^{(k)}(t)}\left( x \right) },t\ge 0, \end{aligned}$$

and

$$\begin{aligned} \underset{t\rightarrow \infty }{\mathop {\lim }}\,F_{B}(t)=\underset{s\rightarrow {{0}^{+}}}{\mathop {\lim }}\,f_{B}(s)=\left\{ \begin{array}{cc} 1, &{} \rho \le 1, \\ \omega< 1, &{} \rho > 1, \end{array} \right. \quad E\left[ b \right] =\left\{ \begin{array}{cc} \frac{\rho }{\lambda (1-\rho )}, &{} \rho < 1, \\ \infty , &{} \rho \ge 1, \end{array} \right. \end{aligned}$$

where \(\omega (0<\omega <1)\) is the root of the equation \(z=f_{\chi }(\lambda -\lambda z)\) in (0, 1).

Further, let \({{b}^{<i>}}\) be the duration of the server’s busy period which begins with i \((\ge 1)\) customers. Due to a Poisson arrival process of customers, the distribution function of \({{b}^{<i>}}\) can be expressed as \(P\left\{ {{b}^{<i>}}\le t \right\} ={F_{B}^{(i)}}(t)\), \(t\ge 0\), \(i\ge 1\).

Next, we introduce the joint probability distribution of the queue size and the server’s busy period by \({{Q}_{j}}(t)=P\left\{ 0\le t<b; N(t)=j \right\} \). Thus, \({{Q}_{j}}(t)\) can be interpreted as the transient probability of queue size being j at time point t during the period (0, b]. It implies that \(N(t)=j\) in \({{Q}_{j}}(t)\) requires the initial state \(N(0)=1\), \((0,t]\subset (0,b]\) and the time point \(t=0\) is the beginning moment of b. Then, the boundary condition is given by \({{Q}_{1}}(0)=1\), \({{Q}_{j}}(0)=0\), \(j>1\).

Lemma 2

Let \(q_{j}^{*}\left( s \right) =\mathop {\int }_{0}^{\infty }{{e}^{-st}}{{Q}_{j}}\left( t \right) dt\) denote the Laplace transform of \({{Q}_{j}}(t)\). For \(\Re \left( s \right) >0\) and \(j\ge 1\), we have the recursive expression of \(q_{j}^{*}(s)\) as follows:

$$\begin{aligned} q_{1}^{*}\left( s \right) =&\ \frac{f_{B}\left( s \right) \bar{f}_{\chi }\left( s+\lambda \right) }{\left( s+\lambda \right) f_{\chi }\left( s+\lambda \right) },\\ q_{j}^{*}\left( s \right) =&\ \frac{f_{B}\left( s \right) }{f_{\chi }\left( s+\lambda \right) }\int _{0}^{\infty }{{e}^{-st}}{\bar{F}_{\chi }}\left( t \right) \frac{{{\left( \lambda t \right) }^{j-1}}}{\left( j-1 \right) !}{{e}^{-\lambda t}}dt\\&+\frac{1}{f_{\chi }\left( s+\lambda \right) }\underset{k=1}{\overset{j-1}{\mathop \sum }}\,\frac{q_{j-k}^{*}\left( s \right) }{{f_{B}^{k}}\left( s \right) }\left\{ f_{B}\left( s \right) -\underset{i=0}{\overset{k}{\mathop \sum }}\,\int _{0}^{\infty }{{e}^{-\left( s+\lambda \right) t}}\frac{{{\left[ \lambda f_{B}\left( s \right) t \right] }^{i}}}{i!}dF_{\chi }\left( t \right) \right\} ,j>1, \end{aligned}$$

where \(f_{B}(s)\) is defined as in Lemma 1. \(\sum \limits _{k=i}^{j}{=0}\) if \(j<i\).

Proof

See Kuang et al. (2022). \(\square \)

Now, we analyze the transient queue length distribution of the system with an arbitrary initial state. Let \({{p}_{ij}}(t)=P\{N(t)=j|N(0)=i\}\) be the conditional probability that queue size is j at any time t with initial state \(N(0)=i\) \((i=0,\) 1, 2, \(\cdots )\), and its Laplace transform can be given by \(p_{ij}^{*}(s)=\int _{0}^{\infty }{{{e}^{-st}}{{p}_{ij}}(t)dt}\), i, \(j=0\), 1, 2, \(\cdots \).

Theorem 1

For \(\Re \left( \text {s} \right) >0\), we have

$$\begin{aligned}&p_{00}^{*}\left( s \right) =\frac{\bar{f}_{\tau }\left( s \right) }{s}\left\{ 1+\frac{f_{\tau }\left( s \right) f_{B}\left( s \right) \bar{f}_{V}\left( s+\lambda \right) }{ \bar{f}_{V}\left( s+\lambda \right) [ 1- \bar{f}_{Y}\left( s+\lambda \right) f_{\tau }\left( s \right) f_{B}\left( s \right) ]-{{\Delta }_{N}}\left( s \right) } \right\} ,\end{aligned}$$
(1)
$$\begin{aligned}&p_{i0}^{*}\left( s \right) =\frac{\bar{f}_{\tau }\left( s \right) }{s}\cdot \frac{{f_{B}^{i}}\left( s \right) \bar{f}_{V}\left( s+\lambda \right) }{ \bar{f}_{V}\left( s+\lambda \right) [ 1- \bar{f}_{Y}\left( s+\lambda \right) f_{\tau }\left( s \right) f_{B}\left( s \right) ]-{{\Delta }_{N}}\left( s \right) },i\ge 1, \end{aligned}$$
(2)

where

$$\begin{aligned} {{\Delta }_{N}}\left( s \right)&=f_{Y}\left( s+\lambda \right) \left[ {f_{B}^{N}}\left( s \right) {{\Phi }_{N}}\left( s \right) +f_{V}\left( s+\lambda -\lambda f_{B}\left( s \right) \right) -{{\Psi }_{N}}\left( s \right) \right] ,\\ f_{V}(s+\lambda )&=\int _{0}^{\infty }{{{e}^{-(s+\lambda )t}}}dF_{V}(t),f_{Y}(s+\lambda )=\int _{0}^{\infty }{{{e}^{-(s+\lambda )t}}}dF_{Y}(t),\\ {{\Phi }_{N}}(s)&=\underset{n=1}{\mathop {\overset{N-1}{\mathop {\sum }}\,}}\,\int _{0}^{\infty }{{f_{\tau }^{N-n}}\left( s \right) \frac{{{[f_{B}(s)\lambda t]}^{n}}}{n!}{{e}^{-\left( s+\lambda \right) t}}dF_{V}\left( t \right) },\\ {{\Psi }_{N}}\left( s \right)&=\underset{n=0}{\mathop {\overset{N-1}{\mathop {\sum }}\,}}\,\int _{0}^{\infty }{\frac{{{[f_{B}(s)\lambda t]}^{n}}}{n!}{{e}^{-\left( s+\lambda \right) t}}dF_{V}\left( t \right) }. \end{aligned}$$

Proof

See Appendix. \(\square \)

Theorem 2

For \(\Re \left( \text {s} \right) >0\), we have

  1. 1.

    If \(j=1,2,\cdots ,N-1,\) then

    $$\begin{aligned} \begin{aligned} p_{0j}^{*}(s)=&\ f_{\tau }(s)q_{j}^{*}(s)+f_{\tau }(s)f_{B}(s)\\&\cdot \frac{s{{f}_{\tau }}(s)q_{j}^{*}(s){{{\bar{f}}}_{Y}}(s+\lambda ){{{\bar{f}}}_{V}}(s+\lambda )+{{f}_{Y}}(s+\lambda )\left[ f_{\tau }^{j}(s){{{\bar{f}}}_{\tau }}(s ){{{\bar{f}}}_{V}}(s+\lambda )+s{{\theta }_{j}}(s) \right] }{s\left\{ {{{\bar{f}}}_{V}}(s+\lambda )\left[ 1-{{{\bar{f}}}_{Y}}(s+\lambda ){{f}_{\tau }}\left( s \right) {{f}_{B}}\left( s \right) \right] -{{\Delta }_{N}}\left( s \right) \right\} },\\ \end{aligned} \end{aligned}$$
    (3)
    $$\begin{aligned} \begin{aligned} p_{ij}^{*}(s)=&\ \sum \limits _{k=1}^{i}{q_{j-i+k}^{*}(s){f_{B}^{k-1}}(s)}+ f_{B}^{i}(s)\\ {}&\cdot \frac{s{{f}_{\tau }}\left( s \right) q_{j}^{*}(s){{{\bar{f}}}_{Y}}(s+\lambda ){{{\bar{f}}}_{V}}(s+\lambda )+{{f}_{Y}}(s+\lambda )\left[ f_{\tau }^{j}(s){{{\bar{f}}}_{\tau }}(s){{{\bar{f}}}_{V}}(s+\lambda )+s{{\theta }_{j}}(s) \right] }{s\left\{ {{{\bar{f}}}_{V}}(s+\lambda )\left[ 1-{{{\bar{f}}}_{Y}}(s+\lambda ){{f}_{\tau }}\left( s \right) {{f}_{B}}\left( s \right) \right] -{{\Delta }_{N}}\left( s \right) \right\} }. \end{aligned} \end{aligned}$$
    (4)
  2. 2.

    If \(j\ge N,\) then

    $$\begin{aligned} \begin{aligned} p_{0j}^{*}(s)=&\ {{f}_{\tau }}q_{j}^{*}(s)+{{f}_{\tau }}(s){{f}_{B}}(s)\\&\cdot \frac{{{f}_{\tau }}(s)q_{j}^{*}(s){{{\bar{f}}}_{Y}}(s+\lambda ){{{\bar{f}}}_{V}}(s+\lambda )+{{f}_{Y}}(s+\lambda ){{\sigma }_{j}}(s)}{{{{\bar{f}}}_{V}}(s+\lambda )\left[ 1-{{{\bar{f}}}_{Y}}(s+\lambda ){{f}_{\tau }}\left( s \right) {{f}_{B}}\left( s \right) \right] -{{\Delta }_{N}}\left( s \right) }, \end{aligned} \end{aligned}$$
    (5)
    $$\begin{aligned} \begin{aligned} p_{ij}^{*}(s)=&\ \sum \limits _{k=1}^{i}{q_{j-i+k}^{*}(s)f_{B}^{k-1}(s)+}f_{B}^{i}(s)\\&\cdot \frac{{{f}_{\tau }}(s)q_{j}^{*}(s){{{\bar{f}}}_{Y}}(s+\lambda ){{{\bar{f}}}_{V}}(s+\lambda )+{{f}_{Y}}(s+\lambda ){{\sigma }_{j}}(s)}{{{{\bar{f}}}_{V}}(s+\lambda )\left[ 1-{{{\bar{f}}}_{Y}}(s+\lambda ){{f}_{\tau }}\left( s \right) {{f}_{B}}\left( s \right) \right] -{{\Delta }_{N}}\left( s \right) }, \end{aligned} \end{aligned}$$
    (6)

    where

    $$\begin{aligned} {{\sigma }_{j}}(s)=&\ {{\theta }_{j}}(s)+\int _{0}^{\infty }{\bar{F}_{V}(t){{e}^{-\left( s+\lambda \right) t}}\frac{{{\left( \lambda t \right) }^{j}}}{j!}}dt,\\ {{\theta }_{j}}(s)=&\ {{\Phi }_{N}}(s)\sum \limits _{k=1}^{N}{q_{j-N+k}^{*}(s)f_{B}^{k-1}(s)}\\&+\sum \limits _{n=N}^{\infty }{\sum \limits _{k=1}^{n}{q_{j-n+k}^{*}(s)f_{B}^{k-1}(s)\int _{0}^{\infty }{\frac{{{(\lambda t)}^{n}}}{n!}{{e}^{-(s+\lambda )t}}d{{F}_{V}}(t)}}}, \end{aligned}$$

    \({{\Delta }_{N}}(s)\) and \({{\Phi }_{N}}(s)\) are stated as in Theorem 1.

Proof

See Appendix. \(\square \)

4 The Recursive Solution of the Steady-State Queue Length Distribution

In this section, based on the transient results presented in Theorems 1 and 2 above, the explicit recursive formulas for the stationary queue-length distribution are obtained by applying L’Hospital’s rule. Furthermore, other critical queueing performance metrics of importance are derived by some algebraic manipulation.

Theorem 3

Let \({{p}_{j}}=\underset{t\rightarrow \infty }{\mathop {\lim }}\,P\{N(t)=j\},j=0,1,2,\cdots \), we have

  1. 1.

    When \(\rho \ge 1,{{p}_{j}}=0,j=0,1,2,\cdots \).

  2. 2.

    When \(\rho <1\), the recursive formulas of \(\left\{ {{p}_{j}},j=0,1,2,\cdots \right\} \) are listed as follows,

    $$\begin{aligned} {{p}_{0}}=(1-\rho )\frac{1-{v}_{0}}{{{M}_{N}}}, \end{aligned}$$
    (7)
    $$\begin{aligned} {{p}_{j}}=\lambda (1-\rho )\frac{\left( 1-{v}_{0} \right) [ \bar{f}_{Y}(\lambda ) {{q}_{j}}+\frac{1}{\lambda }f_{Y}(\lambda ) ]+f_{Y}\left( \lambda \right) {{\theta }_{j}}}{{{M}_{N}}},j=1,2,\cdots , N-1,\quad \end{aligned}$$
    (8)
    $$\begin{aligned} {{p}_{j}}=\lambda (1-\rho )\frac{\left( 1-{v}_{0} \right) \bar{f}_{Y}{{q}_{j}}+f_{Y}\left( \lambda \right) {{\sigma }_{j}}}{{{M}_{N}}}, j=N, N+1, \cdots , \end{aligned}$$
    (9)

    and \(\left\{ {{p}_{j}},j=0,1,2,\cdots \right\} \) forms a probability distribution, where

    $$\begin{aligned} {v}_{0}&=\int _{0}^{\infty }{{{e}^{-\lambda t}}dF_{V}(t)},f_{Y}(\lambda )=\int _{0}^{\infty }{{{e}^{-\lambda t}}dF_{Y}(t)},\\ {{M}_{N}}&=(1-{{v}_{0}})\bar{f}_{Y}(\lambda )+f_{Y}(\lambda )\left[ N\sum \limits _{m=1}^{N-1}{{{v}_{m}}}+\lambda \int _{0}^{\infty }{t{F_{\tau }^{(N-1)}}(t)dF_{V}(t)}, \right] \\ {{q}_{j}}&=\underset{s\rightarrow {{0}^{+}}}{\mathop {\lim }}\,q_{j}^{*}(s)\\&=\frac{1}{f_{\chi }(\lambda )}\int _{0}^{\infty }{\bar{F}_{\chi }(t)\frac{{{(\lambda t)}^{j-1}}}{(j-1)!}}{{e}^{-\lambda t}}dt\\ {}&\quad +\frac{1}{f_{\chi }(\lambda )}\sum \limits _{k=1}^{j-1}{{{q}_{j-k}} \left[ 1-\sum \limits _{i=0}^{k}{\int _{0}^{\infty }{\frac{{{(\lambda t)}^{i}}}{i!}{{e}^{-\lambda t}}dF_{\chi }(t)}} \right] },\\ {{\theta }_{j}}&=\sum \limits _{k=1}^{N}{q_{j-N+k}\sum \limits _{n=1}^{N-1}{{{v}_{n}}}}+\sum \limits _{n=N}^{\infty }{\sum \limits _{k=1}^{n}{q_{j-n+k} {{v}_{n}}}},\\ {{\sigma }_{j}}&={{\theta }_{j}}+\int _{0}^{\infty }{\bar{F}_{V}(t)\frac{{{(\lambda t)}^{j}}}{j!}}{{e}^{-\lambda t}}dt. \end{aligned}$$

Proof

It is noted that the stationary probability of queue length can be calculated by

$$\begin{aligned} {{p}_{j}}=\underset{t\rightarrow \infty }{\mathop {\lim }}\,\sum \limits _{i=0}^{\infty }{P\{N(0)=i\}{{p}_{ij}}(t)}=\sum \limits _{i=0}^{\infty }{P\{N(0)=i\}\underset{t\rightarrow \infty }{\mathop {\lim }}\,{{p}_{ij}}(t)} \end{aligned}$$

and

$$\begin{aligned} \underset{t\rightarrow \infty }{\mathop {\lim }}\,{{p}_{ij}}(t)=\underset{s\rightarrow {{0}^{+}}}{\mathop {\lim }}\,sp_{ij}^{*}(s). \end{aligned}$$

Hence, we have to compute \(\underset{s\rightarrow {{0}^{+}}}{\mathop {\lim }}\,sp_{ij}^{*}(s)\).

  1. 1.

    When \(\rho >1\), due to \(\underset{s\rightarrow {{0}^{+}}}{\mathop {\lim }}\,f_{B}(s)=\omega (0<\omega <1),\) it yields

    $$\begin{aligned} \begin{aligned}&\underset{s\rightarrow {{0}^{+}}}{\mathop {\lim }}\,{{\bar{f}}_{V}}(s+\lambda )\left[ 1-{{{\bar{f}}}_{Y}}(s+\lambda ){{f}_{\tau }}\left( s \right) {{f}_{B}}\left( s \right) \right] -{{\Delta }_{N}}\left( s \right) \\&=(1-{v}_{0})\left\{ 1-\left[ 1-f_{Y}\left( \lambda \right) \right] \omega \right\} \\&\quad -f_{Y}\left( \lambda \right) \left[ {{\omega }^{N}}\underset{n=1}{\mathop {\overset{N-1}{\mathop {\sum }}\,}}\,\int _{0}^{\infty }{\frac{{{\left( \lambda \omega t \right) }^{n}}}{n!}{{e}^{-\lambda t}}dF_{V}\left( t \right) }+f_{V}\left( \lambda -\lambda \omega \right) \right. \\&\quad -\left. \underset{n=0}{\mathop {\overset{N-1}{\mathop {\sum }}\,}}\,\int _{0}^{\infty }{\frac{{{\left( \lambda \omega t \right) }^{n}}}{n!}{{e}^{-\lambda t}}dF_{V}\left( t \right) } \right] \\&= (1-{v}_{0})\left\{ 1-[1-f_{V}(\lambda )]\omega \right\} -f_{Y}(\lambda )[f_{V}(\lambda -\lambda \omega )-{v}_{0}] \\&\quad +f_{Y}\left( \lambda \right) (1-{{\omega }^{N}})\sum \limits _{n=1}^{N-1}{\int _{0}^{\infty }{\frac{{{(\lambda \omega t)}^{n}}}{n!}{{e}^{-\lambda t}}dF_{V}(t)}}. \end{aligned} \end{aligned}$$
    (10)

    We noted that

    $$\begin{aligned} 1-{v}_{0}>f_{V}(\lambda -\lambda \omega )-{v}_{0}>0,1-[1-f_{Y}(\lambda )]\omega>1-[1-f_{Y}(\lambda )]=f_{Y}(\lambda )>0, \end{aligned}$$

    and

    $$\begin{aligned} f_{Y}\left( \lambda \right) \left( 1-{{\omega }^{N}} \right) \sum \limits _{n=1}^{N-1}{\int _{0}^{\infty }{\frac{{{(\lambda \omega t)}^{n}}}{n!}{{e}^{-\lambda t}}dF_{V}(t)}}\ge 0. \end{aligned}$$

    Hence,

    $$\begin{aligned}&\underset{s\rightarrow {{0}^{+}}}{\mathop {\lim }}\,{{\bar{f}}_{V}}(s+\lambda )\left[ 1-{{{\bar{f}}}_{Y}}(s+\lambda ){{f}_{\tau }}\left( s \right) {{f}_{B}}\left( s \right) \right] -{{\Delta }_{N}}\left( s \right) \\&=\left\{ (1-{v}_{0})\left[ 1-\left[ 1-f_{Y}\left( \lambda \right) \right] \omega \right] -f_{Y}\left( \lambda \right) \left[ f_{V}\left( \lambda -\lambda \omega \right) -{v}_{0} \right] \right\} \\&\quad +f_{Y}\left( \lambda \right) \left( \text {1-}{{\omega }^{N}} \right) \sum \limits _{n=1}^{N-1}{\int _{0}^{\infty }{\frac{{{\left( \lambda \omega t \right) }^{n}}}{n!}{{e}^{-\lambda t}}dF_{V}(t)}}\\&\ne 0. \end{aligned}$$

    Combining the expressions presented in Theorems 1 and 2, we can obtain \(\underset{t\rightarrow \infty }{\mathop {\lim }}\, {{p}_{ij}}(t)=\underset{s\rightarrow {{0}^{+}}}{\mathop {\lim }}\,sp_{ij}^{*}(s)=0\) by a direct calculation, i, \(j=0\), 1, 2, \(\cdots \). When \(\rho =1\), due to \(\underset{s\rightarrow {{0}^{+}}}{\mathop {\lim }}\,f_{B}(s)=1\) and \(E\left[ b \right] =\infty \), we have

    $$\begin{aligned} \begin{aligned}&\underset{s\rightarrow {{0}^{+}}}{\mathop {\lim }}\,{{\bar{f}}_{V}}(s+\lambda )\left[ 1-{{{\bar{f}}}_{Y}}(s+\lambda ){{f}_{\tau }}\left( s \right) {{f}_{B}}\left( s \right) \right] -{{\Delta }_{N}}\left( s \right) \\&=(1-{{v}_{0}})f_{Y}\left( \lambda \right) -f_{Y}\left( \lambda \right) \left( \underset{n=1}{\mathop {\overset{N-1}{\mathop {\sum }}\,}}\,{{v}_{n}}+1-\underset{n=0}{\mathop {\overset{N-1}{\mathop {\sum }}\,}}\,{{v}_{n}} \right) \\&=(1-{{v}_{0}})f_{Y}\left( \lambda \right) -f_{Y}\left( \lambda \right) (1-{{v}_{0}}) \\&=0, \end{aligned} \end{aligned}$$
    (11)

    and

    $$\begin{aligned} \begin{aligned}&\underset{s\rightarrow {{0}^{+}}}{\mathop {\lim }}\,\frac{d}{ds}\left\{ {{{\bar{f}}}_{V}}(s+\lambda )\left[ 1-{{{\bar{f}}}_{Y}}(s+\lambda ){{f}_{\tau }}\left( s \right) {{f}_{B}}\left( s \right) \right] -{{\Delta }_{N}}\left( s \right) \right\} \\&=E[b]\left\{ 1-{{v}_{0}}-f_{Y}(\lambda )\left[ 1-\lambda E[V]-\sum \limits _{n=1}^{N-1}{(N-1){{v}_{n}}} \right] \right\} \\&\quad +\frac{(1-{{v}_{0}})[1-f_{Y}(\lambda )]}{\lambda }+f_{Y}(\lambda )\left\{ E[V]+\frac{1}{\lambda }\sum \limits _{n=1}^{N-1}{(N-n){{v}_{n}}} \right\} \\&=\infty \end{aligned} \end{aligned}$$
    (12)

    holds. Applying L’Hospital’s rule leads to \(\underset{s\rightarrow {{0}^{+}}}{\mathop {\lim }}\,sp_{ij}^{*}(s)=0\), i, \(j=0\), 1, 2, \(\cdots \). Therefore, for \(\rho \ge 1\), we have \({{p}_{j}}=0\), \(j=0\), 1, 2 \(\cdots \).

  2. 2.

    When \(\rho <1\), because of \(\underset{s\rightarrow {{0}^{+}}}{\mathop {\lim }}\,f_{B}(s)=1\) and \(E\left[ b \right] =\frac{\rho }{\lambda (1-\rho )}\), we get

    $$\begin{aligned} \begin{aligned}&\underset{s\rightarrow {{0}^{+}}}{\mathop {\lim }}\,\frac{d}{ds}\left\{ {{{\bar{f}}}_{V}}(s+\lambda )\left[ 1-{{{\bar{f}}}_{Y}}(s+\lambda ){{f}_{\tau }}\left( s \right) {{f}_{B}}\left( s \right) \right] -{{\Delta }_{N}}\left( s \right) \right\} \\&=\frac{(1-{{v}_{0}})[1-f_{Y}(\lambda )]}{\lambda (1-\rho )}+\frac{Nf_{Y}\left( \lambda \right) }{\lambda \left( 1-\rho \right) }\sum \limits _{m=1}^{N-1}{{{v}_{m}}} \\&\quad +\frac{\lambda f_{Y}(\lambda )}{\lambda \left( 1-\rho \right) }\int _{0}^{\infty }{t{{F}_{\tau }^{(N-1)}}(t)dF_{V}(t)}. \end{aligned} \end{aligned}$$
    (13)

    By using L’Hospital’s rule again and directly calculating, we can obtain the recursive expressions of \(\left\{ {{p}_{j}},j=0,1,2,\cdots \right\} \). For \(\rho <1\), it is easy to see that

    $$\begin{aligned} \begin{aligned} \sum \limits _{j=0}^{\infty }{{{p}_{j}}}=&\ \frac{(1-\rho )(1-{{v}_{0}})}{{{M}_{N}}}+\frac{\lambda (1-\rho )(1-{{v}_{0}}) \bar{F}_{Y}(\lambda ) }{{{M}_{N}}}\sum \limits _{j=1}^{\infty }{{{q}_{j}}} \\&+\frac{(N-1)(1-\rho )(1-{{v}_{0}})f_{Y}(\lambda )}{{{M}_{N}}}\\ {}&+\frac{\lambda (1-\rho )f_{Y}(\lambda )}{{{M}_{N}}}\left[ \sum \limits _{j=1}^{\infty }{{{\theta }_{j}}}+\int _{0}^{\infty }{\bar{F}_{V}(t){{F}_{\tau }^{(N)}}(t)}dt \right] . \end{aligned} \end{aligned}$$
    (14)

    After calculation and simplification, it follows that

    $$\begin{aligned} \begin{aligned} \sum \limits _{j=1}^{\infty }{{{\theta }_{j}}}&=\sum \limits _{j=1}^{\infty }{\left( \sum \limits _{k=1}^{N}{q_{j-N+k}\sum \limits _{n=1}^{N-1}{{{v}_{n}}}}+\sum \limits _{n=N}^{\infty }{\sum \limits _{k=1}^{n}{q_{j-n+k}\cdot {{v}_{n}}}} \right) } \\&=\sum \limits _{j=1}^{\infty }{\sum \limits _{k=1}^{N}{q_{j-N+k}\sum \limits _{n=1}^{N-1}{{{v}_{n}}}}}+\sum \limits _{j=1}^{\infty }{\sum \limits _{n=N}^{\infty }{\sum \limits _{k=1}^{n}{q_{j-n+k}\cdot {{v}_{n}}}}} \\&=(\sum \limits _{j=1}^{\infty }{{{q}_{j}}}) \left( N\sum \limits _{n=1}^{N-1}{{{v}_{n}}}+\sum \limits _{n=N}^{\infty }{n}\cdot {{v}_{n}} \right) \\&=(\sum \limits _{j=1}^{\infty }{{{q}_{j}}}) \left[ N\sum \limits _{n=1}^{N-1}{{{v}_{n}}}+\lambda \int _{0}^{\infty }{t{{F}_{\tau }^{(N-1)}}(t)}dF_{V}(t) \right] ,\\ \end{aligned} \end{aligned}$$
    (15)
    $$\begin{aligned} \begin{aligned} \text {and}~~~~\sum \limits _{j=1}^{\infty }{{{q}_{j}}}&=E[b]=\frac{\rho }{\lambda (1-\rho )} \end{aligned} \end{aligned}$$
    (16)

    holds. Then, substituting Eqs. (15) and (16) into Eq. (14), \(\sum \limits _{j=0}^{\infty }{{{p}_{j}}}=1\) can be easily obtained. That is, \(\left\{ {{p}_{j}},j=0,1,2,\cdots \right\} \) which satisfies the stationary condition \(\rho <1\) forms a probability distribution. \(\square \)

Theorem 4

When \(\rho <1\) and \(|z |<1\), let P(z) be the probability generating function (p.g.f.) of \(\left\{ {{p}_{j}},j=0,1,2,\cdots \right\} \), then

$$\begin{aligned} \begin{aligned} P(z)=&\ \frac{\left( 1-\rho \right) \left( 1-z \right) f_{\chi }\left( \lambda \left( 1-z \right) \right) }{f_{\chi }\left( \lambda \left( 1-z \right) \right) -z}\\&\cdot \frac{\left( 1-z \right) (1-{{v}_{0}})+f_{Y}(\lambda )\left[ z(1-{{v}_{0}})-f_{V}\left( \lambda \left( 1-z \right) \right) +{{v}_{0}}+\sum \limits _{m=1}^{N-1}{({{z}^{m}}-}{{z}^{N}}){{v}_{m}} \right] }{\left( 1-z \right) {{M}_{N}}}, \end{aligned} \end{aligned}$$
(17)

and the mean of steady-state queue size, denoted by E[L], is presented by

$$\begin{aligned} E[L]=\rho +\frac{{{\lambda }^{2}}E[ {{\chi }^{2}} ]}{2\left( 1-\rho \right) }+\frac{f_{Y}(\lambda )\left\{ \sum \limits _{m=1}^{N-1}{\left[ N(N-1)-m(m-1) \right] {{v}_{m}}}+{{\lambda }^{2}}E[{{V}^{2}}] \right\} }{2{{M}_{N}}}, \end{aligned}$$
(18)

where \({{M}_{N}}\) is determined in Theorem 3, \(f_{\chi }(\lambda (1-z))=\int _{0}^{\infty }{{{e}^{-\lambda (1-z)t}}dF_{\chi }(t)}\), \(f_{V}(\lambda (1-z))=\int _{0}^{\infty }{{{e}^{-\lambda (1-z)t}}dF_{V}(t)}\).

Proof

According to the definition of p.g.f. and the expression of \(p_{j}\) given in Theorem 3, it yields

$$\begin{aligned} \begin{aligned} P(z)=&\sum \limits _{j=0}^{\infty }{{{z}^{j}}{{p}_{j}}}=\frac{\left( 1-\rho \right) \left( 1-{v}_{0} \right) }{{{M}_{N}}}+\frac{\lambda \left( 1-\rho \right) \bar{f}_{Y}\left( \lambda \right) \left( 1-{v}_{0} \right) }{{{M}_{N}}}\sum \limits _{j=1}^{\infty }{{{z}^{j}}{{q}_{j}}}\\&+\frac{\lambda \left( 1-\rho \right) f_{Y}\left( \lambda \right) }{{{M}_{N}}}\sum \limits _{j=1}^{\infty }{{{z}^{j}}{{\theta }_{j}}}+\frac{\left( 1-\rho \right) \left( 1-{v}_{0} \right) f_{Y}\left( \lambda \right) }{{{M}_{N}}}\cdot \frac{z-{{z}^{N}}}{1-z}\\&+\frac{\lambda \left( 1-\rho \right) f_{Y}\left( \lambda \right) }{{{M}_{N}}}\sum \limits _{j=N}^{\infty }{{{z}^{j}}\int _{0}^{\infty }{\bar{F}_{V}(t)\frac{{{(\lambda t)}^{j}}}{j!}}{{e}^{-\lambda t}}dt}. \end{aligned} \end{aligned}$$
(19)

Through calculation and simplification, we get the following equations,

$$\begin{aligned}&\sum \limits _{j=1}^{\infty }{{{z}^{j}}{{q}_{j}}}=\frac{z\left[ 1-f_{\chi }\left( \lambda \left( 1-z \right) \right) \right] }{\lambda \left[ f_{\chi }\left( \lambda \left( 1-z \right) \right) -z \right] },\end{aligned}$$
(20)
$$\begin{aligned}&\sum \limits _{j=1}^{\infty }{{{z}^{j}}{{\theta }_{j}}}=( \sum \limits _{j=1}^{\infty }{{{z}^{j}}{{q}_{j}}} )\left[ \frac{1-{{z}^{N}}}{1-z}\sum \limits _{m=1}^{N-1}{{{v}_{m}}}+\sum \limits _{m=N}^{\infty }{\frac{1-{{z}^{m}}}{1-z}}{{v}_{m}} \right] , \end{aligned}$$
(21)
$$\begin{aligned} \begin{aligned}&\lambda \sum \limits _{j=N}^{\infty }{{{z}^{j}}\int _{0}^{\infty }{\bar{F}_{V}(t)\frac{{{(\lambda t)}^{j}}}{j!}}{{e}^{-\lambda t}}dt}\\&=\frac{1}{1-z}\left\{ {{v}_{0}}-f_{V}\left( \lambda \left( 1-z \right) \right) +{{z}^{N}}\left( 1-{{v}_{0}} \right) +\sum \limits _{m=1}^{N-1}{\left( {{z}^{m}}-{{z}^{N}} \right) {{v}_{m}}} \right\} . \end{aligned} \end{aligned}$$
(22)

Then, substituting Eqs. (20)–(22) into (19) leads to Eq. (17), and Eq. (18) can be derived by using \({{E[L]}}=\frac{d}{dz}\left[ P\left( z \right) \right] |_{z=1}\). \(\square \)

Theorem 5

(Stochastic decomposition structure of the steady-state queue size) For \(\rho <1\), the steady-state queue size studied in this paper can be decomposed into the sum of two independent parts: one is the steady-state queue size of the classic M/G/1 queue that has been studied (see e.g., Cohen 1982), and the other is the additional queue size \({{L}_{d}}\) caused by N-policy and delayed uninterrupted multiple vacation, which is distributed as

$$\begin{aligned} P\left\{ {{L}_{d}}=0 \right\}&=\frac{1-{v}_{0}}{{{M}_{N}}},\end{aligned}$$
(23)
$$\begin{aligned} P\left\{ {{L}_{d}}=j \right\}&=\frac{f_{Y}\left( \lambda \right) (1-{v}_{0})}{{{M}_{N}}}, j=1,2,\cdots ,N-1,\end{aligned}$$
(24)
$$\begin{aligned} P\left\{ {{L}_{d}}=j \right\}&=\frac{f_{Y}\left( \lambda \right) \int _{0}^{\infty }{{{F}_{\tau }^{\left( j+1 \right) }}(t)dF_{V}(t)}}{{{M}_{N}}},j=N,N+1,\cdots , \end{aligned}$$
(25)

where \({{M}_{N}}\) is determined in Theorem 3.

Proof

From the Eq. (17) above, it can be seen that the stochastic decomposition property of the steady-state queue size holds. In order to obtain Eqs. (23)–(25), let

$$\begin{aligned} \begin{aligned} {{P}_{V}}(z)&=\frac{\left( 1-z \right) (1-{{v}_{0}})+f_{Y}(\lambda )\left[ z(1-{{v}_{0}})-f_{V}\left( \lambda \left( 1-z \right) \right) +{{v}_{0}}+\sum \limits _{m=1}^{N-1}{({{z}^{m}}-}{{z}^{N}}){{v}_{m}} \right] }{\left( 1-z \right) {{M}_{N}}} \\&=\frac{1-{{v}_{0}}}{{{M}_{N}}}+\frac{f_{Y}(\lambda )}{{{M}_{N}}}H\left( z \right) \cdot I\left( z \right) , \end{aligned} \end{aligned}$$
(26)

where \(H\left( z \right) =z(1-{{v}_{0}})-f_{V}\left( \lambda \left( 1-z \right) \right) +{{v}_{0}}+\sum \limits _{m=1}^{N-1}{({{z}^{m}}-}{{z}^{N}}){{v}_{m}}\), and \(I\left( z \right) =\frac{1}{1-z}\).

Using a straightforward calculation, the following results are easily obtained.

$$\begin{aligned} {{H}^{(0)}}\left( z \right) |_{z=0}&=H\left( z \right) |_{z=0} =0,{{H}^{(1)}}\left( z \right) |_{z=0}=1-{v}_{0}, \\ {{H}^{(j)}}\left( z \right) |_{z=0}&=0,2\le j\le N-1, \\ {{H}^{(N)}}(z)|_{z=0}&=-N!\sum \limits _{m=1}^{N-1}{{{v}_{m}}}-\int _{0}^{\infty }{{{(\lambda t)}^{N}}{{e}^{-\lambda t}}dF_{V}(t)}, \\ {{H}^{(j)}}\left( z \right) |_{z=0}&=-\int _{0}^{\infty }{{{(\lambda t)}^{j}}{{e}^{-\lambda t}}dF_{V}(t)},j\ge N+1, \\ {{I}^{(j)}}(z){|_{z=0}}&=j!,j\ge 0. \end{aligned}$$

Then, employing

$$\begin{aligned} P\left\{ {{L}_{d}}=j \right\} =\frac{1}{j!}\cdot \frac{{{d}^{j}}}{d{{z}^{j}}}\left[ {{P}_{V}}\left( z \right) \right] |_{z=0} \end{aligned}$$

and

$$\begin{aligned} {{\left[ H\left( z \right) \cdot I\left( z \right) \right] }^{(j)}}=\sum \limits _{k=0}^{j}{C_{j}^{k}}{{H}^{(k)}}\left( z \right) {{I}^{(j-k)}}\left( z \right) , \end{aligned}$$

we can get Eqs. (23)–(25) by carrying some algebraic simplifications, where \({{H}^{(k)}}\left( z \right) \) represents the k-th order derivative of \(H\left( z \right) \) with respect to z, and \(C_{m}^{k}=\frac{m!}{k!(m-k)!}\). \(\square \)

Theorem 6

Let E[W] denote the average waiting time of an arbitrary customer, then for \(\rho <1\), we have

$$\begin{aligned} E[W]=\frac{\lambda E\left[ {{\chi }^{2}} \right] }{2\left( 1-\rho \right) }+\frac{f_{Y}(\lambda )\left\{ \sum \limits _{m=1}^{N-1}{\left[ N(N-1)-m(m-1) \right] {{v}_{m}}}+{{\lambda }^{2}}E[{{V}^{2}}] \right\} }{2\lambda {{M}_{N}}}, \end{aligned}$$
(27)

where \({{M}_{N}}\) is given in Theorem 3.

Proof

According to the model description, we can see that customers are served in a first-come-first-served manner, and the arrival process is a Poisson process with rate \(\lambda (>0)\). It is also observed that in equilibrium, the number of customers in the queue at a departure is equal to the number of customers that arrived during the departing customer’s sojourn time. Therefore, Little’s law holds, and the Eq. (27) can be derived by \(E[W]=\frac{E[L]}{\lambda }-E[\chi ]\). \(\square \)

5 The Optimal Control Policy under the Cost Model

5.1 The Cost Model and Cost Function

This section offers four numerical examples to determine the optimal control policy \({{N}^{*}}\) and the optimal two-dimensional control policy \(({{N}^{*}},{{T}^{*}})\) for minimizing the system cost. Considering actual operating costs of the system, we first establish the cost structure as follows:

  1. 1.

    \(R\equiv \) fixed setup cost of the system for each time (this cost is due to the consumption of switching on the server each time);

  2. 2.

    \(h\equiv \) fixed holding cost for each customer per unit time in the system (the cost arises from the customer’s sojourn time, including the waiting and service times).

Let C(N) donate the long-run expected cost of the system per unit of time. Applying the renewal reward theorem, we get

$$\begin{aligned} \begin{aligned} C\left( N \right)&=\frac{\text {Expected cost within a busy cycle}}{\text {Expected length of a busy cycle}}\\&=hE[L]+\frac{R}{{E\left[ {{I}} \right] }+{E\left[ {{Z}} \right] }}, \end{aligned} \end{aligned}$$
(28)

where E[L] is given by Eq. (18) as mentioned above, I denotes the length of a server’s non-busy period (the time interval from the moment the system becomes empty until the moment the server returns to the system from vacation and provides service), which is similar to the definition in the paper by Luo et al. (2023). Let Z denote the length of a server’s busy period and \({{U}_{b}}\) be the queue size at the beginning of Z, and its probability distribution is given by

$$\begin{aligned} P\left\{ {{U}_{b}}=1 \right\}&=1-f_{Y}\left( \lambda \right) , \\ P\left\{ {{U}_{b}}=N \right\}&=\frac{f_{Y}\left( \lambda \right) }{1-{{v}_{0}}}\sum \limits _{n=1}^{N}{{{v}_{n}}},\\ P\left\{ {{U}_{b}}=n \right\}&=\frac{f_{Y}\left( \lambda \right) }{1-{{v}_{0}}}{{v}_{n}},n=N+1,N+2,\cdots . \end{aligned}$$

Therefore, we can obtain the average value of \({{U}_{b}}\) as \(E\left[ {{U}_{b}} \right] =\frac{{{M}_{N}}}{1-f_{V}\left( \lambda \right) }.\)

Using the above Lemma 1, we can calculate the average value of Z as follows:

$$\begin{aligned} {{{E[Z]}}}=E\left[ b \right] E\left[ {{U}_{b}} \right] =\frac{\rho {{M}_{N}}}{\lambda \left( 1-\rho \right) \left( 1-{v}_{0} \right) },\rho <1. \end{aligned}$$
(29)

Since the queue size at the beginning of Z is equal to the number of customers arriving during I and customers arrival process is a Poisson with rate \(\lambda \) \((>0)\), the average length of the server’s non-busy period can be represented by \(E[I]=\frac{E\left[ {{U}_{b}} \right] }{\lambda }\). Then,

$$\begin{aligned} E[I]+E[Z]=\frac{{{M}_{N}}}{\lambda \left( 1-\rho \right) \left( 1-{v}_{0} \right) }\text {, }\rho <1. \end{aligned}$$
(30)

Substituting Eqs. (18) and (30) into Eq. (28), we have

$$\begin{aligned} \begin{aligned} C(N)=&\ h\left\{ \rho +\frac{{{\lambda }^{2}}E[ {{\chi }^{2}} ]}{2\left( 1-\rho \right) }+\frac{f_{Y}(\lambda )\left\{ \sum \limits _{m=1}^{N-1}{\left[ N(N-1)-m(m-1) \right] {{v}_{m}}}+{{\lambda }^{2}}E[{{V}^{2}}] \right\} }{2{{M}_{N}}} \right\} \\&+\frac{R\lambda \left( 1-\rho \right) \left( 1-{v}_{0} \right) }{{{M}_{N}}}, \end{aligned} \end{aligned}$$
(31)

where \({{M}_{N}}\) is given in Theorem 3.

5.2 Optimal Control Policy without the Average Waiting Time Constraint

From the above Eq. (31), we can see that the cost function C(N) is a non-linear function that depends on the decision variable N. It is too difficult to find the optimal solution of Eq. (31) in an analytical manner. Therefore, we next search for the optimal solution through the following numerical examples.

Example 1

We consider a practical situation related to a maintenance system—an auto repair shop to illustrate the theoretical results of the model. The manager of an auto repair shop invited a repair expert with excellent skills to be responsible for repairing a particular car brand. Considering the needs of the business, the manager asked the expert to wait for a random time Y instead of leaving immediately for a vacation V after all repair work is finished. Once a car needs repair during Y, the repair expert provides service immediately until no more cars need repair. After that, the expert restarts another delay period Y. In order to save costs (including costs of the expert’s appearance and starting repairs), the manager designs the following repair strategy according to the number of arriving cars during V: (i)If no cars are waiting for repair after V expires, the maintenance expert will continue to be on vacation; (ii)If the number of arrivals is greater than or equal to N; the expert immediately repair these cars at the end of V until there is no car again; (iii)If the number of arrivals is less than N but greater than 0, the expert waits for N customers to accumulate in the system before providing repair.

Assume that cars arrive at the auto repair shop according to a Poisson process with the parameter \(\lambda (> 0)\). The repair time of each car, the delay period Y and the time V for the repair expert to continuously repair other brands of cars obey different PH distributions with representation \((\varvec{\alpha },\varvec{L})\), \((\varvec{\beta },\varvec{K})\) and \((\varvec{\gamma },\varvec{S})\) of orders m, n and i, respectively. Vectors \(\varvec{\alpha }=\left( {{\alpha }_{1}},{{\alpha }_{2}},\ldots {{\alpha }_{m}} \right) \), \(\varvec{\beta }=\left( {{\beta }_{1}},{{\beta }_{2}},\ldots {{\beta }_{n}} \right) \) and \(\varvec{\gamma }=\left( {{\gamma }_{1}},{{\gamma }_{2}},\ldots {{\gamma }_{i}} \right) \) can be interpreted as the initial probability vectors among the transient states, where \({\varvec{\alpha }}{{\varvec{e}}_{m}}=1\), \({\varvec{\beta }}{{\varvec{e}}_{n}}=1\) and \({\varvec{\gamma }}{{\varvec{e}}_{i}}=1\). \({{\varvec{e}}_{m}}\), \({{\varvec{e}}_{n}}\) and \({{\varvec{e}}_{i}}\) represent column vectors of dimensions m, n and i with all elements equal to one, respectively. Column vectors \(\varvec{L}^{0}\), \(\varvec{K}^{0}\) and \(\varvec{S}^{0}\) meet the conditions \(\varvec{L{{{e}}_{m}}}+\varvec{L}^{0}=0\), \(\varvec{K{{{e}}_{n}}}+\varvec{K}^{0}=0\) and \(\varvec{S{{{e}}_{i}}}+\varvec{S}^{0}=0\), respectively. According to Eq. (31), the cost function C(N) without the average waiting time constraint can be expressed as

$$\begin{aligned} \begin{aligned} C(N)=&\ h\left\{ -\lambda \varvec{\alpha } {\varvec{{L}}^{-1}}{\varvec{{e}}_{m}}+\frac{{{\lambda }^{2}}\varvec{\alpha } {\varvec{{L}}^{-2}}{\varvec{{e}}_{m}}}{1+\lambda \varvec{\alpha } {\varvec{{L}}^{-1}}{\varvec{{e}}_{m}}}\right. \\&+\left. \frac{{\zeta }({{\psi }_{N}}+2{{\lambda }^{2}}\varvec{\gamma } {\varvec{{S}}^{-2}}{\varvec{{e}}_{i}})}{2\left[ (1-{\eta })(1-{\zeta })+{\zeta }({{\varphi }_{N}}-\lambda \varvec{\gamma } {\varvec{{S}}^{-1}}{\varvec{{e}}_{i}}) \right] } \right\} \\&+\frac{R\lambda \left( 1+\lambda \varvec{\alpha } {\varvec{{L}}^{-1}}{\varvec{{e}}_{m}} \right) (1-{\eta })}{(1-{\eta })(1-{\zeta })+{\zeta }({{\varphi }_{N}}-\lambda \varvec{\gamma } {\varvec{{S}}^{-1}}{\varvec{{e}}_{i}})}, \end{aligned} \end{aligned}$$
(32)

where \({\varvec{{I}}_{n}}\) represents the identity matrix of dimension n,

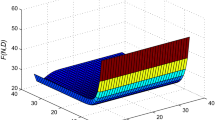
$$\begin{aligned} {\zeta }&=\varvec{\beta } {{(\lambda {\varvec{{I}}_{n}}-\varvec{K})}^{-1}}{\varvec{{K}}^{0}},{\eta }=\varvec{\gamma } {{(\lambda {\varvec{{I}}_{i}}-\varvec{S})}^{-1}}{\varvec{{S}}^{0}},\\ {{\varphi }_{N}}&=\varvec{\gamma } \sum \limits _{k=1}^{N-1}{\left( N-k \right) {{\lambda }^{k}}{{(\lambda {\varvec{{I}}_{i}}-\varvec{S})}^{-k-1}}}{{\varvec{S}}^{0}},\\ {{\psi }_{N}}&=\sum \limits _{k=1}^{N-1}{\left[ N(N-1)-k(k-1) \right] }{{\lambda }^{k}}\varvec{\gamma } {{(\lambda {\varvec{{I}}_{i}}-\varvec{S})}^{-k-1}}{{\varvec{S}}^{0}}. \end{aligned}$$

We set \(R=200\), \(h=3\), \(\lambda =0.8\), \(\varvec{L}=\left( \begin{matrix} -15 &{} 1.5 &{} 0.1 \\ 0.2 &{} -1 &{} 0.2 \\ 0.3 &{} 0.1 &{} -4 \\ \end{matrix} \right) \), \(\varvec{\alpha } ={{\left( \begin{matrix} 0.5 \\ 0.3 \\ 0.2 \\ \end{matrix} \right) }^{\top }}\), \({\varvec{{L}}^{0}}=\left( \begin{matrix} 13.4 \\ 0.6 \\ 3.6 \\ \end{matrix} \right) \), \(\varvec{K}=\left( \begin{matrix} -5 &{} 2 &{} 2 \\ 0.5 &{} -12 &{} 3 \\ 0.8 &{} 0.2 &{} -20 \\ \end{matrix} \right) \), \(\varvec{\beta }={{\left( \begin{matrix} 0.1 \\ 0.8 \\ 0.1 \\ \end{matrix} \right) }^{\top }}\), \({\varvec{{K}}^{0}}=\left( \begin{matrix} 1 \\ 8.5 \\ 19 \\ \end{matrix} \right) \), \(\varvec{S}=\left( \begin{matrix} -2 &{} 1 &{} 0.5 \\ 0.2 &{} -1 &{} 0.4 \\ 0.6 &{} 0.2 &{} -1.2 \\ \end{matrix} \right) \), \(\varvec{\gamma }={{\left( \begin{matrix} 0.3 \\ 0.3 \\ 0.4 \\ \end{matrix} \right) }^{\top }}\), \({\varvec{{S}}^{0}}=\left( \begin{matrix} 0.5 \\ 0.4 \\ 0.4 \\ \end{matrix} \right) \). Then, we obtain the value of C(N) for different values of decision variable N and plot the figure via the MATLAB software (hold 4 digits after the decimal point). The numerical results are displayed in Table 1. Figure 1 plots the curve of C(N) with respect to N.

Table 1 Numerical results for \(C\left( N \right) \) under different N
Full size table
Fig. 1
figure 1

\(C\left( N \right) \) varies with different N

Full size image

From Table 1 and Fig. 1, the optimal value of N is achieved at \({{N}^{*}}=8\) and its corresponding minimum function value \(C({{N}^{*}})=42.5158\).

Example 2

If the random variable V in Example 1 is a fixed length \(T(\ge 0)\), that is, \(P\left\{ V=T \right\} =1\). The two-dimensional cost function, denoted by C(N, T), can be expressed as

$$\begin{aligned} \begin{aligned} C(N,T)=&\ h\left\{ -\lambda \varvec{\alpha } {\varvec{{L}}^{-1}}{\varvec{{e}}_{m}}+\frac{{{\lambda }^{2}}\varvec{\alpha } {\varvec{{L}}^{-2}}{\varvec{{e}}_{m}}}{1+\lambda \varvec{\alpha } {\varvec{{L}}^{-1}}{\varvec{{e}}_{m}}}+\frac{{\zeta }[{{\phi }_{N}}+{{\left( \lambda T \right) }^{2}}]}{2\left[ \left( 1-{{e}^{-\lambda T}} \right) \left( 1-{\zeta } \right) \text {+}{\zeta }({{\vartheta }_{N}}+\lambda T) \right] } \right\} \\&+\frac{R\lambda \left( 1+\lambda \varvec{\alpha } {\varvec{{L}}^{-1}}{\varvec{{e}}_{m}} \right) \left( \text {1}-{{e}^{-\lambda T}} \right) }{\left( 1-{{e}^{-\lambda T}} \right) \left( 1-{\zeta } \right) +{\zeta }({{\vartheta }_{N}}+\lambda T)}, \end{aligned} \end{aligned}$$
(33)

where \({\varvec{{I}}_{n}}\) and \(\zeta \) are determined in Example 1,

$$\begin{aligned} {{\phi }_{N}}=\sum \limits _{k=1}^{N-1}{\left[ N(N-1)-k(k-1) \right] \frac{{{\left( \lambda T \right) }^{k}}}{k!}{{e}^{-\lambda T}}}, {{\vartheta }_{N}}=\sum \limits _{k=1}^{N-1}{\left( N-k \right) }\frac{{{\left( \lambda T \right) }^{k}}}{k!}{{e}^{-\lambda T}}. \end{aligned}$$

Since N is a discrete variable, we will calculate the optimum values of N and T for the cost function C(N, T) through the following algorithm:

  • Step 1: Substituting the system parameters into Eq. (33), and initialize the iteration counter \( N=1\).

  • Step 2: Use MATLAB program to search the optimal numerical solution \(T_{N}^{*}\) of decision variable T so as to minimize the cost function \(C\left( N,T \right) \). The minimum value of the cost function \(C\left( N,T \right) \) can be denoted as \(C\left( N,T_{N}^{*} \right) \).

  • Step 3: Set \(N=N+1\) and repeat the step 2.

  • Step 4: If \(C\left( N+1,T_{N+1}^{*} \right) -C\left( N,T_{N}^{*} \right) >0\), then stop and report \(\left( {{N}^{*}},{{T}^{*}} \right) =\left( {{N}^{*}},T_{N}^{*} \right) \) and \(C\left( N,{{T}^{*}} \right) =C\left( N,T_{N}^{*} \right) \). Otherwise, go to Step 3 and Step 4.

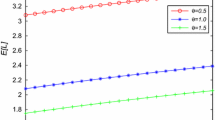
We first choose the cost parameters R, h and the system parameters \(\lambda \), \(\varvec{L}\), \(\varvec{\alpha }\), \(\varvec{K}\), and \(\varvec{\beta }\) to have the same values as in Example 1. Next, we program in MATLAB by using the above algorithm. The obtained numerical results are reported in Table 2. Figure 2 shows the change of C(N, T) for different N and T.

Table 2 Numerical results for \({{T}_{N}}^{*}\) and \(C\left( N,T_{N}^{*} \right) \) under different N
Full size table
Fig. 2
figure 2

The change of C(N, T) for differen N and T

Full size image

We can see from Table 2 that the two-dimensional optimal solution of Eq. (33) \(({{N}^{*}},{{T}^{*}})=(4,10.4066)\) and its corresponding minimum function value \(C({{N}^{*}},{{T}^{*}})=26.3750\). In addition, we can also check the correctness of the results by \(\frac{dC(N,T)}{dT}|_{(N=4,T=T_{4}^{*})} \approx 0\).

5.3 Optimal Control Policy with the Average Waiting Time Constraint

Scholars rarely considered the influence of the length of the customers’ waiting time on the optimal control policy in previous optimization problems. By reducing the number of system startups, the N-policy can save running costs. Nevertheless, it will also increase customers’ waiting times, which will result in lost customers or system congestion if waiting times are too long. It is therefore necessary to examine the optimal control policy under the premise that the average waiting time of an arbitrary customer is less than the threshold \(E[{W}_{0}]\) in order to minimize customer waiting times and trade off costs between customers and system managers. Next, we will discuss the optimal control policy for economizing the system cost under the same conditions as in Example 1 and Example 2.

Example 3

Let the distributions of all random variables be the same as in Example 1. The cost function C(N) with the average waiting time constraint can be expressed as

$$\begin{aligned} \left\{ {\begin{array}{cc} \min C(N), \\ s.t.E[W]\le E[{W}_{0}], \\ \end{array}} \right. \end{aligned}$$
(34)

where C(N) is given by the above Eq. (32), and

$$\begin{aligned} E[W]=\frac{{{\lambda }}\varvec{\alpha } {\varvec{{L}}^{-2}}{\varvec{{e}}_{m}}}{1+\lambda \varvec{\alpha } {\varvec{{L}}^{-1}}{\varvec{{e}}_{m}}}+\frac{{\zeta }({{\psi }_{N}}+2{{\lambda }^{2}}\varvec{\gamma } {\varvec{{S}}^{-2}}{\varvec{{e}}_{i}})}{2\lambda \left[ (1-{\eta })(1-{\zeta })+{\zeta }({{\varphi }_{N}}-\lambda \varvec{\gamma } {\varvec{{S}}^{-1}}{\varvec{{e}}_{i}}) \right] }. \end{aligned}$$

Let the values of all parameters be the same as that in Example 1. We use the MATLAB program to calculate the values of C(N) and E[W] under different values of N and \(E[{W}_{0}]\). All numerical results are reported in Table 3.

Table 3 Numerical results for C(N) and E[W] under different N and \(E[{W}_{0}]\)
Full size table

From Table 3, we can reveal that

  • If \(E[{W}_{0}]=6\), the optimal control threshold value \({{N}^{*}}=8\) and its corresponding minimum cost value \(C({{N}^{*}})=42.5158\) under the constraint condition \(E[W]\le 6\).

  • \(E[{W}_{0}]=4.5\), the optimal control threshold value \({{N}^{*}}=6\) and its corresponding minimum cost value \(C({{N}^{*}})=43.7989\) under the constraint condition \(E[W]\le 4.5\).

  • If \(E[{W}_{0}]=3\), the optimal control threshold value \({{N}^{*}}=3\) and its corresponding minimum cost value \(C({{N}^{*}})=51.7797\) under the constraint condition \(E[W]\le 3\).

Example 4

Let the distributions of all random variables be the same as in Example 2. The cost function C(N, T) with the average waiting time constraint can be expressed as

$$\begin{aligned} \left\{ {\begin{array}{cc} \min C(N,T), \\ s.t.E[W]\le E[{W}_{0}], \\ \end{array}} \right. \end{aligned}$$
(35)

where C(N, T) is given by the above Eq. (33), and

$$\begin{aligned} E[W]=\frac{\lambda \varvec{\alpha } {\varvec{{L}}^{-2}}{\varvec{{e}}_{m}}}{1+\lambda \varvec{\alpha } {\varvec{{L}}^{-1}}{\varvec{{e}}_{m}}}+\frac{{\zeta }({{\phi }_{N}}+{{\left( \lambda T \right) }^{2}})}{2\lambda \left[ \left( 1-{{e}^{-\lambda T}} \right) \left( 1-{\zeta } \right) +{\zeta }({{\vartheta }_{N}}+\lambda T) \right] }. \end{aligned}$$

Let the values of all parameters be the same as that in Example 2. We use the algorithm given in Example 2 to calculate Eq. (35). The numerical results are shown in Table 4.

Table 4 Numerical results for \({{T}_{N}}^{*}\), \(C\left( N,T_{N}^{*} \right) \) and E[W] under different N and \(E[{W}_{0}]\)
Full size table

By Table 4, we can obtain the following conclusions:

  • If \(E[{W}_{0}]=4.5\), the optimal control policy \(({{N}^{*}},{{T}^{*}})=(4,8.4525)\) and its corresponding minimum cost value \(C({{N}^{*}},{{T}^{*}})=26.8370\) under the constraint condition \(E[W]\le 4.5\).

  • If the \(E[{W}_{0}]=3\), the optimal control policy \(({{N}^{*}},{{T}^{*}})=(3,5.4827)\) and its corresponding minimum cost value \(C({{N}^{*}},{{T}^{*}})=30.5611\) under the constraint condition \(E[W]\le 3\).

  • If \(E[{W}_{0}]=1.5\), the optimal control policy \(({{N}^{*}},{{T}^{*}})=(2,2.5408)\) and its corresponding minimum cost value \(C({{N}^{*}},{{T}^{*}})=44.1927\) under the constraint condition \(E[W]\le 1.5\).

6 Conclusions

In this paper, we proposed a new M/G/1 queueing model with delayed uninterrupted multiple vacation under N-policy control and discussed the transient and steady-state properties of the queue size. Our analysis technique differed from traditional analysis methods (e.g., embedded Markov chain and supplementary variable technique). The expressions of the Laplace transform of the transient queue-length distribution with respect to time t were presented. Then, based on the transient analysis, some crucial queueing performance indices were derived. Finally, we set several numerical examples to discuss the optimal control policy to minimize the expected cost when the random variables obey different PH distributions. Our analysis can help policy-makers set a reasonable threshold for cost optimization in many applications, such as maintenance and order-based systems. The system studied in this paper can be extended to more complex queueing models, such as the non-Markovian arrival process of customers and unreliable servers, which can be the future research directions.