A Computational Framework for Material Design

Abstract

A computational framework is proposed that enables the integration of experimental and computational data, a variety of user-selected models, and a computer algorithm to direct a design optimization. To demonstrate this framework, a sample design of a ternary Ni-Al-Cr alloy with a high work-to-necking ratio is presented. This design example illustrates how CALPHAD phase-based, composition and temperature-dependent phase equilibria calculations and precipitation models are coupled with models for elastic and plastic deformation to calculate the stress-strain curves. A genetic algorithm then directs the search within a specific set of composition and processing constraints for the ideal composition and processing profile to optimize the mechanical properties. The initial demonstration of the framework provides a potential solution to initiate the material design process in a large space of composition and processing conditions. This framework can also be used in similar material systems or adapted for other material classes.

Introduction

With the announcement of the Materials Genome Initiative advocating for a 50% reduction in time and cost to develop and deploy new materials, the need to accelerate computational material design approaches has become essential. While there are many different approaches to computational materials design [63, 69, 71, 77], all of the approaches integrate processing, structure, property (PSP) relations to predict a set of desirable material properties for a given application. As noted by Kuehmann and Olson [50], a key challenge of computational materials design is the optimization of several conflicting requirements, which are represented by a variety of processing-structure-property models, to achieve the desired materials performance. To achieve this optimization, the models used must be integrated such that composition, structure, processing variables are tracked as needed. The biggest challenges in this design process are the integration of a variety of models needed and the available experimental and computational data, the flexibility to exchange different models depending on the design application, and the ability to re-assess model parameters for specific alloy systems. There have been a variety of attempts to develop platforms and tools to support materials design for different kinds of material classes and applications. In particular, for Ni-based superalloys, there have been a variety design optimization strategies employed, including using trade-off diagrams [21, 50, 69, 100] and search algorithms [40, 86, 87]. An essential part of all these designs is the control of the precipitation of the γ ^′ strengthening phase and the high temperature properties.

Many strategies are used to design novel alloys for various applications. Reed et al. [69] used thermodynamic equilibria and composition-based models to approximate the PSP relations of a Ni-based superalloy. The alloy composition is selected according to the trade-off diagrams to fulfill the performance requirements. Gheribi et al. [34] combined CALPHAD software, FactSage, with the mesh adaptive direct search algorithm to search the optimum alloy composition and processing conditions for different design objectives. This software provides effective search in a larger parameter space. These two works are computationally efficient but ignored the kinetics of phase transformation during the heat treatment. Saunders et al. [80] integrated the Johnson-Mehl-Avrami equation for γ ^′ precipitation with mechanistic models for yield and creep rupture properties to interpret the PSP relations of Ni-based superalloys. This chain of forward calculations is ideal to optimize the processing conditions, but an extra module should be expected to select the material. Olson used multiple tools to improve the computational material design quality and reduce the number of design iterations [63]. An extra connection between tools and data may create a smooth workflow to initiate a new design project. Another trade-off diagram approach was taken by Crudden et al. [21] which coupled the CALPHAD approach with a data-driven model using an artificial neural network (ANN) to estimate yield strength. Based on the concurrent knowledge and data, this ANN model faithfully interpreted the information in a certain composition domain, but this non-physics based tool may not be applicable in a wider design space. To summarize these design strategies, an integration of phase-based models and data with search algorithm is needed for the next generation of material design.

These design examples demonstrate some of the complexity of materials design and the need to optimize within a framework of conflicting objectives. A variety of efforts have been made to design efficient algorithms, including genetic algorithms (GA) coupled with CALPHAD-based tools [58, 86, 87], atomistic simulations [13, 31, 40], and data-driven approaches [42, 55, 78, 102]. The goal of this work is to develop a platform that integrates federated experimental and computational data repositories with CALPHAD-based tools and mechanistic property models to predict materials behavior and enable materials design using a GA. A model ternary Ni-Al-Cr alloy is chosen to demonstrate this platform.

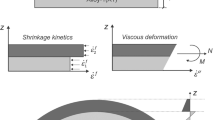
For computational materials design, it is useful to identify key PSP links in a system design chart [65]. The key PSP relations, as seen in Fig. 1a, for Ni-based superalloys used for turbine blades are reviewed to identify the data and models that are to be incorporated in this example. The desired properties for this application include creep resistance, fatigue strength, ductility and toughness, high strength, high temperature phase stability, and oxidation resistance. The strength is optimized by controlling the precipitation and stability of the γ ^′ phase in the γ matrix during the solution treatment and tempering processes. The creep resistance is determined by the lattice mismatch between the γ/γ ^′ phases and diffusion in the γ matrix. The ductility and toughness are dependent on the matrix grain size and the inclusions present. The high temperature phase stability is dependent on avoiding TCP phases precipitating in the matrix during the solution treatment and tempering processes. This work focuses on developing a ternary Ni-Al-Cr alloy that optimizes the strength and the ductility for a given set of processing conditions. Based on this simplification, Fig. 1b highlights critical process-structure-property relations for this work. The critical relations that must be included in this design process include simulation of the precipitation, growth, and coarsening of the γ ^′ phase; prediction the γ/γ ^′ interfacial energy; calculations of solid solution, grain boundary, and dislocation-based strengthening mechanisms; and prediction of the plastic deformation. The details of the models employed will be described in the “ γ ^′ Precipitation” to “Plastic Deformation” sections.

Fig. 1

a The system design chart for γ/γ ^′ Ni-based superalloy. b The focus of the present work

To optimize this design problem, an efficient search algorithm is needed to obtain the solution from the large composition and processing condition spaces. In the present work, we propose a tool which integrates the simulation of γ ^′ precipitation and mechanical property models within the framework of a genetic algorithm (GA) to design a high work-to-necking (E _WTN ) Ni_(1−x−y)Al _x Cr _y ternary alloy.

Computational Framework

Infrastructure Framework

Experimental and computational data, CALPHAD-based tools, and elastic/plastic property models with a design optimization code are integrated using a Python-based environment. The Materials Data Curation System (MDCS) [23] enables the curation and reuse of experimental and computational data. Using the representational state transfer application programming interface (REST-API) enables seamless linkage of these data with the user models and optimization tools. Different user models written in a variety of programming languages (C, Fortran, and Python) are modularized and integrated within the Python-environment. A genetic algorithm is coupled with this framework to optimize the desired properties as a function of composition and processing conditions. In addition, reference data are used with either the GA or basin-hopping algorithm [43] to calibrate models. Figure 2 illustrates how the data and different user models are integrated within this design framework.

Fig. 2

The data flow diagram for the present framework

Four modules with models for phase-based properties are developed to interpret the PSP relations as shown in Fig. 3. To ensure that the model alloy is in the γ/γ ^′ two phase field region at the processing temperature, the thermodynamic equilibrium is calculated using Thermo-Calc [4] with the TCNI6 database [88]. This equilibrium calculation is followed by calculations with the precipitation module for γ ^′ precipitation. The resulting γ ^′ size and volume fraction are the inputs in the materials knowledge systems in Python (PyMKS) [97] which simulates the elastic deformation of the alloy. A constitutive module has been developed for plastic deformation. The work-to-necking is then calculated as the area beneath the stress-strain curve from the initial elastic deformation to necking.

Fig. 3

The flowchart of the computational process

After casting, hot working, solution treatment, and coating, the microstructure of a γ/γ ^′ Ni-base superalloy ideally contains a homogeneous, disordered face centered cubic (FCC, γ) phase. During the tempering treatment at processing temperature (T _p ), the strengthening phase, ordered FCC (γ ^′), precipitates (Fig. 1). The radius and volume fraction of the γ ^′ particles are the important microstructure features affecting the yield stress [19, 49]. The next four sections will review the models used to predict the precipitation, yield strength, elastic and plastic deformation.

γ ^′ Precipitation

The models for the precipitation kinetics, including classic nucleation, diffusion controlled growth, and coarsening, are well developed [12, 14, 66, 67, 85] and have been successfully applied to simulate the γ ^′ precipitation in Ni-based superalloys [3, 5, 64, 65, 68, 74]. Olson et al. validated a similar precipitation model implemented in PrecipiCalc for 3rd generation disk alloys [64, 65]. The phase equilibria and diffusivity data that are needed for these models are obtained from CALPHAD (calculation of phase diagrams) computations using thermodynamic and diffusion mobility databases [11, 25, 71, 79]. In this work, we implement a module to simulate the γ ^′ precipitation during the tempering treatment. The precipitate size and volume fraction are calculated as a function of the processing time. The yield stress (σ _ys ) at service temperature (T _s ) will be estimated from these parameters and the processing time is optimized once the yield stress is maximized.

Nucleation

The nucleation energy, ΔG _nu (J/m ³), for forming the precipitate from the supersaturated solid solution is determined by the chemical driving force, ΔG _ch , and the elastic strain energy, ΔG _el , resulting from different atomic volumes [94]:

$$\begin{array}{@{}rcl@{}} \Delta G_{nu} &=& \Delta G_{ch} + \Delta G_{el} \end{array} $$

(1a)

$$\begin{array}{@{}rcl@{}} \Delta G_{ch} &=& - \frac{Rg T_{p}}{V_{M}^{\gamma^{\prime}}} {\sum}_{i} \bar{X}_{i}^{\gamma^{\prime}} \ln(\frac{a_{i}}{{a_{i}^{e}}}) \end{array} $$

(1b)

$$\begin{array}{@{}rcl@{}} \Delta G_{el} &=& 8 \mu^{\gamma} \frac{1+\nu}{1-\nu} (\frac{l^{\gamma}-l^{\gamma^{\prime}}}{l^{\gamma}+l^{\gamma^{\prime}}})^{2} \end{array} $$

(1c)

Rg is the gas constant; T _p is the processing temperature; $V_{M}^{\gamma ^{\prime }}$ is the molar volume of γ ^′. $\bar {X}_{i}^{\gamma ^{\prime }}$ and ${a_{i}^{e}}$ are the solubility and the thermodynamic activity of element i in γ ^′ phase at equilibrium state at processing temperature. a _i is the thermodynamic activity of the element i. According to Thomas et al., the Poisson ratio, ν, was set to 1/3 [89]. μ ^γ is the shear modulus of γ phase. $l^{\gamma ^{\prime }}$ and l ^γ are the lattice parameters of γ ^′ and γ, respectively, which are calculated from the molar volumes, $V_{M}^{\gamma }$ and $V_{M}^{\gamma ^{\prime }}$, obtained from TCNI6 database: $l=(\frac {4 V_{M}}{N_{A}})^{1/3}$. N _A is Avogadro’s number. Frost et al. proposed a temperature dependent formula based on experimental observations to approximate the shear modulus of the γ phase [33, 89]:

$$ \mu^{\gamma} = \mu^{\gamma}_{0} \left( 1-0.5\frac{T-300}{T_{M}} \right) $$

(2)

$\mu ^{\gamma }_{0}$ is adopted as 112 GPa [30] and 1673 K was chosen as an average melting temperature T _M [33]. The effects from alloy composition are not included in this model.

Table 1 The alloy composition and model parameters used in kinetic simulation: E _int and N ₀ are determined by data fitting; $\protect |\Delta H^{\gamma - \gamma ^{\prime }}|$ and α _int are the calculated values

According to the classic homogeneous nucleation model, the number density of the γ ^′ particles is $N_{t} =\int \dot {J} dt$. $\dot {J}$ is the nucleation rate which can be estimated using [76]:

$$ \dot{J} = Z \beta N_{0} \exp\left( \frac{-\Delta G^{*}}{k_{B} T_{p}} \right) \exp\left( \frac{-t_{incu}}{t} \right) $$

(3)

Z and β are Zeldovich factor and the attachment rate of solute atoms to γ ^′. N ₀ is the number density of initial nucleation sites. t _incu = t ₀/(Z ² β) is the incubation time [76, 94] and t ₀ is the adjustable parameter which is adopted as 1.5 in this work. t is the processing duration. k _B is the Boltzmann constant. $N_{0} \exp \left (\frac {-\Delta G^{*}}{k_{B} T_{p}} \right )$ describes the initial number density distribution as function of the Gibbs energy. ΔG ^∗ is the activation energy for forming a critical γ ^′ nucleus [94]:

$$ \Delta G^{*} = \frac{16 \pi}{3} \frac{E^{3}_{int}}{\Delta G_{nu}^{2}} $$

(4)

E _int is the interfacial energy between γ and γ ^′. The parameters N ₀ and E _int will be assessed later.

Zeldovich factor and the attachment rate of solute atoms to γ ^′ are obtained from [1, 5, 24]:

$$\begin{array}{@{}rcl@{}} Z &=& \frac{V_{M}^{\gamma^{\prime}}}{2 \pi N_{A} {R^{*}}^{2} } \sqrt{\frac{E_{int}}{k_{B} T_{p}}} \end{array} $$

(5a)

$$\begin{array}{@{}rcl@{}} \beta &=& \frac{4 \pi {R^{*}}^{2}}{(l^{\gamma^{\prime}})^{4}} \left[ \sum \frac{(\bar{X}_{i}^{\gamma^{\prime}}-\bar{X}_{i}^{\gamma})^{2}}{\bar{X}_{i}^{\gamma} D_{i}^{\gamma}} \right]^{-1} \end{array} $$

(5b)

$\bar {X}_{i}^{\gamma }$ and $\bar {X}_{i}^{\gamma ^{\prime }}$ are the equilibrium composition of element i of the γ and γ ^′ phases. $D_{i}^{\gamma }$ is the chemical diffusion coefficient of element i in γ which is calculated using Thermo-Calc with TCNI6 and NIST Ni-mobility databases [10, 11].

The critical nucleus size (R ^∗) can be calculated using [94]:

$$ R^{*} = - \frac{2 E_{int}}{ \Delta G_{nu} } $$

(6)

Growth

The γ ^′ precipitates continue to grow, due to the supersaturation of the γ phase. The radius, $R_{t}^{\gamma ^{\prime }}$, of the growing γ ^′ phase can be modeled using a diffusion controlled approach [14]:

$$ \frac{dR_{t}^{\gamma^{\prime}}}{dt} = \frac{D_{i}^{\gamma}}{\xi_{i,t} R_{t}^{\gamma^{\prime}}} \frac{X_{i,t}^{\gamma} - \bar{X}^{\gamma}_{i}}{\bar{X}^{\gamma^{\prime}}_{i}-\bar{X}^{\gamma}_{i}} $$

(7)

Assuming that the γ ^′ phase has an equilibrium composition $\bar {X}^{\gamma ^{\prime }}_{i}$, the growth of the precipitates is dominated by the chemistry of the remaining γ with the supersaturated composition $X_{i,t}^{\gamma }$. $\xi _{i,t} R_{t}^{\gamma ^{\prime }}$ describes the effective diffusion distance from γ/γ ^′ interface and is calculated using the mass balance equation ($X_{i,t}^{\gamma } = (X_{i,0}^{\gamma } - V_{f}^{\gamma ^{\prime }}\bar {X}^{\gamma ^{\prime }}_{i})/(1-V_{f}^{\gamma ^{\prime }})$ [5]) and the mean field approximation based on the volume fraction of γ ^′. The parameter ξ _i,t is calculated using the analytic solution of the diffusion equation in spherical coordinates [14]:

$$ \xi_{i,t} = 1 - \lambda_{i,t}{\pi} \exp(\lambda_{i,t}^{2}) \text{erfc}(\lambda_{i,t}) = \frac{1}{2 \lambda_{i,t}^{2}} \frac{X_{i,t}^{\gamma} - \bar{X}^{\gamma}_{i}}{\bar{X}^{\gamma^{\prime}}_{i}-\bar{X}^{\gamma}_{i}} $$

(8)

λ _i,t is a numerical parameter that can be obtained by the solution of the function: [14, 74].

$$ 2\lambda_{i,t}^{2} - 2\lambda_{i,t}^{3} \sqrt{\pi}exp(\lambda_{i,t}^{2})erfc(\lambda_{i,t}) = \frac{X_{i,t}^{\gamma} - \bar{X}^{\gamma}_{i}}{\bar{X}^{\gamma^{\prime}}_{i}-\bar{X}^{\gamma}_{i}} $$

(9)

Coarsening

Once the composition is fully partitioned, the γ ^′ growth mechanism transforms from a growth to a coarsening process. Perez et al. used a growth equation and linearized form of the Gibbs-Thomson effect to predict the coarsening rate [66]:

$$ \frac{d R_{t}^{\gamma^{\prime}}}{dt} = \frac{8}{27} \frac{E_{int} V_{at}^{\gamma^{\prime}}}{(R^{\gamma^{\prime}})^{2} k_{B} T} \frac{D_{i}^{\gamma} \bar{X}_{i}^{\gamma}}{\bar{X}_{i}^{\gamma^{\prime}} - \bar{X}_{i}^{\gamma}} $$

(10)

$V_{at}^{\gamma ^{\prime }} = \frac {V_{M}^{\gamma ^{\prime }}}{N_{A}}$ is the mean atomic volume of γ ^′.

Parameter Assessment for γ ^′ Precipitation Model in Ni-Al-Cr System

In this example design for an Ni-Al-Cr system, the interfacial energy E _int and initial number density N ₀ are the two remaining parameters that depend on composition and processing conditions. These two parameters are determined using a regression analysis of available experimental data for number density, mean radius of γ ^′ particles, and volume fraction [6, 7, 84]. For Ni-Al-Cr, there are three available data sets that are listed in Table 1 and the digital data is stored in the MDCS. For each alloy composition, the γ ^′ precipitation is simulated and the predicted number density, mean radius, and volume fraction of γ ^′ as a functions of time are compared to the experimental results. The precipitate radius can be correlated to the number density at each numerical time step by the size distribution function [1, 14].

The computed number density at each time step is used to calculate the mean radius of γ ^′ ($\bar {R}^{\gamma ^{\prime }}_{t}$) as the nucleation and growth continue along with the processing time. The volume fraction of γ ^′ (Vf,tγ ^′) is calculated from the area of this size distribution function:

$$\begin{array}{@{}rcl@{}} \bar{R}^{\gamma^{\prime}}_{t} &=& \frac{\sum N_{t} R_{t}^{\gamma^{\prime}}}{\sum N_{t}} \end{array} $$

(11a)

$$\begin{array}{@{}rcl@{}} V_{f,t}^{\gamma^{\prime}} &=& \sum N_{t} \frac{4 \pi (R_{t}^{\gamma^{\prime}})^{3}}{3} \end{array} $$

(11b)

The growth process finishes when the volume fraction and composition of γ ^′ reach the equilibrium values and coarsening begins as modeled by Eq. 10. The number density of particles decreases with increasing γ ^′ radius. Figures 4a and b shows that the predicted number density and mean radius of γ ^′ for the Kt1 sample are close to the experimental results. However, in Fig. 4c, the differences of the volume fractions for these samples are significant. This may be because the size distribution as number density function does not follow the classic nucleation model, or other experimental difficulties. The investigation of the reasons is beyond the scope of the present work. For the Kt2 and Kt3 samples, the equilibrium volume fractions ($\bar {V}_{f}^{\gamma ^{\prime }}$) predicted with the present model agree within about 2 to 5% of the reported experimental values (Fig. 4c). This results in differences in number density and mean radius of γ ^′ , especially for Kt2 sample, compared to the experimental results in Fig. 4a and b.

Fig. 4

Kinetic modeling of Ni-Al-Cr ternary alloys a number density, b average radius, c volume fraction of γ ^′; the points are the experimental results from [6, 7, 84] and the dotted lines are the equilibrium Vfγ ^′ from TCNI6

E _int is determined by the chemical composition and processing temperature and can be modeled as a function of a geometric parameter, α _int , and enthalpy difference between the γ and γ ^′ phases at the interface ($\Delta H^{\gamma - \gamma ^{\prime }}$) [53, 62]. α _int is the ratio of the atomic bonds across the interface to the total number of the atomic bonds of the interface atoms. In this work, we propose α _int as a linear function of the processing temperature. The best agreement with the values of E _int in Table 1, is obtained by:

$$\begin{array}{@{}rcl@{}} E_{int} =\alpha_{int} \cdot |\Delta H^{\gamma - \gamma^{\prime}}| = (3.75 \times 10^{-2} T_{p} - 2.23)\\\times 10^{-6} \cdot |\Delta H^{\gamma - \gamma^{\prime}}| \end{array} $$

(12)

For the present work, it is assumed that the composition dependence of E _int is represented by $|\Delta H^{\gamma - \gamma ^{\prime }}|$. The initial number density of particles is the other adjustable parameter for the phase transformation modeling and is related to the initial microstructure. In this work, we adopt a constant value of N ₀ = 4.0 × 10²⁶ according to the Kt3 sample in Table 1. Ideally a constant value should only be assumed when alloy preparations are the same to ensure similar microstructures.

The two model parameters, E _int and N ₀, are composition and processing history dependent and need to be re-adjusted for new alloy compositions and processing histories. To apply these phase transformation models for material design, i.e., new composition and processing domains, the ability to predict these parameters is needed.

Yield Stress

During tempering, γ ^′ precipitation occurs as described in the “ γ ^′ Precipitation” section. To optimize the strength of the alloy, the optimum tempering conditions must be determined. The strengthening contributions from dislocation shearing or bowing around the γ ^′ precipitates are modeled taking the microstructure and chemistry of the alloy into account. For these models, the volume fraction and mean radius of γ ^′ (Vfγ ^′ and $\bar {R}^{\gamma ^{\prime }}$) are the needed microstructure parameters [49, 54, 93] and the anti-phase boundary energy (E _APB ) is an important chemical parameter that determines whether a weak or strong dislocation coupling effect dominates over the dislocations shearing effect [19, 20, 22]. The models for additional strengthening mechanisms, such as solid solution strengthening and Hall-Petch effect, have also been implemented based on the statistical analyses [49, 73]. Using these strengthening models, the processing conditions (processing temperature and time) are chosen to maximize the yield strength of the microstructure [3, 41, 91].

Once the essential properties of precipitation process are determined, the yield stress (σ _ys ) is calculated. Stress, σ, is described as a sum of contributions from lattice friction, σ ₀, solid solute stress from the matrix phase, σ _SS , grain boundary effect, σ _GB , dislocation strengthening, σ _dis , and precipitation hardening stress, σ _p [72]: (the unit is MPa)

$$ \sigma = \sigma_{0} + \sigma_{SS} + \sigma_{GB} + \sqrt{\sigma^{2}_{dis} + {\sigma^{2}_{p}}}. $$

(13)

According to Thompson [90], the value of the contribution from the lattice friction (σ ₀) can be set to 21.8 MPa for Ni-based alloys. Except for the precipitation hardening stress, the contributions from the other mechanisms can be approximated using the chemical composition of the matrix phase, the grain diameter, d ^γ, and the initial dislocation density in the γ phase, $\rho _{0}^{\gamma }$, [2, 57, 60, 72, 73, 82]:

$$\begin{array}{@{}rcl@{}} \sigma_{SS} &=& \left( 50625 X_{Al,t}^{\gamma} + 113569 X_{Cr,t}^{\gamma} \right)^{1/2} \end{array} $$

(14a)

$$\begin{array}{@{}rcl@{}} \sigma_{GB} &=&\frac{\mu^{\gamma} b}{d^{\gamma}} n^{*} [1-\exp(-\frac{{\Lambda}_{SP} \varepsilon}{b n^{*}})] \end{array} $$

(14b)

$$\begin{array}{@{}rcl@{}} \sigma_{dis} &=& 0.25 \mu^{\gamma} b \sqrt{\rho_{0}^{\gamma}} \end{array} $$

(14c)

where μ ^γ is the shear modulus (2). b is the magnitude of the Burger’s vector which is $l^{\gamma }/\sqrt {2}$ [19]. Λ _SP = 0.15 μm is the average distance between slip planes [52, 72]; ε is the applied strain. n ^∗ is the critical number of dislocations piling up at the grain boundary and is set to be 4 for FCC phase [72]. Grain size and initial dislocation density are process history dependent parameters and are selected as typical values 10 μm and 10¹³ 1/m² for Ni-based alloys in this work. The factors in Eq. 14a were proposed by Mishima et al. which were obtained by the regression analyses of the compressive 0.2% flow stresses of the binary Ni alloys with 0 to 0.08 Al or 0 to 0.08 Cr at 77 K [60]. Although the temperature effect on solid solution strengthening is not included, this model has been successfully applied in different composition and temperature domains [2, 9, 49].

Depending on size, volume fraction, and chemistry of γ ^′, the precipitation hardening stress, σ _p , is determined by different effects: weak (σ _wc ), strong (σ _sc ) dislocation coupling and dislocation bowing between the particles (Orowan’s bowing) (σ _or ) [19, 20, 49, 70]:

$$\begin{array}{@{}rcl@{}} \sigma_{wc} &=& M \frac{E_{APB}}{2b} \left[ \left( \frac{1.91 \bar{R}^{\gamma^{\prime}} E_{APB} V_{f}^{\gamma^{\prime}} }{L_{T}} \right)^{0.5} - V_{f}^{\gamma^{\prime}} \right] \end{array} $$

(15a)

$$\begin{array}{@{}rcl@{}} \sigma_{sc} &=& 0.22 M \frac{\mu^{\gamma} b}{\bar{R}^{\gamma^{\prime}}} \left( \frac{ \pi \bar{R}^{\gamma^{\prime}} E_{APB} V_{f}^{\gamma^{\prime}}}{L_{T}} - V_{f}^{\gamma^{\prime}} \right)^{0.5} \end{array} $$

(15b)

$$\begin{array}{@{}rcl@{}} \sigma_{or} &=& M \frac{\mu^{\gamma} b}{\bar{R}^{\gamma^{\prime}}} \left( \frac{V_{f}^{\gamma^{\prime}}}{\pi}\right)^{0.5} \end{array} $$

(15c)

where M is the Taylor factor and is adopted as 3 [73]; E _APB represents the anti-phase boundary energy. $\bar {R}^{\gamma ^{\prime }}$ and $V_f^{\gamma ^{\prime }}$ are the mean radius and volume fraction of γ ^′. L _T = μ ^γ b ²/2 is the line tension of a dislocation [19].

As the mean radius and volume fraction of γ ^′ increase, the precipitation hardening stress increases after a short processing period and is dominated by the weak dislocation coupling effect. With increasing heat treatment time, the precipitation hardening mechanism changes from a size effect to a composition dependent effect. The competition between larger γ ^′ diameter and anti-phase boundary energy causes the dislocation shearing mechanism to switch from weak dislocation coupling to a lower shearing-stress barrier path that is the strong dislocation coupling effect. As the γ ^′ diameter grows, the strong dislocation coupling stress decreases, as well as the precipitation hardening stress. As the processing time increases, γ ^′ particles become too large to be cut through by dislocations and Orowan’s effect dominates. Therefore, the effective precipitation hardening stress follows the minimum stress path among these three mechanisms [19]. The critical transition point from weak to strong dislocation coupling mechanism is considered as the maximum precipitation hardening stress that can be determined by the competition of size effect ($\bar {R}^{\gamma ^{\prime }}$) and material chemistry (E _APB in [1 1 1] plane). E _APB can be calculated under a single particle, equilibrium assumption: [20, 59]:

$$\begin{array}{@{}rcl@{}} E_{APB,[1 1 1]} &=& \frac{W_{1} - 3W_{2} + 4W_{3}}{\sqrt{3} (l^{\gamma^{\prime}})^{2}} \end{array} $$

(16a)

$$\begin{array}{@{}rcl@{}} W_{1} &=& 0.75 W_{13} \end{array} $$

(16b)

$$\begin{array}{@{}rcl@{}} W_{3} &=& 0.125 W_{13} \end{array} $$

(16c)

$$\begin{array}{@{}rcl@{}} W_{13} &=& \frac{ 3 \Delta H_{eff}^{\gamma} + \Delta H^{ord} \frac{1-\bar{X}_{s}^{\gamma^{\prime}}}{\bar{X}_{s}^{\gamma^{\prime}}} }{24 N_{A} \bar{X}_{s}^{\gamma^{\prime}} \left( 1-\bar{X}_{s}^{\gamma^{\prime}} \right)} \end{array} $$

(16d)

$$\begin{array}{@{}rcl@{}} W_{2} &=& \frac{\Delta H^{ord} \left( 1-\bar{X}_{s}^{\gamma^{\prime}} \right) - \Delta H_{eff}^{\gamma} \bar{X}_{s}^{\gamma^{\prime}} }{12 N_{A} (\bar{X}_{s}^{\gamma^{\prime}})^{2} \left( 1-\bar{X}_{s}^{\gamma^{\prime}} \right) } \end{array} $$

(16e)

where $l^{\gamma ^{\prime }}$ is the lattice parameter of $\gamma ^{\prime }$; W ₁, W ₂, and W ₃ are the bounding energies between center atom and first, second and third nearest neighbours. $\Delta H_{eff}^{\gamma } = \Delta H^{\gamma }/1.1$ is the disordered enthalpy with considering 10% short range ordering effect [59] and $\Delta H^{ord}=\Delta H^{\gamma ^{\prime }}-\Delta H_{eff}^{\gamma }$ is the enthalpy of ordering. $\bar {X}_{s}^{\gamma ^{\prime }} = \bar {X}_{Al}^{\gamma ^{\prime }} + \bar {X}_{Cr}^{\gamma ^{\prime }}$ is the total solubility of γ ^′ at service temperature.

To test the Eq. 16a16 with the TCNi6 database, the APB energy of binary Ni-Al alloys is calculated for service temperature ranging from 473 to 1073 K and the results are presented in Fig. 5. Each open circle is a randomly selected condition where $\bar {X}_{Al}^{\gamma ^{\prime }}$ is the result of the equilibrium calculation while the overall composition X _Al is set to be in the range of 0.09–0.25 and T _p is from 473 K to 1473 K. The other thermochemical properties ($\Delta H^{\gamma }$ and $\Delta H^{\gamma ^{\prime }}$) and the lattice parameter of γ at service temperature are calculated using TCNI6 database. The calculated APB energy is in the range from 0.188 to 0.218 Jm⁻² for the selected domain. Figure 5 shows that the APB energy is higher at lower service temperature and higher Al content in γ ^′ which agrees with the trend reported in [19, 20]. The same model is applied for the Ni-Al-Cr ternary in the domain of X _Al = 0.1 to 0.25, X _Cr = 0.05 to 0.25, T _p = 673 to 1273 K, and T _s = 473 to 1073 K, E _APB of 293 randomly selected samples are calculated and stored in MDCS. The values of E _APB are in the range of 0.06 to 0.18 Jm⁻².

Fig. 5

The calculated E _APB at various T _s ; the open circles are the calculated alloys

Elastic Deformation

The materials knowledge systems (MKS) package is used to determine the elastic deformation with inputs from the yield stress predictions. MKS is a statistical tool using a response variable of the local material state to estimate the local phase or stress status of the microstructure in an applied thermal or strain field [28, 29, 46]. MKS provides efficient calculations to simulate the elastic deformation of the microstructure. The local response variables are obtained from a regression process using the results from a finite element method. In this work, we use the Python version of MKS (PyMKS) to simulate the elastic deformation of the alloy [97]. Finite element calculations using SfePy software [17] are carried out to generate the reference data for PyMKS. The model training in PyMKS is conducted using simple geometries, which are so-called delta microstructures. SfePy calculates the elastic stress of the delta microstructure and PyMKS assessed the model parameters using two-point statistics. With PyMKS, the model can then be applied to more complicated geometries.

The model parameters used by PyMKS are the shear modulus (μ) and Poisson ratio (ν), and the volume fraction of γ ^′, which is taken from the precipitation calculation described in the “ γ ^′ Precipitation” section. The shear moduli are calculated by Eq. 2 where μ ₀ is adopted as 112 GPa for γ and 108 GPa for γ ^′ for Ni-based alloys [30]. In this work, Eq. 2 treats the shear moduli for γ and γ ^′ as constants independent of alloy composition at the same service temperature. Ideally, these two parameters should be composition dependent. Based on these assumptions, Fig. 6a depicts the representative volume element (RVE) at 300 K for the PyMKS calculation. The black and white areas represent 90% γ and 10% γ ^′, respectively, in the two-dimensional 100 ×100 mesh domain. This microstructure is strained by 1% in the x direction at T _p = 1123 K. The periodic boundary condition is defined in y direction. Figure 6b is the elastic stress field obtained from PyMKS. Some modeling errors can be seen as light dots at the interface but are minor in comparison to the overall response as shown in Fig. 7. In this figure, Young’s modulus (Y) calculated by PyMKS is compared to the one calculated by SfePy using the same conditions. These calculations were performed for 16 microstructures with different volume fractions of γ ^′ ranging from 5 to 80%. The Young’s modulus is controlled by the average stress and applied elastic strain. These estimates using the MKS method are compared to finite element (FEM) simulations with the same conditions using SfePy. The results of MKS and FEM are compared in Fig. 7. It shows small differences of Young’s moduli between these two computational methods but SfePy and PyMKS take 22 and 1 s, respectively, in average to finish one calculation. In this work, we adopt μ as the function of service temperature and γ ^′ volume fraction is obtained from the precipitation simulations.

Fig. 6

a The physical model of Vfγ ^′ = 10% (white) in γ (black) used to calculate Young’s modulus. b The calculated elastic stress field created by 1% strain using PyMKS

Fig. 7

The comparison between calculated Young’s modulus (Y) from PyMKS (Y _PyMKS ) to SfePy (Y _SfePy )

Plastic Deformation

After yield strength prediction and PyMKS modeling to find the elastic limit, the plastic deformation is simulated to complete the stress-strain curve. Different approaches are available to model the plastic deformation. The constitutive models to simulate the plastic deformation, such as the power law [36, 37, 96, 100] and hyperbolic sine law [56, 95, 99], require model parameters that capture the strain hardening behavior of the alloy. After fitting the experimental data, the effects from material chemistry, geometry, and testing conditions are no longer distinguished by the model parameters, and, therefore, the trained models can only be used under specific conditions. Other constitutive models include more physical phenomena and provide generic, high-quality results compared to the experiments [15, 26, 45, 47] and require the assessments of the model parameters. The finite element method (FEM) provides an even higher level of accuracy but is computationally more expensive and is commonly not used within an integrated computational design framework [16, 32, 48, 51, 61, 92, 101]. As shown in Fig. 3, we adopt the constitutive model with irreversible thermodynamics model to simulate the plastic deformation of the alloy.

During plastic deformation, the applied mechanical work increases the dislocation density and raises the entropy, S, of the alloy. Considering the energy for dislocation kinetics (dE) and the heat dissipation (dQ) in the testing environment, the energy conservation can be formulated as follows:

$$ dE + dQ = TdS $$

(17)

where dE can be calculated from the total energy for dislocation generation (dW _ge ), glide (dW _gl ), and annihilation (dW _an ). dQ can be estimated from the variation of the internal energy (dU) and the input of the mechanical work (dW). These quantities are described by the following relationships [38, 39, 72]:

$$\begin{array}{@{}rcl@{}} dE &=& dW_{ge} + dW_{gl} + dW_{an} = \frac{1}{2} \mu b^{2} d\rho^{+} \\ &&+ \tau b {\Lambda}_{MFP} d\rho^{+} + \frac{1}{2} \mu b^{2} d\rho^{-} \end{array} $$

(18a)

$$\begin{array}{@{}rcl@{}} dQ &=& dU - dW = \frac{1}{2} \mu b^{2} d\rho - \tau_{dis} d\varepsilon \end{array} $$

(18b)

dρ ⁺ and dρ ⁻ are the generation and annihilation of the dislocation density, respectively. The variation of the dislocation density can be presented as dρ = dρ ⁺ − dρ ⁻. The mean free path of the dislocation motion is obtained from ${\Lambda }_{MFP}= (1/d^{\gamma } + \sqrt {\rho _{0}^{\gamma }})^{-1}$ [8, 27]. Huang et al. proposed that the increasing entropy is presented as a linear function of the shear stress: dS = [𝜃b/(TΛ _MFP )]dτ [38] with 𝜃 being a temperature dependent factor. Combining Eqs. 13 and 18 and using the relation τ = σ/M, the variation of the dislocation density, ρ _{ε + dε} , can be calculated [52]:

$$ \rho_{\varepsilon + d\varepsilon} \,=\, \rho_{\varepsilon} + \frac{(\mu^{\gamma} b^{2} + \tau b {\Lambda}_{MFP}) \frac{\omega}{\dot{\varepsilon}} \exp(-\frac{\Delta G_{\rho}}{k_{B} T}) \rho_{\varepsilon} \,-\, \tau_{dis} }{\frac{1}{8} \theta \mu b^{2} - (\mu b^{2} + \tau b {\Lambda}_{MFP} ) } \Delta \varepsilon $$

(19)

where Δε is the strain increment. ω = 10¹³ is the atomic vibration frequency [39]. $\dot {\varepsilon }$ is strain rate. ΔG _ρ is the energy barrier for the dislocation annihilation. The stress in Eqs. 13 and 14c is accordingly updated by the increasing strain steps. The calculation stops at necking, which occurs when Considère’s criterion, σ = dσ/dε, is fulfilled [83]. The work-to-necking is calculated as the area beneath the stress-strain curve.

The two remaining parameters, 𝜃 and ΔG _ρ , are temperature dependent and are fitted using the experimental stress-strain curves reported by Wu et al. [98] under the strain rate ($\dot {\varepsilon }$) of 1x10⁻³ s⁻¹. These parameters are listed together with the experimental yield points (σ _ys and ε _ys ) from Wu et al. in Table 2. Since no composition dependence needs to be fitted, the experimental values are preferred over the ones from Eq. 13 to prevent the error propagation through the models. By appropriately selecting 𝜃 and ΔG _ρ , the predicted strain hardening rates agree with the experimental results at 1123 and 1273 K, (Fig. 8). To efficiently determine these two parameters, we use a basin-hopping method [43] to minimize the data-prediction error. According to Huang et al. [38], these two parameters are linear functions of the processing temperature. Using the values listed in Table 2, they can be represented as 𝜃 = −0.0356T _p and ΔG _ρ = T _p /600 + 1.188 (eV). Figure 8 shows that the calculated stress-strain curves are in good agreement with the experiments.

Fig. 8

Predicted stress-strain curves at various temperatures; the points are the experimental results from [98]

Table 2 The test samples for plastic deformation model [98]; σ _ys and ε _ys are stress and strain at the yield point

Optimization by Genetic Algorithm

To optimize the design parameters presented in Fig. 1b using the models and data described in the “ γ ^′ Precipitation” section to “Plastic Deformation” section, a genetic algorithm is implemented. A GA is used as it enables random but directional iterative optimization of the design parameters [35]. It has been successfully applied in many material research related problems [13, 42, 58, 87]. Unlike the gradient-based or the other grid search algorithms, each GA process requires a significant number of iterations to converge but it is efficient for multi-objective, multi-dimensional optimizations [35, 75].

Before beginning with the optimization process, the boundaries of the stable two-phase (γ + γ ^′) field are established. Figure 9 shows the γ + γ ^′ regions at 973 and 1473 K and the corresponding boundaries for the design composition space are given in Table 3. Accordingly, the objective of the GA optimization is to search for the optimum X _Al , X _Cr and processing temperature within these ranges to maximize work-to-necking at T _s = 973 K. Individual values in these input ranges are assigned bits in the computer memory in the form of binary numbers. For instance, while 6 bits of memory are used for each variable, the input domain is discretized by a 2⁶ × 2⁶ × 2⁶ mesh and each mesh point is labeled by 18 digits of binary number.

Fig. 9

Phase diagram of Ni-Al-Cr calculated using Thermo-Calc with TCNI6 database at a 973 K and b 1473 K; the FCC_L12 (γ) and FCC_L12#2 (γ ^′), two phase field, is of interested in this work

Table 3 The data ranges used in GA optimization

The GA initially randomly selects 12 samples as the 1st generation and evaluates the resulting alloy samples following the computational steps described in Fig. 3. After the evaluation, this Python-based framework outputs the data and meta-data of each sample to a XML file which is then stored in MDCS using REST API. To continue the search process, only the two samples with highest work-to-necking are kept and the others are ignored, which is the so-called elimination. The reproduction operator duplicates these two samples five times to maintain the same number of the samples for each generation. The match operator and the crossover operator exchange the label numbers in the five new pairs of samples to create the next generation. The last applied operator before the next evaluation is a mutation that is designed to create the variance of the samples. More detailed information about the genetic algorithm can be found in the literature [18, 35, 81]. The crossover and mutation rates are minor as the γ + γ ^′ composition space as determined by the phase diagram is relatively small, and this improves the efficiency of the search. In this work, we apply single crossover by random selection of the label sections and the mutation rate is adopted as 1/(total memory size) (1/ 6 × 6 × 6) [18]. The converge rate is defined as 98%: once the binary label number of the top two samples are 98% identical, the generation is claimed as converged and the search is restarted by random selection for the next generation. Repeating these steps, the GA directs the search until the prescribed number of generations is reached. To optimize the three variables in this work, 12 samples in each generation of 30 generations were used for the search.

Results

Model Testing

Before using the GA to optimize the processing and composition variables, the properties of the two model alloys, listed in Table 4, are selected for the investigation of the correlation between alloy chemistry, processing conditions, and yield stress. At the initial precipitation stage of sample YS1, the high nucleation rate allows the transformation of a large number of small mean radius ($\bar {R}^{\gamma ^{\prime }}$) γ ^′ particles shown in Fig. 10a. As a result of the high number density of particles with a critical size that nucleate in a short time, the mean radius of γ ^′ particles decreases during the initial stage of the transformation. After a certain processing time t, γ ^′ grows and begins to coarsen. As shown in Fig. 10b, during growth and the early coarsening processes, the precipitation hardening stress is dominated by weak dislocation coupling effect, which increases with increasing γ ^′ mean radius and volume fraction. The solid solution stress decreases until thermochemical equilibrium is reached as a result of partitioning of the chemical composition from γ to γ ^′. The decrease of the solid solution stress and the increase of the weak-dislocation-coupling stress result in a smaller increase of the yield stress as seen in Fig. 10b. With the γ ^′ precipitate size increasing, the anti-phase boundary energy becomes more important and the strong dislocation coupling effect dominates. Orowan’s effect plays the key role for alloy YS1 after about 55 min of treatment at processing temperature, and the yield stress decreases with increasing γ ^′ mean radius as given by Eq. 15. In contrast, alloy YS2 shows that the microstructure has a large mean radius and low number density γ ^′ precipitates (Fig. 10c). Orowan’s effect is the main mechanism of precipitation hardening and the contribution from precipitation hardening to the yield stress is relatively low. Comparing YS1 and YS2, one finds that high nucleation and low growth rates are preferred to improve the yield stress.

Fig. 10

The predicted process-structure-yield stress correlations of γ ^′ transformation and σ of a, b YS1 and c, d YS2

Table 4 Predicted input parameters: E _int , E _APB , and Vfγ ^′ for the yield strength model for the two example alloys and the tempering temperature, T _p

Design Optimization Results

The GA is used to optimize the system for the highest work-to-necking (Fig. 1b) within the defined composition and processing space (X _Al , X _Cr , and T _p ). A GA search (Fig. 3) was performed three times producing a total 214 effective samples. The predicted properties of the samples are presented in Figs. 11, 12, and 13. The weak to strong dislocation coupling transition (Fig. 10b) is of interest to determine the processing time for maximizing the yield stress. For alloy YS1, the calculation shows that the maximum yield stress occurs during the coarsening of γ ^′. As given by Eq. 10, the size effect competes against the APB energy effect. This phenomenon is clearly seen in Fig. 11a, b. In the $V_f^{\gamma ^{\prime }}$-$\bar {R}^{\gamma ^{\prime }}$ plot, the alloys with higher volume fraction and smaller mean radius of γ ^′ posses higher precipitation hardening stress. As mentioned in the previous section, higher anti-phase boundary energy means that the γ ^′ particle has higher resistance to dislocation shearing which results in a higher precipitation hardening stress. Figure 11c presents the calculated precipitation hardening stress as function of the alloy composition and processing temperature. Alloys with different X _Al and X _Cr may have similar phase transformation behavior and anti-phase boundary energy and the trend of the precipitation hardening stress is not as clear in these two diagrams. In principle, as Fig. 5 shows, higher X _Al causes higher anti-phase boundary energy that results in higher precipitation hardening stress.

Fig. 11

The predicted precipitation stress σ _p a with the key microstructure parameters b in 3 Vfγ ^′ regions and the solid lines connect the maximum and minimum values of each region c in the domain of model input

Fig. 12

The predicted yield stress σ _ys in the domain of model input

Fig. 13

The predicted work-to-necking (E _WTN ) in the domain of model input

Figure 12 summarizes the predicted yield stress in the input domain while considering the other mechanistic properties (13). After the same processing history of the raw samples, the lattice friction, grain boundary, and dislocation-dislocation hardening stresses are independent from the alloy composition and processing temperature. According to Eq. 14b, the addition of 0.01 to 0.2 mole fraction Al and Cr increases solid solution stress by 22.5 to 100 MPa and 33.7 to 150 MPa, respectively.

The goal of the GA searches is to maximize the work-to-necking. The results of the GA are shown in Fig. 13 and the red points mark the preferred alloys for this example design. In this figure, work-to-necking ranges from 9.62 to 41.25 MPa. In Figs. 12 and 13, it can be seen that the more ductile alloy supports higher work-to-necking. Four selected samples, labeled Opt-H, Opt-M1, Opt-M2, and Opt-L in Fig. 13, of the examined alloys are listed in Table 5. These alloys possess work-to-necking as high (41.25 MPa), medium (∼25 MPa) and low (9.62 MPa) based on the different calculation input sets. Figure 14 shows the predicted volume fraction and mean radius of γ ^′ and yield stress as functions of the processing time. Among these alloys, γ ^′ fraction is lowest in Opt-H. It can also be seen that Opt-H has highest growth rate of the mean γ ^′ radius but lowest volume fraction transformation rate. In this case, γ ^′ transformation is controlled by the particle growth and the microstructure contains low number density of larger radius γ ^′ particles. The yield stress of Opt-H is determined by the transition from strong dislocation coupling to Orowan’s effects that results in better ductility of the alloy.

Fig. 14

The calculated a volume fraction of γ ^′ b mean radius of γ ^′ and (3) yield stress variations as function of processing time of the samples in Table 5

Table 5 The samples selected during the optimization: Opt-H as the highest E _WTN and Opt-L as the the lowest one among 214 samples

The phase transformation behaviors of Opt-M1 Opt-M2 and Opt-L are very similar: high nucleation rate dominates the precipitation process that results in high number density, small γ ^′ particles and higher yield stress. Comparing Opt-M1 to Opt-M2 shows that different alloy compositions and processing conditions can also lead to similar work-to-necking. Figure 14 shows that after different processing times at different temperatures, the combinations of volume fraction, mean precipitate radius, and anti-phase boundary energy result in similar maximum yield stresses as the peak values of Opt-M1 and Opt-M2 in Fig. 14c. Opt-L possesses highest maximum yield stress among these four alloys because it has the highest volume fraction, highest anti-phase boundary energy and smallest mean precipitate radius.

Using the microstructure information at the yield point as input to the mechanistic models, the stress-strain curves are calculated and presented in Fig. 15. The dotted lines are the strain hardening rate ($\frac {d \sigma }{{d \varepsilon }}$) and where they intersect the stress-strain curves (solid) are the necking points of the different alloys. The area beneath the stress-strain curve is the objective of the search, the work-to-necking. Fig. 15 also shows that the Young’s moduli are almost identical. The Young’s modulus is calculated using PyMKS with the input of γ ^′ volume fraction and the results indicate that the volume fraction of γ ^′ has a minor effect to the elastic deformation. To summarize the results in Fig. 11c, 12, and 13, a low yield stress, ductile alloy (OPT-H) is preferred for high work-to-necking alloy according to the models used in the present work.

Fig. 15

The predicted stress-strain curves of the four selected samples, as Table 5, from the optimization process; dash lines represent the strain hardening rates (dσ/dε)

Discussion of Model Assessment and Parameters

The four modules described above consist of general phase-based models which require composition-dependent, microstructure-dependent and adjustable parameters for this specific application. The employed parameters for each module are listed in Fig. 16. To adopt this framework, the sensitivity of the individual model to each parameter and error propagation through the workflow should be noted. Ideally, the model sensitivity is proposed to be examined and validated during the model development process using the data under broad conditions and focusing on a specific physical quantity. At a preliminary design stage, the piecewise information in the processing-structure-property relation is insufficient to validate the model sensitivity in a wide composition space. In this work, we assess the microstructure-dependent and adjustable parameters based on the literature data to suggest the potential alloy and processing temperature for next design iteration. In a real design effort, it can be expected that some of the model parameters will be updated using the results from validation experiments that need to be carried out after promising candidate designs are identified using the GA search. The successful model-validation processes can be used for the next design iteration [44, 64].

Fig. 16

a Parameter value origin and data flow in this framework: the physics-based parameters are calculated using CALPHAD method and physics-based models; empirical parameters are obtained from references; b the values of the adjustable parameters

During the optimization process, the composition-dependent parameters such as phase transition temperature, equilibrium phase composition, lattice parameters, diffusion coefficients, etc. are obtained using Thermo-Calc TC-API with TCNI6 and NIST Ni-mobility databases. These quantities can also be calculated using other databases. Figure 17a shows the equilibrium γ ^′ mole fractions of the Kt1 alloy in Table 1 which are calculated using different thermodynamic databases [25, 88]. It can be seen that the solvus temperature is 20 K lower using the database by Dupin et al. [25] and, therefore, the predicted processing window will be different as well. Figure 17b compares the equilibrium chemical compositions in γ ^′ calculated using these two databases. The errors are 2 to 5% which causes the uncertainties from lattice parameters to elastic energy, chemical driving force and phase transformation kinetics. The CALPHAD method uses a thermodynamic and a mobility database to calculate the diffusion matrix and it can be expected that the diffusion matrix will be different at the same processing temperature and re-assessment of the adjustable parameters may be necessary. However, Campbell et al. found that the effect from using different high-quality thermodynamics databases on the diffusion matrix is within the experimental error citecampbell2002development. Olson et al. found that the effect of uncertainties in the molar volume are acceptable within current model uncertainties [64].

Fig. 17

Comparison of results from calculations using the TCNI6 and Dupin [25] thermodynamic databases: a the mole fraction of γ ^′ b the chemical composition in γ ^′

To test the sensitivity of the framework, the diffusion coefficients are manually changed by ± 20% to repeat the calculation for the Kt1 alloy in Fig. 4. The changes in the phase transformation rates have minor effect on the estimate of the γ ^′ volume fraction compared to the experimental uncertainty in Fig. 18a but result in a ± 10⁵ min processing time to maximize the yield stress. Because the maximum yield stresses are identical (as Fig. 18b), the stress-strain curves for all three cases completely overlap in Fig. 18c. This indicates, as one would expect, that the uncertainty in diffusion coefficients has an effect on the selection of the processing time but not the predicted alloy properties.

Fig. 18

Effect of diffusion coefficients changed by ± 20 % on a average γ ^′ radius, b yield stress, and c stress-strain curve

Other composition-dependent parameters are the energy barrier for dislocation annihilation, ΔG _ρ , and the temperature dependent factor, 𝜃, which are determined for the conditions given by the base element, strain rate and service temperature [38, 72]. For Ni-based alloys, undergoing the same strain rate testing, these two can be treated as service temperature dependent parameters as recommended in the previous section. The microstructure-dependent parameters are determined by the processing history (thermal and mechanical processes). For example, the initial number density of nucleation sites is highly related to the morphology, grain size and shape. This parameter needs to be adjusted for different processing histories, however, as the alloys in the present work are treated by similar pre-processing steps, it is acceptable to use the same value of N ₀ in all the calculations. The atomic bond ratio, α _int , is an indirect but important parameter for extropolating the interfacial energy, E _int , into a broader composition domain. α _int is determined by E _int and $\Delta H^{\gamma - \gamma ^{\prime }}$ which are obtained by the best fit to the experimental number density and CALPHAD calculation. The α _int may need to be re-assessed if different pre-processing steps are used that result in different initial microstructures, dislocation density, etc. or a different thermodynamic databases is used. Since the same thermodynamic database and the same initial conditions are used in the present work, α _int needs to be assessed only once. The remaining model parameters, grain diameter, d ^γ, and initial dislocation density, $\rho _{0}^{\gamma }$, are assigned as physically reasonable constants, 10 μm and 10¹³ 1/m², because of the lack of data or models for predicting these quantities. To validate these models with the assessed parameters requires extensive processing-structure-property data from a consistent experimental environment. As mentioned in the previous paragraph, the model refinements are expected to be carried out in the next design iteration while this framework narrows the composition space by decreasing the γ + γ ^′ phase region.

Summary

A modular python-based framework has been developed that integrates the computational models for desired processing-structure-property correlations as an initial step of the material design process. The goal of the present work is to demonstrate that a modeling chain can be developed and implemented with a GA to identify the potential region in a composition space that satisfies the design requirements based on the selected models and data. The present framework is developed to accommodate the modularized codes that are programmed in various languages. The smooth data flow within this framework supports a plug and play feature that allows switching of individual models for different design objectives.

We selected the Ni-Al-Cr ternary system and work-to-necking as the only design target to demonstrate the design process using this framework. In the present work, the computational models are used to identify the chemical composition and processing conditions in a domain with three variables. The training of these models is conducted individually using published results to avoid error propagation through the simulation process. The simulation process is started using pre-selected compositions and processing temperature regime. A GA performs a search for better performance alloys using the results from the integrated models. The reliability of the search results depends on the generality of the models for a wider input domain and the quality of the data used for model training.

The approach presented here can be expanded to multicomponent systems by including the additional elements from databases and re-assessing the model parameters following the “Discussion of Model Assessment and Parameters” section. The objective/utility function for the GA to evaluate the samples could also be revised for different target performance. Based on similar PSP relations, this framework could also be applied to precipitation hardened alloys such as Co-based superalloys or stainless steels. Also, other design objectives such as the castability, alloy density, and grain coarsening, could be considered by adding additional models to the framework. Therefore, a full alloy design project may require a more sophisticated design optimization strategy to complete the PSP relations. As mentioned, this Python environment easily accommodates user implemented modules and the data can be transmitted straightforwardly through the MDCS. This data-enabled design framework can also be applied to other material systems by switching to other user selected PSP relations. Programming-language friendly features and the potential for automatic parameter assessment, support the future expansion of the design framework. The general concept of the present framework can be extended for the design of novel commercial alloys by employing models with predictive capabilities.