1 Introduction and Background

Longitudinally stiffened plates have been widely used since they are an effective system for axially compressed members. Previous studies on flat panels (Choi et al. 2015; Choi 2013; Choi and Choi 2012) have demonstrated that the local buckling strength could substantially increase along with the rotational stiffness of the closed-section ribs and an approximate solution which reflects the increasing effects was suggested. Meanwhile, steel curved panels have also been in demand for various facilities and large structures such as bridges, buildings, plants and storage facilities, some of the cases might be stiffened by closed-section ribs. However, their design have been conservatively made without reflecting the increasing effect as there have only been few studies as well as an absence of suitable design guides or specifications in regards to the buckling behavior of longitudinally stiffened curved panels.

Since there is a considerable effect which leads to an improvement in compressive strength, thus, it is desirable that the increasing effects or approach proven in the flat plates should be examined and utilized on curved panel. In doing so, geometric differences due to curvature have to be examined closely since the primary difference between a curved panel and a flat plate is that the former has a curvature in the unstressed state, whereas the latter is assumed to be initially flat. Tran et al. (2012) presented on their work equations for the elastic buckling stress of curved panels which was developed in a manner similar to the buckling stress of flat plate, since the use of curved panels are becoming more popular, but there is a lack of specifications and related literature regarding the plate buckling theory are more abundant compared to the buckling theory of curved panels.

The study introduced the buckling coefficient considering the radius of curvature (\(k_{c}^{z}\)) developed by various researchers which quantify the influence of curvature and reflects the difference between the flat and curved panel. The expressions developed by Redshaw (1933) and Timoshenko and Gere (1961) relied on the assumption that for curved panels like for full revolution cylinders, the ultimate load is equal to the critical buckling load, while Stowell (1943) used it in his proposition of a modified form of Redshaw’s expression.

An assumption is made (Stowell 1943) that the critical stress \(\left( {F_{cr} } \right)\) of the curved panel may be expressed in a manner similar to the critical stress of flat plate and factored by \(k_{c}^{z}\) to properly apply the geometric difference, and the formula for the critical compressive stress was derived using the theory of small deflections and the differential equation of the deflection of the panel was given by the Donnell equation. Redshaw (1933) has proposed an approximate formula derived by an energy method without limitations as to curvature for simply supported edges which has a form similar to Stowell’s. His developed expression applied the classical energy approach, while Stowell proposed a modification of Redshaw’s equation to better take into account the boundary condition. Timoshenko and Gere (1961), on the other hand, made an assumption on the form of the displacements so that they satisfy the boundary conditions. He obtained the critical load by substituting the displacement expressions into the equilibrium equations and looked for a value which nullifies the determinants of these equations. Meanwhile, Domb and Leigh’s (2001) expression was calibrated on a numerical database by some curve fitting method. Their work presents the implementation of a nonlinear finite element technique for the prediction of the initial buckling in simply supported curved panels subjected to pure compression.

In this paper, the buckling behaviors of partially restrained curved panels by longitudinally installing closed-section ribs were investigated thoroughly under the loading condition of uniaxial compression. Then, approximate solutions have been suggested in this study for the elastic buckling strength of partially restrained curved panels, which were simply derived from previous studies by reflecting the influential factors to rationally quantify a reinforcing effect due to the rotational stiffness and the influence of curvature, respectively.

Comparative study and trend analysis along several design parameters was conducted to verify the validity and accuracy of the proposed equations by evaluating the correlation of these formulas with the numerical analysis. Through such manner, the approximate equation that can reasonably estimate the elastic buckling strength of curved panel can be identified. Moreover, finite element analyses along with several design parameters were conducted and the influential parameters on the buckling stresses and mode shapes are examined. The correlation of these influential parameters with the suggested equations and numerical analysis was determined. The parametric study also reveals which parameters are affecting the buckling stress and mode shapes significantly. Consequently, this study is to investigate the variation of elastic buckling stresses of longitudinally stiffened curved panels according to the rotational stiffness of the closed-section ribs as well as the effect of the curvature of the panel based on the suggested theoretical approaches and validate the application of these proposed equations.

2 Theoretical Studies

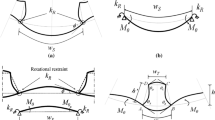
The local buckling mode shape of curved panels elastically restrained by closed-section ribs along both sides is likely to be anticipated as shown in Fig. 1, which is proven through the finite element analysis results in Sect. 4. It is obvious that there is a reinforcing effect existing due to the rotational stiffness of the closed-section ribs during the local buckling of panels. In addition, a geometric effect is necessarily probable to the buckling strength from the originally curved shape of the panels.

Fig. 1
figure 1

Rotationally restrained curved panel model: a buckling behavior of curved panel stiffened by closed-section ribs, b curved panel with elastic restraints, and c rotational restraint stiffness attributable to stiffening by closed-section stiffener

Full size image

Thus, it is rational that the local buckling strength of curved panels longitudinally stiffened with closed-section ribs should consist of the strength increment factor \(\left( {\varPhi \left( {k_{R} } \right)} \right)\) by a reinforcing effect due to the rotational stiffness and the buckling coefficient considering the radius of curvature \(\left( {k_{c}^{z} } \right)\).

From here, the local buckling strength of an elastically restrained curved panel with closed-section ribs is developed by considering \(\varPhi \left( {k_{R} } \right)\). This quantitatively shows the increasing effect of the buckling strength with respect to the rotational stiffness against the rotational displacement \(\left( \phi \right)\), shown in Fig. 1a.

The local buckling of an elastically restrained flat plate was presented in the research study of Choi et al. (2015) and is expressed as:

$$F_{cr} = \varPhi \left( {k_{R} } \right)\frac{{4D\pi^{2} }}{{W_{S}^{2} t_{p} }}$$
(1)

The plate stiffened by closed-section stiffeners is regarded as elastically restrained at the edges. Thus, the isotropic plate can exhibit relatively favorable strength performance at the connected edges on which the closed-section ribs are installed. The explicit formula for the rotational restraint stiffness is

$$k_{R} = \frac{{2EI_{U} }}{h'}\left( {2 - \frac{{W_{T} }}{{2W_{T} + 3h'}}} \right) + \frac{{6EI_{p} }}{{W_{R} }}$$
(2)

where

$$I_{U} = \frac{{t_{u}^{3} }}{12};\;I_{p} = \frac{{t_{p}^{3} }}{12};\;D = \frac{{Et_{p}^{3} }}{{12\left( {1 - \nu^{2} } \right)}}.$$

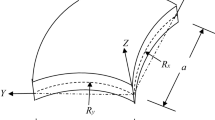
Tran et al. (2012) presented the equations for the elastic buckling stress of simply supported curved panel, as shown in Fig. 2a, which has a similar form as the buckling stress of flat plate and is given by

$$F_{cr} = k_{c}^{z} \frac{{D\pi^{2} }}{{W_{S}^{2} t_{p} }}$$
(3)
Fig. 2
figure 2

Typical buckling mode shape of curved panel under uniform axial compression: a simply supported at both sides, and b with elastic restraints at both sides

Full size image

In contrast, Fig. 2b shows the curved panel elastically restrained by closed-section ribs, which will be used in this study.

Buckling coefficient considering the radius of curvature \(\left( {k_{c}^{z} } \right)\) was introduced to reflect the difference between the flat plate and the curved panel. Different \(k_{c}^{z}\) was theoretically developed by various researchers (Domb and Leigh 2001; Timoshenko and Gere 1961; Stowell 1943; Redshaw 1933). Comparison of the developed expression for the buckling coefficient of previous researchers showed that Timoshenko’s developed formula is approaching closely to the numerical analysis. Thus, the buckling coefficient considering the radius of curvature is given by Eq. (4) (Tran et al. 2012; Timoshenko and Gere 1961).

$$k_{c}^{z} = \left\{ {\begin{array}{*{20}l} {4 + \frac{{3\left( {1 - \nu^{2} } \right)}}{{\pi^{4} }}Z^{2} } \hfill & {{\text{if}}\quad Z \le \frac{{2\pi^{4} }}{{\sqrt {3\left( {1 - \nu^{2} } \right)} }}} \hfill \\ {\frac{4\sqrt 3 }{{\pi^{2} }}Z} \hfill & {{\text{if}}\quad \frac{{2\pi^{4} }}{{\sqrt {3\left( {1 - \nu^{2} } \right)} }} \le Z} \hfill \\ \end{array} } \right.$$
(4)

where \(Z\) is the curvature shape coefficient \(= \frac{{W_{S}^{2} }}{{Rt_{p} }}\).

Accordingly, it is rationally assumed that the buckling stress of partially restrained curved panel could be expressed as

$$F_{cr} = \varPhi \left( {k_{R} } \right)k_{c}^{z} \frac{{D\pi^{2} }}{{W_{S}^{2} t_{p} }}$$
(5)

Based on the form of Eq. (5), three types of \(\varPhi \left( {k_{R} } \right)\) are introduced by modifying the shape functions or simplifying through a regression analysis. The first one was derived by using a 4th order polynomial function as a shape function (Choi and Kim 2016; Choi et al. 2015; Qiao and Shan 2005), which is given by

$$\varPhi \left( {k_{R} } \right) = \frac{{6\left( {1.871\sqrt {{{\tau_{2} } \mathord{\left/ {\vphantom {{\tau_{2} } {\tau_{1} }}} \right. \kern-0pt} {\tau_{1} }}} + {{\tau_{3} } \mathord{\left/ {\vphantom {{\tau_{3} } {\tau_{1} }}} \right. \kern-0pt} {\tau_{1} }}} \right)}}{{\pi^{2} }}$$
(6)

in which

$$\begin{aligned} \tau_{1} & = 124 + 22\frac{{k_{R} W_{S} }}{D} + \frac{{k_{R}^{2} W_{S}^{2} }}{{D^{2} }} \\ \tau_{2} & = 24 + 14\frac{{k_{R} W_{S} }}{D} + \frac{{k_{R}^{2} W_{S}^{2} }}{{D^{2} }} \\ \tau_{3} & = 102 + 18\frac{{k_{R} W_{S} }}{D} + \frac{{k_{R}^{2} W_{S}^{2} }}{{D^{2} }}. \\ \end{aligned}$$

Meanwhile, the \(\varPhi \left( {k_{R} } \right)\) derived when using a harmonic function as a shape function given by

$$w = W\left( {\sin \frac{m\pi x}{L}} \right)\left[ {\left( {1 - \psi } \right)\sin \frac{\pi y}{{W_{S} }} + \frac{\psi }{2}\left( {1 - \cos \frac{2\pi y}{{W_{S} }}} \right)} \right]$$

is expressed as

$$\varPhi \left( {k_{R} } \right) = \frac{1}{2}\sqrt {\frac{{\tau_{1} }}{{\tau_{2} }}} + \frac{{\tau_{3} }}{{4\tau_{2} }}$$
(7)

in which

$$\begin{aligned} \tau_{1} & = 86D^{2} \pi^{2} + 573k_{R} W_{S} D + 86k_{R}^{2} W_{S}^{2} \\ \tau_{2} & = 86D^{2} \pi^{2} + 229k_{R} W_{S} D + 16k_{R}^{2} W_{S}^{2} \\ \tau_{3} & = 172D^{2} \pi^{2} + 458k_{R} W_{S} D + 43k_{R}^{2} W_{S}^{2} . \\ \end{aligned}$$

Through a regression analysis, a simplified form of the strength increment factor (Choi et al. 2018) was obtained which may reasonably replace the strength increment factor of the approximate equations derived using energy method. It is expressed as

$$\varPhi \left( {k_{R} } \right) = 1.15\left( {\frac{3.2D + \kappa }{7.2D + \kappa }} \right)^{1.0} + 0.5$$
(8)

in which

$$\kappa = k_{R} W_{S} .$$

The above theoretically derived approximate equations for partially restrained curved panel using Timoshenko’s developed expression for \(k_{c}^{z}\), since it could better quantify the influence of curvature, will be adopted and the correlation of these buckling strength equations with the numerical analysis will be determined in this paper to verify their validity and accuracy in estimating the elastic buckling stresses.

3 Finite Element Modeling

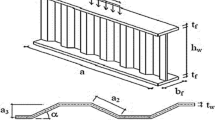
A series of parametric studies were performed through finite element modeling to compare and verify the validity of the approximate formulas. The model of this study is shown in Fig. 3, in which the closed-section rib is cut in half, and the dimensions of the longitudinally stiffened curved panels are presented in Table 1. The closed-section ribs are designed to have sufficient bending stiffness to induce local buckling. \(R\) means the radius of curvature = 2500, 3000, 3500, 4000 and 4500 mm, \(W_{S}\) is the net spacing between the longitudinal stiffeners, \(W_{R}\) is the width of the lower end rib, \(W_{T}\) is the width of the upper end rib, \(t_{p}\) is the thickness of the curved panel, \(t_{u}\) is the thickness of the closed-section rib and \(h\) is the height of the closed-section rib.

Fig. 3
figure 3

Stiffened curved panel model: a section of a curved panel reinforced with a closed-section rib, and b closed-section rib stiffener

Full size image
Table 1 Model dimension
Full size table

For the finite element analysis, the four-node plane element S4R5 provided by the general structural analysis program ABAQUS (2014) was used. Figure 4 shows the finite element mesh, loading and boundary condition of the model. In the model, half u-ribs as longitudinal stiffeners were installed along the unloaded sides to demonstrate the consistent rotational restraint effect on each subpanel. Load distribution was applied at both end sides in the longitudinal direction to exhibit uniform axial compression. To evaluate the increasing effects on the local plate buckling strength due to the rotational stiffness and verify the validity of the proposed equations, variable analysis was performed for the major influential parameters on the stiffened curved panel \(\left( {R,\,W_{S} ,\,t_{p} } \right)\) and closed-section ribs \(\left( {t_{u} ,\,W_{T} ,\,W_{R} ,\,h} \right)\). Furthermore, the isotropic steel has material properties such as modulus of elasticity, \(E = 205,000\,{\text{MPa}}\) and Poisson’s ratio, \(\nu = 0.3\).

Fig. 4
figure 4

Stiffened curved panel model with loading and boundary condition: a boundary condition, and b finite element model with axial loading

Full size image

4 Analysis Results

Eigenvalue analysis was performed on the finite element models to obtain the minimum critical stress and the buckling mode. From the result of the analysis, the buckling behavior of partially restrained curved panels can be figured out. The buckling mode shape obtained from the numerical analysis is shown in Fig. 5. The finite element analysis reveals that the buckling mode is local plate buckling (PB). As can be seen, if the closed-section rib has sufficient section rigidity, a fixed point is formed on the panel reinforced at the location where the closed-section ribs are installed and the local plate buckling behavior occurs at \(W_{S}\) or the effective width.

Fig. 5
figure 5

Local plate buckling (PB): a WS = 285 mm, b WS = 324 mm, c WS = 364 mm, and d WS = 405 mm

Full size image

The local plate buckling strengths were obtained for each case according to the specifications given in Table 1, some representative cases are shown in Table 2, which shows the comparison of the buckling stress \(\left( {F_{cr} } \right)\) of Eq. (5) using the strength increment factor derived from the suggested theoretical approaches, Eqs. (6)–(8) and the \(F_{cr}\) from the finite element analysis. The parametric numerical analyses were conducted according to the rotational restraint stiffness along with several design parameters, some of which are graphically presented in Fig. 6. As shown in Fig. 6, the buckling strength increases as the rotational restraint stiffness increases. Once \(k_{R}\) reached a certain limiting value, the buckling strength does not considerably increase any further. The buckling strength significantly increased compared to the buckling strength with simple supports. It can also be observed from the result of the analysis that the percentage difference is decreasing on the converged region.

Table 2 Numerical analysis results (R = 2500 mm, tp = 10 mm, α = 3)
Full size table
Fig. 6
figure 6

Buckling strength along with rotational stiffness: a WS, b tp, c WR, d h and e R

Full size image

The proposed theoretical approaches for the partially-restrained curved panel, the derived from energy method using polynomial and a harmonic function as a shape function and the simplified equation, are compared. The correlation of these buckling strength equations with the numerical analysis was determined. Figure 7 shows their comparison with the finite element analysis in percentage difference (%). The diagrams represent the tendency or the behavior of the approximate formulas with respect to the parametric ranges of several design parameters. The diagrams show that the \(F_{cr}\) using Eq. (7) has a percentage difference with the numerical analysis that is under 16%, the \(F_{cr}\) using Eq. (6) is under 12% and using Eq. (8) shows a difference of under 8%. It can also be observed that the equations have similar trend. Through this, the influential parameters and the most accurate approach are identified. Based on the result of the analysis, \(W_{S}\) and \(t_{p}\) significantly affects the buckling strength. Figures 6 and 7 shows that the characteristic of the buckling strength along with these two parameters is different compared to the other parameters. Their difference is generally higher especially when using the \(F_{cr}\) of Eq. (7). Figure 7 reveals how close the equations are to the numerically evaluated values especially on the simplified equation, \(F_{cr}\) of Eq. (8), showing a better correlation as compared to the others. These diagrams verified the validity and accuracy for the application of these approximate equations in estimating the elastic buckling stress of the stiffened curved panel. Moreover, Fig. 7a, d remarkably show that there are some erroneous tendencies. There is a sharp curvature, that is, when \(R\) is smaller. While there is a lower strength range when \(W_{S}\) is larger, showing that the difference is increasing. Since there are some ranges that are more erroneous, further study is needed.

Fig. 7
figure 7

Comparative study and trend analysis: a WS, b tp, c WR, and d R

Full size image

5 Conclusions

This study has examined the buckling behavior of partially restrained curved panels stiffened with closed-section ribs under uniaxial compression. A methodology to derive the approximate solutions is suggested for the buckling strength of partially restrained curved panels, which were simply derived by reflecting the influential factors to rationally quantify a reinforcing effect due to the rotational stiffness and the influence of curvature, respectively. Numerical analysis of the longitudinally stiffened isotropic curved panel showed the variation of local plate buckling strength along with several design parameters. It was found that there is greater buckling strength due to the increase in rotational stiffness and the influential parameters on the buckling stress and mode shapes were identified. Comparative study and trend analysis of the equations verified the validity of the proposed equations as the comparison shows how they are approaching closely to the numerically evaluated values. The accuracy of the equations were investigated and it can be suggested that the simplified equation of \(F_{cr}\) using the strength increment factor \(\varPhi \left( {k_{R} } \right)\) of Eq. (8) shows a better correlation and approaching more closely with the numerical analysis. The equations also reflect well the effect of the radius of curvature as well as the enhanced strength attributable to the rotational restraint effect of the closed-section ribs.

The result of this analysis can be used in improving the optimum design section of curved panel structures longitudinally stiffened with closed-section ribs and can also contribute in improving the structural performance and in utilizing more efficiently the curved panels as a member subjected to axial compression by applying closed-section ribs as longitudinal stiffeners. Further study on wider range of panel curvature is needed in order to obtain a more effective design formula and for full implementation of the developed formula.