Introduction

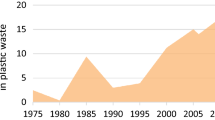
Million tons of plastic are consumed each year. Estimation said that out of this only one-quarter part is recycled. Plastic is prepared from toxic materials like vinyl hydrochloride, benzene, etc. These chemicals cause the precarious health issues and also contaminate our air, soil and water. The huge bulk of industrial plastic is non-biodegradable and if it is degradable then it only starts degrading in about 700 years which means that all the plastic that has ever been produced has not degraded yet. Therefore, these dumped industrial plastics are either burned or recycled. One should recycle all the things of plastic rather than new production and burning. Keep it away from environmental sources such as landfill and ocean. Because when the industrial waste plastic composed in dumping sites, it keeps rotting, spreading odor which cause the air pollution. Hence, rivers and landfill become the target of this various types of pollution which are produced by industrial waste plastic.

About three decades ago, as people’s requirement was not too big so that easy to control the garbage causes. But today’s world has none of the activities which do not generate plastic debris. Instead of this, all stated processes like producing, dumping, burning of plastics, one needs to think beyond this. This paper includes two occurrences to invest particular total budget into health policy and installing recycling machine policy rather than the budget used in new production, burning or dumping of plastic.

In statistical way, Wilcox et al. (2015) has developed a model on how sea birds do effective waste management which help to reduce pollution threat. Song et al. (1999) has tuned a model to determine the optimal conditions and identify environmentally favorable recycle routes by analyzing the sensitivity and optimization methods. Dubey (2010) used optimal investment policy for clean environment and human health policy by considering a nonlinear dynamical model of resource biomass. Pathinathan et al. (2014) took an algorithmic approach and using induced fuzzy cognitive maps which analyze the threats of plastic pollution. Nganda (2007) prepared two models to manage the municipal waste by using integer and mixed integer programming problem. Matar et al. (2014) established a paper for production, recycling and reuses of inventory plastic beverages bottles like EOQ model. Shah et al. (2019) formed a model to optimize two investment policies to control environmental pollution. Donovan et al. (1975) prepared a mathematical model using the concept of two-shot modeling for recycling of plastic. Cairns et al. (2005) has framed a paper on improving options to reuse, reduce and recycle of e-waste to protect consumers, public health and an environment.

In epidemics model proposed by Swan (1990), Branicky et al. (1998), De Pillis and Radunskaya (2001), Gaff and Schaefer (2009), Okosun and Makinde (2014), Rodrigues et al. (2014), Rachah and Torres (2015), Ding et al. (2016) and many more control theory have been applied.

A brief survey tells the information about the plastics and way to optimize the environmental pollution using different approaches of mathematics. This paper has obtained the results using mathematical dynamical model. “Modeling” section deals with development of mathematical model of the problem under consideration. “Stability” section analyzes the local and global stability of the proposed model. Two cost policies for burning and installing recycling machine is optimized in “Optimal investment in health and recycled machine policy” section. All the results are numerically interpreted in “Numerical simulation” section. “Conclusion” section includes the remarkable conclusions from the model.

Material and methods

Modeling

This paper supports for reducing eminence of pollution by moderating plastic consumption and promoting recycling of industrial plastic. This industrial plastic \((P_{L} (t))\)(in tons) is either sends for burning \((B_{n} (t))\)(in tons), dumping \((D(t))\)(in tons) or recycling \((R_{C} (t))\)(in tons) which sources the pollution \((P(t))\)(in ppm) at any time \(t \ge 0\). Here, total budget \((C)\) (in $) is divided into two useful optimum policy, health policy for the society \((C_{h} )\) (in $) and installing recycling machine policy \((C_{m} = C - C_{h} )\) (in $).

The model given in Fig. 1 is formulated by using all parameters mentioned in Table 1 are the rates which connects the state variables known as compartments. The parametric values have been assumed hypothetically.

Fig. 1
figure 1

Diagram of model

Full size image
Table 1 Notation, parameter description and parametric values
Full size table

Hence, the system of differential equation is constructed as,

$$\begin{gathered} \frac{{{\text{d}}P_{L} }}{{{\text{d}}t}} = B - \beta _{1} P_{L} B_{n} - \beta _{2} P_{L} D - \delta _{1} P_{L} R_{C} + \delta _{2} R_{C} - \mu P_{L} \hfill \\ \frac{{{\text{d}}B_{n} }}{{{\text{d}}t}} = \beta _{1} P_{L} B_{n} + \varepsilon D - \eta _{1} B_{n} - \mu B_{n} - \theta _{1} C_{h} B_{n} \hfill \\ \frac{{{\text{d}}D}}{{{\text{d}}t}} = \beta _{2} P_{L} D + \varepsilon D - \eta _{2} D - \gamma D - \mu D + \theta _{2} C_{m} D \hfill \\ \frac{{{\text{d}}R_{C} }}{{{\text{d}}t}} = \delta _{1} P_{L} R_{C} - \delta _{2} R_{C} + \gamma D - \eta _{3} R_{C} - \mu R_{C} \hfill \\ \frac{{{\text{d}}P}}{{{\text{d}}t}} = \eta _{1} B_{n} + \eta _{2} D + \eta _{3} R_{C} - \mu P \hfill \\ \end{gathered}$$
(1)

with \(P_{L} > 0\) and \(D,B_{n} ,R_{C} ,P \ge 0\).

Summing the above differential equations of system (1), we have

$$\begin{aligned} \frac{{\text{d}}}{{{\text{d}}t}}\left( {P_{L} + B_{n} + D + R_{C} + P} \right) & = B - \mu P_{L} - \mu B_{n} - \mu D - \mu R_{C} - \mu P - \theta _{1} C_{h} B_{n} + \theta _{2} C_{m} D \\ & = B - \mu (P_{L} + B_{n} + D + R_{C} + P) \ge 0 \\ \end{aligned}$$

\(\Rightarrow \mathop {\lim }\limits_{t \to \infty } \,\sup (P_{L} + B_{n} + D + R_{C} + P) \le \frac{B}{\mu }\).

Thus, the feasible region of the model is \(\Lambda = \left\{ {(P_{L} ,B_{n} ,D,R_{C} ,P) \in R^{5} :P_{L} + B_{n} + D + R_{C} + P \le \frac{B}{\mu }} \right\}.\)where \(R_{ + }^{5} = \left\{ {(P_{L} ,B_{n} ,D,R_{C} ,P) \in R^{5} :P_{L} > 0,\,\,B_{n} \ge 0,\,D \ge 0,\,R_{C} \ge 0,\,P \ge 0} \right\}.\)

By solving system (1), the solutions are finding out called equilibrium points:

  1. (i)

    \(E_{0} \left( {\frac{B}{\mu },0,0,0,0} \right)\)

  2. (ii)

    \(E_{1} \left( {\frac{{C_{h} \theta_{1} + \eta_{1} + \mu }}{{\beta_{1} }},\frac{{ - C_{h} \mu \theta_{1} + B\beta_{1} - \eta_{1} \mu - \mu^{2} }}{{\beta_{1} (C_{h} \theta_{1} + \eta_{1} + \mu )}},0,0,\frac{{\eta_{1} \left( { - C_{h} \mu \theta_{1} + B\beta_{1} - \eta_{1} \mu - \mu^{2} } \right)}}{{\beta_{1} \mu (C_{h} \theta_{1} + \eta_{1} + \mu )}}} \right)\)

  3. (iii)

    \(E_{2} \left( {\frac{{\delta_{2} + \eta_{3} + \mu }}{{\delta_{1} }},0,0,\frac{{B\delta_{1} - \delta_{2} \mu - \eta_{3} \mu - \mu^{2} }}{{\delta_{1} (\eta_{3} + \mu )}},\frac{{\eta_{3} \left( {B\delta_{1} - \delta_{2} \mu - \eta_{3} \mu - \mu^{2} } \right)}}{{\mu \delta_{1} (\eta_{3} + \mu )}}} \right)\)

  4. (iv)

    \(E^{*} \left( {P_{L}^{*} ,B_{n}^{*} ,D^{*} ,R_{C}^{*} ,P^{*} } \right)\)

where

$$P_{L}^{*} = \frac{{\varepsilon + \eta_{2} + \gamma + \mu - C_{m} \theta_{2} }}{\mu }$$
$$\begin{aligned} B_{n}^{*} & = \varepsilon (( - C_{m} \theta_{2} + \varepsilon + \eta_{2} + \gamma + \mu )( - \delta_{1} \mu ( - C_{m} \theta_{2} + \varepsilon + \eta_{2} + \gamma + \mu ) + \beta_{2} B\delta_{1} ) + (\delta_{2} + \eta_{3} + \mu )( - B\beta_{2}^{2} \\ & \quad + \beta_{2} \mu ( - C_{m} \theta_{2} + \varepsilon + \eta_{2} + \gamma + \mu )))/ - \beta_{2}^{2} \delta_{2} ( - C_{m} \theta_{2} + \varepsilon + \eta_{2} + \mu )(C_{h} \theta_{1} + \eta_{1} + \mu ) + \beta_{1} \delta_{1} ( - C_{m} \theta_{2} \\ & \quad + \varepsilon + \eta_{2} + \mu )^{2} ( - C_{m} \theta_{2} - \eta_{2} - \mu ) + ( - C_{m} \theta_{2} + \varepsilon + \eta_{2} + \mu )((C_{h} \theta_{1} + \eta_{1} + \mu )(\beta_{2} \delta_{1} ( - C_{m} \theta_{2} + \varepsilon + \eta_{2} \\ & \quad + \mu ) - \beta_{2}^{2} (\eta_{3} + \mu )) + \beta_{1} \beta_{2} \delta_{2} (\eta_{3} + \mu ) + \beta_{1} \beta_{2} \eta_{3} (\eta_{2} + \gamma + \mu )) \\ \end{aligned}$$
$$\begin{aligned} D^{*} & = [\delta_{1} ( - C_{m} \theta_{2} + \varepsilon + \eta_{2} + \mu ) - \beta_{2} (\delta_{2} + \eta_{3} + \mu )][(C_{h} \theta_{1} + \eta_{1} + \mu )(\beta_{2} \mu ( - C_{m} \theta_{2} + \varepsilon + \eta_{2} + \mu ) \\ & \quad - B\beta_{2}^{2} ) + ( - C_{m} \theta_{2} + \varepsilon + \eta_{2} + \mu )( - \beta_{1} \mu ( - C_{m} \theta_{2} + \varepsilon + \eta_{2} + \mu ) + B\beta_{1} \beta_{2} )]/\beta_{2} \{ \beta_{2}^{2} \delta_{2} (C_{h} \theta_{1} + \eta_{1} \\ & \quad + \mu )( - C_{m} \theta_{2} - \varepsilon - \mu ) + ( - C_{m} \theta_{2} + \varepsilon + \eta_{2} + \gamma + \mu )[\beta_{1} \delta_{1} ( - C_{m} \theta_{2} + \varepsilon + \eta_{2} + \gamma + \mu )(C_{m} \theta_{2} - \eta_{2} ) \\ & \quad + \beta_{2} \delta_{1} ( - C_{m} \theta_{2} + \varepsilon + \eta_{2} + \mu )(\theta_{1} + \eta_{1} + \mu ) - \beta_{2}^{2} (C_{h} \theta_{1} + \eta_{1} + \mu )(\eta_{3} + \mu ) + \beta_{1} \beta_{2} \delta_{2} ( - C_{m} \theta_{2} + \eta_{2} \\ & \quad + \mu ) + \beta_{1} \beta_{2} \eta_{3} ( - C_{m} \theta_{2} + \eta_{2} + \gamma + \mu ) + \beta_{1} \beta_{2} \mu ( - C_{m} \theta_{2} + \gamma + \mu ) - \beta_{1} \delta_{1} \mu ( - C_{m} \theta_{2} + \varepsilon + \gamma + \mu ) \\ & \quad + \beta_{1} \delta_{1} \mu (C_{m} \gamma \theta_{2} - \eta_{2} (\varepsilon + \eta_{2} + \gamma + \mu ))]\} \\ \end{aligned}$$
$$\begin{aligned} R_{C}^{*} & = \gamma (\beta_{2} (C_{h} \theta_{1} + \eta_{1} + \mu )( - B\beta_{2} + \mu ( - C_{m} \theta_{2} + \varepsilon + \eta_{2} + \gamma + \mu )) + \beta_{1} ( - C_{m} \theta_{2} + \varepsilon + \eta_{2} + \gamma \\ & \quad + \mu )(B\beta_{2} - \mu (C_{m} \theta_{2} + \varepsilon + \eta_{2} + \gamma + \mu ))/\beta_{2} (C_{h} \theta_{1} + \eta_{1} + \mu )( - C_{m} \delta_{1} \theta_{2} ( - C_{m} \theta_{2} + \varepsilon + \eta_{2} + \gamma + \mu ) \\ & \quad - \beta_{2} \delta_{2} ( - C_{m} \theta_{2} + \varepsilon + \eta_{2} + \mu )) + \beta_{1} \delta_{1} \mu (C_{m} \varepsilon \theta_{2} - \eta_{2} \gamma ) + \beta_{2} \delta_{1} (\eta_{2} \mu ( - C_{m} \theta_{2} + \eta_{1} ) + \eta_{1} (\mu (\gamma + \mu ) \\ & \quad + \varepsilon \eta_{2} )) + ( - C_{m} \theta_{2} + \varepsilon + \eta_{2} + \gamma + \mu )(\beta_{1} \delta_{1} ( - C_{m} \theta_{2} + \varepsilon + \eta_{2} + \gamma + \mu )(C_{m} \theta_{2} - \mu ) + \beta_{2} (C_{h} \theta_{1} + \eta_{1} \\ & \quad + \mu )( - \beta_{2} (\eta_{3} + \mu ) + \delta_{1} (\varepsilon \, + \eta_{2} - \mu ) - \beta_{1} \beta_{2} (C_{m} \theta_{2} - \mu )(\delta_{2} + \eta_{3} + \mu ) + \beta_{1} \beta_{2} (\eta_{2} (\delta_{2} + \eta_{3} + \mu ) \\ & \quad + \gamma (\eta_{3} + \mu )) - \beta_{1} \delta_{1} \eta_{2} (\varepsilon + \eta_{2} + \gamma + \mu )) \\ \end{aligned}$$
$$\begin{aligned} P^{*} & = \eta _{2} \mu \{ C_{h} \theta _{1} \beta _{2} [\gamma (\beta _{2} \delta _{2} - \gamma \delta _{1} ) + \beta _{2} ( - \mu (C_{m} \theta _{2} + \delta _{2} + \gamma ) + \eta _{{3\,}} (1 + \eta _{2} + 2\gamma ) - \eta _{2} \delta _{1} (\eta _{2} + 2\mu )) \\ & \quad - \delta _{1} (\mu ^{2} + 2\gamma (\eta _{2} + \mu ))] + C_{m} \theta _{2} [C_{m} \theta _{2} ( - \beta _{1} \beta _{2} (\delta _{2} + \eta _{3} ) + \beta _{1} (3\delta _{1} \gamma - \beta _{2} \eta _{1} )) + \beta _{1} \beta _{2} (2\delta _{2} (\eta _{2} + \mu ) \\ & \quad + 2\eta _{3} (\eta _{2} + \mu )) + \beta _{1} \gamma (2\mu - 3\delta _{1} (2\eta _{2} - 1 - 2\mu ) - \beta _{2} \eta _{1} (\delta _{2} + \eta _{3} - 2\mu (\delta _{1} + \delta _{2} ) - 2\eta _{2} \delta _{1} )] + \beta _{2} [2\varepsilon \gamma ( \\ & \quad - \beta _{1} (\delta _{2} + 2\eta _{3} ) - 2\delta _{1} \eta _{1} ) + \gamma (\beta _{1} ( - 2\delta _{2} (\eta _{2} + \mu ) - \eta _{3} (3\eta _{2} + 3\gamma + 4\gamma \mu )) + 2\eta _{1} (\beta _{2} \eta _{3} - \delta _{1} (\eta _{2} + \beta _{2} \mu )) \\ & \quad + \beta _{2} \mu ^{2} (C_{h} \theta _{1} (\eta _{2} + \mu ) - \mu C_{m} \theta _{2} ) - \beta _{1} ((\delta _{2} + \eta _{3} )(\eta _{2} + \mu )^{2} + \gamma \mu (2\eta _{2} + \gamma + \mu )) - \eta _{1} (\beta _{2} (\delta _{2} + \eta _{3} )(\eta _{2} \, \\ & \quad + \mu ) + \mu \gamma (1 + 2\eta _{3} )) + \beta _{2} \mu ^{2} (\eta _{2} + \mu ) - C_{m} \theta _{2} (C_{h} \theta _{1} (2\delta _{1} \gamma - \beta _{2} (\delta _{2} + \eta _{3} )) + 2\beta _{1} \gamma (\delta _{2} + 2\eta _{3} ) \\ & \quad + 2\delta _{1} \eta _{1} \gamma )]\, - 3\beta _{1} \delta _{1} \gamma (3\eta _{2} (\eta _{2} + \gamma ) + \mu (2\eta _{2} + \gamma + \mu ))\} + C_{m} \theta _{2} \{ \beta _{1} [\beta _{2} \eta _{3} \gamma \mu (2\mu - C_{m} \theta _{2} + 2\gamma - \beta _{2} \eta _{1} )] \\ & \quad + \mu [\varepsilon (\delta _{1} C_{m} \theta _{2} (3\beta _{1} \eta _{2} - \beta _{2} \eta _{1} ) + \beta _{1} \eta _{2} (2\mu \beta _{2} - 3\delta _{1} (\varepsilon + 2\eta _{2} + 2\mu )) - \beta _{2} (\beta _{2} \eta _{1} (\delta _{2} + \eta _{3} ) - 2\delta _{1} (\eta _{1} (\varepsilon \\ & \quad + \mu ) + \mu \eta _{2} ))) + \beta _{2} ( - \mu \beta _{2} (\eta _{3} (\gamma + \eta _{2} ) + \eta _{2} (\delta _{2} + \eta _{1} )) + 2\eta _{2} \mu \delta _{1} (\eta _{2} + \mu )) + C_{m} \theta _{2} \eta _{2} ( - \beta _{2} \delta _{1} (C_{m} \theta _{2} \\ & \quad + \mu ) + \beta _{1} ( - \beta _{2} \mu + 3\delta _{1} (\eta _{2} + \mu ))) + B\beta _{2} (\delta _{1} \eta _{2} (C_{m} \theta _{2} \beta _{1} - C_{h} \theta _{1} \beta _{2} ) + 2\beta _{1} \eta _{2} \delta _{1} (\varepsilon + \gamma + \mu ))\, \\ & \quad - C_{h} \theta _{1} \beta _{2} ^{2} \eta _{3} \gamma ]\} + B\beta _{2} \{ \beta _{2} [C_{h} \theta _{1} (\delta _{1} \eta _{2} (\varepsilon + \mu ) + \beta _{2} (\eta _{2} (\delta _{2} + \mu ) + \eta _{3} (\eta _{2} + \gamma ))) + C_{m} \theta _{2} - \beta _{1} (\eta _{2} (\delta _{2} \, \\ & \quad + \eta _{3} + \mu ) - \eta _{3} \gamma + \delta _{2} \eta _{2} (\varepsilon + \gamma + \mu ) + \varepsilon (\eta _{2} (\eta _{2} + \mu ) + \gamma \eta _{3} ) + \eta _{3} \eta _{2} (\gamma + \mu ) + \gamma \mu (\eta _{3} + \eta _{2} )) + \delta _{1} ( - \eta _{1} (\varepsilon \,\, \\ & \quad + \eta _{2} ) - \eta _{2} \mu - \eta _{2} ^{2} + \varepsilon \eta _{1} (2\eta _{2} + \gamma + \mu ) + \beta _{2} \eta _{1} (\varepsilon ^{2} + \eta _{2} ^{2} ) + \beta _{2} \eta _{2} \mu (\eta _{2} + \mu ) + \delta _{1} \mu \eta _{2} (\mu (\varepsilon + \eta _{1} ) + \gamma (\eta _{2} \\ & \quad + \mu )) - \beta _{2} ^{2} (\delta _{2} (\eta _{1} (\varepsilon + \eta _{2} ) + \eta _{2} \mu ) - \eta _{1} (\eta _{3} + \mu )(\varepsilon + \eta _{2} ))] + \beta _{1} [\delta _{1} \eta _{2} (2(C_{m} \eta _{2} \theta _{2} - \varepsilon (\gamma + \mu ) - \gamma \mu )(\varepsilon \\ & \quad + \mu ^{2} + \gamma ^{2} + 2\eta _{2} (\eta _{2} + \gamma + \mu ))) + \eta _{2} \beta _{2} (\delta _{2} + \eta _{3} + \mu (\eta _{2} + \mu )) + \beta _{2} \eta _{3} \gamma ^{2} - \delta _{1} \eta _{2}^{3} )]\} + \gamma \mu [\gamma \beta _{2} ( - \beta _{1} \eta _{3} (\gamma \\ & \quad + 2\mu ) + \mu \eta _{2} (\beta _{2} \delta _{2} - \delta _{1} ) + \beta _{2} \eta _{1} \eta _{3} ) + \gamma ^{2} \beta _{1} \delta _{1} \eta _{2} + \beta _{2} \mu \eta _{3} (\mu \beta _{1} + \beta _{2} \eta _{1} )] + \beta _{2} \mu \{ \beta _{2} \mu [2\eta _{3} \gamma (\gamma + \mu ) \\ & \quad - 2B\beta _{2} \eta _{2} + 2\varepsilon (\varepsilon \eta _{1} + \mu \eta _{2} ) - \beta _{1} \eta _{2} ((\eta _{2} + \mu )^{2} + \eta _{2} ^{3} + \mu ^{3} + 3\eta _{2} \mu (\eta _{2} + \mu )) + \beta _{2} \eta _{2} \mu ^{2} \delta _{2} (\eta _{2} + 1) + \eta _{1} \eta _{2} \\ & \quad + \eta _{3} \eta _{2} (\eta _{2} + \mu )] + \beta _{2} \delta _{1} [ - \mu \eta _{2} (\mu ^{2} + \eta _{2} ^{2} + \mu \eta _{2} ) + \gamma ^{2} \eta _{1} (\varepsilon - \eta _{2} )]\} + \varepsilon \mu \{ C_{h} \theta _{1} [\beta _{2} \eta _{2} (\beta _{2} (\delta _{2} + \eta _{3} ) \\ & \quad - \delta _{1} (\varepsilon + 2\eta _{2} + 2\mu )) + \beta _{2}^{2} \eta _{3} \gamma + 2\beta _{2} \delta _{1} \eta _{2} (C_{m} \theta _{2} - \gamma )] + C_{m} \theta _{2} [\beta _{1} \beta _{2} (\eta _{2} (\delta _{2} + \eta _{3} ) + \gamma \eta _{3} ) + 2\delta _{1} (\eta _{2} ( \\ & \quad - 3\beta _{1} \gamma + 2\beta _{2} \eta _{1} ) + \beta _{2} \eta _{1} \gamma )] - \delta _{1} [\eta _{1} (\varepsilon ^{2} + \mu ^{2} ) + \varepsilon \mu (2\eta _{1} + \eta _{2} ) + 2\mu \eta _{2} (\eta _{2} + \mu )] + \beta _{1} [\beta _{2} (\eta _{2} ( - (\varepsilon + 2\eta _{2} \\ & \quad + 2\mu )(\delta _{2} + \eta _{3} ) - 2\gamma \mu ) - \varepsilon \eta _{3} \gamma - 2\gamma \eta _{3} (\gamma + \mu )) + 3\delta _{1} \eta _{2} \gamma (\varepsilon + 2\eta _{2} + \gamma + 2\mu ) + 3\delta _{1} \eta _{2} (\mu (\varepsilon + \eta _{2} ) + \mu ^{2} \\ & \quad + \eta _{2} ^{2} ) - \beta _{2} \eta _{2} \mu (\varepsilon + \eta _{2} + 2\mu ) + \varepsilon \delta _{1} \eta _{2} (\varepsilon + \eta _{2} )] + \beta _{2} [ - \delta _{1} (2\eta _{1} \gamma (\varepsilon + \mu ) + \eta _{1} \eta _{2} (3\eta _{2} + 4\mu ) - 2\mu \eta _{2} \gamma ) \\ & \quad + \beta _{2} \eta _{1} (2\eta _{2} (\delta _{2} + \eta _{3} ) + 4\gamma \eta _{3} + \eta _{3} (\varepsilon + \mu ) + \mu (2\eta _{2} + \gamma )) + \beta _{2} \delta _{2} (\eta _{1} (\varepsilon + \mu ) + \eta _{2} \mu )\, + \eta _{3} (\eta _{2} + \gamma )]\} \\ & \quad /\beta _{2} \mu \{ \beta _{2} ^{2} \delta _{2} (C_{m} \theta _{2} - \varepsilon - \eta _{2} - \gamma - \mu )(C_{h} \theta _{1} + \eta _{1} + \mu ) + (C_{m} \theta _{2} - \varepsilon - \eta _{2} - \gamma - \mu )[\beta _{2} \delta _{1} (C_{m} \theta _{2} - \varepsilon - \eta _{2} \\ & \quad - \mu )(C_{h} \theta _{1} + \eta _{1} + \mu ) + \beta _{2} ^{2} (C_{h} \theta _{1} + \eta _{1} + \mu )(\eta _{3} + \mu ) + \beta _{1} \delta _{1} (C_{m} \theta _{2} - \varepsilon - \eta _{2} - \gamma - \mu )(C_{m} \theta _{2} - \eta _{2} \\ & \quad - \mu ) + \beta _{1} \beta _{2} ((C_{m} \theta _{2} - \eta _{2} - \mu )(\delta _{2} + \eta _{3} + \mu ) + \gamma (\eta _{3} + \mu ))]\} \\ \end{aligned}$$

First is pollution-free equilibrium point. Second point is recycling free, third is dumping free and fourth is optimum issue point.

Stability

To scrutinize the stability analysis of model for equilibrium points \(E_{0} ,E_{1} ,E_{2}\) and \(E^{*}\) is very useful. Stepwise stability for each equilibrium point is carried out as follows locally and globally.

Local stability

Jacobian matrix using system (1) is stated which will be used to derive local stability for the model.

$$J = \left[ {\begin{array}{*{20}c} {J_{11} } & { - \beta_{1} P_{L} } & { - \beta_{2} P_{L} } & { - \delta_{1} P_{L} + \delta_{2} } & 0 \\ {\beta_{1} B_{n} } & {J_{22} } & \varepsilon & 0 & 0 \\ {\beta_{2} D} & 0 & {J_{33} } & 0 & 0 \\ {R_{C} \delta_{1} } & 0 & \gamma & {J_{44} } & 0 \\ 0 & {\eta_{1} } & {\eta_{2} } & {\eta_{3} } & { - \mu } \\ \end{array} } \right]$$

where \(J_{11} = - \beta_{1} B_{n} - \beta_{2} D - R_{C} \delta_{1} - \mu ,\) \(J_{22} = - C_{h} \theta_{1} + \beta_{1} P_{L} - \eta_{1} - \mu ,\) \(J_{33} = C_{m} \theta_{2} + \beta_{2} P_{L} - \varepsilon - \eta_{2} - \gamma - \mu\) and \(J_{44} = - \delta_{1} P_{L} - \delta_{2} - \eta_{3} - \mu\).

Theorem 3.1.1

The pollution-free equilibrium point \(E_{0}\) of model is locally asymptotically stable with conditions.

Proof

Jacobian matrix at \(E_{0}\) is as follows:

$$J_{0} = \left[ {\begin{array}{*{20}c} { - \mu } & {\frac{{ - \beta_{1} B}}{\mu }} & {\frac{{ - \beta_{2} B}}{\mu }} & {\frac{{ - \delta_{1} B}}{\mu } + \delta_{2} } & 0 \\ 0 & { - C_{h} \theta_{1} + \frac{{\beta_{1} B}}{\mu } - \eta_{1} - \mu } & \varepsilon & 0 & 0 \\ 0 & 0 & {C_{m} \theta_{2} + \frac{{\beta_{2} B}}{\mu } - \varepsilon - \eta_{2} - \gamma - \mu } & 0 & 0 \\ 0 & 0 & \gamma & {\frac{{\delta_{1} B}}{\mu } - \delta_{2} - \eta_{3} - \mu } & 0 \\ 0 & {\eta_{1} } & {\eta_{2} } & {\eta_{3} } & { - \mu } \\ \end{array} } \right]$$

has eigenvalues,

\(\omega_{1} = - \mu\), \(\omega_{2} = - \mu\), \(\omega_{3} = \frac{{\delta_{1} B}}{\mu } - (\delta_{2} + \eta_{3} + \mu )\), \(\omega_{4} = - C_{h} \theta_{1} + \frac{{\beta_{1} B}}{\mu } - \eta_{1} - \mu\) and \(\omega_{5} = C_{m} \theta_{2} + \frac{{\beta_{2} B}}{\mu } - \varepsilon - \eta_{2} - \gamma - \mu\).

Equilibrium point is stable if all eigenvalues related to Jacobian matrix are negative. Here, only first two eigenvalues are negative. Therefore, the conditions for the equilibrium point \(E_{0} \left( {\frac{B}{\mu },0,0,0,0} \right)\) to be asymptotically stable is,

  1. (i)

    \(({\text{i}})\,\,\delta_{2} + \eta_{3} + \mu > \frac{{\delta_{1} B}}{\mu }\),

  2. (ii)

    \(({\text{ii}})\,\,C_{h} \theta_{1} + \eta_{1} + \mu > \frac{{\beta_{1} B}}{\mu }\) and

  3. (iii)

    \(({\text{iii}})\,\varepsilon + \eta_{2} + \gamma + \mu > C_{m} \theta_{2} + \frac{{\beta_{2} B}}{\mu }\).

\(\square\)

Theorem 3.1.2

The recycling free equilibrium point \(E_{1}\) of model is locally asymptotically stable with conditions.

Proof

Let \(x_{1} = \frac{{C_{h} \theta_{1} + \eta_{1} + \mu }}{{\beta_{1} }}\) and the Jacobian matrix at \(E_{1}\) is,

$$J_{1} = \left[ {\begin{array}{*{20}c} {J_{111} } & { - \beta_{1} x_{1} } & { - \beta_{2} x_{1} } & { - \delta_{1} x_{1} + \delta_{2} } & 0 \\ {\beta_{1} \left( {\frac{ - \mu }{{\beta_{1} }} + \frac{B}{{\beta_{1} x_{1} }}} \right)} & {J_{122} } & \varepsilon & 0 & 0 \\ 0 & 0 & {J_{133} } & 0 & 0 \\ 0 & 0 & \gamma & {J_{144} } & 0 \\ 0 & {\eta_{1} } & {\eta_{2} } & {\eta_{3} } & { - \mu } \\ \end{array} } \right]$$

where \(J_{111} = - \beta_{1} \left( {\frac{ - \mu }{{\beta_{1} }} + \frac{B}{{\beta_{1} x_{1} }}} \right) - \mu\), \(J_{122} = - C_{h} \theta_{1} + \beta_{1} x_{1} - \eta_{1} - \mu\),

\(J_{133} = C_{m} \theta_{2} + \beta_{2} x_{1} - \varepsilon - \eta_{2} - \gamma - \mu\) and \(J_{144} = \delta_{1} x_{1} - \delta_{2} - \eta_{3} - \mu\) has eigenvalues,

\(\omega_{1} = - \mu\), \(\omega_{2} = C_{m} \theta_{2} + \beta_{2} x_{1} - \varepsilon - \eta_{2} - \gamma - \mu\), \(\omega_{3} = \delta_{1} x_{1} - \delta_{2} - \eta_{3} - \mu\) and

\(\omega_{4} = - \frac{1}{{2x_{1} }}\left( \begin{gathered} \left( {\theta_{1} C_{h} x_{1} - x_{1}^{2} \beta_{1} + \eta_{1} x_{1} + \mu x_{1} + B} \right) \pm (C_{h}^{2} \theta_{1}^{2} x_{1}^{2} - 2\theta_{1} C_{h} x_{1}^{3} \beta_{1} + x_{1}^{4} \beta_{1}^{2} \hfill \\ + 2\theta_{1} C_{h} \eta_{1} x_{1}^{2} + 2\theta_{1} C_{h} \mu x_{1}^{2} - 2x_{1}^{3} \beta_{1} \eta_{1} + 2x_{1}^{3} \beta_{1} \mu - 2B\theta_{1} C_{h} x_{1} - 2Bx_{1}^{2} \beta_{1} \hfill \\ \, + \eta_{1}^{2} x_{1}^{2} + 2\eta_{1} \mu x_{1}^{2} + \mu^{2} x_{1}^{2} - 2B\eta_{1} x_{1} - 2B\mu x_{1} + B^{2} )^{\frac{1}{2}} \hfill \\ \end{gathered} \right)\).

Recycling free equilibrium point \(E_{1}\) is asymptotically stable if following conditions hold:

  1. (i)

    \(\delta_{2} + \eta_{3} + \mu > \delta_{1} x_{1}\),

  2. (ii)

    \(\varepsilon + \eta_{2} + \gamma + \mu > C_{m} \theta_{2} + \beta_{2} x_{1}\), and

  3. (iii)

    \(B\left( {C_{h} \theta_{1} + \eta_{1} + x_{1} } \right) > \beta_{1} \mu x_{1}^{2}\).

\(\square\)

Theorem 3.1.3

The dumping free equilibrium point \(E_{2}\) of model is locally asymptotically stable with conditions.

Proof

Let \(x_{2} = \frac{{\delta_{2} + \eta_{3} + \mu }}{{\delta_{1} }}\) and \(x_{3} = \frac{{B - \mu x_{2} }}{{\eta_{3} + \mu }}\) and the Jacobian matrix at \(E_{2}\) is

$$J_{2} = \left[ {\begin{array}{*{20}c} { - \delta_{1} x_{3} - \mu } & { - \beta_{1} x_{2} } & { - \beta_{2} x_{2} } & { - \delta_{1} x_{2} + \delta_{2} } & 0 \\ 0 & {J_{222} } & \varepsilon & 0 & 0 \\ 0 & 0 & {J_{233} } & 0 & 0 \\ {x_{3} \delta_{1} } & 0 & \gamma & {\delta_{1} x_{2} - \delta_{2} - \eta_{3} - \mu } & 0 \\ 0 & {\eta_{1} } & {\eta_{2} } & {\eta_{3} } & { - \mu } \\ \end{array} } \right]$$

where \(J_{222} = - C_{h} \theta_{1} + \beta_{1} x_{2} - \eta_{1} - \mu\), \(J_{233} = C_{m} \theta_{2} + \beta_{2} x_{2} - \varepsilon - \eta_{2} - \gamma - \mu\) has eigenvalues, \(\omega_{1} = - \mu\), \(\omega_{2} = - C_{h} \theta_{1} + \beta_{1} x_{2} - \eta_{1} - \mu\), \(\omega_{3} = C_{m} \theta_{2} + \beta_{2} x_{2} - \varepsilon - \eta_{2} - \gamma - \mu\) and \(\omega_{4} = - \frac{1}{2}\left( \begin{gathered} ( - \delta_{1} x_{2} + x_{3} \delta_{1} + \delta_{2} + \eta_{3} + 2\mu ) \pm (\delta_{1}^{2} x_{2}^{2} - \delta_{1}^{2} x_{2} x_{3} + \delta_{1}^{2} x_{3}^{2} - 2\delta_{1} \delta_{2} x_{3} + \eta_{3}^{2} \hfill \\ + 2\delta_{1} \delta_{2} x_{3} - 2\delta_{1} \eta_{3} x_{2} + \delta_{2}^{2} + 2\delta_{2} \eta_{3} ) \hfill \\ \end{gathered} \right)^{\frac{1}{2}}\).

Dumping free equilibrium point \(E_{2}\) is asymptotically stable if following conditions hold:

  1. (i)

    \(C_{h} \theta_{1} + \eta_{1} + \mu > \beta_{1} \left( {\frac{{\delta_{2} + \eta_{3} + \mu }}{{\delta_{1} }}} \right)\),

  2. (ii)

    \(\varepsilon + \eta_{2} + \gamma + \mu > C_{m} \theta_{2} + \beta_{2} \left( {\frac{{\delta_{2} + \eta_{3} + \mu }}{{\delta_{1} }}} \right)\) and

  3. (iii)

    \(\left( {\eta_{3} + \mu } \right)(x_{3} \delta_{1} + \mu ) + \mu \delta_{2} > \mu \left( {\delta_{2} + \eta_{3} + \mu } \right)\).

\(\square\)

Theorem 3.1.4

The endemic equilibrium point \(E^{*} \left( {P_{L}^{*} ,B_{n}^{*} ,D^{*} ,R_{C}^{*} ,P^{*} } \right)\) of model is locally asymptotically stable with conditions.

Proof

Let, \(x_{11} = \beta_{1} B_{n}^{*} + \beta_{2} D^{*} + R_{C}^{*} \delta_{1} + \mu\), \(x_{22} = C_{h} \theta_{1} - \beta_{1} P_{L}^{*} + \eta_{1} + \mu\),

\(x_{33} = \varepsilon + \eta_{2} + \gamma + \mu - C_{m} \theta_{2} - \beta_{2} P_{L}^{*}\) and \(x_{44} = \delta_{2} + \eta_{3} + \mu - \delta_{1} P_{L}^{*}\).

Jacobian matrix at \(E^{*}\) is,\(J^{*} = \left[ {\begin{array}{*{20}c} { - x_{11} } & { - \beta_{1} P_{L}^{*} } & { - \beta_{2} P_{L}^{*} } & { - \delta_{1} P_{L}^{*} + \delta_{2} } & 0 \\ {\beta_{1} B_{n}^{*} } & { - x_{22} } & \varepsilon & 0 & 0 \\ {\beta_{2} D^{*} } & 0 & { - x_{33} } & 0 & 0 \\ {R_{C}^{*} \delta_{1} } & 0 & \gamma & { - x_{44} } & 0 \\ 0 & {\eta_{1} } & {\eta_{2} } & {\eta_{3} } & { - \mu } \\ \end{array} } \right]\) and has characteristic equation, \(\lambda^{5} + a_{1} \lambda^{4} + a_{2} \lambda^{3} + a_{3} \lambda^{2} + a_{4} \lambda + a_{5} = 0\), where

$$a_{1} = \mu + x_{44} + x_{33} + x_{22} + x_{11}$$
$$\begin{gathered} a_{2} = R_{C}^{*} \delta_{1} \left( {P_{L}^{*} \delta_{1} - \delta_{2} } \right) + B_{n}^{*} P_{L}^{*} \beta_{1}^{2} + D^{*} P_{L}^{*} \beta_{2}^{2} + \mu \left( {x_{11} + x_{22} + x_{33} + x_{44} } \right) \hfill \\ \,\,\,\,\,\, + \left( {x_{11} + x_{44} } \right)\left( {x_{22} + x_{33} } \right) + x_{11} x_{44} + x_{22} x_{33} \hfill \\ \end{gathered}$$
$$\begin{gathered} a_{3} = \left( {P_{L}^{*} \delta_{1} - \delta_{2} } \right)\left( {D^{*} \beta_{2} \gamma + R_{C}^{*} \delta_{1} \left( {x_{22} + x_{33} + \mu } \right)} \right) + \left( {x_{11} x_{22} + B_{n}^{*} P_{L}^{*} \beta_{1}^{2} } \right)\left( {x_{33} + x_{44} } \right) \hfill \\ \,\,\,\,\,\, + x_{33} x_{44} (x_{11} + x_{22} ) + \mu \left( {x_{11} x_{44} + x_{22} x_{33} + \left( {x_{22} + x_{33} } \right)\left( {x_{11} + x_{44} } \right)} \right) + D^{*} P_{L}^{*} \beta_{2}^{2} (x_{22} \hfill \\ \,\,\,\,\, + x_{44} + \mu ) + P_{L}^{*} \beta_{1} (D^{*} \beta_{2} \varepsilon + B_{n}^{*} \beta_{1} \mu ) \hfill \\ \end{gathered}$$
$$\begin{gathered} a_{4} = \mu \left( {x_{33} + x_{44} } \right)\left( {B_{n}^{*} P_{L}^{*} \beta_{1}^{2} + x_{11} x_{22} } \right) + \mu D^{*} P_{L}^{*} \beta_{1} \beta_{2} \varepsilon + \mu D^{*} \beta_{2}^{2} P_{L}^{*} \left( {x_{22} + x_{44} } \right) \hfill \\ \,\,\,\,\,\, + \left( {P_{L}^{*} \delta_{1} - \delta_{2} } \right)\,\left[ {D^{*} \beta_{2} \gamma \left( {\mu + x_{22} } \right) + R_{C}^{*} \delta_{1} \left( {\mu \left( {x_{22} + x_{33} } \right) + x_{22} x_{33} } \right)} \right] + x_{33} x_{44} (\mu \left( {x_{11} + x_{22} } \right) \hfill \\ \,\,\,\,\,\, + B_{n}^{*} P_{L}^{*} \beta_{1}^{2} + x_{11} x_{22} ) + D^{*} P_{L}^{*} \beta_{2} x_{44} \left( {\beta_{1} \varepsilon + \beta_{2} x_{22} } \right) \hfill \\ \end{gathered}$$
$$a_{5} = \mu (x_{22} (P_{L}^{*} \delta_{1} - \delta_{2} )(D^{*} \beta_{2} \gamma + R_{C}^{*} \delta_{1} x_{33} ) + x_{33} x_{44} (B_{n}^{*} P_{L}^{*} \beta_{1}^{2} + x_{11} x_{22} ) + D^{*} P_{L}^{*} \beta_{2} x_{44} (\beta_{1} \varepsilon + \beta_{2} ))$$

A criterion satisfies if all coefficients \(a_{i}\)’s are positive. This gives condition \(P_{L}^{*} \delta_{1} > \delta_{2}\).\(\square\)

Global stability

A graph is basically a pair of sets \(G = (V,E)\), where \(V\) is the set of vertices and \(E\) is the set of edges, formed by pairs \((i,j)\) of vertices. \((i,j)\) stands for the initial vertex and the terminal vertex, respectively. If these vertices are same that is \(i = j\) known as a self-loop, it connects a vertex to itself. A directed graph is made up of a set of vertices which are connected by edges, where these edges have a direction associated with their vertices. A directed graph has path in which the edges are in the same direction is known as directed path. Out-degree \((d^{ + } (i))\) of refers to the number of edges incident from initial vertex \(i\) and the number of edges away from the vertex \(i\), is denoted by in-degree \((d^{ - } (i))\). A weighted graph directed graph \((G,\,A)\) where \(A = (a_{ij} )_{n \times n}\), \(a_{ij} > 0\) is weight of each edge with numerical positive weight if it exists otherwise zero. Product of weight on all edges gives the weight \(w(K)\) of sub-graph. The root vertex has degree one is called root tree. The sub-graph contains all vertices with minimum number of edges are called a spanning tree. The Laplacian matrix \(L = (l_{ij} )\) of \(G\) is defined as:

$$l_{ij} = \left\{ \begin{gathered} - a_{ij} ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,i \ne j, \hfill \\ \sum\nolimits_{i \ne k} {a_{ik} ,\,\,\,\,\,\,i = k.} \hfill \\ \end{gathered} \right.$$
(2)

Theorem 3.2.1 (Kirchhoff’s matrix tree theorem)

For \(n \ge 2\), assume that \(c_{i}\) is the cofactor of \(l_{ii}\) in \(L\). Then \(c_{i} = \sum\nolimits_{{T \in T_{i} }} {{\mathcal{W}}(T),\,i = 1,\,2,\,...,n,}\) where \(T_{i}\) is the set of all spanning tree \(T\) of graph \((G,\,A)\) that are rooted at vertex \(i\). Moreover, if \((G,\,A)\) is strongly connected, then \(c_{i} > 0\) for \(1 \le i \le n\).

Lemma 3.2.1

Let \(c_{i}\) be as given in Kirchhoff’s matrix tree theorem. If \(a_{ij} > 0\) and \(d^{ + } (j) = 1\) for some \(1 \le i,j \le n\), then \(c_{i} a_{ij} = \sum\limits_{k = 1}^{n} {c_{j} a_{jk} }\).

Lemma 3.2.2

Let \(c_{i}\) be as given in the Kirchhoff matrix tree theorem. If \(a_{ij} > 0\) and \(d^{ - } (i) = 1\) for some \(1 \le i,j \le n\), then \(c_{i} a_{ij} = \sum\nolimits_{k = 1}^{n} {c_{k} a_{ki} }\).

Theorem 3.2.2

Suppose that the following assumptions are satisfied:

  1. 1.

    There exist functions \(V_{i} :U \to {\mathbb{R}},\,G_{ij} :U \to {\mathbb{R}}\) and constants \(a_{ij} > 0\) such that for every \(1 \le i \le n\), \(V^{\prime}_{i} \le \sum\nolimits_{j = 1}^{n} {G_{ij} (x)}\) for \(x \in U\).

  2. 2.

    For \(M = [a_{ij} ]\), each directed cycle \(C\) of \((G,\,M)\) has \(\sum\limits_{(s,\,r) \in \varepsilon (C)} {G_{rs} (x) \le 0}\) for \(x \in U\), where \(\varepsilon (C)\) denotes the arc set of the directed cycle \(C\).

Then, the function \(V(x) = \sum\limits_{i = 1}^{n} {c_{i} V_{i} (x)}\), with constants \(c_{i} \ge 0\) as given in the theorem 3.2.1,

satisfies \(V^{\prime} \le 0\), hence, \(V\) is a Lyapunov function for the system.

Theorem 3.2.3

The endemic equilibrium point \(E^{*} \left( {P_{L}^{*} ,B_{n}^{*} ,R_{C}^{*} ,D^{*} ,P^{*} } \right)\) is globally asymptotically stable.

Proof

Using graph theoretical results for global stability, we generate Lyapunov function \(V(t)\) and each \(V_{i}\) is defined as,

\(V_{1} = P_{L} - P_{L}^{*} - P_{L}^{*} ln\frac{{P_{L} }}{{P_{L}^{*} }},\) \(V_{2} = B_{n} - B_{n}^{*} - B_{n}^{*} ln\frac{{B_{n} }}{{B_{n}^{*} }},\) \(V_{3} = D - D^{*} - D^{*} ln\frac{D}{{D^{*} }},\)\(V_{4} = R_{C} - R_{C}^{*} - R_{C}^{*} ln\frac{{R_{C} }}{{R_{C}^{*} }}\) and \(V_{5} = P - P^{*} - P^{*} ln\frac{P}{{P^{*} }}\).

Now, each \(V_{i}\), for \(1 \le i \le 5\) differentiating with respect to \(t\) we have,

$$\begin{aligned} V_{1}^{\prime } & = \left( {1 - \frac{{P_{L}^{*} }}{{P_{L} }}} \right)P_{L}^{\prime } = \left( {1 - \frac{{P_{L}^{*} }}{{P_{L} }}} \right)(B - \beta_{1} P_{L} B_{n} - \beta_{2} P_{L} D - \delta_{1} P_{L} R_{C} + \delta_{2} R_{C} - \mu P_{L} ) \\ & = \beta_{1} P_{L}^{*} B_{n}^{*} \left( {1 - \frac{{P_{L}^{*} }}{{P_{L} }}} \right)\left( {1 - \frac{{P_{L} B_{n} }}{{P_{L}^{*} B_{n}^{*} }}} \right) + \beta_{2} P_{L}^{*} D^{*} \left( {1 - \frac{{P_{L}^{*} }}{{P_{L} }}} \right)\left( {1 - \frac{{P_{L} D}}{{P_{L}^{*} D^{*} }}} \right) \\ & \quad + \delta_{1} P_{L}^{*} R_{C}^{*} \left( {1 - \frac{{P_{L}^{*} }}{{P_{L} }}} \right)\left( {1 - \frac{{P_{L} R_{C} }}{{P_{L}^{*} R_{C}^{*} }}} \right) - \delta_{2} R_{C}^{*} \left( {1 - \frac{{P_{L}^{*} }}{{P_{L} }}} \right)\left( {1 - \frac{{R_{C} }}{{R_{C}^{*} }}} \right) \\ & \quad + \mu P_{L}^{*} \left( {1 - \frac{{P_{L}^{*} }}{{P_{L} }}} \right)\left( {1 - \frac{{P_{L} }}{{P_{L}^{*} }}} \right) \\ & \le a_{12} G_{12} + a_{13} G_{13} + a_{14} G_{14} \\ \end{aligned}$$
$$\begin{aligned} V_{2}^{\prime } & = \left( {1 - \frac{{B_{n}^{*} }}{{B_{n} }}} \right)\left( {\beta_{1} P_{L} B_{n} + \varepsilon D - \eta_{1} B_{n} - \mu B_{n} - \theta_{1} C_{h} B_{n} } \right) \\ & \le \beta P_{L}^{*} B_{n}^{*} \left( {1 - \frac{{B_{n}^{*} }}{{B_{n} }}} \right)\left( {1 - \frac{{P_{L} B_{n} }}{{P_{L}^{*} B_{n}^{*} }}} \right) + \varepsilon D^{*} \left( {1 - \frac{{B_{n}^{*} }}{{B_{n} }}} \right)\left( {1 - \frac{D}{{D^{*} }}} \right) \\ & = a_{21} G_{21} + a_{23} G_{23} \\ \end{aligned}$$
$$\begin{aligned} V_{3}^{\prime } & = \left( {1 - \frac{{D^{*} }}{D}} \right)\left( {\beta_{2} P_{l} D - \varepsilon D - \eta_{2} D - \gamma D - \mu D + \theta_{2} C_{m} D} \right) \\ & \le \beta_{2} P_{L}^{*} D^{*} \left( {1 - \frac{{D^{*} }}{D}} \right)\left( {1 - \frac{{P_{L} D}}{{P_{L}^{*} D^{*} }}} \right) + \theta_{2} C_{m} D^{*} \left( {1 - \frac{{D^{*} }}{D}} \right)\left( {1 - \frac{D}{{D^{*} }}} \right) \\ & = a_{31} G_{31} + a_{33} G_{33} \\ \end{aligned}$$
$$\begin{aligned} V_{4}^{\prime } & = \left( {1 - \frac{{R_{C}^{*} }}{{R_{C} }}} \right)\left( {\delta_{1} P_{L} R_{C} - \delta_{2} R_{C} + \gamma R_{C} - \eta_{3} R_{C} - \mu R_{C} } \right) \\ & \le \delta_{1} P_{L}^{*} R_{C}^{*} \left( {1 - \frac{{R_{C}^{*} }}{{R_{C} }}} \right)\left( {1 - \frac{{P_{L} R_{C} }}{{P_{L}^{*} R_{C}^{*} }}} \right) + \gamma D^{*} \left( {1 - \frac{{R_{C}^{*} }}{{R_{C} }}} \right)\left( {1 - \frac{D}{{D^{*} }}} \right) \\ & = a_{41} G_{41} + a_{43} G_{43} \\ \end{aligned}$$

and

$$\begin{aligned} V_{5}^{\prime } & = \left( {1 - \frac{{P^{*} }}{P}} \right)\left( {\eta_{1} B_{n} + \eta_{2} D + \eta_{3} R_{C} - \mu P} \right) \\ & \le \eta_{1} B_{n}^{*} \left( {1 - \frac{{P^{*} }}{P}} \right)\left( {1 - \frac{{B_{n} }}{{B_{n}^{*} }}} \right) + \eta_{2} D^{*} \left( {1 - \frac{{P^{*} }}{P}} \right)\left( {1 - \frac{D}{{D^{*} }}} \right) + \eta_{3} R_{C}^{*} \left( {1 - \frac{{P^{*} }}{P}} \right)\left( {1 - \frac{{R_{C} }}{{R_{C}^{*} }}} \right) \\ & = a_{52} G_{52} + a_{53} G_{53} + a_{54} G_{54} \\ \end{aligned}$$

where \(a_{12} = a_{21} = \beta_{1} P_{L}^{*} B_{n}^{*}\), \(a_{13} = a_{31} = \beta_{2} P_{L}^{*} D^{*}\), \(a_{14} = a_{41} = \delta_{1} P_{L}^{*} R_{C}^{*}\), \(a_{23} = \varepsilon D^{*}\), \(a_{33} = \theta_{2} C_{m} D^{*}\), \(a_{43} = \gamma D^{*}\), \(a_{52} = \eta_{1} B_{n}^{*}\), \(a_{53} = \eta_{2} D^{*}\) and \(a_{54} = \eta_{3} R_{C}^{*}\) \(\square\).

This above calculation leads to a weighted graph containing each compartment as below:

This weighted graph \((G,\,A)\) includes four vertices presenting the three cycles \(G_{12} + G_{21} = 0,\) \(G_{13} + G_{31} = 0\) and \(G_{14} + G_{41} = 0\) (Fig. 2). Theorem 3.2.2 gives the constants \(c_{i}\)’s, for \(1 \le i \le 5\) to construct a Lyapunov function \(V(x) = \sum\nolimits_{i = 1}^{n} {c_{i} V_{i} (x)}\). Lemma 3.2.2 helps to relate the constants \(c_{i}\)’s which turns out to,

$${{d}^{-}}(3)=1\quad \Rightarrow {{c}_{3}}{{a}_{31}}={{c}_{1}}{{a}_{13}}+{{c}_{2}}{{a}_{23}}+{{c}_{4}}{{a}_{43}}+{{c}_{5}}{{a}_{53}}$$
Fig. 2
figure 2

The weighted graph

Full size image

Let us take \(c_{1} = k_{1} ,c_{2} = k_{2} ,c_{4} = k_{3} ,c_{5} = k_{4}\)

$$\Rightarrow c_{3} = \frac{{k_{1} \beta_{2} P_{L}^{*} + k_{2} \varepsilon + k_{3\,} \gamma + k_{4} \eta_{2} }}{{\beta_{2} P_{L}^{*} }}$$

Since, \(V(t) = \sum\nolimits_{i = 1}^{5} {c_{i} V_{i} (t)} = c_{1} V_{1} + c_{2} V_{2} + c_{3} V_{3} + c_{4} V_{4} + c_{5} V_{5}\)

$$= k_{1} V_{1} + k_{2} V_{2} + \left( {\frac{{k_{1} \beta_{2} P_{L}^{*} + k_{2} \varepsilon + k_{3\,} \gamma + k_{4} \eta_{2} }}{{\beta_{2} P_{L}^{*} }}} \right)V_{3} + k_{3} V_{4} + k_{4} V_{5}$$

where \(k_{i}\)’s for \(1 \le i \le 4\) are arbitrary constants. \(\{ E^{*} \}\).

Here, \(V^{\prime} \le 0\) at equilibrium point i.e.,\(P_{L} = P_{L}^{*}\),\(B_{n} = B_{n}^{*}\),\(R_{C} = R_{C}^{*}\),\(D = D^{*}\) and \(P = P^{*}\) which suggest that \(\{ E^{*} \}\) is the only invariant set in int \((\Lambda )\) indicates that \(E^{*}\) is globally asymptotically stable (Harary 1969; West 1996).

Optimal investment in health and recycled machine policy

Optimal control theory deals with state equations and control variables for finding control by optimizing objective function. The purpose of this paper is to optimizing pollution. Therefore, the objective function is,

$$J(c_{i} ,\Lambda ) = \int\limits_{0}^{T} {(A_{1} P_{L}^{2} + } A_{2} B_{n}^{2} + A_{3} D^{2} + A_{4} R_{C}^{2} + A_{5} P^{2} + w_{1} C_{h}^{2} + w_{2} C_{m}^{2} )\,\,dt$$
(3)

where \(\Lambda\) denotes set of all compartmental variables, \(A_{1} ,A_{2} ,A_{3} ,A_{4} ,A_{5}\) denote non-negative weight constants for compartments \(P_{L} ,B_{n} ,D,R_{C} ,P\), respectively. \(w_{1}\) and \(w_{2}\) are the weight constants for investments on health policy \((C_{h} )\) and installing recycled machine policy \((C_{m} )\), respectively.

As the weight parameter \(w_{1}\) and \(w_{2}\) are constants of the cost applied on the density of burned and recycled plastic for both the policies, respectively, from which the optimal investment condition is normalized. \(C_{h}\) and \(C_{m}\) are the investments for optimizing the burning and recycling, respectively. Now, we will calculate both the values of investment policy from \(t = 0\) to \(t = T\) such that,

$$J(C_{h} (t),C_{m} (t)) = min\{ J(C_{h}^{*} ,\Lambda ),J(C_{m}^{*} ,\Lambda )/(C_{h} ,C_{m} ) \in \phi \}$$

where \(\phi\) is a smooth function on the interval \([0,1]\). The optimal investment policy denoted by \(C_{h}\) and \(C_{m}\) are found by accumulating all the integrands of Eq. (3) using the lower bounds and upper bounds, respectively, with the results of Fleming and Rishel (2012).

For minimizing the investment function in (3), using the Pontrygin’s principle from Pontryagin et al. (1986) by constructing Lagrangian function consisting of state equations and adjoint variables \(\lambda_{1} ,\lambda_{2} ,\lambda_{3} ,\lambda_{4} ,\lambda_{5}\) as follows:

$$\begin{aligned} L(\Lambda ,A_{i} ) & = A_{1} P_{L}^{2} + A_{2} B_{n}^{2} + A_{3} D^{2} + A_{4} R_{C}^{2} + A_{5} P^{2} + w_{1} C_{h}^{2} + w_{2} C_{m}^{2} \\ & \quad + \lambda_{1} (B - \beta_{1} P_{L} B_{n} - \beta_{2} P_{L} D - \delta_{1} P_{L} R_{C} + \delta_{2} R_{C} - \mu P_{L} ) \\ & \quad + \lambda_{2} (\beta_{1} P_{L} B_{n} + \varepsilon D - \eta_{1} B_{n} - \mu B_{n} - \theta_{1} C_{h} B_{n} ) \\ & \quad + \lambda_{3} (\beta_{2} P_{L} D - \varepsilon D - \eta_{2} D - \gamma D - \mu D + \theta_{2} C_{m} D) \\ & \quad + \lambda_{4} (\delta_{1} P_{L} R_{C} - \delta_{2} R_{C} + \gamma D - \eta_{3} R_{C} - \mu R_{C} ) \\ & \quad + \lambda_{5} (\eta_{1} B_{n} + \eta_{2} D + \eta_{3} R_{C} - \mu P) \\ \end{aligned}$$

The partial derivatives of the Lagrangian function with respect to each variable of the compartment gives the adjoint equation variables \(\lambda_{i} = (\lambda_{1} ,\lambda_{2} ,\lambda_{3} ,\lambda_{4} ,\lambda_{5} )\) corresponding to the system which are:

$$\mathop {\lambda_{1} }\limits^{ \bullet } = - \frac{\partial L}{{\partial P_{L} }} = - 2A_{1} P_{L} + (\lambda_{1} - \lambda_{2} )\beta_{1} B_{n} + (\lambda_{1} - \lambda_{3} )\beta_{2} D + (\lambda_{1} - \lambda_{4} )\delta_{1} R_{C} + \lambda_{1} \mu$$
$$\mathop {\lambda_{2} }\limits^{ \bullet } = - \frac{\partial L}{{\partial B_{n} }} = - 2A_{2} B_{n} + (\lambda_{1} - \lambda_{2} )\beta_{1} P_{L} + \eta_{1} (\lambda_{2} - \lambda_{5} ) + \lambda_{2} \mu + \lambda_{2} \theta_{1} C_{h}$$
$$\mathop {\lambda_{3} }\limits^{ \bullet } = - \frac{\partial L}{{\partial D}} = - 2A_{3} D + (\lambda_{1} - \lambda_{3} )\beta_{2} P_{L} + (\lambda_{3} - \lambda_{2} )\varepsilon + (\lambda_{3} - \lambda_{5} )\eta_{2} + (\lambda_{3} - \lambda_{4} )\gamma + \lambda_{3} \mu - \lambda_{3} \theta_{2} C_{m}$$
$$\mathop {\lambda_{4} }\limits^{ \bullet } = - \frac{\partial L}{{\partial R_{C} }} = - 2A_{4} R_{C} + (\lambda_{1} - \lambda_{4} )(\delta_{1} P_{L} - \delta_{2} ) + (\lambda_{4} - \lambda_{5} )\eta_{3} + \mu \lambda_{4}$$
$$\mathop {\lambda_{5} }\limits^{ \bullet } = - \frac{\partial L}{{\partial P}} = - 2A_{5} P + \lambda_{5} \mu$$

The necessary conditions for Lagrangian function \(L\) to be optimal are,

\(\mathop {C_{h} }\limits^{ \bullet } = - \frac{\partial L}{{\partial C_{h} }} = - 2w_{1} C_{h} + \lambda_{2} \theta_{1} B_{n} = 0\) and \(\mathop {C_{m} }\limits^{ \bullet } = - \frac{\partial L}{{\partial C_{m} }} = - 2w_{2} C_{m} - \lambda_{3} \theta_{2} D = 0\).

Hence, we get \(C_{h} = \frac{{\lambda_{2} \theta_{1} B_{n} }}{{2w_{1} }}\) and \(C_{m} = \frac{{ - \lambda_{3} \theta_{2} D}}{{2w_{2} }}\).

The whole computation gives the optimal investment conditions resulting as,

\(C_{h}^{*} = max\left( {a_{1} ,min\left( {b_{1} ,\frac{{\lambda_{2} \theta_{1} B_{n} }}{{2w_{1} }}} \right)} \right)\) and \(C_{m}^{*} = max\left( {a_{2} ,min\left( {b_{2} ,\frac{{ - \lambda_{3} \theta_{2} D}}{{2w_{2} }}} \right)} \right)\).

In this manner, analytical outcomes have been determined for optimized investment. Next section contains the numerical interpretation.

Result and discussion

Numerical simulation

This section illustrates the simulation results which are used to verify the efficacy of this existing model by using the parametric values given in Table 1.

Figure 3 consists of five activities, plastic; it’s burning, dumping, recycling and causes the pollution, which can be depicted from a graph. After approximately 24 days, industrial plastic is sent for dumping then after one month it is recycled; during that period, it is also burned and this results pollution in two months.

Fig. 3
figure 3

Transmission of pollution

Full size image

Figure 4 gives the idea that how total budget is functioning. Initially, for almost two years, it is increasing and then gradually decreases. For simulating the model, here we have considered the total budget as 1 (in 000′ $/ton). Figure 5 advocates that out of total budget, the investment in health policy \((C_{h} )\) is 30% by decreasing the burning of plastic and another in installing recycling machine policy \((C_{m} )\) is 60%. Both cost functions are increasing in same manner then with passage of time it decreases in accordance with the total budget.

Fig. 4
figure 4

Total budget

Full size image
Fig. 5
figure 5

Cost functions

Full size image

Figure 6a and b gives the effect of investment as cost functions on decreasing burning and installing recycling machine, respectively. Investments benefit that burning decreases by 14.88% which can be used for health policy for the society. In the same manner to promote plastic recycling, the cost is invested in installing recycling machine which results in recycling increases by 14.90%.

Fig. 6
figure 6

a Effect of \(C_{h}\) on burning b Effect of \(C_{m}\) on recycling

Full size image

These trajectory graphs in Fig. 7 are plotted with growth rate value of \(B\) = 60%. It recommends that the direction of both the process to pollution is toward to the solution of system (1) that is equilibrium point. As time increases or decreases for an identified period; trajectory remains approaches to critical point.

Fig. 7
figure 7

Trajectory curve of burning and recycling to pollution

Full size image

Figure 8 analyzes the global dynamical behavior of pollution due to dumped plastic. One can observe from this scatter diagram that dumped plastic garbage from industries emits the pollution. It is periodic in nature.

Fig. 8
figure 8

Pollution due to dumping

Full size image

Conclusion

Industrial dumped plastics are sent for either burning or recycling. With our increasing awareness, this paper is useful in how to invest in health policy by reducing the burning of industrial plastic and in installing recycling machine policy for dumped plastic. Local stability for nonlinear dynamic with its differential equations gives sufficient conditions. By using graph theory results, global stability implemented advocates that the model is globally asymptotically stable. This model has been extended by optimizing the cost function. Detailed computations along with its numerical simulation seek to show that the cost function is very effective for the model as it is concerned with the society by controlling pollution and invest in health policy. Supporting recycling is the one good approach to prevent dumped plastic pollution. The time has come and should know that only we people are the solution by either reducing or recycling the plastic usage by re-thinking our life style.