Introduction

Finding the new distributions for modeling the lifetime of the systems such as devices and organisms is an attractive topic in statistics, which is useful in some applied sciences such as biology and engineering. For this purpose, many researches have been published in the statistical literature. Some written books in this topic are Lawless [21], Deshpande and Purohit [12].

The simplest model in the lifetime data analysis is the exponential distribution. Also, the exponential distribution is the basis of many distributions in this topic. In the recent years, the modifications of the exponential distribution have been considered; e.g., the generalized exponential distribution by Gupta and Kundu [15,16,17,18], the exponentiated Weibull distribution by Mudholkar and Srivastava [27], the exponentiated gamma distribution by Nadarajah and Kotz [28], the exponential-geometric distribution by Adamidis and Loukas [3], the modified exponential-Poisson distribution by Preda et al. [29], the modified exponential distribution by Rasekhi et al. [32], the extended exponential geometric distribution by Louzada et al. [24], an extended-G geometric family by Cordeiro et al. [9], the complementary exponentiated exponential geometric distribution by Louzada et al. [23] and an extension of the exponential-geometric distribution by Adamidis et al. [2].

Recently, Bordbar and Nematollahi [7] proposed the modified exponential-geometric distribution via the operation of compounding based on Marshall and Olkin [26] scheme. Motivated to introduce a simple and flexible model to describe phenomenon with monotone hazard rates which are common in reliability and biological studies, the target of this paper is introducing a new model as a competitor for some existing distributions to fit on some data sets. In this purpose, we establish a new modified exponential-geometric (NMEG) distribution similar to the Bordbar and Nematollahi’s [7] idea, which perform better than some of the well-known distributions, especially that introduced by Bordbar and Nematollahi [7], in fitting on some real data sets in terms of some statistical criteria.

This paper is organized as follows: Section 2 introduces the new lifetime model. In Section 3, the various properties of the proposed distribution are investigated. Section 4 discusses finding the maximum likelihood estimators of the parameters. In Section 5, a Monte Carlo simulation study is conducted to investigate the performance of the maximum likelihood estimators. Finally, in Section 6, the proposed distribution is applied on three real data sets.

The NMEG distribution

Given a random variable Y with the distribution function \(F_Y(.)\), Marshall and Olkin [26] introduced a useful method to construct a new distribution function \(F_W(.;\alpha )\) corresponding to a random variable W, by adding a parameter \(\alpha \) as follows:

$$\begin{aligned} F_W(x;\alpha )=\frac{F_Y(x)}{F_Y(x)+\alpha (1-F_Y(x))},\quad x\in {\mathbb {R}},\alpha >0, \end{aligned}$$

where the distribution function \(F_Y(.)\) is called the baseline distribution.

Let us consider the exponential distribution with mean \(1/\beta \), as the baseline distribution. So, we have

$$\begin{aligned} F_W(x;\alpha ,\beta )=\frac{1-e^{-\beta x}}{1-(1-\alpha )e^{-\beta x}},\quad x>0,\alpha ,\beta >0. \end{aligned}$$

Also, the corresponding density function, denoted by \(f_W(.;\alpha ,\beta )\), is obtained as:

$$\begin{aligned} f_W(x;\alpha ,\beta )=\frac{\alpha \beta e^{-\beta x}}{(1-(1-\alpha ) e^{-\beta x})^2},\quad x>0,\alpha ,\beta >0. \end{aligned}$$

Let \(W_1,\ldots , W_Z,\) be a random sample from the density function \(f_W(.;\alpha ,\beta )\) and Z be a random independent variable of W, from the geometric distribution with the density function \(f_Z(x;p)=p (1-p)^{x-1}\), for a natural value of x. By considering the smallest order statistic in the sample \(W_1,\ldots ,W_Z,\) Bordbar and Nematollahi [7] introduced a new modified distribution; but we continue the topic by a minor change in this approach. Suppose that \( X=\max (W_{1},\ldots ,W_{Z})\). Thus, the conditional density function of the random variable X given \(Z=z\), \(f_{X|Z=z}(.;\alpha ,\beta )\), is obtained as following:

$$\begin{aligned} f_{X|Z=z}(x;\alpha ,\beta )= & {} \frac{\alpha \beta z e^{-\beta x}(1- e^{-\beta x})^{z-1}}{(1-{\bar{\alpha }}e^{-\beta x})^{z+1}},\\&\quad \quad x>0 , z\in {\mathbb {N}}, \alpha ,\beta >0, \end{aligned}$$

and consequently, the marginal density function of X is given by

$$\begin{aligned} f_{X}(x;\alpha ,\beta ,p)= & {} \frac{\alpha \beta p e^{-\beta x}}{(p-(p-\alpha )e^{-\beta x})^2}, \nonumber \\&\quad \quad x>0,\alpha ,\beta >0, 0<p<1. \end{aligned}$$
(1)

The latter density function is called the NMEG distribution which is denoted by \(X\sim \mathrm{NMEG}(\alpha ,\beta ,p)\) for the random variable X. In this paper, we intend to consider and investigate the NMEG distribution as previously mentioned. It can be easily seen that the survival function, \({\bar{F}}_{X}(x;\alpha ,\beta )\), and the hazard function, \(h_{X}(x;\alpha ,\beta )\), corresponding to the random variable X are given by

$$\begin{aligned} {\bar{F}}_{X}(x;\alpha ,\beta ,p)=\frac{\alpha e^{-\beta x}}{p-(p-\alpha )e^{-\beta x}}, \end{aligned}$$

and

$$\begin{aligned} h_{X}(x;\alpha ,\beta ,p)=\frac{\beta p}{p-(p-\alpha )e^{-\beta x}}, \end{aligned}$$

respectively. It is necessary to mention that \(\mathrm{NMEG}(\alpha ,\beta ,p)\) reduces to exponential distribution, when \(\alpha =p\). So, throughout paper we consider the case that \(\alpha \ne p\).

Statistical properties

In this section, various properties of the NMEG distribution including the shapes of the density and hazard functions, quantile function, characteristic function and moments, mean residual life and Shannon and Rényi entropies are discussed.

Shape of the density and hazard functions

It is easily seen that the derivative density function in (1) is obtained as :

$$\begin{aligned}&f^{\prime }_X(x;\alpha ,\beta ,p)\\&\quad =\frac{2\alpha \beta ^2 p (\alpha -p) e^{-2\beta x}-\alpha \beta ^2 p e^{-\beta x}(p-(p-\alpha )e^{-\beta x})}{(p-(p-\alpha )e^{-\beta x})^3}. \end{aligned}$$

Obviously, \(\alpha <p\) implies the negativity of the derivative and consequently the reduction of \( f_X(x;\alpha ,\beta ,p)\). If \(\alpha >p\), the value \(x_0=-\frac{1}{\beta }\ln \frac{p}{\alpha -p}\) is the unique root of the equation \(f^{\prime }_X(x;\alpha ,\beta ,p)=0\), such that \(x_0\) maximizes \( f_X(x;\alpha ,\beta ,p)\). Therefore, \(x_0 < 0\) (\(p<\alpha <2p\)) implies the reduction of \( f_X(x;\alpha ,\beta ,p)\) in \(x\ge 0\), and \(x_0 >0\) (\(\alpha >2p\)) implies the increase of \( f_X(x;\alpha ,\beta ,p)\) in \(0\le x\le x_0\) and reduction of \( f_X(x;\alpha ,\beta ,p)\) in \(x\ge x_0\). Thus, the mode of X, denoted by \(M_X\), can be simplified as:

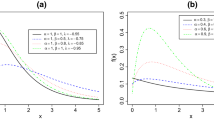
$$\begin{aligned} M_X=\left\{ \begin{array}{rl} 0 , &{} \alpha < 2p ,\\ -\frac{1}{\beta }\ln (\frac{p}{\alpha -p}), &{} \alpha \ge 2p. \end{array} \right. \end{aligned}$$

Left panel of Fig. 1 that represents the plots of density functions for different values of parameters, agrees with the obtained results for the shape of density function.

Clearly, derivative of the hazard function is

$$\begin{aligned} h^\prime _{X}(x,;\alpha ,\beta ,p)= & {} -\frac{\beta ^2 p (p-\alpha )e^{-\beta x}}{(p-(p-\alpha )e^{-\beta x})^2}. \end{aligned}$$

Thus, the hazard function is decreasing if \(\alpha <p\), and it is increasing if \(\alpha >p\). Furthermore, we have

$$\begin{aligned} \lim _{x\rightarrow \infty }h(x;\alpha ,\beta ,p)=\lim _{x\rightarrow \infty }\frac{\beta p}{p-(p-\alpha )e^{-\beta x}}=\beta , \end{aligned}$$

i.e., for large values of x, the hazard function does not depend on \(\alpha \) and p. Right panel of Figure 1 that represents the plots of the hazard functions for different values of parameters, agrees with the all results of this subsection.

Quantile function

The quantile function of \(X\sim \mathrm{NMEG}(\alpha ,\beta ,p)\), denoted by \(Q(u;\alpha ,\beta ,p)\), for \(0<u<1\) is obtained by solving the equation \(F_X(Q(u);\alpha ,\beta ,p)=u\); which is:

$$\begin{aligned} Q(u;\alpha ,\beta ,p)=-\frac{1}{\beta } \ln \left( \frac{p(1-u)}{\alpha u+p(1-u)}\right) . \end{aligned}$$

So, the median of the random variable X, denoted by \(m_X\), is obtained in the following form:

$$\begin{aligned} m_X=Q(0.5;\alpha ,\beta ,p)=-\frac{1}{\beta } \ln \left( \frac{p}{\alpha +p}\right) . \end{aligned}$$

In order to do a Monte Carlo simulation, assume that U be a random variable uniformly distributed on (0,1). Based on inverse transform method, the random variable

$$\begin{aligned} X=-\frac{1}{\beta } \ln \left( \frac{p(1-U)}{\alpha U+p(1-U)}\right) , \end{aligned}$$
(2)

is distributed as \(\mathrm{NMEG}(\alpha ,\beta ,p)\).

Fig. 1
figure 1

The plots of the density and hazard functions for \(\beta=1\), \(p=0.5\) and the values \(\alpha =0.1,0.3,0.8,5\)

Full size image

Characteristic function

In order to obtain Characteristic function, a necessary function which is called hypergeometric function (Bailey [5]) can be applied:

$$\begin{aligned} F_{2,1}(a,b,c,z)=\frac{\varGamma (c)}{\varGamma (b) \varGamma (c-b)}\int _{0}^1\frac{u^{b-1}(1-u)^{c-b-1}}{(1-zu)^a} du, \end{aligned}$$
(3)

such that \(c>b>0\).

Let X be a random variable with \(X\sim \mathrm{NMEG}(\alpha ,\beta ,p)\). Thus, to obtain the characteristic function of X, denoted by \(\varPhi _X(t)\), we have

$$\begin{aligned} \varPhi _{X}(t)= & {} \int _0^\infty e^{itx} \frac{\alpha \beta p e^{-\beta x}}{(p-(p-\alpha ) e^{-\beta x})^2}dx\\= & {} \alpha p \int _0^1 \frac{u^{-it/\beta }}{(p-(p-\alpha )u)^2}du\\= & {} \frac{\alpha p}{p^2} \int _0^1 \frac{u^{-it/\beta }}{(1-\frac{p-\alpha }{p}u)^2}du \\= & {} \frac{\alpha \beta }{p(\beta -it)}F_{2,1}(2,1-\frac{it}{\beta } ,2-\frac{it}{\beta },1-\frac{\alpha }{p} ), \end{aligned}$$

where \(i=\sqrt{-1}\), and the third quality arises from the change of variable \(u=e^{-\beta x}\).

Moments

In order to present a closed form for the moments, we need an important function called the polylogarithm function L(z, r), which is a generalization of Euler’s and Landen’s functions. This function has some integral representations; but we state the represented form in Lewin [22] p. 236 and Prudnikov et al. [31], p. 762, as follows:

$$\begin{aligned} L(z,r)=\frac{z}{\varGamma (r)}\int _{0}^{\infty }\frac{u^{r-1}}{e^u-z} du. \end{aligned}$$

For a nonnegative integer value r, and for any \(z<1\), Jodrá [19] represented another form for L(z, r), which is given by

$$\begin{aligned} L(z,r)=\frac{z}{\varGamma (r+1)}\int _{0}^{1}\frac{(-\ln u)^r}{(1-zu)^2} du. \end{aligned}$$

Here, we use the latter representation of the polylogarithm function.

Let X be a random variable with \(X\sim \mathrm{NMEG}(\alpha ,\beta ,p)\). To obtain the non-central moments of X, for \(r \in {\mathbb {N}}\), we have

$$\begin{aligned} E[X^r]= & {} \int _0^{\infty }x^r \frac{\alpha \beta p e^{-\beta x}}{(p-(p-\alpha )e^{-\beta x})^2} dx\\= & {} \frac{\alpha p}{\beta ^r} \int _0^1 \frac{(-\ln u)^r}{(p-(p-\alpha )u)^2} du\\= & {} \frac{\alpha r! }{\beta ^r (p-\alpha )} L(1-\frac{\alpha }{p}, r). \end{aligned}$$

where the third inequality comes from changing the variable of integration to \(u=e^{-\beta x}\). In the special case \(r=1\),

$$\begin{aligned} E[X]= & {} \frac{\alpha }{\beta (p-\alpha )} L(1-\frac{\alpha }{p},1)=-\frac{\alpha }{\beta (p-\alpha )}\ln (\frac{\alpha }{p})\\= & {} \frac{\ln p-\ln \alpha }{\beta (p-\alpha )}\alpha . \end{aligned}$$

where the second equality follows from the fact that \(L(-z,1)=-\ln (1+z)\); see Adamidis and Loukas [3]. Also, the variance of X is obtained as:

$$\begin{aligned} Var[X]= & {} \frac{ 2\alpha }{\beta ^{2} (p-\alpha )} L(1-\frac{\alpha }{p},2)-\left( \frac{\ln p-\ln \alpha }{\beta (p-\alpha )}\alpha \right) ^2\\= & {} \frac{ \alpha }{\beta ^{2} (p-\alpha )} \left( 2 L(1-\frac{\alpha }{p},2)-\frac{(\ln p-\ln \alpha )^2}{ p-\alpha }\alpha )\right) . \end{aligned}$$

Mean residual life

Given that a unit is of age x, the remaining life after time x is random. The expected value of this random residual life is called the mean residual life (MRL) at time x. According to Cox [10], for a distribution with a finite mean, the MRL completely determines the distribution. Let X be a random variable with \(X\sim \mathrm{NMEG}(\alpha ,\beta ,p)\). The mean residual life of X, denoted by \(\mu (.;\alpha ,\beta ,p)\), is obtained as follows:

$$\begin{aligned} \mu (x;\alpha ,\beta ,p)= & {} \frac{1}{{\bar{F}}_{X}(x;\alpha ,\beta ,p)} \int _x^\infty \frac{\alpha e^{-\beta t}}{p-(p-\alpha ) e^{-\beta t}}dt\\= & {} \frac{1}{{\bar{F}}_{X}(x;\alpha ,\beta ,p)} \frac{\alpha }{\beta } \int _0^{e^{-\beta x}}\frac{du}{p-(p-\alpha )u}\\= & {} -\frac{p-(p-\alpha )e^{-\beta x}}{\beta (p-\alpha ) e^{-\beta x} }\\&\left( \ln (p-(p-\alpha )e^{-\beta x})-\ln p\right) , \end{aligned}$$

where the last equality follows changing variable \(u=e^{-\beta t}\). It is clear that E[X] is also obtained by \(\mu (0;\alpha ,\beta ,p)\).

Entropies

Entropy is a measure of variation or uncertainty of a random variable X. Two popular entropy measures are Rényi and Shannon entropies that introduced by Shannon [34] and Rényi [33], respectively. This subsection provides the closed forms for Shannon and Rényi entropies. The following theorem investigates the Shannon entropy of X.

Theorem 1

Let X be a random variable with \(X\sim \mathrm{NMEG}(\alpha ,\beta ,p)\). The Shannon entropy of X, denoted by \(\eta _X\), is given by

$$\begin{aligned} \eta _X= & {} -\ln \alpha -\ln \beta -\ln p+\alpha \frac{\ln p - \ln \alpha }{p-\alpha }\\&+\frac{2\alpha p}{\alpha -p} \left( \frac{1+\ln p}{p}-\frac{1+\ln \alpha }{\alpha }\right) . \end{aligned}$$

Proof

According to definition of the Shannon entropy, we have

$$\begin{aligned} \eta _{X}= & {} E[-\ln f_X(X;\alpha ,\beta ,p)]\\= & {} -\ln \alpha -\ln \beta -\ln p+\alpha \frac{\ln p - \ln \alpha }{p-\alpha }\\&+2 \int _0^\infty \ln \left( p-(p-\alpha )e^{-\beta x}\right) \frac{\alpha \beta p e^{-\beta x}}{\left( p-(p-\alpha )e^{-\beta x}\right) ^2}dx\\= & {} -\ln \alpha -\ln \beta -\ln p+\alpha \frac{\ln p - \ln \alpha }{p-\alpha }\\&+\frac{2\alpha p}{\alpha -p}\int _p^\alpha \frac{\ln t}{t^2}dt\\= & {} -\ln \alpha -\ln \beta -\ln p+\alpha \frac{\ln p - \ln \alpha }{p-\alpha }\\&+\frac{2\alpha p}{\alpha -p} \left( \frac{1+\ln p}{p}-\frac{1+\ln \alpha }{\alpha }\right) , \end{aligned}$$

where the third equality follows the changing variable \(t=p+(\alpha -p)e^{-\beta x}\), and the last equality is implied using the integral parts.

\(\square \)

Theorem 2

Let X be a random variable with \(X\sim \mathrm{NMEG}(\alpha ,\beta ,p)\). The Rényi entropy of X, denoted by \(R_X(\rho )\) for \(\rho >0\) and \(\rho \ne 0\), is given by

$$\begin{aligned} R_X(\rho )= & {} \frac{1}{1-\rho }\left( \rho (\ln \alpha -\ln p)+(\rho -1)\ln \beta -\ln \rho +\ln F_{2,1}\right. \\&\left. (2\rho ,\rho , 1+\rho ,1-\frac{\alpha }{p})\right) . \end{aligned}$$

Proof

By the definition of the Rényi entropy,

$$\begin{aligned} R_{X}(\rho )= & {} \frac{1}{1-\rho }\ln \left( \int _0^\infty \left( f(x)\right) ^{\rho }dx\right) \\= & {} \frac{1}{1-\rho }\ln \left( (\alpha \beta p)^{\rho } \int _0^\infty \frac{e^{-\rho \beta x}}{\left( (p-(p-\alpha )e^{-\beta x}\right) ^{2\rho }}dx\right) \\= & {} \frac{\rho \ln (\alpha \beta p)}{1-\rho }+ \frac{1}{1-\rho } \ln \left( \frac{1}{\beta } \int _0^1 \frac{u^{\rho -1}}{\left( p-(p-\alpha )u\right) ^{2\rho }}du\right) \\= & {} \frac{\rho \ln (\alpha \beta p)}{1-\rho }+ \frac{1}{1-\rho } \ln \left( \frac{1}{\beta p^{2\rho }}\right. \\&\left. \frac{\varGamma (\rho )\varGamma (1)}{\varGamma (1+\rho )}F_{2,1}(2\rho , \rho , 1+\rho , 1-\frac{\alpha }{p})\right) \\= & {} \frac{1}{1-\rho }\left( \rho (\ln \alpha -\ln p)+(\rho -1)\ln \beta \right. \\&\left. -\ln \rho +\ln F_{2,1}(2\rho ,\rho , 1+\rho ,1-\frac{\alpha }{p})\right) , \end{aligned}$$

where the third equality follows from change variable \(u=e^{-\beta x}\) and the fourth equality follows the equation (3) by the values \(a=2\rho \), \(b=\rho \), \(c=\rho +1\) and \(z=1-\frac{\alpha }{p}\). \(\square \)

Maximum likelihood estimation (MLE)

The MLEs of the parameters of the NMEG distribution are investigated. Let \({\varvec{x}}=(x_1,\ldots ,x_n)\) be a realization of a random sample from a \(\mathrm{NMEG}(\alpha ,\beta ,p)\) distributed population. The log-likelihood function of the parameters is given by

$$\begin{aligned}&\ell _{n}(\alpha , \beta , p;{\varvec{x}})=n\ln (\alpha \beta p)- \beta \sum \limits _{i={1}}^{n}x_{i}-2 \sum \limits _{i={1}}^{n}\ln \\&\quad \left( p-(p-\alpha )e^{-\beta x_{i}}\right) . \end{aligned}$$

Then, the partial derivatives of the log-likelihood function with respect to \(\alpha \), \(\beta \) and p are given by

$$\begin{aligned} \frac{\partial \ell _{n}(\alpha , \beta , p;{\varvec{x}})}{\partial \alpha }= & {} \frac{n}{\alpha }-2\sum \limits _{i={1}}^{n}\dfrac{e^{-\beta x_{i}}}{p-(p-\alpha )e^{-\beta x_{i}}}, \end{aligned}$$
(4)
$$\begin{aligned} \frac{\partial \ell _{n}(\alpha , \beta , p;{\varvec{x}})}{\partial \beta }= & {} \frac{n}{\beta }-\sum \limits _{i={1}}^{n}x_{i}-2\sum \limits _{i={1}}^{n}\dfrac{(p-\alpha ) x_{i}e^{-\beta x_{i}}}{p-(p-\alpha )e^{-\beta x_{i}}}, \end{aligned}$$
(5)
$$\begin{aligned} \frac{\partial \ell _{n}(\alpha , \beta , p;{\varvec{x}})}{\partial p}= & {} \frac{n}{p}-2\sum \limits _{i={1}}^{n}\dfrac{1-e^{-\beta x_{i}}}{p-(p-\alpha )e^{-\beta x_{i}}}. \end{aligned}$$
(6)

It is clear that the MLEs cannot be obtained as a closed form. To solve the problem the numerical methods are needed. But, fortunately, the statistical and mathematical software can solve such systems, in particular, applying R software. The results of the estimators by applying R software in Section 5 are reported. We apply the EM algorithm proposed by Dempster et. al [11] to estimate parameters. The whole data distributions are often defined in terms of their density function as follows:

$$\begin{aligned} f(x,z;\alpha , \beta , p)= & {} f_{x|Z=z} (x;\alpha , \beta ) f_{z} (z;p)\\= & {} \dfrac{\alpha \beta z e^{- \beta x} (1 - e^{- \beta x})^{2-1}}{(1 - {\overline{\alpha }} e^{- \beta x})^{z+1}}\\&(1-p)p^{z-1}~~~~ x> 0,\\&z = 1,2,\ldots , \alpha , \beta > 0,~ p \in (0,1). \end{aligned}$$

Therefore, the expectation step of an EM-algorithm cycle involves computing the conditional expectation of \( (Z | x ; \alpha ^{(h)} , \beta ^{(h)} , p^{(h)}) \). Here, \(( \alpha ^{(h)} , \beta ^{(h)} , p^{(h)}) \) represents the present estimate of \( (\alpha , \beta , p) \). It should be noted that:

$$\begin{aligned} P(Z|x;\alpha , \beta , p) = f(x , z ; \alpha , \beta , p) / f(x; \alpha , \beta , p). \end{aligned}$$

Then, we have

$$\begin{aligned}&P(Z|x;\alpha , \beta , p) \\&\quad =\dfrac{(p-(p-\alpha )e^{-\beta x})^{2} Z[(1-p)(1-e^{-\beta x})]^{z-1}}{(1- {\overline{\alpha }}e^{-\beta x})^{z+1}},~~ z = 1,2 , \ldots . \end{aligned}$$

Thus,

$$\begin{aligned} E(Z|x;\alpha , \beta , p) = \dfrac{p-(p + {\overline{\alpha }}) e^{-\beta x}}{p-(p-\alpha )e^{-\beta x}}. \end{aligned}$$

The maximization step involves completing the maximum likelihood estimation of the vector \( (\alpha , \beta , p) \), where \(Z's \) that are missing are replaced by their conditional expectations \(E(Z|x ; \alpha , \beta ,p) \). Using the expectation–maximization (EM) algorithm \( (\alpha ^{(h+1)} , \beta ^{(h+1)} , p^{(h+1)}) \) is chosen as the \((\alpha , \beta , p) \) value whose maximum is \( l_{n} (\alpha ^{(h)} , \beta ^{(h)} , p^{(h)} , x_{obs})\). Thus, we have

$$\begin{aligned} P^{(h+1)}= & {} \frac{1}{\sum \limits _{i=1}^{n} \Big ( \frac{p^{(h)} - (p^{(h)} + \overline{\alpha (h)}) - e^{- \beta ^{ (h)} x_{i} }}{p^{(h)} - (p^{(h)} - \overline{\alpha ^{(h)}}) - e^{- \beta ^{(h)} x_{i}}} \Big )}\\ \beta ^{(h+1)}= & {} n \Big ( \Big ( \sum \limits _{i=1}^{n} x_{i} \Big ( \frac{p^{(h)} - (p^{(h)} + \overline{\alpha ^{(h)}}) - e^{- \beta ^{(h)} x_{i}}}{p^{(h)}- (p^{(h)} - \overline{\alpha ^{(h)}}) - e^{-\beta ^{(h)}x_{i}}} \Big ) \Big ) \\+ & {} (\alpha ^{(h+1)} + p^{(h)} \sum \limits _{i=1}^{n} \frac{\overline{\alpha ^{(h+1)}} e^{- \beta ^{(h+1)} x_{i}}}{1 - \overline{\alpha ^{(h+1)}} e^{- \beta ^{(h+1)} x_{i}}} \Big )^{-1} \\ \alpha ^{(h+1)}= & {} \frac{n \sum \limits _{i=1}^{n} \frac{p^{(h)} - )p^{(h)} + {\overline{\alpha }}^{(h)}) e^{- \beta ^{(h)} x_{i}}}{p^{(h)} - (p^{(h)} - \alpha ^{(h)}) e^{- \beta ^{(h)} x_{i}}}}{\sum \limits _{i=1}^{n} \mathrm {ln} (1 - \overline{\alpha ^{(h+1)}} - e^{- \beta ^{(h+1)}x_{i}}) + \alpha ^{(h+1)} \sum \limits _{i=1}^{n} \frac{1 - e^{- \beta ^{(h+1)} x_{i}}}{1 - \overline{\alpha ^{(h+1)}} e^{- \beta (h+1)} x_{i}}}\nonumber . \end{aligned}$$

Asymptotic variance and covariance of the MLEs estimator \( J_{n} (\theta ) = E(I_{n} ; \theta ) (I_{n} = I(\theta ; x_{obs})) \) is the observed fisher information matrix with the following elements:

$$\begin{aligned} (I_{n})_{ij} = - \frac{\partial ^{2} l_{n}}{\partial \theta _{i} \partial \theta _{j}},~~~ i,j = 1,2,3. \end{aligned}$$

and expectation should be defined in relation to X distribution. By differentiation of (4), (5), (6), we can define the elements of the symmetric, second-order observed information matrix as follows:

$$\begin{aligned} {(I_{n})_{11}}= & {} \frac{n}{\alpha ^{2}} - 2 \sum \limits _{i=1}^{n} \frac{e^{- \beta x_{i}}}{(p-(p - \alpha )e^{-\beta x_{i}})^{2}}\\ (I_{n})_{12}= & {} 2 p \sum \limits _{i=1}^{n} \frac{x_{i} e^{- \beta x_{i}}}{(p-(p-\alpha ) e^{-\beta x_{i}})^{2}}\\ (I_{n})_{13}= & {} 2p \sum \limits _{i=1}^{n} \frac{e^{- \beta x_{i}}(1- e^{- \beta x_{i}}}{(p-(p-\alpha ) e^{- \beta x_{i}})^{2}}\\ (I_{n})_{22}= & {} \frac{n}{\beta ^{2}} - 2p (p-a) \sum \limits _{i=1}^{n} \frac{x_{i}^{2} e^{- \beta x_{i}}}{(p-(p-a) e^{- \beta x_{i}})^{2}}\\ (I_{n})_{23}= & {} 2(p-a) \sum \limits _{i=1}^{n} \frac{x_{i} e^{-\beta x_{i}}}{(p-(p-a)e^{-\beta x_{i}})^{2}}\\ (I_{n})_{33}= & {} \frac{n}{p^{2}} - 2 \sum \limits _{i=1}^{n} \frac{(1- e^{-\beta x_{i}})^{2}}{(p-(p-\alpha ) e^{- \beta x_{i}})^{2}}. \end{aligned}$$

Hence, \( J_{n} (\theta ) = E(I_{n} ; \theta ) \) can be expressed as follows:

$$\begin{aligned} (J_{n})_{11}= & {} \frac{n}{\alpha ^{2}} - 2 n E\Big ( \frac{e^{- 2 \beta X}}{(p-(p-\alpha ) e^{-\beta X})^{2}} \Big )\\ (J_{n})_{12}= & {} 2 np E\Big ( \frac{X e^{- \beta X}}{(p-(p-\alpha ) e^{- \beta X})^{2}} \Big )\\ (J_{n})_{13}= & {} 2 n E \Big ( \frac{e^{-\beta X} (1 - e^{-\beta X})}{(p-(p-\alpha ) e^{\beta X})^{2}} \Big )\\ (J_{n})_{22}= & {} \frac{n}{\beta ^{2}} 2np (p-\alpha ) E\Big ( \frac{X^{2} e^{-\beta X}}{(p-(p-\alpha ) e^{-\beta X})^{2}} \Big ) \\ (J_{n})_{23}= & {} 2n(p-a) E \Big (\frac{X e^{-\beta X}}{(p-(p-a)e^{-\beta X})^{2}}\Big )\\ (J_{n})_{33}= & {} \frac{n}{p^{2}} - 2 n E \Big ( \frac{(1-e^{-\beta X})^{2}}{(p-(p-\alpha ) e^{-\beta X})^{2}} \Big ). \end{aligned}$$

Simulation study

In this section, the performance of the MLEs is assessed via simulation in terms of the sample size n, and the empirical bias and empirical mean square error (MSE), for different values of parameters. Let \(\varvec{\theta }=(\theta _1,\theta _2,\theta _3)=(\alpha ,\beta ,p)\) be the parameters vector. Given n and \(\varvec{\theta }\), the following algorithm to calculate the biases and MSEs, for \(i=1,2,3\), is applied.

Algorithm 1

  1. (i)

    Generate the values \(x_1,\ldots ,x_n\) from the \(\mathrm{NMEG}(\alpha ,\beta ,p)\) using (2).

  2. (ii)

    Compute \(\hat{\varvec{\theta }}=({\hat{\theta }}_1,{\hat{\theta }}_2,{\hat{\theta }}_3)\) for \(x_1,\ldots ,x_n\).

  3. (iii)

    Repeat the steps (i) and (ii) for 10,000 times.

  4. (iv)

    Obtain the bias and the MSE using the formulas \(\mathrm{bias}({\hat{\theta }}_i)=\frac{1}{10000}\sum _{j=1}^{10000} {\hat{\theta }}_{ij}-\theta _i\) and \(\mathrm{MSE}({\hat{\theta }}_i)=\frac{1}{10000}\sum _{j=1}^{10000} ({\hat{\theta }}_{ij}-\theta _i)^2\), where \({\hat{\theta }}_{ij}\) denotes the MLE of \(\theta _i\) in the jth replication, for \(i=1,2,3\) and \(j=1,\ldots ,10000\).

We applied Algorithm 1 in R software (version 4.0.2) and calculated the empirical biases and MSEs in some cases. Table 1 represents the calculated values. In Table 1, we observed that the biases and the MSEs are small for different values \( \alpha \), \( \beta \) and p. Also we observed that the absolute values of biases and the MSE decrease whenever the sample size n increases.

Table 1 The biases and MSEs (in parentheses) of MLEs for different values of sample sizes n and different values of the parameters
Full size table

Applications

In this section, the comparison of the NMEG with some existing distributions is considered. For this purpose, we consider three real data sets to analyze. In the first set, we show that the NMEG is a good competitor for two important distributions gamma and Weibull as the two-parameter distributions. In the second set, it is observed that the NMEG distribution performs well comparing to a three-parameter distribution. Since the NMEG and the distribution introduced by Bordbar and Nematollahi [7] have approximately the same structures, for the third data set we compare these models and we see that the NMEG is very better. Two sets of real data have decreasing hazard function, and one has increasing hazard function. To identify the shape of the hazard function, the empirical scaled total time on test (TTT) plot is applied. Let F(.) be a distribution function. The TTT concept was introduced by Brunk et al. [8], defined as \(H^{-1}_F(t)=\int _{0}^{F^{-1}(t)}\left( 1-F(u)\right) du\). Also the scaled TTT transform is defined as \(\phi _F(t)=H^{-1}_F(t)/H^{-1}_F(1)\). According to Aarest [1], the hazard function is increasing (decreasing) if \(\phi _F(t)\) is concave (convex) in \(t\in [0,1]\). To determine the behavior of hazard function based on data, the empirical form of \(\phi _F(t)\) is helpful. Let \({\varvec{x}}=(x_1,\ldots ,x_n)\) be an observed vector of a random sample. The empirical scaled TTT transform is given by

$$\begin{aligned} T(i/n)=\frac{\sum _{k=1}^i x_{k:n}-(n-i)x_{i:n}}{\sum _{k=1}^i x_{k:n}},\quad i=0,\ldots ,n, \end{aligned}$$

where \(x_{k:n}\) represents the observed value of kth-order statistics. For \(0\le t \le 1\), T(t) is defined by linear interpolation. The plot of (i/n, T(i/n)) \((i=0,\ldots ,n)\), where consecutive points are connected by straight lines, is called the empirical scaled TTT plot.

The first data set, \(\mathrm{D}_1\), consists of the number of successive failure for the air conditioning system of each member in feet of 13 Boeing 720 jet airplanes. The pooled data with 213 observations are considered here. This data set was analyzed by Adamidis and Loukas for exponential-geometric distribution [3], Proschan for exponential distribution [30], Dahiya and Gurland for Gamma and exponential distribution [13], Gleser for Gamma distribution [14] and Kus for exponential-Poisson distribution [20]. \(\mathrm{D}_1\) is given by as follows:

194, 15, 41, 29, 33, 181, 413, 14, 58, 37, 100, 65, 9, 180, 447, 184, 36, 201, 118, 34, 31, 18, 18, 67, 57, 62, 7, 22, 34, 90, 10, 60, 186, 61, 49, 14, 24, 56, 20, 79, 84, 44, 59, 29, 156, 118, 25, 310, 76, 26, 44, 23, 62, 130, 208, 70 , 101, 208, 74, 57, 48, 29, 502, 12, 70, 21, 29, 386, 59, 27, 153, 26, 326, 55, 320, 56, 104, 220, 239, 47, 246, 176, 182, 33, 15, 104, 35, 23, 261, 87, 7, 120, 14, 62, 47, 225, 71, 246, 21, 42, 20, 5, 12, 120, 11, 3, 14, 71, 11, 14, 11, 16, 90, 1, 16, 52, 95, 97, 51, 11, 4, 141, 18, 142, 68, 77, 80, 1, 16, 106, 206, 82, 54, 31, 216, 46, 111, 39, 63, 18, 191, 18, 163, 24, 50, 44, 102, 72, 22, 39, 3, 15, 197, 188, 79, 88, 46, 5, 5, 36, 22, 139, 210, 97, 30, 23, 13, 14, 359, 9, 12, 270, 603, 3, 104, 2, 438, 50, 254, 5, 283, 35, 12, 130, 493, 487, 18, 100, 7, 98, 5, 85, 91, 43, 230, 3, 130, 102, , 209, 14, 57, 54, 32, 67, 59, 134, 152, 27, 14, 230, 66, 61, 34.

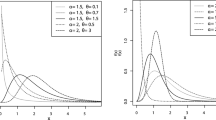
Figure 2 represents the empirical scaled TTT plot of \(\mathrm{D}_1\). This shows that a distribution with decreasing hazard function can be used for \(\mathrm{D}_1\).

Fig. 2
figure 2

Empirical scaled TTT plot of \(\mathrm{D}_1\)

Full size image

Based on a comparison made by Adamidis and Loukas [3], we consider gamma and Weibull distributions to compare as the competing distributions with the following density functions: We fitted the gamma, Weibull and NMEG distributions on \(\mathrm{D}_1\) and computed the MLEs, the corresponding Akaike information criterion (AIC) and AIC with correction (AICc) values for three distributions (see Table 2).

Table 2 MLEs of the parameters of the gamma, Weibull and NMEG distributions and the corresponding AICs and AICcs for fitting to \(\mathrm{D}_1\)
Full size table
Table 3 Goodness-of-fit tests of the gamma, Weibull and NMEG distributions for fitting to \(\mathrm{D}_1\)
Full size table

Table 3 considers goodness-of-fit tests for the three distributions in terms of the Kolmogorov–Smirnov (KS) statistics. In Tables 2 and 3, it is observed that the NMEG distribution is better than the gamma and Weibull distributions. Figure 3 represents the fitted density and distribution functions of gamma, Weibull and NMEG distributions for \(\mathrm{D}_1\). Also, the probability–probability (p-p) plot for the NMEG distribution is presented in Fig. 4.

Fig. 3
figure 3

Fitted density and distribution functions of the gamma, Weibull and NMEG distributions for \(\mathrm{D}_1\)

Full size image
Fig. 4
figure 4

p-p plot of the NMEG distribution for \(\mathrm{D}_1\)

Full size image

The second data set, \(\mathrm{D}_2\), consists of the survival times of guinea pigs injected with the different amount of tubercle bacilli studied by Bjerkedal [6]. \(\mathrm{D}_2\) is given by as follows:

0.1, 0.33, 0.44, 0.56, 0.59, 0.72, 0.74, 0.77, 0.92, 0.93, 0.96, 1, 1, 1.02, 1.05, 1.07, 

1.07, 1.08, 1.08, 1.08, 1.09, 1.12, 1.13, 1.15, 1.16, 1.2, 1.21, 1.22, 1.22, 1.24, 1.3,

1.34, 1.36, 1.39, 1.44, 1.46, 1.53, 1.59, 1.6, 1.63, 1.63, 1.68, 1.71, 1.72, 1.76, 1.83,

1.95, 1.96, 1.97, 2.02, 2.13, 2.15, 2.16, 2.22, 2.3, 2.31, 2.4, 2.45, 2.51, 2.53, 2.54,

2.54, 2.78, 2.93, 3.27, 3.42, 3.47, 3.61, 4.02, 4.32, 4.58, 5.55. Figure 5 represents the empirical scaled TTT plot of \(\mathrm{D}_2\). This shows that a distribution with increasing hazard function can be used for \(\mathrm{D}_2\).

Fig. 5
figure 5

Empirical scaled TTT plot of \(\mathrm{D}_2\)

Full size image

Ahmad et al. [4] introduced a new extended alpha power transformed Weibull (NEAPTW) and showed that it better fits to \(\mathrm{D}_2\) than some other well-known existing distributions. So, we consider the NEAPTW distribution as the competing distribution with the following density function:

$$\begin{aligned} g(x;\alpha ,\beta ,p)= & {} \frac{\beta p x^{p-1} e^{-\beta x^p}}{\alpha - e^{\alpha }}\left( (\ln \alpha ) \alpha ^{1-e^{-\beta x^p}}-\alpha e^{\alpha (1-e^{-\beta x^p})}\right) ,\\&\quad x>0,\alpha ,\beta ,p>0,\alpha \ne e. \end{aligned}$$

We fitted the NMEG distribution to \(\mathrm{D}_2\) and computed the MLEs and the corresponding AIC and AICc criteria values. Table 4 represents the MLEs of the parameters of both distributions and the corresponding AICs and AICcs. The corresponding values to NEAPTW are available in Ahmad et al. [4]. Table 5 considers goodness-of-fit test for both distributions. In Tables 4 and 5, it is observed that the NMEG distribution better fits to \(\mathrm{D}_2\) than the NEAPTW distribution. Figure 6 represents the fitted density and distribution functions of NEAPTW and NMEG distributions for \(\mathrm{D}_2\). Also, the p-p plot for the NMEG distribution is presented in Figure 7.

Table 4 MLEs of the parameters of the NEAPTW and NMEG distributions and the corresponding AICs and AICcs for fitting to \(\mathrm{D}_2\)
Full size table
Table 5 Goodness-of-fit tests of the NEAPTW and NMEG distributions for fitting to \(\mathrm{D}_2\)
Full size table
Fig. 6
figure 6

Fitted density and distribution functions of NEAPTW and NMEG distributions for \(\mathrm{D}_2\)

Full size image
Fig. 7
figure 7

p-p plot of the NMEG distribution for \(\mathrm{D}_2\)

Full size image

The third data set, \(\mathrm{D}_3\) (studied by Maguire et al. [25]), represents the time intervals between two deadly accidents in the mines of the Division no. 5 of Great Britain National Cole Board in 1950. \(\mathrm{D}_3\) is given by as follows: 21, 2, 15, 1, 5, 1, 9, 1, 0, 17, 0, 1, 24, 14, 4, 9, 20, 14, 1, 1, 44, 4, 5, 1, 13, 6, 9, 3.

Figure 8 represents the empirical scaled TTT plot of \(\mathrm{D}_3\). This shows that a distribution with decreasing hazard function is useful for \(\mathrm{D}_3\).

Fig. 8
figure 8

Empirical scaled TTT plot of \(\mathrm{D}_3\)

Full size image

Bordbar and Nematollahi [7] proposed the modified exponential-geometric (MEG) distribution and used it for fitting to \(\mathrm{D}_3\). So, we consider the MEG distribution as the competing distribution with the following density function:

$$\begin{aligned} g(x;\alpha ,\beta ,p)=\frac{\alpha \beta (1-p)e^{-\beta x}}{\left( 1-(1-\alpha )e^{-\beta x}-\alpha p e^{-\beta x}\right) },\quad x>0,\alpha ,\beta >0,0<p<1. \end{aligned}$$

We fitted the NMEG distribution to \(\mathrm{D}_3\) and computed the MLEs and the corresponding AIC and AICc values. Table 6 represents the MLEs of the parameters of both distributions and the corresponding AICs and AICcs. The corresponding values to MEG are available in Bordbar and Nematollahi [7]. Table 7 considers goodness-of-fit test for both distributions. In Tables 6 and 7, it is observed that the NMEG distribution is more practical than the MEG distribution for \(\mathrm{D}_3\). Figure 9 represents the fitted density and distribution functions of MEG and NMEG distributions for \(\mathrm{D}_3\). Also, the p-p plot for the NMEG distribution is presented in Figure 10.

Table 6 MLEs of the parameters of the MEG and NMEG distributions and the corresponding AICs and AICcs for fitting to \(\mathrm{D}_3\)
Full size table
Table 7 Goodness-of-fit tests of the MEG and NMEG distributions for fitting to \(\mathrm{D}_3\)
Full size table
Fig. 9
figure 9

Fitted density and distribution functions of MEG and NMEG distributions for \(\mathrm{D}_3\)

Full size image
Fig. 10
figure 10

p-p plot of the NMEG distribution for \(\mathrm{D}_3\)

Full size image

Conclusion

Due to importance of the monotone hazard rate models in some areas such as reliability and biology, we introduced the NMEG distribution with the monotone hazard function via operation of compounding based on Marshall and Olkin [26] scheme with the baseline exponential distribution. Then, we obtained the quantile function, characteristic function, moments and the Shannon and Rényi entropies in the closed forms in terms of some well-known mathematical functions. Therefore, the log-likelihood equations were obtained and the EM algorithm was presented to calculate the MLEs of parameters. Then, performance of the MLEs was investigated for different values of sample sizes and different values of the parameters using simulation. The simulation results show that the MLEs perform well in terms of bias and MSE criteria.

For application, three real data sets were analyzed using the NMEG distribution and some competitors. To analyze the first data set, which consists of the number of successive failure for the air conditioning system of each member in feet of 13 Boeing 720 jet airplanes, we considered the gamma, Weibull and NMEG distributions. In the second data set which consists of the survival times of guinea pigs injected with the different amount of tubercle bacilli, we considered the NEAPTW and NMEG distributions for analyzing. Finally, to analyze the third data set which represents the time intervals between two deadly accidents in the mines of the Division no. 5 of Great Britain National Cole Board in 1950, the MEG and NMEG distributions were utilized. To compare the NMEG distribution with the competitors in fitting to three real data sets, the AIC and AICc criteria were used and the KS statistic was also applied. Our results show that fit of the NMEG distribution is clearly more suitable than fit of the other competitors.