Optimal dividend strategies in a Cramer–Lundberg model with capital injections and administration costs

Abstract

In this paper, we consider a classical risk model with dividend payments and capital injections in the presence of both fixed and proportionals administration costs. Negative surplus or ruin is not allowed. We measure the value of a strategy by the discounted value of the dividends minus the costs. It turns out, capital injections are only made if the claim process falls below zero. Further, at the time of an injection the company may not only inject the deficit, but inject additional capital C ≥ 0 to prevent future capital injections. We derive the associated Hamilton–Jacobi–Bellman equation and show that the optimal strategy is of band type. By using Gerber–Shiu functions, we derive a method to determine numerically the solution to the integro-differential equation and the unknown value C.

1 Introduction

The idea of controlling the risk exposure of insurance companies by means of their dividend payments goes back to de Finetti [9]. He proposed to consider the expected value of discounted future dividends until the time of ruin. The goal was now to find a strategy which maximises this value. For the classical Cramér–Lundberg model, this problem was first solved by Gerber [11] who showed that an optimal strategy exists and is of the so-called "band-type". Later on, Azcue and Muler [6] extended this model by the possibility to reinsure the insurance portfolio. Albrecher and Thonhauser [1] considered the reserve process under a force of interest, and Thonhauser and Albrecher [22] included an additional term depending on the time of ruin representing some sort of reward for avoiding early ruin. For a diffusion approximation, the dividend maximisation problem was solved by Shreve et al. [21]. For more variants of this problem see Jeanblanc-Piqué and Shiryaev [16], Asmussen and Taksar [3], or Thonhauser and Albrecher [22].

Unfortunately, the optimal dividend strategy resulting in de Finetti’s setting leads almost surely to ruin. Therefore, Dickson and Waters [8] proposed to allow capital injections from the shareholders when the surplus falls below zero to avoid bankruptcy. They considered the value of the discounted cash flow in the classical risk model if the dividends are paid according to a barrier strategy, see also Gerber [14]. Kulenko and Schmidli [17] established the optimality of such barrier strategies (for arbitrary claim size distributions) by maximising the expected difference between the discounted dividend payments and the penalised capital injections for a penalty factor ϕ > 1. In a diffusion framework, an analogous problem has been solved by Shreve et al. [21], see also Lokka and Zervos [18]. Finally, Avram et al. [5] showed the optimality of the barrier dividend strategies in the more general framework of spectrally negative Lévy processes.

The penalty factor in Kulenko and Schmidli [17] can also be interpreted as proportional costs associated with the capital injections. In this paper, we extend this model by adding fixed costs incurring any time at which capital injections are made. We will show that the optimal dividend strategy is not of barrier type any more, but of band type. In a diffusion approximation, the analogous problem was treated by He and Liang [15] and Paulsen [19] who assumed that costs incur with both dividend payments and capital injections. For an overview on various dividend optimisation problems, the reader is directed to Schmidli [20], Albrecher and Thonhauser [2], and Avanzi [4].

Let

$$ X_t = x + ct - \sum_{i=1}^{N_t} Y_i $$

be a classical risk process on a filtered probability space ${(\Upomega, {\mathcal F}, \{{\mathcal F}_t\}_{t\geq 0}, {\mathbb{P}}).\;x\in {\mathbb{R}}}$ is the initial capital, c > 0 is the premium rate, {N _t } _t ≥ 0 is a Poisson process with rate λ > 0, say, and ${\{Y_i\}_{i\in {\mathbb{N}}}}$ is an iid sequence of strictly positive random variables with distribution function G(y). The claim sizes {Y _i } and the claim arrival process {N _t } are assumed to be independent. We assume that ${{\mathbb{E}}[Y_i] = \mu < \infty}$ and, for simplicity, that G(y) is continuous. Note that no positive safety loading needs to be assumed. We use the smallest right-continuous filtration ${\{{\mathcal F}_t\}_{t\geq 0}}$ such that {X _t } _t ≥ 0 is adapted. If we want to indicate that the initial capital is x we will write ${\mathbb{P}}_x$ and ${\mathbb{E}}_x$ for the probability measure and the expectation, respectively. Otherwise, we dismiss the letter x and write ${\mathbb{P}}$ and ${\mathbb{E}}$.

The accumulated dividends process is a non-decreasing, càdlàg process {D _t } _t ≥ 0 with D ₀₋ = 0, the accumulated capital injections are denoted by {Z _t } _t ≥ 0, which also is a non-decreasing, pure jump process with Z ₀₋ = 0. The surplus process then becomes

$$ X^{(D,Z)}_t= X_t-D_t+Z_t \quad X^{(D,Z)}_{0-}=x. $$

The capital injections {Z _t } have to be chosen in such a way that X ^(D,Z) _t  ≥ 0 for all t. That is, a non-negative surplus is required.

We assume that at any time where capital injections are made a lump-sum penalty L has to be paid. As a consequence, the insurance company would possibly prefer to inject not only the minimal amount required but additional capital C for preventing future capital injections (which are costs, in fact). The value of a strategy (D, Z) = {(D _t , Z _t )} _t ≥ 0 is defined as

$$ V^{(D,Z)}(x)= {\mathbb{E}}_x\left[\int\limits_{0-}^\infty e^{-\delta t}\;\hbox{d} D_t - \phi\int\limits_{0-}^\infty e^{-\delta t}\;\hbox{d} Z_t - L\sum_{t\geq 0}e^{-\delta t}{\rm 1\!\!I}_{\{\Updelta Z_t > 0\}}\right] $$

where $\Updelta Z_s = Z_s - Z_{s-}.\; \phi \geq 1$ is a penalty factor. δ > 0 is a discount factor. A strategy (D, Z) is admissible if

$$ {\mathbb{P}}_x[X^{(D,Z)}_t\geq 0\;\hbox{for all}\; t\geq 0]=1. $$

We denote by ${\fancyscript{S}_x}$ the set of all admissible strategies for the initial capital x. We want to maximise V ^(D,Z)(x) over all admissible strategies and to identify the strategy (if it exists) which gives the maximal value. Thus, the value function of our problem is

$$ V(x)= \sup_{(D,Z)\in{\fancyscript{S}}_x}V^{(D,Z)}(x). $$

Note that $\int_{0-}^\infty e^{-\delta t}\;\hbox{d} D_t = \delta\int_{0-}^\infty e^{-\delta t} D_t\;\hbox{d} t$. Since the value of the (not admissible) strategy D _t  = x + c t and Z _t  = 0 is an upper bound for the value of any admissible strategy, we get that $V^{(D,Z)}(x) < x + c/\delta < \infty$ for any admissible strategy. Since D _t  = x + c t and Z _t  = S _t := x + c t − X _t is an admissible strategy, we obtain the lower bound V(x) ≥ x + (c − λμϕ − λL)/δ. This shows that V(x) is finite.

If we had chosen ϕ < 1 then we could make a capital injection of size K and pay it as dividend at the same time. The value would be K(1 − ϕ) − L. This shows that the value function would be infinite. If δ = 0 the value can only exceed $-\infty$ if the safety loading is positive. But then consider a barrier strategy at a high barrier b. Consider the time between the process reaches the barrier for the first time and reaches it again after leaving the barrier. If the barrier is high enough, it is unlikely that a capital injection has to be made and the value of the dividends is larger than the value of the costs. Since the barrier is reached infinitely often, the value of the strategy would become infinite. Since always a higher barrier would be better, there would not exist an optimal strategy.

We first argue that it cannot be optimal to make a capital injection unless the surplus is negative. Suppose x ≥ 0. Let (D, Z) be a strategy allowing capital injections at any time. We assume without loss of generality that Z ₀ > 0 and D ₀ = 0. We construct now another strategy $({\tilde D},{\tilde Z})$ that pays no dividend and no capital injections until some stopping time S to be defined below. At time S the strategy $({\tilde D},{\tilde Z})$ is adjusted in such a way, that the surplus processes coincide from S on. That is, $X^{({\tilde D}, {\tilde Z})}_t = X_t$ for t < S and $X^{({\tilde D},{\tilde Z})}_t = X^{(D,Z)}_t$ for t ≥ S. The following stopping times are illustrated in Fig. 1. Let $\tau_0 = \inf\{t\ge 0: X_t < 0\}$ be the first time where no control leads to a negative surplus, $\sigma_D = \inf\{t\ge 0: D_t > Z_0\}$ be the first time where the initial injection is compensated by paying dividends, $\sigma_Z = \inf\{t\ge 0: Z_t > Z_0\}$ the first time after zero where an injection is made, and S = min{τ₀, σ _D , σ _Z }. We define

$$ {\tilde D}_t = (D_t - (D_S \wedge Z_0))^+,\quad {\tilde Z}_t = (Z_t - D_S + {\tilde D}_S) {\rm 1\!\!I}_{\{t \ge S\}}. $$

Note that the strategy $({\tilde D},{\tilde Z})$ is admissible. The difference of the value between the two strategies is

$$ \begin{aligned} & {L(1-e^{-\delta S} {\rm 1\!\!I}_{\{{\tilde Z}_S > 0, Z_s=Z_0\}}) + \phi Z_0 +\phi (Z_S -Z_0- {\tilde Z}_S)e^{-\delta S} }\\ & \qquad - \int\limits_0^S e^{-\delta t} \;\hbox{d} D_t + e^{-\delta S} {\tilde D}_S \\ & \quad = L(1-e^{-\delta S} {\rm 1\!\!I}_{\{{\tilde Z}_S > 0, Z_s=Z_0\}}) + \phi Z_0 (1-e^{-\delta S}) +\phi (D_S - {\tilde D}_S)e^{-\delta S} \\ & \qquad -\int\limits_0^S e^{-\delta t} \;\hbox{d} D_t + e^{-\delta S} {\tilde D}_S \\ & \quad \ge L(1-e^{-\delta S} {\rm 1\!\!I}_{\{{\tilde Z}_S > 0, Z_s=Z_0\}}) + \phi Z_0 (1-e^{-\delta S}) - \int\limits_0^S \delta e^{-\delta t} D_t\;\hbox{d} t \\ & \quad > L(1-e^{-\delta S} {\rm 1\!\!I}_{\{{\tilde Z}_S > 0, Z_s=Z_0\}}) + \phi Z_0 (1-e^{-\delta S}) - \int\limits_0^S \delta e^{-\delta t} Z_0\;\hbox{d} t \\ & \quad \ge L(1-e^{-\delta S} {\rm 1\!\!I}_{\{{\tilde Z}_S > 0, Z_s=Z_0\}}) > 0. \end{aligned} $$

Thus, the strategy $({\tilde D}, {\tilde Z})$ yields a larger value than (D, Z).

Fig. 1

Construction of the strategy $({\tilde D},{\tilde Z})$ (dashed line) from the strategy (D, Z) (solid line)

If the initial capital is negative, then capital injections at height Z ₀ = |x| + C are made; thus,

$$ V(x)=V(C)-\phi(|x|+C) - L \quad \hbox{for}\; x< 0. $$

(1)

Let us now consider the decision at the time where a capital injection is necessary. Suppose the deficit is z > 0. The insurer decides to make a capital injection of size z + C. A strategy can be chosen, such that $V^{(D,Z)}(C) > V(C) - \varepsilon$. The future value of the strategy becomes then at least $V(C) - \varepsilon - \phi(z+C) - L$. The maximum that can be attained is V(C) − ϕ(z + C) − L. Maximising over C gives $V(-z) = \sup_{C \ge 0} V(C) - \phi(z+C) - L$. One therefore has to maximise V(C) − ϕC. Thus the problem is independent of the deficit z.

We will see below that the function V(x) is continuous and that there is a value x ₁, such that V(x) = V(x ₁) + x − x ₁ for x > x ₁. That is, capital above x ₁ is paid as dividend. This implies that a choice C > x ₁ does not make sense. Therefore, there is $C_0 \in [0,x_1],$ such that $V(C_0) - \phi C_0 = \sup_{C \ge 0} V(C) - \phi C$. It follows readily that any strategy where capital injections are made such that the process is at a level C with V(C) − ϕC < V(C ₀) − ϕC ₀ yields a lower value. In the following we will assume that we already have fixed the value C = C ₀. We therefore only consider strategies where the surplus is at the optimal level C after a capital injection. The reader, however, should be aware that in the case where C is not unique the optimal strategy is not unique.

The capital injections process can be described in the following way. For x ≥ 0 let {D ⁰ _t } be a dividend strategy for the process {X _t } until the surplus process falls below zero for the first time at $\tau_1:=\inf\{t\geq 0: X_t-D_t^0<0\}$. Then Z ⁰ _t  = 0 on [0,τ₁]. Now let

$$ \begin{aligned} {\Updelta Z}_{\tau_1}^0 & = |X_{\tau_1}-D_{\tau_1}^0|+C,\\ Z_t^0 & = \Updelta Z_{\tau_1}^0 \cdot {\rm 1\!\!I}_{t\geq \tau_1},\\ X_t^1 & = X_t-D_t^0+Z_t^0. \end{aligned} $$

Then X ^(D,Z) _t  = X ¹ _t for $t\in[0,\tau_1]$. Suppose now, we have constructed the process ${X^n_t}$ on [0,τ _n ]. Let ${D^n_t}$ be a dividend strategy for ${X^n_t}$ until the surplus process falls below zero at $\tau_{n+1}:=\inf\{t>\tau_n: X^n_t-D_t^n<0\}$. Define

$$ \begin{aligned} {\Updelta Z}_{\tau_{n+1}}^n &= |X_{\tau_{n+1}}^n-D_{\tau_{n+1}}^n|+C,\\ Z_t^n&= \sum_{k=1}^{n+1}\Updelta Z_{\tau_k}^{k-1}\cdot{\rm 1\!\!I}_{t\geq \tau_k},\\ X_t^{n+1} &= X_t^n-D_t^n+Z_t^n.\end{aligned} $$

We have X ^(D,Z) _t  = X ⁿ⁺¹ _t for $t\in[0,\tau_{n+1}], n\geq 0$. By construction, the capital injections at time t depend on the dividend strategy at t and the chosen value C. Therefore, we will in the following use the short notations {Z _t }, {X ^D _t } and V ^D(x) for the capital injection process {Z ^D _t }, the surplus process and the value connected to a strategy {(D _t , Z ^D _t )} if the connection is obvious.

The paper is organised as follows. In Sect. 2 we first study the case of dividends which have a restricted density. We derive the associated Hamilton–Jacobi–Bellman (HJB) equation and identify the optimal strategy. In Sect. 3 we extend the results to a general case of increasing and càdlàg dividend processes. We find an optimal strategy and give a characterisation of the value function among other solutions to the HJB equation. By means of Gerber–Shiu penalty functions (see Gerber and Shiu [13]), we show a possible way to calculate the value function if it is of barrier type and demonstrate it at two examples.

2 Strategies with restricted densities

In this section we only consider dividends that are paid at a restricted rate

• $D_t=\int_0^t U_s \;{\text{d}} s,$

• $0\leq U_t\leq u_0<\infty,$

and denote the strategies {(U _t , Z ^U _t )} by {U _t }. Then

$$ X_t^U= X_t - \int\limits_0^t U_s \;\hbox{d} s + Z_t. $$

The value of such a strategy is

$$ V^U(x)={\mathbb{E}}\left[\int\limits_0^\infty e^{-\delta t}U_t \;\hbox{d} t - \phi\int\limits_{0-}^\infty e^{-\delta t}\;\hbox{d} Z_t - L\sum_{t\geq 0}e^{-\delta t}{\rm 1\!\!I}_{\{\Updelta Z_t > 0\}}\right]. $$

Let us denote the set of the admissible restricted strategies by ${\fancyscript{S}^r_x}$. Then the value function is ${V(x)=\sup_{U\in \fancyscript{S}^r_x}V^U(x)}$. Because of (1) we assume that x ≥ 0. Then Z ₀ = 0.

2.1 The value function and the HJB-equation

We first prove some properties of the value function. The first result also holds for non-restricted dividend payments.

Lemma 1

The value of expected capital injections is bounded from below by −λ(ϕμ + ϕC + L)/δ.

Proof

The worst that may happen is that one has to inject capital for all the claims. Using that the time of the kth claim T _k is Gamma $\Upgamma(\lambda,k)$ distributed, we find that

$$ \begin{aligned} &{\mathbb{E}}\left[ -\phi\sum_{k=1}^\infty (Y_k+C) e^{-\delta T_k} -L\sum_{k=1}^\infty e^{-\delta T_k}\right] \\ &\quad =-(\phi(\mu+C)+ L){\mathbb{E}}\left[ \sum_{k=1}^\infty e^{-\delta T_k}\right] = -(\phi(\mu+ C)+L)\sum_{k=1}^\infty \left( {\frac{\lambda}{\lambda + \delta}}\right)^k \\ & \quad = -(\phi(\mu+ C)+L) {\frac{\lambda} {\lambda + \delta}}\; {\frac{1}{1-{\frac{\lambda}{\lambda + \delta}}}} = -{\frac{\lambda (\phi\mu+\phi C+L)}{\delta}}. \end{aligned} $$

□

Lemma 2

V(x) is bounded by u ₀/δ, increasing and Lipschitz continuous. Moreover, $\lim_{x\to\infty}V(x)=u_0/\delta$.

Proof

That V(x) is increasing and that $V(x)\leq \int_0^\infty u_0 e^{-\delta t} \;{\text {d}} t = u_0/\delta$ is clear. Consider the strategy $U_t=u_0. \, \tau_x^U=\inf\{t: x+(c-u_0)t-\sum_{i=1}^{N_t}Y_i<0\}$ converges to infinity as $x\to\infty$. By bounded convergence, ${{\mathbb{E}}[e^{-\delta \tau_x^U}]}$ converges to zero. By Lemma 1 we have that

$$ \begin{aligned} V(x)\geq& V^U(x) \ge {\mathbb{E}}\left[\int\limits_0^{\tau_x^U} u_0 e^{-\delta t}\;\hbox{d}t - \phi\int\limits_{0-}^\infty e^{-\delta t} \;\hbox{d} Z_t - L\sum_{t\geq 0}e^{-\delta t}{\rm 1\!\!I}_{\{\Updelta Z_t > 0\}}\right]\\ \geq& {\mathbb{E}}\left[\int\limits_0^{\tau_x^U} u_0 e^{-\delta t}\;\hbox{d}t \right] - {\mathbb{E}}\left[e^{-\delta \tau_x^U}\right](\phi(\mu+C)+ L){\frac{\lambda}{\delta}}\to {\frac{u_0}{\delta}}. \end{aligned} $$

Let h > 0 be small. We choose a strategy ${{\tilde{U}}\in \fancyscript{S}^r_{x+ch}}$ with initial capital x + c h and define the strategy

$$ \begin{aligned} U_t& = 0\cdot{\rm 1\!\!I}_{\{T_1< h\}}+\left(0\cdot{\rm 1\!\!I}_{\{t < h\}} + {\tilde{U}}_{t-h}{\rm 1\!\!I}_{\{t \geq h\}}+\right) {\rm 1\!\!I}_{\{T_1\geq h\}},\\ Z_t& = Z_t^0\cdot{\rm 1\!\!I}_{\{T_1< h\}}+\left(0\cdot{\rm 1\!\!I}_{\{t < h\}} + {\tilde{Z}}_{t-h}{\rm 1\!\!I}_{\{t \geq h\}}+\right){\rm 1\!\!I}_{\{T_1\geq h\}}, \end{aligned} $$

where {Z ⁰ _t } denotes the capital injections if no dividend is paid. By Lemma 1, the value connected to Z ⁰ is bounded from below. The first claim happens with density λe ^−λt and T ₁ is larger than h with probability e ^−λh. By conditioning on ${{\mathcal F}_{h\wedge T_1},}$ it follows that

$$ \begin{aligned} V(x) \geq& V^U(x)\\ \geq& {\mathbb{E}}_x\left[{\rm 1\!\!I}_{\{T_1\geq h\}} e^{-\delta h}V^{{\tilde U}}(X^U_{h})\right]\\ &+{\mathbb{E}}_x\left[\left(-\phi\int\limits_0^{T_1}\! e^{-\delta t} \hbox{d} Z^0_t - L\sum_{0\leq t\leq T_1}e^{-\delta t}{\rm 1\!\!I}_{\{\Updelta Z^0_t > 0\}}\right){\rm 1\!\!I}_{\{T_1< h\}}\right] \\ \geq & e^{-(\lambda+\delta)h}V^{\tilde{U}}(x+ch)- {\frac{(1-e^{-\lambda h}) (\phi\mu+ \phi C+L)\lambda}{\delta}}, \end{aligned} $$

and so

$$ \begin{aligned} V(x) \geq& \sup_{\tilde{U}\in {\fancyscript{S}}^r_{x+ch}}e^{-(\lambda+\delta)h}V^{\tilde{U}}(x+ch) - {\frac{(1-e^{-\lambda h}) (\phi(\mu+ C)+L)\lambda}{\delta}}\\ =& e^{-(\lambda+\delta)h}V(x+ch) - {\frac{(1-e^{-\lambda h}) (\phi(\mu+C)+ L)\lambda}{\delta}}. \end{aligned} $$

The Lipschitz-continuity follows now by the boundedness of V

$$ \begin{aligned} 0\leq& V(x+ch)-V(x) \\ \leq& V(x+ch)(1-e^{-(\lambda+\delta)h}) + {\frac{(\phi(\mu+C)+ L)\lambda}{\delta}} (1-e^{-\lambda h})\\ \leq& V(x + c h) (\lambda+\delta)h + {\frac{(\phi(\mu+ C)+L)\lambda^2}{\delta}} h\\ \le& {\frac{u_0}{\delta}}(\lambda+\delta)h + {\frac{(\phi(\mu+ C)+L)\lambda^2}{\delta}} h. \end{aligned} $$

□

V is (locally) Lipschitz continuous and, therefore, absolutely continuous on ${{\mathbb{R}}_{\geq 0}}$. Furthermore, by Rademacher’s Theorem (see for example [10, section 5.8.3]), V is Lebesgue a.e. differentiable with (locally) bounded derivatives. In particular, $V^{\prime}$ is the density of V and V is differentiable at all points where $V^{\prime}$ is continuous. We denote by ${{\mathcal D}\subseteq {\mathbb{R}}_{\geq 0}}$ the set of points x where V(x) is differentiable. Then ${\bar{{\mathcal D}}={\mathbb{R}}_{\geq 0}}$ and ${{\mathcal D}^c={\mathbb{R}}_{\geq 0}\backslash {\mathcal D}}$ is a set with Lebesgue measure zero. In the next section we show that at points of non-differentiability V has derivatives from the right and from the left.

We now formulate the Hamilton–Jacobi–Bellman equation for our problem. We defer the proof of the following theorem to the appendix.

Theorem 1

The function V(x) is differentiable a.e. on $(0,\infty)$ and fulfils the Hamilton–Jacobi–Bellman equation

$$ \begin{aligned} 0&=\sup_{0\leq u\leq u_0}\left\{\vphantom{\lambda\phi\int\limits_x^\infty (1-G(y))\;d y}(c-u)V^{\prime}(x)+u- (\lambda+\delta)V(x)\right.\\ & \quad \left.+\lambda\int\limits_0^x V(x-y) \;d G(y) + \lambda(V(C)-\phi C-L)(1-G(x))\right.\\ & \quad \left.- \lambda\phi\int\limits_x^\infty (1-G(y))\;d y \right\}. \end{aligned} $$

(2)

At points where V(x) is not differentiable, the derivatives from the left and from the right exist and fulfil Eq.  2, respectively, with $V^{\prime}(x-)<V^{\prime}(x+)$.

Equation 2 is linear in u, thus, the argument $\tilde{u}=u(x)$ maximising the left-hand side of Eq. 2 is

$$ u(x)=\left\{ \begin{array}{ll} 0, & \hbox {if } V^{\prime}(x)>1,\\ \min\{c, u_0\}, & \hbox {if } V^{\prime}(x)=1,\\ u_0, & \hbox {if } V^{\prime}(x)<1, \end{array}\right. $$

(3)

where we let $V^{\prime}(x)$ be the derivative from the left if ${x\notin {\mathcal D}}$. Here we used the fact that, if u ₀ < c, any value u solves the Eq. 2. If u ₀ ≥ c, then $V^{\prime}(x)=1$ implies that $(\lambda+\delta)V(x) +\lambda\int_0^{\infty}V(x-y) \;\hbox{d} G(y)=c$ and

$$ \begin{aligned} V(x) &= {\frac{c}{\lambda+\delta}} + {\frac{\lambda} {\lambda+\delta}}\int\limits_0^{\infty}V(x-y) \;\hbox{d} G(y) \\ &= \int\limits_0^\infty \lambda e^{-\lambda t}\left\{\int\limits_0^t c e^{-\delta s}\;\hbox{d} s + e^{-\delta t}\int\limits_0^{x}V(x-y) \;\hbox{d} G(y)\right.\\ & \quad +\left. e^{-\delta t}\int\limits_x^\infty \left[ V(C)-\phi(y-x+C) - L \right]\;\hbox{d} G(y)\right\}\;\hbox{d}t, \end{aligned} $$

i.e. V(x) is the value of a barrier-strategy where the incoming premium is paid as dividend until the first claim occurs. After that, the optimal strategy (if it exists) is followed. The existence of the optimal strategy has still to be shown.

We consider now the value at x = 0. From Eqs. 2 and 14 we get

$$ 0=(c-\tilde{u})V^{\prime}(0)+\tilde{u}-(\lambda+\delta)V(0) +\lambda(V(C)-\phi(\mu+C)-L) $$

where $V^{\prime}(0)$ is the derivative from the right. If $V^{\prime}(0)< 1,$ then $\tilde{u}=u_0,$ i.e. the "optimal" strategy is to pay dividends at the maximal rate. In the case u ₀ > c this means that capital injections are needed to pay dividends from. This cannot be optimal because of the early penalty. Thus we have that $V^{\prime}(0)\geq 1$ for u ₀ > c.

2.2 Characterisation of the solution

Before proving the next lemma, we make the following observations.

• {Z _t } only increases at the claim times. Therefore, it holds in an interval (T _i−1, T _i ) between two claims that $\hbox{d} X^U_t=(c-U_t)\; \hbox{d} t.$

• $X^U_{T_i}= X^U_{T_i-}-Y_{i}+\Updelta Z_{T_i}.$

• ${\rm 1\!\!I}_{\{\Updelta Z_{T_i}>0\}}={\rm 1\!\!I}_{\{Y_{i}>X_{T_i-}\}}.$

• If $X^U_{T_i-}-Y_{i}< 0,$ then the shareholders pay as much that $X^U_{T_i}=X^U_{T_i-}-Y_{i}+\Updelta Z_{T_i}=C;$ i.e., $\Updelta Z_{T_i}= (C + Y_{i}- X^U_{T_i-}){\rm 1\!\!I}_{Y_{i}>X_{T_i-}}$. In this case, the value function fulfils

  $$ V(X^U_{T_i}) (= V(C))= V(X^U_{T_i-}-Y_{i})+( \phi \Updelta Z_{T_i}+ L){\rm 1\!\!I}_{\{\Updelta Z_{T_i}>0\}} $$

  because of the property (1). Thus, it suffices to consider only solutions f to the HJB equation satisfying property (1).

Lemma 3

Let f(x) be an increasing, bounded and positive solution to Eq. 2 with property (1). Then for any admissible strategy U, the process

$$ \begin{aligned} &\left\{f(X_t^U)e^{-\delta t}-f(x)- \sum_{0\leq s\leq t} [f(X_s^U) - f(X_s^U - \Updelta Z_s)]e^{-\delta s}\right.\\ &\left.-\int\limits_0^t\left[(c-U_s)f^{\prime}(X_s^U)\right.\right.\\ &\left.\left.-(\lambda+\delta)f(X_s^U)+\lambda\int\limits_0^\infty f(X_s^U-y)d G(y)\right]e^{-\delta s}\;d s \right\} \end{aligned} $$

is a martingale.

Proof

We have the decomposition

$$ \begin{aligned} f(X^U_t)e^{-\delta t}&=f(X^U_0)+\sum_{i=1}^{N_t}\left[f(X^U_{T_i}- \Updelta Z_{T_i})e^{-\delta T_i}-f(X^U_{T_{i-1}})e^{-\delta T_{i-1}}\right]\\ & \quad + \sum_{0 \le s \le t} [f(X_s^U) - f(X_s^U - \Updelta Z_s)]e^{-\delta s}\\ & \quad +f(X^U_t)e^{-\delta t}-f(X^U_{T_{N_t}})e^{-\delta T_{N_t}}\\ & = f(x)+ \sum_{0 \le s \le t} [f(X_s^U) - f(X_s^U - \Updelta Z_s)]e^{-\delta s}\\ & \quad +\sum_{i=1}^{N_t}[f(X^U_{T_i-}-Y_{i})-f(X^U_{T_i-})]e^{-\delta T_i}\\ & \quad +\sum_{i=1}^{N_t}[f(X^U_{T_i-})e^{-\delta T_i-}-f(X^U_{T_{i-1}})e^{-\delta T_{i-1}}]\\ & \quad +f(X^U_t)e^{-\delta t}-f(X^U_{T_{N_t}})e^{-\delta T_{N_t}}. \end{aligned} $$

From Brémaud [7, p. 27] we have that the process

$$ \begin{aligned} &\left\{\sum_{i=1}^{N_t}\left[f(X^U_{T_i-}-Y_{i}) -f(X^U_{T_i-})\right]e^{-\delta T_i}\right. \\ & \quad \left.- \lambda\int\limits_0^t e^{-\delta s}\int\limits_0^\infty \left(f(X_s^U-y)\;\hbox{d} G(y)-f(X_s^U)\right)\;\hbox{d} s\right\} \end{aligned} $$

is a martingale. Now noting that

$$ f(X^U_{T_i-})e^{-\delta T_i-}-f(X^U_{T_{i-1}})e^{-\delta T_{i-1}}= \int\limits_{T_{i-1}}^{T_i-} \left((c-U_s)f^{\prime}(X^U_s)-\delta f(X^U_s)\right)e^{-\delta s}\;{\text{d}} s $$

and using that T _i  − and T _i−1 can be replaced by T _i ∧ t and T _i−1∧ t, respectively, we get that the process

$$ \begin{aligned} &\left\{f(X^U_t)e^{-\delta t}-f(x)- \sum_{0\leq s\leq t} [f(X_s^U) - f(X_s^U - \Updelta Z_s)]e^{-\delta s}\right.\\ & \quad \left.- \int\limits_0^t \left[(c-U_s)f^{\prime}(X^U_s)\right.\right.\\ & \quad \left.\left.+\lambda \int\limits_0^\infty f(X_s^U-y)\;\hbox{d} G(y) -(\lambda+\delta) f(X^U_s)\right]e^{-\delta s} \;\hbox{d} s\right\} \end{aligned} $$

is a ${\{{\mathcal F}_t\}}$-martingale with expected value 0. □

Now we show that the value function is the unique increasing bounded solution to Eq. 2 and the strategy given by Eq. 3 is optimal.

Theorem 2

Let f(x) be an increasing, bounded and positive solution to Eq. 2 with property (1) and C ≥ 0 chosen such that $f(C) - \phi C = \sup_{x \ge 0} f(x) - {\phi}x$. Then $\lim_{x\to\infty}f(x)=u_0/\delta.$ If u ₀ ≤ c or $f^{\prime}(0)\geq 1,$ then f(x) = V(x), and an optimal strategy is given by (3).

Proof

Since f is bounded, f must converge to a $f(\infty)<\infty$. We first note that $C \le f(C) - f(0) \le f(\infty) - f(0)$. There exists a sequence $x_n\to\infty$ such that $f^{\prime}(x_n)\to 0$. Let u _n  = u(x _n ). By Definition (3), we can assume that u _n  = u ₀. Letting $n\to\infty$ in Eq. 2, yields that

$$ 0 = \left( {c - u_{0} } \right)f^{\prime } \left( {x_{n} } \right) + \lambda \left[ {\int\limits_{0}^{\infty } {f\left( {x_{n} - y} \right){\text{d}}G\left( y \right) - f\left( {x_{n} } \right)} } \right] - \delta f\left( {x_{n} } \right) + u_{0} \mathop{\rightarrow}^{{n\to\infty}} - \delta f\left( \infty \right) + u_{0} $$

showing that $\lim_{x\to\infty}f(x)=u_0/\delta.$

Let now U = U ^* be the strategy given by Eq. 3 and the corresponding $Z^{*}=Z^{U^{*}}.$ From the lemma above and the HJB equation, it follows that

$$ \left\{f(X_t^{U^*})e^{-\delta t} -f(x)+\int\limits_0^t e^{-\delta s}U_s^* \;\hbox{d}s - \sum_{0\leq s\leq t} [f(X_s^{U^*}) - f(X_s^{U^*} - \Updelta Z_s^*)]e^{-\delta s} \right\} $$

is a martingale with expected value 0. If ${\Updelta Z}_s^* > 0,$ then X ^U* _s  = C and $f(X_s^{U^*} - {\Updelta Z}_s^*) = f(C- {\Updelta Z}_s^*)=f(C) - \phi ({\Updelta Z}_s^*-C+C)- L =f(C) - \phi{\Updelta Z}_s^*- L$. Thus

$$ f(x)={\mathbb{E}}\left[f(X_t^{U^*})e^{-\delta t} +\int\limits_0^t e^{-\delta s}U_s^* \;\hbox{d}s -\phi\int\limits_0^t e^{-\delta s}\;\hbox{d}Z^*_s- L\sum_{0\leq s\leq t}e^{-\delta s}{\rm 1\!\!I}_{\{\Updelta Z^*_s>0\}}\right] $$

holds. By the boundedness of f and the bounded convergence theorem, we get that ${{\mathbb{E}}[f(X_t^{U^*})e^{-\delta t}]\to 0 }$ as $t\to\infty$. Since the other terms are monotone, we can interchange the limit and integration and obtain f(x) = V ^U*(x). Here we used the condition $f^{\prime}(0)\geq 1$ which is motivated by the considerations above. For an arbitrary strategy U, Eq. 2 gives that

$$ \begin{aligned} f(x)\geq& {\mathbb{E}}\left[f(X_t^U)e^{-\delta t} +\int\limits_0^t e^{-\delta s}U_s \;\hbox{d} s -\phi\int\limits_0^t e^{-\delta s}\;\hbox{d} Z_s\right. \\ &\left.- L\sum_{0\leq s\leq t}e^{-\delta s}{\rm 1\!\!I}_{\{\Updelta Z_s>0\}}\right], \end{aligned} $$

where we used that

$$ f(X_s^U) \le f(C) + \phi (X_s^U-C) = f(X_s^U-\Updelta Z_s) + \phi \Updelta Z_s + L. $$

Letting $t\to\infty$ shows that f(x) ≥ V ^U(x). Thus, f(x) = V(x). □

3 Unrestricted dividends

In this section, all increasing, adapted and càdlàg processes ${D\in\fancyscript{S}_x}$ are allowed. The value of a strategy D is

$$ V^D(x)={\mathbb{E}}\left[\int\limits_{0-}^\infty e^{-\delta t}\;\hbox{d} D_t -\phi \int\limits_{0-}^\infty e^{-\delta t}\;\hbox{d} Z_t - L\sum_{t\geq 0}e^{-\delta t}{\rm 1\!\!I}_{\{\Updelta Z_t>0\}}\right] $$

and ${V(x)=\sup_{D\in\fancyscript{S}_x}V^D(x)}$ is the value function.

3.1 The value function and the HJB-equation

Again, we start by proving some useful properties of V(x).

Lemma 4

The function V(x) is increasing with

$$ x-y\leq V(x)-V(y)\leq\phi(x-y)+L $$

for 0 ≤ y < x, locally Lipschitz continuous on $[0, \infty)$ and therefore absolutely continuous. For any x ≥ 0,

$$ x + {\frac{c - \lambda (\phi\mu +\phi C+ L)}{\delta}} \leq V(x)\leq x+{\frac{c}{\delta}}. $$

Proof

Consider a strategy D with $V^{D}(y)\geq V(y)-\varepsilon$ for an $\varepsilon >0$. For x ≥ y we define a new strategy as follows: x − y is paid immediately as dividend and then the strategy D with initial capital y is followed. Then for any $\varepsilon >0,$ it holds that

$$ V(x)\geq x-y + V^{D}(y)\geq x-y + V(y)-\varepsilon. $$

Because $\varepsilon$ was arbitrary, V(x) − V(y) ≥ x − y follows. In particular, V is increasing.

For the other direction let $\varepsilon >0$ and D an $\varepsilon$-optimal strategy for initial capital x. For y < x capital injections x − y are made immediately and after that the strategy D is followed. Hence,

$$ V(y)\geq {-}\phi(x-y)-L+V^D(x)\geq {-}\phi(x-y)-L+V(x)-\varepsilon. $$

Because this holds for all $\varepsilon >0,$ we get the inequality

$$ V(x)-V(y)\leq \phi(x-y)+L\;. $$

Consider now the strategy D paying initial capital immediately and then the dividends are paid at rate c, i.e. the whole surplus exceeding 0 is paid as dividend. For such a strategy we have C = 0, since for C > 0 the sum of the dividends would be lower because of the penalty ϕ. Thus, the value of the dividends is

$$ V^D(x)=x+{\mathbb{E}}_x\left[\int\limits_0^\infty e^{-\delta t}c\;\hbox{d} t \right]=x+{\frac{c}{\delta}}. $$

The value of the capital injections is calculated in Lemma 1, which yields the lower bound. We note that for any reasonable strategy, V ^D(x) is an upper bound for the accumulated dividend payments. Not taking the capital injections into account yields the upper bound for the value function.

The local Lipschitz continuity follows by the local boundedness of V as in the proof of Lemma 2.

By Rademacher’s Theorem, the local Lipschitz continuity ensures the existence of the derivative $V^{\prime}(x)$ almost everywhere on $[0,\infty)$. Then $V^{\prime}$ is a density of V. □

We note that since (c − λ(ϕμ + ϕC + L))/δ is the lower bound for V(0), the positivity of V can only be assured, if

$$ c>\lambda (\phi\mu+\phi C+ L). $$

(4)

From the next lemma, it follows that the value function can be calculated as the limit of the value functions from the previous section. The proof is analogous to the proof in Schmidli [20, Section 2.4.2].

Lemma 5

Let V _u (x) be the value function for the restricted dividend strategy in the case u ₀ = u. Then $\lim_{u\to\infty}V_u(x)=V(x)$.

Idea of the proof

Since V _u (x) is increasing in u, it is converging pointwise. The restricted strategy is admissible. Therefore, $\lim_{u\to\infty}V_u(x)\leq V(x)$. Now approximate V(x) by the value of a pure jump dividend strategy {D _t }, which, on its part, can be approximated by a restricted dividend strategy. □

To prove the Hamilton–Jacobi–Bellman equation for this problem, we can repeat the procedure in Schmidli [20, Section 2.4.2].

Theorem 3

The function V(x) is differentiable a.e. on $(0,\infty)$ and fulfils the Hamilton–Jacobi–Bellman equation

$$ \max\left\{c V^{\prime}(x)+\lambda\int\limits_0^\infty V(x-y)\;{\text{d}} G(y) - (\lambda+\delta)V(x), 1-V^{\prime}(x)\right\}=0. $$

(5)

At points where V(x) is not differentiable, the derivatives from the left and from the right exist and fulfil Eq.  5 with $V^{\prime}(x-)=1<V^{\prime}(x+)$.

Idea of the proof

Since we let $u\to\infty,$ it is enough to consider the case u > c. Equation 2 can be written as

$$ \begin{aligned} &\max\left\{c V_u^{\prime}(x)+\lambda\int\limits_0^\infty V_u(x-y)\;\hbox{d} G(y) - (\lambda+\delta)V_u(x),\right.\\ & \left. 1- V^{\prime}_u(x) + {\frac{\lambda\int\limits_0^\infty V_u(x-y)\;\hbox{d} G(y) - (\lambda+\delta)V_u(x) +c}{u-c}} \right\}=0. \end{aligned} $$

The two parts correspond to the different cases u = 0 and u = u ₀ for the restricted problem (see Eq. 2), where the second equation is divided by u ₀. Now show that $V_u^{\prime}(x)\to f(x)$ a.e. for some positive function f(x). Then show that f(x) really is the density of V(x). □

Remark 1

From the theorem above follows that the differentiability of V is only violated at the switching points from paying dividends to paying no dividends.

3.2 The optimal dividend strategy

Motivated by the proof of Theorem 3, we consider the following three sets which will be essential for the definition of the optimal strategy.

• ${{\mathcal A} = \{x\in[0,\infty]: V^{\prime}(x)=1 \;{\text{and}}\; H(x)=c\},}$

• ${{\mathcal B} = \{x\in(0,\infty): V^{\prime}(x)=1 \;{\text{and}}\;H(x)>c\},}$

• ${{\mathcal C} = ({{\mathcal {A}}\cup{\mathcal B})}^c = \{x\in[0,\infty): V^{\prime}(x)>1 \;{\text{and}}\; H(x)>c\}}.$

Here we again mean the derivative from the left if the derivative does not exist. The next lemma discusses some properties of these sets. The proof is deferred to the Appendix.

Lemma 6

• 1. ${{\mathcal A}}$ is closed.

• 2. ${{\mathcal B}}$ is a left-open set, i.e., if ${x\in {\mathcal B},}$ then there exists $\varepsilon>0$ such that ${(x-\varepsilon, x]\subset {\mathcal B}}$.

• 3. If ${(x_0, x]\subset {\mathcal B}}$ and ${x_0\notin {\mathcal B},}$ then ${x_0\in {\mathcal A}}$.

• 4. ${{\mathcal C}}$ is a right-open set, i.e., if ${x\in {\mathcal C},}$ then there exists δ > 0 such that ${[x,x+\delta)\subset {\mathcal C}}$.

• 5. We have ${(\lambda(\phi\mu+\phi C+L)/\delta, \infty)\subset {\mathcal B}}$.

• 6. ${{\mathcal A}, {\mathcal B}\neq \emptyset}$.

Now we define the following strategy D ^*:

• If ${X_t^{D^*}\in {\mathcal A},}$ then we pay a dividend at rate c until the next claim occurs, i.e., $\hbox{d} D^*_t=c\;\hbox{d} t$.

• If ${x:=X_{T-}^{D^*}-Y \in {\mathcal B},}$ then there is a ${x_1=\sup\{z<x: z\notin {\mathcal B}\}}$ such that ${(x_1, x]\subset {\mathcal {B}},}$ and the sum

  $$ \Updelta D^*_t= x-x_1 $$

  is paid as dividend. Then, ${x_1\in{\mathcal A}}$.

• If ${X_t^{D^*}\in {\mathcal C},}$ no dividends are paid.

This is the so called band strategy. By construction, the dividend process D ^* is measurable.

For the constructed strategy D ^* we denote X ^* _t  = X ^D* _t  = X ⁰ _t  − D ^* _t  + Z ^* _t the corresponding surplus process. We again can derive the following facts.

• The process X ^* only jumps at the claim times. Thus, in an interval (T _i-1, T _i ) between two claims holds that ${\hbox{d}X^*_t= c{\rm 1\!\!I}_{\{X^*_t\in{\mathcal C}\}}\; \hbox{d} t.}$

• ${X^*_{T_i}= X^*_{T_i-}-Y_{i}-\Updelta D^*_{T_i}{\rm 1\!\!I}_{\{X^*_{T_i-}-Y_{i}\in {\mathcal B}\}}+\Updelta Z^*_{T_i}{\rm1\!\!I}_{\{X^*_{T_i-}-Y_{i}<0\}}.}$

• ${\rm 1\!\!I}_{\{\Updelta Z^*_{T_i}>0\}}={\rm 1\!\!I}_{\{X^*_{T_i-}-Y_{i}<0\}}\;.$

• It can not be optimal to pay dividends at claim times when the surplus falls below zero, i.e. when capital injections are needed. Thus, ${\rm 1\!\!I}_{\{\Updelta D^*_{T_i}>0\}}=1-{\rm 1\!\!I}_{\{\Updelta Z^*_{T_i}>0\}}$.

• If $X^*_{T_i-}-Y_{i}< 0,$ then the shareholders pay as much that $X^*_{T_i-} = C;$ i.e., $\Updelta Z^*_{T_i}= -(X^*_{T_i-}-Y_{i})+C$. In this case, the value function fulfils

  $$ V(X^*_{T_i})(= V(C))= V(X^*_{T_i-}-Y_{i})+( \phi\Updelta Z^*_{T_i}+ L){\rm 1\!\!I}_{\{\Updelta Z^*_{T_i}>0\}} $$

  because of the property (1). Thus, it suffices to consider only solutions f to the HJB equation with the property (1).

Theorem 4

The strategy D ^* is optimal, i.e., V*(x) = V ^D*(x) = V(x).

Proof

Similarly to the proof of Lemma 3, we get that the process

$$ \begin{aligned} &\left\{V(X^*_t)e^{-\delta t}-V(x)+ \sum_{i=0}^{N_t}\Updelta D^*_{T_i}e^{-\delta T_i}-\sum_{i=1}^{N_t}(\phi \Updelta Z^*_{T_i}+L){\rm 1\!\!I}_{\{\Updelta Z^*_{T_i}>0\}} e^{-\delta T_i}\right.\\ & \quad - \int\limits_0^t \left[c V^{\prime}(X^*_s) +\lambda \int\limits_0^\infty V(X_s^*-y)\;\hbox{d} G(y) -(\lambda+\delta) V(X^*_s)\right]{\rm 1\!\!I}_{\{X_s^*\in {\mathcal C}\}}e^{-\delta s} \;\hbox{d} s\\ & \quad \left.- \int\limits_0^t \left[\lambda \int\limits_0^\infty V(X_s^*-y)\;\hbox{d} G(y) -(\lambda+\delta) V(X^*_s)\right]{\rm 1\!\!I}_{\{X_s^*\in {\mathcal A}\}}e^{-\delta s} \;\hbox{d} s\right\} \end{aligned} $$

is a martingale. On ${{\mathcal C}}$ we have $V^{\prime}(X_s^*)>1$ and the first term of (5) vanishes. On ${{\mathcal A}}$ both terms of (5) are zero, therefore

$$ \lambda \int\limits_0^\infty V(X_s^*-y)\;\hbox{d} G(y) -(\lambda+\delta) V(X^*_s)=-c\;. $$

Thus, we get that

$$ \begin{aligned} & \left\{V(X^*_t)e^{-\delta t}-V(x)+ \sum_{i=0}^{N_t}\Updelta D^*_{T_i}e^{-\delta T_i}+ \int\limits_0^t c{\rm 1\!\!I}_{\{X_s^*\in {\mathcal A}\}}e^{-\delta s} \;\hbox{d} s\right.\\ & \quad \left.-\sum_{i=1}^{N_t}( \phi\Updelta Z^*_{T_i}+L){\rm 1\!\!I}_{\{\Updelta Z^*_{T_i}>0\}} e^{-\delta T_i}\right\} \end{aligned} $$

is a martingale with expected value 0. From the martingale property we get that

$$ \begin{aligned} V(x)&= {\mathbb{E}}\left[V(X^*_t)e^{-\delta t}+ \sum_{i=0}^{N_t}\Updelta D^*_{T_i}e^{-\delta T_i}+ \int\limits_0^t c{\rm 1\!\!I}_{\{X_s^*\in {\mathcal A}\}}e^{-\delta s} \;\hbox{d} s\right.\\ &\quad \left.-\sum_{i=1}^{N_t}(\phi\Updelta Z^*_{T_i}+L){\rm 1\!\!I}_{\{\Updelta Z^*_{T_i}>0\}} e^{-\delta T_i}\right]. \end{aligned} $$

Since V(X ^* _t )e ^−δt ≤ V((x + ct)∨ C ^*) e ^−δt ≤ ((x + ct)∨ C ^* + c/δ)e ^−δt converges to 0 as $t\to\infty,$ we have that

$$ \lim_{t\to\infty}{\mathbb{E}}[V(X^*_t)e^{-\delta t}]=0 $$

by the bounded convergence theorem. By monotone convergence we finally get that

$$ \begin{aligned} V(x) & = \lim_{t\to\infty}{\mathbb{E}}\left[\int\limits_0^t c{\rm 1\!\!I}_{\{X_s^*\in{\mathcal A}\}}e^{-\delta s} \;\hbox{d} s + \sum_{i=0}^{N_t}\Updelta D^*_{T_i}e^{-\delta T_i}\right. \\ & \quad \left.- \phi\sum_{i=1}^{N_t} e^{-\delta T_i}\Updelta Z^*_{T_i} - L \sum_{0\leq s\leq t}e^{-\delta s}{\rm 1\!\!I}_{\{\Updelta Z_s^*>0\}}\right]\\ & =\left. {\mathbb{E}}\left[\int\limits_0^\infty e^{-\delta s} \;\hbox{d} D_s^* - \phi\int\limits_0^\infty e^{-\delta s} \;\hbox{d} Z^*_s- L \sum_{0\leq s<\infty}e^{-\delta s}{\rm 1\!\!I}_{\{\Updelta Z_s^*>0\}}\right]\right.\\ & = V^*(x). \end{aligned} $$

□

Remark 2

If ${\phi > 1, C\in {\mathcal B}}$ cannot be optimal. Thus ${C\in {\mathcal A}}$ or ${C\in {\mathcal C}}$. If ϕ = 1, it follows from Lemma 4 that V(x) − x ≥ V(C) − C for x ≥ C. Since C is optimal we also have V(x) − x ≤ V(C) − C, therefore equality holds, i.e. V(x) = V(C) + x − C for x ≥ C. That is, the capital injection is such that the surplus is at the maximal level in ${{\mathcal A}}$.

3.3 Characterisation of the solution

3.3.1 The minimality property of the solution

Because we do not have an explicit solution nor an initial value, we need to characterise the solution V(x) among other possible solutions.

Theorem 5

V(x) is the minimal solution to Eq. 5 with C chosen such that V(C) − ϕC becomes maximal. If f(x) is a solution with only positive jumps of its derivative fulfilling property (1) and a linear growth condition f(x) ≤ κ₁ x + κ₂ for some positive constants κ₁, κ₂ and all x ≥ 0, then f(x) = V(x).

Proof

Let f be a solution to the HJB equation with property (1) and C chosen such that f(C) − ϕC becomes maximal. Then f(x) is increasing. Consider the process X ^* under the optimal strategy and denote the optimal surplus after a capital injection by C ^*. We have then, as in the proof of Theorem 4, that the process

$$ \begin{aligned} &\left\{f(X^*_t)e^{-\delta t}-f(X^*_0)-\sum_{i=1}^{N_t} \left[f(X^*_{T_i}) - f(X^*_{T_i} - \Updelta Z^*_{T_i})\right]e^{-\delta T_i}\right.\\ & \quad + \sum_{i=1}^{N_t}\left[f(X^*_{T_i-})- f(X^*_{T_i-}-Y_{i}-\Updelta D^*_{T_i})\right]{\rm 1\!\!I}_{\{X^*_{T_i-}-Y_{i}\in {\mathcal B}\}}e^{-\delta T_i}\\ & \quad - \int\limits_0^t \left[cf^{\prime}(X^*_s)+\lambda \!\int\limits_0^\infty\!\!\! f(X_s^*-y)\;\hbox{d} G(y) -(\lambda+\delta) f(X^*_s)\right]{\rm 1\!\!I}_{\{X_s^*\in {\mathcal C}\}}e^{-\delta s} \;\hbox{d} s\\ & \quad \left.- \int\limits_0^t \left[\lambda\! \int\limits_0^\infty\!\!\! f(X_s^*-y)\;\hbox{d} G(y) -(\lambda+\delta) f(X^*_s)\right]{\rm 1\!\!I}_{\{X_s^*\in{\mathcal A}\}}e^{-\delta s} \;\hbox{d} s\right\} \end{aligned} $$

is a martingale with expected value 0. Since $f^{\prime}(x)\geq 1,$ we have f(x) ≥ f(X ^*₀ ) + D ^*₀ and $f(X^*_{T_i-})-f(X^*_{T_i-}-Y_{i}-\Updelta D^*_{T_i})\geq \Updelta D^*_{T_i}.$ By Eq. 5

$$ cf^{\prime}(X^*_s)+\lambda \int\limits_0^\infty f(X_s^*-y)\;\hbox{d} G(y) -(\lambda+\delta) f(X^*_s)\leq 0 $$

and

$$ \lambda \int\limits_0^\infty f(X_s^*-y)\;\hbox{d} G(y) -(\lambda+\delta) f(X^*_s)\leq -cf^{\prime}(X_s^*)\leq -c. $$

Noting that if $X^*_{T_i} - {\Updelta Z}^*_{T_i}=C^*- {\Updelta Z}^*_{T_i}=X^*_{T_i-} - Y_{i}<0,$ then, since f(C) − ϕC is maximal, we also have

$$ \begin{aligned} f(X^*_{T_i}) - f(X^*_{T_i} - \Updelta Z^*_{T_i}) & = f(C^*) - [f(C) - \phi(\Updelta Z^*_{T_i}-C^* +C)-L] \\ & \le \phi \Updelta Z^*_{T_i} + L. \end{aligned} $$

This yields

$$ \begin{aligned} f(x) \geq & {\mathbb{E}}\left[f(X^*_t)e^{-\delta t}+ \sum_{i=0}^{N_t}\Updelta D^*_{T_i}e^{-\delta T_i}+\int\limits_0^t e^{-\delta s}c{\rm 1\!\!I}_{\{X^*_s\in {\mathcal A}\}}\;\hbox{d} s\right.\\ & \left.-\sum_{i=1}^{N_t}(\phi \Updelta Z^*_{T_i}+L){\rm 1\!\!I}_{\{\Updelta Z^*_{T_i}>0\}} e^{-\delta T_i}\right]\\ \geq & {\mathbb{E}}\left[\int\limits_0^t e^{-\delta s} \;\hbox{d} D^*_s - \phi\int\limits_0^t e^{-\delta s} \;\hbox{d} Z^*_s -L \sum_{0\leq s\leq t}e^{-\delta s} {\rm 1\!\!I}_{\{\Updelta Z^*_s>0\}}\right] \end{aligned} $$

and, therefore, by monotone convergence, f(x) ≥ V ^D*(x) = V(x).

Suppose that, additionally, f satisfies a linear growth condition. Define

$$ \begin{aligned} \tilde{H}(x)&=(\lambda+\delta)f(x)-\lambda\int\limits_0^x f(x-y)\hbox{d} G(y)\\ & \quad -\lambda(f(C)-\phi C-L)(1-G(x))+\lambda\phi\int\limits_x^\infty (1-G(y))\hbox{d}y \end{aligned} $$

and the following sets:

• ${\tilde{{\mathcal{A}}} = \{x\in[0,\infty): f^{\prime}(x)=1 \;\hbox{and}\; \tilde{H}(x)=c\},}$

• ${{\tilde{\mathcal{B}}} = \{x\in(0,\infty): f^{\prime}(x)=1 \;\hbox{and}\; \tilde{H}(x)>c\},}$

• ${{\tilde{\mathcal{C}}} = ({\tilde{\mathcal{A}}}\cup{\tilde{\mathcal{B}}})^c = \{x\in[0,\infty): f^{\prime}(x)>1 \;\hbox{and}\; \tilde{H}(x)>c\}}$.

The results of Lemma 6 remain valid. Let $\tilde{D}$ be the strategy corresponding to f(x) defined in the same way as D ^*, i.e. if the current ${x\in {\tilde{\mathcal{A}}},}$ then every incoming premium is paid as dividend; if ${x=X_{T-}^{\tilde{D}}-Y \in {\tilde{\mathcal{B}}},}$ then the sum $\Updelta \tilde{D}_t= x-x_1$ is paid as dividend reducing the reserve process to the next point ${x_1\in {\tilde{\mathcal{A}}}}$ which is smaller than x; if ${x\in {\tilde{\mathcal{C}}},}$ no dividend is paid. In the same way as in Theorem 4 we find that the process

$$ \begin{aligned} &\left\{f(X^{\tilde{D}}_t)e^{-\delta t}-f(x)+ \sum_{i=0}^{N_t}\Updelta \tilde{D}_{T_i}e^{-\delta T_i}+ \int\limits_0^t c{\rm 1\!\!I}_{\{X_s^{\tilde{D}}\in {\tilde{{\mathcal{A}}}}\}}e^{-\delta s} \;\hbox{d} s\right.\\ & \quad \left.-\sum_{i=1}^{N_t}( \phi\Updelta Z^{\tilde{D}}_{T_i}+L){\rm 1\!\!I}_{\{\Updelta Z^{\tilde{D}}_{T_i}>0\}} e^{-\delta T_i}\right\} \end{aligned} $$

is a martingale with expected value 0. Taking expectations and letting $t\to\infty$ yields the assertion since $f(X^{\tilde{D}}_t)e^{-\delta t}\leq f((x+ct)\vee C)e^{-\delta t}$ tends to zero as $t\to\infty$ by the linear growth condition. Thus we get $f(x)=V^{\tilde{D}}\leq V(x)$ and therefore f(x) = V(x). □

Remark 3

The condition that f(C) − ϕC is maximal is needed in order to exclude solutions with a non-optimal choice of C.

3.3.2 Dividends at zero

We now consider the case where dividends are paid in zero. Then ${0\in {\mathcal A}, V^{\prime}(0)=1}$ and H(0) = c. It follows that

$$ V(0)={\frac{c+\lambda(V(C)-\phi C-L-\phi\mu)}{\lambda+\delta}}. $$

By Lemma 6, there exists $x_0 \leq \infty$ such that ${(0,x_0)\subset {\mathcal B}}$ because ${{\mathcal B}}$ is left-open and only elements of ${{\mathcal A}}$ can be lower boundaries of subsets of ${{\mathcal B}}$. Thus, V(x) is the value of the barrier strategy with barrier at zero for $x\in[0,x_0],$ i.e. all surplus exceeding zero is paid as dividends. Of special interest is the case C = 0, where

$$ V(0)={\frac{c-\lambda(\phi\mu+L)}{\delta}}. $$

Since $1-V^{\prime}(x)=0$ is fulfilled obviously, we consider the first part of the HJB equation (5) which reads

$$ \begin{aligned} & c+\lambda\int\limits_0^x\left(x-y+ {\frac{c-\lambda(\phi\mu+L)} {\delta}}\right)\;\hbox{d} G(y)\\ & \quad +\lambda\int\limits_x^\infty \left({\frac{c-\lambda(\phi\mu+L)} {\delta}}-L-\phi(y-x)\right)\;\hbox{d} G(y) \\ & \quad - (\lambda+\delta)\left(x+ {\frac{c-\lambda(\phi\mu+L)} {\delta}}\right)\leq 0. \end{aligned} $$

This is equivalent to

$$ \lambda L\; G(x)+\int\limits_0^x(\lambda(\phi-1)(1- G(y))- \delta)\;\hbox{d} y\leq 0. $$

(6)

The condition simplifies to λL G(x) ≤ δx in the case ϕ = 1. The condition also simplifies if G(x) is concave. Then the left hand side of Eq. 6 is concave as a function of x. The condition is fulfilled if the derivative of the left hand side in zero is non-positive. That is, λL g(0) + λ(ϕ − 1) − δ ≤ 0, where g(x) is the density of the claim size distribution. This can be written as

$$ g(0)\leq {\frac{\delta-\lambda(\phi-1)}{\lambda L}}. $$

Note that δ > λ(ϕ − 1) is necessary. It should further be noted that condition (6) is necessary for a barrier in zero and C = 0.

3.3.3 No dividends at zero and ϕ > 1

If $V^{\prime}(0)>1,$ i.e. ${0\in {\mathcal C},}$ then no dividends are paid in zero. We already know that ${C\in{\mathcal A}}$ or ${C\in{\mathcal C}}$. In particular, V is differentiable at C. Since C maximises V(C) − ϕC, we find $V^{\prime}(C)=\phi$ if C ≠ 0. It follows that ${C \notin {\mathcal A}}$ since $V^{\prime}(x) = 1$ for all ${x \in {\mathcal A}}$.

If C = 0 and $V^{\prime}(C)=V^{\prime}(0)=\phi,$ then, in the case of positive safety loading c > λμ, 

$$ V(0)={\frac{cV^{\prime}(0)-\lambda\phi\mu-\lambda L} {\delta}}=\phi{\frac{c-\lambda\mu}{\delta}}-{\frac{\lambda L} {\delta}} $$

was increasing in ϕ, which is not possible. Thus, $V^{\prime}(C)\neq \phi$ for ϕ > 1.

For small initial values, V(x) is the value of a barrier strategy on [0, b] for some (locally) optimal barrier b. We assume that C < b. Then we could apply the method from Gerber and Shiu [13] and Gerber et al. [12] to determine the value function at least for $x\in[0,b]$.

Let τ be the first time the (uncontrolled) surplus process X _t falls below zero and τ^b the time of ruin of the controlled surplus process X ^D _t if dividends are paid according to the barrier strategy with a barrier b. Then we can write

$$ \begin{aligned} V(x)&={\mathbb{E}}_x\left[\int\limits_0^{\tau^b} e^{-\delta t}\;\hbox{d} D_t\right]\\ & \quad -\phi {\mathbb{E}}_x\left[e^{-\delta \tau^b} |X_{\tau^b}|{\rm 1\!\!I}_{\tau^b<\infty}\right]+(V(C)-\phi C-L){\mathbb{E}}_x\left[e^{-\delta \tau^b} {\rm 1\!\!I}_{\tau^b<\infty}\right]. \end{aligned} $$

Consider now the functions

$$ \begin{aligned} \sigma(x)&={\mathbb{E}}_x\left[e^{-\delta \tau} |X_\tau|{\rm 1\!\!I}_{\tau<\infty}\right],\\ \psi(x)&={\mathbb{E}}_x\left[e^{-\delta \tau} {\rm 1\!\!I}_{\tau<\infty}\right],\\ \sigma^b(x)&={\mathbb{E}}_x\left[e^{-\delta \tau^b} |X^D_{\tau^b}|{\rm 1\!\!I}_{\tau^b<\infty}\right],\\ \psi^b(x)&={\mathbb{E}}_x\left[e^{-\delta \tau^b} {\rm 1\!\!I}_{\tau^b<\infty}\right]. \end{aligned} $$

These functions are the Gerber–Shiu penalty functions with w(x, y) = y for σ(x) and w(x,y) = 1 for ψ(x), see formula (2.10) of Gerber and Shiu [13]. They fulfil the integro-differential equation

$$ 0=ch^{\prime}(x)-(\lambda+\delta)h(x)+\lambda\int\limits_0^x h(x-y)\;\hbox{d} G(y)+\lambda \Uppi(x) $$

(7)

with

$$ \Uppi(x)=\int\limits_x^\infty w(x,y-x)\;\hbox{d} G(y). $$

Let ρ be the unique positive solution to Lundberg’s fundamental equation

$$ \lambda+\delta -c\xi=\lambda \hat{g}(\xi)=\lambda\int\limits_0^\infty e^{-\xi y}\;\hbox{d} G(y). $$

Then the initial value can be determined by

$$ h(0)={\frac{\lambda}{c}}\int\limits_0^\infty e^{-\rho x}\Uppi(x)\;\hbox{d} x. $$

For A fixed, denote by V ^A,b the function

$$ \begin{aligned} V^{A,b}(x)&= {\mathbb{E}}_x\left[\int\limits_0^{\tau^b} e^{-\delta t}\;\hbox{d} D_t\right]\\ & \quad -\phi {\mathbb{E}}_x\left[e^{-\delta \tau^b} |X^D_{\tau^b}|{\rm 1\!\!I}_{\tau^b<\infty}\right]+(A-L){\mathbb{E}}_x\left[e^{-\delta \tau^b} {\rm 1\!\!I}_{\tau^b<\infty}\right]\;. \end{aligned} $$

where τ^b is the time of ruin if a barrier strategy with barrier b = b(A) is applied. Let V ^b be the value of the expected discounted dividends until ruin, i.e., ${V^b(x)={\mathbb{E}}_x\left[\int\limits_0^{\tau^b} e^{-\delta t}\;\hbox{d}D_t\right]}.$ Then we can write

$$ V^{A,b}(x)=V^b(x)-\phi \sigma^b(x)+(A-L)\psi^b(x)\;. $$

Note that A = V(C) − ϕC ≥ V(0). Let

$$ \chi(x)={\mathbb{E}}_x\left[e^{-\delta \tau+\rho X_\tau}{\rm 1\!\!I}_{\{\tau<\infty\}}\right] $$

be a penalty function with w(x, y) = e ^−ρy. Gerber and Shiu [13] showed that V ^b can be expressed as

$$ V^b(x)={\frac{e^{\rho x}-\chi (x)}{\rho e^{\rho b}-\chi^{\prime}(b)}}. $$

(8)

Further Gerber et al. [12] obtained for σ^b(x) and ψ^b(x) the following dividends-penalty identity

$$ \begin{aligned} \sigma^b(x)=& \sigma(x)-\sigma^{\prime}(b)V^b(x),\\ \psi^b(x)=& \psi(x)-\psi^{\prime}(b)V^b(x) \end{aligned} $$

(9)

for 0 ≤ x ≤ b. Combining Eqs. 8 and 9 yields

$$ V^{A,b}(x)=V^b(x)\left[1+\phi \sigma^{\prime}(b)-(A-L)\psi^{\prime}(b)\right]-\phi \sigma(x)+(A-L)\psi(x). $$

We have that $(V^{A,b})^{\prime}(b)=(V^{b})^{\prime}(b)=1$ and for the penalty functions holds $\sigma(\infty)=\psi(\infty)=\chi(\infty)=0$ and

$$ \begin{aligned} \psi(0)=& {\frac{\lambda}{c}}\int\limits_0^\infty e^{-\rho x}(1-G(x))\hbox{d} x,\\ \sigma(0)=& {\frac{\lambda}{c}}\int\limits_0^\infty e^{-\rho x}\int\limits_x^\infty(1-G(y))\hbox{d}y\,\hbox{d}x,\\ \chi(0)=& {\frac{\lambda} {c}}\int\limits_0^\infty e^{-\rho x}x\hbox{d} G(x). \end{aligned} $$

Thus, V ^A,b(x) is determined by the functions σ(x), ψ(x) and χ(x).

Since σ(x), ψ(x) and χ(x) do not depend on b, we can find an optimal b ^* = b ^*(A) which maximises V ^A,b(x) by maximising the expression

$$ {\frac{1+\phi \sigma^{\prime}(b)-(A-L)\psi^{\prime}(b)}{\rho e^{\rho b}-\chi^{\prime}(b)}}. $$

Then b ^* is independent of x (for x ≤ b ^*). By maximising V ^A,b*(x) − ϕx, we can find an optimal C ^* = C ^*(A). Finally, we solve the equation V ^A,b*(C ^*) − ϕC ^* = A to find the correct A. For this purpose we observe the following.

Denote by A ^* the correct A and τ^*, b ^*, C ^* the time of ruin, the optimal barrier and the optimal level for the capital injections corresponding to A ^*. Let A > A ^* and τ^b, b, C the analogous notation for A. For A ^* must hold V ^{A*, b*}(C ^*) − ϕC ^* = A ^*. Then we have

$$ \begin{aligned} & V^{A,b}(C)-\phi C-A\\ & \quad =(V^{A,b}(C)-\phi C-A)-(V^{A^*,b^*}(C^*)-\phi C^*-A^*)\\ & \quad \leq (V^{A,b}(C)-\phi C)-(V^{A^*,b^*}(C)-\phi C)-(A-A^*)\\ & \quad = V^{A,b}(C)-V^{A^*,b^*}(C)-(A-A^*)\\ & \quad \leq V^{A,b}(C)-V^{A^*,b}(C)-(A-A^*)\\ & \quad ={\mathbb{E}}_{C}\left[\int\limits_0^{\tau^b} e^{-\delta t} \hbox{d} D_t-\phi e^{-\delta \tau^b} |X_{\tau^b}|{\rm 1\!\!I}_{\tau^b<\infty}+(A-L) e^{-\delta \tau^b} {\rm 1\!\!I}_{\tau^b < \infty}\right]\\ & \qquad -{\mathbb{E}}_{C}\left[\int\limits_0^{\tau^b} e^{-\delta t} \hbox{d} D_t-\phi e^{-\delta \tau^b} |X_{\tau^b}|{\rm 1\!\!I}_{\tau^b<\infty}+(A^*-L)e^{-\delta \tau^b} {\rm 1\!\!I}_{\tau^b<\infty}\right]\\ & \qquad -(A-A^*)\\ & \quad =(A-A^*)\left({\mathbb{E}}_{C}\left[e^{-\delta \tau^b} {\rm 1\!\!I}_{\tau^b < \infty}\right]-1 \right)\\ &\quad < 0, \end{aligned} $$

where the first inequality follows by the maximality property of V ^A*,b*(C ^*) − ϕC ^*. The second inequality holds because the value V ^A*,b*(x) for the optimal barrier b ^* is greater than the value V ^A*,b(x) of the strategy with the non-optimal barrier b. If A < A ^*, in the analogous way we get that

$$ V^{A,b}(C)-\phi C -A \geq (A^*-A)\left(1-{\mathbb{E}}_{C^*}\left[e^{-\delta \tau^*} {\rm 1\!\!I}_{\tau^*<\infty}\right]\right)> 0. $$

Thus, the function $A\longmapsto V^{A,b}(C)-\phi C -A$ is decreasing. In this way, A ^* = V(C ^*) − ϕC ^* can be found.

Remark 4

V ^A,b(x) is the unique solution to Eq. 7 on [0, b], see Gerber et al. [12]. Thus, V ^A*,b* is unique on [0, b ^*].

3.3.4 No dividends a zero and ϕ = 1

In this case, we know that C is the largest value in ${{\mathcal A}}$. If ${{\mathcal A}}$ consists only of one point b, then the optimal strategy is a pure barrier strategy with a barrier b, and we have C = b. We can determine the value function in the same way as described above omitting calculating C.

3.3.5 Piecewise construction of the solution

Assume that it is optimal to pay dividends according to a barrier strategy with barrier at x ₀ for some x ₀ ≥ 0 in a bounded interval [0, a], and for x > a it is optimal to pay no dividends in some interval. Additionally assume that we already know the value function v on [0, x ₀], i.e., $v:[0,x_0]\rightarrow [0,\infty)$ is a given continuous and increasing function. If C ≤ x ₀ (in fact, we assume that $C < \inf\{x: V^{\prime}(x) = 1\},$ so C is below the lowest barrier), then for x > x ₀, we are looking for a solution to the equation

$$ \begin{aligned} 0 & =c u^{\prime}(x)+\lambda\int\limits_{x-x_0}^x v(x-y)\;\hbox{d} G(y)+\lambda\int\limits_0^{x-x_0}u(x-y)\;\hbox{d} G(y)\\ & \quad +\lambda(v(C)-\phi C-L)(1-G(x))-\lambda\phi\int\limits_x^\infty (1-G(y))\;\hbox{d} y \\ & \quad -(\lambda+\delta)u(x)\\ v(x_0) & = u(x_0), \end{aligned} $$

(10)

where u≡ v on $(-\infty,x_0].$

Similarly to Albrecher and Thonhauser [1] we can show the next result (for the proof see the Appendix).

Lemma 7

Let x ₀ ≥ 0. For any continuous and increasing function $v:[0,x_0]\rightarrow [0,\infty)$ there exists a unique, in $(x_0,\infty)$ differentiable and strictly increasing solution $u:[x_0,\infty)\rightarrow[0,\infty)$ to (10) with u(x ₀) = v(x ₀).

Now we describe an algorithm to determine the value function piecewise. The procedure is similar to Schmidli [20] (see also Albrecher and Thonhauser [1]).

Step 1:

Check condition (6). If it is fulfilled for $x \in (0,x_0),$ then V(x) = x + (c − λ(ϕμ + L))/δ for all x ≤ x ₀, where x ₀ is chosen maximal. If $x_0 = \infty,$ we have solved the problem. If x ₀ > 0, we expect that we have found the solution on [0,x ₀] and go to Step 3. If x ₀ = 0, no dividend will be paid in zero and we proceed with Step 2.

Step 2:

We expect for small x a barrier strategy. In order to fix the first barrier, we proceed as in Sect. 3.3.3. Let f ₀(x) be a solution to Eq. 5 with the (locally) optimal x ₀ and C. Define

$$ v_0(x)= \left\{ \begin{array}{lll} f_{0} (x) & : & x \le x_{0}\\ x - x_{0}+ f_{0}(x_{0}) & : & x > x_{0} \end{array}\right. $$

If now v ₀ fulfils the HJB equation, then the value function is V(x) = v ₀(x). If not, go to Step 3.

Step 3:

For n ≥ 0, we are looking for some interval ${(x_n,a)\in {\mathcal B}}$. If some adjoining interval [a, x _n+1) belongs to ${{\mathcal C},}$ then we have to find a solution to Eq. 10. Suppose that we have constructed v _n (x) and x _n . Let f _n+1(x; y) be a function such that f _n+1(x; y) = v _n (x) for x ≤ y and f _n+1(x; y) is a solution to Eq. 10 for x > y, i.e.,

$$ \begin{aligned} 0 & =cf^{\prime}_{n+1}(x;y)+\lambda\int\limits_{x-y}^x v_n(x-z)\hbox{d} G(z)\\ & \quad +\lambda\int\limits_0^{x-y}f_{n+1}(x-z;y)\hbox{d} G(z)+\lambda(v_n(C)-\phi C-L)(1-G(x))\\ & \quad -\lambda\phi\int\limits_x^\infty (1-G(z))\hbox{d} z-(\lambda+\delta)f_{n+1}(x;y). \end{aligned} $$

Then we have to choose the smallest y > x _n such that the derivative $f^{\prime}_{n+1}(\cdot;y)$ has its minimum at 1, i.e.,

$$ a=\inf\{y> x_n | \inf_{x>y} f^{\prime}_{n+1}(x;y)=1\}, $$

where the derivative is taken with respect to the first argument. If a is chosen too small then the derivative $f^{\prime}_{n+1}(x;\cdot)$ will be larger than 1 and will not reach 1 again. If a is chosen too large, then the derivative will reach a value smaller than 1. The point x _n+1 can now be determined as

$$ x_{n+1}:=\sup\{x\geq a| f^{\prime}(x;a)=1\}. $$

Let

$$ v_{n+1}(x)= \left\{ \begin{array}{lll} f_{n+1}(x;a) & : & x\leq x_{n+1}\\ x- x_{n+1}+ f_{n+1}(x_{n+1};a) & : & x> x_{n+1} \end{array}\right. $$

If v _n+1(x) solves (5), then it is the value function. If not, we repeat the procedure in Step 3. The algorithm terminates because of Lemma 6.

Step 4:

Control, whether V(C) − ϕC is maximal. If not, denote the solution obtained in Step 3 by V ₁(x) and let $C_1 = \arg\max\{V_1(x) - \phi x\}. \, {\text {Let}} V_2(x) = V_1(C_1) + \phi (x-C_1)-L$ for x < 0. Solve the problem with the corresponding V ₂(x) for x < 0, i.e.,

$$ \begin{aligned} 0 & =cV_2^{\prime}(x)-(\lambda+\delta)V_2(x)+\lambda\int\limits_0^x V_2(x-y)\hbox{d} G(y)\\ & \quad +\lambda(V_1(C_1)-\phi C_1-L)(1-G(x))-\lambda\phi\int\limits_x^\infty (1-G(y))\hbox{d} y. \end{aligned} $$

Note that V ₂(x) will not be continuous in 0. The solution V ₂(x) has the following interpretation. After the first capital injection, one has to follow the strategy that gives V ₁(x). Find the optimal strategy until the first capital injection. Repeating this step give a policy improvement, that will converge to the optimal value function and therefore to the optimal strategy.

3.4 Examples

3.4.1 Exponentially distributed claim sizes

We consider the case with exponentially distributed claim sizes, i.e., G(y) = 1 − e ^−αy and ${\mathbb{E}}[Y]=\mu=1/\alpha$.

We start by looking for the candidate points of the set ${\mathcal {A}}.$ Since H(x) = c and $V^{\prime}(x)=1$ on ${{\mathcal A},}$ we have to differentiate the function

$$ \begin{aligned} V(x) &= {\frac{c} {\lambda+\delta}}+ {\frac{\lambda } {\lambda+\delta}}\left[\int\limits_0^x V(x-y)\alpha e^{-\alpha y}\hbox{d} y +(V(C)-\phi C-L)e^{-\alpha x}\right. \\ & \quad \left.- \phi \int\limits_x^\infty e^{-\alpha y} \hbox{d} y\right]\\ &= {\frac{c}{\lambda+\delta}}+ {\frac{\lambda }{\lambda+\delta}}e^{-\alpha x}\left[\int\limits_0^x V(y)\alpha e^{\alpha y}\hbox{d} y + V(C)-\phi C-L- \phi {\frac{1}{\alpha}}\right] \end{aligned} $$

where we used the representation Eq. 14. This yields

$$ 1=V^{\prime}(x)= {\frac{c\alpha}{\lambda+\delta}}- {\frac{\delta \alpha}{\lambda+\delta}}V(x) $$

and therefore

$$ V(x)= {\frac{c\alpha-(\lambda+\delta)}{\delta \alpha}}. $$

(11)

Since V(x) is strictly increasing, this equation can only be fulfilled for at most one point, i.e., ${{\mathcal A}}$ consists of at most one point, b say. Because ${{\mathcal A}}$ is not empty, a point b exists. By Lemma 6, b is the lower boundary of ${{\mathcal B}}$. Thus, a barrier strategy with a barrier b is optimal.

We now want to determine the parameters for which b = 0 and therefore V(x) = x + V(0) for V(0) = (c − λ(L + ϕ/α))/δ. Then, by Eq. 6, we have to check whether

$$ \begin{aligned} F(x)=&\lambda (1-e^{-\alpha x})L -\delta x+\lambda(\phi-1)\int\limits_0^x e^{-\alpha y}\hbox{d} y\\ =& \lambda (1-e^{-\alpha x})\left(L+{\frac{\phi-1} {\alpha}}\right) -\delta x\leq 0 \end{aligned} $$

for all x ≥ 0. The first derivative of F, 

$$ F^{\prime}(x)=(\lambda\alpha L+\lambda(\phi -1))e^{-\alpha x}-\delta $$

is a decreasing function, i.e., F(x) is strictly concave. Therefore, it is non-positive if and only if $F^{\prime}(0)\leq 0,$ i.e. if

$$ \delta\geq \lambda\alpha L+\lambda(\phi -1). $$

Let δ < λαL + λ(ϕ − 1). Then b > 0. Let ρ and R be the positive and the negative solution to Lundberg’s equation

$$ cs^2-(\lambda+\delta-\alpha c)s-\alpha\delta=0, $$

i.e.,

$$ \begin{aligned} \rho &= {\frac{\lambda+\delta-\alpha c + \sqrt{(\lambda+\delta-\alpha c)^2 + 4\alpha\delta c}}{2c}},\\ R &= {\frac{\lambda+\delta-\alpha c -\sqrt{(\lambda+\delta-\alpha c)^2 + 4\alpha\delta c}}{2c}} \end{aligned} $$

By Gerber and Shiu [13], we know that ψ(x) = ψ(0)e ^Rx, σ(x) = σ(0)e ^Rx and χ(x) = χ(0)e ^Rx with

$$ \psi(0)= {\frac{\lambda} {c(\rho+\alpha)}},\\ \quad \sigma(0)= {\frac{\lambda} {c\alpha(\rho+\alpha)}},\\ \quad \chi(0)={\frac{\lambda\alpha} {c(\rho+\alpha)^2}}. $$

Then, for A fixed, we can find an optimal b(A) by maximising the function

$$ {\frac{1+\phi\sigma(0)Re^{Rb}-(A-L)\psi(0)Re^{Rb}}{\rho e^{\rho b}-\chi(0)Re^{Rb}}}. $$

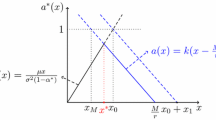
As an illustration, we let λ = 1.8, α = 0.5, δ = 0.3, c = 11, L = 2 and ϕ = 1.2. Then b ^* = 4.313 is the optimal barrier height and C ^* = 0.1047 is the optimal capital injections level which are reached for A ^* = 18.087; see Fig. 2.

Fig. 2

V(x) for Exp(1)-distributed claim sizes

3.4.2 Gamma-distributed claim sizes

We choose the Γ(2,1)-distribution for the claim sizes i.e. $G(x)=1-(x+1)e^{-x}.$

First we check whether $f(x)=x+(c-\lambda(\phi\mu+L))/\delta$ is the value function. By Eq. 6, we have to verify the condition

$$ \begin{aligned} F(x)& \quad =\lambda G(x)L-\delta x+\lambda(\phi-1)\int\limits_0^x (y+1) e^{-y}\hbox{d} y\\ & \quad = \lambda e^{-x} \left[ (1-\phi -L)x +2(1-\phi)-L\right]\\ & \qquad -\lambda(2(1-\phi)-L) -\delta x\\ & \quad \leq 0. \end{aligned} $$

The first derivative of F(x) is $F^{\prime}(x)= \lambda e^{-x}((\phi -1+L)x+\phi-1)-\delta$. The second derivative is $F^{\prime\prime}(x) = \lambda e^{-x}(L-(\phi-1+L)x)$. We see that the function F(x) is first convex and then concave. Since $F(0)=0, F^{\prime}(0)=\lambda(\phi-1)-\delta$ and F is continuous, we can conclude that if δ ≤ λ(ϕ − 1), then the derivative in zero is positive and F(x) ≥ 0 on some interval $[0,\varepsilon)$. Therefore, f(x) is not the value function on $[0,\infty)$. Moreover, for the value function V(x) we get $V^{\prime}(0)>1$. To find the barrier b and the capital injection level C we use the approach of Sect. 3.3.3. Let R ₂ < R ₁ < 0 < ρ be the solutions to Lundberg’s equation

$$ cs^3+(2c-(\lambda+\delta))s^2+(c-2(\lambda+\delta))s-\delta=0. $$

Then we have

$$ \psi(0)={\frac{\lambda(\rho+2)}{c(\rho+1)^2}},\\ \quad \sigma(0)={\frac{\lambda(2\rho+3)}{c(\rho+1)^2}},\\ \quad \chi(0)={\frac{2\lambda}{c(\rho+1)^3}} $$

and

$$ \psi(x)=K_1 e^{R_1 x}+K_2e^{R_2x}\;,\sigma(x)=\tilde{K}_1 e^{R_1 x}+\tilde{K}_2e^{R_2x}\;, \chi(x)=\hat{K}_1 e^{R_1 x}+\hat{K}_2e^{R_2x} $$

with

$$ \begin{aligned} K_1&= {\frac{-c\psi(0)(1+R_1)^2+\lambda(R_1+2)} {c(\rho-R_1)(R_1-R_2)}},\\ K_2&={\frac{c\psi(0)(1+R_2)^2-\lambda(R_2+2)} {c(\rho-R_2)(R_1-R_2)}},\\ \tilde{K}_1&= {\frac{-c\sigma(0)(1+R_1)^2+\lambda(2R_1+3)} {c(\rho-R_1)(R_1-R_2)}},\\ \tilde{K}_2&={\frac{c\sigma(0)(1+R_2)^2-\lambda(2R_2+3)} {c(\rho-R_2)(R_1-R_2)}}, \end{aligned} $$

and

$$ \begin{aligned} \hat{K}_1 &= \frac{1} {c(\rho+1)^2(\rho-R_1)(R_1-R_2)} \\ & \quad\times \left( -c\chi(0)\left[ \rho^2(R_1+1)^2+R_1^2(2\rho+1)+2(\rho+2\rho R_1+R_1)\right]\right.\\ &\quad \left.+\lambda(\rho+R_1+2)\right), \end{aligned} $$

$$ \begin{aligned} \hat{K}_2&={\frac{1} {c(\rho+1)^2(\rho-R_2)(R_1-R_2)}} \\ &\quad \times\left( c\chi(0)\left[ \rho^2(R_2+1)^2+R_2^2(2\rho+1)+2(\rho+2\rho R_2+R_2)\right]\right.\\ & \quad \left.-\lambda(\rho+R_2+2)\right). \end{aligned} $$

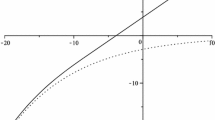
For a numerical example, let λ = 4, c = 10, δ = 0.1, ϕ = 1.3, L = 2. Then, for A ^* = 5.463 we get the (globally) optimal barrier level b ^* = 11.4143 and the optimal capital level C ^* = 3.7026; see Fig. 3.

Fig. 3

V(x) for $\Upgamma(2,1)$-distributed claim sizes: barrier strategy

Appendix

Proof of Theorem 1

Let h > 0 and fix $u\in [0,u_0].$ If x = 0 we suppose u ≤ c, if x > 0 we let h be small enough such that x + (c − u)h ≥ 0, i.e. the reserve process does not fall below zero because of the dividend payments. Let K > 0 be the Lipschitz-constant. Choose $\varepsilon > 0$ and ${n\in\mathbb{N} }$ such that $K (x+(c-u)h)/n<\varepsilon/2$ and let x _k  = k(x + (c − u)h)/n for 0 ≤ k ≤ n. For initial capital $x^{\prime}$ where $x_k\leq x^{\prime}< x_{k+1},$ we choose a strategy {U ^k _t } with $V^{U^k}(x_k)> V(x_k)-\varepsilon/2.$ Then, by the Lipschitz continuity of V(x), it holds that

$$ V^{U^k} (x^{\prime})\geq V^{U^k}(x_k)> V(x_k)-\varepsilon/2 > V(x^{\prime}) - K (x^{\prime} -x_k)-\varepsilon/2 > V(x^{\prime}) - \varepsilon. $$

Thus, for all $x^{\prime}\in[0, x+(c-u)h]$ we can find a measurable strategy $\tilde{U}$ such that $V^{\tilde{U}}(x^{\prime})> V(x^{\prime})-\varepsilon.$

Consider now the strategy

$$ U_t=\left\{ \begin{array}{ll} u, & 0\leq t< h\wedge T_1,\\ \tilde{U}_{t-h}, & t\geq h\wedge T_1, \end{array}\right. \qquad Z_t=\left\{ \begin{array}{ll} 0, & 0\leq t< h\wedge T_1, \\ \tilde{Z}_{t-h}, & t\geq h\wedge T_1. \end{array}\right. $$

Conditioning on ${{\mathcal F}_{h\wedge T_1}}$ yields

$$ \begin{aligned} V(x) & \geq V^{U}(x)= {\mathbb{E}}\left[\int\limits_{0}^{h\wedge T_1-} e^{-\delta t}u \;\hbox{d} t +e^{-\delta (h\wedge T_1)}V^{\tilde{U}}(X_{h\wedge T_1})\right] \\ & ={\mathbb{E}}\left[\left(\int\limits_{0}^{h} e^{-\delta t}u \;\hbox{d} t +e^{-\delta h}V^{\tilde{U}}(X_{h})\right){\rm 1\!\!I}_{T_1> h}\right.\\ & \quad \left. +\left(\int\limits_{0}^{ T_1-} e^{-\delta t}u \;\hbox{d} t +e^{-\delta T_1}V^{\tilde{U}}(X_{ T_1})\right){\rm 1\!\!I}_{T_1\leq h} \right]\\ & =\left. e^{-\lambda h}\int\limits_0^{h}u e^{-\delta t}\;\hbox{d} t +e^{-(\delta+\lambda) h}V^{\tilde{U}}(x+(c-u)h)\right.\\ & \quad +\int\limits_0^h\lambda e^{-\lambda t}\left\{\int\limits_0^{t}u e^{-\delta s}\;\hbox{d} s\right.\\ & \quad \left. +e^{-\delta t}\int\limits_0^\infty V^{\tilde{U}}(x+(c-u)t-y) \;\hbox{d} G(y)\right\}\;\hbox{d} t\;\\ &\left.\geq e^{-\lambda h}\int\limits_0^{h}u e^{-\delta t}\;\hbox{d} t +e^{-(\delta+\lambda) h}V(x+(c-u)h)\right.\\ & \quad +\int\limits_0^h\lambda e^{-\lambda t}\left\{\int\limits_0^{t}u e^{-\delta s}\;\hbox{d} s\right. \\ & \quad \left. +e^{-\delta t}\int\limits_0^\infty V(x+(c-u)t-y) \;\hbox{d} G(y)\right\}\;\hbox{d} t- \varepsilon. \end{aligned} $$

The constant $\varepsilon$ is arbitrary, thus, we let tend it to zero. If we rearrange the terms and divide them by h, then we get

$$ \begin{aligned} 0 & \geq {\frac{V(x+(c-u)h)-V(x)}{h}}-{\frac{1-e^{-(\lambda+\delta) h}}{h}}V(x+(c-u)h)\\ & \quad +e^{-\lambda h}{\frac{1}{h}}\int\limits_0^h u e^{-\delta t} \;\hbox{d} t + {\frac{1}{h}}\int\limits_0^h \lambda e^{-\lambda t}\left[\int\limits_0^t u e^{-\delta s}\;\hbox{d} s\right.\\ & \quad \left. +e^{-\delta t}\int\limits_{0}^{\infty}V(x+(c-u)t-y)\; d G(y)\right]\;\hbox{d} t. \end{aligned} $$

(12)

Now we choose a strategy W(h) = {W _t (h)} with V ^W(h)(x) ≥ V(x) − h ². There exists w _h such that ${{\mathbb{E}}[\int_0^{h\wedge T_1}(W_s(h)-w_h)e^{-\delta s}\;\hbox{d} s]=0}.$ Let $w_t^{\prime}$ denote W _t (h) conditioned on T ₁ > t and $a(t)=\int_0^t(c-w_s^{\prime})\;\hbox{d} s$. In the same way as above, we can derive

$$ \begin{aligned} &0 \leq h+ {\frac{V(x+a(h))-V(x)}{h}}-{\frac{1-e^{-(\lambda+\delta) h}} {h}}V(x+a(h))\\ & \quad +e^{-\lambda h}{\frac{1}{h}}\int\limits_0^h w_h e^{-\delta t} \;\hbox{d} t + {\frac{1}{h}}\int\limits_0^h \lambda e^{-\lambda t}\left[\int\limits_0^t w_h e^{-\delta s}\;\hbox{d} s \right.\\ & \quad \left. +e^{-\delta t}\int\limits_{0}^{\infty}V(x+a(t)-y) \;\hbox{d} G(y)\right]\;\hbox{d} t. \end{aligned} $$

All terms with exception of the second and the forth one converge. We choose a sequence h _n  → 0 such that

$$ \lim_{n\to \infty}{\frac{V(x+a(h_n))-V(x)} {h_n}}=\limsup_{h\downarrow 0}{\frac{V(x+a(h))-V(x)}{h}}. $$

This limit is finite by the local Lipschitz continuity. Without loss of generality, we can assume that $w_{h_n}$ converges to some value $\tilde{u}$. Then a(h _n )/h _n converges to $c-\lim w_{h_n}^{\prime}=c-\lim w_{h_n}=c-\tilde{u}$ and

$$ \begin{aligned} \lim_{n\to \infty}{\frac{V(x+a(h_n))-V(x)}{h_n}}=& \lim_{n\to \infty}{\frac{V(x+a(h_n))-V(x)}{a(h_n)}}\;{\frac{a(h_n)}{h_n}}\\ =& (c-\tilde{u})V^{\prime}(x). \end{aligned} $$

The sequence {$w_{j_n}$} fulfils (12), and so equality holds for $u=\tilde{u}$.

We can repeat the above procedure for any subsequence $w_{j_n}$ that converges to $\hat{u},$ say. Then for the limit

$$ \lim_{n\to\infty}{\frac{V(x+a(j_n))-V(x)}{j_n}} $$

we get

$$ \limsup_{h\downarrow 0}{\frac{V(x+a(h))-V(x)} {h}}+\hat{u}=(\lambda+\delta)V(x)-\lambda \int\limits_{0}^{\infty}V(x-y) \;\hbox{d} G(y) $$

such that $\tilde{u}=\hat{u}$ and the limit

$$ \limsup_{h\downarrow 0}{\frac{V(x+a(h))-V(x)} {h}}=(c-\tilde{u})\lim_{h\downarrow 0}{\frac{V(x+(c-\tilde{u})h)-V(x)}{(c-\tilde{u})h}} $$

is unique. If now ${x\in{\mathcal D},}$ the above limit is $(c-\tilde{u})V^{\prime}(x)$. Otherwise we have shown the differentiability at x from the right if $c>\tilde{u}$ and the differentiability at x from the left if $c<\tilde{u}$. We do not distinguish the notation first and write for both derivatives the Hamilton–Jacobi–Bellman equation

$$ \sup_{0\leq u\leq u_0}\left\{(c-u)V^{\prime}(x)+u-(\lambda+\delta)V(x) +\lambda \int\limits_0^{\infty}V(x-y) \;\hbox{d} G(y)\right\}=0 , $$

(13)

where we have

$$ \begin{aligned} &\int\limits_0^{\infty}V(x-y) \;\hbox{d} G(y)\\ & \quad = \int\limits_0^x V(x-y) \;\hbox{d} G(y) + \int\limits_x^\infty (V(C)- \phi(y-x+C)-L)\;\hbox{d} G(y)\\ & \quad = \int\limits_0^x V(x-y) \;\hbox{d} G(y)\\ &\qquad + (V(C)-\phi C-L)(1-G(x))- \phi\int\limits_x^\infty (1-G(y))\;\hbox{d} y, \end{aligned} $$

(14)

because of the property (1).

Equation 13 is linear in u, thus, the argument $\tilde{u}=u(x)$ maximising the left-hand side of Eq. 13 is

$$ u(x)=\left\{ \begin{array}{ll} 0, & \hbox {if} \quad V^{\prime}(x)>1,\\ \in[0, u_0], & \hbox {if}\quad V^{\prime}(x)=1,\\ u_0, & \hbox {if} \quad V^{\prime}(x)<1. \end{array}\right. $$

Consider now the function

$$ H(x):= (\lambda+\delta)V(x)-\lambda \int\limits_0^{\infty}V(x-y) \;\hbox{d} G(y). $$

(15)

Since V(x − y) ≤ V(x) for y ≥ 0, it follows by the bounded convergence theorem and continuity of V(x) that H(x) is a continuous function on ${\mathbb{R}}.$ The HJB equation (13) reads

$$ (c-\tilde{u})V^{\prime}(x)+\tilde{u} - H(x)=0. $$

(16)

for any ${x\in {\mathcal D}}$ and $\tilde{u}=u(x).$

Let u ₀ < c. Then we have shown the differentiability from the right with

$$ \begin{array}{lllll} V^{\prime}(x+)> 1 &\Leftrightarrow& \tilde{u}=0 &\Leftrightarrow& H(x)> c,\\ V^{\prime}(x+)<1 &\Leftrightarrow& \tilde{u}=u_0 &\Leftrightarrow& H(x)< c,\\ V^{\prime}(x+)=1 &\Leftrightarrow& \tilde{u}\;\hbox{arbitr.} &\Leftrightarrow& H(x)=c. \end{array} $$

Suppose, H(x) > c. Then, by continuity, there exist $\varepsilon>0$ and an interval ${{\mathcal U}_\varepsilon(x)}$ such that H(z) > c for any ${z\in {\mathcal U}_\varepsilon(x)}.$ Let {x _n } be a sequence in ${{\mathcal U}_\varepsilon(x)\cap {\mathcal D}}$ tending to x from left. For any x _n Eq. 16 holds. Denote $\tilde{u}_n= u(x_n)$. Then, H(x _n ) > c and from Eq. 16 $\tilde{u}_n=0$ follows. Therefore, $u=\lim_{n\to\infty}\tilde{u}_n=0$ and we get that V is differentiable from the left with

$$ V^{\prime}(x-)=\lim_{n\to\infty}{\frac{H(x_n)-\tilde{u}_n} {c-\tilde{u}_n}}={\frac{H(x)}{c}}=V^{\prime}(x+)>1. $$

If H(x) < c, in an analogous way we get $H(x_n)<c, \tilde{u}_n=u_0$ and therefore u = u ₀ such that $V^{\prime}(x-)=V^{\prime}(x+)<1$.

If H(x) = c, differentiability follows because we can choose u arbitrarily.

Thus, for u ₀ < c, we have proved that V is continuously differentiable and fulfils Eq. 13. We denote this solution by $V_{u_0} (x)$.

We consider now the case u ₀ = c. We can follow from Eq. 16 that

$$ \begin{array}{lll} V^{\prime}(x+)>1 \Leftrightarrow \tilde{u}=0 &\Leftrightarrow& H(x)>c,\\ ((V^{\prime}(x-)<1 \Leftrightarrow \tilde{u}=u_0) \;\;{or}\;\; (V^{\prime}(x)=1 \Leftrightarrow \tilde{u}\;\hbox{arbitr.})) &\Leftrightarrow& H(x)=c. \end{array} $$

If H(x) > c, then, by similar arguments as above, we derive that V is differentiable at x with $V^{\prime}(x)>1$ and HJB equation (13) is fulfilled with u = 0.

Let now H(x) = c. Then, H(z) ≥ c for any ${z\in {\mathcal U}_\varepsilon(x)}$. Suppose, $V^{\prime}(x-)<1$. For a sequence x _n ↓ x with H(x _n ) > c we get that $\tilde{u}_n=0$ and therefore V is differentiable from the right with $V^{\prime}(x+)=1$. In this case (13) is again fulfilled. If there is a sequence with H(x _n ) = c, then we get differentiability at x.

The last case to consider is u ₀ > c. Then

$$ \begin{array}{lll} V^{\prime}(x)=1 \Leftrightarrow \tilde{u}\;\hbox{arbitr.} &\Leftrightarrow& H(x)=c,\\ ((V^{\prime}(x-)<1 \Leftrightarrow \tilde{u}=u_0) \;\;{or}\;\; (V^{\prime}(x+)>1 \Leftrightarrow \tilde{u}=0)) &\Leftrightarrow& H(x)>c. \end{array} $$

If H(x) = c, then differentiability follows similarly to above.

Let H(x) > c. Suppose that $V^{\prime}(x+)>1$ and $\tilde{u}=0$. Let {x _n } be a sequence in ${{\mathcal U}_\varepsilon(x)\cap{\mathcal D}}$ with x _n ↑ x. If $u=\lim_{n\to\infty}\tilde{u}_n=0,$ then we get differentiability with $V^{\prime}(x)>1$. If u = u ₀, then V is differentiable from the left with $V^{\prime}(x-)<V^{\prime}(x+)$ and both derivatives solve Eq. 13.

Suppose that V′(x −) < 1 and $\tilde{u}=u_0$. For a sequence x _n ↓ x we again have to choose either u = 0 or u = u ₀. The choice u = 0 shows that V is differentiable from the right with $V^{\prime}(x+)>1$ and both derivatives solve Eq. 13. If u = u ₀, then differentiability follows with $V^{\prime}(x)<1$.

Proof of Lemma 6

The proof is based on Schmidli [20, Section 2.4.2].

• 1. Since H is continuous, H(x) ≥ c for all $x\in[0,\infty)$ and {c} is closed, the set $\{x\in[0,\infty): H(x)=c\}$ is closed.

• 2. Let ${x\in {\mathcal B}}$. Since ${{\mathcal A}}$ is closed, there must be $\varepsilon>0$ such that ${(x-\varepsilon, x)\subset {\mathcal A}^c}$ because, otherwise, ${x\in {\mathcal A}}$. Since ${(x-\varepsilon, x)\subset{\mathcal C}^c,}$ we get ${(x-\varepsilon, x)\subset{\mathcal B}}$.

• 3. Let $\{x_n\}\subset (x_0, x]$ such that x _n ↓ x ₀. Then, $V^{\prime}(x_n)=1$ and H(x _n ) > c. By continuity, $V^{\prime}(x_0)=1$ and H(x ₀) = c, since, otherwise, ${x_0\in {\mathcal B}}$.

• 4. If ${x\in{\mathcal C},}$ then, by the continuity of H, there must be a δ > 0 such that ${[x,x+\delta)\subset {\mathcal A}^c}$. If there would be some ${x_1\in {\mathcal B}}$ within this interval, we could follow the existence of an ${x_0\in {\mathcal A}}$ with x ₀ < x ₁ such that ${(x_0,x_1] \subset {\mathcal B}}$. Since ${x\notin {\mathcal B}}$ this x ₀ has also to be in the interval [x, x + δ) which is a contradiction. Therefore, ${[x,x+\delta)\subset {\mathcal B}^c}$ and ${[x,x+\delta)\subset {\mathcal C}}$.

• 5. Let C be chosen optimally. Since V(x) is strictly increasing, we get $V(x)-\int\limits_0^x V(x-y)\;{\text{d}} G(y)\geq V(x)(1-G(x))$ and therefore

  $$ \begin{aligned} & (\lambda+\delta)V(x)-\lambda\int\limits_0^x V(x-y)\hbox{d} G(y)\\ & \qquad -\lambda(V(C)-\phi C-L)(1-G(x))+\lambda\phi\int\limits_x^\infty (1-G(y))\hbox{d} y\\ & \quad \geq \lambda V(x)(1-G(x))+\delta V(x)-\lambda (V(C)-\phi C-L)(1-G(x))\\ & \quad = \delta V(x)+\lambda(1-G(x))(V(x)-V(C)+\phi C+L)\\ &\quad \geq \delta V(x). \end{aligned} $$

  The last inequality holds because obviously V(x) − V(C) ≥ 0 for x ≥ C. For x < C we have by Lemma 4 that V(x) − V(C) ≥  − ϕ(C − x) − L and thus V(x) − V(C) + ϕC + L ≥ ϕx ≥ 0.

  From Lemma 4 we can follow that for any $x>\lambda(\phi\mu+\phi C+L)/\delta$

  $$V(x)\geq x+ \frac{c- \lambda(\phi\mu+\phi C+L)}{\delta}>\frac{\lambda(\phi\mu+\phi C+L)}{\delta}+\frac{c- \lambda(\phi\mu+\phi C+L)}{\delta}=\frac{c}{\delta}$$

  holds. Assume now that there is $x>\lambda(\phi\mu+\phi C+L)/\delta$ with $V^\prime(x-)>1.$ Then $V^\prime(z)>1$ for all z ≥ x. To prove this claim, we suppose that there is $z={\text{inf}}\{y>x:V^\prime(y)=1\}<\infty.$ For this point we have

  $$1=V^\prime(z)=\frac{(\lambda+\delta)V(x)-\lambda\int_0^\infty V (x-y) \text{d}G(y)}{c}\geq \frac{\delta V(z)}{c}\\>\frac{\delta V(x)}{c}>1,$$

  which is a contradiction. Thus,

  $$V^\prime(z)\geq \frac{\delta}{c}V(z)$$

  for all z ≥ x, or equivalently, $\log(V(z)/V(x))\geq (z-x)\delta/c,$ i.e. V(x) is exponentially increasing on $[x,\infty).$ This is a contradiction to Lemma 4. Thus, $V^\prime(x-)=1.$

• 6. The assertion follows from the forth and fifth point.

Proof of Lemma 7

Let $\varepsilon={\frac{c}{2(2\lambda+\delta)}}$ and denote by $CI[x_0,x_0+\varepsilon)$ the set of all continuous and increasing functions $u:[x_0,x_0+\varepsilon)\rightarrow [0,\infty)$. For a $u\in CI[x_0,x_0+\varepsilon),$ let

$$ \begin{aligned} \bar{u}(x)& = {\frac{1} {c}}\left[(\lambda+\delta)u(x)-\lambda\int\limits_{x-x_0}^x v(x-y)\hbox{d} G(y)-\lambda\int\limits_0^{x-x_0}u(x-y)\hbox{d} G(y)\right.\\& \quad \left.-\lambda (v(C)-\phi C-L)(1-G(x))+\lambda\phi\int\limits_x^\infty(1-G(y))\hbox{d} y\right]. \end{aligned} $$

By the continuity of u and $v, \bar{u}$ is continuous for x ≥ 0. Define now for $u\in CI[x_0,x_0+\varepsilon)$

$$ T_u(x)=\int\limits_{x_0}^x \bar{u}(s)\;{\text{d}} s + v(x_0)\;. $$

Because of the monotonicity of u and v and v(x ₀) = u(x ₀) we get

$$ \begin{aligned} c\bar{u}(x)& = (\lambda+\delta)u(x)-\lambda\int\limits_{x-x_0}^x v(x-y)\hbox{d} G(y)-\lambda\int\limits_0^{x-x_0}u(x-y)\hbox{d} G(y)\\ & \quad -\lambda (v(C)-\phi C-L)(1-G(x))+\lambda\phi\int\limits_x^\infty (1-G(y))\hbox{d} y\\ &\geq (\lambda+\delta)u(x)-\lambda v(x_0)(G(x)-G(x-x_0))-\lambda u(x)G(x-x_0) \\ & \quad -\lambda v(C)(1-G(x))\\ &\geq \delta u(x)+\lambda u(x)-\lambda u(x)G(x)-\lambda v(C)(1-G(x))\\ & = \delta u(x)+\lambda (1-G(x))(u(x)- v(C))\\ &\geq \delta u(x)\\ & > 0. \end{aligned} $$

By the positivity of u and v, we get the upper bound for $\bar{u}(x)$

$$ c\bar{u}(x)\leq (\lambda+\delta)u(x)+\lambda(\phi C +L+\phi\mu). $$

It follows that T _u is increasing, positive and continuous for $x\in [x_0, x_0+\varepsilon)$. For $u_1, u_2\in CI[x_0,x_0+\varepsilon)$ holds

$$ \begin{aligned} &c(\bar{u}_1(x)-\bar{u}_2(x))\\ &=(\lambda+\delta)(u_1(x)-u_2(x))-\lambda \int\limits_0^{x-x_0}(u_1(x-y)-u_2(x-y))\hbox{d} G(y)\\ & \leq (\lambda+\delta)\left\|u_1-u_2\right\|+\lambda \left\|u_1-u_2\right\|G(x-x_0)\\ & \leq(2\lambda+\delta)\left\|u_1-u_2\right\|, \end{aligned} $$

where $\left\|\cdot\right\|$ is the supremum norm. It follows

$$ T_{u_1}(x)-T_{u_2}(x)\leq \varepsilon {\frac{2\lambda+\delta} {c}}\left\|u_1-u_2\right\|\leq {\frac{1} {2}}\left\|u_1-u_2\right\|\;. $$

Interchanging u ₁ and u ₂ yields $\left\|T_{u_1}-T_{u_2}\right\|\leq {\frac{1} {2}}\left\|u_1-u_2\right\|,$ i.e. T is a contraction on $CI[x_0,x_0+\varepsilon)$. This proves the existence of a $u\in CI[x_0,x_0+\varepsilon)$ such that

$$ u(x)=T_u(x)=\int\limits_{x_0}^x \bar{u}(s)\hbox{d} s + v(x_0). $$

This provides $u^{\prime}(x)=\bar{u}(x)$ everywhere in $[x_0, x_0+\varepsilon)$. Thus we get the existence of a unique solution to Eq. 10 with the required properties on $[x_0, x_0+\varepsilon)$.

Since $\varepsilon$ does not depend on x ₀, we have shown the existence of a unique solution on $[x_0,\infty)$.