1 Introduction

The transportation of fluids caused by the constant contraction and relaxation of a channel is commonly known as peristalsis [1]. Such motion has diverse applications in different fields of modern era, in the human/animal body, motion of physiological fluids in vessels (like intestines, ureter, stomach, etc.) and blood vessels (like capillaries, veins, arteries, etc.). Other applications include urine moving to bladder from kidneys [2], motion of food through the esophagus, chime moving in the intestines, intrauterine unsolidified motion, and spermatozoa flow in ductus efferentes of masculine reproductive system. Similarly, motion by ovum in feminine uterine tube, transfer of lymph in veins, and vasomotion of arterioles, capillaries, and venules also follow the motion of peristaltic. In the field of bio-locomotion, the same analogy of peristalsis can be found in earthworms as an outer motion doing geonautical mobility very efficiently supported by the excretion of lubricating mucus. In addition, the same phenomenon is being followed in soil sciences where air is being forced through burrows [3]. Roller/finger pumps also work on this phenomenon, and besides, modern micro- and nanorobots are principally based on mechanisms of peristaltic [4]. Since the major investigation by Latham [5], many theoretical as well as experimental contributions are being made in research to understand the peristaltic flows in different scenarios. A review of the basic literature can be viewed in Jaffrin and Shapiro [6]. Burns and Parkes theoretically studied the peristaltic motion in [7]. Work by Chow [8], Mishra and Rao [9], Shapiro et al. [10], and Takabatake and Ayukawa [11] has motivated some interest in recent years. However, scope of these studies is limited to Newtonian fluids.

The famous Navier–Stokes equations are unable to describe the flow characteristics of many complex fluids such as suspensions, liquid detergents, oils, drilling muds, and grease. Several researchers addressed this difficulty by suggesting diversified non-Newtonian fluid models. But, then these mathematical models raise the challenge of solving highly nonlinear and much more complicated when compared with the Navier–Stokes model. One such model is named as Johnson–Segalman model which is suitable for viscoelastic flows and designed to tolerate non-affine deformation [12]. This model has distinct characteristic when compared to other fluid models in the sense that for simple shear flow, it permits non-monotonic change in shear stress with the increase (decrease) in the rate of deformation. Some non-Newtonian fluids possess an exciting property called spurt. It refers to an abnormal rise in volume for a small rise in pressure gradient. Spurt occurrence based on the above-mentioned non-monotonic change is discussed in detail in [13,14,15,16,17].

The term "nanofluid" refers to a type of fluids in which nanoparticles are uniformly disseminated throughout the base fluid, such as water, oil, and ethylene glycol. Nanofluids gained enormous attention in start of twenty-first century. Even after two decades of this century, these fluids are still a source of attention for various researchers as these have strong effects on related flow characteristics in various areas of interest. Choi [18] was first one, who proposed nanofluids. Experimental as well as theoretical studies show that nanofluids improve thermo-physical properties when compared with ordinary fluids. Nanoparticles have random motion, often called Brownian motion, in liquids and possibly collide in nanofluids. Collision is suggested to be one possible reason for enhancement of thermal conductivity. Nanofluids when associated with peristalsis have important applications in medical field including cancer treatment and drug delivery, chemical engineering including chemicals transportation, and mechanical engineering field. In recent times, such a collective study of peristalsis and nanofluids [19,20,21,22,23,24,25] has been modeled for physiological flows to examine the effects of nanofluids on peristaltic motion.

The study of the influence of magnetic force in peristaltic transport is crucial from a biological perspective. Physiological fluids include biomagnetic fluids as a subpart. Furthermore, investigation of magnetohydrodynamics (MHD) in biomagnetic flows has an immense importance in medicinal field. Some examples include observing the blood flow rates, magnetic equipment for cell separation, and evaluating strong magnetic field effects on the cardiovascular system. Considering these wide ranges of applications, many researchers have studied the MHD of biomagnetic flow under various considerations [26,27,28]. Electrical machines performing magnetic resonance imaging (MRI) tests are based on similar idea. Also, magnetic field in the presence of nanofluid plays a major role in medical applications like cancer therapy and existing medication distribution (Tripathi and Beg [29]). Nanofluids made of titanium nanoparticles are used to treat cancer patients by radiation having magnetic attributes destroying tumor cells without damaging strong tissues. Knowing the physical importance of nanofluids with magnetism, Sucharitha et al. [30] studied the MHD flow of nanofluid in a non-uniform channel with effects of Joule heating. Some important contributions are made in research on nanofluids, taking thermophoresis effects with Brownian motion to study motion [31,32,33,34,35,36,37,38,39,40].

Double-diffusion phenomena refer to the mixing of fluids with two constituents with distinct molecular diffusivities. Such phenomena are observed in oceanography, solid-state physics, astrophysics, chemical processes, biology, and geophysics [41]. Also, in industries, solar ponds, crystal manufacturing, storage tanks of natural gas, and metal solidification processes double diffusion is observed. Some researchers have used double-diffusive convection in analyzing peristaltic movement. The same effects in the presence of nanofluid were analyzed in [42] by Noreen et al. More research work can be found on double diffusion in [20, 43,44,45,46,47,48].

In most of the early work on peristalsis, no-slip conditions are used to study the flow. However, effects of slip condition are always of interest in applied sciences due to their practical applications. Combination of both slip conditions and nanoparticles is of great interest for researchers because of their key role thermal systems utilized by industries. Slip effect is based on such a motion in which velocity of particles is perturbed adjacent to the surface/boundary. Navier established the idea of the slip phenomenon, which states that shear stress and fluid velocity rate near the surface are proportional. Afterward, the concept of partial slip on boundaries was investigated by several researchers with various fluid models and different geometries [49,50,51,52,53,54].

The effects of multiple slip conditions on the peristaltic flow with magnetic field for Johnson–Segalman nanofluid incorporating double-diffusive convection are considered for the present problem. To the best of our knowledge, such combination was not studied for Johnson–Segalman nanofluids before. Such a combination can provide basis for further theoretical and practical research in drug delivery systems. Effects of various parameters on bolus formation in the flow may also be utilized in diseases management. Also, consideration of electromagnetic waves expands the horizon of the study to the application in cancer therapy as well. This study will help in assessment of chyme movement in the gastrointestinal tract and in regulating the intensity of magnetic field of the blood flow during surgery.

2 Basic Equations

The basic equations of incompressible Johnson–Segalman nanofluids are defined as follows [44]:

The continuity equation for the incompressible fluid is defined as

$${\text{div}}V = 0,$$
(1)

Navier–Stoke equation is defined as

$$\begin{aligned} \rho_{f} \left( \frac{{{\text{d}}V}}{{{\text{d}}\hat{t}}} \right) &= {\text{div}}\tau + \rho f + g\left\{\left( 1 -\Theta_{0}\right)\rho_{f0}\right.\\ & \quad \left\{\beta_{T} \left(T - T_{0}\right) + \beta_{C} \left(C - C_{0}\right)\right\} \\ &\quad \left.- \left(\rho_{p} -\rho_{f0}\right)\left( \Theta - \Theta_{0} \right)\right\}, \end{aligned}$$
(2)

The energy equation is defined as

$$\left( {\rho c} \right)_{f} \left( {\frac{dT}{{dt}}} \right) = k\nabla^{2} T + \left( {\rho c} \right)_{p} \left\{ {D_{B} \left( {\nabla \Theta \cdot \nabla T} \right)} \right. + \left( {\frac{{D_{T} }}{{T_{0} }}} \right)\nabla T \cdot \nabla T\} + D_{TC} \nabla^{2} C,$$
(3)

The solute concentration is defined as

$$\frac{{{\text{d}}C}}{{{\text{d}}t}} = D_{s} \nabla^{2} C + D_{CT} \nabla^{2} T,$$
(4)

The nanoparticle fraction equation is defined as

$$\frac{{{\text{d}}\Theta }}{{{\text{d}}t}} = D_{B} \nabla^{2} \Theta + \left( {\frac{{D_{T} }}{{T_{0} }}} \right)\nabla^{2} T,$$
(5)

where \(\rho_{f}\) denotes the base fluid density,\(V\) stands for the velocity vector,\(\tau\) is the stress tensor, \({\text{d/d}}t\) represents the derivative of material time, \(g\) stands for the acceleration, \(f\) denotes the body force,\(\rho_{{f_{0} }}\) is the fluid density at \(T_{0}\), \(\rho_{{\text{p}}}\) denotes the particles density, \(T\) denotes the temperature, \(C\) is the concentration, \(D_{{\text{T}}}\) is the thermophoretic diffusion, \(\Theta\) stands for the nanoparticle volume fraction, \(D_{{\text{B}}}\) is the Brownian diffusion, \(D_{CT}\) is the Soret diffusively, \(D_{s}\) is the solutal diffusively, \(D_{{{\text{TC}}}}\) is the Dufour diffusively, \(\beta_{{\text{C}}}\) is the volumetric solutal expansion coefficient of a fluid, \(\beta_{{\text{T}}}\) is the volumetric thermal expansion coefficient of a fluid, \(k\) is the thermal conductivity, \(\left( {\rho c} \right)_{p}\) is the heat capacity of nanoparticle, and \(\left( {\rho c} \right)_{f}\) stands for the fluid heat capacity.

The Johnson–Segalman fluid stress tensor is defined by [16]

$$\tau = - {\text{PI}} + \sigma ,$$
(6)
$$\sigma = 2\mu D + S,$$
(7)
$$S + \xi \left[ {\frac{{{\text{d}}S}}{{{\text{d}}t}} + S\left( {W - \beta D} \right) + (W - \beta D)^{T} S} \right] = 2\eta D,$$
(8)
$$D = \frac{1}{2}\left( {{\text{grad}}\left( V \right) + {\text{grad}}\left( V \right)^{*} } \right),$$
(9)
$$W = \frac{1}{2}\left( {{\text{grad}}\left( V \right) - {\text{grad}}\left( V \right)^{*} } \right),$$
(10)

where \(P,\) \(I,\) \((\mu ,\) \(\eta ),\) \(\xi ,\) \(\beta ,\) \(D,\) and \(W\) denote the pressure, identity tensor, dynamic viscosities, relaxation time, slip parameter, velocity gradient symmetric, and skew symmetric part, respectively. Note that model (6) reduces to the Maxwell fluid model for \(\beta = 1\) and \(\mu = 0,\) and for \(\mu = 0 = \xi,\) we receive the classical Navier–Stokes fluid model.

3 Mathematical Formulation

Let us consider Johnson–Segalman fluid nanofluid and examined the flow within condensed, electrically confined dual dimensional conduit with a diameter of \(d_{1} + d_{2}\). Cartesian coordinates are drawn by keeping the center of channel at \(X\)-axis and cross-sectional region on Y-axis. The sinusoidal wave moves smoothly on the wall along the channel. The values of temperatures, solvent concentrations, and nanoparticle fraction are calculated as \(T = T_{0}\), \(C = C_{0}\), \(\Theta = \Theta_{0} ,\) \(\left( {{\text{at }}y = H_{1} } \right),\) and \(T = T_{1}\), \(C = C_{1}\), \(\Theta = \Theta_{1}\) (at \(y = H_{2}\)). Magnetic flux remained constant at an angle \(\Gamma\). Magnetic Reynolds number is kept very low, while electric field is taken as null. Resultantly, induced magnetic flux is not considerable in comparison with applied magnetic flux.

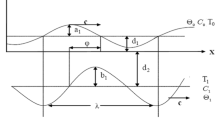
The geometrical shape is defined in Fig. 1, and mathematical expression of geometry of problem is defined as [16]

$$Y = d_{1} + d_{3} \cos \left( {\frac{2\pi }{\lambda }\left( {X - ct} \right)} \right) = H_{1} ,$$
$$Y = - d_{2} - d_{4} \cos \left( {\frac{2\pi }{\lambda }\left( {X - ct} \right) + \varphi } \right) = H_{2} ,$$
(11)

where \(c\) denotes the wave of speed, \(t\) stands for the time, \((d_{3} ,\) \(d_{4} )\) represents the wave amplitudes, \((d_{1} ,\) \(d_{2} )\) stands for the channel width, \(\lambda\) denotes the wavelength, and \(\varphi\) stands for the phase difference with a range of \(0 \le \varphi \le \pi .\) At \(\varphi = 0,\) channel is symmetric with out-of-phase waves and \(\varphi = \pi\) represents a channel with a phase wave. Moreover, wave amplitudes (\(d_{3} ,d_{4}\)), channel width \((d_{1} ,\) \(d_{2} ),\) and phase difference \(\varphi\) satisfy the following criterion \(d_{4}^{2} + d_{3}^{2} + 2d_{3} d_{4} \cos \varphi \le \left( {d_{1} + d_{2} } \right)^{2}\).

Fig. 1
figure 1

Geometrical shape of the walls

Full size image

Velocity for two-dimensional and directional flow is

$$V = \left( {U\left( {X,Y,t} \right),V\left( {X,Y,t} \right),0} \right).{ }$$
(12)

Using Eq. (12), Eqs. (1)–(10) become

$$\frac{\partial U}{{\partial X}} + \frac{\partial V}{{\partial Y}} = 0,$$
(13)
$$\begin{aligned} & \rho \left( \frac{\partial }{\partial t} + U\frac{\partial }{\partial X} + V\frac{\partial }{\partial Y} \right)U = - \frac{\partial P}{{\partial X}} + \mu \left( {\frac{{\partial^{2} U}}{{\partial X^{2} }} + \frac{{\partial^{2} U}}{{\partial Y^{2} }}} \right) \\ & \quad + \frac{{\partial S_{XX} }}{\partial X} + \frac{{\partial S_{XY} }}{\partial Y} - \sigma B_{0}^{2} \cos \Gamma \left( {U\cos \Gamma - V\sin \Gamma } \right)\\ &\quad + g\left\{\left( {1 - \Theta_{0} }\right)\rho_{f0}\left\{ \beta_{T} \left( {T - T_{0} } \right) + \beta_{C} \left( {C - C_{0} } \right)\right\}\right. \\ & \quad \left. - \left( {\rho_{p} - \rho_{f0} } \right)\left( \Theta - \Theta_{0} \right)\right\}, \end{aligned}$$
(14)
$$\begin{aligned} \rho \left( {\frac{\partial }{\partial t} + U\frac{\partial }{\partial X} + V\frac{\partial }{\partial Y}} \right)V & = - \frac{\partial P}{{\partial Y}} + \mu \left( {\frac{{\partial^{2} V}}{{\partial X^{2} }} + \frac{{\partial^{2} V}}{{\partial Y^{2} }}} \right) \\&+ \frac{{\partial S_{YX} }}{\partial X} + \frac{{\partial S_{YY} }}{\partial Y} \\ &\quad+ \sigma B_{0}^{2} \sin \Gamma \left( {U\cos \Gamma - V\sin \Gamma } \right), \\ \end{aligned}$$
(15)
$$\begin{aligned} \left( {\rho c} \right)_{f} \left( {\frac{\partial }{\partial t} + U\frac{\partial }{\partial X} + V\frac{\partial }{\partial Y}} \right)T &= k\left( {\frac{{\partial^{2} T}}{{\partial X^{2} }} + \frac{{\partial^{2} T}}{{\partial Y^{2} }}} \right) + \left( {\rho c} \right)_{p} \\ & \quad\times \left\{ {D_{B} \left( {\frac{\partial \Theta }{{\partial X}}\frac{\partial T}{{\partial X}} + \frac{\partial \Theta }{{\partial Y}}\frac{\partial T}{{\partial Y}}} \right)} \right. \hfill \\ &\left. {\left( {\frac{{D_{T} }}{{T_{0} }}} \right)\left[ {\left( {\frac{\partial T}{{\partial X}}} \right)^{2} + \left( {\frac{\partial T}{{\partial Y}}} \right)^{2} } \right]} \right\} \\ &\quad+ D_{TC} \left( {\frac{{\partial^{2} C}}{{\partial X^{2} }} + \frac{{\partial^{2} C}}{{\partial Y^{2} }}} \right),{ } \hfill \\ \end{aligned}$$
(16)
$$\left( {\frac{\partial }{\partial t} + U\frac{\partial }{\partial X} + V\frac{\partial }{\partial Y}} \right)C = D_{s} \left( {\frac{{\partial^{2} C}}{{\partial X^{2} }} + \frac{{\partial^{2} C}}{{\partial Y^{2} }}} \right) + D_{TC} \left( {\frac{{\partial^{2} T}}{{\partial X^{2} }} + \frac{{\partial^{2} T}}{{\partial Y^{2} }}} \right),$$
(17)
$$\left( {\frac{\partial }{\partial t} + U\frac{\partial }{\partial X} + V\frac{\partial }{\partial Y}} \right)\Theta = D_{B} \left( {\frac{{\partial^{2} \Theta }}{{\partial X^{2} }} + \frac{{\partial^{2} \Theta }}{{\partial Y^{2} }}} \right) + \left( {\frac{{D_{T} }}{{T_{0} }}} \right)\left( {\frac{{\partial^{2} T}}{{\partial X^{2} }} + \frac{{\partial^{2} T}}{{\partial Y^{2} }}} \right),$$
(18)
$$\begin{aligned} 2\eta \frac{\partial U}{{\partial X}} & = S_{XX} + \xi \left( {\frac{\partial }{\partial t} + U\frac{\partial }{\partial X} + V\frac{\partial }{\partial Y}} \right)S_{XX} - 2\xi \beta S_{XX} \frac{\partial U}{{\partial X}} \\ & \quad \quad + \xi \left[ {\left( {1 - \beta } \right)\frac{\partial V}{{\partial X}} - \left( {1 + \beta } \right)\frac{\partial U}{{\partial Y}}} \right]S_{XY} , \\ \end{aligned}$$
(19)
$$\begin{aligned} \eta \left( {\frac{\partial U}{{\partial Y}} + \frac{\partial V}{{\partial X}}} \right) &= S_{XY} + \xi \left( {\frac{\partial }{\partial t} + U\frac{\partial }{\partial X} + V\frac{\partial }{\partial Y}} \right)S_{XY} \\&\quad + \frac{\xi }{2}\left[ {\left( {1 - \beta } \right)\frac{\partial U}{{\partial Y}} - \left( {1 + \beta } \right)\frac{\partial V}{{\partial X}}} \right]S_{XX} \hfill \\ &\quad + \frac{\xi }{2}\left[ {\left( {1 - \beta } \right)\frac{\partial V}{{\partial X}} - \left( {1 + \beta } \right)\frac{\partial U}{{\partial Y}}} \right]S_{YY} , \hfill \\ \end{aligned}$$
(20)
$$\begin{aligned} 2\eta \frac{\partial V}{{\partial Y}} & = S_{YY} + \xi \left( {\frac{\partial }{\partial t} + U\frac{\partial }{\partial X} + V\frac{\partial }{\partial Y}} \right)S_{YY} - 2\xi \beta S_{YY} \frac{\partial V}{{\partial Y}} \\ & \quad + \xi \left[ {\left( {1 - \beta } \right)\frac{\partial U}{{\partial Y}} - \left( {1 + \beta } \right)\frac{\partial V}{{\partial X}}} \right]S_{XY}.\end{aligned}$$
(21)

Now introduce Galilean transformations in fixed frame \(\left( {X,Y} \right)\) and wave frame \(\left( {x,y} \right)\) as

$$\begin{aligned} &v = V, u = U - c, y = Y, x = X - ct, p\left( {x,y} \right) \\ & \quad = P\left( {X,Y,t} \right),\end{aligned}$$
(22)

and define non-dimensional parameters [16, 47, 48]

$$\begin{aligned} & \overline{v} = \frac{v}{c}, \overline{x} = \frac{x}{\lambda }, \overline{u} = \frac{u}{c},\overline{y} = \frac{y}{{d_{1} }}, \delta = \frac{{d_{1} }}{\lambda },\overline{t} = \frac{ct}{\lambda }, \\ & d = \frac{{d_{2} }}{{d_{1} }}, h_{2} = \frac{{H_{2} }}{{d_{2} }}, b = \frac{{d_{4} }}{{d_{1} }}, h_{1} = \frac{{H_{1} }}{{d_{1} }},a = \frac{{d_{3} }}{{d_{1} }}, \\ &\overline{p} = \frac{{d_{1}^{2} p\left( x \right)}}{{\left( {\mu + \eta } \right)c\lambda }}, \Pr = \frac{{\left( {\rho c} \right)_{f} \upsilon }}{k},\\ & {\text{Re}} = \frac{{\rho_{f} cd_{1} }}{\mu }, \upsilon = \frac{\mu }{{\rho_{f} }}, Le = \frac{\upsilon }{{D_{s} }}, \\ & Ln = \frac{\upsilon }{{D_{B} }}, v = - \delta \frac{\partial \psi }{{\partial x}},u = \frac{\partial \psi }{{\partial y}}, \\ & G_{rc} = \frac{{g\left( {1 - \Theta_{0} } \right)\rho_{f0} \beta_{c} \left( {C_{1} - C_{0} } \right)d_{1}^{2} }}{\mu c},\\ & G_{rF} = \frac{{g\left( {\rho_{p} - \rho_{f0} } \right)\left( {\Theta_{1} - \Theta_{0} } \right)}}{\mu c}d_{1}^{2} , \\ & N_{t} = \frac{{\left( {\rho c} \right)_{p} D_{T} \left( {T_{1} - T_{0} } \right)}}{{T_{0} k}}, \\ & \theta = \frac{{T - T_{0} }}{{T_{1} - T_{0} }}, \gamma = \frac{{C - C_{0} }}{{C_{1} - C_{0} }}, \Omega = \frac{{\Theta - \Theta_{0} }}{{\Theta_{1} - \Theta_{0} }}, \\ & Wi = \frac{c\xi }{{d_{1} }}, \overline{S} = \frac{{d_{1} }}{\mu c}S, N_{CT} = \frac{{D_{CT} \left( {T_{1} - T_{0} } \right)}}{{\left( {C_{1} - C_{0} } \right)D_{s} }}, \\ & N_{TC} = \frac{{D_{CT} \left( {C_{1} - C_{0} } \right)}}{{k\left( {T_{1} - T_{0} } \right)}},\\ & G_{rt} = \frac{{gd_{1}^{2} \left( {1 - \Theta_{0} } \right)\left( {T_{1} - T_{0} } \right)\rho_{f0} \beta_{T} }}{\mu c},\\ & N_{b} = \frac{{\left( {\rho c} \right)_{p} D_{B} \left( {\Theta_{1} - \Theta_{0} } \right)}}{k}, \\ &M = \sqrt {\frac{\sigma }{\mu }} B_{0} d_{1} , \end{aligned}$$
(23)

where \(\theta ,\) \(\delta ,\) \(\gamma ,\) \(N_{b} ,\) \({\text{Re}} , G_{rF} ,\) \(Pr,\) \(Le,\) \(G_{rt} ,\) \(G_{rc} ,\) \(N_{CT} ,\) \(Ln,\) \(N_{t} ,\) \(\Omega ,\) \(N_{TC} , \mu , k\) represent the temperature, wave number, solutal (species) concentration, Brownian motion, Reynolds number, nanoparticle Grashof number, Prandtl number, Lewis number, thermal Grashof number, solutal Grashof number, Soret parameter, nanofluid Lewis number, thermophoresis parameter, nanoparticle fraction, Dufour parameter, viscosity of fluid, and thermal conductivity, respectively.

Equation (5) is satisfied automatically using Eqs. (12) and (13), and Eqs. (6) to (10) in the wave frame (by dropping bars) become

$$\begin{aligned} {\text{Re}} \delta \left( {\psi_{xy} \psi_{y} - \psi_{yy} \psi_{x} } \right) & = - \left( {\frac{\mu + \eta }{\mu }} \right)\frac{\partial p}{{\partial x}} + \delta \frac{{\partial S_{xx} }}{\partial x} \\ & \quad + \frac{{\partial S_{xy} }}{\partial y} + \left( {\delta^{2} \frac{{\partial^{3} \psi }}{{\partial x^{2} \partial y}} + \frac{{\partial^{3} \psi }}{{\partial y^{3} }}} \right) \\ & \quad - M^{2} \cos \Gamma \left( {\left( {\psi_{y} + 1} \right)\cos \Gamma + \delta \psi_{x} \sin \Gamma } \right) \\ & \quad + G_{rt} \theta + G_{rc} \gamma - G_{rF} \Omega,\end{aligned}$$
(24)
$$\begin{aligned} & {\text{Re}}\;\delta ^{3} \left( {\psi _{{xy}} \psi _{x} - \psi _{{xx}} \psi _{y} } \right) = - \left( {\frac{{\mu + \eta }}{\mu }} \right)\frac{{\partial p}}{{\partial y}} \\&\quad + \delta ^{2} \frac{{\partial S_{{xy}} }}{{\partial x}} + \delta \frac{{\partial S_{{yy}} }}{{\partial y}} - \delta ^{2} \left( {\delta ^{2} \frac{{\partial ^{3} \psi }}{{\partial x^{3} }} + \frac{{\partial ^{3} \psi }}{{\partial x\partial y^{2} }}} \right) \\ & \quad \quad + M^{2} \delta \sin \Gamma \left( {\left( {\psi _{y} + 1} \right)\cos \Gamma + \psi _{x} \delta \sin \Gamma } \right), \\ \end{aligned}$$
(25)
$${\text{Re}}\, Pr\,\delta \left( {\theta_{x} \psi_{y} - \theta_{y} \psi_{x} } \right) = \left( {\theta_{yy} + \delta^{2} \theta_{xx} } \right) + N_{TC} \left( {\delta^{2} \gamma_{xx} + \gamma_{yy} } \right) + N_{b} \left( {\delta^{2} \Omega_{x} \theta_{x} + \theta_{y} \Omega_{y} } \right) + N_{t} \left( {\delta^{2} \left( {\theta_{x} } \right)^{2} + \left( {\theta_{y} } \right)^{2} } \right),$$
(26)
$${\text{Re}}\, \delta Le\,\left( {\gamma_{x} \psi_{y} - \gamma_{y} \psi_{x} } \right) = \left( {\delta^{2} \gamma_{xx} + \gamma_{yy} } \right) + N_{CT} \left( {\delta^{2} \theta_{xx} + \theta_{yy} } \right),$$
(27)
$${\text{Re}}\, \delta Ln\,\left( {\psi_{y} \Omega_{x} - \psi_{x} \Omega_{y} } \right) = \left( {\delta^{2} \Omega_{xx} + \Omega_{yy} } \right) + \frac{{N_{t} }}{{N_{b} }}\left( {\delta^{2} \theta_{xx} + \theta_{yy} } \right),$$
(28)
$$\begin{aligned} \left( {\frac{2\delta \eta }{\mu }} \right)\frac{{\partial^{2} \psi }}{\partial x\partial y} & = S_{xx} + \delta Wi\left( {\frac{\partial \psi }{{\partial y}}\frac{\partial }{\partial x} - \frac{\partial \psi }{{\partial x}}\frac{\partial }{\partial y}} \right)S_{xx} \\ & \quad- 2\beta Wi\delta \frac{{\partial^{2} \psi }}{\partial x\partial y} \\ &\quad - Wi\left( {\delta^{2} \left( {1 - \beta } \right)\frac{{\partial^{2} \psi }}{{\partial x^{2} }} + \left( {1 + \beta } \right)\frac{{\partial^{2} \psi }}{{\partial y^{2} }}} \right)S_{xy},\end{aligned}$$
(29)
$$\begin{aligned} \frac{\eta }{\mu }\left( {\frac{{\partial^{2} \psi }}{{\partial y^{2} }} - \delta^{2} \frac{{\partial^{2} \psi }}{{\partial x^{2} }}} \right) & = S_{xy} + Wi\delta \left( {\frac{\partial \psi }{{\partial y}}\frac{\partial }{\partial x} - \frac{\partial \psi }{{\partial x}}\frac{\partial }{\partial y}} \right)S_{xy} \\ &\quad + \frac{Wi}{2}\left( {\left( {1 - \beta } \right)\frac{{\partial^{2} \psi }}{{\partial y^{2} }} + \delta^{2} \left( {1 + \beta } \right)\frac{{\partial^{2} \psi }}{{\partial x^{2} }}} \right)S_{xx} \\ &\quad - \frac{Wi}{2}\left( {\delta^{2} \left( {1 - \beta } \right)\frac{{\partial^{2} \psi }}{{\partial x^{2} }} + \left( {1 + \beta } \right)\frac{{\partial^{2} \psi }}{{\partial y^{2} }}} \right)S_{yy},\end{aligned}$$
(30)
$$- \left( {\frac{2\delta \eta }{\mu }} \right)\frac{{\partial^{2} \psi }}{\partial x\partial y} = S_{yy} + Wi\,\delta \,\left( {\frac{\partial \psi }{{\partial y}}\frac{\partial }{\partial x} - \frac{\partial \psi }{{\partial x}}\frac{\partial }{\partial y}} \right)S_{yy} + 2\,\beta\, \delta Wi\frac{{\partial^{2} \psi }}{\partial x\partial y}S_{yy} + Wi\left( {\left( {1 - \beta } \right)\frac{{\partial^{2} \psi }}{{\partial y^{2} }} + \delta^{2} \left( {1 + \beta } \right)\frac{{\partial^{2} \psi }}{{\partial x^{2} }}} \right)S_{xy} .$$
(31)

Using lubricant approach ( \(\delta < < 1,\) \({\text{Re}} \to 0\)), Eqs. (14) to (18) are now reduced as

$$0 = - \left( {\frac{\mu + \eta }{\mu }} \right)\frac{\partial p}{{\partial x}} + \frac{{\partial S_{xy} }}{\partial y} + \frac{{\partial^{3} \psi }}{{\partial y^{3} }} - M^{2} \cos^{2} \Gamma \left( {\frac{\partial \psi }{{\partial y}} + 1} \right) + G_{rt} \theta + G_{rc} \gamma - G_{rF} \Omega ,$$
(32)
$$0 = - \frac{\partial p}{{\partial y}},$$
(33)
$$\frac{{\partial^{2} \theta }}{{\partial y^{2} }} + N_{TC} \frac{{\partial^{2} \gamma }}{{\partial y^{2} }} + N_{b} \left( {\frac{\partial \Omega }{{\partial y}}\frac{\partial \theta }{{\partial y}}} \right) + N_{t} \left( {\frac{\partial \theta }{{\partial y}}} \right)^{2} = 0,$$
(34)
$$\frac{{\partial^{2} \gamma }}{{\partial y^{2} }} + N_{CT} \frac{{\partial^{2} \theta }}{{\partial y^{2} }} = 0,$$
(35)
$$\frac{{\partial^{2} \Omega }}{{\partial y^{2} }} + \frac{{N_{t} }}{{N_{b} }}\frac{{\partial^{2} \theta }}{{\partial y^{2} }} = 0,$$
(36)

where

$$S_{xx} = Wi\left( {1 + \beta } \right)\frac{{\partial^{2} \psi }}{{\partial y^{2} }}S_{xy} ,$$
(37)
$$\left( {\frac{\eta }{\mu }} \right)\frac{{\partial^{2} \psi }}{{\partial y^{2} }} = S_{xy} + \frac{Wi}{2}\left( {1 - \beta } \right)\frac{{\partial^{2} \psi }}{{\partial y^{2} }}S_{xx} - \frac{Wi}{2}\left( {1 + \beta } \right)\frac{{\partial^{2} \psi }}{{\partial y^{2} }}S_{yy} ,$$
(38)
$$S_{yy} = - Wi\left( {1 - \beta } \right)\frac{{\partial^{2} \psi }}{{\partial y^{2} }}S_{xy} .$$
(39)

Now reducing pressure from Eqs. (19) and (20) and using Eq. (24), we now have the following expression:

$$\frac{{\partial^{2} S_{xy} }}{{\partial y^{2} }} + \frac{{\partial^{4} \psi }}{{\partial y^{4} }} - M^{2} \cos^{2} \Gamma \frac{{\partial^{2} \psi }}{{\partial y^{2} }} + G_{rt} \frac{\partial \theta }{{\partial y}} + G_{rc} \frac{\partial \gamma }{{\partial y}} - G_{rF} \frac{\partial \Omega }{{\partial y}} = 0,$$
(40)
$$S_{xy} = \frac{{\left( {\frac{\eta }{\mu }} \right)\left( {\frac{{\partial^{2} \psi }}{{\partial y^{2} }}} \right)}}{{1 + Wi^{2} \left( {1 - \beta^{2} } \right)\left( {\frac{{\partial^{2} \psi }}{{\partial y^{2} }}} \right)^{2} }},$$
(41)
$$\begin{aligned} & \frac{{\partial^{2} }}{{\partial y^{2} }}\left[ {\frac{{\left( {\frac{\eta }{\mu } + 1} \right)\left( {\frac{{\partial^{2} \psi }}{{\partial y^{2} }}} \right) + Wi^{2} \left( {1 - \beta^{2} } \right)\left( {\frac{{\partial^{2} \psi }}{{\partial y^{2} }}} \right)^{3} }}{{1 + Wi^{2} \left( {1 - \beta^{2} } \right)\left( {\frac{{\partial^{2} \psi }}{{\partial y^{2} }}} \right)^{2} }}} \right] - M^{2} \cos^{2} \Gamma \frac{{\partial^{2} \psi }}{{\partial y^{2} }} \\ & \quad + G_{rt} \frac{\partial \theta }{{\partial y}} + G_{rc} \frac{\partial \gamma }{{\partial y}} - G_{rF} \frac{\partial \Omega }{{\partial y}} = 0.\end{aligned}$$
(42)
$$\begin{aligned} \left( {\frac{{\mu + \eta }}{\eta }} \right)\frac{{\partial p}}{{\partial x}} & = \frac{\partial }{{\partial y}}\left( {\frac{{\partial ^{2} \psi }}{{\partial y^{2} }}} \right)\left[ {\frac{{\frac{\eta }{\mu }\left( {\frac{{\partial ^{2} \psi }}{{\partial y^{2} }}} \right)}}{{1 + Wi^{2} \left( {1 - \beta ^{2} } \right)\left( {\frac{{\partial ^{2} \psi }}{{\partial y^{2} }}} \right)}}} \right] \\ & \quad + \frac{{\partial ^{3} \psi }}{{\partial y^{3} }} - M^{2} \cos ^{2} \Gamma \left( {\frac{{\partial \psi }}{{\partial y}} + 1} \right)\\ & \quad + G_{{rt}} \theta + G_{{rc}} - G_{{rF}} \Omega \end{aligned}$$
(43)

After using binomial expansion for small \(Wi^{2}\), Eqs. (42) and (43) may be simplified to

$$\begin{aligned} & \frac{{\partial^{2} }}{{\partial y^{2} }}\left[ {\frac{{\partial^{2} \psi }}{{\partial y^{2} }} + Wi^{2} \lambda_{1} \left( {\frac{{\partial^{2} \psi }}{{\partial y^{2} }}} \right)^{3} + Wi^{4} \lambda_{2} \left( {\frac{{\partial^{2} \psi }}{{\partial y^{2} }}} \right)^{5} } \right] \\ & \quad - M^{2} \cos^{2} \Gamma \frac{{\partial^{2} \psi }}{{\partial y^{2} }} + G_{rt} \frac{\partial \theta }{{\partial y}} + G_{rc} \frac{\partial \gamma }{{\partial y}} - G_{rF} \frac{\partial \Omega }{{\partial y}} = 0,\end{aligned}$$
(44)
$$\begin{aligned} \frac{{\partial p}}{{\partial x}} & = \frac{{\partial ^{3} \psi }}{{\partial y^{3} }} + Wi^{2} \lambda _{1} \frac{\partial }{{\partial y}}\left[ {\left( {\frac{{\partial ^{2} \psi }}{{\partial y^{2} }}} \right)^{3} } \right]\\ &\quad + Wi^{4} \lambda _{2} \frac{\partial }{{\partial y}}\left[ {\left( {\frac{{\partial ^{2} \psi }}{{\partial y^{2} }}} \right)^{5} } \right] - M^{2} \cos ^{2} \Gamma \left( {\psi _{y} + 1} \right) \\ & \quad \quad + G_{{rt}} \theta + G_{{rc}} \gamma - G_{{rF}} \Omega , \\ \end{aligned}$$
(45)
$$\lambda_{1} = \frac{{\left( {\beta^{2} - 1} \right)\eta }}{{\left( {\eta + \mu } \right)}},{ }\lambda_{2} = \left( {\beta^{2} - 1} \right)\lambda_{1} .$$
(46)

In wave frame, the boundary conditions for the initiate problem are given as

$$\psi = \frac{F}{2}, {\text{at}} \,y = h_{1} \left( x \right),$$
$$\psi = - \frac{F}{2}, {\text{at}} \,y = h_{2} \left( x \right),$$
$$\frac{\partial \psi }{{\partial y}} + \omega_{1} \left( {\frac{{\partial^{2} \psi }}{{\partial y^{2} }} + S_{xy} } \right) = - 1\,{\text{on}}\, y = h_{1} \left( x \right),$$
$$\frac{\partial \psi }{{\partial y}} - \omega_{1} \left( {\frac{{\partial^{2} \psi }}{{\partial y^{2} }} + S_{xy} } \right) = - 1\, {\text{on}}\, y = h_{2} \left( x \right),$$
$$\theta + \omega_{2} \frac{\partial \theta }{{\partial y}} = 0,\,{\text{on}}\, y = h_{1} \left( x \right),$$
(47)
$$\theta - \omega_{2} \frac{\partial \theta }{{\partial y}} = 1,\;{\text{on}}\, y = h_{2} \left( x \right),$$
(48)
$$\gamma + \omega_{3} \frac{\partial \gamma }{{\partial y}} = 0,{\text{ on }}y = h_{1} \left( x \right),$$
$$\gamma - \omega_{3} \frac{\partial \gamma }{{\partial y}} = 1, {\text{on}} y = h_{2} \left( x \right),$$
(49)
$$\Omega + \omega_{4} \frac{\partial \Omega }{{\partial y}} = 0, \;{\text{on}} y = h_{1} \left( x \right),$$
$$\Omega - \omega_{4} \frac{\partial \Omega }{{\partial y}} = 1, \;{\text{on}} y = h_{2} \left( x \right).$$
(50)

If \(\omega_{1} ,\) \(\omega_{2} ,\) \(\omega_{3} ,\) and \(\omega_{4}\) in the above-mentioned conditions are all zero, there are no-slip conditions.

The mean flow \(Q\) is computed in dimensionless form as follows:

$$Q = F + 1 + d,$$
(51)

where

$$F = \int_{{h_{2} \left( x \right)}}^{{h_{1} \left( x \right)}} {\frac{{\partial \psi }}{{\partial y}}dy = \psi \left( {h_{1} \left( x \right)) - \psi (h_{2} \left( x \right)} \right),}$$
(52)

where

$$h_{1} \left( x \right) = 1 + a\cos 2\pi x,\;h_{2} \left( x \right) = - d - b\cos (2\pi x + \varphi ).$$
(53)

3.1 Special Case:

  • The results of [16] can also be retrieved as a special case of an existing problem in the absence of double-diffusive convection (\(G_{rt} = 0 = G_{rc} = G_{rF}\)), slip conditions (\(\omega_{1} = \omega_{2} = \omega_{3} = \omega_{4} = 0\)), and \(M = 0.\)

  • The results of [9] can also be retrieved as a special case of an existing problem in the absence of double-diffusive convection (\(G_{rt} = 0 = G_{rc} = G_{rF}\)), non-Newtonian fluid (\(\lambda_{1} = 0 = \lambda_{2}\)), slip conditions (\(\omega_{1} = \omega_{2} = \omega_{3} = \omega_{4} = 0\)), and \(M = 0.\)

Flowchart: Flowchart showing the hierarchy of the ongoing problem

figure a

4 Numerical Solution and Validation

Due to nonlinearity of partial differential equations, finding exact solutions to Eqs. (21)–(25) is extremely challenging. Differential equations are solved using the NDSolve command in the MATHEMATICA software. This command is based on different types of numerical methods. Some of these methods are: Explicit Euler, midpoint rule method, midpoint rule method with Gragg smoothing, and linearly implicit Bader‐smoothed midpoint rule method. Settings are kept at default in which equations are solved numerically by the best suitable method for solving the system of equations. Table 1 is generated to show the comparison of the present work with the available literature. It is depicted from Table 1 that in the absence of slip, the numerical solution satisfied the boundary conditions at \(y = h_{1} \left( x \right)\) and \(y = h_{2} \left( x \right)\).and our numerical results matches with Hayat et al. [16] and viscous fluid [4] in the absence of double-diffusive convection and slip parameter.

Table 1 Comparison with the available literature
Full size table

5 Results and Discussion

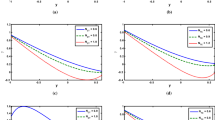
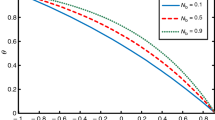
In this section, graphical depiction is achieved as a result of numerical computation to solutions. To analyze the importance of temperature on several parameters such as thermophoresis \(N_{{\text{t}}}\), Brownian motion \(N_{{\text{b}}}\), Soret \(N_{CT}\), Dufour\(N_{TC}\), and temperature slip \(\omega_{2},\) Fig. 2a, b is plotted. As noticed in Fig. 2a and b, the temperature profile increases when thermophoresis \(N_{t}\) and Brownian motion \(N_{{\text{b}}}\) parameters are enhanced. Because of the rise in Brownian motion and thermophoretic effects, nanoparticles actively travel from the wall toward the fluid, vastly increasing temperature. The similar behavior is noted for the case of Soret \(N_{CT}\) and Dufour \(N_{TC}\) parameters. The temperature profile shows its increasing behavior by enhancing values of \(N_{CT}\) and \(N_{TC}\) (Fig. 2c and d). To study the impact of partial slip parameter of temperature \(\omega_{2}\) , Fig. 2e is drawn. It is notable in Fig. 2e that temperature profile decreases in the zone when \(y \in \left[ { - 0.3, - 0.1} \right]\) but when \(y \in \left[ { - 0.1,0.65} \right]\) the temperature profile increases due to increasing values of temperature slip parameter \({\varvec{\omega}}_{2} .\) Because of the slip, the kinetic energy between fluid particles increases, raising the fluid temperature (Fig. 2e). To explore the significance of concentration on thermophoresis \(N_{{\text{t}}}\), Brownian motion \(N_{{\text{b}}}\), Soret \(N_{CT}\), Dufour\(N_{TC}\), and slip parameter of concentration \(\omega_{3}\) , Fig. 3a–e is plotted. It is noted from Fig. 3a–e that the concentration profile decreases by enhancing thermophoresis \(N_{{\text{t}}}\), Brownian motion \(N_{{\text{b}}}\), Soret \(N_{CT}\), Dufour \(N_{TC}\), and slip constraint of concentration \(\omega_{3}\). Figure 4a–e is displayed to examine the effect of nanoparticle fraction on several parameters such as thermophoresis \(N_{{\text{t}}}\), Brownian motion \(N_{{\text{b}}}\), Soret parameter \(N_{CT} ,\) Dufour parameter\(N_{TC}\), and slip parameter of nanoparticle fraction \(\omega_{4} .\) As shown in Fig. 4a, increasing Brownian motion \(N_{{\text{b}}}\) raises the density of nanoparticles fraction. Furthermore, in the cases of \(N_{{\text{t}}}\), \(N_{CT} ,\) \(N_{TC}\) , and\(\omega_{4}\), opposite behavior is observed. By growing the values of \(N_{CT} ,\) \(N_{t} ,\) \(N_{TC}\) and\(\omega_{4}\), the nanoparticle fraction drops (Fig. 4b–e). This is owing to the fact that when \({\varvec{N}}_{{\varvec{t}}}\) grows, the fluid viscosity falls, resulting in a smaller volume fraction occupied by the less dense particles. Moreover, since the channel walls generate less disturbance to the fluid particles due to the slip effect, higher values of \({\varvec{\omega}}_{4}\) cause the concentration to decrease. As a result, the mass transfer rate of nanoparticles is slowed. Figure 5a–f shows the changes in pressure rise \(\left(\Delta p\right)\) vs mean flow rate \(\left(Q\right)\) for multiple slip parameter \(\beta\) values \(,\) Weissenberg number \(Wi,\) Hartmann number \(M,\) velocity slip constraint \({\omega }_{1},\) thermophoresis \({N}_{t},\) and thermal Grashof number \({G}_{rt}\). It clearly shows that raising\(\beta\),\(M\), and \(Wi\) increases the pumping rate in the pumping region " \(\Delta p>0"\) and in free pumping region " \(\Delta p=0".\) In the copumping region " \(\Delta p<0"\), the pumping rate decreases when\(\beta\),\(M\), and \(Wi\) increase (Fig. 5a–c). The velocity slip constraint \({\omega }_{1}\) has the opposite conduct on pressure rise when compared with\(\beta\),\(M\), and \(Wi\) (Fig. 5d). Here, pumping rate decreases in pumping zone " \(\Delta p>0"\) and in free pumping zone " \(\Delta p=0"\) by increasing velocity slip parameter\({\omega }_{1}\). The pumping rate increases in pumping region " \(\Delta p>0",\) in free pumping region "\(\Delta p=0"\) , and in copumping region "\(\Delta p<0"\) by increasing \({N}_{t}\) and \({G}_{rt}\) values (Fig. 5e and f). Figure 6a and d reveals the deviations of \(dp/dx\) against \(x\) for different slip parameter \(\beta ,\) Hartmann number \(M,\) Weissenberg number \(Wi,\) and thermophoresis \({N}_{t}\) values \(.\) It is found that in broader parts of channel \(x\in [\mathrm{0,0.4}]\) and \(x\in [\mathrm{0.6,1}]\), the pressure gradient is comparatively small. This means that the flow can pass through without creating a significant pressure gradient. To keep the flux flowing through the narrow region of the channel\(x\in [\mathrm{0.4,0.6}]\), a higher-pressure gradient is necessary. When the values of \(\beta ,\) \(M\) and \(Wi\) are increased, the pressure gradient is observed to grow (Fig. 6a–c) but it reduces as the \({N}_{t}\) values are increased (Fig. 6d). Figure 7a–f demonstrates the impact of velocity on \(\beta ,\) \({\omega }_{1},\) \(M,\) \({G}_{rF},\) \({N}_{t},\) and\({N}_{TC}\). It is noticed in Fig. 7a that when \(y\in [\mathrm{0,0.5}]\) the magnitude of velocity decreases by increasing \(\beta\) values. Figure 7b shows that increasing \(M\) values decreases the magnitude of velocity for \(y\in [-\mathrm{0.3,0}]\) and \(y\in [\mathrm{0.55,0.68}]\), whereas increasing \(M\) values increases the magnitude of velocity when \(y\in [\mathrm{0,0.5}]\). The velocity at the walls is seen to be reduced as \({\varvec{M}}\) increases. In reality, increasing the magnetic number increases the Lorentz force, which acts as a retarding force at the walls, reducing fluid speed. Figure 7c shows the effect of the slip parameter of velocity\({\omega }_{1}\). Figure 7c shows that increasing \({\omega }_{1}\) values decreases the magnitude of velocity when \(y\in [-0.3,-0.25]\) and\(y\in [\mathrm{0.4,0.68}]\), whereas increasing \({\omega }_{1}\) values increases the magnitude of velocity when \(y\in [-\mathrm{0.25,0.4}]\). The slip effect in the channel causes the fluid particles to stray, slowing the fluid velocity. The influence of \({G}_{rF},\) \({N}_{t},\) and \({N}_{TC}\) on velocity is studied in Fig. 7d–f. The magnitude of velocity increases when \(y\in [-\mathrm{0.3,0.2}]\) due to reduction in the drag force but reduces when \(y\in [\mathrm{0.2,0.85}]\) by increasing \({G}_{rF},\) \({N}_{t},\) and \({N}_{TC}\).

Fig. 2
figure 2

Profile of temperature for \({N}_{t},\) \({N}_{b},\) \({N}_{CT},\) \({N}_{TC},\) and \({\omega }_{2}\)

Full size image
Fig. 3
figure 3

Profile of concentration for \({N}_{t},\) \({N}_{b},\) \({N}_{CT},\) \({N}_{TC},\) and \({\omega }_{3}\)

Full size image
Fig. 4
figure 4

Profile of nanoparticle fraction for \({N}_{b},\) \({N}_{t},\) \({N}_{CT},\) \({N}_{TC},\) and \({\omega }_{4}\)

Full size image
Fig. 5
figure 5

Profile of pressure rise for \(\beta ,\) \(M,\) \(Wi,\) \({\omega }_{1},\) \({N}_{t},\) and \({G}_{rt}\)

Full size image
Fig. 6
figure 6

Profile of pressure gradient for \(\beta ,\) \(M,\) \(Wi,\) and \({N}_{t}\)

Full size image
Fig. 7
figure 7

Profile of velocity for \(\beta ,\) \(M,\) \({\omega }_{1},\) \({G}_{rF},\) \({N}_{t},\) and \({N}_{TC}\)

Full size image

Figures 8, 9, 10, and 11 are plotted to show the effect of streamlines. As shown in Fig. 8, increasing the velocity slip parameter \({\omega }_{1}\) reduces the quantity of trapped boluses in both the top and lower parts of the channel. By raising \({N}_{TC}\) and \({G}_{rF}\) values, the quantity of trapped bolus grows in the upper part of the channel, while the size of trapped bolus increases in the lower section (Figs. 9 and 10). By raising the slip parameter of temperature \({\omega }_{2}\), the size of the trapped bolus decreases in the top half of the channel, while the size of the trapped bolus increases in the lower half of the channel (Fig. 11).

Fig. 8
figure 8

Streamlines for \({\omega }_{1}\)

Full size image
Fig. 9
figure 9

Streamlines for \({N}_{TC}\)

Full size image
Fig. 10
figure 10

Streamlines for \({G}_{rF}\)

Full size image
Fig. 11
figure 11

Streamlines for \({\omega }_{2}\)

Full size image

6 Concluding Remarks

This section provides a final remark on the ongoing problem. The primary purpose of a new study is to determine the importance and impacts of slip on double-diffusive convection flows. Numerical methodologies can be utilized to solve nonlinear equations, and graphical results can be employed to evaluate various embedded constraints. The major significant findings are as follows:

  • The temperature profile increases when thermophoresis \({N}_{t}\) and Brownian motion \({N}_{b}\) parameters are enhanced. By increasing \({N}_{t}\), nanoparticle concentration becomes higher which cause the temperature profiles to rise. Increasing \(N_{b}\) increases the average kinetic energy, and hence, it causes an increase in temperature profiles.

  • The solutal concentration profile decreases by enhancing all the diffusion parameters, viz. thermophoresis\(N_{{\text{t}}}\), Brownian motion\(N_{{\text{b}}}\), Soret \(N_{CT}\) , and Dufour \(N_{TC}\) parameter. Also, solutal concentration profiles are found decreasing as slip parameter \(\omega_{3}\) intensifies \(.\)

  • The density of nanoparticles fraction raises by increasing Brownian motion \(N_{{\text{b}}}\) because it increases the average kinetic energy and hence particles move it effects the motion of nano particles. However, opposite behavior is noted in the case of \(N_{{\text{t}}}\), \(N_{CT} ,\) \(N_{TC},\) and \(\omega_{4}\).

  • The enhancement of slip effect \(\omega_{1}\) inside the channel for Johnson–Segalman nanofluids with double-diffusive effects is found flow resisting as it causes the fluid particles to stray, slowing the fluid velocity. However, opposite behavior is observed near the boundary wall of the channel.

  • The velocity at the walls is seen to be enhanced as the Hartmann number \(M\) increases. This means that when magnetic effects are dominating the viscous effects that speed of fluid near walls tends to increase.

  • The volume of trapped bolus grows in the upper part of the channel as \(N_{TC}\) and \(G_{rF}\) values are increased, while the size of trapped bolus expands in the lower part.