Thermal analysis of peristaltic flow of nanosized particles within a curved channel with second-order partial slip and porous medium

Abstract

In a thermo-dynamical system, maximum transfer of energy takes the center of attention. Industrial advancement in recent years augmented the need for efficient heat transfer and cooling process both at the microscale and at the larger scale. The porous medium provides an advantage on fins or inserts due to its greater surface area in contact and hence enhances heat transfer rates. Nanofluids use nanosized particles with very high thermal conductivity uniformly distributed in base fluids which increases the conductivity of the base fluid ridiculously. Both the Porous matrix and nanofluid play a vital role in enhancing the heat transfer rate. In this paper, the transport of nanosized particles within a non-Darcy porous curved channel is assumed. The flow is induced by a peristaltic wave. Higher-order slip effects are also encountered. The flow problem is modeled using the so-called Buongiorno’s formulation. It is assumed that the wave on the wall has a long wavelength as compare to its amplitude; also, creeping flow assumption is added leading to small values of Reynolds’ number. The equations are solved analytically, and the exact solutions are achieved. Graphical and tabular outputs are displayed alongside detailed discussion.

Introduction

Porous materials provide a variety of advantages over conventional engineering designs. The irregular motion of fluids helps and provides a uniform mixture of fluids which is also helpful in maintaining temperature distribution. More surface area in contact increases the heat transfer rate and controls the rate of the chemical reaction. Also, it helps in the improvement in heat flux absorption. Considering the advantages, many experimental and theoretical scientists prefer investigation of heat transfer in a system exploiting several different types of materials which use porous spaces. Technology advancement and a rise in manufacturing at a smaller level increase the use of the porous medium. Advancement in micro- and nano-manufacturing makes such porous materials easy to use in thermo-chemical machines or systems. Mathematically, the flow rate through a porous space is defined using Darcy’s law [1] which states that the cross-sectional area in the transverse direction to flow and gradient of pressure are directly proportional to flow rate. If the Reynolds number has moderate values, the inertial forces tend to become significant. In this case, an inertial term called Forchheimer’s term [2] is included in traditional Darcy’s law. This term tends to add nonlinearity in flow rate. Porous medium can be used as insulators and heat transfer promoters in different systems. On account of such advantages, heat and fluid flow through porous media find marvelous applications in hydrology, geothermal energy systems, petroleum reservoirs, crude oil and gas production, heat exchanger design, catalytic reactors, grain storage, fermentation process, analyze the water movement in reservoirs, analyze the beds of fossil fuels, solar receivers, etc. [3,4,5,6,7].

The idea of adding solid particles in the liquid to enhance the conductivity of liquids was floated about a century ago when Maxwell established mathematical relations of the electrical conductivity of solid particles. But, these experiments and theoretical studies have been conducted with milli or micrometer size particles. These particles tend to settle down quickly or form an aggregation. Also, they resist flow and cause a drop in pressure. To add to that a large number of particles is needed to improve the thermal conductivity of the fluid. Considering the adverse effects and limited advantage of the solid–liquid suspension, these fluids cannot hit the limelight. With the advanced modern technology, particles of a size less than 100 nm are prepared of the metals and their oxides with better thermal conductivity and mechanical and magnetic performance based on the requirement of the system. These nanoparticles are uniformly dispersed in Newtonian and non-Newtonian base fluids. These are stable suspended nanoparticles with typical dimensions of the order of 10 nm. The term “nanofluid” was first used by Choi [8]. It was one of the promising aspects of thermal conductivity enhancement of fluids. Later, different mathematical models, namely homogenous flow model [9], dispersion model [10] and the Buongiorno’s model [11], were developed in brainstorm ways. Many researchers [12,13,14,15,16,17,18,19] analyzed the transport of momentum and energy in the channel and through different geometries for nanofluids.

Peristalsis is the involuntary wavelike contraction and relaxation movements of muscles mostly in digestive tracts. The transport process is well controlled due to soft and flexible nature of the walls. Hence, it leads to many possibilities of the waveform and on the walls and bolus pressure. Further research in this field is being done, and positive steps have been taken to build some instruments which involve such transport mechanism. Many machines such as a heart–lung machine, finger pumps, etc., are developed employing the mechanism of peristalsis. Latham [20] was the first to coin the name of such transport. Many authors [21,22,23,24,25] carried on their investigation into the related areas and found interesting outcomes for the diverse flow situation.

Some of the most exciting studies in recent years are Ellahi et al. [26] explore peristaltic transportation of non-Newtonian nanofluids through a Darcy type porous medium. They also studied the effects of a porous medium in energy loss and hence explored entropy generation and Bejan number graphically. Das et al. [27] in 2018 analyzed water-based nanofluid saturating the porous tube. The effects of the magnetic field are observed on flow and entropy generation. Copper particles are chosen as nanoparticles. Hayat et al. [28] investigated Williamson nanofluid transported with the help of the peristaltic wave on the tube. The effect of endoscope presence is also encountered. Hayat et al. [29] also worked on the transport of nanofluid in a compliant channel driven by the peristaltic wave. They also considered convective conditions and radiative heat transfer in this study. Bhatti et al. [30] address nonlinear thermal radiation effects on peristaltic pumping of viscoelastic fluid. They also incorporated the effects of electromagnetohydrodynamics and Darcy type porous medium. Mathematical modeling of partial wall slip on magneto-nanofluid in a curved channel was addressed by Hayat et al. [31]. They assumed porous space saturated with Jeffery-type base fluid with suspended nanoparticle. Mekheimer et al. [32] find the application of peristaltic blood flow in cancer therapy. They assumed nanosized gold particles in third-grade fluid in the catheter. Bhatti et al. [33] discussed electro-kinetically modulated peristaltic propulsion. They assumed magnetized nanofluid and analyzed heat transport. Entropy analysis was also made in a microchannel. Reddy and Makinde [34] worked on the MHD peristaltic transport of non-Newtonian linear viscoelastic nanofluid through an asymmetric channel. Hasona et al. [35] investigated the MHD Jeffrey nanofluid with temperature-dependent viscosity for the application in the oil refinery. Abou-Zeid [36] employed HPM to find the solutions of non-Newtonian nanofluid in eccentric annuli. The flow is driven by the peristaltic wave, and a constant magnetic field is applied perpendicular to the flow. Mohamed and Abou-zeid [37] again extended the work with micropolar Casson nanofluid. Kothandapani and Prakash [38] worked out the solutions for a mathematical model of MHD nanofluid in a tapered asymmetric channel with the porous medium.

Systems are absolutely desired for the purpose of cooling of any machines which perform energy transport. Such machines are widely used in power plants, factories and transportation. Nowadays, the technique involving both nanofluid and porous media finds considerable attention from many researchers and great demand from industry-based thermal systems. The rationale behind it is that in porous media the contact area increases, while nanoparticles dispersed in nanofluid upsurge the effective thermal conductivity leading to the dramatic enhancement of the efficiency of typical industrial thermal systems. The investigation regarding the viscous fluid flow through a closed porous geometry with flexible walls driven by the peristaltic wave is of enduring significance in view of its applications.

Because of the aforementioned relevance of peristaltic flow in the porous medium, authors have been motivated to explore an unsteady heat transfer problem using nanofluids. Such aspect of the study has not been discussed yet. It is also extendable that this study provides an analytic solution for highly nonlinear coupled system of differential equations with non-homogeneous second-order partial slip conditions. Then, the authors offered physical results based on the graphical behavior of various key results shown under the influence of observable parameters.

Mathematical modeling

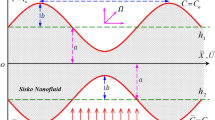
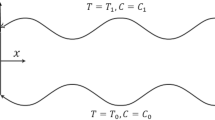
Let us assume a curved two-dimensional channel having flexible walls and executing peristaltic waves along its radial direction. Moreover, the enclosure contains a saturation of nanofluid considered in a porous medium. The flow is considered to be incompressible. The conduit of half-width a twisted in circular form having center O along with the radius $\alpha$ is deliberated (geometry can be found in [31]). The flow inside is stimulated through sinusoidal waves of minute amplitude $b$ running along the walls of the channel. Furthermore, the lower wall of the channel is sustained at, respectively, the steady temperatures $T_{0}$ and nanoparticles distribution $C_{0}$, and the upper wall is having the said quantities with magnitudes $T_{1} \;{\text{and}}\; C_{1}$.The disciplinary expressions for the nanofluid transport in cylindrical curvilinear coordinates $\left( {\bar{R},\bar{X}} \right)$ are organized as follows [31]:

$$\begin{aligned} & \frac{\partial V}{{\partial \overline{t} }} + \overline{V} \frac{{\partial \overline{V} }}{{\partial \overline{R} }} + \frac{{\alpha \overline{U} }}{{\alpha + \overline{R} }}\frac{{\partial \overline{V} }}{{\partial \overline{X} }} - \frac{{\overline{U}^{2} }}{{\alpha + \overline{R} }} = - \frac{1}{\rho }\frac{{\partial \overline{P} }}{{\partial \overline{R} }} \\ & + \upsilon \left[ {\frac{1}{{\alpha + \overline{R} }}\frac{\partial }{{\partial \overline{R} }}\left\{ {(\alpha + \overline{R} )\frac{{\partial \overline{V} }}{{\partial \overline{R} }}} \right\} + \left( {\frac{\alpha }{{\alpha + \overline{R} }}} \right)^{2} \frac{{\partial^{2} \overline{V} }}{{\partial \overline{X}^{2} }} - \frac{{\overline{V} }}{{(\alpha + \overline{R} )^{2} }} + \frac{2\alpha }{{(\alpha + \overline{R} )^{2} }}\frac{\partial U}{{\partial \overline{X} }}} \right], \\ \end{aligned}$$

(1)

$$\begin{aligned} & \frac{{\partial \overline{U} }}{{\partial \overline{t} }} + \overline{V} \frac{{\partial \overline{U} }}{{\partial \overline{R} }} + \frac{{\alpha \overline{U} }}{{\alpha + \overline{R} }}\frac{{\partial \overline{U} }}{{\partial \overline{X} }} + \frac{{\overline{UV} }}{{\alpha + \overline{R} }} = - \frac{\alpha }{{\rho (\alpha + \overline{R} )}}\frac{{\partial \overline{P} }}{{\partial \overline{X} }} \\ & + \upsilon \left[ {\frac{1}{{\alpha + \overline{R} }}\frac{\partial }{{\partial \overline{R} }}\left\{ {(\alpha + \overline{R} )\frac{{\partial \overline{U} }}{{\partial \overline{R} }}} \right\} + \left( {\frac{\alpha }{{\alpha + \overline{R} }}} \right)^{2} \frac{{\partial^{2} \overline{U} }}{{\partial \overline{X}^{2} }} - \frac{{\overline{U} }}{{(\alpha + \overline{R} )^{2} }} + \frac{2\alpha }{{(\alpha + \overline{R} )^{2} }}\frac{{\partial \overline{V} }}{{\partial \overline{X} }}} \right] \\ & + (1 - C_{0} )\rho g_{\upalpha} (T - T_{0} ) + (\rho_{\text{p}} - \rho )g_{\upbeta} (C - C_{0} ) - \frac{\mu }{{k_{1} }}\overline{U} , \\ \end{aligned}$$

(2)

$$\begin{aligned} & \frac{\partial T}{{\partial \overline{t} }} + \overline{V} \frac{\partial T}{{\partial \overline{R} }} + \frac{{\overline{U} \alpha }}{{\alpha + \overline{R} }}\frac{\partial T}{{\partial \overline{X} }} = \frac{\kappa }{{(\rho C)_{\text{p}} }}\left[ {\frac{{\partial^{2} T}}{{\partial \overline{R}^{2} }} + \frac{1}{{(\alpha + \overline{R} )}}\frac{\partial T}{{\partial \overline{R} }} + \left( {\frac{\alpha }{{\alpha + \overline{R} }}} \right)^{2} \frac{{\partial^{2} T}}{{\partial \overline{X}^{2} }}} \right] \\ & + \tau \left[ {D_{\text{B}} \left( {\frac{\partial C}{{\partial \overline{R} }}\frac{\partial T}{{\partial \overline{R} }} + \left( {\frac{\alpha }{{\alpha + \overline{R} }}} \right)^{2} \frac{\partial C}{{\partial \overline{X} }}\frac{\partial T}{{\partial \overline{X} }}} \right) + \frac{{D_{\text{T}} }}{{T_{\text{M}} }}\left( {\left( {\frac{\partial T}{{\partial \overline{R} }}} \right)^{2} + \left( {\frac{\alpha }{{\alpha + \overline{R} }}} \right)^{2} \left( {\frac{\partial T}{{\partial \overline{X} }}} \right)^{2} } \right)} \right] \\ & + \frac{\mu }{{(\rho C)_{\text{p}} }}\left[ {4\left( {\frac{{\partial \overline{V} }}{{\partial \overline{R} }}} \right)^{2} + \left( {\frac{{\partial \overline{U} }}{{\partial \overline{R} }} + \frac{{\overline{U} }}{{\alpha + \overline{R} }} + \frac{{\partial \overline{V} }}{{\partial \overline{X} }}} \right)^{2} } \right], \\ \end{aligned}$$

(3)

$$\begin{aligned} & \frac{\partial C}{{\partial \overline{t} }} + \overline{V} \frac{\partial C}{{\partial \overline{R} }} + \frac{{\overline{U} \alpha }}{{\alpha + \overline{R} }}\frac{\partial C}{{\partial \overline{X} }} = D_{\text{B}} \left( {\frac{{\partial^{2} C}}{{\partial \overline{R}^{2} }} + \frac{1}{{\alpha + \overline{R} }}\frac{\partial C}{{\partial \overline{R} }} + \left( {\frac{\alpha }{{\alpha + \overline{R} }}} \right)^{2} \frac{{\partial^{2} C}}{{\partial \overline{X}^{2} }}} \right) \hfill \\ & + \frac{{D^{\text{T}} }}{{T_{\text{M}} }}\left( {\frac{{\partial^{2} T}}{{\partial \overline{R}^{2} }} + \frac{1}{{\alpha + \overline{R} }}\frac{\partial T}{{\partial \overline{R} }} + \left( {\frac{\alpha }{{\alpha + \overline{R} }}} \right)^{2} \frac{{\partial^{2} T}}{{\partial \overline{X}^{2} }}} \right). \hfill \\ \end{aligned}$$

(4)

In above relations, $\rho_{\text{p}}$ indicates density for nanosized particles, $\kappa$ indicates the thermal conductivity, $c_{\text{p}}$ shows specific heat, $C$ is the nanoparticles concentration, $T$ comes for temperature gradient, $\beta$ indicates the expansion within concentration, $k_{1}$ is permeability of free space and $g$ is the gravitational acceleration.

The above equations involve unsteady terms in the fixed frame. To transform them into a steady format, we detach from the static frame to the moving frame $\left( {\bar{r},\bar{x}} \right)$ traveling with the wave speed c. The two frames are connected by the following transformations:

$$\bar{x} = \bar{X} - c\bar{t}, \;\bar{r} = \bar{R},\; \bar{u} = \bar{U} - c,\; \bar{v} = \bar{V}, \; \bar{p} = \bar{P}.$$

The above-defined system of equations can be manipulated in the wave frame as

$$\begin{aligned} & \overline{v} \frac{{\partial \overline{v} }}{{\partial \overline{r} }} + \frac{{\alpha \overline{u} }}{{\alpha + \overline{r} }}\frac{{\partial \overline{v} }}{{\partial \overline{x} }} - \frac{{\overline{u}^{2} }}{{\alpha + \overline{r} }} = - \frac{1}{\rho }\frac{{\partial \overline{p} }}{{\partial \overline{r} }} \\ & + \upsilon \left[ {\frac{1}{{\alpha + \overline{r} }}\frac{\partial }{{\partial \overline{r} }}\left\{ {(\alpha + \overline{r} )\frac{{\partial \overline{v} }}{{\partial \overline{r} }}} \right\} + \left( {\frac{\alpha }{{\alpha + \overline{r} }}} \right)^{2} \frac{{\partial^{2} \overline{v} }}{{\partial \overline{x}^{2} }} - \frac{{\overline{v} }}{{(\alpha + \overline{r} )^{2} }} + \frac{2\alpha }{{(\alpha + \overline{r} )^{2} }}\frac{{\partial \overline{u} }}{{\partial \overline{x} }}} \right], \\ \end{aligned}$$

(5)

$$\begin{aligned} & \overline{v} \frac{{\partial \overline{u} }}{{\partial \overline{r} }} + \frac{{\alpha \overline{u} }}{{\alpha + \overline{r} }}\frac{{\partial \overline{u} }}{{\partial \overline{x} }} + \frac{{\overline{uv} }}{{\alpha + \overline{r} }} = - \frac{\alpha }{{\rho (\alpha + \overline{r} )}}\frac{{\partial \overline{p} }}{{\partial \overline{x} }} \\ & + \upsilon \left[ {\frac{1}{{\alpha + \overline{r} }}\frac{\partial }{{\partial \overline{r} }}\left\{ {(\alpha + \overline{r} )\frac{{\partial \overline{u} }}{{\partial \overline{r} }}} \right\} + \left( {\frac{\alpha }{{\alpha + \overline{r} }}} \right)^{2} \frac{{\partial^{2} \overline{u} }}{{\partial \overline{x}^{2} }} - \frac{{\overline{u} }}{{(\alpha + \overline{r} )^{2} }} + \frac{2\alpha }{{(\alpha + \overline{r} )^{2} }}\frac{{\partial \overline{v} }}{{\partial \overline{x} }}} \right] \\ & + (1 - C_{0} )\rho g_{\upalpha} (T - T_{0} ) + (\rho_{\text{p}} - \rho )g_{\upbeta} (C - C_{0} ) - \frac{\mu }{{k_{1} }}(\overline{u} + c), \\ \end{aligned}$$

(6)

$$\begin{aligned} & - c\frac{\partial T}{{\partial \overline{x} }} + \overline{v} \frac{\partial T}{{\partial \overline{r} }} + \frac{{(\overline{u} + \overline{c} )\alpha }}{{\alpha + \overline{r} }}\frac{\partial T}{{\partial \overline{x} }} = \frac{\kappa }{{(\rho C)_{\rm p} }}\left[ {\frac{{\partial^{2} T}}{{\partial \overline{r}^{2} }} + \frac{1}{{(\alpha + \overline{r} )}}\frac{\partial T}{{\partial \overline{r} }} + \left( {\frac{\alpha }{{\alpha + \overline{r} }}} \right)^{2} \frac{{\partial^{2} T}}{{\partial \overline{x}^{2} }}} \right] \\ & + \tau \left[ {D_{\rm B} \left( {\frac{\partial C}{{\partial \overline{r} }}\frac{\partial T}{{\partial \overline{r} }} + \left( {\frac{\alpha }{{\alpha + \overline{r} }}} \right)^{2} \frac{\partial C}{{\partial \overline{x} }}\frac{\partial T}{{\partial \overline{x} }}} \right) + \frac{{D_{\rm E} }}{{T_{\text{M}} }}\left( {\left( {\frac{\partial T}{{\partial \overline{r} }}} \right)^{2} + \left( {\frac{\alpha }{{\alpha + \overline{r} }}} \right)^{2} \left( {\frac{\partial T}{{\partial \overline{x} }}} \right)^{2} } \right)} \right] \\ & + \frac{\mu }{{(\rho C)_{\text{p}} }}\left[ {4\left( {\frac{{\partial \overline{v} }}{{\partial \overline{r} }}} \right)^{2} + \left( {\frac{{\partial \overline{u} }}{{\partial \overline{r} }} + \frac{{\overline{u} + c}}{{\alpha + \overline{r} }} + \frac{{\partial \overline{v} }}{{\partial \overline{x} }}} \right)^{2} } \right], \\ \end{aligned}$$

(7)

$$\begin{aligned} &- c\frac{\partial C}{{\partial \overline{x} }} + \overline{v} \frac{\partial C}{{\partial \overline{r} }} + \frac{{(\overline{u} + c)\alpha }}{{\alpha + \overline{r} }}\frac{\partial C}{{\partial \overline{x} }} = D_{\text{B}} \left( {\frac{{\partial^{2} C}}{{\partial \overline{r}^{2} }} + \frac{1}{{\alpha + \overline{r} }}\frac{\partial C}{{\partial \overline{r} }} + \left( {\frac{\alpha }{{\alpha + \overline{r} }}} \right)^{2} \frac{{\partial^{2} C}}{{\partial \overline{x}^{2} }}} \right) \\ & + \frac{{D_{\text{T}} }}{{T_{\text{M}} }}\left( {\frac{{\partial^{2} T}}{{\partial \overline{r}^{2} }} + \frac{1}{{\alpha + \overline{r} }}\frac{\partial T}{{\partial \overline{r} }} + \left( {\frac{\alpha }{{\alpha + \overline{r} }}} \right)^{2} \frac{{\partial^{2} T}}{{\partial \overline{x}^{2} }}} \right). \\ \end{aligned}$$

(8)

Now we translate our quantities in dimensionless form by following appropriate transformations

$$\left. \begin{aligned} x & = \frac{{2\pi \overline{x} }}{\lambda },\;\eta = \frac{{\overline{r} }}{a},\;u = \frac{{\overline{u} }}{c},\;v = \frac{{\overline{v} }}{c},\;\text{Re} = \frac{\rho ca}{\mu },\;p = \frac{{2\pi a^{2} }}{\lambda \mu c}\overline{p} ,\;h = \frac{{\overline{H} }}{a},\;\delta = \frac{2\pi a}{\lambda },\;k = \frac{\alpha }{a},\;\phi = \frac{{C - C_{0} }}{{C_{1} - C_{0} }}, \\ \theta & = \frac{{T - T_{0} }}{{T_{1} - T_{0} }},\,{\text{Nt}} = \frac{{\tau D_{\text{T}} T_{0} }}{{T_{\text{M}} }},\,\Pr = \frac{{\mu c_{\text{p}} }}{\kappa },\,{\text{Da}} = \frac{{k_{1} }}{{\eta^{2} }},\,{\text{Ec}} = \frac{{c^{2} }}{{c_{\text{p}} T_{0} }},\,{\text{Nb}} = \frac{{\tau D_{\text{B}} C_{0} }}{\upsilon },\, \\ {\text{Gr}} & = \frac{{(1 - c_{0} )\alpha gT_{0} \eta^{2} }}{c\upsilon },\,{\text{Gc}} = \frac{{(\rho_{\text{p}} \rho )\beta gc_{0} \eta^{2} }}{c\mu }. \\ \end{aligned} \right)$$

Incorporating the above non-dimensional parameters in Eqs. (4), (5) and (6), and then adopting the limitation for extensive wavelength $({\text{i}} . {\text{e}} .,\;\delta \approx 0(1))$ along with low Reynolds number $(\text{Re} \approx 0(1))$, following resulting form of the governing equations is secured:

$$\frac{\partial p}{\partial r} = 0,$$

(9)

$$- \frac{k}{\eta + k}\frac{\partial p}{\partial x} + \frac{1}{(\eta + k)}\frac{\partial }{\partial \eta }\left[ {(\eta + k)\left( {\frac{\partial u}{\partial \eta }} \right)} \right] - \left[ {\frac{(u + 1)}{{(\eta + k)^{2} }}} \right] + {\text{Gr}}\theta + {\text{Gc}}\phi - \frac{(u + 1)}{\text{Da}} = 0,$$

(10)

$$\frac{1}{\Pr }\left( {\frac{{\partial^{2} \theta }}{{\partial \eta^{2} }}\frac{1}{(\eta + k)}\frac{\partial \theta }{\partial \eta }} \right) + {\text{Ec}}\left( {\frac{\partial u}{\partial \eta } - \frac{(u + 1)}{(\eta + k)}} \right)^{2} + {\text{Nb}}\left( {\frac{\partial \theta }{\partial \eta }\frac{\partial \phi }{\partial \eta }} \right) + {\text{Nt}}\left( {\frac{\partial \theta }{\partial \eta }} \right)^{2} = 0,$$

(11)

$$\frac{{\partial ^{2} \phi }}{{\partial \eta ^{2} }} + \frac{1}{{(\eta + k)}}\frac{{\partial \phi }}{{\partial \eta }} + \frac{{{\text{Nt}}}}{{{\text{Nb}}}}\left( {\frac{{\partial ^{2} \theta }}{{\partial \eta ^{2} }} + \frac{1}{{(\eta + k)}}\frac{{\partial \theta }}{{\partial \eta }}} \right) = 0.$$

(12)

The dimensionless second-order slip boundary conditions for the current analysis have the following form [25]

$$\left. \begin{aligned} & u = \mp \beta_{1} \frac{\partial u}{\partial \eta } \mp \beta_{2} \frac{{\partial^{2} u}}{{\partial \eta^{2} }} - 1 {\text{ at }}\eta = \pm h = \pm (1 + \phi^{\prime } \sin x), \hfill \\ & \theta \pm \gamma \frac{\partial \theta }{\partial \eta } = \left\{ {\begin{array}{*{20}l} {0\,{\text{at }}\eta = h} \\ {1\,{\text{at }}\eta = - h,} \\ \end{array} } \right. \, \hfill \\ & \phi \pm \gamma_{1} \frac{\partial \phi }{\partial \eta } = \left\{ {\begin{array}{*{20}l} {0\,{\text{at }}\eta = h} \\ {1\,{\text{at }}\eta = - h,} \\ \end{array} } \right. \hfill \\ \end{aligned} \right\}$$

(13)

where $\beta_{1} , \beta_{2} , \gamma$ and $\gamma_{1}$ stand for the first-order, second-order, thermal and concentration slip parameter, correspondingly.

Analytical solutions

Above obtained governing expressions are coupled and are very complicated differential equations with complex boundary conditions that cannot be solved directly by any appropriate exact method, so we handle the issue by highly converging analytical technique [36]. The homotopy equations for above-defined unknowns are summarized as below:

$$\left. {\begin{array}{*{20}l} {\left( {1 - \tilde{\lambda }} \right){\rm E}\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{u} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{u} _{0} } \right) + \tilde{\lambda }\left( { - \frac{k}{{\eta + k}}\frac{{\partial p}}{{\partial x}} + \frac{1}{{(\eta + k)}}\frac{\partial }{{\partial \eta }}\left[ {(\eta + k)\left( {\frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{u} }}{{\partial \eta }}} \right)} \right] - \left[ {\frac{{(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{u} + 1)}}{{(\eta + k)^{2} }}} \right] + {\text{Gr}}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\theta } + {\text{Gc}}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varphi } - \frac{{(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{u} + 1)}}{{{\text{Da}}}}} \right) = 0,} \hfill \\ {\left( {1 - \tilde{\lambda }} \right){\rm E}\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\theta } - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\theta } _{0} } \right) + \tilde{\lambda }\left( {\frac{1}{{{\text{Pr}}}}\left( {\frac{{\partial ^{2} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\theta } }}{{\partial \eta ^{2} }}\frac{1}{{(\eta + k)}}\frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\theta } }}{{\partial \eta }}} \right) + {\text{Ec}}\left( {\frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{u} }}{{\partial \eta }} - \frac{{(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{u} + 1)}}{{(\eta + k)}}} \right)^{2} + {\text{Nb}}\left( {\frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\theta } }}{{\partial \eta }}\frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varphi } }}{{\partial \eta }}} \right) + {\text{Nt}}\left( {\frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\theta } }}{{\partial \eta }}} \right)^{2} } \right) = 0,} \hfill \\ {\left( {1 - \tilde{\lambda }} \right){\rm E}\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varphi } - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varphi } _{0} } \right) + \tilde{\lambda }\left( {\frac{{\partial ^{2} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varphi } }}{{\partial \eta ^{2} }} + \frac{1}{{(\eta + k)}}\frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varphi } }}{{\partial \eta }} + \frac{{{\text{Nt}}}}{{{\text{Nb}}}}\left( {\frac{{\partial ^{2} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\theta } }}{{\partial \eta ^{2} }} + \frac{1}{{(\eta + k)}}\frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\theta } }}{{\partial \eta }}} \right)} \right) = 0.} \hfill \\ \end{array} } \right\}$$

(14)

Above revealed factors $\tilde{\lambda },\;E,\;{\check{u}},\;{\check{\theta }},\;\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\phi } ,\;\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{u} _{0} ,\;\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\theta } _{0} ,\;{\check{\phi }}_{0}$ are currently representing the embedding parameter, the linear operator, proposed solutions for velocity, temperature distribution and nanoparticles concentration and their corresponding initial guesses, respectively. The linear operator E used here is given as $E = {\raise0.7ex\hbox{${\partial^{2} }$} \!\mathord{\left/ {\vphantom {{\partial^{2} } {\partial \eta^{2} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\partial \eta^{2} }$}}$, and the initial guesses are considered as

$${\check{u}}_{0} = \frac{1}{2}\left({- h^{2} + \eta^{2} - 2h\beta_{1} - \frac{{2\eta \beta_{2}}}{{h + \beta_{1}}}} \right),{\check{\theta}}_{0} = {\check{\phi}}_{0} = \frac{1}{2} - \frac{\eta}{{2\left({h + \gamma} \right)}}.$$

At this stage, we propose the following series form solutions:

$${\check{u}} = u_{0} + \tilde{\lambda}u_{1} + \tilde{\lambda}^{2} u_{2} + \cdots$$

$${\check{\theta}} = \theta_{0} + \tilde{\lambda}\theta_{1} + \tilde{\lambda}^{2} \theta_{2} + \cdots$$

$${\check{\phi}} = \phi_{0} + \tilde{\lambda}\phi_{1} + \tilde{\lambda}^{2} u\phi_{2} + \cdots$$

We incorporate the above expressions in equations defined in (14). By equating the powers of $\tilde{\lambda}$, we get the systems of differential equations which can be solved easily on Mathematica or any other mathematical software. The solutions for the velocity component u, the temperature profile $\theta$ and the nanoparticles concentration $\phi$ for $\lambda \to 1,$ have been acquired as

$$\begin{aligned} & u = \frac{1}{2}\left( { - h^{2} + \eta^{2} - 2h\beta_{1} - \frac{{2\eta \beta_{2} }}{{h + \beta_{1} }}} \right) + C_{1} + \eta C_{2} - \frac{1}{{2{\text{Da}}\left( {h + \gamma } \right)\left( {h + \beta_{1} } \right)}}(2{\text{Da}}k{\text{d}}p / {\text{d}}x \\ & \left( {h + \gamma } \right)\eta \left( {h + \beta_{1} } \right) - \frac{1}{12}\left( {h + \gamma } \right)\eta^{4} \left( {h + \beta_{1} } \right) - 2{\text{Da}}k^{2} {\text{d}}p / {\text{d}}x\left( {h + \gamma } \right){\text{Log}}\left[ {k + \eta } \right]\left( {h + \beta_{1} } \right) \\ & - \frac{{2{\text{Da}}k{\text{d}}p}}{{{\text{d}}x\left( {h + \gamma } \right)\eta {\text{Log}}\left[ {k + \eta } \right]\left( {h + \beta_{1} } \right)}} + \frac{1}{2}\left( {h + \gamma } \right)\eta^{2} \left( {h + \beta_{1} } \right) \\ & \left( {{\text{Da}}\left( {3 + {\text{Gc}} + {\text{Gr}}} \right) + h^{2} + 2h\beta_{1} } \right) + {\text{Da}}\left( {h + \gamma } \right){\text{Log}}\left[ {k + \eta } \right]( - \left( {h + \beta_{1} } \right) \\ & \left( {h^{2} - k^{2} + 2h\beta_{1} } \right) + 2k\beta_{2} ) + \frac{1}{6}\eta^{3} \left( { - {\text{Da}}\left( {{\text{Gc}} + {\text{Gr}}} \right)\left( {h + \beta_{1} } \right) + 2\left( {h + \gamma } \right)\beta_{2} } \right)), \\ \\ \end{aligned}$$

$$\begin{aligned} & \theta = \frac{1}{2} - \frac{\eta }{{2\left( {h + \gamma } \right)}} + C_{3} + \eta C_{4} - \frac{1}{{12\left( {h + \gamma } \right)^{2} \left( {h + \beta_{1} } \right)^{2} }}(6\left( {h + \gamma } \right)\eta \left( {h + \beta_{1} } \right)^{2} + {\text{Ec}}k\Pr \\ & \left( {h + \gamma } \right)^{2} \eta^{3} \left( {h + \beta_{1} } \right)^{2} + \frac{1}{4}{\text{Ec}}\Pr \left( {h + \gamma } \right)^{2} \eta^{4} \left( {h + \beta_{1} } \right)^{2} - 6\left( {h + \gamma } \right)\eta {\text{Log}}\left[ {k + \eta } \right] \\ & \left( {h + \beta_{1} } \right)^{2} + \left( {h + \beta_{1} } \right)(h\left( {{\text{Nb}} + {\text{Nt}} + {\text{Ec}}\left( {2h^{2} - k^{2} } \right)\left( {h + \gamma } \right)^{2} } \right) + \beta_{1} ({\text{Nb}} + {\text{Nt}} + {\text{Ec}}(6h^{2} \\ & - k^{2} )\left( {h + \gamma } \right)^{2} + 4{\text{Ec}}h\left( {h + \gamma } \right)^{2} \beta_{1} ) - 4 - k\left( {h + \gamma } \right)^{2} \beta_{2} ) - 3\left( {h + \gamma } \right) {\text{Log}}\left[ {k + \eta } \right](h^{2} (2k \\ & + {\text{Ec}}h^{4} \Pr \left( {h + \gamma } \right) - 2{\text{Ec}}h^{2} k^{2} \Pr \left( {h + \gamma } \right) + {\text{Ec}}k^{4} \Pr \left( {h + \gamma } \right)) + 4{\text{Ec}}h\left( {3h^{2} - k^{2} } \right)\Pr \left( {h + \gamma } \right)\beta_{1}^{3} \\ & + 4{\text{Ec}}h^{2} \Pr \left( {h + \gamma } \right)\beta_{1}^{4} + 4{\text{Ec}}k\Pr \left( {h + \gamma } \right)\beta_{2} \left( { - h^{3} + hk^{2} + k\beta_{2} } \right) + \beta_{1}^{2} (2k + 13{\text{Ec}}h^{4} \Pr \left( {h + \gamma } \right) \\ & - 10{\text{Ec}}h^{2} k^{2} \Pr \left( {h + \gamma } \right) + {\text{Ec}}k^{4} \Pr \left( {h + \gamma } \right) - 8{\text{Ec}}hk\Pr \left( {h + \gamma } \right)\beta_{2} ) + 2\beta_{1} (h(2k + 3Ech^{4} \Pr \\ & \left( {h + \gamma } \right) - 4{\text{Ec}}h^{2} k^{2} \Pr \left( {h + \gamma } \right) + {\text{Ec}}k^{4} \Pr \left( {h + \gamma } \right)) + 2{\text{Ec}}k\left( { - 3h^{2} + k^{2} } \right)\Pr \left( {h + \gamma } \right)\beta_{2} ))), \\ \\ \end{aligned}$$

$$\phi = \frac{1}{2} - \frac{\eta }{{2\left( {h + \gamma_{1} } \right)}} + C_{5} + \eta C_{6} + \frac{{\left( {{\text{Nb}} + {\text{Nt}}} \right)\left( { - \eta + \left( {k + \eta } \right){\text{Log}}\left[ {k + \eta } \right]} \right)}}{{2{\text{Nb}}\left( {h + \gamma_{1} } \right)}},$$

where the constants $C_{i} , \;i = 1,2,3,4,5,6$ are given in “Appendix.”

The expression of $\frac{{{\text{d}}p}}{{{\text{d}}x}}$ in the form of mean flow rate $Q$ can be evaluated as

$$\begin{aligned} & \frac{{{\text{d}}p}}{{{\text{d}}x}} = (3( - {\text{Da}}h(2\left( {{\text{Gc}}h^{5} \pi + {\text{Gr}}h^{5} \pi + 5\left( {h + \gamma } \right)\left( { - 3hk^{3} \pi - 3Q + h^{3} \pi \left( {3k + 4C_{2} } \right)} \right)} \right) \\ & + 15\left( {h^{2} - k^{2} } \right)^{2} \pi \left( {h + \gamma } \right)\left( { - {\text{Log}}\left[ { - h + k} \right] + {\text{Log}}\left[ {h + k} \right]} \right)) - {\text{Da}}(2({\text{Gc}}h^{5} \pi + {\text{Gr}}h^{5} \pi \\ & + 5\left( {h + \gamma } \right)\left( { - 3hk^{3} \pi - 3Q + h^{3} \pi \left( {9k + 4C_{2} } \right)} \right)) + 15\left( {3h^{4} - 4h^{2} k^{2} + k^{4} } \right)\pi \left( {h + \gamma } \right) \\ & \left( { - {\text{Log}}\left[ { - h + k} \right] + Log\left[ {h + k} \right]} \right))\beta_{1} + 30{\text{Da}}h\pi \left( {h + \gamma } \right)( - 2hk + \left( {h - k} \right)\left( {h + k} \right) \\ & \left( {{\text{Log}}\left[ { - h + k} \right] - {\text{Log}}\left[ {h + k} \right]} \right))\beta_{1}^{2} + 2\pi \left( {h + \gamma } \right)(2h\left( {h^{4} + 5{\text{Da}}\left( {2h^{2} + 3k^{2} } \right)} \right) + 15{\text{Da}}k \\ & \left( { - h^{2} + k^{2} } \right)\left( {{\text{Log}}\left[ { - h + k} \right] - {\text{Log}}\left[ {h + k} \right]} \right))\beta_{2} ))/(10{\text{Da}}k\pi \left( {h + \gamma } \right)( - 16h^{3} + 6hk^{2} \\ & + 3\left( {h - k} \right)^{2} \left( {2h + k} \right){\text{Log}}\left[ { - h + k} \right] + 3\left( {2h - k} \right)\left( {h + k} \right)^{2} {\text{Log}}\left[ {h + k} \right])\left( {h + \beta_{1} } \right)) \\ \end{aligned}$$

Numerical Solutions

The pressure increase $\Delta p$ over per unit wavelength $\lambda$ is characterized as

$$\Delta p = \mathop \int \limits_{0}^{\lambda } \left( {\frac{{{\text{d}}p}}{{{\text{d}}x}}} \right){\text{d}}x.$$

Here the definite integral cannot be evaluated easily because the expression ${\text{d}}p / {\text{d}}x$ contains logarithmic terms, so it is evaluated numerically by numerical integration (NIntegrate) technique in Mathematica. The data obtained for $\Delta p$ against the flow rate $- 1 < Q < 1$ under the varying values of $\beta_{1} \;{\text{and}}\; \beta_{2}$ by retaining other parameters fixed are given in the following Table 1.

Table 1 Data of $\Delta p \;{\text{for}}\; Q$ against $\beta_{1}$ and $\beta_{2}$

Graphical results and explanation

In above analysis, we have analyzed the analytical investigation of nanofluid concentration through a curved channel having porous medium by considering second-order partial slip at the surfaces. In this section, we have described the outcomes for several physical parameters on considerable quantities, the pressure rise, nanoparticles concentration, temperature distribution and velocity profile by drawing graphs under the variation of pertinent parameters. For this purpose, we have presented the graphs of obtained quantities in Figs. 1–16. Figures 1–3 reflect the graphs of pressure rise $\Delta p$ against the domain of flow rate $Q$ to examine the effects of $\beta_{1} ,\beta_{2} \;{\text{and}}\;{\text{Da}}$. In Figs. 4–6, the graphs for nanoparticle concentration $\phi$ have been sketched against independent variable $\eta$ under the variety of $\gamma_{1} ,{\text{Nb }}\;{\text{and}}\;{\text{Nt}}$. The temperature profile $\theta$ along $\eta$ has been portrayed in Figs. 7–11 with the variation of $\beta_{1} ,\beta_{2} ,{\text{Nb}},\;{\text{Nt}}\; {\text{and}}\;\gamma$. From Figs. 12–16, we can suggest the behavior of velocity profile $u$ plotted with radial coordinate $\eta$ along the changing magnitudes of $\beta_{1} ,\;\beta_{2} ,\;{\text{Da}},\;{\text{Gc}}\;{\text{and}}\;{\text{Gr}}.$

Fig. 1

Alteration of $\Delta p$ for $\beta_{1}$ for fixed $\gamma = 2,\;{\text{Gr}} = 0.3,\;\beta_{2} = 0.3,\;{\text{Da}} = 0.2,\;{\text{Gc}} = 1,\;k = 2,\;\phi^{\prime } = 0.6.$

Pressure rise phenomenon

Figure 1 is plotted to examine the change in $\Delta p$ with different magnitude of slip parameter $\beta_{1}$. It is noticed here that in the pumping region $(\Delta p > 0$, the pressure rise enhances but in the augmented pumping area, it declines with the increase in values of the slip parameter $\beta_{1}$. It is decided from this plot that slip of the walls affects the peristaltic pumping and gives the free pumping at $\Delta p = - 20$. The effect of parameter $\beta_{2}$ on $\Delta p$ has been reported as within the pumping region pressure rise decreases and in domain $Q \in [0.3 - 2],\,\,\Delta p$ gives linear relation with $\;\beta_{2}$, allowing free pumping region to be at $\Delta p = 0$ (see Fig. 2). In Fig. 3, we can see that there is no free pumping region, i.e., the region at which pressure rise curves cross each other. The profile of $\Delta p$ decreases with porosity parameter Da throughout the region.

Fig. 2

Alteration of $\Delta p$ for $\beta_{2}$ for fixed $\gamma = 2,\;{\text{Gr}} = 0.3,\;\beta_{1} = 0.3,\;{\text{Da}} = 0.2,\;{\text{Gc}} = 1,\;k = 2,\;\phi^{\prime } = 0.6.$

Fig. 3

Alteration of $\Delta p$ for $Da$ for fixed $\gamma = 2,\;{\text{Gr}} = 0.3,\;\beta_{1} = 0.1,\;\beta_{2} = 0.2,\;{\text{Gc}} = 1,\;k = 2,\;\phi^{\prime } = 0.1.$

Nanoparticles concentration

Figures 4–6 have been drawn to examine the behavior of $\emptyset$ under the variation of slip parameter $\gamma_{1} , \;{\text{Brownian}}\;{\text{parameter}}\;{\text{Nb}}\;{\text{and}}\;{\text{thermopherosis}} \;{\text{Nt}}$, respectively. It is depicted from Fig. 4 that $\emptyset$ is behaving inversely with the increasing amount of $\gamma_{1}$ in the region lower to the central line and in the neighborhood of center on upper side while giving opposite relation in the upper portion of the channel. Figure 5 suggests that Brownian motion parameter Nb is describing increasing characteristics on the profile of nanoparticles concentration throughout the considered channel which is in line with the physical happening that Brownian motion generates the more dense amount of nanoparticles. We can observe from Fig. 6 that there is an inverse relation between nanoparticles concentration and thermophoresis parameter Nt everywhere in the channel as physically thermophoresis accounts for starting the mechanism of diffusion, which is also in accordance with the findings reported in a numerical investigation [26].

Fig. 4

Alteration of $\phi$ for $\gamma_{1}$ for fixed $\beta_{1} = 0.1,$ $\beta_{2} = 0.1,$ $x = 0.2,$ $Q = 2,$ ${\text{Nt}} = 0.1,$ $\Pr = 0.1,$ ${\text{Da}} = 0.1,$ ${\text{Nb}} = 1,$ ${\text{Ec}} = 1,$ $k = 2,$ $\phi^{\prime } = 0.1.$

Fig. 5

Alteration of $\phi$ for ${\text{Nb}}$ for fixed $\beta_{1} = 0.1,$ $\beta_{2} = 0.1,$ $x = 2,$ $Q = 2,$ ${\text{Nt}} = 1,$ $\Pr = 0.5,$ ${\text{Da}} = 0.1,$ $\gamma_{1} = 1,$ ${\text{Ec}} = 1,$ $k = 2,$ $\phi^{\prime } = 0.3.$

Fig. 6

Alteration of $\phi$ for ${\text{Nt}}$ for fixed $\beta_{1} = 0.1,$ $\beta_{2} = 0.1,$ $x = 0.2,$ $Q = 2,$ $\gamma_{1} = 0.1,$ $\Pr = 0.5,$ ${\text{Da}} = 0.1,$ ${\text{Nb}} = 1,$ ${\text{Ec}} = 1,$ $k = 2,$ $\phi^{\prime } = 0.3.$

Temperature profile

From Figs. 7 and 8, it is concluded that temperature profile $\theta$ is rising with the increase in first-order slip parameter $\beta_{1}$. But the variation is small as noticed on the lower side of the channel when contrasted with the upper portion which is totally against the behavior of temperature gradient under the increasing values of the second-order slip parameter $\beta_{2}$. It is noticed from Figs. 9 and 10 that Brownian motion parameter Nb and thermophoresis parameter Nt are affecting the temperature distribution in an increasing fashion which reflects that more energy is produced under the variation of these two parameters. From Fig. 11, it is obvious that slip parameter $\gamma$ is lowering the temperature gradient in lower edge but affecting in opposite manner in the central and upper fields.

Fig. 7

Alteration of $\theta$ for $\beta_{1}$ for fixed ${\text{Nt}} = 1,$ $\beta_{2} = 0.1,$ $x = 0.2,$ $Q = 2,$ $\gamma = 0.5,$ $\Pr = 0.5,$ ${\text{Da}} = 0.1,$ ${\text{Nb}} = 0.1,$ ${\text{Ec}} = 1,$ $k = 2,$ $\phi^{\prime } = 0.2.$

Fig. 8

Alteration of $\theta$ for $\beta_{2}$ for fixed $\beta_{1} = 0.3,$ ${\text{Nt}} = 1,$ $x = 0.2,$ $Q = 2,$ $\gamma = 0.3,$ $\Pr = 0.5,$ ${\text{Da}} = 0.1,$ ${\text{Nb}} = 0.1,$ ${\text{Ec}} = 1,$ $k = 1.1,$ $\phi^{\prime } = 0.1.$

Fig. 9

Alteration of $\theta$ for $N_{b}$ for fixed $\beta_{1} = 0.3,$ $Nt = 0.5,$ $x = 0.2,$ $Q = 2,$ $\gamma = 0.3,$ $\Pr = 0.5,$ $Da = 0.1,$ $Ec = 1,$ $\beta_{2} = 0.1,$ $k = 1.1,$ $\phi ' = 0.1.$

Fig. 10

Alteration of $\theta$ for ${\text{Nt}}$ for fixed $\beta_{1} = 0.3,$ ${\text{Ec}} = 1,$ $x = 0.2,$ $Q = 2,$ $\gamma = 0.3,$ $\Pr = 0.5,$ ${\text{Da}} = 0.1,$ ${\text{Nb}} = 0.5,$ $\beta_{2} = 0.1,$ $k = 1.1,$ $\phi^{\prime } = 0.1.$

Fig. 11

Alteration of $\theta$ for $\gamma$ for fixed $\beta_{1} = 0.2,$ ${\text{Ec}} = 1,$ $x = 0.2,$ $Q = 2,$ $\Pr = 0.5,$ ${\text{Nt}} = 0.1,$ ${\text{Da}} = 0.1,$ ${\text{Nb}} = 0.5,$ $\beta_{2} = 0.1,$ $k = 1.1,$ $\phi^{\prime } = 0.1.$

Velocity field

Figures 12–16 have been presented to measure the impacts of parameters $\beta_{1} ,\; \beta_{2} ,\;{\text{Da}},\;{\text{Gc}}\;{\text{and}}\;{\text{Gr}},$, respectively, on velocity field $u$. From all these diagrams, it is obtained clearly that velocity profile is varying in parabolic format. Figures 12 and 13 analyze that velocity has gone to increase under the slip parameter $\beta_{1}$ but goes down with the second-order slip factor $\beta_{2}$ due to increase in viscosity under the influence of greater second-order partial slip. The impact of porous medium on fluid velocity can be analyzed from Fig. 14. It accounts for the observation that velocity is depending upon porosity in inverse proportion which is due to the physical aspect that more pores in the surface will affect the flow in reducing its speed causing much liquid to be saturated in pores and exerting a resistance to the velocity. It is evaluated from Figs. 15 and 16 which is admitting the characteristics of fluid velocity for various increasing influence of respective local nanoparticle Grashof number Gc and local temperature Grashof number Gr with the domain of radial component $\eta$, that more the magnitudes of Gc and Gr, more faster is the fluid flow which is due to the decrease in viscosity under nanoparticles heat and mass transfer.

Fig. 12

Alteration of $u$ for $\beta_{1}$ for fixed $x = 0.2,$ $Q = 2,$ ${\text{Gr}} = 1,$ $\gamma = 0.2,$ ${\text{Da}} = 0.2,$ ${\text{Gc}} = 1,$ ${\text{Nb}} = 0.5,$ $\beta_{2} = 0.2,$ $k = 2,$ $\phi^{\prime } = 0.1.$

Fig. 13

Alteration of $u$ for $\beta_{2}$ for fixed $x = 0.2,$ $Q = 2,$ ${\text{Gr}} = 1,$ $\gamma = 0.2,$ ${\text{Da}} = 0.2,$ ${\text{Gc}} = 1,$ ${\text{Nb}} = 0.5,$ $\beta_{1} = 0.2,$ $K = 2,$ $\phi^{\prime } = 0.1.$

Fig. 14

Alteration of $u$ for i for fixed $x = 0.2,$ $Q = 2,$ ${\text{Gr}} = 1,$ $\gamma = 0.2,$ ${\text{Da}} = 0.2,$ ${\text{Gc}} = 1,$ ${\text{Nb}} = 0.5,$ $\beta_{2} = 0.2,$ $k = 2,$ $\phi = 0.1.$

Fig. 15

Alteration of $u$ for ${\text{Gc}}$ for fixed $x = 0.2,$ $Q = 2,$ $Gr = 1,$ $\gamma = 0.2,$ ${\text{Da}} = 0.2,$ $\beta_{1} = 0.1,$ ${\text{Nb}} = 0.5,$ $\beta_{2} = 0.2,$ $k = 2,$ $\phi^{\prime } = 0.1.$

Fig. 16

Alteration of $u$ for ${\text{Gr}}$ for fixed $x = 0.2,$ $Q = 2,$ $\beta_{1} = 0.1,$ $\gamma = 0.2,$ ${\text{Da}} = 0.2,$ $Gc = 1,$ $\beta_{2} = 0.2,$ $k = 2,$ $\phi^{\prime } = 0.1.$

Conclusions

The above all discussion depicts the investigation for peristaltic flow for nanofluid in a curved channel via considering second-order slip at the walls beneath the constraints for lengthy wavelength as well as low Reynolds numerals. From above study, the following key points are deduced.

• 1. The pressure rise profile is increasing with $\beta_{1}$ in half region and decreasing in rest of the domain, while opposite behavior is seen with ${\text{Da}}$ and $\beta_{2}$.

• 2. The nanoparticles concentration decreases with $\gamma_{1} \;{\text{and}}\;{\text{Nt}}$ while increases with ${\text{Nb}} .$

• 3. It is concluded that the temperature profile $\theta$ gets increased with $\beta_{1}$ and $\gamma$; however, it decreases with $\beta_{2}$.

• 4. It is seen that the velocity $u$ is increasing with $\beta_{1}$ and ${\text{Gr}}$, but inverse behavior is reported for the parameters $\beta_{2}$, ${\text{Da}}$ and ${\text{Gr}}$.

• 5. It is finally observed that the slip parameters $\beta_{1}$ and $\beta_{2}$ have totally opposite readings for whole the analysis.

Appendix

The constants used in solutions are elaborated as

$$\begin{aligned} & C_{1} = \frac{1}{{24{\text{Da}}\left( {h - k} \right)^{2} \left( {h + k} \right)^{2} \left( {h + \gamma } \right)\left( {h + \beta_{1} } \right)}}(h\left( {h - k} \right)^{2} \left( {h + k} \right)^{2} \left( {h + \gamma } \right)(6{\text{Da}}(3 + {\text{Gc}} \\ & + {\text{Gr}})h^{2} + 5h^{4} - 6{\text{Da}}\left( {h - k} \right)\left( {h + k - 2k{\text{d}}p / {\text{d}}x} \right){\text{Log}}\left[ { - h + k} \right] - 6{\text{Da}}\left( {h + k} \right)(h - k \\ & + 2k{\text{d}}p / {\text{d}}x){\text{Log}}\left[ {h + k} \right]) - 24h^{2} \left( {h - k} \right)\left( {h + k} \right)\left( {{\text{Da}} - h^{2} + k^{2} } \right)\left( {h + \gamma } \right)\beta_{1}^{3} + 4\left( {h + \gamma } \right) \\ & \beta_{1}^{2} (\left( {h - k} \right)\left( {h + k} \right)(3{\text{Da}}\left( {{\text{Gc}} + {\text{Gr}}} \right)h^{3} - 3{\text{Da}}\left( {2 + {\text{Gc}} + {\text{Gr}}} \right)hk^{2} + 11h^{3} \left( {h - k} \right)\left( {h + k} \right) \\ & - 3{\text{Da}}\left( {h - k} \right)\left( {h + k} \right)\left( {\left( {h - k{\text{d}}p / {\text{d}}x} \right){\text{Log}}\left[ { - h + k} \right] + \left( {h + k{\text{d}}p / {\text{d}}x} \right){\text{Log}}\left[ {h + k} \right]} \right)) - 12{\text{Da}} \\ & h^{2} k\beta_{2} ) + 12\beta_{2} ( - {\text{Da}}\left( {h - k} \right)\left( {h + k} \right)(h^{2} ({\text{Gc}}\left( {h - k} \right)\left( {h + k} \right) + {\text{Gr}}\left( {h - k} \right)\left( {h + k} \right) + 2k \\ & d\left( {1 + p/{\text{d}}x} \right)\left( {h + \gamma } \right)) + k\left( { - h^{2} + k^{2} } \right)\left( {h + \gamma } \right)\left( {{\text{Log}}\left[ { - h + k} \right] + {\text{Log}}\left[ {h + k} \right]} \right)) + 2h(2{\text{Da}}k^{2} \\ & + \left( {h^{2} - k^{2} } \right)^{2} )\left( {h + \gamma } \right)\beta_{2} ) + \beta_{1} (\left( {h - k} \right)^{2} \left( {h + k} \right)^{2} \left( {h + \gamma } \right)(6{\text{Da}}\left( {7 + 3{\text{Gc}} + 3{\text{Gr}}} \right)h^{2} + 25h^{4} \\ & + 6{\text{Da}}\left( { - 3h^{2} + k^{2} \left( {1 - 2{\text{d}}p/{\text{d}}x} \right) + 4hk{\text{d}}p/{\text{d}}x} \right){\text{Log}}\left[ { - h + k} \right] - 6{\text{Da}}(3h^{2} - k^{2} + 2k(2h \\ & + k){\text{d}}p/{\text{d}}x){\text{Log}}\left[ {h + k} \right]) - 12{\text{Da}}h({\text{Gc}}\left( {h^{2} - k^{2} } \right)^{2} + {\text{Gr}}\left( {h^{2} - k^{2} } \right)^{2} + 2k( - k^{2} p + h^{2} (2 \\ & + {\text{d}}p/{\text{d}}x))\left( {h + \gamma } \right))\beta_{2} )), \\ \end{aligned}$$

$$\begin{aligned} & C_{2} = \frac{1}{{12\left( {h + \gamma } \right)\left( {h + \beta_{1} } \right)^{2} }}(h(h\left( {h\left( { - \left( {{\text{Gc}} + {\text{Gr}}} \right)h + 12kdp/dx} \right) + 12k{\text{d}}p/{\text{d}}x\gamma } \right) + 3\left( {h + \gamma } \right) \\ & \left( {\left( {h - k} \right)\left( {h + k - 2k{\text{d}}p/{\text{d}}x} \right){\text{Log}}\left[ { - h + k} \right] - \left( {h + k} \right)\left( {h + k\left( { - 1 + 2{\text{d}}p/{\text{d}}x} \right)} \right){\text{Log}}\left[ {h + k} \right]} \right)) \\ & + \frac{1}{{{\text{Da}}\left( {h^{2} - k^{2} } \right)^{2} }}(12{\text{Da}}h\left( {h - k} \right)k\left( {h + k} \right)\left( {h + \gamma } \right)\beta_{1}^{3} + 2\left( {h + \gamma } \right)\beta_{2} (\left( {h - k} \right)\left( {h + k} \right)(h \\ & \left( {h^{2} \left( {h - k} \right)\left( {h + k} \right) + 3{\text{Da}}\left( {\left( {4 + {\text{Gc}} + {\text{Gr}}} \right)h^{2} - k^{2} \left( {2 + {\text{Gc}} + {\text{Gr}} - 2{\text{d}}p/{\text{d}}x} \right)} \right)} \right) + 3{\text{Da}}k( - h^{2} \\ & + k^{2} )\left( {{\text{Log}}\left[ { - h + k} \right] - {\text{Log}}\left[ {h + k} \right]} \right)) - 6{\text{Da}}k\left( {h^{2} + k^{2} } \right)\beta_{2} ) - 3\beta_{1}^{2} ({\text{Da}}\left( {h - k} \right)\left( {h + k} \right)({\text{Gc}}h^{2} \\ & \left( {h - k} \right)\left( {h + k} \right) + {\text{Gr}}h^{2} \left( {h - k} \right)\left( {h + k} \right) + 2k\left( { - 3h^{2} + k^{2} } \right)\left( {h + \gamma } \right) - 2\left( {h - k} \right)\left( {h + k} \right)\left( {h + \gamma } \right) \\ & \left( {\left( {h - k{\text{d}}p/{\text{d}}x} \right){\text{Log}}\left[ { - h + k} \right] - \left( {h + k{\text{d}}p/{\text{d}}x} \right){\text{Log}}\left[ {h + k} \right]} \right)) - 4h\left( {\left( {h^{2} - k^{2} } \right)^{2} + {\text{Da}}\left( {h^{2} + k^{2} } \right)} \right) \\ & \left( {h + \gamma } \right)\beta_{2} ) + \beta_{1} ( - {\text{Da}}\left( {h - k} \right)^{2} \left( {h + k} \right)^{2} (2h\left( {2{\text{Gc}}h^{2} + 2{\text{Gr}}h^{2} - 3k\left( {1 + 2{\text{d}}p/{\text{d}}x} \right)\left( {h + \gamma } \right)} \right) \\ & + 3\left( {h + \gamma } \right)(\left( { - 3h^{2} + k^{2} \left( {1 - 2{\text{d}}p/{\text{d}}x} \right) + 4hk{\text{d}}p/{\text{d}}x} \right){\text{Log}}\left[ { - h + k} \right] + (3h^{2} + 4hk{\text{d}}p/{\text{d}}x + k^{2} \\ & \left( { - 1 + 2{\text{d}}p/{\text{d}}x} \right)){\text{Log}}\left[ {h + k} \right])) + 6(3\left( {h^{3} - hk^{2} } \right)^{2} + {\text{Da}}(\left( {6 + {\text{Gc}} + {\text{Gr}}} \right)h^{4} + k^{4} (4 + {\text{Gc}} + {\text{Gr}} \\ & - 2{\text{d}}p/{\text{d}}x) - 2h^{2} k^{2} \left( {3 + {\text{Gc}} + {\text{Gr}} - p} \right)))\left( {h + \gamma } \right)\beta_{2} ))), \\ \end{aligned}$$

$$\begin{aligned} & C_{3} = \frac{1}{{48\left( {h - k} \right)\left( {h + k} \right)\left( {h + \gamma } \right)^{2} \left( {h + \beta_{1} } \right)^{2} }}(h^{2} \left( {h - k} \right)\left( {h + k} \right)( - h{ \Pr }(6\left( {{\text{Nb}} + {\text{Nt}}} \right)\left( {h + 2\gamma } \right) \\ & + {\text{Ec}}h\left( {h + \gamma } \right)^{2} \left( {13h^{2} - 6k^{2} + 16h\gamma } \right)) + 6\left( {h + \gamma } \right)((h\left( { - 2 + {\text{Ec}}\left( {h^{2} - k^{2} } \right)^{2} { \Pr }} \right) + 2\left( {k - \gamma } \right) + {\text{Ec}} \\ & \left( {h^{2} - k^{2} } \right)^{2} { \Pr }\gamma ){\text{Log}}\left[ { - h + k} \right] + \left( {h\left( {2 + {\text{Ec}}\left( {h^{2} - k^{2} } \right)^{2} { \Pr }} \right) + {\text{Ec}}\left( {h^{2} - k^{2} } \right)^{2} { \Pr }\gamma + 2\left( {k + \gamma } \right)} \right) \\ & {\text{Log}}\left[ {h + k} \right])) + 24{\text{Ec}}h{ \Pr }\left( {h + \gamma } \right)^{2} (h^{2} \left( { - h^{2} + k^{2} + 4h\gamma } \right) + \left( {3h^{4} - 4h^{2} k^{2} + k^{4} } \right)({\text{Log}}\left[ { - h + k} \right] \\ & + {\text{Log}}\left[ {h + k} \right]))\beta_{1}^{3} + 24{\text{Ec}}h^{2} { \Pr }\left( {h + \gamma } \right)^{2} \left( {2h\gamma + \left( {h - k} \right)\left( {h + k} \right)\left( {{\text{Log}}\left[ { - h + k} \right] + {\text{Log}}\left[ {h + k} \right]} \right)} \right) \\ & 24{\text{Ec}}k{ \Pr }\left( {h + \gamma } \right)^{2} \beta_{2} (h\left( {h - k} \right)\left( {h + k} \right)\left( { - h^{2} + \left( {h - k} \right)\left( {h + k} \right)\left( {{\text{Log}}\left[ { - h + k} \right] + {\text{Log}}\left[ {h + k} \right]} \right)} \right)\beta_{1}^{4} \\ & - 24{\text{Ec}}k{ \Pr }\left( {h + \gamma } \right)^{2} \beta_{2} (h\left( {h - k} \right)\left( {h + k} \right)\left( { - h^{2} + \left( {h - k} \right)\left( {h + k} \right)\left( {{\text{Log}}\left[ { - h + k} \right] + {\text{Log}}\left[ {h + k} \right]} \right)} \right) \\ & + k\left( { - 2h\gamma - \left( {h - k} \right)\left( {h + k} \right)\left( {{\text{Log}}\left[ { - h + k} \right] + {\text{Log}}\left[ {h + k} \right]} \right)} \right)\beta_{2} ) - \beta_{1}^{2} (h{ \Pr }(6\left( {h - k} \right)\left( {h + k} \right)({\text{Nb}} \\ & + {\text{Nt}})\left( {h + 2\gamma } \right) + {\text{Ec}}h\left( {h + \gamma } \right)^{2} \left( {61h^{4} - 67h^{2} k^{2} + 6k^{4} - 16h\left( {2h^{2} + k^{2} } \right)\gamma } \right)) - 6\left( {h - k} \right)\left( {h + k} \right) \\ & \left( {h + \gamma } \right)(\left( {h\left( { - 2 + {\text{Ec}}\left( {13h^{4} - 10h^{2} k^{2} + k^{4} } \right){ \Pr }} \right) + 2\left( {k - \gamma } \right) + {\text{Ec}}\left( {13h^{4} - 10h^{2} k^{2} + k^{4} } \right){ \Pr }\gamma } \right) \\ & {\text{Log}}\left[ { - h + k} \right] + (h\left( {2 + {\text{Ec}}\left( {13h^{4} - 10h^{2} k^{2} + k^{4} } \right){ \Pr }} \right) + {\text{Ec}}\left( {13h^{4} - 10h^{2} k^{2} + k^{4} } \right){ \Pr }\gamma + 2(k + \\ & \gamma )){\text{Log}}\left[ {h + k} \right]) + 48{\text{Ec}}hk{ \Pr }\left( {h + \gamma } \right)^{2} \left( {2h\gamma + \left( {h - k} \right)\left( {h + k} \right)\left( {{\text{Log}}\left[ { - h + k} \right] + {\text{Log}}\left[ {h + k} \right]} \right)} \right)\beta_{2} ) \\ & + 2\beta_{1} (h\left( {h - k} \right)\left( {h + k} \right)( - h{ \Pr }\left( {6\left( {{\text{Nb}} + {\text{Nt}}} \right)\left( {h + 2\gamma } \right) + {\text{Ec}}h\left( {h + \gamma } \right)^{2} \left( {25h^{2} - 6k^{2} + 16h\gamma } \right)} \right) + 6 \\ & \left( {h + \gamma } \right)(\left( {h\left( { - 2 + {\text{Ec}}\left( {3h^{4} - 4h^{2} k^{2} + k^{4} } \right){ \Pr }} \right) + 2\left( {k - \gamma } \right) + {\text{Ec}}\left( {3h^{4} - 4h^{2} k^{2} + k^{4} } \right){ \Pr }\gamma } \right) \\ & {\text{Log}}\left[ { - h + k} \right] + \left( {h\left( {2 + {\text{Ec}}\left( {3h^{4} - 4h^{2} k^{2} + k^{4} } \right){ \Pr }} \right) + {\text{Ec}}\left( {3h^{4} - 4h^{2} k^{2} + k^{4} } \right){ \Pr }\gamma + 2\left( {k + \gamma } \right)} \right) \\ & {\text{Log}}\left[ {h + k} \right])) - 12{\text{Ec}}k{ \Pr }\left( {h + \gamma } \right)^{2} (h^{2} \left( { - h^{2} + k^{2} + 4h\gamma } \right) + \left( {3h^{4} - 4h^{2} k^{2} + k^{4} } \right)({\text{Log}}\left[ { - h + k} \right] \\ & + {\text{Log}}\left[ {h + k} \right]))\beta_{2} )), \\ \end{aligned}$$

$$\begin{aligned} & C_{4} = \frac{1}{{24\left( {h - k} \right)\left( {h + k} \right)\left( {h + \gamma } \right)^{2} \left( {h + \beta_{1} } \right)^{2} }}(h^{2} \left( {h - k} \right)\left( {h + k} \right)(2h\left( {6 + {\text{Ec}}h^{3} k{ \Pr }} \right) + 2{\text{Ec}}k(7h^{3} \\ & - 3hk^{2} ){ \Pr }\gamma - 6{\text{Ec}}k\left( { - 2h^{2} + k^{2} } \right){ \Pr }\gamma^{2} + 3(h\left( { - 2 + {\text{Ec}}\left( {h^{2} - k^{2} } \right)^{2} { \Pr }} \right) + 2\left( {k - \gamma } \right) + {\text{Ec}} \times \\ & \left( {h^{2} - k^{2} } \right)^{2} { \Pr }\gamma ){\text{Log}}\left[ { - h + k} \right] - 3\left( {h\left( {2 + {\text{Ec}}\left( {h^{2} - k^{2} } \right)^{2} { \Pr }} \right) + {\text{Ec}}\left( {h^{2} - k^{2} } \right)^{2} { \Pr }\gamma + 2\left( {k + \gamma } \right)} \right) \\ & {\text{Log}}\left[ {h + k} \right]) + 12{\text{Ec}}h\left( {3h^{2} - k^{2} } \right){ \Pr }\left( {h + \gamma } \right)(2k\gamma + \left( {h - k} \right)\left( {h + k} \right)({\text{Log}}\left[ { - h + k} \right] - {\text{Log}}[h + \\ & k]))\beta_{1}^{3} + 12{\text{Ec}}h^{2} { \Pr }\left( {h + \gamma } \right)\left( {2k\gamma + \left( {h - k} \right)\left( {h + k} \right)\left( {{\text{Log}}\left[ { - h + k} \right] - {\text{Log}}\left[ {h + k} \right]} \right)} \right)\beta_{1}^{4} - 12{\text{Ec}}k \\ & \Pr \left( {h + \gamma } \right)\left( { - 2k\gamma - \left( {h - k} \right)\left( {h + k} \right)\left( {{\text{Log}}\left[ { - h + k} \right] - {\text{Log}}\left[ {h + k} \right]} \right)} \right)\beta_{2} \left( { - h^{3} + hk^{2} + k\beta_{2} } \right) + \\ & 2\beta_{1} (h\left( {h - k} \right)\left( {h + k} \right)(2h\left( {6 + {\text{Ec}}h^{3} k{ \Pr }} \right) + 2{\text{Ec}}k\left( {13h^{3} - 3hk^{2} } \right){ \Pr }\gamma - 6{\text{Ec}}k\left( { - 4h^{2} + k^{2} } \right) \\ & { \Pr }\gamma^{2} + 3\left( {h\left( { - 2 + {\text{Ec}}\left( {3h^{4} - 4h^{2} k^{2} + k^{4} } \right){ \Pr }} \right) + 2\left( {k - \gamma } \right) + {\text{Ec}}\left( {3h^{4} - 4h^{2} k^{2} + k^{4} } \right){ \Pr }\gamma } \right) \\ & {\text{Log}}\left[ { - h + k} \right] - 3\left( {h\left( {2 + {\text{Ec}}\left( {3h^{4} - 4h^{2} k^{2} + k^{4} } \right){ \Pr }} \right) + {\text{Ec}}\left( {3h^{4} - 4h^{2} k^{2} + k^{4} } \right){ \Pr }\gamma + 2\left( {k + \gamma } \right)} \right) \\ & {\text{Log}}\left[ {h + k} \right]) - 6{\text{Ec}}k\left( { - 3h^{2} + k^{2} } \right){ \Pr }\left( {h + \gamma } \right)( - 2k\gamma - \left( {h - k} \right)\left( {h + k} \right)({\text{Log}}\left[ { - h + k} \right] - {\text{Log}}[h + \\ & k]))\beta_{2} ) + \beta_{1}^{2} (2h\left( {h - k} \right)\left( {h + k} \right)\left( {6 + {\text{Ec}}h^{3} k{ \Pr }} \right) + 2{\text{Ec}}k\left( {43h^{5} - 34h^{3} k^{2} + 3hk^{4} } \right){ \Pr }\gamma + 6{\text{Ec}}k \\ & \left( {14h^{4} - 11h^{2} k^{2} + k^{4} } \right){ \Pr }\gamma^{2} + 3\left( {h - k} \right)\left( {h + k} \right)((h\left( { - 2 + {\text{Ec}}\left( {13h^{4} - 10h^{2} k^{2} + k^{4} } \right){ \Pr }} \right) + 2 \\ & \left( {k - \gamma } \right) + {\text{Ec}}\left( {13h^{4} - 10h^{2} k^{2} + k^{4} } \right){ \Pr }\gamma ){\text{Log}}\left[ { - h + k} \right] - (h\left( {2 + {\text{Ec}}\left( {13h^{4} - 10h^{2} k^{2} + k^{4} } \right){ \Pr }} \right) \\ & + {\text{Ec}}\left( {13h^{4} - 10h^{2} k^{2} + k^{4} } \right){ \Pr }\gamma + 2\left( {k + \gamma } \right)){\text{Log}}\left[ {h + k} \right]) - 24{\text{Ec}}hk{ \Pr }\left( {h + \gamma } \right)(2k\gamma + \left( {h - k} \right) \\ & \left( {h + k} \right)\left( {{\text{Log}}\left[ { - h + k} \right] - {\text{Log}}\left[ {h + k} \right]} \right))\beta_{2} )), \\ \end{aligned}$$

$$C_{5} = \frac{{\left( {{\text{Nb}} + {\text{Nt}}} \right)\left( {\left( {h - k + \gamma_{1} } \right){\text{Log}}\left[ { - h + k} \right] - \left( {h + k + \gamma_{1} } \right){\text{Log}}\left[ {h + k} \right]} \right)}}{{4{\text{Nb}}\left( {h + \gamma_{1} } \right)}},$$

$$C_{6} = - \frac{{\left( {{\text{Nb}} + {\text{Nt}}} \right)\left( { - 2h + \left( {h - k + \gamma_{1} } \right){\text{Log}}\left[ { - h + k} \right] + \left( {h + k + \gamma_{1} } \right){\text{Log}}\left[ {h + k} \right]} \right)}}{{4{\text{Nb}}\left( {h + \gamma_{1} } \right)^{2} }}.$$