1 Introduction

Support vector machine (SVM) [1, 2] may be called the flagship of classification in machine learning. Since SVM offers one of the most robust and accurate methods among all well-known algorithms such as k-nearest neighborhood (k-NN), artificial neural networks (ANN), decision trees (DT), it is considered to be tried in classification. It has a solid theoretical basis, requires few samples for training and works stable with a large number of dimensions. SVM [3] has been one of the most developed and used methods of recent years, based on solid mathematical principles such as Lagrangian duality optimization [4] and kernel function [5] trick approaches, in classification tasks of supervised machine learning methods. Classification with supervised learning [6–8] is a method of machine learning [1, 9] task that categorically predicts class to which a particular instance belongs. Kernel function methods attract the attention of machine learning researchers due to their robust mathematical infrastructure, higher accuracy rates and relatively fast training times compared to other machine learning methods such as k-NN, ANN and DT in solving nonlinear problems. Although there are quite a lot of kernel function varieties, basic ones are linear, polynomial, Gaussian or in other words radial basis function (RBF) and sigmoid kernels [9] in classification. However, the kernel selection [2] issue, aimed at which kernel function is required to classify data most accurately, is an important research topic in recent years. Also, novel kernel function types [10–17] are produced continuously from large mathematical functions space since a wide variety of nonlinearly separable dataset are available in the real world. Kernels were applied to many areas including different dataset in literature [18,19,20]. In order to select the most suitable kernel for the topological structure of the dataset, kernel variety in literature should be increased.

Authors in [21] proposed a framework which can be applied on kernels and transform them more accurately in terms of clustering, classification and dimensionality reduction of dataset. They prepared a synthetic dataset in 3D spiral form and used a common repository dataset. In experiments, their geometry aware kernels improved performance. In study [22], a modified fuzzy c-means clustering algorithm based on Mahalanobis distance that takes into samples’ correlation account has been proposed and success achieved in terms of reducing effect of outliers and obtaining high classification accuracy. In [12], construction methods of some orthogonal polynomial kernels and proposed triangular-Chebyshev and triangular-Legendre kernels were compared with universal kernels via classification and regression scenarios. Proposed ones could achieve classification and regression tasks more accurately. Jiang et. al [14] proposed stationary Mahalanobis distance-induced kernels in SVM with applications in credit risk evaluation. They focused on stationary kernel construction where they assumed distance between two simultaneously translated vectors would be the same as the one without translation. Proposed kernels were appropriate for credit risk evaluation and over classical machine learning methods by meaning of performance. Baek and Kim [23] studied SVM’s computational expense and proposed a new look up table based on a less costly optimal additive kernel. However, results showed that their proposed kernel is not higher than Gaussian kernel in accuracy. Ding et al. have proposed a kernel modifying the traditional RBF kernel of SVM, which they call random radial basis function (RRBF), in which kernel parameters can be randomly assigned and expand a single parameter to multivalued parameters of finite length. In experimental studies, datasets with 13 binary and 5 multi-class labels were used. As a result of experimental comparisons, they stated that RRBF outperforms RBF, polynomial, extreme learning machine (ELM), Chebyshev and Hermite kernels for both binary and multi-class classification datasets [24]. Another study by Ding et al. is the random compact Gaussian (RCG) kernel, which they proposed by combining random feature mapping used in the extreme learning machine (ELM) kernel with a traditional Gaussian kernel. Unlike their proposed method ELM kernel, all parameters in RCG kernel are randomly assigned. Random feature mapping saves the parameter selection time of RCG core and implicit mapping saves core computation time of RCG core. Experiments on both classification and regression datasets have reported that RCG tends to achieve better generalization performance than other kernels [25].

In the studies reviewed above, it is seen that improved new kernels via modification where kernels modified accordingly Mercer condition, distance metric where used metric provides positive semi-definition criteria and numerical trick like lookup tables. The Gaussian kernel in classification problems is referenced in the literature very often since it accurately classifies most of common datasets. Moreover, recent studies on kernels for the SVM are compared with Gaussian kernels especially on nonlinearly separable datasets. In this study, we have proposed a new kernel named adaptive Gaussian (AG). AG uses a mean-based method for preprocess of input vectors of training dataset and \(\rho \) parameter selection method based on standard deviation. The contributions of this study are listed as follows:

  1. (1)

    The proposed method offers an adaptive kernel method by calculating the standard deviation value depending on the norms of the input vectors instead of the variance parameter in the Gaussian kernel.

  2. (2)

    It performs automatic calculation by disabling the manually determined parameter specific to the problem in the traditional Gaussian kernel.

  3. (3)

    Since it does not need problem-specific parameters, it can be applied directly and practically to all classification problems.

This paper is organized as follows; in the first section, the literature about SVM and Gaussian kernels has been introduced. In the second section, SVM has been briefly explained. In the third section, the theoretical approach of the proposed kernel function has been discussed. In the fourth section, experimental results have been presented and compared to well-known kernel functions and in the last section, this paper is summarized.

2 Support Vector Machine

SVM is a supervised learning model in machine learning used to classify binary or multiple datasets of linear or nonlinear separable type. Since the Lagrangian dual problem is used as an optimization approach in the SVM classifier, the number of training processes is saved, and a significant speed advantage is obtained compared to other algorithms. Thus, SVM is successful in high-volume datasets, as well as in high-dimensional problems with few data. Support vectors with hyperplanes are used for a linearly separable dataset as given in Fig. 1.

Fig. 1
figure 1

Linear SVM classifier with hyperplane and margin

Full size image

Given \(m\) training pairs \(\left({x}_{1},{y}_{1}\right),\dots \dots ,({x}_{m},{y}_{m})\), where \({x}_{i}\in {R}^{n}\), with \(i=\mathrm{1,2},\dots ,m\), is an input vector labeled by \({xy}_{i}\in \{-1,+1\}\), the linear SVM classifier searches for an optimal separating hyperplane given in Fig. 1.

$$ \langle \omega ,x\rangle + b = 0 $$
(1)

\(\omega \in {R}^{n}\) is the normal vector to the hyperplane and \(b\) is a scalar. Equation (1) is obtained by solving the following convex quadratic programming problem below:

$$ \mathop {\min }\limits_{{\omega ,\tau_{i} }} {\mkern 1mu} \frac{{\left\| \omega \right\|^{2} }}{2} + C\left(\sum\limits_{i = 1}^{n} {\tau_{i} } \right) $$
(2)
$$ {\text{subject to: }}\left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {y(\langle \omega ,x\rangle + b) \ge 1 - \tau_{i} } \\ {\tau_{i} \ge 0} \\ \end{array} \, } \\ \end{array} {\text{ with, }}i = 1,2,...,m,} \right. $$
(3)

where C is a regularity parameter greater than zero, which balances the significance between maximization of margin width and minimization of training error. The slack variable \({\tau }_{i}\in R\) is the soft margin error of the \(i\)th training sample. The solution of Eqs. 2 and 3 is obtained by finding the saddle point of the Lagrange function and a decision function of the form given in Eq. 4.

$$ f(y) = {\text{sgn}}(\langle \omega ,x\rangle + b) = {\text{sgn}}\left(\sum\limits_{i = 1}^{m} {a_{i} } y_{i} x_{i}^{T} x + b\right) $$
(4)

The problems, caused by the nonlinear topology of datasets, can be solved by mapping datasets to multi-dimensional space by the kernel functions, which can be divided into a linearly separable problem. SVMs with kernel functions are created for nonlinearly separable data. These kernel functions are basically polynomial, Gaussian and sigmoid. The Gaussian kernel function allows the separation of nonlinearly separable data by mapping the input vector to Hilbert space. The Gaussian kernel is an exponential function including norm and real constant given in Eq. 5.

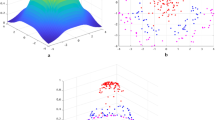
$$ {K}_{G} (u,v) = \exp \left( { - \frac{{\left\| {u - v} \right\|_{2}^{2} }}{{2\rho^{2} }}} \right) $$
(5)

where \(u\) and \(v\) are input vectors, the Euclidean norm [26] in the numerator part of the exponential expression is obtained with input vectors, and \(\rho \) in the denominator part is a real constant, which is an arbitrary value. Gaussian kernel function decays exponentially in the input feature space and uniformly in all directions around the support vector, inducing to hyper-spherical contours of the kernel function. When using the Gaussian kernel in SVM, input vectors of the kernel are generally raw form; however in [27, 28] applied a correction method as the mean of input vectors. Width of each bell-shaped surface is directly proportional to \(\rho \). The parameter \(\rho \) that gives optimal width can be found by trying. Experimental process of finding \(\rho \) is an iterative approach that consumes time and power. Therefore, the development of an efficient method for tuning \(\rho \) to an optimal width for the data would be an important solution for SVM classification problems. A stationary state of a Gaussian kernel can be represented as bell shaped with three-dimensional surface and data distributions given in Fig. 2.

Fig. 2
figure 2

Behavior of SVM with Gaussian kernel on nonlinear separable dataset; a 3D Gaussian surface b nonlinearly separable dataset c dataset mapped to Hilbert space by Gaussian kernel

Full size image

Other basic kernel functions used in SVM are linear kernel given in Eq. 6 and polynomial kernel given in Eq. 7.

$$ {K}_{{{\text{Lin}}}} (u,v) = \left\langle {u,v} \right\rangle $$
(6)
$$ {K}_{{{\text{Pol}}}} (u,v) = \left( {\left\langle {u,v} \right\rangle + 1} \right)^{n} $$
(7)

where \(n\) is degree of polynomial.

3 The Kernel Approximation

Let \(\left\{{x}_{n}\right\}\) be a sequence in the metric space \(\left(X,d\right)\). If there is an N number in the form of

$$d({x}_{n},{x}_{m})<\epsilon $$
(8)

for \(\forall \epsilon >0\) and \(\forall k,l\ge N\), the \(\left\{{x}_{n}\right\},\) a sequence is called the Cauchy sequence. The metric space to which every Cauchy sequence is convergent is the complete metric space. On the other hand, a normed space and \(d\left({x}_{n},{x}_{m}\right)\) is defined by

$$d\left({x}_{n},{x}_{m}\right)=\| {x}_{n}-{x}_{m}\| $$
(9)

in that case \(d\) is a metric. Further, the complete inner product space as metric space is named Hilbert space \(H\).

The kernel function \(K:X\times X\to R\) is defined by

$$ {K}(u,v) = \left\langle {\varphi (u),\varphi (u)} \right\rangle_{{H}} $$
(10)

where the space \(H\) is a feature space of \(K\) and \(\varphi :X\times X\to H\) is a feature map. Also, from the property of the inner product \(h,g\in H\) be given by.

$$ g(x) = \sum\limits_{i = 1}^{m} {\eta_{i} {K}(v_{i} ,u)} {\text{ and }}h(x) = \sum\limits_{i = 1}^{n} {\lambda_{i} {K}(v_{i} ,u)} $$
(11)

Then

$$ \begin{aligned} \left\langle {g,h} \right\rangle &= \sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{n} {\eta_{i} \lambda_{i} } {K}(u_{i} ,v_{j} ) = } \sum\limits_{i = 1}^{m} {\eta_{i} h(u_{i} ) }\\ &= \sum\limits_{j = 1}^{n} {\lambda_{j} g(v_{j} )} \end{aligned} $$
(12)

Theorem 1 (Mercer) [3]

To be a valid SVM kernel, for \(\varphi \left(u\right)\), the following integration should always be nonnegative for the given kernel function \(K\left(u,v\right)\)

$$ \int {\int \, } {K}(u,v)\varphi (u)\varphi (u)dudv \ge 0 $$
(13)

If \(K\left(u,v\right)\) is a kernel and \(\kappa \) is the kernel matrix with \({\kappa }_{i,j}=K\left(u,v\right)\),

$$ \varsigma^{T} \kappa \varsigma = \sum\limits_{i,j} {\varsigma_{i} \varsigma_{j} } {K}(u,v) = \left\langle {\varphi (u),\varphi (v)} \right\rangle = \left\| {\sum\limits_{i} {\varsigma_{i} } \varphi (u)} \right\|^{2} \ge 0 $$
(14)

4 Proposed Method

In SVM and statistics, we take advantage of kernels, which are measures of the similarity between two examples. Most features of SVM are determined by the choice of kernel function. The use of different kernel functions represents the inner product in different feature space. The Gaussian kernel in classification problems is referenced in literature very often since it accurately classifies most of common datasets. Gaussian kernel function decays exponentially in the input feature space and uniformly in all directions around the support vector, inducing to hyper-spherical contours of the kernel function. The Gaussian kernel is defined by

$$ {\rm K}(u,v) = \exp \left( { - \gamma \left\| {u - v} \right\|_{2}^{2} } \right), $$
(15)

where \(\gamma =\frac{-1}{2{\rho }^{2}}\) and \(\rho \) is a positive real constant and \(\| .\| \) is the Euclidean norm for vectors. In addition to possessing the advantages of the Gaussian kernel, we present a new kernel named adaptive Gaussian (AG) in Eq. 16.

$$ {K}_{{{\text{AG}}}} (u,v) = \exp \left( { - \frac{{\left\| {u - v} \right\|^{2} - \delta (\left\| {u - v} \right\|^{2} ) + \Omega }}{{\delta (\left\| {u - v} \right\|^{2} )}}} \right) $$
(16)

where \(\delta \left(\bullet \right)\) is the standard deviation function and Ω is as shown in Eq. 17.

$$ \Omega = \left\{ {\begin{array}{*{20}c} {\left| {\min \left( {\left\| {u - v} \right\|^{2} - \delta (\left\| {u - v} \right\|^{2} )} \right)} \right|,} & {\min \left( {\left\| {u - v} \right\|^{2} - \delta (\left\| {u - v} \right\|^{2} )} \right) < 0} \\ {0,} & {{\text{otherwise}}} \\ \end{array} } \right. $$
(17)

To avoid division by zero, a term is added to the denominator of the equation as in Eq.18.

$$ {K}_{{{\text{AG}}}} (u,v) = \exp \left( { - \frac{{\left\| {u - v} \right\|^{2} - \delta (\left\| {u - v} \right\|^{2} ) + \Omega }}{{\delta (\left\| {u - v} \right\|^{2} ) + \varepsilon }}} \right) $$
(18)

\(\varepsilon \) is a negligible number to avoid a division by zero. Equation 19 is defined to simplify reading complexity.

$$ \xi = \left\| {u - v} \right\|^{2} - \delta (\left\| {u - v} \right\|^{2} ) $$
(19)

As a result, the equation of the proposed kernel function, Eq. 20, is obtained.

$$ {K}_{AG} (u,v) = \exp \left( { - \frac{\xi + \Omega }{{\delta (\left\| {u - v} \right\|^{2} ) + \varepsilon }}} \right) $$
(20)

The denominator of the proposed kernel function adapts to the input vectors. At the same time, adaptation is provided by calculating squared norm of the differences of input vectors and their standard deviations in the numerator part. Therefore, the proposed kernel function is considered adaptive. With the piecewise function Ω used in the numerator part, if its minimum value is below zero, its absolute value is calculated and an offset operation is applied to the entire dataset.

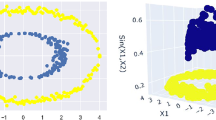
To simplify the understanding of the adaptive property, visualization can be made on a dataset whose property space is two dimensional. As a result of all the vectors entering the kernel according to the vector in the center, in other words, in the central static state, distributed vectors on a three-dimensional bell-shaped surface are obtained. These vectors in Hilbert space can now be easily classified with SVM. The bell curve of the AG corresponding to input vectors in different value ranges and the bell curves of the Gaussian kernel are compared in Fig. 3.

Fig. 3
figure 3

AG vs. Gaussian kernel function curves a data between −1 and 1 b data between −5 and 5 c data between −10 and 10 d data between −100 and 100

Full size image

The AG kernel function adapts to different data intervals and creates an optimal Gaussian bell curve. With this adaptive feature of the AG, the problem of finding optimum value of the parameter \(\rho \) which is an arbitrary real constant value in the Gauss kernel function is eliminated. The time complexity of a conventional Gaussian kernel is \(O(d{N}_{\mathrm{SV}})\), where \({N}_{\mathrm{SV}}\) is the number of support vectors and d is the number of features [25]. In the time complexity of the proposed method, the standard deviation of the norm of the input vectors is calculated in addition to the Gaussian kernel. In the time complexity, the d-dimensional standard deviation calculation cost is added for each support vector, and thus, the time complexity of the proposed method is found as \(O((d+d){N}_{\mathrm{SV}})\).

5 Experimental Results

In order to test the accuracy of the proposed method in experimental studies, a total of 25 datasets, 17 of which are KEEL-dataset repository and 8 of them UCI machine learning repository, were used as shown in Table 1. The MATLAB platform was used to implement the AG into SVM. The real constant of Gauss kernel functions \(\gamma \) values is taken as default value 1. In addition, the degree of polynomial kernel function is taken as the default value of 2.

Table 1 Datasets used in experimental studies
Full size table

Figure 4 shows the \(k\)-fold cross-validation technique for the datasets given to the classifier model. Here, the \(k\)-value is determined as 10. We use a common procedure of tenfold cross-validation to run the experiments. Cross-validation is the process of creating grouped datasets by selecting different amounts of samples from the same dataset.

Fig. 4
figure 4

k-fold cross-validation of the dataset

Full size image

The cross-validation technique is used to measure the predictive ability of a machine learning model on previously unseen data with less bias. Each dataset used in our experiments is divided into ten subgroups with an approximately equivalent number of samples. Thus, ten runs are performed for each dataset during the training and testing process of machine learning models. Then, by calculating their mean accuracy values, the overall success rate of machine learning models was obtained.

Accuracy (ACC), F-measure (FM) and Matthews correlation coefficient (MCC) metrics were used to measure classification success of the proposed method. ACC is a commonly used metric to measure the classification success of a model. The ACC value is equal to the ratio of correct predictions of a classifier to the total number of samples in a dataset. However, only model accuracy is not sufficient in imbalanced datasets.

$$ {\text{ACC}} = \frac{{{\text{TP}} + {\text{TN}}}}{{{\text{TP}} + {\text{TN}} + {\text{FP}} + {\text{FN}}}} $$
(21)

F1-score is obtained by calculating the harmonic mean of the precision and recall values. It is more appropriate to use this scale instead of the ACC to avoid choosing a wrong classifier model in imbalanced datasets.

$$ {\text{FM}} = \frac{2}{{{\text{TPR}}^{ - 1} + {\text{PPV}}^{ - 1} }} $$
(22)

Matthews correlation coefficient (MCC) is a correlation coefficient between observed and predicted binary classifications. Like most correlation coefficients, the MCC ranges from −1 to 1. A higher correlation between observed and predicted values is better estimation. Coefficient −1 represents the total disagreement between prediction and observation, coefficient 0 is not better than a random prediction, and + 1 represents a perfect estimate.

$$ {\text{MCC}} = \frac{{{\text{TP}} \times {\text{TN}} - {\text{FP}} \times {\text{FN}}}}{{\sqrt {\left( {{\text{TP}} + {\text{FP}}} \right)\left( {{\text{TP}} + {\text{FN}}} \right)\left( {{\text{TN}} + {\text{FP}}} \right)\left( {{\text{TN}} + {\text{FN}}} \right)} }} $$
(23)

Table 2 shows the proposed method and the results of the classification processes applied on 25 datasets of other SVM kernels. As seen from the table, it is obvious that the proposed kernel ACC and FM are better than other methods. The proposed kernel and polynomial kernel have very close scores in terms of MCC.

Table 2 Comparison of classification results
Full size table

Figure 5 shows the general classification accuracies of SVM kernel according to dataset repositories. It is seen that the proposed method has higher classification accuracy on both KEEL and UCI dataset repositories compared to other kernels.

Fig. 5
figure 5

Overall classification accuracy of SVM kernels according to dataset repositories

Full size image

In Table 3, Wilcoxon signed-rank test is given to test whether there is a difference between the two measurement results obtained from the datasets in experimental studies. In the hypothesis test, significance level was determined as 0.05. According to the test results obtained from the hypothesis test, it is seen that the proposed method is significantly different from other SVM kernels.

Table 3 Wilcoxon signed-rank test results (α = 0.05)
Full size table

In recent years, many kernel functions have been proposed for the SVM. Comparison results of some of them with the proposed method are given in Table 4.

Table 4 Comparison of classification results of the proposed method and reported results of state-of-the-art SVM kernels
Full size table

6 Conclusion

The use of kernel functions in SVM is one of the popular studies of recent years, and efforts to develop new kernel functions are given in detail in the introduction section. Especially the success of the Gaussian kernel function, which is one of the basic kernel functions, on nonlinear separable datasets is obvious. This kernel function is introduced and its usage in SVM is explained. The fact that the Gauss function depends on an arbitrary real constant parameter causes the problem of finding the optimal value of the parameter in the training process. In this study, an adaptive kernel function is proposed by making an improvement on the Gaussian kernel, which is an effective kernel function. The proposed kernel function was used in SVM classifiers and applied in 25 well-known datasets and comparisons were made with the basic kernel functions: Gaussian, linear and polynomial. As a result of the comparisons of the experimental studies, the proposed model achieved a higher success than other kernel functions with 84.7% ACC and 73.6% FM. Although the Gaussian kernel function provides 81.9% overall classification accuracy, the proposed method offers approximately 3% better than Gaussian kernel. It has been shown that the proposed method in the study can be used effectively in SVM classification problems. According to the test results obtained from the hypothesis test, it is seen that the proposed method is significantly different from other SVM kernels. The proposed kernel function can be applied in future studies in different metric spaces.