Adaptive Arctan kernel: a generalized kernel for support vector machine

Abstract

Support Vector Machines (SVMs) can learn from high-dimensional and small amounts of training data, thanks to effective optimization methods and a diverse set of kernel functions (KFs). The adaptability of SVM to numerous real-world problems has increased interest in the SVM method, and studies conducted with this method carry significant weight in various fields. The fixed parameter “AtanK” for KFs must be specified before the SVM model training process. Therefore, determining the appropriate kernel parameter values can be timE−consuming and may lead to slow convergence of the SVM model. On the other hand, the method provides faster and more robust convergence due to the adaptive parameter in the SVM model. In this study, a new Adaptive Arctan (AA) KF, tailored to the characteristics of different datasets, is proposed as an enhancement to the AtanK KF for the SVM algorithm. The proposed AA KF is compared with experimental results on 30 public KEEL and UCI datasets, alongside AtanK, adaptive Gaussian, Radial Basis Function, linear, and polynomial KFs. The results demonstrate that the proposed AA KF outperforms the other KFs, and it exhibits superior learning ability.

1 Introduction

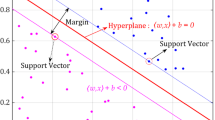
The support vector machine (SVM) is a machine learning model developed by Vapnik. It is used in clustering and regression problems, especially in classification [1,2,3]. SVM is a non-parametric, supervised machine learning method based on statistical learning theory [4]. Researchers widely prefer SVM for classification algorithms due to its successful performance, robust mathematical infrastructure, and relatively fast speed [5, 6]. In SVM, mapping is performed to transfer data samples to a dimensional space, and the classification process begins with the hyperplane that separates the two classes. Samples close to the boundaries are defined as support vectors. The separation of SVM training samples into different subgroups using support vectors is determined by the choice of kernel functions (KFs). Although there are various types of KFs, the basic ones for classification are Linear, Polynomial, Gaussian, Radial Based Function (RBF), and Sigmoid kernels [7,8,9,10]. The choice of KFs has a significant impact on the classification performance in SVM. SVM can mitigate the shortcomings of existing models, such as overfitting, reliance on a single consideration factor, and the inability to generate predictions for lengthy periods. As a supervised learning model, SVM is an effective statistical machine learning tool for classifying datasets of both linear and nonlinear separable types. One of the key features that makes SVM advantageous is its use of the Lagrange binary optimization problem. This allows for the optimal number of training iterations, resulting in a significant time advantage compared to other machine learning methods. SVM excels on datasets that require substantial memory and datasets with many features but few samples.

A Kernel Function (KF) transforms the input data into Hilbert space within the Support Vector Machine (SVM), creating intervals for the hyperplane to classify the data. While there are several well-known KFs, new proposals continue to emerge every day. The most renowned and successful KFs can be categorized as linear, *Gaussian, RBF, polynomial, and AtanK. Some of these functions include a parameter with an arbitrary value. This arbitrary value can be manually adjusted according to the dataset, and classification in the SVM is performed using the most suitable version of the KF for the dataset. FinE−tuning the optimal arbitrary value based on the dataset requires time and results in a high processing load. Although the Gaussian KF is one of the most well-known KFs with parameters, recent studies have also introduced parameters for AtanK. In Eqs. (1) and (2), the Gaussian KF and AtanK KF are presented, respectively.

$$ K(s,q) = \exp \left( { - \frac{{\left\| {s - q} \right\|_{2}^{2} }}{{2\sigma^{2} }}} \right) $$

(1)

$$ K\left( {s,q} \right) = \frac{2}{\pi }\arctan \left( {\frac{{\sigma^{2} }}{{\left\| {s - q} \right\|_{2}^{2} }}} \right) $$

(2)

where $s$ and $q$ are input vectors. These vectors are expressed in KFs with the Euclidean norm. $\sigma$ is a real number, which is an arbitrary value. These KFs vary smoothly in the input feature space in all directions around the support vector, resulting in hyper-spherical contours of the KF.

KFs are expressed as a set of mathematical functions used to process input data [11]. KFs play a crucial role in solving nonlinear problems with the aid of a linear classifier. In the context of the SVM architecture, KFs are employed to achieve accurate data separation by transforming the nonlinear structure of the input dataset from a higher-dimensional space to a linear structure [12]. Furthermore, KFs are recommended to simplify complex computations, enabling the creation of hyperplanes in higher dimensions without increasing complexity. In summary, KFs are utilized to address nonlinear problems. Additionally, given the unique characteristics of each dataset, identifying the most appropriate KF for optimal data classification has become a significant research focus in recent years [13].

Selecting appropriate KFs can be a challenging process. To choose the most suitable KF for the characteristics of the dataset in use, the performance of SVM algorithms with different KFs is compared. Additionally, parameter tuning for each KF is a timE−consuming process. Therefore, proposing an adaptive KF that can adjust to the data, rather than attempting to find the optimal function by experimenting with KFs having various parameter values, reduces a substantial workload. The adaptive approach enables SVM to diminish parameter dependency in KFs during classification and regression processes [14].

The Linear, Polynomial, Sigmoid, Gaussian, and RBF kernels are widely used in the literature [15]. However, many studies in the literature have observed that new functions are proposed to outperform existing KFs. Elen and colleagues introduced a new KF called Adaptive Gaussian (AG), inspired by the Gaussian kernel used in the SVM [13]. In their study, Anna et al proposed a new KF by combining three types of KFs: polynomial, RBF, and Fourier [7]. As a result of the experimental evaluation, they reported that the combined KF offers better performance than other KFs. Ding et al introduced a new KF, the random radial basis function (RRBF). The proposed RRBF outperforms traditional RBF and other KFs [16]. Negri et al presented two new KFs for classifying remotely sensed images in their study [17]. They reported that the proposed new KFs perform well on both remote sensing and real-world datasets compared to other functions. In the study by Tian and Li, the ArcTan KF (AtanK) is proposed as an alternative to the Gaussian KF to increase the practicality of the SVM [18]. They reported that the proposed AtanK has better efficiency and robustness than the polynomial kernel, Gaussian kernel, and exponential radial basis functions. Khan et al introduced a new KF, a combination of polynomial and RBF, to improve the performance of the SVM used to classify protein structures. They reported that they achieved better performance than other machine learning algorithms with the proposed hybrid KF SVM [19]. In the study by Li and He, an adaptive KF is proposed to enhance the classification performance of the SVM [20]. In the study by Ba et al, a soft sensing method based on least square the SVM regression with multi-core learning was proposed. In the proposed model, they reported that they used the RBF, polynomial, and sigmoid KFs to construct the multiple kernel structure [21]. The adaptive arctan KF proposed in this study outperformed the KFs suggested in the literature in the experimental evaluations conducted on 30 public UCI datasets.

In this study, a new Adaptive Arctan (AA) KF is proposed to align with the characteristics of various datasets in the SVM classification algorithm. It often consumes a significant amount of time to determine the most suitable parameter value when applying KFs to the SVM problems. However, the proposed AA KF SVM can ascertain the most appropriate parameter during the initial run, enabling quicker classification with optimal performance during the learning process. Instead of a fixed $\sigma$ parameter value used in the AtanK function, the AA KF, capable of adjusting itself to each dataset, is suggested. Consequently, the SVM model delivers faster and more accurate classification. The proposed AA KF permits us to construct hyperplanes in higher dimensions without increasing complexity. Furthermore, the overfitting issue commonly observed in the SVM can be effectively addressed with the proposed AA KF. The proposed AA KF is compared with AtanK, AG, RBF, LIN, and POL KFs through experiments conducted on 30 public UCI datasets. The results indicate that the proposed AA KF outperforms other KFs and exhibits superior learning capabilities.

The contributions of this study are listed as follows:

• The new adaptive arctan KF is proposed.

• The proposed adaptive arctan KF has a better learning ability.

• Since it does not need problem-specific parameters, it can be applied directly and practically to all classification problems.

Motivation to the SVM and KF are presented in Section 2 of the study. Proposed adaptive arctan KF is presented in Section 3, experimental results are presented in Section 4, and conclusions are discussed in section 5.

2 Motivation

2.1 Support vector machine

The AtanK function is used in SVM, where the input vectors of the kernel are in their raw form. This function is unimodal and symmetric about the third axis. For small values of $\sigma$, the function exhibits a Gaussian-like bell-shaped curve, while at large values, it assumes a plateau-like shape. Although the variation in this shape scale is effective in separating the classes in the Hilbert space, it is determined through testing the parameter $\sigma$, which provides the optimum plateau width. This experimental process involves an iterative method that is timE−consuming and power-intensive. Therefore, there is a need for an efficient method to determine the optimum value of $\sigma$ based on the data. In this study, drawing inspiration from the AtanK function and the Adaptive Gaussian KF, a statistical model that adapts to the data within the function instead of $\sigma$ is proposed. A snapshot of the AtanK function can be represented as a plateau in the context of threE−class synthetic data distributions and a threE−dimensional surface, as shown in figure 1.

Figure 1

Behavior of the SVM with AtanK on nonlinear separable synthetic 3 class dataset; (a) 3D AtanK surface with $\sigma = 5$, (b) Nonlinearly separable synthetic 3 class dataset, (c) Dataset mapped to Hilbert space by AtanK.

2.2 Kernel trick

Let $\left\{ {s_{k} } \right\},$ be a sequence in the $\left( {S,d} \right)$ metric space. If there is M number such as

$$ d\left( {s_{k} ,s_{l} } \right) < \varepsilon $$

(3)

is called Cauchy sequence for $\forall \varepsilon > 0$ and $\forall k,l \ge M$. . Every Cauchy sequence in the full metric space is convergent. A distance in the norm space is defined by

$$ d\left( {s_{k} ,s_{l} } \right) = \left\| {s_{k} - s_{l} } \right\| $$

(4)

Also, the complete inner product space in metric space is called Hilbert space $H$.

$$ K\left( {s,q} \right) = \left\langle {\gamma \left( s \right),\gamma \left( q \right)} \right\rangle_{H} $$

(5)

is defined as $K:S \times S \to R$ KF by means of inner product. Here, $H$ is feature space of $K$ and $\gamma :S \times S \to H$ is feature map. Further, with the inner product’s property, $f,g \in H$ be gin by

$$ \begin{aligned} f\left( s \right) & = \sum\limits_{i = 1}^{k} {\eta_{i} K\left( {s_{i} ,s} \right)} , \\ g\left( q \right) & = \sum\limits_{j = 1}^{l} {\lambda_{j} K\left( {q_{j} ,q} \right)} \\ \end{aligned} $$

(6)

Then

$$ \begin{aligned} \left\langle {f,g} \right\rangle & = \sum\limits_{i = 1}^{k} {\sum\limits_{j = 1}^{l} {\eta_{i} \lambda_{j} K\left( {s_{i} ,q_{j} } \right)} } \\ & = \sum\limits_{i = 1}^{k} {\eta_{i} g\left( {s_{i} } \right)} = \sum\limits_{j = 1}^{l} {\lambda_{j} f\left( {q_{j} } \right)} \\ \end{aligned} $$

(7)

Mercer Theorem. For the kernel $K\left(s,q\right)$ with $\gamma \left(s\right)$, integral in Eq. (8) should always provide non-negativity, the purpose of being a valid SVM KF [1].

$$ \int {\int {K\left( {s,q} \right)\gamma \left( s \right)\gamma \left( q \right)} } dsdq \ge 0 $$

(8)

If $\kappa$ is the kernel matrix of $K\left(s,q\right)$ KF with ${\kappa }_{i,j}=K\left(s,q\right)$,

$$ \begin{aligned} \rho^{T} \kappa \rho & = \sum\nolimits_{i,j} {\rho_{i} \rho_{j} K\left( {s,q} \right)} = \left\langle {\gamma \left( s \right),\gamma \left( q \right)} \right\rangle \\ & = \left\| {\sum\nolimits_{i} {\rho_{i} } \gamma \left( s \right)} \right\|^{2} \ge 0 \\ \end{aligned} $$

(9)

3 Adaptive Arctan kernel function

KFs in the SVM are similarity scales between two samples. The selection of a kernel function is an important process for the SVM and has a significant impact on the results. The kernel function expresses the inner product in the feature space. The Gaussian, as given in Eq. (1), is one of the most preferred and efficient classifying KFs. In this study, we drew inspiration from the Gaussian KF and the AtanK function provided in Eq. (2). The arctan part in the AtanK function creates the curve shape, while the $2/\pi$ factor sets the upper limit on the vertical axis to 1. Although $2/\pi$ is convenient for visualization, it does not affect the SVM classification process. According to AtanK, the arctan KF given in Eq. (10) is proposed as a simpler and non-adaptive function.

$$ K_{A} \left( {s,q} \right) = \arctan \left( { - \frac{{\left\| {s - q} \right\|^{2} }}{{\sigma^{2} }}} \right) $$

(10)

Negativity in parentheses prevents the inversion of the curve. This negativity actually aids in visualization. Although the highest value of the proposed arctan KF is 0, it does not introduce any negativity in the SVM classification process. Figure 2 displays the graphs of the proposed arctan KF at various $\sigma$ values. As the value of $\sigma$ increases, it becomes evident that the arctan KF transitions from a bell-shaped form to a plateau.

Figure 2

Plot of the Arctan Kernel function at various $\sigma$ values.

Instead of the arbitrary $\sigma$ value in Eq. (10), the adaptive arctan (AA) KF given in Eq. (11) is proposed to adapt to the data.

$$ K_{AA} \left( {s,q} \right) = \arctan \left( { - \frac{{\left\| {s - q} \right\|^{2} - \delta \left( {\left\| {s - q} \right\|^{2} } \right) + \omega }}{{\delta \left( {\left\| {s - q} \right\|^{2} } \right)}}} \right) $$

(11)

While the $\sigma$ value is determined manually in the AtanK KF, the proposed kernel function (AA KF) adapts to different problems by calculating the inverse tangent of the input vector with a coefficient obtained depending on the standard deviation in the input vector. In order to handle division by a value in undefined or infinite results, which can occur if the standard deviation is equal to zero, division by a very small $\alpha$ value is provided in Eq. (12).

$$ K_{AA} \left( {s,q} \right) = \arctan \left( { - \frac{{\left\| {s - q} \right\|^{2} - \delta \left( {\left\| {s - q} \right\|^{2} } \right) + \omega }}{{\delta \left( {\left\| {s - q} \right\|^{2} } \right) + \alpha }}} \right) $$

(12)

where $\delta \left( \cdot \right)$ is a function of the standard deviation, $\alpha$ is an extremely small number to eliminate dividing by zero and $\omega$ is as shown in Eq. (13).

$$ \omega = \left\{ {\begin{array}{*{20}l} {\left| {\left\| {s - q} \right\|^{2} - \delta \left( {\left\| {s - q} \right\|^{2} } \right)} \right|,} \hfill & {\left\| {s - q} \right\|^{2} < \delta \left( {\left\| {s - q} \right\|^{2} } \right)} \hfill \\ {0,} \hfill & {otherwise} \hfill \\ \end{array} } \right. $$

(13)

The proposed AA KF's denominator in parentheses responds to the input vectors. Simultaneously adaptation is supplied by computing the square norm of the input vector differences and their standard deviations in the numerator. As a result, the proposed AA kernel is regarded as adaptable. When the numerator portion of the piecewise function $\omega$ is utilized, if the numerator part's minimum value is less than zero, the numerator part's absolute value is computed, and an offset operation is then performed on the whole dataset.

A dataset with a two-dimensional property space can be used for visualization to simplify the comprehension of the adaptive property. Distributed vectors on a 3D bell or plateau-shaped surface are formed due to all the vectors entering the kernel in alignment with the central vector or in the central static state. These Hilbert space vectors can now be quickly categorized using the SVM. In figure 3, bell and plateau curves of the AtanK function, and the bell and plateau curves of the AA KF corresponding to inputectors in various value ranges, are contrasted. The AA KF, which creates a smooth bell curve distribution regardless of the data range, offers an adaptive feature. Thus, the problem of finding the optimum value of the parameter $\sigma$ in Arctan KF and AtanK function, which is an arbitrary real constant value, is eliminated with the AA KF.

Figure 3

The proposed AA vs. arctangent function on various input data ($x$) intervals. (a) $- 1 \le x \le 1$, (b) $- 5 \le x \le 5$, (c) $- 10 \le x \le 10$, (d) $- 100 \le x \le 100$.

4 Experimental results

In experimental studies, two repository datasets, namely KEEL, and UCI, were used to evaluate the performance of the proposed kernel function. The Gaussian KFs $\sigma$ parameter value was taken default value 1. Additionally, the polynomial kernel degree value was taken default value 2. The steps used in the experimental studies for the AA KF are shown in figure 4. In order to test the performances of machine learning algorithms, the $k$-fold crossover method is used as shown in figure 5.

Figure 4

Process steps of experimental studies for KFs.

Figure 5

k-fold cross validation of the dataset [13].

In the study, the $k$-fold value was determined as five for the experimental evaluation. The cross-validation method is a widely used method to evaluate the predictive performance of models. In the $k$-fold cross-validation method, the data set is randomly divided into $k$ subgroups of approximately equal size. Thus, $k$ runs are performed for each data set in the training and testing process of machine learning models.

Then, the average accuracy values were calculated and the overall success rate of the model was obtained. The two repository datasets, namely KEEL, and UCI used for the experimental evaluation are presented in tables 1 and 2 as balanced, imbalanced. To measure how the proposed kernel function generalizes to different data distributions, six different synthetic datasets are given in table 3. Visualizations of the synthetic datasets are given in figure 6.

Table 1 Benchmark balanced datasets for evaluation of the SVM kernels.

Table 2 Benchmark imbalanced datasets for evaluation of the SVM kernels.

Table 3 Synthetic datasets for evaluation of the SVM kernels.

Figure 6

Visualizations of the synthetic datasets.

The performances of classification algorithms were compared according to the criteria of accuracy (ACC), and F₁-score, respectively Eqs. (14) and (15) [22,23,24,25].

$$ Accuracy = \frac{TP + TN}{{TP + FP + TN + FN}} $$

(14)

$$ F_{1} = \frac{2TP}{{2TP + FP + FN}} $$

(15)

The experimental results of the proposed Adaptive Arctan (AA) KF and the AtanK, AG, RBF, LIN, and POL KFs on the 30 datasets are presented in tables 4, 5, 6 and 7.

Table 4 Accuracy rates of kernels for the KEEL and UCI balanced datasets.

Table 5 Accuracy rates of kernels for the KEEL and UCI imbalanced datasets.

Table 6 Confidence Interval Profile of KFs for balanced and imbalanced datasets (for accuracy rates).

Table 7 F₁-scores of KF for the KEEL and UCI balanced datasets.

Tables 4 and 5 show the experimental results performed on the KEEL and UCI datasets. When analyzing table 4, we observe that the proposed AA KF achieves an average best accuracy value of 0.8488 on the balanced distributed data sets. The closest average accuracy value to the proposed KF is seen as polynomial (PO) 0.8479. The worst success rate on balanced datasets was obtained with the AtanK KF. It is given in table 4 that the multi-class dataset Zoo achieved higher success compared to other KFs. In table 5, it can be observed that the suggested AA KF achieved an average best accuracy value of 0.8832 on imbalanced distributed data sets. In addition, the closest average success rate to the proposed AA KF was observed as 0.8236 with the RBF kernel. It has been observed that the best success rate on the multiclass dataset Yeast is associated with the proposed AA KF. Consequently, tables 4 and 5 display that a high success rate was achieved on multi-class datasets. The AA KF, when tested on both balanced and imbalanced datasets, yielded significantly better results than the original AtanK function. In table 6, confidence intervals at a 95% confidence level were also calculated for each kernel. The proposed AA KF exhibits a more favorable confidence interval profile with a higher mean and a narrower interval compared to other kernels.

Tables 7 and 8 present the results of the F₁-score criterion from experiments performed on the KEEL and UCI datasets. Table 7 shows that the average best F₁-score, which is 0.7821, belongs to the proposed AA KF on balanced distributed datasets. The mean F₁-score value closest to AA KF is 0.7816 in PO KF. Additionally, the worst F₁-score on balanced datasets was 0.3410 in AtanK KF. Table 8 shows that the best average F₁-score value is 0.6916 for AA SF over imbalanced distributed datasets. Furthermore, the average success rate closest to AA KF is observed as 0.6675 in PO CF. Additionally, the worst F₁-score on imbalanced datasets was obtained as 0.2716 in the AtanK function. It has been observed that much better results are obtained with AA KF when tested on both balanced and unbalanced datasets compared to the original AtanK function. A graphic is shown in figure 7 for the accuracy and F₁-score results of the KFs on the KEEL and UCI datasets.

Table 8 F₁-scores of KF for the KEEL and UCI imbalanced datasets.

Figure 7

Mean classification results of the SVM kernels on KEEL and UCI repositories. (a) Accuracy, (b) F1-score.

In table 9, the proposed AA KF exhibits a better confidence interval profile with a higher mean and a smaller interval compared to the other kernels. Figure 7 shows the general classification accuracies of the SVM kernel according to dataset repositories. It is seen that the proposed method (AA) has higher classification accuracy on both the KEEL and UCI dataset repositories compared to other kernels.

Table 9 Confidence interval profile of KFs for balanced and imbalanced datasets (for F₁-scores).

The experimental results of the proposed Adaptive Arctan (AA) and AtanK, AG, RBF, LIN, and POL kernels on the six synthetic datasets are presented in tables 10 and 11. The mean accuracy and F₁-scores of the kernel functions on the synthetic datasets are shown in figures 8 and 9 respectively.

Table 10 Test accuracies of the synthetic datasets.

Table 11 Test F1-scores of the synthetic datasets.

Figure 8

Mean accuracy of the kernel functions on synthetic datasets.

Figure 9

Mean F1-scores of the kernel functions on synthetic datasets.

Tables 10 and 11 present the results of the accuracy and F1-score criterion from experiments performed on the synthetic datasets. It is observed that the proposed AA KF gives better accuracy and F1-score results in four out of six synthetic datasets compared to other KFs.

In tables 12 and 13, Wilcoxon signed-rank test was used to determine whether there is a difference between the measurement findings of two kernels via results obtained from the data sets in the experimental evaluations. The level of significance for the hypothesis test was determined as 0.05. The proposed adaptive arctan (AA) KF can be clearly distinguished from other KFs, as shown in the test results obtained from the hypothesis test.

Table 12 Comparison of the Wilcoxon signed-rank test results ($p=0.05$) for balanced datasets.

Table 13 Comparison of the Wilcoxon signed-rank test results ($p=0.05$) for imbalanced datasets.

When table 14 is analyzed, it is observed that the proposed AA KF on average takes shorter time than AtanK and AG, but takes longer time than the other kernels.

Table 14 Execution times (in sec.) of KF for the KEEL and UCI imbalanced datasets.

In this study, we propose a new AA KF that adapts to the characteristics of various datasets. The AA KF is obtained by hybridizing the AG and AtanK KFs. When using KFs in SVM, a significant amount of time is required to determine the most suitable $\sigma$ value for real-world problems. Our proposed SVM with the AA KF streamlines the learning process, as it employs a statistical model in the initial run instead. Instead of using a fixed $\sigma$ parameter as in the AtanK function, we introduce the AA KF with an adaptive structure tailored to each dataset. This modification results in faster and more efficient convergence for the SVM model. In the results we obtained, it is evident that the SVM model, when used with the proposed KF, performs exceptionally well on the KEEL and UCI datasets. No single method consistently delivers accurate F₁-score values across all datasets, as each dataset possesses unique characteristics. However, the proposed AA KF outperforms most of the previously suggested KFs in terms of average accuracy for the KEEL and UCI repositories.

5 Conclusion

The SVM is preferred by researchers in classification algorithms due to its successful performance, robust mathematical infrastructure, and relatively fast speed. Kernel functions (KFs) have a significant impact on both the performance and computational costs of SVMs. During the training process of the SVM model, manually determining the constant arbitrary value parameter of the AtanK KF can be timE−consuming and may lead to slow convergence of the SVM model. On the other hand, by introducing an adaptive KF into the SVM model, it's possible to obtain the most suitable Hilbert space decompositions for the datasets and the SVM during the training process. As a result, the SVM can achieve faster and better convergence. In this study, a new Adaptive Arctan (AA) KF is proposed for the SVM algorithm, which adapts to the characteristics of different datasets. Experimental evaluations were conducted on 30 public KEEL and UCI datasets using the proposed AA KF as well as AtanK, AG, RBF, linear, and polynomial kernels. The results indicate that the AA KF outperforms the other KFs and exhibits superior learning ability. Future work aims to finE−tune hyper parameters, including computational cost, kernel parameters, and the penalty constant. Additionally, in future studies, performance evaluation will extend to hybrid models involving real-time data and transfer learning. There is also an intention to introduce a new SVM kernel by incorporating an optimized ANN weight vector with a meta-heuristic optimization method, transformed into a Bayesian-optimized the SVM kernel.