A Theoretical Investigation on the Heat Transfer Ability of Water-Based Hybrid (Ag–Au) Nanofluids and Ag Nanofluids Flow Driven by Electroosmotic Pumping Through a Microchannel

Abstract

This article explores the peristaltically regulated electroosmotic pumping of water-based hybrid (Ag–Au) nanofluids through an inclined asymmetric microfluidic channel in a porous environment. A newly developed model termed as modified Buongiorno model which studies the impact of thermophoretic and Brownian diffusion phenomenon along with the inclusion of thermophysical attributes of nanoparticles is employed to predict the heat transfer attributes. Governing equations of the present model are linearized through Debye–Hückel and lubrication linearization principle. Mathematical software Maple 17 is applied to simulate the numerical results. Salient attributes of the electroosmotic peristaltic pumping subject to various physical parameters are assessed through graphical results. Visualization of fluid flow is presented by preparing contour plots for stream function. Moreover, a comparative study for water-based hybrid (Ag–Au) nanofluid and the silver nanofluid is made. It is found that the hybridity of nanofluid facilitates to achieve a much higher heat transfer rate as compared to silver-water nanofluid and thermophysical properties are remarkably improved in the case of hybrid nanofluids. The heat transfer rate is inversely related to the size of suspended nanoparticles. Furthermore, the mechanism of heat transfer is boosted through electroosmosis by reducing the thickness of the electric double layer and applying the electric field. This model will be applicable to developing biomicrofluidics devices for drug delivery systems.

1 Introduction

Pumping is essential to the function of transport phenomena to propel the fluids from one part to another part. Various types of pumping mechanisms are utilized to solve the propose of industries and others. While studying the natural transport phenomena like the movement of food bolus in the digestive system, blood flow in blood vessels, urine flow in the ureter, etc., peristaltic pumping [1, 2] plays an important role to transport the physiological fluids. This pumping mechanism is one of the oldest pump designs. This pumping mechanism has been utilized in industries for developing the various types of peristaltic pumps [3, 4]. A very interesting overview of peristaltic pumping is presented by Esser et al. [5] where they have discussed the classification and comparison of peristaltic pumps with biological pumps, technical pumping systems; biomimetic pumping systems, and comparison of pump performance.

While studying the transport phenomena in microscale, the very latest pumping mechanism known as electroosmotic pumping is frequently utilized for microfluidic systems. Electroosmotic pumping is one of the electrokinetic mechanisms, and it is defined as the movement of electrolyte solutions relative to the charged surface under the electric field effects. Wang et al. [6] reviewed the emerging development of electroosmotic pumps which can be utilized in designing micro- and nanofluidic devices and constructing their microplatforms. In another work of Wang et al. [7], they have presented the various features of electroosmotic pumps, introduced the fabrication technologies, and discussed their applications. Sarah and Li [8] reported the electroosmotic pumping in a rectangular microchannel and analyzed the liquid transport. Ramos et al. [9] investigated the electroosmotic flow of electrolyte at small-voltage amplitudes and higher-voltage amplitudes. They have reported that the flow regimes are opposite to each other for both cases. Edwards et al. [10] studied the pump efficiency and mechanical power for various pump shapes and also discussed the interesting applications for microfluidics. They observed that flow rates of 0.19–2.30 μL/min are noted for the range of 40–400 V. Zhao and Liao [11] investigated the pressure-driven flow under the non-isothermal condition. They have concluded that pumping performances for isothermal and non-isothermal models are dissimilar in presence of Joule heating. Nisar et al. [12] have discussed the applications of the electroosmotic pumps based on MEMS drug delivery systems. Manshadi et al. [13] presented a non-Newtonian fluid model power-law model to examine the fluid pumping and voltage requirement.

An interesting review [14] on electroosmotic pumps (mechanical and non-mechanical micropumps) and its biomedical applications were reported. Detail pieces of information about various types of micropumps like piezoelectric (PZT) micropumps; electrostatic and electroactive polymer composite micropumps; thermal actuation micropumps; electromagnetic (EM) actuation micropumps; magnetohydrodynamic (MHD) micropumps; electrohydrodynamic (EHD) micropumps; electroosmotic (EO) micropumps; bubble-type and evaporation-type micropumps; electrowetting (EW) and electrochemical micropumps and its applications in cell culturing; blood transport; drug delivery, etc., were also provided in this review. Another review [15] presented the developments in electroosmotic pumping from 2009 to 2018 in microflow analysis and discussed the characterization of electroosmotic pumps (EOP) like open channel EOP, packed column EOP, porous monolith EOP, porous membrane EOP, etc., and their applications. All the above studies focused on the peristaltic pumping models and electroosmotic pumping models. Considering the biomedical applications of electroosmotic pumping with adding the peristaltic pumping to enhance the performance of the pumping process and efficiency of the pumps, some of the recent mathematical models [16,17,18,19,20,21] have been reported in the literature to examine the combined effects of electroosmosis and peristalsis mechanisms for designing the future scope of smart pumps for use of biomedical applications.

In the recent development in heat transfer analysis, thermal systems, and nanotechnology, dissimilar nanoparticles are being suspended in the base fluids (to prepare the hybrid nanofluids) in the mixture or composite form to improve the heat transfer performance, i.e., thermal conductivity of the conventional fluids and nanofluids for making adequate for ultra-high cooling applications and thermal systems. However, the thermophysical properties of hybrid nanofluids depend on various physical parameters like shape, size of nanoparticles, the volume fraction of nanoparticles, types of base fluids (Newtonian fluid or non-Newtonian fluids), and other additives. The concept of using hybrid nanofluids [22] is to find out better thermal networks and synergistic effects of nanomaterials. However, many major challenges are still there in practical applications like the cost of nanoparticles, production process, stability, and many others discussed in this review report. Another review [23] on emerging development and applications of nanofluids has been reported. Mahanthesh et al. [24] investigated the heat transfer phenomenon of magneto-composite hybrid nanofluid over an isothermal wedge under the impact of space and temperature-dependent heat source. They considered the C₂H₆O₂–H₂O as a base fluid along with silver and MoS₂ as hybrid nanoparticles and utilized Runge–Kutta–Fehlberg method to solve the coupled nonlinear equations. The nonlinear convective flow of three different fluids, namely water, Al₂O₃-water nanofluid, and Cu-Al₂O₃-water hybrid nanofluid, due to rotating vertical planar plate is investigated by Ashlin and Mahanthesh [25]. They included the effect of internal heat generation and Rosseland’s radiative heat on fluid flow analysis. Considering the promising demands of the recent research in hybrid nanofluids and its applications, many more review reports [26,27,28] have been presented and various aspects of its signs of progress have been discussed. Inspired by the huge applications of hybrid nanofluids, some of the numerical and experimental works [29,30,31,32,33,34] have been investigated for examining the thermal performance of the hybrid nanofluids in which the works [33, 34] were considered the Ag–Au alloys for the hybrid nanofluids.

After a depth review of the literature on electroosmotic pumping, peristaltic pumping, and hybrid nanofluids presented above, it is found that none of the studies have reported the electroosmotic pumping of hybrid nanofluids with Ag–Au nanoparticles; however, a very recent investigation on the electroosmotic flow of hybrid nanofluid with TiO₂, Al₂O₃ and Cu nanoparticles has been reported by Prakash et al. [35]. Electroosmotically aided peristaltic pumps to provide many advantages such as maintain high flow rates and less contact of pumping materials with mechanical parts. Furthermore, the fluid flow can also be controlled through the actuation of electrodes. Such pumps are highly recommended for cooling circuits and in other microfluidic devices. Filling this gap, a mathematical model on hybrid nanofluid flow driven by electroosmotic pumping is developed in the present paper. A comparative study between hybrid nanofluids and nanofluids is also done to examine the thermal performance. The findings of the present model may be applicable in various thermal systems and management and develop a future scope of hybrid nanotechnology.

2 Mathematical Formulation

2.1 Flow Regime

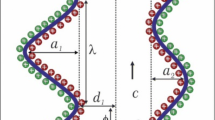
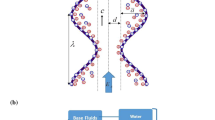
Here the peristaltic transport of aqueous hybrid nanofluid through an asymmetric microchannel is analyzed. The asymmetric microchannel is assumed to be inclined at an angle α with the vertical axis. Silver and gold nanoparticles of average diameter 25 nm are chosen to be dispersed in the aqueous base fluid at an initial temperature of 25 °C. To develop the hybrid nanofluid, initially, silver-water nanofluid is prepared and then gold nanoparticles are dispersed in silver-water nanofluid to get silver-gold + water hybrid nanofluid. Therefore, subscript 1 is used to designate the properties of silver nanoparticles and subscript 2 represents the gold nanoparticles properties. Peristaltic pumping is generated by propagating a sinusoidal wave of wavelength λ and speed c along the channel walls. Further, the electroosmotic phenomenon is induced to support the peristaltic pumping by applying an assisting electric field across an electric double layer generated by the aqueous ionic solution. The mathematical formulation of the problem is done by choosing the Cartesian coordinate system ($\tilde{X}$, $\tilde{Y},\tilde{t}$). The schematic configuration for the inclined asymmetric microchannel is depicted in Fig. 1. Mathematical expression for wall geometry is given as:

Fig. 1

Schematic representation of the physical setup of the problem

$$\begin{aligned} & \tilde{H}_{1} \left( {\tilde{X},\bar{t}} \right) = - b_{1} - d_{1} \sin \left( {\frac{2\pi }{\lambda }\left( {\tilde{x} - c\tilde{t}} \right)} \right), \\ & \tilde{H}_{2} \left( {\tilde{X},\bar{t}} \right) = b_{1} + d_{2} \sin \left( {\frac{2\pi }{\lambda }\left( {\tilde{X} - c\tilde{t}} \right) + \varphi } \right), \\ \end{aligned}$$

(1)

where b₁ and the b₂ symbolize the half-width of the lower and upper channel, respectively, d₁ and d₂ the amplitude of the lower and upper peristaltic wave, and $\varphi$ the phase angle between the waves.

2.2 Governing Equations

In this analysis, hybrid nanofluid is assumed to be incompressible. Buongiorno model in combination with the Hamilton–Crosser model for hybrid nanofluid is employed for mathematical modeling of aqueous hybrid nanofluid. Both gold and silver particles are taken in a cylindrical shape. The thermophysical properties of nanoparticles and the base fluid calculated at 298 K are indicated in Table 1. Fluid flow is being influenced by the presence of mixed convection and porous medium. The impact of thermal radiation on heat transfer procedure is also considered. Further, no-slip boundary conditions are satisfied by the fluid at channel walls.

Table 1 Thermophysical properties of pure water and silver nanoparticles

Subject to the above inferences, the momentum, energy, and concentration equations are derived as [36]:

$$\frac{{\partial \tilde{U}}}{{\partial \tilde{X}}} + \frac{{\partial \tilde{V}}}{{\partial \tilde{Y}}} = 0,$$

(2)

$$\begin{aligned} & \rho_{hnf} \left( {\frac{{\partial \tilde{U}}}{{\partial \tilde{t}}} + \tilde{U}\frac{{\partial \tilde{U}}}{{\partial \tilde{X}}} + \tilde{V}\frac{{\partial \tilde{U}}}{{\partial \tilde{Y}}}} \right) = - \frac{{\partial \tilde{P}}}{{\partial \tilde{X}}} + \mu_{hnf} \left( {\frac{{\partial^{2} \tilde{U}}}{{\partial \tilde{X}^{2} }} + \frac{{\partial^{2} \tilde{U}}}{{\partial \tilde{Y}^{2} }}} \right) + \rho_{\text{e}} E_{{\tilde{X}}} - \frac{{ \mu_{hnf} }}{{K_{1}^{*} }}\tilde{U} \\ & \quad + \rho_{hnf} g\sin \left( \alpha \right) + \left( {\rho \gamma } \right)_{hnf} g\left( {\tilde{T} - T_{0} } \right) + \rho_{hnf} \beta_{{\tilde{\varPhi }}} g\left( {\tilde{\varPhi } - \varPhi_{0} } \right), \\ \end{aligned}$$

(3)

$$\begin{aligned} & \rho_{hnf} \left( {\frac{{\partial \tilde{V}}}{{\partial \tilde{t}}} + \tilde{U}\frac{{\partial \tilde{V}}}{{\partial \tilde{X}}} + \tilde{V}\frac{{\partial \tilde{V}}}{{\partial \tilde{Y}}}} \right) = - \frac{{\partial \tilde{P}}}{{\partial \tilde{Y}}} + \mu_{hnf} \left( {\frac{{\partial^{2} \tilde{V}}}{{\partial \tilde{X}^{2} }} + \frac{{\partial^{2} \tilde{V}}}{{\partial \tilde{Y}^{2} }}} \right) - \frac{{ \mu_{hnf} }}{{K_{1}^{*} }}\tilde{V} \\ & \quad + \rho_{hnf} g\cos \left( \alpha \right), \\ \end{aligned}$$

(4)

$$\begin{aligned} & \left( {\rho C} \right)_{hnf} \left( {\frac{{\partial \tilde{T}}}{{\partial \tilde{t}}} + \tilde{U}\frac{{\partial \tilde{T}}}{{\partial \tilde{X}}} + \tilde{V}\frac{{\partial \tilde{T}}}{{\partial \tilde{Y}}}} \right) = K_{hnf} \left( {\frac{{\partial^{2} \tilde{T}}}{{\partial \tilde{X}^{2} }} + \frac{{\partial^{2} \tilde{T}}}{{\partial \tilde{Y}^{2} }}} \right) + \tau \cdot L^{t} \\ & \quad + \left( {\rho C} \right)_{\text{p}} D_{\text{B}} \left( {\frac{{\partial \tilde{\varPhi }}}{{\partial \tilde{X}}}\frac{{\partial \tilde{T}}}{{\partial \tilde{X}}} + \frac{{\partial \tilde{\varPhi }}}{{\partial \tilde{Y}}}\frac{{\partial \tilde{T}}}{{\partial \tilde{Y}}}} \right) + \frac{{D_{\text{T}} }}{{\tilde{T}_{0} }}\left( {\rho C} \right)_{\text{p}} \left( {\left( {\frac{{\partial \tilde{T}}}{{\partial \tilde{X}}}} \right)^{2} + \left( {\frac{{\partial \tilde{T}}}{{\partial \tilde{Y}}}} \right)^{2} } \right) - \frac{{\partial q_{\text{r}} }}{{\partial \tilde{Y}}}, \\ \end{aligned}$$

(5)

$$\left( {\frac{{\partial \tilde{\varPhi }}}{{\partial \tilde{t}}} + \tilde{U}\frac{{\partial \tilde{\varPhi }}}{{\partial \tilde{X}}} + \tilde{V}\frac{{\partial \tilde{\varPhi }}}{{\partial \tilde{Y}}}} \right) = D_{\text{B}} \left( {\frac{{\partial^{2} \tilde{\varPhi }}}{{\partial \tilde{X}^{2} }} + \frac{{\partial^{2} \tilde{\varPhi }}}{{\partial \tilde{Y}^{2} }}} \right) + \frac{{D_{\text{T}} }}{{\tilde{T}_{0} }}\left( {\frac{{\partial^{2} \tilde{T}}}{{\partial \tilde{X}^{2} }} + \frac{{\partial^{2} \tilde{T}}}{{\partial \tilde{Y}^{2} }}} \right).$$

(6)

where

$$L\, = \,{\text{grad}}\left( {\vec{V}} \right).$$

According to Roseland’s approximation, the radiation energy emitted by a body per unit of time is given by [37]

$$q_{\text{r}} = - \frac{{16\sigma^{*} }}{{3\kappa^{*} }}T_{0}^{3} \frac{{\partial \tilde{T}}}{{\partial \tilde{Y}}},$$

with $\kappa^{*}$ and $\sigma^{*}$ being the coefficient of mean absorption and the Stefan–Boltzmann constant, respectively. Further, in the above equations, $\tilde{P}$, $K_{1}^{*} ,$ $\rho_{\text{e}} , g$, $\left( {\rho \gamma } \right)_{hnf}$, $D_{\text{T}}$, $D_{\text{B}}$, $\left( {\rho C} \right)_{hnf}$, $\tilde{T}_{0}$, $\beta_{{\tilde{\varPhi }}} ,$ $\tilde{\varPhi }$, $\tilde{T}$, $\mu_{hnf}$, $\rho_{hnf}$, $K_{hnf}$ and $\left( {\rho C} \right)_{\text{p}}$ portend the pressure force, the porosity parameter, the charge number density, volume expansion coefficient for heat, the parameter of thermophoretic and Brownian diffusion coefficient for hybrid nanofluid calculated by the same way as defined by Buongiorno [38], the specific heat capacity for hybrid nanofluid, the temperature maintained at the lower wall, volume expansion coefficient for mass transfer, the temperature of hybrid nanofluid, the nanoparticle volume fraction, the viscosity and the density of the hybrid nanofluid, the thermal conductivity for hybrid nanofluid and the specific heat for nanoparticles, respectively. Furthermore, the term $\rho_{hnf} g\sin \left( \alpha \right)$ in Eq. (3) occurs due to inclination of the microchannel with $\alpha$ being the angle of inclination with $\tilde{X}$-axis and the term $\tau \cdot L^{t}$ in Eq. (5) arises due to the viscous dissipation with $\tau$ representing the stress tensor.

The general mixture rule is utilized to calculate the density, specific heat capacity and thermal expansion for hybrid nanofluid, and the correlations are given by:

$$\rho_{hnf} = \left( {1 - \varPhi_{2} } \right)\left[ {\left( {1 - \varPhi_{1} } \right)\rho_{bf} + \varPhi_{1} \rho_{s1} } \right] + \varPhi_{2} \rho_{s2} ,$$

(7)

$$\left( {\rho C} \right)_{hnf} = \left( {1 - \varPhi_{2} } \right)\left[ {\left( {1 - \varPhi_{1} } \right)\left( {\rho C} \right)_{bf} + \varPhi_{1} \left( {\rho C} \right)_{s1} } \right] + \varPhi_{2} \left( {\rho C} \right)_{s2} ,$$

(8)

$$\left( {\rho \gamma } \right)_{hnf} = \left( {1 - \varPhi_{2} } \right)\left[ {\left( {1 - \varPhi_{1} } \right)\left( {\rho \gamma } \right)_{bf} + \varPhi_{1} \left( {\rho \gamma } \right)_{s1} } \right] + \varPhi_{2} \left( {\rho \gamma } \right)_{s2} ,$$

The effective thermal conductivity for hybrid nanofluid is predicted by the Hamilton–Crosser model and the Brinkman model is employed for effective viscosity of hybrid nanofluid as [39]:

$$\begin{aligned} & K_{hnf} = K_{nf} \left( {\frac{{K_{s2} + \left( {M - 1} \right)K_{nf} - \left( {M - 1} \right)\varPhi_{2} \left( {K_{nf} - K_{s2} } \right)}}{{K_{s2} + \left( {M - 1} \right)K_{nf} + \varPhi_{2} \left( {K_{nf} - K_{s2} } \right)}}} \right) , \\ & K_{nf} = K_{bf} \left( {\frac{{K_{s1} + \left( {M - 1} \right)K_{bf} - \left( {M - 1} \right)\varPhi_{1} \left( {K_{bf} - K_{s1} } \right)}}{{K_{s1} + \left( {M - 1} \right)K_{bf} + \varPhi_{1} \left( {K_{bf} - K_{s1} } \right)}}} \right) \\ \end{aligned}$$

(9)

$$\frac{{ \mu_{hnf} }}{{\mu_{bf} }} = \frac{1}{{\left( {1 - \varPhi_{1} } \right)\left( {1 - \varPhi_{2} } \right)}} = A,$$

(10)

Here $\varPhi_{1}$ and $\varPhi_{2}$ denote the volume fraction for silver and gold nanoparticles, respectively, M is the shape parameter, $\rho_{s}$ the density of nanoparticles, $\rho_{bf}$ the density of water, $K_{s}$ and $K_{bf}$ the thermal conductance of solid nanoparticles and water, respectively, and $\gamma_{s}$ and $\gamma_{bf}$ the thermal expansion for nanoparticle and the water, respectively.

From the theory of electrostatics, the electric charge distribution $\tilde{E}$ in the vicinity of the diffuse layer is described by the Poisson equation as:

$$\nabla^{2} \tilde{E} = - \frac{{\rho_{e} }}{{\varepsilon_{0} \varepsilon }},$$

(11)

where ε designates the dielectric constant for the solution, $\varepsilon_{0}$ the dielectric constant of vacuum and the net charge density $\rho_{\text{e}}$ is given by:

$$\rho_{\text{e}} = ez\left( {n^{ + } - n^{ - } } \right),$$

(12)

here e denotes the electron charge, and $n^{ - }$ and $n^{ + }$ are the anions and cations with bulk concentration n₀ and z is the valency of ions.

As the flow is unsteady in the fixed coordinates system ($\tilde{X}$, $\tilde{Y},\tilde{t}$) therefore a frame is attached with the peristaltic wave which moves with it and the flow becomes steady in the moving frame of reference ($\bar{X}$, $\bar{Y}, \tilde{t}$). The correlations for flow quantities in both frames of references are:

$$\bar{X} = \tilde{X} - c\tilde{t},\bar{U} = \tilde{U} - c, \bar{Y} = \tilde{Y},$$

$$\bar{V} = \tilde{V}, \bar{P}\left( {\bar{X},\bar{Y}} \right) = \tilde{P}\left( {\tilde{X},\tilde{Y},\tilde{t}} \right),$$

The dimensionless parameters involved in the non-dimensional analysis of the flow problem are listed as:

$${\begin{aligned} & x = \frac{{\bar{X}}}{\lambda }, \,\,y = \frac{{ \bar{Y}}}{{b_{1} }},\,\, p = \frac{{\bar{P}b_{1}^{2} }}{{\mu_{bf} c}},\,\,u = \frac{{\bar{U}}}{c},\,\,v = \frac{{\bar{V}}}{c},\,\, n = \frac{{\tilde{n}}}{{n_{0} }},\,\,{\text{Br}} = {\text{Ec}} \Pr , \\ & h_{1} = \frac{{\tilde{H}_{1} }}{{b_{1} }},\,\, h_{2} = \frac{{\tilde{H}_{2} }}{{d_{1} }},\,\,\Pr = \frac{{\mu_{bf} C_{\text{p}} }}{{K_{bf} }} , \,\,\delta = \frac{{b_{1} }}{\lambda },\,\, \theta = \frac{{\tilde{T} - \tilde{T}_{0} }}{{\overline{{\tilde{T}_{1} - \tilde{T}_{0} }} }},\,\,{\text{Gr}}_{\text{c}} = \frac{{\rho_{bf} g\beta_{{\bar{\varPhi }}} b_{1}^{2} \varPhi_{0} }}{{\mu_{bf} c}}, \\ & K_{1} = \frac{{K_{1}^{*} }}{{b_{1}^{2} }},\,\,\varPhi = \frac{{\tilde{\varPhi } - \varPhi_{0} }}{{\varPhi_{0} }} ,\,\,E = \frac{{ez\bar{E}}}{{k_{\text{B}} \hat{T}_{\text{avg}} }},\,\,{\text{Re}} = \frac{{\rho_{bf} cb_{1} }}{{\mu_{bf} }},\,\,{\text{Fr}} = \frac{{c^{2} }}{{gb_{1} }} \\ & U_{\text{HS}} = - \frac{{\varepsilon_{0} \varepsilon k_{\text{B}} \hat{T}_{\text{avg}} E_{x} }}{{ez\mu_{bf} c}},\,\, k = \sqrt {\frac{{2n_{0} e^{2} z^{2} b_{1}^{2} }}{{\varepsilon_{0} \varepsilon k_{\text{B}} \hat{T}_{\text{avg}} }}} = \frac{{b_{1} }}{{\lambda_{\text{d}} }}, \,\,N_{\text{t}} = \frac{{D_{{\bar{T}}} \tau^{*} \rho_{bf} \left( {\tilde{T}_{1} - \tilde{T}_{0} } \right)}}{{\tilde{T}_{0} \mu_{bf} }} , \\ & N_{\text{b}} = \frac{{D_{\text{B}} \tau^{*} \rho_{\text{b}} \varPhi_{0} }}{{\mu_{bf} }}, \tau^{*} = \frac{{\left( {\rho c} \right)_{\text{p}} }}{{\left( {\rho c} \right)_{bf} }},\,\,{\text{Ec}} = \frac{{c^{2} }}{{c_{\text{p}} \left( {\bar{T}_{1} - \bar{T}_{0} } \right)}},\,\,{\text{Gr}}_{\text{t}} = \frac{{\rho_{bf} g\gamma_{bf} b_{1}^{2} \left( {T_{1} - T_{0} } \right)}}{{\mu_{bf} c}}, \\ & A_{1} = \frac{{\left( \rho \right)_{hnf} }}{{\left( \rho \right)_{bf} }},L = \frac{{\left( {\rho \gamma } \right)_{hnf} }}{{\left( {\rho \gamma } \right)_{bf} }}, \varPsi = \frac{{\tilde{\varPsi }}}{{cb_{1} }} , R = \frac{{16\sigma^{*} T_{0}^{3} }}{{3k^{*} \mu_{bf} C_{bf} }}. \\ \end{aligned}}$$

(13)

where Pr portend the Prandtl number, Ec the Eckert number, Br the Brinkmann number, R the radiation parameter, N_b the coefficient of Brownian diffusion, N_t the thermophoretic parameter, Ψ the stream function, Re the Reynolds number, ${\text{Gr}}_{\text{c}}$ the mass transfer Grashof number, Fr the Froude number, U_HS the Helmholtz–Smoluchowski velocity, ${\text{Gr}}_{\text{t}}$ the temperature Grashof number, k the Debye length parameter, K₁ the parameter for porosity, and Φ and θ the dimensionless nanoparticle concentration and temperature, respectively.

Inserting non-dimensional numbers and velocity components defined in terms of stream function as defined below:

$$u = \varPsi_{y} , v = - \delta \varPsi_{x} ,$$

(14)

and then adopting the lubrication approximation theory, Eqs. (2)–(6) and (11)–(12) in their dimensionless form are:

$$\frac{\partial p}{\partial x} = A\frac{{\partial^{3} \psi }}{{\partial y^{3} }} + U_{{\text{HS}}} \frac{{\partial^{2} E}}{{\partial y^{2} }} - \frac{A}{{K_{1} }}\left( {\frac{\partial \psi }{\partial y} + 1} \right) + \frac{{\text{Re}}}{{\text{Fr}}}A_{1} { \sin }\left( \alpha \right) + {\text{Gr}}_{{\text{t}}} L\theta + {\text{Gr}}_{{\text{c}} }A_{1} \varPhi ,$$

(15)

$$A\frac{{\partial^{4} \psi }}{{\partial y^{4} }} + U_{\text{HS}} \frac{{\partial^{3} E}}{{\partial y^{3} }} - \frac{A}{{K_{1} }}\frac{{\partial^{2} \psi }}{{\partial y^{2} }} + {\text{Gr}}_{\text{t}} L\frac{\partial \theta }{\partial y} + {\text{Gr}}_{\text{c}} A_{1} \frac{\partial \varPhi }{\partial y} = 0,$$

(16)

$$\left( {\frac{{K_{hnf} }}{{K_{\text{b}} }} + \Pr R} \right)\frac{{\partial^{2} \theta }}{{\partial y^{2} }} + { \Pr }N_{\text{b}} \frac{\partial \theta }{\partial y}\frac{\partial \varPhi }{\partial y} + { \Pr }N_{\text{t}} \left( {\frac{\partial \theta }{\partial y}} \right)^{2} + {\text{Br}}\,A\left( {\frac{{\partial^{2} \psi }}{{\partial y^{2} }}} \right)^{2} = 0,$$

(17)

$$\frac{{\partial^{2} \varPhi }}{{\partial y^{2} }} + \frac{{N_{\text{t}} }}{{N_{\text{b}} }}\frac{{\partial^{2} \theta }}{{\partial y^{2} }} = 0,$$

(18)

$$\frac{{\partial^{2} E}}{{\partial y^{2} }} = k^{2} \left( {\frac{{n^{ - } - n^{ + } }}{2}} \right).$$

(19)

Utilizing the Boltzmann distribution function defined below as [36]:

$$n^{ \pm } = {\text{e}}^{ \mp E} = {\text{e}}^{{ \mp \frac{{ez\bar{E}}}{{k_{\text{B}} \hat{T}}}}} ,$$

(20)

in Eq. (19) which characterizes the distribution of ions in the fluid medium, we get

$$\frac{{\partial^{2} E}}{{\partial y^{2} }} = k^{2} \sinh \left( E \right),$$

(21)

As for the wide range of PH of ionic solutions, the zeta potential established across electric double layer is not more than 25 mV; therefore, Eq. 21 is linearized under the approximation of small zeta potential termed as Debye–Hückel linearization principle, and we get:

$$\frac{{\partial^{2} E}}{{\partial y^{2} }} = k^{2} E,$$

(22)

Subject to the following boundary conditions for electric potential,

$$E|_{{y = h_{1} }} = \xi , E|_{{y = h_{2} }} = \xi ,$$

(23)

integrating Eq. (22) results in the following expression

$$E = \xi \frac{{{ \cosh }\left( {\frac{k}{2}\left( {h_{1} + h_{2} - 2y} \right)} \right)}}{{{ \cosh }\left( {\frac{k}{2}\left( {h_{1} - h_{2} } \right)} \right)}}.$$

(24)

The appropriate boundary conditions in the non-dimensional form are expressed as:

$$\begin{aligned} & \psi = - \frac{F}{2},\frac{\partial \psi }{\partial y} = - 1,\, \theta = 0,\, \varPhi = 0\,\,{\text{at}}\,\,y = h_{1} = - 1 - \varepsilon_{1} \sin \left( {2\pi X} \right), \\ & \psi = \frac{F}{2},\frac{\partial \psi }{\partial y} = - 1, \,\theta = 1, \,\varPhi = 0\,\,{\text{at}}\,\,y = h_{2} = d + \varepsilon_{2} \sin \left( {2\pi X + \varphi } \right), \\ \end{aligned}$$

(25)

where F is the volumetric flow rate and is derived as:

$$F = Q - 1 - d,$$

in which Q is a time-mean flow rate calculated for a single period of the wave.

Pressure rise across one period of the wave is calculated by integration pressure gradient over the range of [0,1] as:

$$\Delta P_{\lambda } = \mathop \int \limits_{0}^{1} \frac{{{\text{d}}p}}{{{\text{d}}x}}{\text{d}}x,$$

Heat transfer rate is calculated as:

$$Z = \frac{\partial h}{\partial x}\left( {\frac{\partial \theta }{\partial y}} \right)_{{y \to h_{2} }}.$$

2.3 Solution Methodology

The reduced system of the equations obtained from the mathematical formulation of the flow problem is highly nonlinear and cannot be executed directly for the analytical solution; therefore, the solution is approximated through built-in numerical technique “dsolve numeric” in Maple 17. This solution is then plotted graphically to visualize the pattern of velocity, temperature, and concentration profile through Maple and Mathematica. Additionally, graphical results are also obtained for pressure rise per wavelength and the stream function.

3 Results and Discussion

This section is devoted to a brief graphical illustration of the governing problem. Graphical results are prepared to manifest the significance of involved parameters on flow properties such as axial velocity, concentration, streamlines, temperature, and pressure rise per wavelength. A comparative study for hybrid nanofluid and silver nanofluid is presented. The bar graphs are prepared to visualize the variation in the heat transfer coefficient for both hybrid and silver-water nanofluid. Both silver and gold nanoparticles are taken in an equal amount of 0.06 vol% and the effect of raising the volume fraction of nanoparticles to 0.2 vol% is analyzed. The average diameter of both types of nanoparticles is taken to be 25 nm, and the initial temperature is 298 K. Under these assumptions, the Prandtl number for water is found to be 6.068. At the volume fraction of 0.06 vol% for each type of nanoparticles and a temperature difference of 10 K, the thermophoretic and the Brownian diffusion parameters are found to be N_t = 4.1683 × 10⁻⁵ and N_b = 1.35412 × 10⁻⁵, respectively.

Figure 2a–f is plotted to portray the influence of the Debye length parameter, HS velocity, nanoparticle volume fraction, porosity parameter, and Grashof number for temperature and mass transfer on the axial velocity. It can be seen through plots that the velocity of the fluid exhibits a parabolic profile with the velocity of hybrid nanofluid lower than the velocity of silver-water nanofluid. Figure 2a manifests the outcomes of the Debye length parameter on velocity. Since Debye length is inversely related to the width of the electric double layer, an enhancement in k corresponds to a thin EDL which refers to an inhomogeneous distribution of electric potential in the fluid medium. Hence a larger potential difference accelerates the fluid flow. Figure 2b encloses the outcomes of HS velocity parameter U_HS on the velocity of hybrid nanofluid and silver + water nanofluid. A negative value of U_HS refers to an electric field in the positive X-direction, U_HS = 0 means no electric field, and U_HS > 0 corresponds to an opposing electric field. It can be noticed that for assisting electric field, velocity is maximum and it is minimum for an opposing electric field. From Brinkman’s relation for the viscosity of hybrid nanofluid, it is obvious that viscosity of the hybrid nanofluid tends to rise for increasing the fraction of nanoparticle in water; therefore, velocity profile diminishes via larger nanoparticle volume fraction as depicted in Fig. 2c. Figure 2d is drawn to delineate the development in the velocity profile for the rise in the porosity parameter. Fluid flow is being accelerated for enhancement in K₁ as less resistance is experienced by the fluid for raising the number of pores in the asymmetric microchannel. Figure 2e and f provides insight to alteration in velocity profile for larger thermal and mass transfer Grashof number. The resulting graphs demonstrate that velocity tends to rise significantly for larger Gr_t, however, a reduction in velocity is observed for increasing Gr_c. This result is physically valid as for larger Gr_t, the temperature rises to produce an enhancement in kinetic energy of fluid particles which strengthens the velocity. However, an increase in Gr_c elevates the concentration of fluid which reduces the speed of fluid due to strong viscous forces.

Fig. 2

Axial velocity distribution u(y) for k, U_HS, Φ_1, Φ₂, K₁, Gr_t, and Gr_c

In the moving frame of reference, streamlines have usually the same shapes like that of channel walls. But under some particular conditions, some streamlines split and trap an amount of fluid called the fluid bolus. This procedure is termed as trapping which is an inherent property of peristalsis. It is very useful in the proper transportation of food and other liquid within the human body. Figures 3, 4, 5 and 6 are prepared to visualize the fluid flow pattern of hybrid nanofluid for distinct values of pertinent parameters. Figure 3a–c delineates the impact of the porosity parameter on the trapping phenomenon. The resulting panels clarify that there is only a minor alteration in the volume of trapped bolus for an enhancement in the porosity parameter. The impression of the Debye length parameter on the pattern of streamlines is manifested through Fig. 4a–c. For varying values of k, the size of the trapped bolus near the upper wall of the channel is shrunk as observed through resulting plots. Figure 5a–c exhibits the impact of multiple values of the HS velocity parameter on streamline behavior. It has been found that for the electric field in the direction of peristalsis, a large number of streamlines are trapped in the vicinity of channel walls. In the absence of an electric field, there is a reduction in the trapping region and the number of closed streamlines. However, in the case of resisting electric field, the volume of trapping bolus shrinks near the upper wall of the asymmetric microchannel and the size of the trapping bolus is magnified near the lower wall. Figure 6a–c depicts the circulatory flow pattern for increasing the nanoparticle volume fraction in the base fluid. There is a slight decline in the size of the trapped bolus through enhancement in the number of dispersed nanoparticles in water ionic solution.

Fig. 3

Streamlines for a K₁ = 0.3, b K₁ = 0.5, and c K₁ = 0.7

Fig. 4

Streamlines for a k = 2, b k = 2.5, and c k = 3

Fig. 5

Streamlines for a U_HS = − 2, b U_HS = 0, and c U_HS = 2

Fig. 6

Streamlines for a Φ₁, Φ₂ = 0.03, b Φ₁, Φ₂ = 0.06, and c Φ₁, Φ₂ = 0.09

Figure 7a–g reveals the development in pressure rise per wavelength of both hybrid and silver nanofluid for variation in different physical parameters of interest. A positive value of ΔP_λ physically implies that pressure force is acting in the opposite direction of the flow and a positive value corresponds to an assisting pressure force. It has been found that ΔP_λ is larger for hybrid nanofluid when compared with the pressure rise per wavelength in the case of silver nanofluid. Figure 7a discloses the impact of the Debye length parameter k on pressure rise per wavelength. As a reduction in the electric double layer stimulates the flow of the fluid, therefore, ΔP_λ declines via a rise in k. Pressure rise per wavelength significantly decays when the direction of the electric field is changed from backward direction to forward direction as indicated in Fig. 7b. Obviously, in that case, the electric field assists the peristaltic pumping of nanofluid which decreases the pressure force in a positive direction. The decreasing impact of Reynolds number on ΔP_λ is manifested through Fig. 7c. Figure 7d displays the pressure rise per wavelength profile for three distinct values Froude number. It is concluded that ΔP_λ is inversely related to the Froude number. As it is clear from the mathematical formulation of the problem that for an increase in Froude number, the effect of gravitation force on flow phenomenon is strengthened which tends to accelerate the flow. An enhancement in nanoparticle volume fraction in the base fluid resists the flow therefore, a rise in the retarding pressure force is noticed for the addition of a larger number of nanoparticles in the base fluid (see Fig. 7e). The variation in pressure rise per wavelength in response to a rise in inclination angle is exhibited through Fig. 7f. It has been found that ΔP_λ grows when the asymmetric microchannel is inclined at a larger angle with the horizontal axis.

Fig. 7

Pressure rise per wavelength ∆P_λ for k, U_HS, Re, Fr, Φ₁, Φ₂, and α

Figure 8a–f is plotted to examine the development in the temperature profile of hybrid nanofluid and silver + water nanofluid for diverse active parameters. It has been found that the temperature of hybrid nanofluid is less than the temperature of silver/water nanofluid and graphs for temperature profile are satisfying the no-slip boundary conditions imposed on the channel walls. Physically, the thermal conductance properties of hybrid nanofluids are higher when compared with mono nanofluids. Due to the enhanced capability of heat transfer of hybrid nanofluid, they are preferred over regular nanofluid in many mechanical cooling systems. Figure 8a outlines the consequences of rising the radiation parameter on the temperature profile of hybrid and regular nanofluid. A reverse impact of R on θ(y) is noted through the resulting panel. This result is well justified as for the rising radiation parameter, and the intensity of thermal radiations tends to decay which reduces the temperature of nanofluids. Increasing nanoparticle volume fraction in the base fluid enhances the cooling efficiency of nanofluid which results in net decay in the temperature profile of the fluid as illustrated through Fig. 8b. The effect of the average diameter of nanoparticles on the net temperature of the fluid is elucidated through Fig. 8c. Using the smaller nanoparticles favors the free movement which results in the enhancement of microconvection of nanoparticles. This free movement of nanoparticles enhances the collision between nanoparticles and the molecules of the base fluid, and consequently, the temperature of the nanofluid is maximum for small nanoparticles. However, when larger nanoparticles are dispersed in the fluid medium, the Brownian diffusion of nanoparticles is retarded which results in the reduction of the temperature. Figure 8d presents an enhancement in temperature profile via a larger Debye length parameter. Since reducing EDL thickness results in enhancement of the effectiveness of electric body forces which results in a heated fluid. Figure 8e portrays the influence of the direction of HS velocity on θ(y). It is noteworthy that temperature is amplified when the direction of the electric field is the same as that of the direction of flow and it significantly declines for the opposite direction of the electric field.

Fig. 8

Temperature profile θ(y) for R, Φ₁, Φ₂, d_p, k, and U_HS

The influence of different involved parameters on the distribution of nanoparticles within the fluid medium is interpreted through Fig. 9a–e. Figure 9a analyzes the advancement in the concentration of nanoparticles for rising values of radiation parameter. Since the viscosity of the fluid escalates for enlargement in the radiation parameter, nanoparticle volume fraction grows at the center of the asymmetric microchannel. Figure 9b displays the impact of Φ₁ and Φ₂ on the distribution of nanoparticles in the fluid medium. It is quite obvious that when a larger amount of nanoparticles are dispersed in the fluid, the number of nanoparticles at a point in the medium also rises. Figure 9c manifests that when a larger temperature difference is imposed between the channel walls, the concentration of nanoparticles decays significantly. It is due to enhancement in thermophoretic diffusion of nanoparticles and the amplification in the strength of buoyancy forces which cause the nanoparticles to diffuse out of the microchannel. Figure 9d exhibits the variation in Φ(y) for rising values of k. As a stronger potential difference is maintained across the fluid medium when the width of EDL is reduced therefore a decreases in nanoparticle concentration is produced. Figure 9e evaluates the consequence of electric field directions on the concentration profile of particles. It has been revealed that the concentration of nanoparticles is minimum for negative values of U_HS, and it is maximized for positive values.

Fig. 9

Nanoparticle volume fraction Φ(y) for R, Φ₁, Φ₂, ∆T, k, and U_HS

Figure 10a–e preserves the alterations in heat transfer rate for varying different parameters involved in the mathematical formulation of the problem for both hybrid and regular nanofluid through bar graphs. Notably, there is a remarkable enhancement in the magnitude of the heat transfer coefficient when hybrid nanofluids are utilized instead of regular nanofluids. Figure 10a presents the heat transfer rate for variation in the HS velocity parameter. The heat transfer rate is more pronounced in the case of assisting the electric field when compared with the heat transfer coefficient for an opposing electric field. It is quite obvious that the heat transfer mechanism is boosted with a fast-moving fluid and it has been discussed earlier that the velocity of the fluid rises for an assisting electric field which is the reason behind enhancement in the magnitude of heat transfer coefficient. The impact of the radiation parameter on the process of heat transfer is manifested in Fig. 10b. A decaying trend in heat transfer toward enhancing R is noticed. As the heat transfer rate is directly related to the temperature of the fluid and larger values of R correspond to thermal radiations of decreased intensity; therefore, the heat transfer rate is decelerated via R. To examine the influence of nanoparticle volume fraction on heat transfer, Fig. 10d is prepared. As the thermal conductivity of nanofluid is directly related to the number of nanoparticles suspended in the base fluid therefore, the magnitude of heat transfer significantly rises for the larger volume fraction of particles. The heat transfer mechanism of nanofluid is strongly affected by the size of nanoparticles being suspended in the base fluid. Figure 10c clarifies that the magnitude of heat transfer coefficient escalates for smaller sized nanoparticles. The effects of the Debye length parameter on the heat transfer rate are presented in Fig. 10e. As there is an inverse relationship between k and EDL thickness and a thin EDL corresponds to the enhanced kinetic energy of fluid particles, heat transfer rate intensifies for a rise in k.

Fig. 10

Heat transfer rate for U_HS, R, d_p, Φ₁, Φ₂, and k

A comparison of velocity and temperature profile of limiting case of currently performed analysis and the previously published work carried out by Prakash et al. [40] is presented in Tables 2 and 3, respectively. A close agreement can be clearly observed from these tables.

Table 2 Comparison of velocity profile of current investigation and the results obtained by Prakash et al. [40]

Table 3 Comparison of temperature profile of current investigation and the results obtained by Prakash et al. [40]

4 Concluding Remarks

This article deals with the numerical simulation of the electroosmotic pumping of water-based hybrid nanofluid (Ag–Au/water) through an inclined asymmetric microchannel in a porous environment. Graphical results are prepared to deliberate the influence of involved parameters on the flow and thermal phenomena. The deduced results of this investigation are summarized as:

• It has been noticed that when a volume fraction of 6% of silver nanoparticles is added in water, an increment of up to 31% in its thermal conductivity is obtained. However, when an equal amount of gold nanoparticles is added to this silver-water nanofluid, its thermal conductivity rises to 71.53%.

• The hybridity of nanofluid produces a major improvement in the heat transfer rate of the moving fluid; therefore, it can be concluded that hybrid nanofluid is a more efficient cooling agent than the regular nanofluid.

• The drag force experienced by the nanofluid is strengthened by enhancing nanoparticle volume fraction in the base fluid.

• The circulatory flow of the fluid is accelerated by assisting electric field and retarded by the opposing electric field.

• Nanofluid with smaller nanoparticles has a boosted rate of heat transfer.

• Both velocity and the temperature of hybrid and silver nanofluid are developed by reducing electric double layer thickness.

• The absolute value of the heat transfer coefficient grows for larger Debye length parameter.

The above findings may help in developing the smart electroosmotic pumping devices for transport phenomena of the microscale volume of liquids and geometries to solve the various purpose of biomedical applications.