Introduction

Electroosmosis [1] is a mechanism of electrokinetics which means the osmosis (i.e., the movement of molecules/liquids from less concentrated solution to a more concentrated solution) under the influence of the electric field. Electrokinetics is the new branch of mechanics that deals with the relation between the motion of aqueous solutions/particles and electroosmotic/electrophoretic forces. Electroosmosis [2] has recently been receiving vital interest in diverse applications in chemical analysis, medical diagnostics, material synthesis, drug delivery, environmental detection, and monitoring. It is also applicable to various phenomena like the movement of ions and aqueous solution in micro- and nanochannels, thermomigration and thermodiffusion in aqueous solutions, etc.

Peristaltic transport [3, 4] is a natural transport mechanism that deals with the physiological transport phenomena utilizing successive muscle contraction and relaxation. Peristaltic propulsion of compressible Jeffrey fluid through a porous channel under the effect of magnetic field is studied by Saleem et al. [5]. Bhatti et al. [6] utilized the Jeffrey fluid model to study the intra-uterine flow of the fluid with suspended nanoparticles by considering the compliant wall boundary conditions. Ellahi et al. [7] performed an investigation on the peristaltic flow of water-based aluminum oxide nanofluid through a symmetric channel in the presence of thermal radiation and analyzed the process of entropy generation through the fluid flow. The impact magnetic zinc oxide nanoparticles on the flow of blood through tapered arteries using the Jefferey fluid model is investigated by Zhang et al. [8]. They also performed the analysis on the entropy generation during the fluid flow. Saleem et al.[9] studied the peristaltic pumping of Casson nanofluid through a duct having the elliptical cross section. The combined study of electroosmosis and peristalsis [10, 11] develops a new branch of the biomicrofluidics where the physiological flows can be analyzed under the effects of external electric fields. Inspired by the biomicrofluidics applications of peristalsis and electroosmosis, many mathematical models [12,13,14,15,16,17,18,19,20,21,22,23] have been developed to investigate the peristaltic transport phenomena modulated by the electroosmosis. Electroosmosis flow driven by peristaltic pumping with entropy generation has been analyzed Ranjit and Shit [12]; Sisko fluid has been done by Akram et al. [13]; electrothermal transport of nanofluids has been studied by Tripathi et al. [14]; transportation of ionic liquid in porous microchannel has been examined by Ranjit et al.[15], heat and mass transfer analysis in two-phase flow has been computed by Bhatti et al.[16]; Williamson ionic nanoliquids in the presence of thermal radiation have been presented by Prakash and Tripathi [17]; of ionic nanoliquids in biomicrofluidics channel has been investigated by Prakash et al. [18]; non-Newtonian Jeffrey fluid in asymmetric has been studied by the Tripathi et al.[19]; heat transfer analysis in blood flow has been investigated by Prakash et al.[20]; thermal analysis of Casson fluids has been added by Reddy et al.[21]; thermal analysis of Sutterby nanofluids has been presented by Akram et al. [22]; entropy generation in porous media has been analyzed by Noreen and Qurat [23]. After a depth reviewed of the literature on electroosmosis modulated peristaltic pumping, it is concluded that flow, pumping, and thermal characteristics are strongly magnified by the electroosmosis mechanism. Many biomicrofluidics devices can be engineered based on their findings. However, no such investigation is available in the literature which deals with the Single-walled nanotubes (SWCNTs) suspended nanofluids flow driven by the combined effects of electroosmosis and peristalsis.

Single-walled nanotube (SWCNT) is a CNT that exhibits electric properties that are different from multi-walled carbon nanotube (MWNT). SWCNT has various applications in polymers [24], high-performance supercapacitors [25], catalysts [26], gas-discharge tubes in telecom networks [27], energy conversion [28], drug delivery [29], sensors [30], etc. Motivated by the wide applications of the SWCNT in various fields of science and engineering, some interesting mathematical models [31,32,33,34,35,36,37,38,39] have been developed to study the peristaltic transport of SWCNT suspended nanofluids with permeable walls [31]; MHD slip flow over stretching surface [32]; induced magnetic field and heat flux [33]; variable viscosity and wall properties [34]; velocity and thermal slips in the mixed convection [35]; micropolar fluid in a rotating fluid [36]; curved channel with variable viscosity [37]; radiative nanofluid flow with double stratification [38]. Raza et al. [39] examined the effect of the induced magnetic field and different types of carbon nanotubes on heat transfer characteristics of saltwater transported by using a peristaltic pump through a permeable channel. In all the mathematical models, it is concluded that the temperature of the nanofluid diminishes with increasing the nanoparticle volume fraction of SWCNTs. It is also noted that velocity and pressure distribution are also highly affected by the SWCNTs. Nevertheless, the above studies have not considered the electroosmosis mechanism which is most demandable in the field of biomicrofluidics devices for drug delivery systems.

Considering the gaps in the literature and motivated by the vital role of SWCNTs suspended nanofluids flow driven by the combined effects of electroosmosis and peristalsis, the main goal here is to formulate a new mathematical model to study the effects of electric and magnetic fields on peristaltic pumping of SWCNTs nanofluids in the microchannel and investigate the heat transfer characteristics of nanofluid flowing through the electroosmotic peristaltic pump. Considering the more realistic microchannel, velocity slip and thermal slip boundary conditions have been employed to find out the solution. The perturbation method is used to obtain a series solution up to a more accurate approximate solution. Numerical computations have been made for graphical results and a detailed discussion has also been presented for the physical interpretation of the model. Finally, concluding remarks of computed results have been given. The findings of the present model can be applicable in biomicrofluidics applications like drug delivery systems and diagnosis of the diseases. Furthermore, biomicrofluidic pumps eliminate the requirements of mechanical parts utilized to propagate the peristaltic waves which remove the possibility of the frictional forces caused by rollers on the channel walls and also reduces the costs of such pumps. So it can be concluded that electroosmotic pumps and more efficient with an additional advantage of consuming less energy.

Mathematical formulation

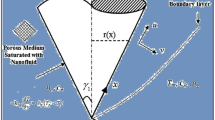
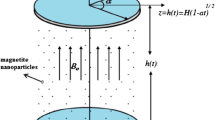
Here, the flow of electrically conducting water-based ionic nanoliquid with the suspension of SWCNT driven by combined peristalsis and electroosmosis through a symmetric channel is examined. Ionic nanoliquid is assumed to be z:z symmetric, i.e., valence of cations and anions is the same. Electroosmotic forces are generated by the application of the external electric field across the EDL in the axial direction. The consequences of mixed convection and viscous dissipation are also accounted. The impact of thermal radiation incorporating the radiative heat flux term specified by Rosseland approximation is analyzed. A constant magnetic field of strength B0 is applied in the transverse direction

$$\vec{B} = \left( {0,\,B_{\text{o}} ,\,0} \right),$$

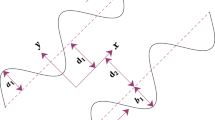
The peristaltic flow is engendered by propagating sinusoidal wave trains with wavelength λ and constant speed c along the walls of the channel in the axial direction. The mathematical formulation is carried out in Cartesian coordinates (\(\overline{x}, \overline{y},\overline{t}\)). The velocity components in the axial direction \(\overline{x}\) and transverse direction \(\overline{y}\) are denoted by \(\overline{u}\) and \(\overline{v}\) respectively. The geometry of the considered problem is given in Fig. 1.

Fig. 1
figure 1

Geometry of the problem

Full size image

The mathematical model for flow regime is expressed as

$$y = \pm \overline{H}\left( {\overline{x},\overline{t}} \right) = \pm d \pm a\sin \left( {\frac{2\pi }{\lambda }\left( {\overline{x} - c\overline{t}} \right)} \right),$$
(1)

where d designates half-width of the channel and a is the amplitude of sinusoidal waves.

Governing equations

Constitutive equations for current flow problem subject to considered flow conditions are formulated as [14]:

$$\frac{{\partial \overline{u}}}{{\partial \overline{x}}} + \frac{{\partial \overline{v}}}{{\partial \overline{y}}} = 0,$$
(2)
$$\rho_{{{\text{nf}}}} \left( {\frac{{\partial \overline{u}}}{{\partial \overline{t}}} + \overline{u}\frac{{\partial \overline{u}}}{{\partial \overline{x}}} + \overline{v}\frac{{\partial \overline{u}}}{{\partial \overline{y}}}} \right) = - \frac{{\partial \overline{p}}}{{\partial \overline{x}}} + \mu_{{{\text{nf}}}} \left( {\frac{{\partial^{2} \overline{u}}}{{\partial \overline{x}^{2} }} + \frac{{\partial^{2} \overline{u}}}{{\partial \overline{y}^{2} }}} \right) - \sigma B_{0}^{2} \overline{u} + \rho_{{\text{e}}} E_{{\overline{\text{x}}}} + \left( {\rho \gamma } \right)_{{{\text{nf}}}} g\left( {\overline{T} - \overline{T}_{0} } \right),$$
(3)
$$\rho_{{{\text{nf}}}} \left( {\frac{{\partial \overline{v}}}{{\partial \overline{t}}} + \overline{u}\frac{{\partial \overline{v}}}{{\partial \overline{x}}} + \overline{v}\frac{{\partial \overline{v}}}{{\partial \overline{y}}}} \right) = - \frac{{\partial \overline{p}}}{{\partial \overline{y}}} + \mu_{{{\text{nf}}}} \left( {\frac{{\partial^{2} \overline{v}}}{{\partial \overline{x}^{2} }} + \frac{{\partial^{2} \overline{v}}}{{\partial \overline{y}^{2} }}} \right) + \rho_{{\text{e}}} E_{{\overline{\text{y}}}} ,$$
(4)
$$\frac{{\partial \overline{T}}}{{\partial \overline{t}}} + \overline{u}\frac{{\partial \overline{T}}}{{\partial \overline{x}}} + \overline{v}\frac{{\partial \overline{T}}}{{\partial \overline{y}}} = \alpha_{{{\text{nf}}}} \left( {\frac{{\partial^{2} \overline{T}}}{{\partial \overline{x}^{2} }} + \frac{{\partial^{2} \overline{T}}}{{\partial \overline{y}^{2} }}} \right) + \tau \cdot L^{\text{t}} - \frac{{\partial q_{{\text{r}}} }}{{\partial \overline{y}}},$$
(5)

where

$$L = {\text{grad}}\left( {\vec{V}} \right).$$
(6)

Here, \(q_{{\text{r}}}\) is the radiative heat flux which is characterized by Rosseland approximation, assuming that heat flux is dominant in \(\overline{y}\) direction only, as [39, 41]:

$$\overline{{q_{{\text{r}}} }} = \frac{{ - 16\sigma^{*} }}{{3k^{*} }}T_{0}^{3} \frac{{\partial \overline{T}}}{{\partial \overline{y}}},$$
(7)

in above relations, \(\overline{p}\), (ργ)nf, σ, ρnf, ρe, \(E_{{\overline{\text{x}}}}\), \(E_{{\overline{\text{y}}}} ,\) τ, μnf and σnf specify the pressure, the effective thermal expansion of nanoliquid, electric conductivity, effective density of nanoliquid, charge number density, electrokinetic body forces in \(\overline{x}\) and \(\overline{y}\) directions, stress tensor, the effective viscosity of nanoliquid, and effective thermal diffusivity of nanoliquid, respectively. The effective thermal conductivity of CNT suspension is described by Xue model. The effective properties of SWCNT-water nanofluid are given as [40]:

$$\begin{gathered} \rho_{{{\text{nf}}}} = \left( {1 - \Phi } \right)\rho_{{\text{b}}} + \Phi \rho_{{{\text{SWCNT}}}} , \,\mu_{{{\text{nf}}}} = \frac{{\mu_{{\text{b}}} }}{{\left( {1 - \Phi } \right)^{2.5} }}, \hfill \\ \left( {\rho c_{{\text{p}}} } \right)_{{{\text{nf}}}} = \left( {1 - \Phi } \right)\left( {\rho c_{{\text{p}}} } \right)_{{\text{b}}} + \Phi \left( {\rho c_{{\text{p}}} } \right)_{{{\text{SWCNT}}}} , \, \alpha_{{{\text{nf}}}} = \frac{{k_{{{\text{nf}}}} }}{{\left( {\rho c_{{\text{p}}} } \right)_{{{\text{nf}}}} }}, \hfill \\ k_{{{\text{nf}}}} = k_{{\text{b}}} \left( {\frac{{\left( {1 - \Phi } \right) + 2\Phi \frac{{k_{{{\text{SWCNT}}}} }}{{k_{{{\text{SWCNT}}}} - k_{{\text{b}}} }}\ln \left( {\frac{{k_{{{\text{SWCNT}}}} + k_{{\text{b}}} }}{{2k_{{\text{b}}} }}} \right)}}{{\left( {1 - \Phi } \right) + 2\Phi \frac{{k_{{\text{b}}} }}{{k_{{{\text{SWCNT}}}} - k_{{\text{b}}} }}\ln \left( {\frac{{k_{{{\text{SWCNT}}}} + k_{{\text{b}}} }}{{2k_{{\text{b}}} }}} \right)}}} \right), \hfill \\ \end{gathered}$$
(8)

with \(\rho_{{\text{b}}}\) being the density of water, \(\rho_{{{\text{SWCNT}}}}\) the density of single-wall carbon nanotubes, \(k_{{\text{b}}}\) and \(k_{{{\text{SWCNT}}}}\) the thermal conductivity of water and SWCNTs, respectively, and Φ the volume fraction of SWCNTs.

Poisson equation is utilized to characterize electric potential φ generated across EDL as [17]:

$$\nabla^{2} \overline{\varphi } = - \frac{{\rho_{{\text{e}}} }}{{\varepsilon_{0} }},$$
(9)

where ρe denotes the electric charge number density given by:

$$\rho_{{\text{e}}} = ez\left( {n^{ + } - n^{ - } } \right),$$
(10)

where e specifies electric charge, n+ and n− are anions and cations having bulk concentration, n0 and z the charge balance of ionic species.

The distribution of ions within the fluid is described by employing Nernst–Planck equation

$$\frac{{\partial \overline{n}^{ \pm } }}{{\partial \overline{t}}} + \overline{u}\frac{{\partial \overline{n}^{ \pm } }}{{\partial \overline{x}}} + \overline{v}\frac{{\partial \overline{n}^{ \pm } }}{{\partial \overline{y}}} = D\left( {\frac{{\partial^{2} \overline{n}^{ \pm } }}{{\partial \overline{x}^{2} }} + \frac{{\partial^{2} \overline{n}^{ \pm } }}{{\partial \overline{y}^{2} }}} \right) \pm \frac{Dze}{{k_{{\text{B}}} \hat{T}}}\left( {\frac{\partial }{{\partial \overline{x}}}\left( {\overline{n}^{ \pm } \frac{\partial \varphi }{{\partial \overline{x}}}} \right) + \frac{\partial }{{\partial \overline{y}}}\left( {\overline{n}^{ \pm } \frac{\partial \varphi }{{\partial \overline{y}}}} \right)} \right),$$
(11)

with the assumption that the EDL is not intersecting the centerline and ionic distribution is steady in order to obtain the stable Boltzmann distribution of cations and anions. In the above equation, D defines the ionic diffusivity, \(\hat{T}\) the mean temperature of the ionic solution and kB is Boltzmann constant.

Following transformation are used to transform the laboratory frame (\(\overline{x}, \,\overline{y},\,\overline{t}\)) to wave frame (\(\tilde{x},\,\tilde{y},\,\overline{t}\))

$$\begin{gathered} \tilde{x} = \overline{x} - c\overline{t}, \,\tilde{u} = \overline{z} - c,\, \tilde{y} = \overline{y}, \hfill \\ \tilde{v} = \overline{v}, \,\tilde{p}\left( {\tilde{x},\tilde{y},\overline{t}} \right) = p\left( {\overline{x},\overline{y},\overline{t}} \right), \hfill \\ \end{gathered}$$
(12)

In order to facilitate this analysis, the following dimensionless quantities are introduced:

$$\begin{gathered} x = \frac{{\tilde{x}}}{\lambda },\, y = \frac{{\tilde{y}}}{d}, \,p = \frac{{\tilde{p}d}}{{\mu_{{\text{b}}} c}},\, u = \frac{{\tilde{u}}}{c},\,v = \frac{{\tilde{v}}}{c},\,n = \frac{{\overline{n}}}{{n_{0} }}, \hfill \\ h = \frac{{\overline{H}}}{d},\,\Pr = \frac{{\mu_{{\text{b}}} c_{{\text{p}}} }}{{k_{{\text{b}}} }} , \,\delta = \frac{d}{\lambda }, \,\theta = \frac{{\overline{T} - \overline{T}_{0} }}{{\overline{{T_{0} }} }},\,L = \frac{{\left( {\rho \gamma } \right)_{{{\text{nf}}}} }}{{\left( {\rho \gamma } \right)_{{\text{f}}} }}, \hfill \\ \varphi = \frac{{ez\overline{\varphi }}}{{k_{{\text{B}}} \hat{T}}} ,\,U = - \frac{{\varepsilon_{0} k_{{\text{B}}} \hat{T}E_{{\text{x}}} }}{{ez\mu_{{\text{b}}} c}}, \,k = \sqrt {\frac{{2n_{0} e^{2} z^{2} d^{2} }}{{\varepsilon_{0} k_{{\text{B}}} \hat{T}}}} , \hfill \\ {\text{Re}} = \frac{{\rho_{{\text{b}}} cd}}{{\mu_{{\text{b}}} }},\, \overline{\Psi } = \frac{\Psi }{cd},\,{\text{Rd}} = \frac{{16\sigma^{*} }}{{3k^{*} \mu_{{\text{b}}} c_{{\text{p}}} }}\overline{{T_{0} }}^{3} ,\, Gr = \frac{{\rho_{{\text{b}}} g\gamma_{{\text{b}}} d^{2} T_{0} }}{{\mu_{{\text{b}}} c}}, \hfill \\ Ec = \frac{{c^{2} }}{{c_{{\text{p}}} \overline{{T_{0} }} }},\,{\text{Br}} = {\text{Ec}}\Pr , \,M^{2} = \frac{{\sigma B_{0}^{2} d^{2} }}{{\mu_{{\text{b}}} }}. \hfill \\ \end{gathered}$$
(13)

In which Pr represents the Prandtl number, δ the wave number, θ the dimensionless temperature, U the Helmholtz—Smoluchowski velocity, k the Debye length parameter which is inversely related to EDL thickness, Re the Reynolds number, Rd the radiation parameter, Gr the Grashof number, Ec the Eckert number, Br the Brinkman number and M is the Hartmann number.

Current problem can be simplified to a notable extent by introducing stream function as:

$$u = \frac{\partial \Psi }{{\partial x}}, \,v = - \delta \frac{\partial \Psi }{{\partial x}},$$
(14)

Substituting Eqs. (12), (13) and (14) in Eqs. (2)–(5) and Eqns. (9)–(11) and adopting long wavelength and low Reynolds number approximation, we get following reduced system of the equations:

$$\frac{1}{{\left( {1 - \Phi } \right)^{2.5} }}\frac{{\partial^{4} \psi }}{{\partial y^{4} }} - M^{2} \frac{{\partial^{2} \psi }}{{\partial y^{2} }} + U\frac{{\partial^{3} \varphi }}{{\partial y^{3} }} + {\text{Gr}}L\frac{\partial \theta }{{\partial y}} = 0$$
(15)
$$\frac{\partial p}{{\partial x}} = \frac{1}{{\left( {1 - \Phi } \right)^{2.5} }}\frac{{\partial^{3} \psi }}{{\partial y^{3} }} - M^{2} \frac{\partial \psi }{{\partial y}} + U\frac{{\partial^{2} \varphi }}{{\partial y^{2} }} + {\text{Gr}}L\theta ,$$
(16)
$$\left( {A + {\text{Pr}}\,{\text{Rd}}} \right)\frac{{\partial^{2} \theta }}{{\partial y^{2} }} + \frac{{{\text{Br}}}}{{\left( {1 - \Phi } \right)^{2.5} }}\left( {\frac{{\partial^{2} \psi }}{{\partial y^{2} }}} \right)^{2} = 0,$$
(17)
$$\frac{{\partial^{2} \varphi }}{{\partial y^{2} }} = k^{2} \left( {\frac{{n^{ - } - n^{ + } }}{2}} \right),$$
(18)
$$\frac{{\partial^{2} n^{ \pm } }}{{\partial y^{2} }} \pm \frac{\partial }{\partial y}\left( {n^{ \pm } \frac{\partial \varphi }{{\partial y}}} \right) = 0,$$
(19)

Equation (19) is solved subject to the suitable boundary conditions and the resulting solution is expressed as:

$$n^{ \pm } = e^{ \mp \varphi } ,$$
(20)

Poisson–Boltzmann paradigm is obtained by combining Eqs. (18) and (20)

$$\frac{{\partial^{2} \varphi }}{{\partial y^{2} }} = k^{2} {\text{sinh}}\left( \varphi \right).$$
(21)

Simplification of the above equation can be done by applying the Debye–Hückel approximation principle which uses an assumption of lower zeta potential across EDL as:

$$\frac{{\partial^{2} \varphi }}{{\partial y^{2} }} = k^{2} \varphi .$$
(22)

Direct integration of Eq. (22) is performed subject to boundary conditions given below

$$\varphi |_{y = h} = 1,\quad \left. {\frac{\partial \varphi }{{\partial y}}} \right|_{y = 0} = 0,$$
(23)

and the resulting electric potential function is given as:

$$\varphi = \frac{{{\text{cosh}}\left( {ky} \right)}}{{{\text{cosh}}\left( {kh} \right)}},$$
(24)

Using Eq. (24) in Eqs. (15)–(17), we get

$$\frac{1}{{\left( {1 - \Phi } \right)^{2.5} }}\frac{{\partial^{4} \psi }}{{\partial y^{4} }} - M^{2} \frac{{\partial^{2} \psi }}{{\partial y^{2} }} + Uk^{3} \frac{{{\text{sinh}}\left( {ky} \right)}}{{{\text{cosh}}\left( {kh} \right)}} + {\text{Gr}}L\frac{\partial \theta }{{\partial y}} = 0,$$
(25)
$$\left( {A + {\text{Pr}}\,{\text{Rd}}} \right)\frac{{\partial^{2} \theta }}{{\partial y^{2} }} + \frac{{{\text{Br}}}}{{\left( {1 - \Phi } \right)^{2.5} }}\left( {\frac{{\partial^{2} \psi }}{{\partial y^{2} }}} \right)^{2} = 0,$$
(26)

The associated boundary slip conditions are:

$$\psi = 0,\frac{{\partial^{2} \psi }}{{\partial y^{2} }} = 0 \quad {\text{at}}\,y\, = \,0,$$
(27)
$$\psi = F, \frac{\partial \psi }{{\partial y}} = - 1 - \frac{\gamma }{{\left( {1 - \Phi } \right)^{2.5} }}\frac{{\partial^{2} \psi }}{{\partial y^{2} }} \quad {\text{at}}\,y = h = 1 + \varepsilon \sin \left( {2\pi x} \right),$$
(28)
$$\frac{\partial \theta }{{\partial y}} = 0\,{\text{at}}\, y = 0, \quad \theta + \eta \frac{\partial \theta }{{\partial y}} = 0,\,{\text{at}}\,y = h.$$
(29)

Here, γ and \(\eta\) designate the dimensionless velocity slip parameter and thermal slip parameter respectively and F is dimensionless flow rate given as

$$F = Q - 1,$$
(30)

with Q being time mean flow rate.

The heat transfer rate can be computed as:

$$Z = \frac{\partial h}{{\partial x}}\frac{\partial \theta }{{\partial y}}_{\text{y} \to \text{h}} .$$
(31)

Solution procedure

The system of Eqs. (25)–(29) resulting from mathematical formulation and simplification of the problem is nonlinear and cannot be solved for the exact solution. However, an approximate analytical solution can be obtained by reducing the nonlinearity of the above system by employing a regular perturbation method. For this purpose, series expansion of involved flow quantities about small Brinkman number are considered as:

$$\begin{aligned} \psi & = \mathop \sum \limits_{i = 0}^{n} {\text{Br}}^{\text{i}} \psi_{\text{i}} = \psi_{0} + {\text{Br}}\psi_{1} \ldots , \\ p & = \mathop \sum \limits_{i = 0}^{n} {\text{Br}}^\text{i} p_\text{i} = p_{0} + {\text{Br}}p_{1} \ldots , \\ \theta & = \mathop \sum \limits_{i = 0}^{n} {\text{Br}}^{\text{i}} \theta_\text{i} = \theta_{0} + {\text{Br}}\theta_{1} \ldots . \\ \end{aligned}$$
(32)

And truncating these series up to O(Br2) only. Plugging above expressions in Eqs. (25)–(26) and boundary conditions (27)–(29), following systems of the zeroth and first order are obtained:

Zeroth-order system

$$\frac{1}{{\left( {1 - \Phi } \right)^{2.5} }}\frac{{\partial^{4} \psi_{0} }}{{\partial y^{4} }} - M^{2} \frac{{\partial^{2} \psi_{0} }}{{\partial y^{2} }} + Uk^{3} \frac{{{\text{sinh}}\left( {ky} \right)}}{{{\text{cosh}}\left( {kh} \right)}} + {\text{Gr}}L\frac{{\partial \theta_{0} }}{\partial y} = 0,$$
(33)
$$\frac{{\partial p_{0} }}{\partial x} = \frac{1}{{\left( {1 - \Phi } \right)^{2.5} }}\frac{{\partial^{3} \psi_{0} }}{{\partial y^{3} }} - M^{2} \frac{{\partial \psi_{0} }}{\partial y} + Uk^{2} \frac{{{\text{cosh}}\left( {ky} \right)}}{{{\text{cosh}}\left( {kh} \right)}} + {\text{Gr}}L\theta_{0}$$
(34)
$$\left( {A + {\text{PrRd}}} \right)\frac{{\partial^{2} \theta_{0} }}{{\partial y^{2} }} = 0,$$
(35)
$$\psi_{0} = 0,\,\frac{{\partial^{2} \psi_{0} }}{{\partial y^{2} }} = \, 0,\quad {\text{at}}\,y = 0,$$
(36)
$$\psi_{0} = F, \frac{{\partial \psi_{0} }}{\partial y} = - 1 - \frac{\gamma }{{\left( {1 - \Phi } \right)^{2.5} }}\frac{{\partial^{2} \psi_{0} }}{{\partial y^{2} }}, at y = h = 1 + \varepsilon \sin \left( {2\pi x} \right),$$
(37)
$$\frac{{\partial \theta_{0} }}{\partial y} = 0\quad {\text{at}}\,y = 0,\quad \theta_{0} + \eta \frac{{\partial \theta_{0} }}{\partial y} = 0,\quad {\text{at}}\,y = h.$$
(38)

First-order system

$$\frac{1}{{\left( {1 - \Phi } \right)^{2.5} }}\frac{{\partial^{4} \psi_{1} }}{{\partial y^{4} }} - M^{2} \frac{{\partial^{2} \psi_{1} }}{{\partial y^{2} }} + {\text{Gr}}L\frac{{\partial \theta_{1} }}{\partial y} = 0,$$
(39)
$$\frac{{\partial p_{1} }}{\partial x} = \frac{1}{{\left( {1 - \Phi } \right)^{2.5} }}\frac{{\partial^{3} \psi_{1} }}{{\partial y^{3} }} - M^{2} \frac{{\partial \psi_{1} }}{\partial y} + GrL\theta_{1} ,$$
(40)
$$\left( {A + {\text{Pr}}\,{\text{Rd}}} \right)\frac{{\partial^{2} \theta_{1} }}{{\partial y^{2} }} + \frac{1}{{\left( {1 - \Phi } \right)^{2.5} }}\left( {\frac{{\partial^{2} \psi_{0} }}{{\partial y^{2} }}} \right)^{2} = 0,$$
(41)
$$\psi_{1} = 0, \frac{{\partial^{2} \psi_{1} }}{{\partial y^{2} }} = 0 \quad {\text{at}}\,y = 0$$
(42)
$$\psi_{1} = 0, \frac{{\partial \psi_{1} }}{\partial y} = - \frac{\gamma }{{\left( {1 - \Phi } \right)^{2.5} }}\frac{{\partial^{2} \psi_{1} }}{{\partial y^{2} }},\quad {\text{at}}\,y = h = 1 + \varepsilon \sin \left( {2\pi x} \right),$$
(43)
$$\frac{{\partial \theta_{1} }}{\partial y} = 0\quad {\text{at}}\,y = 0,\quad \theta_{1} + \eta \frac{{\partial \theta_{1} }}{\partial y} = 0,\quad {\text{at}}\,y = h.$$
(44)

These zeroth- and first-order system of equations are solved separately for an exact solution using mathematical software Mathematica and resulting solution for stream function, temperature, and pressure gradient are given below as:

$$\begin{aligned} \psi & = \frac{1}{{96}}{\text{Br}}\left( {96A3 - \frac{{4C_{2} ^{2} {\text{e}}^{{ - 2{\text{M}}\sqrt {\text{T y}}}} {\text{Gr}}L}}{{M^{5} \left( {A + \Pr \,{\text{Rd}}} \right)T^{{5/2}} }} + \frac{{4C_{1} ^{2} {\text{e}}^{{2{\text{M}}\sqrt {\text{T y}}}} {\text{Gr}}L}}{{M^{5} \left( {A + \Pr \,{\text{Rd}}} \right)T^{{5/2}} }} + \frac{{96A_{2} {\text{e}}^{{ - {\text{M}}\sqrt {\text{T y}}}} }}{{M^{2} T}} + \frac{{96A_{1} {\text{e}}^{{{\text{M}}\sqrt {\text{T y}}}} }}{{M^{2} T}} + 96A_{4} y} \right. \\ & \quad - \frac{{96{\text{e}}^{{ - {\text{M}}\sqrt {\text{T y}}}} {\text{Gr}}k^{2} L\left( {C_{1} {\text{e}}^{{2{\text{M}}\sqrt {\text{T y}}}} \left( { - k + M\sqrt T } \right)^{3} \left( { - k + 2M\sqrt T } \right) + C_{2} \left( {k + M\sqrt T } \right)^{3} \left( {k + 2M\sqrt T } \right)} \right)TU\cosh \left[ {ky} \right]\text{Sech} \left[ {hk} \right]}}{{\left( {A + \Pr \,{\text{Rd}}} \right)\left( {k - 2M\sqrt T } \right)\left( {k + 2M\sqrt T } \right)\left( {k^{2} - M^{2} T} \right)^{4} }} \\ & \quad - \frac{{96{\text{e}}^{{ - {\text{M}}\sqrt {\text{T y}}}} {\text{Gr}}k^{2} L\left( {C_{2} \left( {k - 2M\sqrt T } \right)\left( {k - M\sqrt T } \right)^{3} + C_{1} {\text{e}}^{{2{\text{M}}\sqrt {\text{T y}}}} \left( {k + M\sqrt T } \right)^{3} \left( {k + 2M\sqrt T } \right)} \right)TU\cosh \left[ {ky} \right]\text{Sech} \left[ {hk} \right]}}{{\left( {A + \Pr Rd} \right)\left( {k - 2M\sqrt T } \right)\left( {k + 2M\sqrt T } \right)\left( {k^{2} - M^{2} T} \right)^{4} }} \\ & \quad + \frac{{96\left( {C_{1} + C_{2} } \right){\text{Gr}}Ly^{2} \cosh \left[ {hk} \right]\left( { - 4k^{4} MT^{{3/2}} U + \left( {C_{1} - C_{2} } \right)\left( {k^{2} - M^{2} T} \right)^{2} \cosh \left[ {hk} \right]} \right)\left( {\cosh \left[ {2hk} \right] + \sinh \left[ {2hk} \right]} \right)}}{{M^{3} \left( {A + \Pr \,{\text{Rd}}} \right)T^{{3/2}} \left( {k^{2} - M^{2} T} \right)^{2} \left( {1 + \cosh \left[ {2hk} \right] + \sinh \left[ {2hk} \right]} \right)^{2} }} \\ & \quad - \frac{{32{\text{Gr}}Ly^{3} \left( {2C_{1} C_{2} \left( {k^{2} - M^{2} T} \right)^{2} - k^{6} T^{2} U^{2} + 2C_{1} C_{2} \left( {k^{2} - M^{2} T} \right)^{2} \cosh \left[ {2hk} \right]} \right)\left( {\cosh \left[ {2hk} \right] + \sinh \left[ {2hk} \right]} \right)}}{{M^{2} \left( {A + \Pr Rd} \right)T\left( {k^{2} - M^{2} T} \right)^{2} \left( {1 + \cosh \left[ {2hk} \right] + \sinh \left[ {2hk} \right]} \right)^{2} }} \\ & \quad - \frac{{96{\text{e}}^{{ - {\text{M}}\sqrt {\text{T y}}}} {\text{Gr}}k^{2} L\left( {C_{1} {\text{e}}^{{2{\text{M}}\sqrt {\text{T y}}}} \left( { - k + M\sqrt T } \right)^{3} \left( { - k + 2M\sqrt T } \right) + C_{2} \left( {k + M\sqrt T } \right)^{3} \left( {k + 2M\sqrt T } \right)} \right)TU\text{Sech} \left[ {hk} \right]\sinh \left[ {ky} \right]}}{{\left( {A + \Pr Rd} \right)\left( {k - 2M\sqrt T } \right)\left( {k + 2M\sqrt T } \right)\left( {k^{2} - M^{2} T} \right)^{4} }} \\ & \quad + \frac{{96{\text{e}}^{{ - {\text{M}}\sqrt {\text{T y}}}} {\text{Gr}}k^{2} L\left( {C_{2} \left( {k - 2M\sqrt T } \right)\left( {k - M\sqrt T } \right)^{3} + C_{1} {\text{e}}^{{2{\text{M}}\sqrt {\text{T y}}}} \left( {k + M\sqrt T } \right)^{3} \left( {k + 2M\sqrt T } \right)} \right)TU\text{Sech} \left[ {hk} \right]\sinh \left[ {ky} \right]}}{{\left( {A + \Pr {\text{Rd}}} \right)\left( {k - 2M\sqrt T } \right)\left( {k + 2M\sqrt T } \right)\left( {k^{2} - M^{2} T} \right)^{4} }} \\ & \quad + \left. {\frac{{6{\text{Gr}}k^{3} LT^{2} U^{2} \text{Sech} \left[ {hk} \right]^{2} \sinh \left[ {2ky} \right]}}{{\left( {A + \Pr {\text{Rd}}} \right)\left( {2k - M\sqrt T } \right)\left( {2k + M\sqrt T } \right)\left( {k^{2} - M^{2} T} \right)^{2} }}} \right)\left( {e^{{ - {\text{M}}\sqrt {\text{T}} \left( {\text{h + y}} \right)}} } \right.\left( {e^{{{\text{M}}\sqrt {\text{T}} \left( {\text{h + 2y}} \right)}} \left( {\left( {F + h} \right)\left( {k^{2} - M^{2} T} \right) - hk^{2} TU} \right)} \right. \\ & \quad + {\text{e}}^{{{\text{hM}}\sqrt {\text{T}} }} \left( { - \left( {F + h} \right)\left( {k^{2} - M^{2} T} \right) + hk^{2} TU} \right) - {\text{e}}^{{{\text{M}}\sqrt {\text{T y}}}} y\left( {k^{2} \left( { - 1 + TU + FM\left( {\sqrt T - M\gamma } \right)} \right) + M^{2} T\left( {1 + FM\left( { - \sqrt T + M\gamma } \right)} \right)} \right) \\ & \quad + {\text{e}}^{{{\text{M}}\sqrt {\text{T}} \left( {2{\text{h + y}}} \right)}} y\left( {M^{2} T\left( {1 + FM\left( {\sqrt T + M\gamma } \right)} \right) - k^{2} \left( {1 - TU + FM\left( {\sqrt T + M\gamma } \right)} \right)} \right) + 2{\text{e}}^{{{\text{M}}\sqrt {\text{T}} \left( {2{\text{h + y}}} \right)}} kTU\text{Sech} \left[ {hk} \right] \\ & \quad \left( {hM\sqrt T \cosh \left[ {hM\sqrt T } \right] + \left( { - 1 + hM^{2} \gamma } \right)\sinh \left[ {hM\sqrt T } \right]} \right)\sinh \left[ {ky} \right] + kU({\text{e}}^{{{\text{M}}\sqrt {\text{T}} \left( {{\text{h}} + 2{\text{y}}} \right)}} \left( {T - hk^{2} \gamma } \right) + {\text{e}}^{{{\text{hM}}\sqrt {\text{T}} }} \\ & \quad \left( { - T + hk^{2} \gamma } \right) + {\text{e}}^{{{\text{M}}\sqrt {\text{T y}}}} y\left( { - MT^{{3/2}} - k^{2} \gamma + M^{2} T\gamma } \right) - {\text{e}}^{{{\text{M}}\sqrt {\text{T}} \left( {2{\text{h + y}}} \right)}} y\left( { - k^{2} \gamma + MT\left( {\sqrt T + M\gamma } \right)} \right))\tanh \left[ {hk} \right])) \\ & \quad {{} \mathord{\left/ {\vphantom {{} {\left( {2\left( {k^{2} - M^{2} T} \right)\left( {hM\sqrt T \cosh \left[ {hM\sqrt T } \right] + \left( { - 1 + hM^{2} \gamma } \right)\sinh \left[ {hM\sqrt T } \right]} \right)} \right),}}} \right. \kern-\nulldelimiterspace} {\left( {2\left( {k^{2} - M^{2} T} \right)\left( {hM\sqrt T \cosh \left[ {hM\sqrt T } \right] + \left( { - 1 + hM^{2} \gamma } \right)\sinh \left[ {hM\sqrt T } \right]} \right)} \right),}} \\ \end{aligned}$$
$$\begin{aligned} \frac{{{\text{d}}p}}{{{\text{d}}x}} & = \frac{1}{{8M^{2} }}e^{{ - 2{\text{hM}}\sqrt {\text{T}} }} \left( { - 1/\left( {\left( {A + \Pr {\text{Rd}}} \right)T^{2} \left( { - k^{2} + M^{2} T} \right)^{3} } \right){\text{Br}} \text{Sech} \left[ {hk} \right]^{2} \left( {C_{2} ^{2} {\text{Gr}}k^{6} L - 8C_{1} C_{2} e^{{2{\text{hM}}\sqrt {\text{T}}}} {\text{Gr}}k^{6} L} \right.} \right. \\ & \quad + C_{1} ^{2} e^{{4{\text{hM}}\sqrt {\text{T}}}} {\text{Gr}}k^{6} L - 2C_{1} ^{2} e^{{2{\text{hM}}\sqrt {\text{T}}}} {\text{Gr}}hk^{6} LM\sqrt T + 2C_{2} ^{2} e^{{2{\text{hM}}\sqrt {\text{T}} }} {\text{Gr}}hk^{6} LM\sqrt T - 3C_{2} ^{2} {\text{Gr}}k^{4} L \\ & \quad M^{2} T + 24C_{1} C_{2} e^{{2{\text{hM}}\sqrt {\text{T}}}} {\text{Gr}}k^{4} LM^{2} T - 3C_{1} ^{2} e^{{4{\text{hM}}\sqrt {\text{T}}}} {\text{Gr}}k^{4} LM^{2} T + 4C_{1} C_{2} e^{{2{\text{hM}}\sqrt {\text{T}}}} {\text{Gr}}h^{2} k^{6} LM^{2} T \\ & \quad + 6C_{1} ^{2} e^{{2{\text{hM}}\sqrt {\text{T}}}} {\text{Gr}}hk^{4} LM^{3} T^{{3/2}} - 6C_{2} ^{2} e^{{2{\text{hM}}\sqrt {\text{T}}}} {\text{Gr}}hk^{4} LM^{3} T^{{3/2}} - 4AA4e^{{2{\text{hM}}\sqrt {\text{T}}}} k^{6} M^{4} T^{2} + 3C_{2} ^{2} {\text{Gr}}k^{2} \\ & \quad LM^{4} T^{2} - 24C_{1} C_{2} e^{{2{\text{hM}}\sqrt {\text{T}}}} {\text{Gr}}k^{2} LM^{4} T^{2} + 3C_{1} ^{2} e^{{4{\text{hM}}\sqrt {\text{T}}}} {\text{Gr}}k^{2} LM^{4} T^{2} - 12C_{1} C_{2} e^{{2{\text{hM}}\sqrt {\text{T}}}} {\text{Gr}}h^{2} k^{4} LM^{4} T^{2} \\ & \quad - 4A4e^{{2{\text{hM}}\sqrt {\text{T}}}} k^{6} M^{4} \Pr {\text{Rd}}T^{2} - 6C_{1} ^{2} e^{{2{\text{hM}}\sqrt {\text{T}}}} {\text{Gr}}hk^{2} LM^{5} T^{{5/2}} + 6C_{2} ^{2} e^{{2{\text{hM}}\sqrt {\text{T}}}} {\text{Gr}}hk^{2} LM^{5} T^{{5/2}} + 12AA4 \\ & \quad e^{{2{\text{hM}}\sqrt {\text{T}}}} k^{4} M^{6} T^{3} - C_{2} ^{2} {\text{Gr}}LM^{6} T^{3} + 8C_{1} C_{2} e^{{2{\text{hM}}\sqrt {\text{T}}}} {\text{Gr}}LM^{6} T^{3} - C_{1} ^{2} e^{{4{\text{hM}}\sqrt {\text{T}}}} {\text{Gr}}LM^{6} T^{3} + 12C_{1} C_{2} e^{{2{\text{hM}}\sqrt {\text{T}}}} \\ & \quad {\text{Gr}}h^{2} k^{2} LM^{6} T^{3} + 12A4e^{{2{\text{hM}}\sqrt {\text{T}}}} k^{4} M^{6} \Pr {\text{Rd}}T^{3} + 2C_{1} ^{2} e^{{2{\text{hM}}\sqrt {\text{T}}}} {\text{Gr}}hLM^{7} T^{{7/2}} - 2C_{2} ^{2} e^{{2{\text{hM}}\sqrt {\text{T}}}} {\text{Gr}}hLM^{7} T^{{7/2}} \\ & \quad - 12AA4e^{{2{\text{hM}}\sqrt {\text{T}}}} k^{2} M^{8} T^{4} - 4C_{1} C_{2} e^{{2{\text{hM}}\sqrt {\text{T}}}} {\text{Gr}}h^{2} LM^{8} T^{4} - 12A4e^{{2{\text{hM}}\sqrt {\text{T}}}} k^{2} M^{8} \Pr {\text{Rd}}T^{4} + 4AA4e^{{2{\text{hM}}\sqrt {\text{T}}}} M^{{10}} T^{5} \\ & \quad + 4A4e^{{2{\text{hM}}\sqrt {\text{T}}}} M^{{10}} \Pr {\text{Rd}}T^{5} - 16C_{2} e^{{{\text{hM}}\sqrt {\text{T}}}} {\text{Gr}}k^{4} LM^{3} T^{{5/2}} U + 16C_{1} e^{{3{\text{hM}}\sqrt {\text{T}}}} {\text{Gr}}k^{4} LM^{3} T^{{5/2}} U + 4e^{{2{\text{hM}}\sqrt {\text{T}}}} {\text{Gr}}k^{8} L \\ & \quad T^{2} U^{2} - 4e^{{2{\text{hM}}\sqrt {\text{T}}}} {\text{Gr}}k^{6} LM^{2} T^{3} U^{2} - 2e^{{2{\text{hM}}\sqrt {\text{T}}}} {\text{Gr}}h^{2} k^{8} LM^{2} T^{3} U^{2} + 2e^{{2{\text{hM}}\sqrt {\text{T}}}} {\text{Gr}}h^{2} k^{6} LM^{4} T^{4} U^{2} - 2C_{2} ^{2} {\text{Gr}}k^{6} LM \\ & \quad \sqrt T \eta - 2C_{1} ^{2} e^{{2{\text{hM}}\sqrt {\text{T}}}} {\text{Gr}}k^{6} LM\sqrt T \eta + 2C_{2} ^{2} e^{{2{\text{hM}}\sqrt {\text{T}}}} {\text{Gr}}k^{6} LM\sqrt T \eta + 2C_{1} ^{2} e^{{4{\text{hM}}\sqrt {\text{T}}}} {\text{Gr}}k^{6} LM\sqrt T \eta + 8C_{1} C_{2} \\ & \quad e^{{2{\text{hM}}\sqrt {\text{T}}}} {\text{Gr}}hk^{6} LM^{2} T\eta + 6C_{2} ^{2} {\text{Gr}}k^{4} LM^{3} T^{{3/2}} \eta + 6C_{1} ^{2} e^{{2{\text{hM}}\sqrt {\text{T}}}} {\text{Gr}}k^{4} LM^{3} T^{{3/2}} \eta - 6C_{2} ^{2} e^{{2{\text{hM}}\sqrt {\text{T}}}} {\text{Gr}}k^{4} LM^{3} T^{{3/2}} \\ & \quad \eta - 6C_{1} ^{2} e^{{4{\text{hM}}\sqrt {\text{T}}}} {\text{Gr}}k^{4} LM^{3} T^{{3/2}} \eta - 24C_{1} C_{2} e^{{2{\text{hM}}\sqrt {\text{T}}}} {\text{Gr}}hk^{4} LM^{4} T^{2} \eta - 6C_{2} ^{2} {\text{Gr}}k^{2} LM^{5} T^{{5/2}} \eta - 6C_{1} ^{2} e^{{2{\text{hM}}\sqrt {\text{T}}}} {\text{Gr}} \\ & \quad k^{2} LM^{5} T^{{5/2}} \eta + 6C_{2} ^{2} e^{{2{\text{hM}}\sqrt {\text{T}}}} {\text{Gr}}k^{2} LM^{5} T^{{5/2}} \eta + 6C_{1} ^{2} e^{{4{\text{hM}}\sqrt {\text{T}}}} {\text{Gr}}k^{2} LM^{5} T^{{5/2}} \eta + 24C_{1} C_{2} e^{{2{\text{hM}}\sqrt {\text{T}}}} {\text{Gr}}hk^{2} LM^{6} T^{3} \\ & \quad \eta + 2C_{2} ^{2} {\text{Gr}}LM^{7} T^{{7/2}} \eta + 2C_{1} ^{2} e^{{2{\text{hM}}\sqrt {\text{T}}}} {\text{Gr}}LM^{7} T^{{7/2}} \eta - 2C_{2} ^{2} e^{{2{\text{hM}}\sqrt {\text{T}}}} {\text{Gr}}LM^{7} T^{{7/2}} \eta - 2C_{1} ^{2} e^{{4{\text{hM}}\sqrt {\text{T}}}} {\text{Gr}}LM^{7} T^{{7/2}} \eta \\ & \quad - 8C_{1} C_{2} e^{{2{\text{hM}}\sqrt {\text{T}}}} {\text{Gr}}hLM^{8} T^{4} \eta - 8C_{2} e^{{{\text{hM}}\sqrt {\text{T}}}} {\text{Gr}}k^{6} LM^{2} T^{2} U\eta - 8C_{1} e^{{3{\text{hM}}\sqrt {\text{T}}}} {\text{Gr}}k^{6} LM^{2} T^{2} U\eta + 8C_{2} e^{{{\text{hM}}\sqrt {\text{T}}}} {\text{Gr}}k^{4} \\ & \quad LM^{4} T^{3} U\eta + 8C_{1} e^{{3{\text{hM}}\sqrt {\text{T}}}} {\text{Gr}}k^{4} LM^{4} T^{3} U\eta - 4e^{{2{\text{hM}}\sqrt {\text{T}}}} {\text{Gr}}hk^{8} LM^{2} T^{3} U^{2} \eta + 4e^{{2{\text{hM}}\sqrt {\text{T}}}} {\text{Gr}}hk^{6} LM^{4} T^{4} U^{2} \eta \\ & \quad - 16\left( {C_{1} + C_{2} } \right)e^{{2{\text{hM}}\sqrt {\text{T}}}} {\text{Gr}}k^{4} LM^{2} T^{2} \left( { - k^{2} + M^{2} T} \right)U\left( {h + \eta } \right)\cosh \left[ {hk} \right](C_{2} ^{2} GrL\left( {k^{2} - M^{2} T} \right)^{3} (1 - 2M\sqrt T \eta \\ & \quad \left. { + 2e^{{2{\text{hM}}\sqrt {\text{T}}}} M\sqrt T \left( {h + \eta } \right)} \right) - 4C_{2} e^{{{\text{hM}}\sqrt {\text{T}}}} {\text{Gr}}L\left( {2k^{4} M^{2} T^{2} U\left( {2M\sqrt T + k^{2} \eta - M^{2} T\eta } \right) + C_{1} e^{{{\text{hM}}\sqrt {\text{T}}}} \left( { - k^{2} + M^{2} T} \right)^{3} } \right. \\ & \quad \left. {\left( { - 2 + h^{2} M^{2} T + 2hM^{2} T\eta } \right)} \right) + e^{{2{\text{hM}}\sqrt {\text{T}} }} \left( {M^{2} T^{2} \left( { - k^{2} + M^{2} T} \right)\left( {4AA4M^{2} \left( {k^{2} - M^{2} T} \right)^{2} + 4A4M^{2} \Pr {\text{Rd}}} \right.} \right. \\ & \quad \left( {k^{2} - M^{2} T} \right)^{2} - Grk^{4} LTU^{2} ) + 8C_{1} e^{{{\text{hM}}\sqrt {\text{T}}}} {\text{Gr}}k^{4} LM^{2} T^{2} U\left( {2M\sqrt T - k^{2} \eta + M^{2} T\eta } \right) + C_{1} ^{2} {\text{Gr}}L\left( {k^{2} - M^{2} T} \right)^{3} \\ & \quad \left. {\left. {\left( { - 2M\sqrt T \left( {h + \eta } \right) + e^{{2{\text{hM}}\sqrt {\text{T}}}} \left( {1 + 2M\sqrt T \eta } \right)} \right)} \right)} \right)\cosh \left[ {2hk} \right] - 8C_{2} e^{{{\text{hM}}\sqrt {\text{T}}}} {\text{Gr}}k^{5} LM^{2} T^{2} U\sinh \left[ {2hk} \right] \\ & \quad - 8C_{1} e^{{3{\text{hM}}\sqrt {\text{T}}}} {\text{Gr}}k^{5} LM^{2} T^{2} U\sinh \left[ {2hk} \right] - 8C_{2} e^{{{\text{hM}}\sqrt {\text{T}}}} {\text{Gr}}k^{3} LM^{4} T^{3} U\sinh \left[ {2hk} \right] - 8C_{1} e^{{3{\text{hM}}\sqrt {\text{T}}}} {\text{Gr}}k^{3} LM^{4} T^{3} \\ & \quad U\sinh \left[ {2hk} \right] - 8C_{2} e^{{{\text{hM}}\sqrt {\text{T}}}} {\text{Gr}}k^{5} LM^{3} T^{{5/2}} U\eta \sinh \left[ {2hk} \right] + 8C_{1} e^{{3{\text{hM}}\sqrt {\text{T}}}} {\text{Gr}}k^{5} LM^{3} T^{{5/2}} U\eta \sinh \left[ {2hk} \right] \\ & \quad + 8C_{2} e^{{{\text{hM}}\sqrt {\text{T}}}} {\text{Gr}}k^{3} LM^{5} T^{{7/2}} U\eta \sinh \left[ {2hk} \right] - 8C_{1} e^{{3{\text{hM}}\sqrt {\text{T}}}} {\text{Gr}}k^{3} LM^{5} T^{{7/2}} U\eta \sinh \left[ {2hk} \right] + 2e^{{2{\text{hM}}\sqrt {\text{T}}}} {\text{Gr}}k^{7} LM^{2} T^{3} U^{2} \\ & \quad \left. {\eta \sinh \left[ {2hk} \right] - 2e^{{2{\text{hM}}\sqrt {\text{T}}}} {\text{Gr}}k^{5} LM^{4} T^{4} U^{2} \eta \sinh \left[ {2hk} \right]} \right) + \left( {4e^{{{\text{hM}}\sqrt {\text{T}}}} M^{4} \left( {M^{2} T\left( { - 1 + FM\left( {\sqrt T - M\gamma } \right) + e^{{2{\text{hM}}\sqrt {\text{T}}}} } \right.} \right.} \right. \\ & \quad \left. {\left( {1 + FM\left( {\sqrt T + M\gamma } \right)} \right)} \right) - k^{2} \left( { - 1 + TU + FM\left( {\sqrt T - M\gamma } \right) + e^{{2{\text{hM}}\sqrt {\text{T}}}} \left( {1 - TU + FM\left( {\sqrt T + M\gamma } \right)} \right)} \right) + kU \\ & \quad \left. {\left. {\left( { - \left( {1 + e^{{2{\text{hM}}\sqrt {\text{T}}}} } \right)MT^{{3/2}} + \left( { - 1 + e^{{2{\text{hM}}\sqrt {\text{T}}}} } \right)k^{2} \gamma - \left( { - 1 + e^{{2{\text{hM}}\sqrt {\text{T}}}} } \right)M^{2} T\gamma } \right)\tanh \left[ {hk} \right]} \right)} \right)/ \\ & \quad \left. {\left( {\left( {k^{2} - M^{2} T} \right)\left( {hM\sqrt T \cosh \left[ {hM\sqrt T } \right] + \left( { - 1 + hM^{2} \gamma } \right)\sinh \left[ {hM\sqrt T } \right]} \right)} \right)} \right), \\ \end{aligned}$$
$$ \begin{aligned} \theta & = \frac{1}{{8\left( {A + \Pr Rd} \right)}}Br\left( { - \frac{{16C_{1} C_{2} hk^{2} M^{2} \eta }}{{\left( {k^{2} - M^{2} T} \right)^{2} }} - \frac{{2C_{2}^{2} e^{ - 2{\text{hM}}\sqrt {\text{T}} } k^{4} \eta }}{{MT^{3/2} \left( {k^{2} - M^{2} T} \right)^{2} }} + \frac{{2C_{1}^{2} e^{2{\text{hM}}\sqrt {\text{T}} } k^{4} \eta }}{{MT^{3/2} \left( {k^{2} - M^{2} T} \right)^{2} }} + \frac{{8C_{1} C_{2} hk^{4} \eta }}{{T\left( {k^{2} - M^{2} T} \right)^{2} }} + \frac{{4C_{2}^{2} e^{ - 2{\text{hM}}\sqrt {\text{T}} } k^{2} M\eta }}{{\sqrt{T} \left( {k^{2} - M^{2} T} \right)^{2} }}} \right. \\ & \quad - \frac{{4C_{1}^{2} e^{2{\text{hM}}\sqrt {\text{T}} } k^{2} M\eta }}{{\sqrt{T} \left( {k^{2} - M^{2} T} \right)^{2} }} - \frac{{2C_{2}^{2} e^{ - 2{\text{hM}}\sqrt {\text{T}} } M^{3} \sqrt{T} \eta }}{{\left( {k^{2} - M^{2} T} \right)^{2} }} + \frac{{2C_{1}^{2} e^{2{\text{hM}}\sqrt {\text{T}} } M^{3} \sqrt{T} \eta }}{{\left( {k^{2} - M^{2} T} \right)^{2} }} + \frac{{8C_{1} C_{2} hM^{4} T\eta }}{{\left( {k^{2} - M^{2} T} \right)^{2} }} - \frac{{16C_{2} e^{ - {\text{hM}}\sqrt {\text{T}} } k^{4} U\eta }}{{\left( {k^{2} - M^{2} T} \right)^{2} }} \\ & \quad - \frac{{16C_{1} e^{{\text{hM}}\sqrt {\text{T}} } k^{4} U\eta }}{{\left( {k^{2} - M^{2} T} \right)^{2} }} + \frac{{4\left( {C_{1} + C_{2} } \right)y\left( { - 4k^{4} MT^{3/2} U + \left( {C_{1} - C_{2} } \right)\left( {k^{2} - M^{2} T} \right)^{2} {\text{cosh}} \left[ {hk} \right]} \right){\text{Sech}} \left[ {hk} \right]}}{{MT^{3/2} \left( {k^{2} - M^{2} T} \right)^{2} }} \\ & \quad - \frac{{4\left( {C_{1} + C_{2} } \right)\left( {h + \eta } \right)\left( { - 4k^{4} MT^{3/2} U + \left( {C_{1} - C_{2} } \right)\left( {k^{2} - M^{2} T} \right)^{2} {\text{cosh}} \left[ {hk} \right]} \right){\text{Sech}} \left[ {hk} \right]}}{{MT^{3/2} \left( {k^{2} - M^{2} T} \right)^{2} }} \\ & \quad + \frac{{2e^{ - 2{\text{hM}}\sqrt {\text{T}} } \left( { - C_{2}^{2} \left( {k^{2} - M^{2} T} \right)^{2} + C_{1}^{2} e^{4{\text{hM}}\sqrt {\text{T}} } \left( {k^{2} - M^{2} T} \right)^{2} + 4C_{1} C_{2} e^{2{\text{hM}}\sqrt {\text{T}} } hM\sqrt{T} \left( {k^{2} - M^{2} T} \right)^{2} - 2e^{2{\text{hM}}\sqrt {\text{T}} } hk^{6} MT^{5/2} U^{2} } \right)\eta {\text{Sech}} \left[ {hk} \right]^{2} }}{{MT^{3/2} \left( {k^{2} - M^{2} T} \right)^{2} }} \\ & \quad - 1/\left( {MT^{2} \left( {k^{2} - M^{2} T} \right)^{2} \left( { - k^{2} M + M^{3} T} \right)} \right)e^{ - 2{\text{hM}}\sqrt {\text{T}} } {\text{Sech}} \left[ {hk} \right]^{2} (\left( {k^{2} - M^{2} T} \right)^{3} \left( {C_{2}^{2} + C_{1}^{2} e^{4{\text{hM}}\sqrt {\text{T}} } + 4C_{1} C_{2} e^{2{\text{hM}}\sqrt {\text{T}} } h^{2} M^{2} T} \right) \\ & \quad \,{\text{cosh}} \left[ {2hk} \right] - \left( {k^{2} - M^{2} T} \right)( - C_{1}^{2} e^{4{\text{hM}}\sqrt {\text{T}} } k^{4} + 2C_{1}^{2} e^{4{\text{hM}}\sqrt {\text{T}} } k^{2} M^{2} T - C_{1}^{2} e^{4{\text{hM}}\sqrt {\text{T}} } M^{4} T^{2} - C_{2}^{2} \left( {k^{2} - M^{2} T} \right)^{2} \\ & \quad \left. { - 4C_{1} C_{2} e^{2{\text{hM}}\sqrt {\text{T}} } h^{2} M^{2} T\left( {k^{2} - M^{2} T} \right)^{2} + 2e^{2{\text{hM}}\sqrt {\text{T}} } h^{2} k^{6} M^{2} T^{3} U^{2} - e^{2{\text{hM}}\sqrt {\text{T}} } k^{4} M^{2} T^{3} U^{2} {\text{cosh}} \left[ {2hk} \right]} \right) \\ & \quad - 16e^{{\text{hM}}\sqrt {\text{T}} } k^{3} M^{2} T^{2} U{\text{cosh}} \left[ {hk} \right]\left( {2\left( {C_{2} - C_{1} e^{2{\text{hM}}\sqrt {\text{T}} } } \right)kM\sqrt{T} {\text{cosh}} \left[ {hk} \right] + \left( {C_{2} + C_{1} e^{2{\text{hM}}\sqrt {\text{T}} } } \right)\left( {k^{2} + M^{2} T} \right){\text{sinh}} \left[ {hk} \right]} \right) \\ & \quad + 1/\left( {MT^{2} \left( {k^{2} - M^{2} T} \right)^{2} \left( { - k^{2} M + M^{3} T} \right)} \right)e^{ - 2{\text{M}} {\sqrt {\text{T}}} {\text{y}}} {\text{Sech}} \left[ {hk} \right]^{2} \left( {\left( {k^{2} - M^{2} T} \right)^{3} \left( {C_{2}^{2} + C_{1}^{2} e^{4{\text{M}} {\sqrt {\text{T}}} {\text{y}}} + 4C_{1} C_{2} e^{2{\text{M}} {\sqrt {\text{T}}} {\text{y}}} M^{2} Ty^{2} } \right)} \right. \\ & \quad \,{\text{cosh}} \left[ {2hk} \right] - \left( {k^{2} - M^{2} T} \right)( - C_{1}^{2} e^{4{\text{M}} {\sqrt {\text{T}}} {\text{y}}} k^{4} + 2C_{1}^{2} e^{4{\text{M}} {\sqrt {\text{T}}} {\text{y}}} k^{2} M^{2} T - C_{1}^{2} e^{4{\text{M}} {\sqrt {\text{T}}} {\text{y}}} M^{4} T^{2} - C_{2}^{2} \left( {k^{2} - M^{2} T} \right)^{2} \\ & \quad \left. { - 4C_{1} C_{2} e^{2{\text{M}}{\sqrt {\text{T}}} {\text{y}}} M^{2} T\left( {k^{2} - M^{2} T} \right)^{2} y^{2} + 2e^{2{\text{M}} {\sqrt {\text{T}}} {\text{y}}} k^{6} M^{2} T^{3} U^{2} y^{2} - e^{2{\text{M}}{\sqrt {\text{T}}} {\text{y}}} k^{4} M^{2} T^{3} U^{2} {\text{cosh}} \left[ {2ky} \right]} \right) \\ & \quad \left. { - 16e^{{\text{M}} {\sqrt {\text{T}}} {\text{y}}} k^{3} M^{2} T^{2} U{\text{cosh}} \left[ {hk} \right]\left( {2\left( {C_{2} - C_{1} e^{2{\text{M}} {\sqrt {\text{T}}} {\text{y}}} } \right)kM\sqrt{T} {\text{cosh}} \left[ {ky} \right] + \left( {C_{2} + C_{1} e^{2{\text{M}} {\sqrt {\text{T}}} {\text{y}}} } \right)\left( {k^{2} + M^{2} T} \right){\text{sinh}} \left[ {ky} \right]} \right)} \right) \\ & \quad + \frac{{4e^{ - {\text{hM}}\sqrt {\text{T}} } k^{3} \sqrt{T} U\left( { - 4C_{2} M + 4C_{1} e^{2{\text{hM}}\sqrt {\text{T}} } M + e^{{\text{hM}}\sqrt {\text{T}} } k^{2} \sqrt{T} U} \right)\eta {\text{tanh}} \left[ {hk} \right]}}{{\left( {k^{2} - M^{2} T} \right)^{2} }} \\ & \quad \left. { + \frac{{2e^{ - 2{\text{hM}}\sqrt {\text{T}} } \left( { - C_{2}^{2} + C_{1}^{2} e^{4{\text{hM}}\sqrt {\text{T}} } + 4C_{1} C_{2} e^{2{\text{hM}}\sqrt {\text{T}} } hM\sqrt{T} } \right)\eta {\text{tanh}} \left[ {hk} \right]^{2} }}{MT^{3/2} }} \right). \end{aligned} $$

Results and discussion

Figures 2a–e are plotted to examine the variations in velocity profile with change the magnitude of various parameters. It has been observed that the velocity of the ionic aqueous solution is larger than the velocity profile of SWCNTs + water ionic nanofluid. This result also supports the physical properties, i.e., thermal conductivity of carbon nanotubes which tends to dissipate heat more rapidly as compared to pure water. As a result, fluid particles have less kinetic energy in the case of SWCNTs + water nanofluid and hence velocity profile decreases. Thermophysical properties of the physical parameters such as specific heat capacity, density, thermal conductivity, and thermal expansion coefficient for SWCNTs and water are listed in Table 1. Keeping in view that the relative permittivity of the water is 80 and applying the electric field strength of up to 1kVcm−1, the magnitude of Helmholtz–Smoluchowski velocity is approximately equal to 2 cm−1. Further, with the bulk ionic concentration ranging from 1 μM to 1 mM, the range of Debye length parameter k is found to be from O(1)–O(100). The nanoparticle volume fraction is chosen to be 0.2 vol%; however, the effect of varying nanoparticle volume fraction from 0.1 to 0.3 vol% is also presented. The Prandtl number for water typically varies from 1.7 to 13.7.

Fig. 2
figure 2

a–e Velocity profile u(y) for different values of the k, \(M\), Gr, U and γ

Full size image
Table 1 Thermophysical properties of pure water and single-wall carbon nanotubes (see Ref. [33])
Full size table

Figure 2a reveals an enhancement in velocity for larger Debye length parameter k. Physically conveying, a rise in k tends to decay in EDL thickness which mainly strengthens electroosmotic forces responsible for electroosmotic velocity in the direction of peristaltic pumping. As a result, fluid is accelerated by increasing the Debey length parameter. Figure 2b demonstrates that raise in Hartmann number produces a decrease in the velocity field. It is well-known that increasing values of Hartmann number (M) results in the generation of strong Lorentz force which are opposing forces in nature. These forces resist the acceleration of fluid particles and hence velocity decreases. Figure 2c illustrates the response of velocity profile toward different values of Helmholtz–Smoluchowski (HS) velocity parameter. It is the velocity generated by the acceleration of ionic species due to electroosmotic forces. It can be seen through resulting sketch that velocity is maximum for a negative value of U and it is minimum for the positive value of U. This behavior of velocity can be well-justified by the fact that U = −1 corresponds to an assisting electric field, i.e., electric field in direction of peristaltic pumping, U = 0 means no electric field and U = 1 corresponds to opposing electric body forces. It can be analyzed from Fig. 2d that velocity increases via larger Grashof number Gr. As Grashof number is associated with the temperature difference generated within the fluid medium and a way to quantify the strength of buoyancy forces over viscous forces. A rise in Grashof number physically means that buoyancy forces are dominant over viscous forces which tend to enhance velocity profile. The impact of the velocity slip parameter on axial velocity is shown in Fig. 2e. It is found that velocity is decreasing function of slip velocity experienced by the fluid at channel walls.

Figure 3a–f are plotted to visualize the impact of various embedded parameters on temperature distribution. Figure 3a reveals an enhancement in temperature toward rising values of Debye length parameter k. The resulting graph displays growth in temperature as k increases. This behavior is valid physically since for larger k, the kinetic energy of fluid particles enhances, and an improvement in temperature is noticed. It is also noticed that in the presence of SWCNTs, ionic solution of water possesses a lower temperature. As the suspension of carbon nanotubes causes an enhancement in thermal conductivity of water therefore heat is being removed rapidly from the system. Due to such tremendous property of carbon nanotube suspensions, they are widely used as a coolant in the industrial domain. The decaying trend in temperature distribution via radiation parameter is demonstrated in Fig. 3b. Figure 3c indicates that temperature drops for positive HS velocity parameter but it grows for a negative value. The reason behind this response is that an assisting electric field, i.e., for U = −1, accelerates the fluid particles and more heat is generated. Consequently, the temperature rises. However, for U = 1, the electric field opposes fluid flow and a reduction in kinetic energy of fluid particles occurs which tends to reduce the temperature. The evolution of temperature distribution is noticed for increasing Brinkman number through Fig. 3d. Since Brinkman number is associated with viscous dissipation which is the process of heat generation via shear stress; therefore, more heat is produced as Br is increased. Consequently, the temperature rises. The impression of SWCNTs volume fraction on θ is shown in Fig. 3e. The temperature profile declines when the quantity of CNTs in the base fluid increases. With the addition of more carbon nanotubes, the thermal conductivity of base fluid enhances; therefore, heat is dissipated from the system more rapidly. Variation in temperature of fluid for various values of temperature slip parameter is revealed through Fig. 3f. It is noted that temperature enhances when the thermal slip parameter (η) is increased.

Fig. 3
figure 3

a–f Temperature profile θ(y) for different values of the k, Rd, U, Br, Φ, and η

Full size image

Streamline is one of the key flow characteristics of fluid dynamics. It is important to examine the streamline patterns under the effects of the physical parameters that affect the flow characteristics. It has a great significance in flow visualization. A key attribute of peristaltic flow is associated with the circulation of streamline termed as trapping which results in the formation of the trapped volume of fluids is called a bolus. This trapped bolus is carried along the peristaltic waves. This phenomenon is very useful in the transportation of fluid in a proper manner within the body. Figures 4–7 are drawn to analyze the trapping phenomenon subject to variation in various sundry parameters for SWCNTs + water nanofluid. Figure 4a–c captures the impact of the Debye length parameter (k) on trapping. It can be noticed that the size of the trapping bolus is enlarged for growing values of k due to the mobilization of ionic species through the fluid medium. Figure 5a–c indicates that there is a reduction in the size of trapping bolus as Hartmann number increases. It is mainly due to the retardation offered by the Lorentz forces o the fluid flow which controls the velocity of the fluid. Figure 6a–c reveals that when an electric field is applied in the direction of peristaltic propulsion then a large number of streamlines are observed and trapped bolus are also formed in this case. However, when the external electric field is removed, trapping bolus is disappeared from the streamline patterns. Also, it can be witnessed through Fig. 6c that when an opposing electric field is applied, trapping phenomenon again occurs but, in this case, the number of streamlines is smaller as compared to previous cases. Possibly it can be due to a reduction in the fluid velocity because in this case, electroosmotic velocity is occurring in the opposite direction of peristaltic pumping. Variation in trapping phenomenon for larger Grashof number (Gr) is reported through Fig. 7a–c. It is depicted that the size of the trapping bolus expands for a larger value of Gr. This behavior of circulatory flow pattern is well-justified as larger Grashof number corresponds to dominance of buoyancy forces over opposing viscous forces which in turn facilitates the flow pattern and the occurrence of the circulating streamlines.

Fig. 4
figure 4

Stream lines for SWCNT + H2O for a k = 2, b k = 2.2 and c k = 2.4

Full size image
Fig. 5
figure 5

Stream lines for SWCNT + H2O for a M = 0.2, b M = 0.7 and c M = 1.2

Full size image
Fig. 6
figure 6

Stream lines for SWCNT + H2O for a U = −2, b U = 0 and c U = 2

Full size image
Fig. 7
figure 7

Stream lines for SWCNT + H2O for a Gr = 6, b Gr = 7 and c Gr = 8

Full size image

Figure 8a–e provide insight into the response of pressure gradient for development in various pertinent parameters. Figure 8a characterizes the influence of the Debye length parameter (k) on the pressure gradient. With a rise in k, pressure gradient declines. It is also observed that the pressure gradient is higher for pure water as compared with SWCNTs + water nanofluid. For larger k, the motion of ions in the diffuse layer is boosted therefore pressure decreases in the direction of peristaltic pumping. In response to the rise in Grashof number, pressure gradient increases as manifested through Fig. 8b. It is clarified from Fig. 8c that pressure gradient increases in the forward direction when the electric field supports the peristaltic transport. However, for the case of no electric field and the opposing electric field, the assisting pressure gradient tends to drops because in case of no electric field pressure gradient is only generated due to peristaltic pumping and the net assisting pressure gradient is lower when compared with the case of forwarding electric field. In the case of the opposing electric field, the negative electroosmotic velocity generates the retarding pressure gradient in the opposite direction of peristaltic pumping which causes a reduction in net assisting pressure gradient. Variation in pressure gradient via a larger Hartmann number (M) is explored through Fig. 8d. It is obvious that the pressure gradient drops when the magnitude of M increases. The pressure gradient profile is improved when slip forces experienced by the fluid at channel walls (see Fig. 8e).

Fig. 8
figure 8

Pressure gradient for variation in k, Gr, U, M, and γ

Full size image

Variations in heat transfer rate via various involved parameters are displayed through bar graphs in Fig. 9.

Fig. 9
figure 9

Heat transfer coefficient for SWCNTs-water nanofluid

Full size image

In Fig. 9, blue-colored bars represent the variation in heat transfer rate for Prandtl number and it is found that the magnitude of heat transfer rate decays for larger Prandtl number. It is quite obvious as the Prandtl number is the measure of momentum diffusivity over thermal diffusivity and larger Prandtl number tends to slow down the thermal diffusion process. As a result, a reduction in the magnitude of heat transfer coefficient od observed. In Fig. 9, orange-colored bars manifests the alteration in heat transfer for Brinkmann number. A rise in Br corresponds to enhance the strength of the viscous dissipative forces which heats the fluid. Consequently, the heat transfer rate grows significantly. Further, it is noticed that the heat transfer coefficient decays via a larger radiation parameter. As the absorption power of the fluid is inversely related to the radiation parameter, increasing Rd produces a decay in temperature of the fluid, which in turn decreases the magnitude of the heat transfer coefficient. Figure 9 shows that electroosmotic phenomenon boosts the heat transfer rate when it is established in such a way that it assists the peristaltic pumping. However, a decline is noticed in the case of the opposing electric field.

A comparison of velocity and temperature has been performed between the investigation performed by N.S. Akbar [40] and limiting case of current problem and presented in Tables 2 and 3, respectively. A close agreement between the solution is given in Tables 2 and 3.

Table 2 Comparison of velocity profile of current investigation and the results obtained by N.S. Akbar[40]
Full size table
Table 3 Comparison of temperature profile of current investigation and the results obtained by N.S. Akbar[40]
Full size table

Conclusions

In this model, a theoretical study on electroosmotically modulated peristaltic pumping of SWCNTs + water ionic nanofluids subject to the influence of thermal radiation and the transverse magnetic field is investigated. Fluid flow is analyzed in the presence of buoyancy forces, and the impact of heat dissipation due to viscous forces is also considered. The slip boundary conditions for velocity and the temperature are implemented across the channel walls. The complexity of the nonlinear and coupled set of equations is reduced by adopting the regular perturbation technique and an approximate solution of the problem is obtained. Based on the numerical computations and discussion, the key outcomes of the present analysis are:

  • An increase in the Debye length parameter tends to raise velocity and diminish the pressure in the forward direction.

  • Trapping bolus size expands with increasing the magnitude of the Debye length parameter.

  • Temperature increases with adding the electric field and diminishes with opposing the electric field.

  • Flow and pumping characteristics improve with adding the electric field and reduces with opposing the electric field.

  • Development in the velocity slip parameter decelerates axial flow and elevates the pressure gradient.

  • The addition of SWCNTs in base fluid tends to decay the temperature profile due to enhancement in thermal conductance of the base fluid.

  • Trapping phenomena are strongly affected by adding and opposing the electric field.

  • The thermal slip parameter produces an enhancement in temperature distribution.

The findings of the present model can be applicable in biomicrofluidics applications like controlled drug delivery systems during cancer therapy to target and diagnose the diseased cell. Also this model can be used to enhance the efficiency of various cooling systems and solar heat collectors.