1 Introduction

In recent years, the urban underground space engineering, particularly the subway, has been developing rapidly due to the increasingly dense population of the super-metropolitan all over the world with the associated traffic congestion. So the shield construction method has also become the main construction techniques of the urban subway tunnel because of its advantages with the low construction site requirements, the high ground subsidence control safety, the environmental protection, the good construction quality and the energy saving [1,2,3,4]. However, the shield tunnel face becomes very unstable because of the disturbed zone ahead of the tunnel face by the shield tunnelling [4,5,6]. Different degrees of ground subsidence accidents caused by shield tunnelling happen frequently in Shanghai, Guangzhou, Beijing and so on [3, 4, 7]. How to maintain the stability of the tunnel face has become a key problem to ensure the safety of shield construction and reduce the environmental impact. The analysis shows that the instability of the shield tunnel face is mainly caused by two reasons [1, 4, 8, 9]. The first reason is that the support pressure is probably excessive. For the EPB shield, the ground surface uplift will appear in front of the shield. The second reason is that the support pressure is too small possibly. The soil–water pressure ahead of tunnel face cannot be balanced, resulting in the ground surface subsidence in front of the shield. Compared with the past tunnel accidents, the recent shield tunnelling accidents show that the engineering accidents appear more frequent and more serious largely due to the less support pressure of the tunnel face [10,11,12]. Therefore, the minimum supporting force of the tunnel face has been a hot research topic.

The relevant research on the ultimate supporting force of shield tunnel face mainly includes the following four methods: model test method [4, 13,14,15], numerical simulation [1, 10,11,12, 15,16,17], limit equilibrium method [2, 15, 18,19,20,21,22,23] and limit analysis method [8, 23,24,25,26]. These four methods have their own advantages. For example, the physical model test can provide the convincing experimental data in spite of the high cost, the numerical simulation has great difference due to the multitudinous hypotheses, and the limit analysis method needs to take the energy dissipation theory and appear too complicated. So the three above-mentioned methods are difficult to be popularized individually in the practical engineering. However, the limit equilibrium method can get the definite analytic formula through the simple analysis. The application is quite ideal. So the massive studies have been carried based on this. Murayama formula is an excellent example. It simplifies the three-dimensional problem into two-dimensional plane problem to deal with and also causes the limitation of its formula. According to the three-dimensional wedge shape calculation model established by Born [5], Jancsecz & Steiner [14] set up the equilibrium equation through the force balance of the wedge block and finally obtained the calculation formula. But this model does not consider the arching effect of sandy soil, and the result is not accurate enough. For this reason, Wei Gang et al. [18] improved the model and established the trapezoidal wedge model, but the trapezoidal wedge model did not consider the shear strength of the soil on the side of the slider, and it was only suitable for sandy soil. So Hu Wenting [19] further improved the trapezoidal slider inclination angle to unknown quantity and get the best value through the later optimization search on the basis of the model by Wei Gang et al. [18], yet its calculation formula is only applicable to sandy soil. According to Chengdu sand pebble, Bai Yongxue [11] obtained the support pressure of shield tunnel face by the trapezoidal wedge calculation model, where the lateral triangle of the sliding block and the interaction force between its top and the external soil of the sliding block are considered in the derivation process. Although the calculation formula has certain reference value for sand pebble formation, its calculation model cannot accurately predict the tunnel face support pressure of the shield in the sandy cobble stratum.

Based on the existing deficiencies of the above-mentioned shield tunnel face support pressure research, an improved three-dimensional trapezoidal wedge calculation model in this paper is proposed in accordance with the 8600-mm-diameter shield tunnel in the sand pebble of the Chengdu Metro Line 18. The improved calculation model not only takes into account the influence of the wedge sliding block side soil, but also the obtained support pressure formula can also be used to optimize the outer edge length of the wedge-shaped slider and get the optimal value. Then, the parameter analysis is carried out, and the main influencing factors of the limit support pressure are discussed. Finally, the slip surface is verified by the numerical simulation, and the theoretical limit support pressure is verified by practical engineering cases.

2 Three-Dimensional Limit Equilibrium Solution

2.1 Establishment of Theoretical Calculation Model

The trapezoidal wedge calculation model is set up after considering the arching effect after horizontal unloading during shield tunnelling. On this basis, an improved trapezoidal wedge calculation model is proposed as shown in Fig. 1, which takes into account the influence between pebble and pebble, pebble and sand near the slip interface. The vertical slip failure along the interface will emerge under this condition. In three-dimensional calculation model in Fig. 1, α and β of the trapezoid wedge shape are \( \alpha = 60^{\text{o}} \) and \( \beta = 45^{\text{o}} +\frac{\varphi}{2} \)

Fig. 1
figure 1

Three-dimensional calculation model of trapezoid wedge shape

Full size image

The action direction of the different forces on the trapezoidal sliding block is shown in Fig. 2. P is the total supporting force of shield cutter head acting on tunnel face. F represents the force of upper trapezoid prism acting on the trapezoidal sliding block. G stands for the deadweight of trapezoidal sliding block. N1, N2, N3 are representative for the normal force on the corresponding surface, respectively. T1, T2, T3 delegate sliding friction force on corresponding surface, respectively.

Fig. 2
figure 2

Force diagram of sliding trapezoidal wedge

Full size image

2.2 Basic Assumptions

The following assumptions need to be made before establishing the minimum support pressure:

(1) The soil is a homogeneous, isotropic rigid plastic material following the Mohr–Coulomb yielding criteria. The calculating formula of the shear strength τ on the sliding surface is as follows:

$$ \tau = c + \sigma \tan \varphi $$
(1)

where the c is the cohesive force of soil, the \( \sigma \) is the normal stress on shear surface, the \( \varphi \) is the internal friction angle of soil.

(2) There is no cohesive force between the sand pebble, and the influence of cohesive force c is neglected in the calculation, c = 0.

(3) In the vicinity of the slip interface, the vertical slip failure along the interface will happen as a result of the influence among the pebbles. It is assumed that the L1 is a variable, as shown in Fig. 1, and the optimal value will be obtained through a later optimization search.

(4) The contact surface between the trapezoid and the tunnel face is square, and its area is equal to the tunnel face of the tunnel. That is:

$$ L = d\sqrt \pi/2 $$
(2)

(5) The vertical stress on the inclined plane and vertical plane of trapezoidal body increases linearly with depth.

2.3 Establishment of Equilibrium Equations

The normal force N3 and the friction force T3 on the trapezoidal side ADEN of the trapezoidal sliding block are required directional decomposition before establishing the equilibrium equation of friction. The normal force on the trapezoidal side ADEN is perpendicular to the trapezoid side. T3 is sliding friction force opposite to the motion direction of the trapezoidal sliding block. The direction is parallel to the trapezoidal side ADEN and has angle β with the horizontal plane. The schematic diagram of the sliding trapezoidal wedge block and the leading plane used for the solution is seen in Fig. 3.

Fig. 3
figure 3

Sliding trapezoidal wedge and schematic drawing

Full size image

Combined with each force direction in Fig. 2, the vertical force balance equation of the trapezoidal sliding block is expressed as follows:

$$ F + G = 2T_{3} \sin \beta + T_{2} + T_{1} \sin \beta + N_{1} \cos \beta $$
(3)

The force balance equation in the horizontal direction of trapezoidal sliding block is as follows:

$$ P + 2T_{3} \cos \beta \sin \alpha + T_{1} \cos \beta = N_{2} + 2N_{3} \cos \alpha + N_{1} \sin \beta $$
(4)

Available from (3):

$$ N_{1} = \frac{{F + G - T_{2}}}{\cos \beta} - 2T_{3} \tan \beta - T_{1} \tan \beta $$
(5)

By substituting (5) into (4), an unknown quantity N1 can be eliminated. The expression of minimum support force in the limit state is:

$$ P = \left({F + G} \right)\tan \beta - T_{2} \tan \beta - 2T_{3} \left({\tan \beta \sin \beta + \cos \beta \sin \alpha} \right) + N_{2} + 2N_{3} \cos \alpha - T_{1} \left({\tan \beta \sin \beta + \cos \beta} \right) $$
(6)

2.4 Solutions Under Each Unknown Quantity

The seven unknown quantities, including F, G, N2, N3, T1, T2, T3, are in the preceding formula (6), which are calculated in turn. Weight G of trapezoidal sliding blocks can be calculated from formula (7):

$$ G = \gamma \cdot \left[{L^{2} + L_{1} h_{1} + \sqrt {L^{2} \cdot L_{1} h_{1}}} \right] \cdot h/3 $$
(7)

Force F acting on the upper trapezoidal prism of the trapezoidal sliding blocks is obtained as follows:

$$ F = \sigma_{v} \cdot A $$
(8)

where \( A = (L + L_{1}) \times h/2 \)

The \( \sigma_{v} \) is obtained based on the Terzaghi theory, as shown in Fig. 4. According to the stress balance of the soil column element, we can obtain:

$$ A\sigma_{v} + A\gamma {\text{d}}z = A(\sigma_{v} + {\text{d}}\sigma_{v}) + D(k_{0} \sigma_{v} \tan \varphi){\text{d}}z $$
(9)

Where \( D = L + L_{1} + \frac{2h}{\sin \alpha} \).

Fig. 4
figure 4

Computational model of loose soil pressure

Full size image

By solving (9) by the boundary condition \( Z =0,\sigma_{v} = P_{0} \), we can obtain the three-dimensional earth pressure at any depth.

$$ \sigma_{v} = \frac{\gamma \lambda}{{k_{0} \tan \varphi}} \cdot \left({1 - e^{{- \frac{{k_{0} \tan \varphi z}}{\lambda}}}} \right) + P_{0} \cdot e^{{- \frac{{k_{0} \tan \varphi z}}{\lambda}}} $$
(10)

The \( \lambda \) is obtained by the formula (7).

$$ \lambda = \frac{A}{D} = \frac{{(L + L_{1})h\sin \alpha}}{{(L + L_{1})2\sin \alpha + 4h}} $$
(11)

Substitute (10) into (8):

$$ F = \left[{\frac{{\gamma \lambda \left({1 - e^{{- \frac{{k_{0} \tan \varphi z}}{\lambda}}}} \right)}}{{k_{0} \tan \varphi}} + P_{0} \cdot e^{{- \frac{{k_{0} \tan \varphi z}}{\lambda}}}} \right] \cdot \frac{{(L + L_{1}) \times h}}{2} $$
(12)

(3) Shear T1 on the inclined plane ABMN of trapezoidal is

$$ T_{1} = S_{ABMN} (c + \bar{\sigma}\tan \varphi) $$
(13)

Where \( \bar{\sigma} \) is the average compressive stress, \( T_{1} = N_{1} \tan \varphi \) due to \( c =0 \).

According to formula (5), \( T_{1} \) can be changed to the formula (14):

$$ T_{1} = \frac{{(F + G - T_{2})\tan \varphi}}{\cos \beta (1 + \tan \beta \tan \varphi)} - \frac{{2T_{3} \tan \beta \tan \varphi}}{(1 + \tan \beta \tan \varphi)} $$
(14)

(4) N3 and T3 on both sides of the wedge

The \( \sigma_{v} \) is the vertical stress at the top of the sliding block. It can be calculated according to the loose soil pressure theory of Terzaghi. With the increase in the covering depth, the vertical soil pressure of the sliding surface on both sides of the sliding block increases with the covering depth.

$$ \sigma_{h} = k_{0} (\sigma_{v} + \gamma \cdot y^{\prime}) $$
(15)

where \( k_{0} \) is the soil side pressure coefficient, \( k_{0} = 1 - \sin \varphi \)

The lateral trapezoid ADEM and BCFM of the trapezoidal sliding block are the plane of the vertical horizontal plane, and the lateral trapezoid positive pressure N3 of the sliding block is mainly provided by the horizontal directional force of the soil, so it is perpendicular to the lateral trapezoid plane, and its expression is:

$$ N_{3} = \int_{A} {\sigma_{h} {\text{d}}A} $$
(16)

Integral and simplified:

$$ N_{3} = \frac{{k_{0} h\left[{3\sigma_{v} \left({L + h_{1}} \right) + \gamma \left({L^{2} + Lh_{1} + h_{1}^{2}} \right)} \right]}}{6\sin \alpha} $$
(17)

Then:

$$ T_{3} = \frac{{k_{0} h\left[{3\sigma_{v} \left({L + h_{1}} \right) + \gamma \left({L^{2} + Lh_{1} + h_{1}^{2}} \right)} \right]}}{6\sin \alpha} \cdot \tan \varphi $$
(18)

(5) Shear force \( N_{2} \) and pressure \( T_{2} \) on the vertical MNEF of the wedge

The stress distribution of the vertical MNEF and its calculation process is similar to \( N_{3} \), \( T_{3} \).

$$ N_{2} = L_{1} k_{0} \sigma_{v} h_{1} + L_{1} k_{0} \gamma \frac{{h_{1}^{2}}}{2} $$
(19)

Then:

$$ T_{2} = \left({L_{1} k_{0} \sigma_{v} h_{1} + L_{1} k_{0} \gamma \frac{{h_{1}^{2}}}{2}} \right)\tan \varphi $$
(20)

Based on the above F, G, N2, N3, T1, T2, T3, the limit support pressure P can be obtained by substituting the seven unknown quantities obtained into the formula (6), but the P at this time is about the concentrated force on the tunnel face, which is divided by the tunnel face area to obtain the minimum pressure of the earth bunker, that is:

$$ \sigma_{P} = \frac{4P}{{\pi d^{2}}} $$
(21)

3 Results and Analysis of Minimum Support Pressure

3.1 The Optimized Search of L1

The \( \sigma_{P} \) obtained by the formula (21) is a functional equation about L1. Strictly speaking, the \( \sigma_{P\max} \) can be obtained by means of \( \partial \sigma_{P}/\partial L_{1} =0 \). And the minimum limit support pressure by this equation is to maintain the stability of the tunnel face. L1 at this time is the optimal solution. However, the application of the above method will greatly increase the calculation workload because the formula is too complicated. So it tries to draw the function image in this paper and find out that the maximum point in the image is the optimal solution.

In order to find the optimal solution, the analogy analysis by the two trial calculations will be carried on. Assuming that the tunnel diameter is 6 m, the soil weight is 20 kN/m, the covering depth is 6 m, the ground load is 0, and then the L1 with \( \sigma_{P} \) at different internal friction angles is calculated, as shown in Fig. 5.

Fig. 5
figure 5

Optimal search of L1 under different internal friction angles (D = 6 m)

Full size image

Assuming that the tunnel diameter is 8 m, the soil mass is 20 kN/m, the covering depth is 8 m, the ground load is 0, and then the L1 with \( \sigma_{P} \) at different internal friction angles is calculated, as shown in Fig. 6.

Fig. 6
figure 6

Optimal search of L1under different internal friction angles (D = 8 m)

Full size image

The following results can be obtained from the analogical analysis of Figs. 5 and 6: (1) The range of L1 is not (0, L), but in a range of (0, L). L1 is related to the internal friction angle \( \varphi \). And the smaller the value of the internal friction angle \( \varphi \) is, the larger the value range of L1is. (2) As the L1 increases, the \( \sigma_{P} \) increases slightly and subsequently remains unchanged. After the L1 reaches half of the excavation diameter, the \( \sigma_{P} \) begins to drop until L1 takes all the values as it grows with L1. The change trend of \( \sigma_{P} \) will be more obvious when the internal friction angle \( \varphi \) becomes smaller. As it grows with \( \varphi \), the change trend of \( \sigma_{P} \) will become smaller. And after the internal friction angle \( \varphi \) is more than 30°, the change of range \( \sigma_{P} \) (the difference between the maximum and the minimum) will not exceed 2 kPa.

Based on the aforementioned conclusion (2), a half of the tunnel excavation diameter can be used as the optimal solution about L1 in the subsequent calculation, i.e. the position marked by the vertical lines in Figs. 5 and 6. In order to ensure that the limit support pressure value obtained by the internal friction angles is safe, the minimum support pressure \( \sigma_{P} \) obtained under the optimal solution is guaranteed. And it is safe to satisfy all the calculation results applied in engineering practice.

3.2 Relationship Between Internal Friction Angle and Ultimate Support Pressure

The internal friction angle \( \varphi \) is an important parameter which causes the limit support pressure change. In order to obtain the relationship between the internal friction angle and the ultimate support pressure, it is assumed that the tunnel diameter is 5 m, the soil weight is 16.1kN/m3 and the ground load is 0 kPa. According to the conclusion of the optimized search about L1, the unknown L1 is 2.5 m by the calculation model of this paper. So the relationship between the limit support pressure \( \sigma_{P} \) and the internal friction angle \( \varphi \) is obtained as shown in Fig. 7.

Fig. 7
figure 7

Limit support pressure under different internal friction angles

Full size image

The following analysis results can be obtained from Fig. 7:

(1) When the friction angle \( \varphi \) of the soil is small (less than 25°), the limit support pressure \( \sigma_{P} \) of tunnel depth ratio H/D = 1 is less than that of H/d = 2 and H/D = 3.

(2)When the soil friction angle \( \varphi \) increases, the tunnel depth has little influence on the calculation result of the limit support pressure \( \sigma_{P} \). And when the friction angle of the soil is large, the limit support pressure \( \sigma_{P} \) is hardly affected by the tunnel covering depth.

(3) The greater the internal friction angle is, the less the ultimate support pressure becomes.

These three conclusions are the same as those obtained by other three-dimensional limit equilibrium models [2, 11, 27].

3.3 Relationship Between Tunnel Diameter and Ultimate Support Pressure

The different tunnel diameter also affects the value of limit support pressure. In this paper, it is assumed that the internal friction angle of soil is 38°, the soil weight is 16.1kN/m3 and the ground load is 0. The relationship between diameter and limit support pressure can be obtained by calculation, as shown in Fig. 8. The following results can be derived from Fig. 8:

Fig. 8
figure 8

Limit support pressure under different diameters

Full size image

(1) The tunnel diameter is proportional to the limit support pressure, that is, the larger the diameter is, and the higher the required limit support pressure value is.

(2) Compared with the previous conclusions, the results of this paper show the same trend, but the results are great. And with the increase in diameter, the gap with the previous conclusions will gradually increase.

(3) The calculation result of the limit support pressure in this paper is too large. On the one hand, the normal force and sliding friction force considered on each surface are more comprehensive because the sliding surface is set up. On the other hand, it also shows that the limit support pressure required for sand pebble formation is greater than that of other strata.

4 Verification of the Analytical Model

4.1 Verification of the Slip Surface by the Numerical Simulation

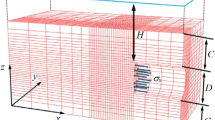
During shield tunnelling, the unstable collapse in front of tunnel face is caused by the improper control of support pressure. It is owned by the large deformation and the failure of the geotechnical engineering problem. Therefore, Flac3D is used better to simulate the failure characteristics. In this paper, the shield tunnel model established by Flac3D is illustrated in Fig. 9.

Fig. 9
figure 9

3D numerical calculation model

Full size image

The model is described as the following assumptions:

(1) The cross section of the shield tunnel is circular with symmetrical slip surface. In order to better observe the morphology of the slip tunnel face, it can be observed taking half the radial tunnels.

(2)The shield tunnelling is a progressive process. The research is focused on the tunnel face instability of slip form, regardless of the actual shield tunnelling process. Therefore, a certain length after tunnel face is carried out and the segment support is simulated timely. The segment is simulated by shell element built-in software. It is assumed that \( \sigma_{\text{s}} \) is the support stress at the centre of the tunnel face and \( \sigma_{t} \) is the static earth pressure at the centre of the tunnel. According to the classical soil mechanics formula, it can obtain:

$$ \sigma_{t} = k_{0} \gamma h $$
(22)

Where k0 is the lateral pressure coefficient of soil, γ is the weight of soil, h is the distance from the centre of the tunnel to the ground.

(3) The support ratio of the shield is \( \upsigma_{s}/\upsigma_{t} \). If λ = 1, the support stress acting on the tunnel face is sufficient to balance the earth pressure in front of the tunnel face. If 0 < λ<1, it means the support stress force is less than the soil pressure, so it will induce a certain displacement to the tunnel face. With the decrease in the λ, the displacement will increase gradually. When the decrease in λ is very small, the tunnel face displacement increases sharply. This moment, λ, is the limit support stress ratio, which is denoted as λ0. The support ratio is set by the Fish function, and the support stress in the limit state can be reached by the λ0 back calculation. In the calculation model, tunnel diameter D is 6 m and the covered depth C is 12 m. The physical and mechanical indexes of the materials are shown in Table 1.

Table 1 Mechanics parameters of materials
Full size table

Figure 10 indicates that the instability and the slip pattern in front of tunnel face without support pressure are made of the five basic descriptions of sliding blocks in front of tunnel face. (1) The sliding block in front of the tunnel face can be divided into two parts, the upper part and lower part. And the boundary line is approximately the top of the tunnel. (2) The upper sliding block is cylindrical and develops upward to the surface. This is roughly the same as the shape of the ground crater caused by the shield tunnel face instability case as shown in Fig. 11. (3) The lower part of the instability model is wedge-shaped. Unstable soil mass slides along the wedge surface of the tunnel face, which eventually leads to the instability and destruction of the entire tunnel face. The instability slip surface ahead of tunnel face agrees basically with the trapezoid wedge shape of the three-dimensional calculation model in Fig. 1. It is reasonable that the instability slip surface ahead of tunnel face is assumed to be the trapezoid wedge shape.

Fig. 10
figure 10

Instability slip surface ahead of tunnel face: a displacement slip diagram of instability ahead of tunnel face, b velocity vector slip diagram of instability ahead of tunnel face

Full size image
Fig. 11
figure 11

Ground subsidence shape caused by shield tunnel face instability

Full size image

4.2 Verification of Theoretical Limit Support Pressure

Besides, theoretical limit support pressure can be also verified by the numerical simulation results and the measured field results.

The Chengdu Metro Line 18 civil engineering 1 standard shield section starts from the South Railway Station and arrives at Jincheng Square Station. The rock strata traversed by the tunnel in this section are mainly medium-dense pebble soil < 3-8-2 > , dense pebble soil < 3-8-3 > and medium-weathered mudstone < 5-1-3 > . The maximum covered depth of the line is about 38 m, the outer diameter of the segment is 8.3 m, the inner diameter is 7.5 m, the thickness of the segment is 0.4 m and the 1.5 m wide segment is adopted. The stratum parameters are shown in Table 2. The measured support pressure from the left line between ZDK10 + 550 station and ZDK10 + 580 station is selected in this paper. The section mainly passes through the sand pebble stratum, and its average covered depth is 9.5 m. The average distance between groundwater level and the axis of tunnel face is 6.5 m. The measured pressure in soil chamber is mostly between 30 kPa and 32 kPa, and some of them reach 110 kPa to 116 kPa, which fluctuates greatly.

Table 2 Stratum parameter table
Full size table

When considering the situation containing groundwater, in order to simplify the calculation, without considering the seepage effect of groundwater, the calculation formula of the limit support pressure that only calculates the hydrostatic pressure is as follows:

$$ \sigma^{\prime}_{P} = \frac{{4P^{\prime}}}{{\pi d^{2}}} +\gamma_{w} H_{w} $$
(24)

Where: γw-Unit weight of water, 10kN/m3; Hw-Distance from groundwater level to the centre of the tunnel; P′-The limit support pressure calculated according to effective unit weight; σ′p-limit support pressure considering groundwater.

The theoretical calculation results, the numerical simulation results and the field measured data derived in this paper are presented in Table 3. It can be determined that compared with the numerical simulation results, the calculation formula derived in this paper is more comprehensive. Therefore, it has higher safety and is more consistent with the field measured data. It shows that the calculation formula has strong applicability in sand pebble stratum. The existence of groundwater has a great influence on the ultimate support pressure, especially in the sand pebble stratum with good permeability. The field measured data are roughly 1.4 times of the limit support pressure, and there is no abnormality during the tunnelling process, so the safety factor can be set to 1.4. In the subsequent setting of the soil warehouse pressure, 1.4 times of the limit support pressure value deduced in this paper is used as the dwell value during the subsequent construction.

Table 3 Comparison of calculation results
Full size table

5 Conclusions

On the basis of considering the characteristics of sand and pebble, an improved three-dimensional wedge shape calculation model is proposed, and the analytical formula is obtained by using the limit equilibrium method. The optimal solution of the limit support pressure is analysed when the trapezoid bottom is half of the tunnel diameter. The influence factors of the support pressure are analysed based on the optimal solution. And it is deduced that the larger the covering depth is, the greater the required limit support pressure is. But when the tunnel is in deep strata, the covering depth has little effect on the limit support pressure. The greater the internal friction of the soil is, the smaller the required limit support pressure becomes. And when other formation parameters are fixed, the larger the tunnel diameter is, the greater the required limit support pressure is. Finally, the calculation model has strong applicability to sand pebble formation based on the numerical simulation results and the field data of Chengdu Metro Line 18.