1 Introduction

The most important role in safe construction of shielding tunneling is how to keep up the tunnel face stability. Lots of experimental [1–3] and theoretical works [4–9] have been done on the failure mechanism and limit support pressure of shield tunnel face. The most widely adopted method to estimate the minimum limit support pressure in engineering practice is the Murayama formula [10]. This formula was derived from a 2D limit equilibrium model. Obviously, tunnel face stability is a 3D problem; rational analysis should be derived from a 3D model. The 3-D effects of stability analysis have been clearly shown in related problems (i.e., slope stability [11]).

Various numerical methods have been used in the deformation, stress, and stability analysis of tunnel excavation face [12]. Elastoplastic FE analysis was employed to study the failure mode and the limit support pressure of tunnel face [13–15]. Discrete element modeling, Lagrangian analysis of continua, and numerical stress analysis were adopted to study the failure mechanism and support characteristics of the tunnel face [3, 16–18]. Comparing to the complicated numerical simulation, an analytical method is more acceptable to engineering practice. A wedge model [19], which is based on the silo theory, was applied to estimate the limit support pressure [5]. Based on the wedge model, Anagnostou [20] obtained a design equation to estimate the limit support pressure, and Anagnostou and Perazzelli [21] further investigated the effects of the support pressure distribution and free unsupported span on the tunnel face stability. The influences of the heterogeneity of soft soils [22] and bolt reinforcement [7] on tunnel face stability were investigated by the wedge model. Although wedge model gives out an analytical solution to limit support pressure, it requires a preliminary assumption of failure mode. The accuracy of the calculation strongly relies on the adopted failure mode. Limit analysis method was used to obtain an upper and lower bound solution to limit support pressure [4]. Comparing to the limit equilibrium method, upper bound limit analysis can optimize the failure mechanism and produce a better solution [23, 24], especially when the optimized failure mechanism was adopted [25]. In recent years, upper bound limit analysis method was extended to wide range of tunnel and ground conditions [26, 27], i.e., multi-layered soil [28, 29]. Although the limit analysis method can produce correct solution to limit support pressure, the complicated calculating procedure hinders its application in engineering, especially in the case of seepage condition.

In soft ground area with high water table line, shield tunnel often locates below the water table line. The underground water seepage shows great influence on tunnel face stability [30–33]. Most theoretical method analyzing shield tunnel face stability under seepage condition is to introduce a seepage force into an existing model; the seepage force can be obtained by numerical analysis in advance [34]. By considering the seepage force in force equilibrium, the wedge model was modified to estimate the limit support pressure under a seepage condition [5]. The slices method [20] was adopted to study tunnel face stability under seepage condition [35, 36]. Based on the failure mode of Leca and Dormieux [4], Lee et al. [37] gave out an upper bound solution to the limit support pressure by introducing the work of seepage force into energy equation. Lu et al. [38] proposed a failure mechanism of shield tunnel face under seepage condition, based on which an upper bound limit solution was obtained. However, the ignorance of seepage force on the failure mode often induces inaccurate result. Numerical study has shown that the failure mode of tunnel face will be changed by seepage, especially when the water level is high [39].

This paper aims to predict the limit support pressure in shallow tunnels with seepage numerically and analytically. The contents of the paper are organized as follows; the face stability of shield shallow tunnel was first studied by the 3D FE simulation. The formula to calculate the limit support pressure was rearranged by the superposition of cohesion, surcharge, and soil weight multiplied by their corresponding coefficients. The varying characteristics of these coefficients obtained from analytical and numerical results were analyzed. According to the seepage analysis of the tunnel face, the analytical expression of the water head distribution was obtained. The seepage force was calculated according to the water head distribution, and a 3D limit equilibrium method was established. The method was employed to analyze the Qiangjiang cross-river shield tunnel face stability; the obtained limit support pressure was compared with the numerical simulation.

2 FE Simulation of Shallow Shield Tunnel Face Under Seepage Condition

The relationship of displacement and support pressure in shallow shield tunnel face found in cohesive-frictional soils was obtained by a 3D finite-element simulation. The elastic-perfectly plastic model with Mohr–Coulomb failure criterion was used in the simulation. The tunnel diameter D was 10 m, the tunnel depth C was 10 m, the distance between the water level and tunnel top H was 10 m, and the surcharge load q was 20 kpa. The 20-node quadrilateral element with pore water pressure was used, and the mesh is shown in Fig. 1. The x-directions of the oyz plane and rear plane were fixed, the y-directions of the oxz plane and rear plane were constrained, the bottom surface of the model was fixed, and the surface between soil and lining was fixed. The unit weight of the soil γ was 17 kN/m3, Young’s modulus E was 30 Mpa, and Poisson ratio ν was 0.3.

Fig. 1
figure 1

The 3D finite-element mesh for the stability analysis of shield tunnel

Full size image

The numerical simulation steps are as follows:

  1. (1)

    The initial stress state induced by the soil weight and the surcharge load was calculated.

  2. (2)

    The soil elements at the excavation area were removed, and a uniform distributed initial support pressure σs0 was applied to the tunnel face. The displacement was setting zero after the computation. To reflect the real stress state of tunnel face before excavation, σs0 was set as the earth pressure at rest \(\left( {\sigma_{{{\text{s}}0}} = K_{0} \left[ {q + \gamma \left( {C + D/2} \right)} \right],K_{0} = 1 - \sin \varphi } \right)\) [13].

  3. (3)

    The support pressure was decreased by hybrid incremental iterative method until the tunnel face collapsed; the deformation caused by the decrease of support pressure was obtained.

The relationship between the support pressure and horizontal displacement at the midpoint of tunnel face is shown in Fig. 2. The deformation increases with the decrease in support pressure. The soil deformation grows rapidly and reaches an active failure state when support pressure approaches a certain value. The decrease in the soil friction angle pulls up the curve and results of a high limit support pressure. As shown in Fig. 3, the failure mode of the tunnel face becomes flattened under seepage condition.

Fig. 2
figure 2

Relationship between support pressure and displacement at the center-point of tunnel face (C/D = 1)

Full size image
Fig. 3
figure 3

The displacement and equivalent plastic strain at collapse

Full size image

In order to analyze the effect of soil cohesion on the tunnel face stability, the cohesion was set as 5, 10, 15, 20, and 30 kPa in numerical simulation. The failure mode of the excavation faces was obtained when φ = 35°, C/D = 1 and H/D = 1. As shown in Fig. 4, the failure modes are almost the same when c equals to 5 and 30 kPa; the cohesion shows little influence on failure mode. The effect of the friction angle on the failure mode was obtained. The collapse modes of the tunnel face when friction angles were 5°, 15°, 25°, 35°, and 45° are shown in Fig. 5. The expanding trend of collapse zone to ground surface is obvious when the friction angle is low. With the friction angle increase, the slope of the failure surface increases. The effect of the tunnel depth was further studied when C/D (ratio of cover and tunnel diameter) was 0.5, 1, 2, and 3. The failure modes obtained from numerical simulations are shown in Fig. 6, and the change of C/D values shows little influence on the failure mode of soil near the tunnel face. The effect of the water level on the failure mode is shown in Fig. 7, the increase in water levels flattens failure mode.

Fig. 4
figure 4

The failure mode of tunnel face with different cohesion of soil

Full size image
Fig. 5
figure 5

The failure mode of tunnel face with different friction angles of soil

Full size image
Fig. 6
figure 6

The failure mode under different tunnel depth conditions

Full size image
Fig. 7
figure 7

The failure mode under different water level conditions

Full size image

3 The Limit Support Pressure Without Seepage

3.1 Wedge Equilibrium Model

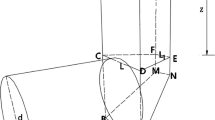
The wedge model [5] is a widely used 3D limit equilibrium method of the tunnel face stability analysis. As shown in Fig. 8, the equilibrium of the wedge requires enough support pressure. To calculate the vertical earth pressure, σ v is above the sliding wedge. The soil in loosen zone is assumed a column, and the vertical forces of a soil column element are shown in Fig. 9. The governing equation and the boundary condition are [5] as follows:

$$\left\{ {\begin{array}{*{20}l} {d\sigma_{\text{v}} + \frac{{2B(1 + \tan \;\alpha )(c + K_{0} \sigma_{\text{v}} \tan \varphi )}}{A\;\tan \alpha }dz - \gamma dz = 0} \hfill \\ {\left. {\sigma_{\text{v}} } \right|_{z = 0} \; = q} \hfill \\ \end{array} } \right\}$$
(1)

where A = B 2/tan(α) is the area of the cross section. The rectangular section of the wedge model is not in accordance with the round shape, and the round area should be converted by BD = πd 2 /4 (B is the width of wedge, D is the height of the wedge, and d is the diameter of the round tunnel). If B = D, then B 2 = πd 2/4. α is the inclination angle of the wedge (as shown in Fig. 8), K 0 is the earth pressure coefficient at rest.

Fig. 8
figure 8

The schematic of 3D wedge limit equilibrium model

Full size image
Fig. 9
figure 9

The schematic of earth pressure calculation

Full size image

The solution of Eq. (1) is as follows:

$$\sigma_{\text{v}} = \frac{B\gamma - 2c(1 + \tan \alpha )}{{2K_{0} (1 + \tan \;\alpha )\tan \varphi }}\left[ {1 - e^{{ - \frac{{2K_{0} z\tan \;\varphi (1 + \tan \;\alpha )}}{B}}} } \right] + qe\frac{{2K_{0} z\tan \varphi (1 + \tan \alpha )}}{B}$$
(2)

where γ is the soil gravity, and z is the depth.

According to the force equilibrium of the wedge,

$$\left\{ {\begin{array}{*{20}l} {P_{\text{s}} = N\;\sin \alpha - T\cos \alpha - 2T'\cos \alpha } \hfill \\ {\frac{{\sigma_{\text{v}} B^{2} }}{\tan \alpha } + G = N\cos \alpha + T\sin \alpha + 2T'\sin \alpha } \hfill \\ \end{array} } \right\}$$
(3)

where P s is the limit support force, T is the friction force on the sliding plane abef, N is the normal forces on the sliding plane abef, T’″ is the friction force on the wedge side ade or bcf, \(N' = K_{0} \gamma z\) is the normal force on wedge side ade or bcf, and G is gravity force of the wedge.

The gravity force of the wedge can be calculated by multiplying the soil weight by the volume of wedge:

$$G = \int_{0}^{B} {\frac{\gamma Bz}{\tan \alpha }} dz = \frac{{B^{3} \gamma }}{2\tan \alpha }.$$
(4)

The friction force T can be obtained by multiplying the shear strength of soil by the area of abef, and friction force T′ can be obtained by multiplying the shear strength of soil by the area of ade or bcf:

$$\left\{ {\begin{array}{*{20}l} {T = \frac{{cB^{2} }}{\sin \alpha } + N\tan \varphi } \hfill \\ {T' = \frac{{B^{2} \left[ {c + K_{0} (\sigma_{v} + \frac{B\gamma }{3})\tan \varphi } \right]}}{2\tan \alpha }} \hfill \\ \end{array} } \right\}.$$
(5)

By solving Eq. (3), the limit support pressure can be obtained:

$$\begin{aligned} \sigma_{\text{s}} = & \frac{{\sigma_{v} (\sin \alpha - \cos \alpha \tan \varphi )}}{\tan \alpha (\sin \alpha \tan \varphi + \cos \alpha )} + \frac{B\gamma (\sin \alpha - \cos \alpha \tan \varphi )}{2\tan \alpha (\sin \alpha \tan \varphi + \cos \alpha )} - \frac{{c + K_{0} (\sigma_{v} + \frac{B\gamma }{3})\tan \varphi }}{\tan \alpha (\sin \alpha \tan \varphi + \cos \alpha )} \\ & - \frac{c}{\sin \alpha (\sin \alpha \tan \varphi + \cos \alpha )}\quad \\ \end{aligned}$$
(6)

The derived Eq. (6) is also available from previous studies [5].

3.2 Superposition of the Limit Support Pressure

After substituting Eq. (2) into Eq. (6), the formula calculating the limit support pressure is obtained. Following the superposition method which is widely used in bearing capacity analysis and recently used in calculating lateral earth pressure on retaining walls [40], the obtained limit support pressure can be rearranged as cohesion, surcharge load, and soil weight multiplied by their influence coefficients:

$$\sigma_{\text{s}} = {\text{cN}}_{\text{c}} + {\text{qN}}_{\text{q}} + 0.5\gamma {\text{DN}}_{\gamma } .$$
(7)

The coefficient of the cohesion is:

$$\begin{aligned} N_{\text{c}} = & \frac{{ - \sin \alpha + \cos \alpha \tan \varphi + K_{0} \tan \varphi }}{{K_{0} \tan \varphi \tan \alpha (\cos \alpha + \sin \alpha \tan \varphi )}}.\left( {1 - e^{{\frac{{ - 2K_{0} C\tan \varphi (1 + \tan \alpha )}}{B}}} } \right) \\ & - \frac{\sin \alpha + \tan \alpha }{\tan \alpha \sin \alpha (\sin \alpha \tan \varphi + \cos \alpha )}, \\ \end{aligned}$$
(8)

where C is the thickness of the soil above tunnel top.

The coefficient of the surcharge load is:

$$N_{\text{q}} = \frac{\sin \alpha - \cos \alpha \tan \varphi }{\tan \alpha (\sin \alpha \tan \varphi + \cos \alpha )}.\;e^{{\frac{{ - 2K_{0} C\tan \varphi (1 + \tan \alpha )}}{B}}} - \frac{{K_{0} \tan \varphi }}{\tan \alpha (\sin \alpha \tan \varphi + \cos \alpha )},$$
(9)

The coefficient of the soil gravity is:

$$\begin{aligned} N_{\gamma } = \frac{{\sin \alpha - \cos \alpha \tan \varphi - K_{0} \tan \varphi }}{{K_{0} \tan \alpha \tan \varphi (1 + \tan \alpha )(\sin \alpha \tan \varphi + \cos \alpha )}} \cdot \left[ {1 - e^{{\frac{{ - 2K_{0} C\tan \varphi (1 + \tan \alpha )}}{B}}} } \right] \hfill \\ \quad \quad + \frac{{\sin \alpha - \cos \alpha \tan \varphi + \frac{{4K_{0} \tan \varphi }}{3}}}{\tan \alpha (\sin \alpha \tan \varphi + \sin \alpha )}. \hfill \\ \end{aligned}$$
(10)

These influence coefficients can be calculated in advance and listed as a table or a figure; the limit support pressure can be easily calculated once the soil strength parameters are given.

3.3 Numerical Solution of the Influence Coefficients

It is shown by Eq. (7) that if any two of c, q and γ are zero, the coefficient corresponding to the non-zero term can be obtained. To obtain rational results, six series of numerical simulations were employed. The finite-element mesh and boundary condition are the same with Chapter 2. In the first two series, the soil gravity and the surcharge load were kept the same, and the soil cohesion varied. Substituting the limit support pressure into Eq. (7), N c was obtained. In the second two series simulations, the soil cohesion and surcharge load were kept the same, and the friction angle varied. The obtained numerical results of the limit support pressure gave out N γ . Following the same way, N q was obtained.

The results of N c obtained from numerical simulation and Eq. (8) are shown in Fig. 10. N c increases with the friction angle φ and decreases with the tunnel cover-to-diameter ratio C/D. In the case of small φ value, C/D shows strong influence on N c, and with the increase of φ, C/D shows less influence on N c. As shown in Fig. 10, when the friction angle is between (10°, 25°), the wedge model gives out almost the same value with the numerical simulation. When the friction angle is beyond of this range, the results of the wedge model deviates slightly from numerical results, and this deviation increases with the friction angle. The results of N q from the numerical simulation and Eq. (9) are shown in Fig. 11. N q decreases with φ when C/D is constant; it approaches zero when φ reaches a certain value (about 25°). Due to the arching effect of frictional soil, the surcharge load and the soil weight were balanced, so the tunnel face can sustain stability by itself. When the tunnel depth C/D is large enough, the calculated result from Eq. (9) is close to the numerical result. However, when C/D is small, Eq. (9) gives out slightly larger N q value than the numerical result. The calculated N γ from Eq. (10) and the numerical simulation are shown in Fig. 12. N γ decreases with friction angle φ, when φ is small, and the tunnel cover-to-diameter ratio C/D shows significant influence on N γ . When φ is large enough (about >30°), N γ becomes independent of C/D. The calculated value by Eq. (10) compares well with the numerical result. The soil weight plays a critical role of the limit support pressure; the comparison indicates that the wedge model can give out reasonable limit support pressure.

Fig. 10
figure 10

The relationship between N c and friction angle

Full size image
Fig. 11
figure 11

The relationship between N q and friction angle

Full size image
Fig. 12
figure 12

The relationship between N γ and friction angle

Full size image

4 Solution of the Limit Support Pressure Under Seepage Condition

4.1 The Water Head Distribution Near Tunnel Face

Based on the numerical results, the pore water pressures along the horizontal centerline of the tunnel face and the vertical direction were obtained. By referring to the method of Perazzelli [35], the water head can be expressed as:

$$h(x,z) = \left[ {1 - e^{{ - b\frac{x}{D} + a\left( {1 - \frac{z'}{D}} \right)}} } \right]\Delta h,$$
(11)

where D is the tunnel diameter, Δh is the distance between the water level and datum, z′ is the distance between the analysis point and datum, and a and b are the fitting parameters.

According to the water head distribution which is shown in Fig. 13, the water heads in the wedge block and loosen zone were fitted separately. In the wedge, the datum was the horizontal plane which goes through the tunnel center, where \(\Delta h = (H + D/2),\;z' = z - D/2\). The water head in the wedge can be fitted by Eq. (11). As shown in Fig. 14a, the fitting curve coincides with the numerical result. In the loosen zone, the datum is the horizontal plane which goes through the tunnel face top. Using Δh = H, a = 3.5, Eq. (11) was adopted to fit the distribution of the water head in the vertical direction. As shown in Fig. 14b, the fitting result coincides with the numerical simulation.

Fig. 13
figure 13

The distribution of water head around the shield tunnel face

Full size image
Fig. 14
figure 14

The analytical expression of the waterhead

Full size image

4.2 The Earth Pressure on the Wedge

When the seepage is considered, the stress of a soil column element is shown in Fig. 15, and the equilibrium requires:

$$\begin{aligned} (\sigma_{v} + d\sigma_{v} )BD\cot \omega + \gamma 'BD\cot \omega dz =\; & \sigma_{v} BD\cot \omega - f_{z} BD\cot \omega dz \\ & + 2(c + K_{0} \sigma_{v} \tan \varphi )(B + D\cot \omega )dz, \\ \end{aligned}$$
(12)

where f z is the seepage force of the unit volume Eq.  (12) can be simplified as:

$$\frac{{d\sigma_{\text{v}} }}{dz} - \frac{{K_{0} \tan \varphi }}{U}\sigma_{\text{v}} = \frac{c}{U} - \gamma^{\prime} - f_{\text{z}} ,$$
(13)

where the coefficient of the earth pressure at rest is K 0 = 1−sinφ, c, φ are the cohesive strength and friction angle, γ′ is the effective gravity, U = BD cotω/[2(B + Dcotω)], and the seepage force of unit volume f x, f y, f z are:

$$\begin{aligned} f_{\text{x}} = - \gamma_{\text{w}} \frac{\partial h}{\partial x} \hfill \\ f_{\text{y}} = - \gamma_{\text{w}} \frac{\partial h}{\partial y} \hfill \\ f_{\text{z}} = - \gamma_{\text{w}} \frac{\partial h}{\partial z} \hfill \\ \end{aligned}$$
(14)
Fig. 15
figure 15

The sketch of forces acting on an infinitesimal prism element

Full size image

By solving Eq. (13), the earth pressure of the loosen zone is obtained. According to Eq. (11), the fitting function of the water head distribution in loosen zone is used to calculate the seepage force. For simplicity, assuming the surface surcharge loading is 0, the boundary condition at z = 0 becomes:

$$\gamma_{\text{w}} \lambda \Delta h_{1} = \frac{1}{BD\tan \omega }\int_{D}^{D + C} {\int_{0}^{D\cot \omega } {\int_{ - B/2}^{B/2} {f_{z} e^{{ - K_{0} \tan \varphi (z - D)/U}} } } } dydxdz,$$
(15)

where γ w is the water gravity.

By solving Eq. (13), the earth pressure of the loosen zone above the wedge is:

$$\sigma_{\text{v}} = \frac{U\gamma ' - c}{{K_{0} \tan \varphi }}\left( {1 - e^{{ - K_{0} \tan \varphi \frac{C}{U}}} } \right) + \lambda \gamma_{\text{w}} \Delta h_{1} .$$
(16)

The first term of the right-hand side of Eq. (16) can be regarded as the vertical effective stress; it can be obtained by Terzaghi’s loosen earth pressure theory. The second term (\(\lambda \gamma_{w} \Delta h_{1}\)) indicates seepage force on the earth pressure, and \(\Delta h_{1}\) is the water head on top of tunnel:

$$\lambda = \frac{{aU\cos \varphi \left( {1 - e^{{ - \frac{aC}{D} - \frac{{CK_{0} \tan \varphi }}{U}}} } \right)\left( {1 - e^{ - b\cot \omega } } \right)}}{{b\left( {aU\cos \varphi + DK_{0} \sin \varphi } \right)\cot \omega }}.$$
(17)

The force above the wedge block is obtained by the Terzaghi’s loosening earth pressure as follows:

$$P_{\text{v}} = \sigma_{\text{v}} {{BD}}\cot \omega .$$
(18)

4.3 The Calculation of the Limit Support Pressure

As shown in Fig. 16, the failure mode in the wedge model coincides with the numerical results of no seepage. However, the mode will be changed if seepage exists. The forces on the wedge are shown in Fig. 17. F X and F Z are the horizontal and vertical seepage forces. Without seepage, the angle of the failure plane with horizontal plane is π/4 + φ/2. Under seepage condition, the rotation angle caused the change of the total force direction is:

$$\delta = \tan^{ - 1} \left( {\frac{{f_{\text{x}} }}{{f_{\text{z}} + \sigma '}}} \right) = \tan^{ - 1} \left( {\frac{{\gamma_{\text{w}} i_{\text{x}} }}{{\gamma_{\text{w}} i_{\text{z}} + \sigma '}}} \right),$$
(19)

where σ’ is the effective stress of soil.

Fig. 16
figure 16

The failure mode of the tunnel face

Full size image
Fig. 17
figure 17

The sketch of forces acting on wedge

Full size image

The inclination angle of the wedge is:

$$\omega = \omega (\varphi ,i_{\text{z}} ,i_{\text{x}} ,\frac{{\gamma^{\prime}}}{{\gamma_{{_{\text{w}} }} }}) = \frac{\pi }{4} + \frac{\varphi }{2} - \delta .$$
(20)

According to the force equilibrium of the wedge:

$$\left\{ \begin{aligned} & P_{\text{s}} = F_{\text{x}} + N\sin \omega - \left( {T_{\text{s}} + T} \right)\cos \omega \hfill \\ & P_{\text{v}} + G + F_{\text{z}} = N\cos \omega + \left( {T_{\text{s}} + T} \right)\sin \omega \hfill \\ \end{aligned} \right.,$$
(21)

where P s is the support force, N is the normal force acting on the surface of the wedge, and G is the gravity of the wedge.

The gravity G is:

$$G = \int_{0}^{D} {\gamma 'Bz\cot \omega dz} = \frac{1}{2}B\gamma '\cot \omega D^{2} .$$
(22)

The total shear force T on the slope of the wedge is:

$$\begin{aligned} T =\; & \frac{BD}{\sin \omega }c + N\tan \varphi = \frac{BD}{\sin \omega }c + \tan \varphi \cos \omega P_{\text{v}} \\ & + \frac{1}{2}\cot \omega \tan \varphi \cos \omega B\gamma 'D^{2} \hfill \\ & + \tan \varphi \cos \omega F_{\text{z}} + S\tan \varphi \sin \omega - \tan \varphi \sin \omega F_{\text{x}} . \hfill \\ \end{aligned}$$
(23)

The total lateral shear force T s on the wedge is:

$$T_{s} = 2\int_{0}^{D} {\left( {c + K_{0} \sigma_{z} \tan \varphi } \right)z\cot \omega dz} = \cot \omega cD^{2} + K_{0} \tan \varphi \left( {\frac{{P_{v} D}}{B} + \frac{{2\cot \omega \gamma 'D^{3} }}{3}} \right).$$
(24)

By Gaussian integration, the volume integral is converted to a surface integral, and the horizontal and vertical seepage forces F x and F z in the wedge block are:

$$F_{\text{x}} = \gamma_{\text{w}} \left( {\iint\limits_{\text{abcd}} {\text{hds}} - \sin \omega \iint\limits_{\text{abef}} {\text{hds}}} \right),$$
(25)
$$F_{\text{z}} = \gamma_{\text{w}} \left( {\cos \omega \iint\limits_{\text{abef}} {{\text{hds}} - \iint\limits_{\text{cdef}} {\text{hds}}}} \right),$$
(26)

where the water head distribution h in the wedge can be obtained from Eq. (11).

By solving Eq. (21), the limit support pressure, which is used to keep up tunnel face stability, is:

$$\sigma_{\text{s}} = N_{{{\text{c}}1}} c + 0.5N_{\gamma }^{'} \gamma 'D + N_{\text{sz}} \frac{{F_{\text{z}} }}{\text{BD}} + \frac{{F_{\text{x}} }}{\text{BD}} + F,$$
(27)

where the coefficients N c1, \(N_{\gamma }^{'}\), \(N_{\text{SZ}}\), and F are:

$$N_{{{\text{c}}1}} = \frac{{ - \sin \omega + \cos \omega \tan \varphi + \frac{{DK_{0} \tan \varphi }}{B}}}{{K_{0} \tan \varphi \tan \omega \left( {\cos \omega + \tan \varphi \sin \omega } \right)}} \times \left( {1 - e^{{ - \frac{{CK_{0} \tan \varphi }}{U}}} } \right) - \frac{{\csc \omega + \frac{D}{B}\cot \omega }}{\cos \omega + \tan \varphi \sin \omega }$$
(28)
$$\begin{aligned} N_{\gamma }^{'} =\; & \frac{{2U\cot \omega \left( {\sin \omega - \frac{{DK_{0} \tan \varphi }}{B} - \cos \omega \tan \varphi } \right)}}{{DK_{0} \tan \varphi (\cos \omega + \tan \varphi \sin \omega )}}\left( {1 - e^{{ - \frac{{CK_{0} \tan \varphi }}{U}}} } \right) \hfill \\ & + \frac{{\sin \omega - \cos \omega \tan \varphi + \frac{{4DK_{0} \tan \varphi }}{3B}}}{\tan \omega (\cos \omega + \tan \varphi \sin \omega )} \hfill \\ \end{aligned}$$
(29)
$$N_{\text{SZ}} = \frac{\sin \omega - \tan \varphi \cos \omega }{{\left( {\cos \omega + \tan \varphi \sin \omega } \right)}}$$
(30)
$$F = \frac{{\gamma_{w} \Delta h_{1} \lambda \left( {\sin \omega - \frac{{DK_{0} \tan \varphi }}{B} - \cos \omega \tan \varphi } \right)\cot \omega }}{\cos \omega + \tan \varphi \sin \omega }.$$
(31)

The support pressure σ s changes with water level. When the water level is higher than ground surface, σ s can be calculated by Eq. (27). However, when the water level is below the ground surface (H < C), the calculation of the loosening earth pressure above the wedge needs adjusting. In the loosen zone, the effective gravity is used below the water level, and the influence of seepage force is considered. Regarding the soil weight above the water level as surcharge, Eq. (16) becomes:

$$\sigma_{v} = \frac{{U\gamma^{\prime} - c}}{{K_{0} \tan \varphi }}\left( {1 - e^{{ - K_{0} \tan \varphi \frac{H}{U}}} } \right) + \lambda^{\prime}\gamma_{w} \Delta h_{1} + \frac{{U\gamma_{0} - c}}{{K_{0} \tan \varphi }}\left( {1 - e^{{ - K_{0} \tan \varphi \frac{C - H}{U}}} } \right)e^{{ - \frac{{K_{0} H\tan \varphi }}{U}}} ,$$
(32)

where \(\gamma_{0}\) is the soil weight above the water level, and \(\lambda '\) is

$$\lambda ' = \frac{{aU\cos \varphi \left( {1 - e^{{ - \frac{aH}{D} - \frac{{HK_{0} \tan \varphi }}{U}}} } \right)\left( {1 - e^{ - b\cot \omega } } \right)}}{{b\left( {aU\cos \varphi + DK_{0} \sin \varphi } \right)\cot \omega }}.$$
(33)

By substituting Eq. (33) into Eq. (21), the total limit support pressure is:

$$\sigma_{\text{s}} = N_{{{\text{c}}1}} c + 0.5D(N^{\prime}_{\gamma 1} \gamma^{\prime} + N_{\gamma 1} \gamma_{0} ) + N_{\text{SZ}} F_{\text{Z}} + F_{\text{X}} + F,$$
(34)

where \(N_{{{\text{c}}1}}\), \(N_{\text{SZ}}\), and F are the same with Eqs. (28), (30), and (31):

$$\begin{aligned} N^{\prime}_{\gamma 1} =\; & \frac{{2U\cot \omega \left( {\sin \omega - \frac{{DK_{0} \tan \varphi }}{B} - \cos \omega \tan \varphi } \right)}}{{DK_{0} \tan \varphi (\cos \omega + \tan \varphi \sin \omega )}}\left( {1 - e^{{ - \frac{{HK_{0} \tan \varphi }}{U}}} } \right) \\ & + \frac{{\sin \omega - \cos \omega \tan \varphi + \frac{{4DK_{0} \tan \varphi }}{3B}}}{\tan \omega (\cos \omega + \tan \varphi \sin \omega )} \\ \end{aligned}$$
(35)
$$N_{\gamma 1} = \frac{{\frac{2U\cot \omega }{{DK_{0} \tan \varphi }}\left( {1 - e^{{ - \frac{{K_{0} (C - H)\tan \varphi }}{U}}} } \right)e^{{ - \frac{{2K_{0} H(1 + \tan \omega )\tan \varphi }}{B}}} }}{\cos \omega + \tan \varphi \sin \omega }\left( {\sin \omega - \frac{{DK_{0} \tan \varphi }}{B} - \cos \omega \tan \varphi } \right).$$
(36)

4.4 Parametric Study of the Limit Support Pressure

When the tunnel diameter d is 10 m, and the saturated unit weight of soil is 21 kN/m3, the limit support pressure calculated by the theoretical model and numerical simulation in different H/D is shown in Fig. 18. When water level is high, there is a deviation from the analytical solution to the numerical results. To ensure safety, we take D/B = 0.87 (by assuming B = d, and d is the tunnel diameter). For comparison, the solution to the limit support pressure was obtained by assuming D = d. In this case, the limit support pressure is underestimated. The variation in the support pressure on the friction angle and cohesion are shown in Figs. 19 and 20. The limit support pressure calculated by the theoretical model from different friction angle coincides with the numerical result. The limit support pressures calculated by the theoretical model from different cohesion are close to the numerical results when the cohesion is small. The comparison of the failure mode in limit equilibrium model and numerical simulation is shown in Fig. 21. The angle of the failure line of traditional model (solid line) is ω = π/4 + φ/2, and the angle in modified model (dotted line) can be calculated by Eq. (19). As shown in Fig. 21, the rotation angles are 11.74°, 17.70°, and 19.48° with the increase in water level, the modified failure modes coincide with the numerical results. The limit support pressures calculated by the theoretical model under different water level conditions are shown in Fig. 22. Validating by the numerical results, the model can reflect the nonlinear relationship between the water level and the limit support pressure.

Fig. 18
figure 18

The influence of H/D on limit support pressure

Full size image
Fig. 19
figure 19

The variation of limit support pressure with fiction angle

Full size image
Fig. 20
figure 20

The variation of limit support pressure with cohesion

Full size image
Fig. 21
figure 21

The variation of failure mechanism with water level

Full size image
Fig. 22
figure 22

The variation of limit support pressure with water level

Full size image

5 Application in Qianjiang Cross-River Shield Tunnel

The proposed model was used to determine the limit support pressure of the Qianjiang shield Tunnel. The Qianjiang shield Tunnel locates in Hangzhou bay area, and it connects Xiaoshan district of Hangzhou and Haining city. The tunnel has two tubes and six lanes, the external diameter of the shield tunnel is 15.43 m, and the length of the tunnel is 4.45 km, with 2.5 km long of which beneath the Qianjiang river. According to the historic hydrologic records, the highest tide level in recent years reached 7.75 m, and the lowest tide level was −2.34 m. The average tidal level of the past several years was 3.87 m, and the lowest tide level was 0.67 m. The distribution of the soil layer is shown in Table 1. Five typical sections (shown in Fig. 23) from south to north be selected to study the variation in the limit support pressure. To analyze the influence of the tide level on the stability of the tunnel face, the limit support pressure in normal water level and the highest tide level was calculated. The limit support pressures on five sections are shown in Fig. 24, the analytical solution of limit support pressure compares well with the numerical results. The analytical solution in [41] was underestimated; the reason is that the influence of the seepage on failure mode was neglected.

Table 1 The properties of the soil layer in typical cross section
Full size table
Fig. 23
figure 23

Typical cross sections of the Qianjiangriver shield tunnel

Full size image
Fig. 24
figure 24

The variation of the limit support pressure of Qianjiang river shield tunnel

Full size image

6 Conclusion

The failure mode and minimum limit support pressure on the shield shallow tunnel face found in cohesive-frictional soils were obtained by the 3D elasto-plasticity finite-element simulation. Adopting a limit equilibrium wedge model, a formula calculating the support pressure was deduced. The formula was rearranged as the superposition of the soil cohesion, surcharge load, and the soil weight multiplied by corresponding influence coefficients. The varying characteristics of those coefficients with the friction angle of soil and the tunnel cover-to-diameter ratio were obtained and compared with numerical results. By the deformation–seepage coupled numerical analysis, the failure mode of the tunnel face with the seepage was obtained. The failure mode was found to change from a global mode to local one with the increase in friction angle and cover-to-diameter ratio. By fitting the numerical results, the expression of water head around the tunnel face was obtained, and the seepage force on the tunnel face was calculated. After including seepage force in the wedge model and considering the change of failure mode induced by seepage, a modified analytical solution to limit support pressure under seepage condition was proposed. The proposed method was used in the stability analysis of the Qianjiang shield tunnel, and the influence of tide on the limit support pressure was obtained.