A New Fusion of ASO with SA Algorithm and Its Applications to MLP Training and DC Motor Speed Control

Abstract

An improved version of atom search optimization (ASO) algorithm is proposed in this paper. The search capability of ASO was improved by using simulated annealing (SA) algorithm as an embedded part of it. The proposed hybrid algorithm was named as hASO-SA and used for optimizing nonlinear and linearized problems such as training multilayer perceptron (MLP) and proportional-integral-derivative controller design for DC motor speed regulation as well as testing benchmark functions of unimodal, multimodal, hybrid and composition types. The obtained results on classical and CEC2014 benchmark functions were compared with other metaheuristic algorithms, including two other SA-based hybrid versions, which showed the greater capability of the proposed approach. In addition, nonparametric statistical test was performed for further verification of the superior performance of hASO-SA. In terms of MLP training, several datasets were used and the obtained results were compared with respective competitive algorithms. The results clearly indicated the performance of the proposed algorithm to be better. For the case of controller design, the performance evaluation was performed by comparing it with the recent studies adopting the same controller parameters and limits as well as objective function. The transient, frequency and robustness analysis demonstrated the superior ability of the proposed approach. In brief, the comparative analyses indicated the proposed algorithm to be successful for optimization problems with different nature.

1 Introduction

Optimization can be described as the process of achieving optimal parameters of a given system with a lower cost. Development of optimization algorithms has gained an incredible attention since the optimization problems can be encountered in a variety of fields such as engineering, science, economics and business [1,2,3]. A real-world optimization problem may be solved if it can be formulated in terms of mathematical form. Various deterministic algorithms are available to solve such problems. However, a considerable amount of those problems has specific characteristics such as non-continuous and non-differentiable nature, too many decision variables and objective functions and thus cannot be solved effectively using conventional mathematical programming approaches [4]. Therefore, alternative methods are required in the case of such problems instead of conventional techniques.

Metaheuristic algorithms have gained an incredible attention among alternative techniques due to their flexible and simple structure along with the ability of random search and avoidance of local optima. Therefore, metaheuristic algorithms have been studied extensively as an alternative and effective way of tackling such problems [5,6,7,8] since they are powerful tools to handle previously mentioned problems. Those types of problems are inspired from real-world physical phenomena or biological behavior of species and can be categorized into three classes such as physics based, evolution based and swarm based [9]. In metaheuristic algorithms, the problem is considered as a black box (although those algorithms are derived from nature) and the algorithm attempts to solve the problem without concerning the nature of the problem. Therefore, they can easily be implemented to real-world problems. It is worth to note that some real-world optimization problems are subjected to constraints of inequality and/or equality and thus known as constraint optimization problems and require constraint handling techniques. There are different available constraint handling strategies, such as famous penalty and multi-objective approaches, that can be found in the literature. The readers are referred to Refs. [10] and [11] for more details.

Some of the examples of metaheuristic algorithms can be listed as squirrel search [12], the ant lion optimizer [13], artificial ecosystem-based optimization [14], slime mould [15], Henry gas solubility optimization [16], Harris hawks optimization [4], Manta ray foraging optimization [9], butterfly optimization [17], symbiotic organisms search [18], artificial bee colony [19], emperor penguins colony [20], sine cosine [21] and kidney inspired [22] algorithms. The reason of having a variety of metaheuristic algorithms derives from No Free Lunch theorem [23]. According to this theorem, there is not any optimization algorithm capable of finding the optimal solution for every optimization problem. Therefore, no algorithm can solve all optimization problems, with different type and nature, effectively than any other option. Instead, each of them can be quite successful for specific set of problems. Atom search optimization (ASO) [24] algorithm is one of those algorithms that have been developed for tackling specific optimization problems as stated by No Free Lunch theorem.

ASO is a recently developed population-based metaheuristic algorithm that was inspired from molecular dynamics [24] and proposed for dealing a variety of optimization problems [25]. It considers the potential function along with the interaction force and geometric constraint. ASO has already been successfully implemented to solve a variety of problems such as hydrogeologic parameter estimation [24], feature selection [26,27,28], centralized thermoelectric generation system in heterogeneous temperature difference [29], dispersion coefficient estimation in groundwater [25], peak sidelobe level reduction [30], automatic voltage regulator [31], optimal power flow [32], modular multilevel converters [33] and modeling fuel cells [34] along with line loss and cost minimization of shunt capacitors [35].

Despite the popularity of metaheuristic algorithms, there are drawbacks such as local minima stagnation and immature convergence. Those are two critical problems in metaheuristics which are caused by their randomized exploration and exploitation operators and thus need to be addressed. Several strategies have been proposed to overcome the respective weaknesses of metaheuristic algorithms. Hybridization is an outstanding method among the proposed approaches since it provides more effective results via synthesizing the best aspects of the algorithms which helps exhibiting a more robust behavior and greater flexibility against difficult problems [36]. Therefore, it has found a place as a demanding trend [37]. Similar to many other metaheuristics, original ASO algorithm also suffers from premature convergence and local optima stagnation [38] and thus requires improvement in order to balance the exploration and exploitation. Developing an improved version of ASO is feasible although the successful implementation of it to the problems listed in the previous paragraph is a good indication of its ability. Further improvement in terms of its capability can be obtained by achieving a balance between exploration and exploitation stages. The latter would help the algorithm to perform better compared to its implementation with the original version. To do so, simulated annealing (SA) algorithm [39], a well-known algorithm that has good local search capabilities, can be used for hybridization. The latter is one of the algorithms that was recently hybridized with other metaheuristic algorithms to solve different types of optimization problems [40,41,42,43,44,45,46,47,48,49].

SA [39] is a stochastic and single solution-based algorithm that simulates the metallurgical process of annealing in which high temperature molecules with high energy levels move against other molecules relatively easy and temperature is decreased slowly to reach a steady state condition with minimum energy level. Similar to ASO, several applications of SA algorithm are also available in the literature. Some those applications can be listed as solution of clustering problem [50], multiple non-consecutive processing of parts on a machine [51], placement of virtual machine for optimum power consumption in data centers [52], optimal estimation of solar cell model parameters [53], optimization of pressure-swing distillation process [54], minimization of the fuel cost and the gas emissions [55], solution for a green vehicle routing problem with fuel consumption [56] and optimal design of supercritical carbon dioxide compressor [57] along with several structural optimization problems [58,59,60,61]. SA is an easy to implement metaheuristic algorithm that is strong in terms of local search and requires less computation time [62]. Therefore, SA algorithm can be interconnected in such a way that a new hybrid model can be constructed. In this way, the solution quality of ASO algorithm can be improved.

A crucial idea in the SA, which makes it to be considered as a hill-climbing technique, is the acceptance of lower quality solutions to escape from local optima using a probability function. Also, SA has only one control parameter to set, which is called temperature and usually reduced monotonically over the search. Therefore, SA algorithm requires minimum number of evaluations for finding optimal solutions due to having a simple structure with easy implementation and a strong local search ability [63]. This is also the motivation of this paper which adopts SA to overcome the previously mentioned drawbacks of ASO algorithm and thus obtain a better structure to solve the optimization problems of various types.

In light of the fact mentioned above, this paper proposes a novel hybrid ASO and SA (hASO-SA) algorithm by considering the lack of balance between exploration and exploitation stages of ASO and incredible local search ability of SA algorithm. The developed hybrid algorithm adopts SA algorithm as an embedded part of the ASO algorithm instead of running both algorithms one by one. That helps SA to operate for worse solutions so that the potential of neighborhood solutions is not neglected. As stated above, the aim of this paper is to achieve an improved version of ASO so that it can be implemented to various optimization problems with greater capability. To do so, eight well-known classical and four CEC2014 benchmark functions of unimodal, multimodal, hybrid and composition types, five classification data sets for nonlinear multilayer perceptron (MLP) training system, and proportional-integral-derivative (PID) controller design for linearized DC motor speed control system were used as different optimization problems for performance evaluation of the proposed hybrid algorithm.

In terms of test functions, the performance evaluations were carried out using classical benchmark functions of Sphere, Rosenbrock, Step, Quartic, Schwefel, Rastrigin, Ackley and Griewank [64] as well as CEC2014 functions [65]. The obtained results were compared with six stochastic algorithms such as particle swarm optimization (PSO), gravitational search (GSA), wind driven optimization (WDO) and genetic algorithm (GA) along with SA and original ASO algorithms. Moreover, hybrid versions of PSO and cuckoo search (CS) algorithms, merged with SA, were also used for performance comparison. The proposed hASO-SA algorithm was run with the same swarm size and the maximum number of iterations for a fair comparison with the stated algorithms. The statistical results obtained for the adopted test functions showed that the best results were achieved via the proposed algorithm. Further performance validation was also carried out using Wilcoxon signed-rank test [66] has been used to prove that the capability of the proposed hybrid hASO-SA algorithm was not by chance.

Likewise, datasets of Iris, Balloon, XOR, Breast cancer and Heart [67] were adopted for MLP training to observe the performance of the proposed algorithm for nonlinear optimization problems. The obtained results for the latter case were compared with the MLP training results that were achieved by using grey wolf optimization (GWO), ant colony optimization (ACO), probability-based incremental learning (PBIL), particle swarm optimization (PSO) and evolutionary strategies (ES) algorithms along with original ASO algorithm. All algorithms were run under similar conditions for a fair comparison and the lower average and standard deviation of mean square error were achieved via the proposed approach which is an indication of better performance.

Similar to benchmark function and MLP training cases, PID controller design for DC motor was also performed by comparing the obtained results with grey wolf-based PID (GWO/PID), sine cosine-based PID (SCA/PID) and atom search optimization-based PID (ASO/PID) controllers. The reason of using the latter algorithms was because of similar set of parameters for both the controller and motor, in addition to the same objective function, so that a fair comparison can be performed. Transient and frequency responses showed the proposed method helps in achieving a better performing system along with a better robustness. The DC motor system also proved the ability of the proposed algorithm to be considerably successful than its counterparts for real-world engineering problems. In summary, the comparisons for all adopted systems have demonstrated that the proposed hybrid hASO-SA algorithm has better performance for a variety of problems having different nature.

1.1 Previous Works on MLP Training

Artificial neural networks mimic human brain via computational models and broadly used for complex nonlinear problems [68]. The MLP is part of the hidden layered feed forward neural networks [69]. It is also an extensively adopted neural network and requires training on particular application [70]. Deterministic approaches can be found in the literature in terms of algorithms used for neural network training [71]; however, slow convergence and local optima stagnation are the issues that the training process suffers from. Therefore, training such structure requires a better algorithm in order to overcome the latter issues. To do so, several metaheuristic algorithms have been proposed so far. Some of those algorithms can be listed as grey wolf [72, 73] and improved grey wolf optimization [74], ant lion optimization [75], chimp optimization [76], grasshopper optimization [77], salp swarm [78] and multiple leader salp swarm [79], hybrid Nelder-Mead and dragonfly [80], hybrid particle swarm optimization and gravitational search [81], magnetic optimization [82] and biogeography-based optimization [83] along with hybrid monarch butterfly and artificial bee colony optimization [84] algorithms. Novel algorithms that can provide further improvement for the MLP training is feasible despite the presented promise of the methods listed above. The latter may also be achieved through improvement of existing algorithms instead of development of new ones from the scratch. In light of the above fact, this study attempts to achieve such a novel algorithm that can perform better compared to other available approaches. Therefore, the hybridization of ASO algorithm with SA technique is proposed in this study to deal with the training MLP which can help to achieve a better algorithm for such a purpose.

1.2 Previous Works on Controller Design for DC Motor

The use of DC motors can be found in almost all of the industrial applications [85] due to their lower price and maintenance cost along with easier control. Robotics, paper mills, machine tools and textile industry are a few to name the industrial applications of DC motors. Several examples of controllers such as PID, FOPID, fuzzy logic or neural networks can be found in the literature [86]. Since DC motors provide an observable test bed for performance evaluations and comparisons, their speed control has been an application area for many metaheuristics algorithms as a real-world engineering application. There are various examples in terms of metaheuristic optimization algorithms for controlling DC motors. Some of those examples can be listed as stochastic fractal search [87], kidney-inspired [88], teaching–learning-based optimization [89], particle swarm optimization [90], swarm learning process [91], ant colony optimization [92], Harris hawks optimization [86], sine cosine [93], grey wolf optimization [94], chaotic atom search optimization [95], flower pollination [96] and improved sine cosine [97] along with genetic [98] and improved genetic [99] algorithms. As part of this study, we have implemented the new proposed approach for similar purpose as well as to assess the performance quality of the proposed hybrid algorithm for such a real-world engineering problem. Similar to the motivation explained in the previous section, this study aims to develop a novel approach that can achieve a more stable structure, compared to existing techniques, for the stated system in terms of transient and frequency responses as well as robustness.

2 Overview of ASO, SA and Proposed hASO-SA Algorithms

2.1 ASO Algorithm

ASO is a population-based global optimization technique inspired by molecular dynamics [25]. Basically, it is a mathematical representation of atomic motion which behaves according to classical mechanics [100]. According to Newton’s second law, relationship of an atomic system can be written as in Eq. (1):

$$ a_{i} = \frac{{F_{i} + G_{i} }}{{m_{i} }} $$

(1)

where $F_{i}$ and $G_{i}$ represent interaction and constraint forces that act on ith atom together. The acceleration and the mass of atom i is denoted by $a_{i}$ and $m_{i}$, respectively. In dimension d and at time t, the interaction force that acts on ith atom due to jth atom can be expressed as in Eq. (2). The latter one is a revised version of The Lennard–Jones (L–J) potential [101] to prevent the atoms from the case where they cannot converge to a specific point.

$$ F_{ij}^{'} \left( t \right) = - \eta \left( t \right)\left[ {2\left( {h_{ij} \left( t \right)} \right)^{13} - \left( {h_{ij} \left( t \right)} \right)^{7} } \right] $$

(2)

$\eta \left( t \right)$ is called the depth function and is defined as in Eq. (3) where $\alpha$ represents the depth weight and T denotes the maximum number of iterations. This function is used for arrangement of the repulsion or attraction regions.

$$ \eta \left( t \right) = \alpha \left( {1 - \frac{t - 1}{T}} \right)^{3} e^{{ - \frac{20t}{T}}} $$

(3)

$h_{ij} \left( t \right)$ is expressed as given in Eq. (4) where r is the distance between two atoms, $h_{\hbox{min} }$ is the lower bound, and $h_{\hbox{max} }$ is the upper bound. The latter function helps repulsion, attraction or equilibrium to occur.

$$ h_{ij} \left( t \right) = \left\{ {\begin{array}{*{20}l} {h_{\hbox{min} } ,\quad \frac{{r_{ij} \left( t \right)}}{\sigma \left( t \right)} < h_{\hbox{min} } } \hfill \\ {\frac{{r_{ij} \left( t \right)}}{\sigma \left( t \right)},\quad h_{\hbox{min} } \le \frac{{r_{ij} \left( t \right)}}{\sigma \left( t \right)} \le h_{\hbox{max} } } \hfill \\ {h_{\hbox{max} } ,\quad \frac{{r_{ij} \left( t \right)}}{\sigma \left( t \right)} > h_{\hbox{max} } } \hfill \\ \end{array} } \right. $$

(4)

The exploration is improved by having lower limit of repulsion ($h = 1.1$) and upper limit of attraction ($h = 1.24$). To represent the limits as explained previously, the terms of $g_{0}$ and u, provided in Eq. (5), are equal to 1.1 and 1.24, respectively.

$$ \begin{aligned} & h_{\hbox{min} } = g_{0} + g\left( t \right) \\ & h_{\hbox{max} } = u \\ \end{aligned} $$

(5)

Drift factor is expressed by g which is used to allow the algorithm to drift from exploration to exploitation and given as in Eq. (6).

$$ g\left( t \right) = 0.1 \times \sin \left( {\frac{\pi }{2} \times \frac{t}{T}} \right) $$

(6)

$\sigma \left( t \right)$, given in Eq. (4), denotes the length scale, which represents the collision diameter, and is defined as follows

$$ \sigma \left( t \right) = \left\| {x_{ij} \left( t \right), \frac{{\mathop \sum \nolimits_{{j \in K{\text{best}}}} x_{ij} \left( t \right)}}{K\left( t \right)}} \right\|_{2} $$

(7)

where $K{\text{best}}$ denotes an atom population that includes the best function values of first K atoms. The function $F^{{\prime }}$ behavior with respect to values of $\eta \left( t \right)$ (corresponding to h values) is illustrated in Fig. 1.

Fig. 1

Corresponding F′ function behavior with different η values

The sum of components having random weights in dth dimension that act on ith atom (due to other atoms) can be expressed as total force and is given as in Eq. (8) where ${\text{rand}}_{j}$ represents a random number in $\left[ {0,1} \right]$.

$$ F_{i}^{d} \left( t \right) = \mathop \sum \limits_{{j \in K{\text{best}}}} {\text{rand}}_{j} F_{ij}^{d} \left( t \right) $$

(8)

In molecular dynamics, atomic motion is greatly affected from the geometric constraint. In ASO, this is simplified by supposing a covalent bond between each atom and the best atom. Therefore, the constraint of atom i can be written as

$$ \theta_{i} \left( t \right) = \left[ {\left| {x_{i} \left( t \right) - x_{\text{best}} \left( t \right)} \right|^{2} - (b_{{i,{\text{best}}}} )^{2} } \right] $$

(9)

where $x_{\text{best}} \left( t \right)$ represents the best atom position at iteration t, whereas $b_{{i,{\text{best}}}}$ denotes the fixed bond length between the best and the ith atoms. Thus, the constraint force can be acquired as

$$ G_{i}^{d} \left( t \right) = \lambda \left( t \right)\left( {x_{\text{best}}^{d} \left( t \right) - x_{i}^{d} \left( t \right)} \right) $$

(10)

where $\lambda \left( t \right)$ is the Lagrangian multiplier and defined as in Eq. (11).

$$ \lambda \left( t \right) = \beta e^{{ - \frac{20t}{T}}} $$

(11)

In the latter, $\beta$ is the multiplier weight. The acceleration of atom i at time t can be written as in Eq. (12) where $m_{i} \left( t \right)$ is the mass of atom i at time t.

$$ a_{i}^{d} \left( t \right) = \frac{{F_{i}^{d} \left( t \right)}}{{m_{i}^{d} \left( t \right)}} + \frac{{G_{i}^{d} \left( t \right)}}{{m_{i}^{d} \left( t \right)}} $$

(12)

As the latter equation express, an atom with a bigger mass provides a better function fitness value, thus causing a reduced acceleration. The mass of atom i can be computed as in Eq. (13).

$$ m_{i} \left( t \right) = \frac{{M_{i} \left( t \right)}}{{\mathop \sum \nolimits_{j = 1}^{N} M_{j} \left( t \right)}} $$

(13)

$$ M_{i} \left( t \right) = e^{{ - \frac{{{\text{Fit}}_{i} \left( t \right) - {\text{Fit}}_{\text{best}} \left( t \right)}}{{{\text{Fit}}_{\text{worst}} \left( t \right) - {\text{Fit}}_{\text{best}} \left( t \right)}}}} $$

(14)

${\text{Fit}}_{\text{best}} \left( t \right)$ represents the atom with minimum fitness value and ${\text{Fit}}_{\text{worst}} \left( t \right)$ denotes the maximum fitness value at iteration t. The latter fitness values are expressed as given in Eqs. (15) and (16), respectively. ${\text{Fit}}_{i} \left( t \right)$ is a representation of function fitness value of atom i at iteration t.

$$ {\text{Fit}}_{\text{best}} \left( t \right) = \min_{{i\epsilon \left( {1,2, \ldots N} \right)}} {\text{Fit}}_{i} \left( t \right) $$

(15)

$$ {\text{Fit}}_{\text{worst}} \left( t \right) = \max_{{i\epsilon \left( {1,2, \ldots N} \right)}} {\text{Fit}}_{i} \left( t \right) $$

(16)

The velocity and the position of atom i at iteration ($t + 1$) can be expressed as follows in order to simplify the algorithm.

$$ \nu_{i}^{d} \left( {t + 1} \right) = {\text{rand}}_{i}^{d} \nu_{i}^{d} \left( t \right) + a_{i}^{d} \left( t \right) $$

(17)

$$ x_{i}^{d} \left( {t + 1} \right) = x_{i}^{d} \left( t \right) + \nu_{i}^{d} \left( {t + 1} \right) $$

(18)

Each atom requires to have higher possible interactions with many atoms having better fitness values as its K neighbors in order to improve the exploration at the beginning of iterations. On the contrary, each atom requires to have fewer possible interactions with atoms having better fitness values as its K neighbors to improve the exploitation. Here, K represents a time-dependent function and is calculated as in Eq. (19) in order to show the gradual decrease with respect to number of iterations.

$$ K\left( t \right) = N - \left( {N - 2} \right) \times \sqrt {\frac{t}{T}} $$

(19)

2.2 SA Algorithm

This algorithm mimics the annealing process in metallurgy and classified as a single-based solution method [39]. Basically, the process is performed by heating and cooling stages which consequently helps in generating uniform crystals with less defects. The SA starts with an initial value set for random solution of $X_{i}$ and determines a neighborhood solution of $X_{i}^{{\prime }}$. Then, it computes the fitness value for $X_{i}$ and $X_{i}^{{\prime }}$. If the fitness value of $X_{i}^{'}$ (F($X_{i}^{{\prime }}$)) is smaller than that of $X_{i}$ (F($X_{i}$)), then SA sets $X_{i}$ = $X_{i}^{{\prime }}$. Meanwhile, SA may replace the solution of $X_{i}$ by solution of $X_{i}^{{\prime }}$ even if the fitness values do not have the latter relationship. The replacement for such a case depends on the probability p as defined in Eq. (20):

$$ p = e^{{ - \frac{\Delta F}{{T_{k} }}}} ;\;\Delta F = F\left( {X_{i}^{{\prime }} } \right) - F\left( {X_{i} } \right) $$

(20)

where F and T denote control parameters of fitness function and temperature, respectively. The algorithm will not replace $X_{i}$ by $X_{i}^{{\prime }}$ if $p < {\text{rand}}\left( {0,1} \right)$; however, a replacement will happen on the contrary case. The SA algorithm later reduces the value of the temperature using the following equation where $\mu$ denotes the cooling coefficient, which is a random constant between 0 and 1.

$$ T_{k + 1} = \mu T_{k} $$

(21)

2.3 Proposed Hybrid hASO-SA Algorithm

The proposed hASO-SA algorithm is a hybrid version of ASO and SA algorithms. The SA is local search metaheuristic algorithm, and it is widely used to solve continuous and discrete optimization problems [39]. The ability of escaping local minimum via hill-climbing moves is one of the main benefits of SA which is useful in terms of searching for a global solution. Therefore, a hybrid approach is proposed with this work by introducing SA is to assist the ASO in terms of avoiding local minimum. Also, it helps increasing the level of diversity while searching for optimum solution in the search space. The novel hybrid hASO-SA algorithm exploits the fast-optimal search capability and hill-climbing property of ASO and SA algorithms, respectively, and proposed to solve various optimization problems.

A flowchart of the proposed hASO-SA is illustrated in Fig. 2. As can be seen from the flowchart, the proposed hybrid algorithm starts with defining the parameters of ASO and SA algorithms first along with initializing a random set of atoms with their velocities and a fitness value set to infinity. Once this achieved, the iterations begin by calculating the fitness value for each atom and then the obtained fitness value is compared with the best fitness value. In the case of better values, the algorithm updates the best solution and fitness value and the rest of the steps in the flow chart are executed. However, the proposed hybrid algorithm gives a chance the current solution even if the current fitness value is not better than the best one. In such a case, the algorithm generates a new solution in a neighborhood of current solution and evaluates the newly generated solution based on the justification of probability. That means the SA behaves as an embedded part of the ASO and operates to justify the neighborhood solution in the case of current solution without better fitness values.

Fig. 2

Flowchart for the hASO-SA algorithm

Based on the justification, the best solution may or may not be updated by the algorithm. In such a scenario, SA is nicely operating as part of the ASO only for fitness values that are worse than the best one so that any potential neighborhood is not passed directly by just looking at the fitness value. It is also worth to note that the hybrid algorithms have a disadvantage of requiring more computational time despite their better performing ability. However, in the proposed algorithm, the fundamental steps of SA technique have been embedded into ASO algorithm which consequently reduced the computational time considerably than expected.

3 Experimental Setup and Results

3.1 Classical and CEC2014 Benchmark Functions

Eight well-known classical and four CEC2014 benchmark functions were employed to achieve an extensive performance evaluation of the proposed hASO-SA algorithm. Those benchmark functions can be assessed under four main types such as unimodal and multimodal, hybrid and composition functions. Therefore, the performance of various optimization algorithms can effectively be measured using them. A summary of employed benchmark functions is provided in Table 1.

Table 1 Details of used classical and CEC2014 benchmark functions

The functions from of $F_{1} \left( x \right) - F_{4} \left( x \right)$ are unimodal functions. They have one global optimum and no local optimum. On the other hand, the functions from $F_{5} \left( x \right)$ to $F_{8} \left( x \right)$ are multimodal functions. These ones have considerable number of local optima. In addition to the above, hybrid functions of $F_{9} \left( x \right)$ and $F_{10} \left( x \right)$ were also adopted. The variables of the latter functions are separated into different subdivisions randomly and either unimodal or multimodal functions are used to replace those subdivisions. Moreover, composition functions are represented by $F_{11} \left( x \right)$ and $F_{12} \left( x \right)$ in the table. Similar to the case in the hybrid functions, the variables of those composition functions are also randomly separated into different subdivisions; however, those subdivisions are constructed by using the basic and hybrid functions. Hybrid and composition benchmark functions are more complex and challenging than the basic unimodal and multimodal benchmark functions, thus presenting more challenging optimization problems. The latter two types of benchmark functions are specifically suitable for testing the potential performance of the algorithms for solving real-world problems. References [38, 64, 65] provide a detailed description of all employed functions.

3.2 Compared Algorithms

The comparisons were carried out using eight stochastic algorithms by utilizing aforementioned test functions. The algorithms used for comparison include three popular algorithms such as PSO, GA and SA, along with three of recently proposed algorithms such as GSA, WDO and original ASO. In addition, further comparative performance evaluations were carried out using two additional hybrid algorithms which were developed based on SA by using particle swarm optimization (hPSO-SA) and cuckoo search (hCS-SA) algorithms.

SA is inspired from the certain rate of heating and cooling used in metallurgy for heating materials [39]. This is a probabilistic approach that seeks for the global optimum of a search space in a fixed amount of time. This algorithm has parameters of initial temperature, temperature reduction rate and mutation rate and those parameters were set to have values of 0.1, 0.98 and 0.5, respectively [24].

GA is an evolutionary algorithm that is inspired from biological evolutionary theory [102]. This algorithm tends to exceptional in terms of finding good global solutions. It adopts selection, crossover and mutation operations to achieve high quality solutions. The latter parameters for this study were chosen to be Roulette wheel for selection, 0.8 for crossover and 0.4 for mutation [24].

PSO is an algorithm that mimics the flocking behavior of birds in the sky [103]. It adopts individual and social group learning to update the velocities and positions of a population. In this way, it searches for the desired goal. This algorithm has a good ability in terms of local search. In this study, the PSO parameters of cognitive and social constants were chosen to be 2 for each. The inertia constant was set to decrease linearly from 0.8 to 0.2 [24].

GSA is another algorithm used for comparison which is a competitive search algorithm [64]. This algorithm is based on the gravitational law and thus makes the agents to interact using the motional law. The attraction can lead to generation of attractive force and this helps in facilitating all agents to move toward the agent with the heavier mass. The parameters of this algorithm were set to 100 and 20 for initial gravitational constant and decreasing coefficient, respectively [24].

The last algorithm used for comparison is WDO which is inspired from the motion of earth’s atmosphere [104]. In here, each small parcel of air moves by following the Newton’s second law. This algorithm has a good global search ability and approximates the global optimum by updating the velocity and position of each parcel using gradient, Coriolis, gravitational and friction forces. The parameter values for this study were set to 3, 0.2 and 0.4 for RT coefficient, gravitational constant and Coriolis effect, respectively. The maximum allowable speed was set to 0.3, whereas the constant in the update equations was 0.4 [24].

In addition of above algorithms, hybrid structures of PSO and CS algorithms (hPSO-SA and hCS-SA, respectively) were also merged with SA and used for comparison. The PSO algorithm used in hPSO-SA is already mentioned briefly in one of the above paragraphs. CS algorithm in hCS-SA is a population-based optimization algorithm and simulates the parasitic breeding behavior of some cuckoo species [105]. Those species lay their eggs on the nests of host birds. Depending on the discovery of the replacement of the eggs by the host bird, the eggs may be thrown, or the nest may be abandoned. In this study, the parameters of CS algorithm were chosen as $\beta = 1.5$ for Lévy flight and $P_{a} = 0.25$ for mutation probability [105].

3.3 Statistical Results and Discussion

The proposed hASO-SA algorithm was run 50 times along with a chosen swarm size of 50 and the maximum number of iterations of 1000 in order to achieve a fair comparison with SA, GA, PSO, GSA, WDO and ASO algorithms [24]. The statistical results obtained for the adopted test functions using listed algorithms are presented in Table 2 by highlighting the best mean results in bold.

Table 2 Comparisons of results for unimodal, multimodal, hybrid and composition functions

Considering the presented numerical values in the table, the proposed hybrid hASO-SA algorithm provided the best statistical values compared to other competitive algorithms, including original ASO, for functions of $F_{2} \left( x \right)$, $F_{4} \left( x \right)$, $F_{5} \left( x \right)$, $F_{9} \left( x \right)$, $F_{10} \left( x \right)$, $F_{11} \left( x \right)$ and $F_{12} \left( x \right)$. In addition, it has also found the same values as its other closest competitors in functions of $F_{3} \left( x \right)$, $F_{6} \left( x \right)$, $F_{7} \left( x \right)$ and $F_{8} \left( x \right)$. The proposed hASO-SA algorithm is behind the WDO algorithm only for the function of $F_{1} \left( x \right)$. The results in Table 2 demonstrate the good optimizing performance of the proposed hASO-SA compared to its competitive algorithms (including the basic ASO) on the benchmark functions, including unimodal, multimodal, hybrid and composition functions.

3.4 Nonparametric Test Analysis

The superiority of an algorithm may generally occur by chance, due to stochastic nature, if the comparison is performed based on statistical criteria such as best, mean and standard deviation. Because of 50 independent runs, the probability of the latter case is low for this study. However, a nonparametric statistical test was also performed to compare the results of each run and decide on the significance of the results. In this work, a nonparametric test named Wilcoxon signed-rank test [66] has been used to prove the superiority of the proposed hybrid hASO-SA algorithm. This test is performed at $5{\text{\% }}$ significant level for the hASO-SA versus other competitive algorithms, and the obtained $p$ values are provided in Tables 3 and 4. The $p$ values less than 0.05 indicate significant difference between the algorithms. The column W (winner) in Table 3 and 4 reveals the results of the test where the sign of ‘=’ is an indication of no significant difference between hASO-SA and the competitive algorithm, whereas the signs of ‘+’ and ‘−’ are of significantly better and worse performances of hASO-SA, respectively, compared to its competitive algorithms.

Table 3 Wilcoxon signed-rank test results for hASO-SA versus SA, GA, PSO and GSA

Table 4 Wilcoxon signed-rank test results for hASO-SA versus WDO, ASO, hPSO-SA and hCS-SA

The results of Tables 3 and 4 showed that the hASO-SA algorithm presents better performance with great effectiveness with respect to other algorithms. Moreover, the corresponding statistical results for each function in 50 runs are listed in Table 5. This table shows the proposed hASO-SA algorithm outperforming all other algorithms significantly for unimodal, multimodal, hybrid and composition benchmark functions.

Table 5 Statistical results of Wilcoxon signed-rank test obtained by proposed hASO-SA

4 Application of hASO-SA in Training MLP

4.1 MLP

MLP can be regarded as a distinctive class of feedforward neural networks. Neurons are organized in one-direction in MLPs. MLPs has a layered structure where data transition occurs. The structure of MLPs can be imagined as parallel layers which are named as input layer, hidden layer and output layer. Figure 3 illustrates an MLP with those three layers where n denotes the number of input nodes, h is hidden layer, and m shows output nodes. The MLP output is calculated in few steps. Firstly, the weighted sums are calculated using Eq. (22) where $W_{ij}$ denotes the connection weight from input layer’s ith node to the hidden layer’s jth node, $X_{i}$ represents the ith input, and $\theta_{j}$ is the bias of the jth hidden node.

$$ s_{j} = \mathop \sum \limits_{i = 1}^{n} \left( {W_{ij} X_{i} } \right) - \theta_{j} ,\quad j = 1,2, \ldots ,h $$

(22)

Fig. 3

Structure of MLP neural network

Secondly, each hidden node’s output is calculated as in Eq. (23).

$$ S_{j} = {\text{sigmoid}}\left( {s_{j} } \right) = \frac{1}{{1 + e^{{ - s_{j} }} }},\quad j = 1,2, \ldots ,h $$

(23)

After calculating the outputs of hidden nodes, the final outputs are defined as in Eqs. (24) and (25) where $\omega_{jk}$ denotes the connection weight from hidden node j to the output node k.

$$ o_{k} = \mathop \sum \limits_{j = 1}^{h} \left( {\omega_{jk} S_{j} } \right) - \theta_{k}^{{\prime }} ,\quad k = 1,2, \ldots ,m $$

(24)

$$ O_{k} = {\text{sigmoid}}\left( {o_{k} } \right) = \frac{1}{{1 + e^{{ - o_{k} }} }},\quad k = 1,2, \ldots ,m $$

(25)

In MLP training, the biases and connection weights are playing a critical role. The quality of MLP’s final output depends on the biases and weights. Therefore, training an MLP means finding optimum values for biases and weights which helps in achieving desirable outputs for defined inputs.

4.2 hASO-SA-Based MLP Trainer

It is feasible to train MLPs in three different methods using metaheuristic methods. The first method includes finding optimal connection weights and biases. In this way, metaheuristics help in achieving minimum error for an MLP. In this method, the MLP architecture remains as it is during the learning process. The second method is about finding an appropriate architecture for an MLP using metaheuristics in the case of a specific problem. Tuning parameters such as learning rate of the gradient-based learning algorithm and momentum is the third method that metaheuristics can be used.

The first method explained above was adopted to implement the proposed hASO-SA since the learning algorithm is required to minimize the MLP error by achieving the convenient weights and biases. An important aspect in MLP training is the representation of biases and weights. Three methods are available to represent them such as binary, matrix and vector [106]. In this paper, the vector method was utilized for representation of biases and weights. The objective function should be defined after representation of biases and weights in vector form in order to evaluate each candidate solution of the algorithm. In this study, the mean square error (MSE) was chosen as objective function which is formulated as:

$$ E = \mathop \sum \limits_{k = 1}^{q} \frac{{\mathop \sum \nolimits_{i = 1}^{m} \left( {o_{i}^{k} - d_{i}^{k} } \right)^{2} }}{q} $$

(26)

where m is the number of outputs, q is the number of training samples, $d_{i}^{k}$ is the desired output of the ith input unit when the kth training sample is used, and $o_{i}^{k}$ is actual output of the ith input unit when the kth training sample appears in the input. Figure 4 represents the overall process of MLP training using proposed hybrid hASO-SA algorithm. As can be seen, the hASO-SA algorithm provides MLP with weights/biases and receives average MSE for all training samples. The hASO-SA algorithm iteratively changes the weights and biases to minimize average MSE of all training samples.

Fig. 4

hASO-SA-based MLP trainer

4.3 Experimental Setup and Analysis of Results on Classification Datasets

Five classification datasets (XOR, Balloon, iris, Heart and Breast cancer) was used to benchmark the proposed hASO-SA algorithm. Those datasets were obtained from [67]. Each candidate solution was selected from a range of $\left[ { - 10, 10} \right]^{D}$ randomly in the training algorithm. The population size of candidate solutions was chosen to be 200 for Iris, Heart and Breast cancer and 50 for XOR and Balloon classification problems. Maximum number of iterations (generations) is 250. The datasets were classified as presented in Table 6.

Table 6 Classification datasets

The algorithm was implemented on datasets for 10 times. The results that were obtained from those datasets are shown from Tables 7, 8, 9, 10 and 11 which provide average (AVE), and standard deviation (STD) of the best mean square error (MSE) acquired in the last iteration of the algorithm. Obviously, the lower average and standard deviation of MSE in the last iteration is an indication of better performance. The performance of the proposed hASO-SA was evaluated by comparing with a variety of algorithms such as classical ASO, ACO, GWO, PBIL, PSO and ES algorithms which was adopted to solve these classification problems [70, 72]. Compared algorithms for training an MLP for hASO-SA algorithm were acquired from Refs. [70, 72].

Table 7 Experimental results for the XOR classification problem

Table 8 Experimental results for the Balloon classification problem

Table 9 Experimental results for the Iris classification problem

Table 10 Experimental results for the Breast cancer classification problem

Table 11 Experimental results for the Heart classification problem

The collected datasets, shown in Table 6, have different difficulty levels, e.g., Heart dataset is considered to be difficult, whereas XOR is simple [67]. The large number of training samples make the problem less difficult, whereas the large number of features causes neural network with larger size and hence increases the difficulty of the problem as more weights need to be determined.

The results of the considered datasets are provided in the following subsections. According to this comprehensive study, the hASO-SA algorithm can be highly recommended to be used in MLP training due to its high exploratory behavior. The latter specification provides high local optima avoidance while training MLP. In addition, the proposed hybrid hASO-SA algorithm has high exploitative behavior as well which helps hASO-SA-based trainer to be able to converge rapidly toward the global optimum for different datasets.

4.3.1 XOR Dataset

This is a well-known nonlinear benchmark classification problem. Recognizing the number of 1’s in the input vector is the objective of this problem. The output is 1 in the case of odd number of input vector consisting of 1 s and 0 for even number of 1 s that form the input vector. The MLP with 3-7-1 structure was used to solve this problem. Numerical results are presented in Table 7 which clearly indicates the proposed hASO-SA algorithm’s performance to be better in solving this problem by avoiding the sub-optimal solutions.

4.3.2 Balloon Dataset

The Balloon dataset includes 16 instances having 4 attributes such as color, age, act and size which are in string format. An MLP structure of 4-9-1 was used for classification. The acquired results are presented in Table 8 which shows that the hASO-SA provides the minimum error. The classification rates of all algorithms are the same and is 100%.

4.3.3 Iris Dataset

This dataset includes 150 samples that can be treated under three classes (Virginica, Versicolor and Setosa). Sepal width and length along with petal width and length are the four features that are present in those samples. An MLP having structure of 4-9-3 was used for solving this classification problem. The obtained results are provided in Table 9. The hASO-SA provides better performance to train MLP-based on the average value of the square error and classification rate. The comparative results showed the superior performance of hASO-SA compared to other algorithms.

4.3.4 Breast Cancer Dataset

This dataset consists of 9 attributes and 699 instances. The attributes include marginal adhesion and uniformity of cell shape and size along with clump thickness [107]. The output is 2 for benign cancer, whereas 4 for malignant cancer. The MLP structure of 9-19-1 was adopted for classification. Table 10 provides the results of this problem. As can be seen the hASO-SA provides the best mean square error in terms of average value and classification rate which is a clear indication of better search ability of the proposed algorithm in terms of escaping local optima.

4.3.5 Heart Dataset

This dataset includes 267 images and was created for diagnosing the cardiac tomography images. 22 features were extracted from those images to summarize them. The MLP with 22-45-1 structure was trained by utilizing 80 instances. The condition of a patient can be expressed as normal or not normal using binary form of the dataset. Table 11 lists the results. The table clearly shows that the proposed hASO-SA is capable of providing better results and classification rate than other algorithms.

5 Application of hASO-SA to PID Controller Design in DC Motor Speed Control

5.1 Speed Control of DC Motor System

DC motors are devices that basically convert the electrical energy into mechanical form. The speed control of a DC motor is important to perform a specific work. This can be achieved either manually by an operator or automatically by adopting control devices. Figure 5 illustrates the block diagram of a DC motor system. The relationship between the speed of the motor ($\omega$) and the applied voltage ($E_{\text{a}}$) under no load ($T_{\text{Load}} = 0$) is provided in Eq. (27).

$$ G_{\text{Plant}} \left( s \right) = \frac{\varOmega \left( s \right)}{{E_{\text{a}} \left( s \right)}} = \frac{{K_{\text{m}} }}{{\left( {L_{\text{a}} s + R_{\text{a}} } \right)\left( {Js + B} \right) + K_{b} K_{\text{m}} }} $$

(27)

Fig. 5

Block diagram of a DC motor

The rest of the parameters for DC motor speed control, given in the latter equation, along with the respective values used for this work are listed in Table 12 [93,94,95].

Table 12 DC motor parameters [93,94,95]

5.2 DC Motor with PID Controller

PID controllers are the most popular controller type in engineering due to their simple structure and high efficiency. The transfer function of a PID controller is provided in Eq. (28) where $K_{\text{p}}$, $K_{\text{i}}$ and $K_{\text{d}}$ are gains of proportional, integral and derivative terms, respectively.

$$ G_{\text{Controller}} \left( s \right) = K_{\text{p}} + \frac{{K_{\text{i}} }}{s} + K_{\text{d}} s $$

(28)

The closed loop block diagram of a DC motor with PID controller is given in Fig. 6. The closed loop transfer function of a DC motor having a unit feedback is given as in Eq. (29).

$$ T_{\text{closed - loop}} \left( s \right) = \frac{\varOmega \left( s \right)}{{\varOmega_{\text{ref}} \left( s \right)}} = \frac{{G_{\text{Plant}} \left( s \right)G_{\text{Controller}} \left( s \right)}}{{1 + G_{\text{Plant}} \left( s \right)G_{\text{Controller}} \left( s \right)}} $$

(29)

Fig. 6

Block diagram of DC motor with PID controller

Using the parameters listed in Table 12 provides the following transfer function.

$$ T_{\text{closed - loop}} \left( s \right) = \frac{{15\left( {K_{\text{d}} s^{2} + K_{\text{p}} s + K_{\text{i}} } \right)}}{{1.08s^{3} + 6.1s^{2} + 1.63s + 15\left( {K_{\text{d}} s^{2} + K_{\text{p}} s + K_{\text{i}} } \right)}} $$

(30)

5.3 hASO-SA-Based PID Controller Design

The objective function was chosen to be ITAE for this study in order to achieve better speed control. The ITAE objective function is given by [93,94,95] as:

$$ J_{\text{ITAE}} = \mathop \int \limits_{0}^{{t_{\text{sim}} }} t\left| {e\left( t \right)} \right|{\text{d}}t $$

(31)

where $e\left( t \right)$ denotes the error signal and is equal to $\omega_{ref} - \omega \left( t \right),$ whereas $t_{sim}$ is the simulation time and were chosen to be $2 s$ for this study. The upper and lower bounds of the optimization problem are also the limits of the controller parameters and given in Eq. (32) [93,94,95].

$$ 10^{ - 3} \le K_{\text{p}} , K_{\text{i}} , K_{\text{d}} \le 20 $$

(32)

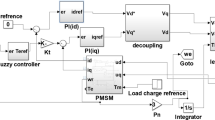
The application of the proposed hASO-SA algorithm to DC motor speed control system is illustrated in Fig. 7. The stability of DC motor speed control system increases to the highest level after completion of the detailed optimization procedure provided in the figure.

Fig. 7

The procedure of applying the proposed hASO-SA algorithm to DC motor speed control

In the optimization module provided in Fig. 7, the swarm size (number of atoms) and the maximum number of iterations (stopping criteria) were set to be 40 and 30, respectively. The value of the ITAE objective function given in Eq. (31) was calculated for each atom in the swarm by integrating the proposed hASO-SA with the DC motor system using MATLAB/Simulink environment. The proposed algorithm was run for 25 times, and the PID parameters corresponding minimum ITAE value were found to be $K_{\text{p}} = 18.4258$, $K_{\text{i}} = 3.3082$ and $K_{\text{d}} = 3.1755$.

5.4 Comparative Simulation Results

The proposed hASO-SA-based controller’s performance was evaluated by comparing it with the most recent studies published in prestigious journals using a variety of analysis. The most convenient approaches chosen for comparison were ASO/PID [95], GWO/PID [94] and SCA/PID [93] controllers since those approaches adopted the same DC motor parameters, ITAE objective function and the limits of the controller parameters. PID controller parameters that were optimized with different algorithms are presented in Table 13.

Table 13 Optimized controller parameters using different algorithms

In addition, the closed loop transfer functions of DC motor with the proposed hASO-SA/PID, ASO/PID [95], GWO/PID [94] and SCA/PID [93] are given in Eqs. (33), (34), (35) and (36), respectively. The analyses of time and frequency domain along with robustness were performed using the latter equations.

$$ T_{\text{hASO - SA}} \left( s \right) = \frac{{47.63s^{2} + 276.4s + 49.62}}{{1.08s^{3} + 53.73s^{2} + 278s + 49.62}} $$

(33)

$$ T_{\text{ASO}} \left( s \right) = \frac{{36.54s^{2} + 179.2s + 30.78}}{{1.08s^{3} + 42.64s^{2} + 180.8s + 30.78}} $$

(34)

$$ T_{\text{GWO}} \left( s \right) = \frac{{13.94s^{2} + 103.5s + 8.439}}{{1.08s^{3} + 20.04s^{2} + 105.1s + 8.439}} $$

(35)

$$ T_{\text{SCA}} \left( s \right) = \frac{{7.953s^{2} + 67.52s + 7.89}}{{1.08s^{3} + 14.05s^{2} + 69.15s + 7.89}} $$

(36)

Based on the simulation results, it can clearly be seen that the usage of the hASO-SA algorithm provides significantly better transient and frequency responses compared to three algorithms from the recent literature. Furthermore, the suggested hASO-SA/PID controller design is more robust to the variations in the system parameters than the other competitive algorithms-based controller designs.

5.4.1 Transient Response Analysis

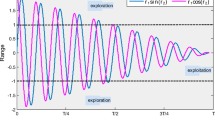
The step responses of DC motor (normalized speed responses) using the proposed hASO-SA/PID, ASO/PID [95], GWO/PID [94] and SCA/PID [93] controllers are illustrated in Fig. 8. As can be observed from the figure, the speed of DC motor reaches the steady state value quickly without any overshoot. This behavior confirms the superiority of the proposed hASO-SA algorithm over ASO, GWO and SC algorithms. Also, the comparative results of maximum overshoot, rise time and settling time for a tolerance band of ± 2% are provided in Table 14. Moreover, the ITAE objective function values are also given in the table. As can be seen from numerical and graphical outcomes, the speed response of a DC motor with the proposed hASO-SA/PID controller is more stable and has no overshoot.

Fig. 8

The comparison of DC motor step responses

Table 14 Comparison of transient response analysis results

5.4.2 Frequency Response Analysis

The Bode diagram of a DC motor speed control system provides information about frequency response. The comparative Bode plots of the different approaches are given in Fig. 9. Gain margin, phase margin and bandwidth of the system can be calculated easily from this figure. Important parameters of frequency response such as bandwidth, gain and phase margin, obtained from Fig. 9, are presented in Table 15. The best value is shown in bold. The numerical values presented in the table clearly show that the proposed hASO-SA/PID-based system has the best frequency response.

Fig. 9

Comparative Bode diagrams

Table 15 Comparison of frequency response analysis results

5.4.3 Robustness Analysis

The output of any system may be affected undesirably due to unexpected sudden changes. It is crucial to design the system from having undesired responses. Therefore, a robustness analysis was performed by observing the behavior of the system which were altered separately with $\pm 25\%$ for $R_{\text{a}}$ and with $\pm 20\%$ for $K_{\text{m}}$. The latter action created four possible operating scenarios. The scenarios and their comparative time domain performance analysis simulation results are presented in Table 16. The best values are shown in bold.

Table 16 Performance comparisons for parametric uncertainty

Likewise, the comparative speed step responses for all scenarios is depicted from Figs. 10, 11, 12 and 13. It is clear from the latter figures that despite the changes occurring in the system parameters, the proposed hASO-SA/PID controller has the least rise time and settling time values with no overshoot in all scenarios except Scenario I and Scenario II with a negligible overshoot percentage while compared to other controllers optimized by ASO, GWO and SCA. As can be seen from the results listed in the table and demonstrated in the figures, the proposed hASO-SA/PID controller has not affected from the change of the parameters. Also, the proposed hASO-SA/PID has better robustness performance compared to ASO/PID [95], GWO/PID [94] and SCA/PID [93] controllers.

Fig. 10

Comparative speed responses for Scenario I

Fig. 11

Comparative speed responses for Scenario II

Fig. 12

Comparative speed responses for Scenario III

Fig. 13

Comparative speed responses for Scenario IV

6 Conclusion

A novel hybrid metaheuristic algorithm based on ASO and SA algorithms was proposed in this work by embedding the SA technique into ASO algorithm. The specific configuration helped improving search capability of ASO without costing considerably longer computational time. Several optimization problems with different nature were utilized to observe the performance of the proposed hybrid hASO-SA algorithm. Classical benchmark functions of Sphere, Rosenbrock, Step, Quartic, Schwefel, Rastrigin, Ackley and Griewank as well as CEC2014 test functions, were adopted for initial assessment of the algorithm. Those functions are of unimodal, multimodal, hybrid and composition types and help effectively measuring the performance of the proposed algorithm. The performance comparisons were carried out with PSO, GA, GSA and WDO along with SA and original ASO, using respective test functions, in order to demonstrate the superiority of the proposed algorithm. Moreover, SA-based hybrid versions of PSO (hPSO-SA) and CS (hCS-SA) algorithms were also used to provide a stronger comparison. The statistical results obtained from those benchmark functions clearly showed the greater capability of the proposed hASO-SA, compared to the algorithms listed above, in terms of achieving values for the metrics of the best, mean and standard deviation. Apart from those statistical values, a nonparametric test named Wilcoxon signed-rank test was also adopted to prove the superiority of the proposed hybrid hASO-SA algorithm was not by chance.

Further assessment was performed by using the proposed algorithm for MLP training, as a nonlinear system, in order to observe the ability of the proposed algorithm for an optimization problem with different nature. To do so, Balloon, Iris, XOR, Heart and Breast cancer datasets were used since they have different difficulty levels, and, similar to the previous case, the performance of the algorithm was compared with other metaheuristics of ASO, GWO, PSO, ACO, ES and PBIL algorithms. The results from those datasets showed the proposed hASO-SA algorithm to be better compared to the listed algorithms since it provided the lowest average and standard deviation of the best mean square error.

A PID controller design for DC motor speed control was also performed as a final evaluation process as it is a widely used test bed for performance assessment of the algorithms. The obtained hASO-SA/PID controller was compared with other algorithms-based PID controllers such as ASO/PID, GWO/PID and SCA/PID controllers since those studies adopted the same parameters for DC motor and the limits of the controller as well as the same objective function. The speed response of DC motor has found to be more stable with no overshoot compared to the same system with different algorithms. In addition, the frequency response was also found to be the best among the competitive algorithms. Moreover, the system presented better robustness, in the case of the changes occurring in the system parameters with the implementation of the proposed hybrid algorithm.

In conclusion, the implementation of the proposed hASO-SA algorithm to problems with different nature showed that this algorithm is a powerful technique for various optimization problems. The proposed hybrid algorithm also has the potential to provide better performance characteristics in several other optimization problems of different types for future studies. Some of those applications can be listed as feature selection and photovoltaic cell parameter estimation along with controller design for automatic voltage regulator and magnetic ball suspension systems.