1 Introduction

Peristaltic flow is produced due to contraction and expansion of wall channel. Blood inside the small blood vessels can transfer through peristaltic flow. The idea of peristaltic flow was firstly given by Latham [1] in his PhD studies. Srinivas et al. [2, 3] presented the result of peristaltic motion of a Jeffrey fluid in the presence of magnetic field through a porous medium [4] and investigated the peristaltic flow of magnetohydrodynamic. For cylindrical tubes, the peristaltic motion for micropolar fluid is discussed by Muthu et al. [5]. Other researchers examined the effect of magnetic field through a porous medium [6,7,8,9]. Tsiklauri and Beresnev [10] examined the peristaltic motion of compressible Maxwell fluid. They examined viscoelastic effect on the fluid dynamics by studying about compressibility of the liquid for Maxwell fluid in a circular tube. They set up that for non-Newtonian regime, on the tube wall the fluid might flow in opposite direction to the direction of the movement of waves. Nadeem and Akram [11] discussed the peristaltic transport of a Williamson in an asymmetric channel. For Maxwell fluid, peristaltic flow in the presence of effect of magnetic field and Hall effect over a porous medium was observed by Elkoumy et al. [12]. After their research, they concluded that for mean velocity distribution, relaxation time shows the decreasing effect.

The study of electrically conducting fluid with magnetic properties is known as magnetohydrodynamics. Many researchers examined magnetohydrodynamics (MHD) motion for an electrically conducting and viscous fluid. Existence of pressure gradient for magnetohydrodynamics bounded sheets is discussed by Gribben [13]. In porous medium, flow of compressible fluid along peristaltic mechanism is given by Aarts and Ooms [14]. They found that on the net flow rate influence of compressibility of liquid is strong and for compressible liquid Reynolds number plays an important role than for an incompressible liquid.

The term compliant wall means that flexible walls have elastic quality due to which deformation and motion for the fluid occur, which can cause change in behavior. A study on stability of compliant walls and their impact on Couette flow over a spring plate was conducted by Shankar and Kumaran [15]. There are several applications about wall collapsing and their results on fluid flow. For nanofluid, Abbas et al. [16] examined the compliant wall effect for peristaltic motion of a fluid in the presence of peristaltic flow and entropy and its impact over a channel. Wall properties show decrease in entropy and temperature by increasing wall stiffness and tension. Over a porous medium, flowing of a fluid is a focus of common attention and has appeared as a distinct field of examination. Flow for a porous medium is defined by Darcy’s law. Compliant wall is excited by the muscles, whose tension controls its deformation. Set of equations ruled the action of these muscles which can be related for movement of compliant walls in terms of variables. In a microchannel, Abdel-Wahab and Mekheimer [17] studied the effects of compressible viscous fluid flow that was made by surface acoustic wave with compliant wall. Nadeem et al. [18] deal with the effect of compliant wall for peristaltic motion of fluid. Most of the researchers observed the peristaltic motion for effect of wall compliance, and most of these discussed about interaction of fluid and walls, which is essential in peristaltic flow [19,20,21].

In past, researchers examined the compressible fluid for distinct parameters [14, 15, 22] and mostly they worked for incompressible peristaltic fluids flow. Also, homotopy perturbation method (HPM) was used by many researchers to obtain the solutions. And some researchers applied the extended homotopy perturbation method. Our goal is to study the effect occurred on the microchannel due to porous medium, magnetic field under symmetric boundary condition with compliant wall effect. In a microchannel, flow is generated due to wavy movement of a compressible Jeffrey fluid in the presence of constant magnetic field. We assume that, in microchannel, originally the fluid is stationary, (i.e., the zeroth-order pressure gradient is ignored at the beginning). This article is the extension of [17] from compressible viscous fluid to compressible Jeffrey fluid in addition to magnetic field and wall properties which are taken into account.

The main objective of this article is to examine the wavy motion of a compressible Jeffrey fluid in the presence of magnetic field with compliant walls effect over a porous medium and also to check the effects of various parameters on fluid. Assume that channel contains stationary fluid in it. To obtain the solution of the problem, we use the perturbation method.

Sectionwise, this paper is elaborated as: Sect. 1 presents the introduction; in Sect. 2, we discuss about mathematical modeling of the problem. Solution is obtained in Sect. 3. Graphical results of the solutions are discussed in Sect. 5. Section 6 presents the conclusion of the article. For non-Newtonian system, the fluid may flow in opposite direction to the direction of the travelling wave.

2 Mathematical Modeling

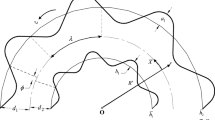
A compressible, electrically conducting and Jeffrey fluid in a two-dimensional symmetric network is considered as depicted in Fig. 1.

Fig. 1
figure 1

Geometry of the problem

Full size image

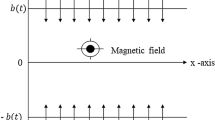
Flow is due to sinusoidal wave of small-amplitude travelling on the flexible walls of the channel, which are considered compliant wall over a porous medium. Constant magnetic field acting in y-direction is analyzed, and the induced magnetic field is neglected. Introducing the Cartesian coordinates in which the x-axis is taken along the center line and the y-axis is normal to it.

The relevant flow equations for compressible Jeffrey fluid in general form are stated as:

$$ \frac{\partial \rho }{{\partial t}} + \left( {{\varvec{V}}\nabla \rho } \right) + \rho \left( {\nabla {\varvec{V}}} \right) = 0, $$
(1)
$$ \rho \frac{{\partial {\varvec{V}}}}{\partial t} + \rho \left( {{\varvec{V}}.\nabla } \right){\varvec{V}} = - \nabla p + \nabla .{\varvec{S}} + {\varvec{R}} + {\varvec{J}} \times {\varvec{B}} + \frac{\mu }{3}\nabla \left( {\nabla .{\varvec{V}}} \right), $$
(2)

where \(\mu ,\rho ,p {\text{and}} t \) are the respective dynamic viscosity, density, pressure and time, whereas \({\varvec{J}}\), \({\varvec{V}}\) and \({\varvec{B}}\) examine the electric current, velocity vector and magnetic vector.

For Jeffrey fluid, extra stress tensor S is expressed as [23]:

$$ \left( {1 + \lambda_{1} \frac{\partial }{\partial t}} \right){\varvec{S}} = \mu \left( {1 + \lambda_{2} \frac{\partial }{\partial t}} \right){\varvec{A}}_{1} , $$
(3a)

where \({\lambda }_{1}\) represents the relaxation time and \({\lambda }_{2}\) is the retardation time; \({{\varvec{A}}}_{1}\) denotes the first Rivlin–Ericksen tensor which is defined as:

$${{\varvec{A}}}_{1}=\left(grad {\varvec{V}}\right)+{(grad {\varvec{V}})}^{T},$$
(3b)

Darcy’s resistance R is defined as

$$\left(1+{\lambda }_{1}\frac{\partial }{\partial t}\right){\varvec{R}}=-\frac{\mu \phi }{K}\left(1+{\lambda }_{2}\frac{\partial }{\partial t}\right){\varvec{V}},$$
(4)

where \(0<\phi <1\), \(K\) (> 0). The conducting liquid is passed over a uniform magnetic field \({B}_{0}\). In case of small magnetic Reynolds number, induced magnetic field b is neglected, and in the presence of body force \({\varvec{J}}\times {\varvec{B}}={\varvec{\sigma}}\boldsymbol{ }({\varvec{V}}\times {\varvec{B}})\times {\varvec{B}}\), only the magnetic field B is present and electric field is ignored, so the current becomes \({\varvec{J}}={\varvec{\sigma}}\boldsymbol{ }({\varvec{V}}\times {\varvec{B}})\) (\(\sigma \) is the conductivity of electric field).

Characteristic response of fluid to a compression is given by equation:

$$\frac{1}{\rho }\frac{\partial \rho }{\partial p}={k}_{c}.$$
(5)

Here, compressibility of the fluid is represented by \({k}_{c}\). The solution of the above equation is

$$\rho ={\rho }_{0}\mathit{exp}\left({k}_{c}\left(p-{p}_{c}\right)\right),$$
(6)

Here, \({\rho }_{0}\) signifies the density and \({p}_{c}\) identifies the reference pressure.

In component form, continuity and momentum equations for Jeffrey compressible fluid take the following form:

$$\frac{\partial \rho }{\partial t}+u\frac{\partial \rho }{\partial x}+v\frac{\partial \rho }{\partial y}+\rho \left(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\right)=0,$$
(7)
$$\begin{aligned}\left(1+{\lambda }_{1}\frac{\partial }{\partial t}\right)\left[\rho \left(\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}\right)\right]\\=-\left(1+{\lambda }_{1}\frac{\partial }{\partial t}\right)\frac{\partial p}{\partial x}+\mu \left(1+{\lambda }_{2}\frac{\partial }{\partial t}\right)\left[{\nabla }^{2}u+\frac{1}{3}\frac{\partial }{\partial x}\left(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\right)\right]\\-\sigma {B}_{0}^{2}\left(1+{\lambda }_{1}\frac{\partial }{\partial t}\right)u-\frac{\mu \phi }{k}\left(1+{\lambda }_{2}\frac{\partial }{\partial t}\right)u,\end{aligned}$$
(8)
$$\begin{aligned}\left(1+{\lambda }_{1}\frac{\partial }{\partial t}\right)\left[\rho \left(\frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}\right)\right]\\=-\left(1+{\lambda }_{1}\frac{\partial }{\partial t}\right)\frac{\partial p}{\partial y}+\mu \left(1+{\lambda }_{2}\frac{\partial }{\partial t}\right)\left[{\nabla }^{2}v+\frac{1}{3}\frac{\partial }{\partial y}\left(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\right)\right]\\-\frac{\mu \phi }{k}\left(1+{\lambda }_{2}\frac{\partial }{\partial t}\right)v,\end{aligned}$$
(9)

The compliant wall is modeled as spring-backed plate, and their movement is directed vertically. Let \(\eta \) and \(- \eta \) represent the vertical displacement of upper wall and lower wall, and \(\eta (x,t)\) is given by:

$$\eta \left(x,t\right)=a\mathit{cos}\left[\frac{2\pi }{\lambda }\left(x-ct\right)\right],$$
(10)

where amplitude is denoted by \({\varvec{a}}\), wavelength by \({\varvec{\lambda}}\) and speed by c of the wave.

The flow equation for compliant wall may be expressed as \(L\left(\eta \right)=p-{p}_{0}\), where L is the operator that shows the motion of compliant wall:

$$L=-T\frac{{\partial }^{2}}{\partial {x}^{2}}+m\frac{{\partial }^{2}}{\partial {t}^{2}}+d\frac{\partial }{\partial t}+B\frac{{\partial }^{4}}{\partial {x}^{4}}+{K}^{*}.$$
(11)

The longitudinal tension per unit width is represented by T, \(m\) is the mass per unit area, \(B\) shows the flexural rigidity, \(d\) is the wall damping coefficient, and \({K}^{*}\) is the spring stiffness of the plate. Due to motion of the fluid, pressure p is produced, and \({p}_{0}\) is the pressure on the outer surface of the wall. Assume that \({p}_{0}\)= 0. Thus, for no slip the appropriate boundary conditions are

$$u\left(x,\pm d\pm \eta ,t\right)=0,$$
(12)
$$v\left(x,\pm d\pm \eta ,t\right)=\pm \frac{\partial \eta (x,t)}{\partial t},$$
(13)

For compliant wall at y = \(\pm d\pm \eta \),

$$\begin{aligned}&\left(1+{\lambda }_{1}\frac{\partial }{\partial t}\right)\frac{\partial L}{\partial x}\\&\quad =-\left(1+{\lambda }_{1}\frac{\partial }{\partial t}\right)\left[\rho \left(\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}\right)\right]\\&\qquad +\mu \left(1+{\lambda }_{2}\frac{\partial }{\partial t}\right)\left[{\nabla }^{2}u+\frac{1}{3}\frac{\partial }{\partial x}\left(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\right)\right]\\&\qquad -\sigma {B}_{0}^{2}\left(1+{\lambda }_{1}\frac{\partial }{\partial t}\right)u-\frac{\mu \phi }{k}\left(1+{\lambda }_{2}\frac{\partial }{\partial t}\right)u.\end{aligned}$$
(14)

Introducing non-dimensional variables and parameters,

$$\stackrel{\sim }{x}=\frac{x}{d}, \stackrel{\sim }{y}=\frac{y}{d}, \stackrel{\sim }{\eta }=\frac{\eta }{d},\stackrel{\sim }{u}=\frac{u}{c},\stackrel{\sim }{v}=\frac{v}{c},\stackrel{\sim }{\rho }=\frac{\rho }{{\rho }_{0}},\stackrel{\sim }{t}=\frac{ct}{d},\stackrel{\sim }{{\lambda }_{1}}=\frac{c}{d}{\lambda }_{1}, \stackrel{\sim }{{\lambda }_{2}}=\frac{c}{d}{\lambda }_{2}, \stackrel{\sim }{p}=\frac{p}{{\rho }_{0}{c}^{2}},\stackrel{\sim }{{p}_{c}}=\frac{{p}_{c}}{{\rho }_{0}{c}^{2}},\stackrel{\sim }{\tau }=\frac{c\tau }{d}.$$

The dimensionless parameters are

$$\varepsilon =\frac{a}{d},\chi ={k}_{c}{\rho }_{0}{c}^{2},M=\frac{d\sigma }{{\rho }_{0}c}{B}_{0}^{2},R=\frac{{\rho }_{0}cd}{\mu }, \alpha =\frac{2\pi d}{\lambda } .$$

These parameters represent the amplitude ratio, compressibility parameter, magnetic parameter, Reynolds number and wave number.

The dimensionless wall parameters are

$$\stackrel{\sim }{T}=\frac{{T\rho }_{0}d}{{\mu }^{2}},\stackrel{\sim }{d}=\frac{{d}^{2}}{\mu },\stackrel{\sim }{B}=\frac{{B\rho }_{0}d}{\mu },\stackrel{\sim }{m}=\frac{m}{d{\rho }_{0}},\stackrel{\sim }{{K}^{*}}=\frac{{K}^{*}{d}^{3}{\rho }_{0}}{{\mu }^{2}}.$$

By using these variables, the above equations become

$$\rho =\mathrm{exp}\left(\chi \left(p-{p}_{c}\right)\right),$$
(15)
$$\frac{\partial \rho }{\partial t}+ u\frac{\partial \rho }{\partial x}+v\frac{\partial \rho }{\partial y}+\rho \left(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\right)=0,$$
(16)
$$\begin{aligned}\left(1+{\lambda }_{1}\frac{\partial }{\partial t}\right)\left[\rho \left(\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}\right)\right]\\=-\left(1+{\lambda }_{1}\frac{\partial }{\partial t}\right)\frac{\partial p}{\partial x}+\frac{1}{R}\left(1+{\lambda }_{2}\frac{\partial }{\partial t}\right)\left[{\nabla }^{2}u+\frac{1}{3}\frac{\partial }{\partial x}\left(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\right)\right]\\-M\left(1+{\lambda }_{1}\frac{\partial }{\partial t}\right)u-\frac{1}{K}\left(1+{\lambda }_{2}\frac{\partial }{\partial t}\right)u,\end{aligned}$$
(17)
$$\begin{aligned}\left(1+{\lambda }_{1}\frac{\partial }{\partial t}\right)\left[\rho \left(\frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}\right)\right]\\=-\left(1+{\lambda }_{1}\frac{\partial }{\partial t}\right)\frac{\partial p}{\partial y}+\frac{1}{R}\left(1+{\lambda }_{2}\frac{\partial }{\partial t}\right)\left[{\nabla }^{2}v+\frac{1}{3}\frac{\partial }{\partial y}\left(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\right)\right]\\-\frac{1}{K}\left(1+{\lambda }_{2}\frac{\partial }{\partial t}\right)v,\end{aligned}$$
(18)
$$\eta \left(x,t\right)=\varepsilon \mathrm{cos}(\alpha (x-t)),$$
(19)
$$ u = 0, \ldots {\text{at}}\,y = \pm 1 \pm \eta $$
(20)
$$ v = \pm \frac{\partial \eta }{{\partial t}}, \ldots {\text{at}}\,y = \eta $$
(21)
$$\begin{aligned} & \left(1+{\lambda }_{1}\frac{\partial }{\partial t}\right)\frac{\partial }{\partial x}[-\frac{T}{{R}^{2}}\frac{{\partial }^{2}}{\partial {x}^{2}}+m\frac{{\partial }^{2}}{\partial {t}^{2}}+\frac{d}{R}\frac{\partial }{\partial t}+\frac{B}{{R}^{2}}\frac{{\partial }^{4}}{\partial {x}^{4}}+\frac{{K}^{*}}{{R}^{2}}]\eta \\ & \quad =-\left(1+{\lambda }_{1}\frac{\partial }{\partial t}\right)\left[\rho \left(\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}\right)\right]\\ & +\frac{1}{R}\left(1+{\lambda }_{2}\frac{\partial }{\partial t}\right)\left[{\nabla }^{2}u+\frac{1}{3}\frac{\partial }{\partial x}\left(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\right)\right]\\ & -M\left(1+{\lambda }_{1}\frac{\partial }{\partial t}\right)u-\frac{1}{K}\left(1+{\lambda }_{2}\frac{\partial }{\partial t}\right)u,\\ & \quad \ldots \,at\, y=\pm 1\pm \eta,\end{aligned}$$
(22)

For solving system of equation, we assume steady case in which u = \({u}_{0}\left(y\right)\), v = 0, and taking pressure gradient constant, i.e.,\(\frac{\partial p}{\partial x}=\frac{dp}{dx}=\mathrm{constant}\).

For this boundary value problem, exact solution is given as:

$${u}_{0}\left(y\right)=\frac{R}{{\delta }^{2}}\frac{dp}{dx}\left(\frac{\mathrm{cosh}\delta y-\mathrm{cosh}\delta }{\mathrm{cosh}\delta }\right),$$
(23)

where \({\delta }^{2}=MR+\frac{R}{K}\),

3 Perturbation Solution

To find the solution of the above nonlinear equations, we use the regular perturbation method for that we define the perturbed unknown quantities for small values of \(\varepsilon \) in the following form:

$$\begin{aligned}p={p}_{0}+\varepsilon {p}_{1}\left(x,y,t\right)+{\varepsilon }^{2}{p}_{2}\left(x,y,t\right)+\dots ,\\u=\varepsilon {u}_{1}\left(x,y,t\right)+{\varepsilon }^{2}{u}_{2}\left(x,y,t\right)+\dots ,\\v=\varepsilon {v}_{1}\left(x,y,t\right)+{\varepsilon }^{2}{v}_{2}\left(x,y,t\right)+\dots ,\\\rho =1+\varepsilon {\rho }_{1}\left(x,y,t\right)+{\varepsilon }^{2}{\rho }_{2}\left(x,y,t\right)+\dots\end{aligned}$$
(24)

Equating the like powers of \(\upvarepsilon \), we obtain (24):

For \({\varvec{\varepsilon}}\):

$${\rho }_{1}=\chi {p}_{1},$$
(25a)
$$\frac{\partial {\rho }_{1}}{\partial t}+\frac{\partial {u}_{1}}{\partial x}+\frac{\partial {v}_{1}}{\partial y}=0,$$
(25b)
$$\begin{aligned}&\left(1+{\lambda }_{1}\frac{\partial }{\partial t}\right)\frac{\partial {u}_{1}}{\partial t}\\&\quad =-\left(1+{\lambda }_{1}\frac{\partial }{\partial t}\right)\frac{\partial {p}_{1}}{\partial x}\\&\qquad +\frac{1}{R}\left(1+{\lambda }_{2}\frac{\partial }{\partial t}\right)\left[\frac{{\partial }^{2}{u}_{1}}{\partial {x}^{2}}+\frac{{\partial }^{2}{u}_{1}}{\partial {y}^{2}}+\frac{1}{3}\frac{\partial }{\partial x}\left(\frac{\partial {u}_{1}}{\partial x}+\frac{\partial {v}_{1}}{\partial y}\right)\right]\\&\qquad -M\left(1+{\lambda }_{1}\frac{\partial }{\partial t}\right){u}_{1}-\frac{1}{K}\left(1+{\lambda }_{2}\frac{\partial }{\partial t}\right){u}_{1},\end{aligned}$$
(25c)
$$\begin{aligned}&\left(1+{\lambda }_{1}\frac{\partial }{\partial t}\right)\frac{\partial {v}_{1}}{\partial t}\\&\quad =-\left(1+{\lambda }_{1}\frac{\partial }{\partial t}\right)\frac{\partial {p}_{1}}{\partial y}\\&\qquad +\frac{1}{R}\left(1+{\lambda }_{2}\frac{\partial }{\partial t}\right)\left[\frac{{\partial }^{2}{v}_{1}}{\partial {x}^{2}}+\frac{{\partial }^{2}{v}_{1}}{\partial {y}^{2}}+\frac{1}{3}\frac{\partial }{\partial y}\left(\frac{\partial {u}_{1}}{\partial x}+\frac{\partial {v}_{1}}{\partial y}\right)\right]\\&\qquad -\frac{1}{K}\left(1+{\lambda }_{2}\frac{\partial }{\partial t}\right){v}_{1},\end{aligned}$$
(25d)

For \({{\varvec{\varepsilon}}}^{2}:\)

$${\rho }_{2}=\chi {p}_{2}+\frac{1}{2}{\chi }^{2}{p}_{1}^{2},$$
(26a)
$$\frac{\partial {\rho }_{2}}{\partial t}+{u}_{1}\frac{\partial {\rho }_{1}}{\partial x}+{v}_{1}\frac{\partial {\rho }_{1}}{\partial y}+\frac{\partial {u}_{2}}{\partial x}+\frac{\partial {v}_{2}}{\partial y}+{\rho }_{1}\left(\frac{\partial {u}_{1}}{\partial x}+\frac{\partial {v}_{1}}{\partial y}\right)=0,$$
(26b)
$$\begin{aligned}&\left(1+{\lambda }_{1}\frac{\partial }{\partial t}\right)(\frac{\partial {u}_{2}}{\partial t}+{u}_{1}\frac{\partial {u}_{1}}{\partial x}+{v}_{1}\frac{\partial {u}_{1}}{\partial y}+{\rho }_{1}\frac{\partial {u}_{1}}{\partial t})\\ &=-\left(1+{\lambda }_{1}\frac{\partial }{\partial t}\right)\frac{\partial {p}_{2}}{\partial x}\\ &\quad+\frac{1}{R}\left(1+{\lambda }_{2}\frac{\partial }{\partial t}\right)\left[\frac{{\partial }^{2}{u}_{2}}{\partial {x}^{2}}+\frac{{\partial }^{2}{u}_{2}}{\partial {y}^{2}}+\frac{1}{3}\frac{\partial }{\partial x}\left(\frac{\partial {u}_{2}}{\partial x}+\frac{\partial {v}_{2}}{\partial y}\right)\right]\\ &\quad-M\left(1+{\lambda }_{1}\frac{\partial }{\partial t}\right){u}_{2}-\frac{1}{K}\left(1+{\lambda }_{2}\frac{\partial }{\partial t}\right){u}_{2},\end{aligned}$$
(26c)
$$\begin{aligned}&\left(1+{\lambda }_{1}\frac{\partial }{\partial t}\right)(\frac{\partial {v}_{2}}{\partial t}+{u}_{1}\frac{\partial {v}_{1}}{\partial x}+{v}_{1}\frac{\partial {v}_{1}}{\partial y}+{\rho }_{1}\frac{\partial {v}_{1}}{\partial t})\\ &\quad=-\left(1+{\lambda }_{1}\frac{\partial }{\partial t}\right)\frac{\partial {p}_{2}}{\partial y}\\ &\quad+\frac{1}{R}\left(1+{\lambda }_{2}\frac{\partial }{\partial t}\right)\left[\frac{{\partial }^{2}{v}_{2}}{\partial {x}^{2}}+\frac{{\partial }^{2}{v}_{2}}{\partial {y}^{2}}+\frac{1}{3}\frac{\partial }{\partial y}\left(\frac{\partial {u}_{2}}{\partial x}+\frac{\partial {v}_{2}}{\partial y}\right)\right]\\ &\quad-\frac{1}{K}\left(1+{\lambda }_{2}\frac{\partial }{\partial t}\right){v}_{2},\end{aligned}$$
(26d)

Equations (20)–(22) represent the boundary condition by using Taylor expansion method about \(y=\pm 1\) and also use these expansions into boundary conditions, and by using Eq. (24), we write sines and cosines in exponential powers:

For \({\varvec{\varepsilon}}:\)

$${u}_{1}\left(x,\pm 1,t\right)=0,$$
(27)
$${v}_{1}\left(x,\pm 1,t\right)=\mp \frac{\iota \alpha }{2}\left({e}^{\iota \alpha \left(x-t\right)}-{e}^{\iota \alpha \left(x-t\right)}\right),$$
(28)
$$\begin{aligned} & -\left(1-\iota \alpha {\lambda}_{1}\right) \frac{\iota \alpha }{2{R}^{2}}\Big[-T{\alpha}^{2}\left({e}^{\iota \alpha \left(x-t\right)}-{e}^{\iota \alpha\left(x-t\right)}\right)\\ & +m{\alpha }^{2}{R}^{2}\left({e}^{\iota\alpha \left(x-t\right)}-{e}^{\iota \alpha\left(x-t\right)}\right) \\ & \quad - B{\alpha }^{4}\left({e}^{\iota \alpha \left(x-t\right)}-{e}^{\iota \alpha \left(x-t\right)}\right)-{K}^{*}\left({e}^{\iota \alpha \left(x-t\right)}-{e}^{\iota \alpha \left(x-t\right)}\right)\Big]\\&\quad +\left(1-\iota \alpha {\lambda }_{1}\right)\frac{D{\alpha }^{2}}{2R}\left({e}^{\iota \alpha \left(x-t\right)}+{e}^{\iota \alpha \left(x-t\right)}\right)\\&=\left(1+{\lambda }_{1}\frac{\partial }{\partial t}\right)\frac{\partial {u}_{1}}{\partial t}+\frac{1}{R}\left(1+{\lambda }_{2}\frac{\partial }{\partial t}\right)\\ & \quad \times\left[\frac{{\partial }^{2}{u}_{1}}{\partial {x}^{2}}+\frac{{\partial }^{2}{u}_{1}}{\partial {y}^{2}}+\frac{1}{3}\frac{\partial }{\partial x}\left(\frac{\partial {u}_{1}}{\partial x}+\frac{\partial {v}_{1}}{\partial y}\right)\right]\\&\quad -M\left(1+{\lambda }_{1}\frac{\partial }{\partial t}\right){u}_{1}-\frac{1}{K}\left(1+{\lambda }_{2}\frac{\partial }{\partial t}\right){u}_{1},\end{aligned}$$

After simplification, the above equation becomes

$$\begin{aligned}&\left(1-\iota \alpha {\lambda }_{1}\right)&\frac{\iota }{2}{\delta }_{1}\left({e}^{\iota \alpha \left(x-t\right)}-{e}^{-\iota \alpha \left(x-t\right)}\right)+\left(1-\iota \alpha {\lambda }_{1}\right)\frac{1}{2}{\delta }_{2}\left({e}^{\iota \alpha \left(x-t\right)}+{e}^{-\iota \alpha \left(x-t\right)}\right)\\ &=- \left(1+{\lambda }_{1}\frac{\partial }{\partial t}\right)\frac{\partial {u}_{1}\left(x,\pm 1,t\right)}{\partial t}\\ &+\frac{1}{R}\left(1+{\lambda }_{2}\frac{\partial }{\partial t}\right)\left[\frac{{\partial }^{2}{u}_{1}\left(x,\pm 1,t\right)}{\partial {x}^{2}}+\frac{{\partial }^{2}{u}_{1}\left(x,\pm 1,t\right)}{\partial {y}^{2}}\right.\\ &\quad\left.+\frac{1}{3}\frac{\partial }{\partial x}\left(\frac{\partial {u}_{1}\left(x,\pm 1,t\right)}{\partial x}+\frac{\partial {v}_{1}\left(x,\pm 1,t\right)}{\partial y}\right)\right]\\ &-M\left(1+{\lambda }_{1}\frac{\partial }{\partial t}\right){u}_{1}\left(x,\pm 1,t\right)-\frac{1}{K}\left(1+{\lambda }_{2}\frac{\partial }{\partial t}\right){u}_{1}\left(x,\pm 1,t\right).\end{aligned}$$
(29)

where

$${\delta }_{1}=\frac{\alpha }{{R}^{2}}\left(-{\alpha }^{2}T+{\alpha }^{2}{R}^{2}m-{\alpha }^{4}B-{K}^{*}\right),$$
$${\delta }_{2}=\frac{{\alpha }^{2}}{{R}^{2}}\left(dR\right).$$

For \({{\varvec{\varepsilon}}}^{2}:\)

$${u}_{2}\left(x,\pm 1,t\right)\pm \frac{1}{2}\left({e}^{\iota \alpha \left(x-t\right)}+{e}^{-\iota \alpha \left(x-t\right)}\right){u}_{1y}\left(x,\pm 1,t\right)=0,$$
(30)
$${v}_{2}\left(x,\pm 1,t\right)\pm \frac{1}{2}\left({e}^{\iota \alpha \left(x-t\right)}+{e}^{-\iota \alpha \left(x-t\right)}\right){v}_{1y}\left(x,\pm 1,t\right)=0$$
(31)

Third boundary condition is not needed for this order.

The solutions of the above systems can be obtained with the help of the following supposed form of solutions for all the systems:

$$\begin{aligned}&{u}_{1}\left(x,y,t\right)={U}_{1}\left(y\right){e}^{\iota \alpha \left(x-t\right)}+\stackrel{-}{{U}_{1}}\left(y\right){e}^{-\iota \alpha \left(x-t\right)},\\&{v}_{1}\left(x,y,t\right)={V}_{1}\left(y\right){e}^{\iota \alpha \left(x-t\right)}+\stackrel{-}{{V}_{1}}\left(y\right){e}^{-\iota \alpha \left(x-t\right)},\\&{p}_{1}\left(x,y,t\right)={P}_{1}\left(y\right){e}^{\iota \alpha \left(x-t\right)}+\stackrel{-}{{P}_{1}}\left(y\right){e}^{-\iota \alpha \left(x-t\right)},\\&{\rho }_{1}\left(x,y,t\right)=\chi {P}_{1}\left(y\right){e}^{\iota \alpha \left(x-t\right)}+\chi \stackrel{-}{{P}_{1}}\left(y\right){e}^{-\iota \alpha \left(x-t\right)},\end{aligned}$$
(32)
$$\begin{aligned}&{u}_{2}\left(x,y,t\right)={U}_{20}\left(y\right)+{U}_{2}\left(y\right){e}^{2\iota \alpha \left(x-t\right)}+\stackrel{-}{{U}_{2}}\left(y\right){e}^{-2\iota \alpha \left(x-t\right)},\\&{v}_{2}\left(x,y,t\right)={V}_{20}\left(y\right)+{V}_{2}\left(y\right){e}^{2\iota \alpha \left(x-t\right)}+\stackrel{-}{{V}_{2}}\left(y\right){e}^{-2\iota \alpha \left(x-t\right)}\\&{p}_{2}\left(x,y,t\right)={P}_{20}\left(y\right)+{P}_{2}\left(y\right){e}^{2\iota \alpha \left(x-t\right)}+\stackrel{-}{{P}_{2}}\left(y\right){e}^{-2\iota \alpha \left(x-t\right)},\\&{\rho }_{2}\left(x,y,t\right)={D}_{20}\left(y\right)+{D}_{2}\left(y\right){e}^{2\iota \alpha \left(x-t\right)}+\stackrel{-}{{D}_{2}}\left(y\right){e}^{-2\iota \alpha \left(x-t\right)},\end{aligned}$$
(33)

Here, overbar denotes the complex conjugate.

With the help of these solutions, the above boundary value problems take the form:

$${V}_{1}^{\mathrm{^{\prime}}}+\iota \alpha {U}_{1}=\iota \alpha \chi {P}_{1},$$
$$-\iota \alpha {\gamma }^{*}{U}_{1}=-\iota \alpha {\gamma }^{*}{P}_{1}+\frac{1}{R}\left[{U}_{1}^{"}-\left({\alpha }^{2}+\frac{R}{K}+MR{\gamma }^{*}\right){U}_{1}\right]+\frac{\iota \alpha }{3R}\left({V}_{1}^{^{\prime}}+\iota \alpha {U}_{1}\right),$$
$$-\iota \alpha {\gamma }^{*}{V}_{1}=-{\gamma }^{*}{{P}_{1}}^{^{\prime}}+\frac{1}{R}\left[{V}_{1}^{"}-\left({\alpha }^{2}+\frac{R}{K}\right){V}_{1}\right]+\frac{1}{3R}\frac{d}{dy}\left({V}_{1}^{^{\prime}}+\iota \alpha {U}_{1}\right),$$
$${U}_{1}\left(\pm 1\right)=0,$$
$${V}_{1}\left(\pm 1\right)=\mp \frac{\iota \alpha }{2},$$
$${U}_{1}^{{^{\prime}}{^{\prime}}}\left(\pm 1\right)=\left({\alpha }^{2}+\frac{R}{K}+MR{\gamma }^{*}-\iota \alpha {\gamma }^{*}R-\frac{{\alpha }^{2}}{3}\right){U}_{1}\left(\pm 1\right)-\frac{\iota \alpha }{3}{V}_{1}^{^{\prime}}\left(\pm 1\right)+{\gamma }^{*}R\omega .$$
(34)
$${D}_{20}=\chi {P}_{20}+{\chi }^{2}{P}_{1}\stackrel{-}{{P}_{1}},$$
$${V}_{20}^{^{\prime}}=-\chi \left({V}_{1}{\stackrel{-}{{P}_{1}}}^{^{\prime}}+\stackrel{-}{{V}_{1}}{P}_{1}^{^{\prime}}+{{V}_{1}}^{^{\prime}}\stackrel{-}{{P}_{1}}+{\stackrel{-}{{V}_{1}}}^{^{\prime}}{P}_{1}\right),$$
$$\frac{1}{R}{U}_{20}^{"}-\left(\frac{1}{K}+M\right){U}_{20}=\iota \alpha \chi {P}_{1}\stackrel{-}{{U}_{1}}-\iota \alpha \chi \stackrel{-}{{P}_{1}}{U}_{1}+\stackrel{-}{{V}_{1}}{U}_{1}^{^{\prime}}+{V}_{1}{\stackrel{-}{{U}_{1}}}^{^{\prime}},$$
$${U}_{20}\left(\pm 1\right)\pm \frac{1}{2}\left(\stackrel{-}{{U}_{1}^{^{\prime}}}\left(\pm 1\right)+{U}_{1}^{^{\prime}}\left(\pm 1\right)\right)=0,$$
$${V}_{20}\left(\pm 1\right)\pm \frac{1}{2}\left[{\stackrel{-}{{V}_{1}}}^{^{\prime}}\left(\pm 1\right)+{V}_{1}^{^{\prime}}\left(\pm 1\right)\right]=0.$$
(35)

Here, complex parameters are

$${\gamma }_{1}=1-\iota \alpha {\lambda }_{1, }{\gamma }_{2}=1-\iota \alpha {\lambda }_{2},$$
$${\gamma }^{*}=\frac{{\gamma }_{1}}{{\gamma }_{2}}.$$

Aarts and Ooms [14] presented the procedure for the solution of equations, and Mekheimer [24] also followed the respective techniques.

Thus, by omitting the lengthy calculations solution of first-order equations for velocity and pressure, one has

$${V}_{1}\left(y\right)={C}_{1}\mathrm{sinh}{a}_{1}y+{C}_{2}\mathrm{sinh}{a}_{2}y,$$
$${U}_{1}\left(y\right)={b}_{1}{C}_{1}\mathrm{cosh}{a}_{1}y+{b}_{2}{C}_{2}\mathrm{cosh}{a}_{2}y+{C}_{3}\chi ,$$
(36)

And solution of second-order Eq. (35) is:

$${V}_{20}=-\chi \left({V}_{1}\stackrel{-}{{P}_{1}}+{P}_{1}\stackrel{-}{{V}_{1}}\right)+{D}_{1},$$
$${U}_{20}\left(y\right)={D}_{2}\mathrm{cosh}\delta y+{D}_{3}\mathrm{sinh}\delta y+E\left(y\right),$$
$${P}_{20}\left(y\right)={D}_{4}-\frac{4\chi }{3R}H\left(y\right)-\frac{1}{K}{\int }_{-1}^{y}{V}_{20}\left(r\right)dr-{\int }_{-1}^{y}F(r)dr$$
(37)

Net axial velocity is defined as:

$$<g> =\frac{1}{T}{\int }_{0}^{T}g\left(x,y,t\right)dt,$$
(38)
$$T=\frac{2\pi }{\alpha },$$

Mean axial velocity is:

$$< u > = \varepsilon^{2} U_{20} \left( y \right).$$
(39)

4 Appendix

Variable and parameters for the first-order solution are:

$$\gamma ={\gamma }^{*}R-\frac{\iota \alpha \chi }{3}, {\beta }^{2}={\alpha }^{2}-\iota \alpha {\gamma }^{*}R+\frac{R}{K}+MR{\gamma }^{*},$$
$${\beta }_{1}^{2}={\alpha }^{2}-\iota \alpha {\gamma }^{*}R+\frac{R}{K},$$
$${a}_{1}^{2}=\frac{\left({\beta }^{2}+{\nu }^{2}\right)+\sqrt{{\left({\beta }^{2}+{\nu }^{2}\right)}^{2}-4{\beta }_{1}^{2}{\nu }_{1}^{2}}}{2},$$
$${a}_{2}^{2}=\frac{\left({\beta }^{2}+{\nu }^{2}\right)-\sqrt{{\left({\beta }^{2}+{\nu }^{2}\right)}^{2}-4{\beta }_{1}^{2}{\nu }_{1}^{2}}}{2},$$
$${b}_{1}=\chi \frac{({a}_{1}^{2}-{\beta }_{1}^{2})}{\gamma {a}_{1}}+\frac{\iota {a}_{1}}{\alpha }, {b}_{2}=\chi \frac{({a}_{2}^{2}-{\beta }_{1}^{2})}{\gamma {a}_{2}}+\frac{\iota {a}_{2}}{\alpha },$$
$${C}_{1}={\gamma }^{*}R\omega \frac{\mathrm{sinh}{a}_{2}}{G}+\frac{\iota \alpha }{2}{a}_{2}({b}_{2}{a}_{2}+\frac{\iota \alpha }{3})\frac{\mathrm{cosh}{a}_{2}}{G},$$
$${C}_{2}=-{\gamma }^{*}R\omega \frac{\mathrm{sinh}{a}_{1}}{G}-\frac{\iota \alpha }{2}\frac{1}{\mathrm{sinh}{a}_{2}}[1+({a}_{2}^{2}{b}_{2}+\frac{\iota \alpha }{2}{a}_{2})\frac{\mathrm{cosh}{a}_{2}\mathrm{sinh}{a}_{1}}{G}],$$
$${C}_{3}=0,$$

\(\omega =-\frac{\iota \alpha }{2{R}^{2}}(-{\alpha }^{2}T+{\alpha }^{2}{R}^{2}m\)+\(\iota \alpha Rd-{\alpha }^{4}B-{K}^{*}),\)

$${\nu }^{2}=\frac{-\frac{4\iota }{3}{\alpha }^{3}\chi +{\alpha }^{2}{\gamma }^{*}R\left(1-\chi \right)-\frac{\iota \alpha \chi R}{K}}{{R\gamma }^{*}-\frac{4\iota \alpha \chi }{3}},$$
$${\nu }^{2}=\frac{-\frac{4\iota }{3}{\alpha }^{3}\chi +{\alpha }^{2}{\gamma }^{*}R\left(1-\chi \right)-\iota \alpha \chi R(M{\gamma }^{*}+\frac{1}{K})}{{R\gamma }^{*}-\frac{4\iota \alpha \chi }{3}},$$
$${g}_{1}={a}_{1}\mathit{cos}h{a}_{1} {g}_{2}={a}_{2}\mathit{cos}h{a}_{2}$$
$${{g}_{3}=a}_{1}\mathrm{sinh}{a}_{2}\mathrm{cosh}{a}_{1}-{a}_{2}\mathrm{cosh}{a}_{2}\mathrm{sinh}{a}_{1},$$
$$W={\alpha }^{2}+\frac{R}{K}+MR{\gamma }^{*}-\iota \alpha {\gamma }^{*}R-\frac{{\alpha }^{2}}{3},$$
$$G={b}_{1}{a}_{1}{g}_{1}\mathit{sin}h{a}_{2}-{b}_{2}{a}_{2}{g}_{2}\mathit{sin}h{a}_{1}+\frac{\iota \alpha }{3}{g}_{3},$$

By using boundary conditions, the complex constants for the second-order solutions are:

$${D}_{1}=0,$$
$${D}_{4}={P}_{20}\left(-1\right)+\frac{4\chi }{3R}H\left(-1\right),$$
$${D}_{2}=\frac{-1}{2(\mathrm{cosh}\delta )}\left[{\beta }_{2}+{\beta }_{3}+E\left(1\right)+E\left(-1\right)\right],$$
$${D}_{3}=\frac{-1}{2(\mathrm{sinh}\delta )}\left[{\beta }_{2}-{\beta }_{3}+E\left(1\right)-E\left(-1\right)\right],$$
$$F=\iota \alpha \chi {P}_{1}\stackrel{-}{{V}_{1} }-\iota \alpha \chi \stackrel{-}{{P}_{1}}{V}_{1}+{V}_{1}\stackrel{-}{{{V}_{1}}^{\mathrm{^{\prime}}}}+{V}_{1}^{\mathrm{^{\prime}}}\stackrel{-}{{V}_{1} }-\iota \alpha {U}_{1}{\stackrel{-}{V}}_{1}+\iota \alpha \stackrel{-}{{U}_{1}}{V}_{1},$$
$$H=\frac{d}{dy}\left({P}_{1}\stackrel{-}{{V}_{1}}+\stackrel{-}{{P}_{1}}{V}_{1}\right),$$
$${\beta }_{2}=\frac{1}{2}\left({U}_{1}^{^{\prime}}\left(1\right)+\stackrel{-}{{U}_{1}^{^{\prime}}}\left(1\right)\right), {\beta }_{3}=-\frac{1}{2}\left({U}_{1}^{^{\prime}}\left(-1\right)+\stackrel{-}{{U}_{1}^{^{\prime}}}\left(-1\right)\right),$$
$$ \begin{aligned} E\left(y\right) & =R\left\{\frac{{j}_{1}}{{\left({a}_{1}+\stackrel{-}{{a}_{1}}\right)}^{2}-{\delta }^{2}}\mathrm{cosh}\left({a}_{1}+\stackrel{-}{{a}_{1}}\right)y+\frac{{j}_{11}}{{\left({a}_{1} -\stackrel{-}{{a}_{1}}\right)}^{2}-{\delta }^{2}}\right. \\ & \quad \left. \mathrm{cosh}\left({a}_{1}-\stackrel{-}{{a}_{1}}\right)y+\frac{{j}_{2}}{{\left({a}_{1}+\stackrel{-}{{a}_{2}}\right)}^{2}-{\delta }^{2}}\right. \\ & \quad \left. \mathrm{cosh}\left({a}_{1}+\stackrel{-}{{a}_{2}}\right)y+\frac{{j}_{22}}{{\left({a}_{1}-\stackrel{-}{{a}_{2}}\right)}^{2}-{\delta }^{2}} \right. \\ & \quad \left. \mathrm{cosh}\left({a}_{1}-\stackrel{-}{{a}_{2}}\right)y+\frac{{j}_{3}}{{\left({a}_{2}+\stackrel{-}{{a}_{1}}\right)}^{2}-{\delta }^{2}}\mathrm{cosh}\left({a}_{2}+\stackrel{-}{{a}_{1}}\right)y\right. \\ & \quad \left. +\frac{{j}_{33}}{{\left({a}_{2}-\stackrel{-}{{a}_{1}}\right)}^{2}-{\delta }^{2}} \mathrm{cosh}\left({a}_{2}-\stackrel{-}{{a}_{1}}\right)y+\frac{{j}_{4}}{{\left({a}_{2}+\stackrel{-}{{a}_{2}}\right)}^{2}-{\delta }^{2}}\right. \\ & \quad \left.\mathrm{cosh}\left({a}_{2}+\stackrel{-}{{a}_{2}}\right)y+\frac{{j}_{44}}{{\left({a}_{2}-\stackrel{-}{{a}_{2}}\right)}^{2}-{\delta }^{2}}\mathrm{cosh}\left({a}_{2}-\stackrel{-}{{a}_{2}}\right)y\right\},\end{aligned} $$
$${j}_{1}=\frac{1}{2}\left({a}_{1}{C}_{1}\stackrel{-}{{b}_{1}}\stackrel{-}{{C}_{1}}+\stackrel{-}{{a}_{1}}\stackrel{-}{{C}_{1}}{b}_{1}{C}_{1}+\stackrel{-}{{a}_{1}}\stackrel{-}{{b}_{1}}\stackrel{-}{{C}_{1}}{C}_{1}+{a}_{1}{b}_{1}{C}_{1}\stackrel{-}{{C}_{1}}\right),$$
$${j}_{2}=\frac{1}{2}\left({a}_{1}{C}_{1}\stackrel{-}{{b}_{2}}\stackrel{-}{{C}_{2}}+\stackrel{-}{{a}_{2}}\stackrel{-}{{C}_{2}}{b}_{1}{C}_{1}+\stackrel{-}{{a}_{2}}\stackrel{-}{{b}_{2}}\stackrel{-}{{C}_{2}}{C}_{1}+{a}_{1}{b}_{1}{C}_{1}\stackrel{-}{{C}_{2}}\right)$$
$${j}_{3}=\frac{1}{2}\left({a}_{2}{C}_{2}\stackrel{-}{{b}_{1}}\stackrel{-}{{C}_{1}}+\stackrel{-}{{a}_{1}}\stackrel{-}{{C}_{1}}{b}_{2}{C}_{2}+\stackrel{-}{{a}_{1}}\stackrel{-}{{b}_{1}}\stackrel{-}{{C}_{1}}{C}_{2}+{a}_{2}{b}_{2}{C}_{2}\stackrel{-}{{C}_{1}}\right),$$
$${j}_{4}=\frac{1}{2}\left({a}_{2}{C}_{2}\stackrel{-}{{b}_{2}}\stackrel{-}{{C}_{2}}+\stackrel{-}{{a}_{2}}\stackrel{-}{{C}_{2}}{b}_{2}{C}_{2}+\stackrel{-}{{a}_{2}}\stackrel{-}{{b}_{2}}\stackrel{-}{{C}_{2}}{C}_{2}+{a}_{2}{b}_{2}{C}_{2}\stackrel{-}{{C}_{2}}\right),$$
$${j}_{11}=\frac{1}{2}\left({a}_{1}{C}_{1}\stackrel{-}{{b}_{1}}\stackrel{-}{{C}_{1}}+\stackrel{-}{{a}_{1}}\stackrel{-}{{C}_{1}}{b}_{1}{C}_{1}-\stackrel{-}{{a}_{1}}\stackrel{-}{{b}_{1}}\stackrel{-}{{C}_{1}}{C}_{1}-{a}_{1}{b}_{1}{C}_{1}\stackrel{-}{{C}_{1}}\right),$$
$${j}_{22}=\frac{1}{2}\left({a}_{1}{C}_{1}\stackrel{-}{{b}_{2}}\stackrel{-}{{C}_{2}}+\stackrel{-}{{a}_{2}}\stackrel{-}{{C}_{2}}{b}_{1}{C}_{1}-\stackrel{-}{{a}_{2}}\stackrel{-}{{b}_{2}}\stackrel{-}{{C}_{2}}{C}_{1}-{a}_{1}{b}_{1}{C}_{1}\stackrel{-}{{C}_{2}}\right),$$
$${j}_{33}=\frac{1}{2}\left({a}_{2}{C}_{2}\stackrel{-}{{b}_{1}}\stackrel{-}{{C}_{1}}+\stackrel{-}{{a}_{1}}\stackrel{-}{{C}_{1}}{b}_{2}{C}_{2}-\stackrel{-}{{a}_{1}}\stackrel{-}{{b}_{1}}\stackrel{-}{{C}_{1}}{C}_{2}-{a}_{2}{b}_{2}{C}_{2}\stackrel{-}{{C}_{1}}\right),$$
$${j}_{44}=\frac{1}{2}\left({a}_{2}{C}_{2}\stackrel{-}{{b}_{2}}\stackrel{-}{{C}_{2}}+\stackrel{-}{{a}_{2}}\stackrel{-}{{C}_{2}}{b}_{2}{C}_{2}-\stackrel{-}{{a}_{2}}\stackrel{-}{{b}_{2}}\stackrel{-}{{C}_{2}}{C}_{2}-{a}_{2}{b}_{2}{C}_{2}\stackrel{-}{{C}_{2}}\right).$$

5 Graphical Results and Discussion

This section shows the graphical results in order to discuss the impact of different parameters on the mean velocity at the boundaries \({D}_{wall}\), the perturbation function, and the mean velocity and reversal flow at the boundaries. Perturbation method is used with amplitude ratio (\({\varvec{\varepsilon}}\)) treated as a parameter, so set the small parameter (\({\varvec{\varepsilon}}<1\)). The graphs also show the state at which backward flow occurs. Various parameters are used to show their graphical effects on velocity distribution and at wall boundaries, in which longitudinal tension, wall damping, compressibility parameter, relaxation and retardation time are included.

Fung and Yih [25] define the perturbation function of mean velocity G(y) as

$$G\left(y\right)=\frac{-200}{{\alpha }^{2}{R}^{2}}\left[E\left(y\right)-E\left(1\right)\right].$$
(40)

Figure 2a–i shows different results in conduct of G(y) for different values of M, K, relaxation time \({\lambda }_{1},\) retardation time \({\lambda }_{2},\) compressibility parameter \(\chi \) and compliant wall parameter d and T. For MHD perturbation function, different values of M are discussed. Figure 2a shows that graph of G(y) reduces when magnetic field increases. Figure 2b shows the decreasing effect of K on perturbation function G(y), i.e., by increasing K the velocity perturbation G(y) decreases. Figure 2c, d shows results on velocity perturbation for relaxation time \({\lambda }_{1}\) in the absence and presence of M. Figure 2c depicts that perturbation function decreases by increasing \({\lambda }_{1}\) in the absence of M (i.e., M = 0). Also in Fig. 2d, perturbation function G(y) shows same decreasing result for relaxation time \({\lambda }_{1}\) when M = 2. Figure 2e, f exhibits the influence of \({\lambda }_{2}\) and M on velocity perturbation function. Figure 2e shows that in the absence of M, retardation time \({\lambda }_{2}\) shows decreasing result on G(y), whereas for M = 2, the graph of perturbation function in Fig. 2f gives the increasing result for increasing value of \({\lambda }_{2}.\) In Fig. 2g, the compressibility parameter \(\chi \) shows decreasing effect on perturbed velocity G(y) in the presence of magnetic field (M = 0.4). Figure 2h, i represents the result for compliant wall parameter d and T. In Fig. 2h, wall damping coefficient d has increasing result on G(y) and also T shows same response, i.e., by increasing T graph of perturbation function G(y) increases (Fig. 2i).

Fig. 2
figure 2figure 2

a The velocity perturbation function G(y) for: \(\alpha =0.5, \chi =0.1, {\lambda }_{1}=0.7, {\lambda }_{2}=0.4, R=10, T=10, K=0.5, B=50, d=0.1, m=0.5, {K}^{*}=3.3.\) b The velocity perturbation function G(y) for: \(\alpha =0.5, \chi =0.1, {\lambda }_{1}=0.7, {\lambda }_{2}=0.4, R=10, T=10, M=1.5, B=50, d=0.1, m=0.5, {K}^{*}=1.3.\) c The velocity perturbation function G(y) for: \(\alpha =0.5, {K}_{n}=0.1,\chi =0.01, {\lambda }_{2}=0.6, R=100, M=0, K=1, T=30, B=2, m=0.01 {K}^{*}=1,d=0.05.\) d The velocity perturbation function G(y) for: \(\alpha =0.5, \chi =0.01, {\lambda }_{2}=0.6, R=100, M=2, K=0.5, T=30, B=2, m=0.01 {K}^{*}=1,d=0.05.\) e The velocity perturbation function G(y) for: \(\alpha =0.5, {K}_{n}=0.15,\chi =0.4 , {\lambda }_{1}=0.7, R=10, M=0, K=0.5, T=30, B=2, m=0.01 {K}^{*}=1.5,d=0.05.\) f The velocity perturbation function G(y) for: \(\alpha =0.5, \chi =0.01, {\lambda }_{1}=0.8, R=100, M=2.0, K=1, T=30, B=2, m=0.1 {K}^{*}=1,d=0.05.\) g The velocity perturbation function G(y) for: \(\alpha =0.5, { \lambda }_{1}=0.7 , {\lambda }_{2}=0.5, R=10, M=0.4, K=1, T=30, B=2, m=0.1 {K}^{*}=1.3,d=0.5.\) h The velocity perturbation function G(y) for: \(\alpha =0.5, \chi =0.15,{ \lambda }_{1}=1.2 , {\lambda }_{2}=0.7, R=100, M=2.0, K=1, T=30, B=2, m=0.01 {K}^{*}=1.3.\) i The velocity perturbation function G(y) for: \(\alpha =0.5, \chi =0.01,{ \lambda }_{1}=1.2 , {\lambda }_{2}=0.7, R=100, M=2.0, K=1, B=2, m=0.01 {K}^{*}=1.3,d=0.05.\)

Full size image

Figure 3a–g examines the change in mean axial velocity with respect to y for several values of M, \(\chi \), relaxation and retardation time \({\lambda }_{1}\) and \({\lambda }_{2}\), permeability parameter and coefficient of wall damping d and wall tension T. Figure 3a shows that backward flow of velocity is obtained when magnetic number increases for R = 1. Due to magnetic field, there occurs deceleration in action of reversal flow till the effect of M is about to vanish in the center line of the channel. Figure 3b illustrates that by increasing relaxation time \({\lambda }_{1}\) there occurs increase in mean velocity and decrease in reversal flow of velocity, and opposite result is obtained for retardation time \({\lambda }_{2}\) (Fig. 3c). Figure 3d describes the behavior of mean axial flow with compressibility parameter\(\chi \). It is to be noted that by increasing compressibility parameter reversal flow decreases. Figure 3e depicts that by increasing the permeability parameter K velocity distribution also increases, and reason is that more fluid passes through permeability parameter and decrease in reversal flow is observed. Figure 3f, g shows the change in mean axial velocity and reversal flow of velocity for parameters of compliant wall d and T. Figure 3f shows that there is a possibility that by increasing value of d mean flow increases and also reversal flow decreases about center line but increases about boundaries. It is observed in Fig. 3g that T shows a small variation in the reversal flow, i.e., backward flow decreases. This means that by increasing value of T reversal flow becomes fast.

Fig. 3
figure 3figure 3

a The variation mean-axial velocity for: \(\alpha =0.5, ,\chi =0.05,{ \lambda }_{1}=1.2 , {\lambda }_{2}=0.5, R=1, K=1, T=10, B=2, m=0.05, {K}^{*}=3.3,d=0.01.\) b The variation mean-axial velocity for: \(\alpha =0.5, {K}_{n}=0.15, M=0.05,\chi =0.05, {\lambda }_{2}=0.5, R=1, K=1.3, T=20, B=20, m=0.01, {K}^{*}=3.3,d=0.5.\) c The variation mean-axial velocity for: \(\alpha =0.5, \chi =0.3,{ \lambda }_{1}=0.7 , R=10, K=3.3, T=20, B=20, m=0.01, M=0.05, {K}^{*}=3.3,d=0.5.\) d The variation mean-axial velocity for: \(\alpha =0.5, { \lambda }_{1}=1.2 , {\lambda }_{2}=0.5, R=20, K=3.3, T=10000, B=2, m=0.01, d=0.5, {K}^{*}=3.3,M=0.01.\) e The variation mean-axial velocity for: \(\alpha =0.9, \chi =0.5,{ \lambda }_{1}=0.4 , {\lambda }_{2}=0.7, R=5, T=20, B=20, m=0.01, M=0.2, {K}^{*}=3.3,d=0.1.\) f The variation mean-axial velocity for: \(\alpha =0.5, \chi =0.5,{ \lambda }_{1}=0.4 , {\lambda }_{2}=0.7, R=10, K=1, T=200, B=20, m=0.01, {K}^{*}=0.1,M=0.2.\) g The variation mean-axial velocity for:\(\alpha =0.5,\chi =0.2,{ \lambda }_{1}=1.2 , {\lambda }_{2}=0.5, R=20, K=1, B=2, m=0.01, {K}^{*}=3.3,d=0.5 M=2.\)

Full size image

Figure 4a–f shows the change in \({D}_{wall}\)(= \({U}_{20}\left(1\right)\)) with the wave number \(\alpha \) for various values of \(\chi \) the compressibility parameter, coefficient of wall damping d, magnetic field, wall tension T, relaxation time \({\lambda }_{1}\) and retardation time \({\lambda }_{2}\). Figure 4a shows that for increase in magnetic parameter graph shows decreasing effect. Figure 4b shows that velocity flow at the \({D}_{wall}\) boundary increases by increasing compressibility parameter \(\chi \) for any value of wave number \(\alpha \). Figure 4c shows the increasing effect on boundaries of mean velocity by increasing the wall damping d. Figure 4d, e shows the effect on \({D}_{wall}\) with wave number \(\alpha \) for different values of relaxation and retardation time. Figure 4d shows that \({\lambda }_{1}\) has an increasing effect on \({D}_{wall}\). By increasing compliant wall parameter d, \({D}_{wall}\) with wave number \(\alpha \) shows increasing response in Fig. 4c. In Fig. 4e, graph shows the same result as for relaxation time, i.e., effect on \({D}_{wall}\) increases by increasing value of retardation time \({\lambda }_{2}\). Figure 4f shows that variation of mean velocity analogous to \({D}_{wall}\) boundary decreases when the wall tension T increases.

Fig. 4
figure 4

a Change in \({D}_{wall}\) with wave number \(\alpha \) for: \(R=10, K=1,{\lambda }_{1}=0.7, {\lambda }_{2}=0.4, {K}_{n}=0.15, {K}^{*}=3.3, d=0.5, T=30, \chi =0.001, m=0.01, B=2. \) b Change in \({D}_{wall}\) with wave number \(\alpha \) for: \(M=2, R=10,{K}_{n}=0.1, K=1, {\lambda }_{1}=0.7, {\lambda }_{2}=0.4, T=30, {K}^{*}=1.3, B=2, m=0.01, d=0.5.\) c Change in \({D}_{wall}\) with wave number \(\alpha \) for: \(R=15, K=1,{\lambda }_{1}=1.2, {\lambda }_{2}=0.5, {K}_{n}=0.1, {K}^{*}=3.3, M=0, T=30, \chi =0.001, m=0.01, B=2.\) d Change in \({D}_{wall}\) with wave number \(\alpha \) for: \(R=100, K=3.5,M=2, {\lambda }_{2}=1.2, {K}_{n}=0.1, {K}^{*}=1.3, d=0.5, T=30, \chi =0.001, m=0.01, B=200.\) e Change in \({D}_{wall}\) with wave number \(\alpha \) for: \(R=10, M=1.5, K=1.5,{\lambda }_{1}=0.8, {K}_{n}=0.1, {K}^{*}=1.3, d=0.5, T=30, \chi =0.001, m=0.01, B=2.\) f Change in \({D}_{wall}\) with wave number \(\alpha \) for: \(R=15, K=20,{\lambda }_{1}=1.2, {\lambda }_{2}=0.5, {K}_{n}=0.1, {K}^{*}=3.3, d=0.5,, \chi =0.001, m=0.01, B=200.\)

Full size image

6 Conclusion

In study of peristaltic transport of MHD, compressible, Jeffrey fluid over a porous medium with effect of compliant walls is analyzed, and this article shows the results of combined effect of wall parameters, relaxation and retardation time, compressibility and permeability parameter in the absence and presence of magnetic effect. The main points of the problem are:

  • The \({D}_{wall}\) increases when compliant wall coefficient d increases, whereas opposite result is obtained for T.

  • The \({D}_{wall}\) increases for relaxation and retardation time.

  • The magnetic field shows decreasing result for perturbation function G(y), and for mean velocity, backward flow occurs.

  • Effect of permeability on perturbed function is decreasing, while on velocity distribution K has an increasing effect.

  • The compressibility parameter χ gives decreasing effect on perturbation function and increasing effect for mean velocity flow.

  • Compliant wall parameter T has an increasing effect for perturbed function and mean axial flow, while d has decreasing effect for G(y) and shows increasing graph for velocity distribution.