1 Introduction

In both scientific and biophysical flows, the flow within channels and pipes with permeable walls is very important. Examples include sodium cooling, soil mechanics, binary gas diffusion, ablation cooling, combustion of a solid rocket motor, blood circulation, artificial dialysis, cosmetics, food preservation and air modeling in the respiratory system. A significant number of theoretical studies on the continuous, incompressible, and laminar flow along injection/suction on the walls have been performed in recent decades. In a porous two-dimensional tube, the flow of viscous and incompressible fluid was examined by several authors. Asghar et al. [1] applied the symmetry method to solve the viscous fluid flow problem inside the channel with porous plates. Makukula et al. [2] proposed a numerical technique to study incompressible viscous fluid flow streaming through two moving porous plates. Xinhui Si et al. [3] studied the laminar flow of the micropolar fluid within an expanding/contracting channel having porous plates. Using the variation parameter method, Sobamowo [4] discussed laminar flow inside a porous channel. In order to solve the problem of viscous fluid flow inside a porous channel along with a slip boundary condition, Ashwini et al. [5] applied a computer-extended series method and HAM. This examination asserts that the suggested techniques converge to the solution for sufficiently large values of Reynolds number. Bhatti et al. [6] considered unsteady Stokes flow with periodic suction and injection on two parallel porous plates having slippage effects. Graphical findings uncovered that axial and radial velocity profiles were considerably affected by the slip parameter. If an adequate magnetic field is applied, the velocity distribution can be restricted. Such a conclusion was drawn by Farooq et al. [7] during the investigation of MHD fluid flow inside the non-uniform penetrable channel with slip phenomena.

Some biophysical flux applications include expanding–contracting channels, for instance, the respiratory system in blood and airflow, mock dialysis, filtration, and birth flux of the gas. For such applications, several researchers have looked at the Newtonian/non-Newtonian flow across expanding–contracting channels for various types, such as using similarities of space and time and two disruptions named as permeation Reynolds number and ratio of expansion to walls. Raza et al. [8] examined the existence of multiple solutions for nanofluid flow inside the penetrable channel having expanding/contracting walls. This research shows that the triple solution exists just for the suction case. Akinshilo [9] constructed the problem of nanofluid flow passing inside the channel with expanding/contracting penetrable walls and provided meaningful information to control heat transfer and shear stress. Using the Buongiorno model, Ali et al. [10] examined the impact of heat transfer on expanding/contracting walls and observed that for expanding walls the Nusselt number prominently increases with thermophoretic diffusion parameter as compared to the contracting walls.

In food preservation, instrumentation, lubrication, tribology, and viscometry, the investigation of Newtonian/non-Newtonian fluid flow using TD characteristics is of excellent significance. For example, the effect of viscosity as a function of temperature had been discussed by some authors [11, 12] for plane Poiseuille flow. In their analyses, the impact of variable viscosity on the constancy of flows inside the channel with permeable plates was studied when both plates of channels have different temperatures. In another analysis, Pinarbasi and Liakopoulos [13] held the channel walls fixed and restricted their attention to the role of viscosity as a function of temperature in a channel by examining stability. The effect of varying viscosity on the flow was analyzed by [14] inside the channel with porous walls having different temperatures. However, Sinah et al. [15] studied the variable viscosity effects with velocity slip and temperature difference for MHD non-Newtonian fluid in an asymmetric channel. By assuming the thermal conductivity along with variational viscosity, the flow of an incompressible NN fluid with nth-order chemical reaction was studied by Animasaun [16]. The study to investigate the effects of variational viscosity for steady natural convective fully developed flow in an annular micro-channel placed in a vertical direction in the company of wall having different temperatures and velocity slip was presented by [17]. An exact solution of the steady, incompressible, mixed convective flow of the viscous liquid was obtained via taking viscosity as a function of temperature in a vertical channel having heated walls [18].

While dealing and controlling NN fluid flows, heat transfer plays a very significant role. NN fluid flow dynamics is a specific challenge for mathematicians, engineers, and physicists. CF is one of the NN fluids that functions as an elastic solid, and there is a yield shear stress in its constitutive equation. Jam, toothpaste, soup, tomato pulp, and rich fruit nectars are considered as CF. Srinivas et al. [19] theoretically examined the phenomena of the CF flow containing chemically reactive species in a channel. In the existence of thermal radiation, they found that the CF parameter increases the velocity distribution. Kumam et al. [20] inspected the impact of entropy generation on CF inside rotating channels which was exposed to thermal radiation. Entropy generation escalated due to Reynolds number, while decreased with the magnetic parameter. Manjunatha et al. [21] observed that by considering variable viscosity, it is conceivable to escalated frictional force and peristaltic pumping efficiency while studying the impact of slip and heat transfer on CF inside an inclined tube with variable viscosity. Alzahrani et al. [22] numerically discussed the entropy generation on CF flow in an enclosure with convection as well as with thermal radiation. CF parameter and thermal radiation raise the kinetic energy of the system.

Heat transfer plays a significant role in the problems involving NN fluid flows. CF is a shear-thinning NN fluid that should get infinite viscosity at zero shear rate and no flow until yield stress is generated. Therefore, the intention of the present study is to explore how heat transfer affects the asymmetric, MHD flow of the non-Newtonian CF within channel having expanding–contracting walls. The transmission of heat varies point to point at a distance from the wall and also influenced by the thermal radiation. The channel walls have pores with dissimilar permeability, and fluid’s viscosity is taken as a function of temperature.

2 Physical Formulation and Derivation

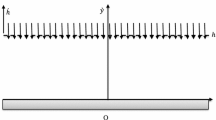
Consider the 2D, laminar, unsteady, and incompressible MHD flow of NN fluid (CF) with viscosity taken as a function of temperature. The flow is through a lengthened rectangular channel with porous walls, unveiling appropriately large facet ratio of height “b”. We suppose that both the upper and lower walls are expanding or contracting uniformly with a time-dependent rate b′(t) having different permeabilities vl and vw. As shown in Fig. 1, flow configuration [23] is described by using the Cartesian coordinate system, in which the x-axis is along the center of the channel and axial velocity u is parallel to it, while normal velocity v is taken along the normal, i.e., y-direction.

Fig. 1
figure 1

Flow model of the study

Full size image

Further, under the assumption of small electromagnetic force and electric conductivity, an exterior and normal magnetic field of uniform intensity is also taken into account over the flow. For incompressible CF model, the constitutive equation [24, 25] is given as

$$\tau^{1/2} = \tau_{c}^{1/2} + \left( {\mu \left( {T_{f} } \right)} \right)^{1/2} \gamma^{1/2}\quad \tau > \tau_{c}$$
(1a)

or

$$\tau_{ij} = \left\{ {\begin{array}{*{20}c} {2\left( {\mu \left( {T_{f} } \right) + p_{y} /\sqrt {2\pi } } \right)e_{ij} ,\quad \pi > \pi_{c} } \\ { 2\left( {\mu \left( {T_{f} } \right) + p_{y} /\sqrt {2\pi_{c} } } \right)e_{ij} ,\quad \pi < \pi_{c} } \\ \end{array} } \right.$$
(1b)

Here \(\pi = e_{ij } e_{ij } .\)

The velocity as well as temperature profile for the under-consideration problem are

$${\mathbf{V}} = \left[ {u\left( {y,t} \right),v\left( {y,t} \right),0} \right],\quad T_{f} = T_{f} \left( {y,t} \right).$$
(2)

Applying the above assumptions and utilizing Eqs. (1) and (2), the flow equations governing the flow with the dependence of viscosity on temperature are

$$\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0,$$
(3)
$$\frac{\partial u}{\partial t} + u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} = - \frac{1}{\rho }\frac{{\partial p^{*} }}{\partial x} + \frac{1}{\rho }\left( {1 + \frac{1}{\beta }} \right)\left[ {\frac{\partial }{\partial x}\left\{ {\mu \left( {T_{f} } \right)\frac{\partial u}{\partial x}} \right\} + \frac{\partial }{\partial y}\left\{ {\mu \left( {T_{f} } \right)\frac{\partial u}{\partial y}} \right\}} \right] - \frac{{\delta \beta_{0}^{2} }}{\rho }u,$$
(4)
$$\frac{\partial v}{\partial t} + u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y} = - \frac{1}{\rho }\frac{{\partial p^{*} }}{\partial y} + \frac{1}{\rho }\left( {1 + \frac{1}{\beta }} \right)\left[ {\frac{\partial }{\partial x}\left\{ {\mu \left( {T_{f} } \right)\frac{\partial v}{\partial x}} \right\} + \frac{\partial }{\partial y}\left\{ {\mu \left( {T_{f} } \right)\frac{\partial v}{\partial y}} \right\}} \right],$$
(5)
$$\rho C_{p} \left( {\frac{{\partial T_{f} }}{\partial t} + u\frac{{\partial T_{f} }}{\partial x} + .\frac{{\partial T_{f} }}{\partial y}} \right) = K\left( {\frac{{\partial^{2} T_{f} }}{{\partial x^{2} }} + \frac{{\partial^{2} T_{f} }}{{\partial y^{2} }}} \right) - \frac{{\partial q_{r} }}{\partial y}.$$
(6)

Associated boundary conditions are

$$\left. \begin{aligned} & u = 0,\quad v = - v_{l} = - A_{0} b^{\prime}(t),\quad T_{f} = T_{0} \quad {\text{at}}\quad y = - b(t), \\ & u = 0,\quad v = - v_{w} = - A_{1} b^{\prime}(t),\quad T_{f} = T_{w} \quad {\text{at}}\quad y = b(t). \\ \end{aligned} \right\}$$
(7)

Here, \(v_{l} ,v_{w}\) are the constant values of permeabilities at \(y = - b\left( {\text{t}} \right)\) and \(y = b(t)\), respectively, \(A_{0} = \frac{{v_{l} }}{{b^{\prime}\left( t \right)}}\), \(A_{1} = \frac{{v_{w} }}{{b^{\prime}\left( t \right)}}\) and \(T_{0} > T_{w}\).

Throughout the literature, there is more than one mathematical model explaining the dynamics of TD viscosity. Here, we use the viscosity model by [26] to analyze the viscosity variation because of temperature and subsequently given by Prasad et al. [27]

$$\mu \left( q \right) = 1 + \varepsilon \left( {1 - q} \right),$$
(8)

Using the below parameters

$$\psi = \frac{\upsilon x}{b\left( t \right)}f\left( {\eta ,t} \right),\quad \eta = \frac{y}{b(t)},\quad q\left( \eta \right) = \frac{{T_{f} - T_{w} }}{{T_{o} - T_{w} }}.$$
(9)

Here, temperature Tf at a distance \(\eta\) from the wall can be expressed as [28]

$$T_{f} = T_{w} + \sum C_{m} q\left( \eta \right)\left( {\frac{x}{b(t)}} \right)^{m} ,$$
(10)

where m is the power-law index.

Roseland approximation for radiation [29, 30] is given by

$$q_{r} = - \frac{{4\sigma^{*} }}{{3K^{*} }} \frac{{\partial T_{f}^{4} }}{\partial y}.$$
(11)

Taylor series is used for the expansion of about \(T_{\infty }\) due to the difference in temperature during flow, while terms having higher-order might be neglected.

$$T_{f}^{4} = T_{\infty } \left( {4T_{\infty }^{2} T_{f} - 3T_{\infty }^{3} } \right).$$
(12)

Invoking Eqs. (8)–(12) in Eqs. (4)–(6) and removing pressure term, we obtain the following dimensionless form:

$$\left( {1 + \frac{1}{\beta }} \right)\left( {\begin{array}{*{20}c} {\left( {1 + \varepsilon (1 - q} \right))f_{\eta \eta \eta \eta } } \\ { - \varepsilon f_{\eta \eta } q_{\eta \eta } - 2\varepsilon f_{\eta \eta \eta } q_{\eta } } \\ \end{array} } \right) + \alpha \left( {\eta f_{\eta \eta \eta } + 3f_{\eta \eta } } \right) + ff_{\eta \eta \eta } - f_{\eta \eta } f_{\eta } - b^{2} \upsilon^{ - 1} f_{\eta \eta t} - M^{2} f_{\eta \eta } = 0,$$
(13)
$$\left( {1 + Nr} \right)q'' + \Pr \left[ {\alpha \left( {mq + \eta q^{\prime}} \right) - mf^{\prime}q + fq^{\prime}} \right] = 0,$$
(14)

and Eq. (7) becomes

$$\left. {\begin{array}{*{20}l} {f\left( { - 1} \right)} \hfill & = \hfill & {R_{0} , f_{\eta } \left( { - 1} \right) = 0, q\left( { - 1} \right) = 1,} \hfill \\ {f\left( 1 \right)} \hfill & = \hfill & {R_{1} , f_{\eta } \left( 1 \right) = 0, q\left( 1 \right) = 0.} \hfill \\ \end{array} } \right\}$$
(15)

Here \(\alpha = \frac{{b\left( t \right)b^{\prime}\left( t \right)}}{\upsilon },\) \(R_{1} = \frac{{v_{w} b}}{\upsilon }\) and \(R_{0} = \frac{{v_{l} b}}{\upsilon }\). R1 and R0 are negative for suction and positive for injection.

Following Uchida and Aoki [31] and assuming \(R_{1} F = f\) and \(al = x\) with \(\alpha\) as constant and \(F = F\left( \eta \right),\) Eqs. (13) and (14) become

$$\left( {1 + \frac{1}{\beta }} \right)\left( {\begin{array}{*{20}c} {\left( {1 + \varepsilon (1 - q} \right)) F^{''''} } \\ { - \varepsilon F^{''} q^{\prime\prime} - 2\varepsilon F^{'''} q^{\prime}} \\ \end{array} } \right) + \alpha \left( {\eta F^{'''} + 3F^{\prime\prime}} \right) + R\left( {F F^{'''} - F^{\prime} F^{''} } \right) - M^{2} F^{''} = 0,$$
(16)
$$\left( {1 + Nr} \right)q^{\prime\prime} + \Pr \left[ {\alpha \left( {mq + \eta q^{\prime}} \right) + R\left( {Fq^{\prime} - mF^{\prime}q} \right)} \right] = 0.$$
(17)

and Eq. (15) becomes

$$\left. {\begin{array}{*{20}l} F \hfill & = \hfill & {A, F^{\prime} = 0 , q = 1\,{\text{on }} \eta = - 1 , } \hfill \\ F \hfill & = \hfill & {1, F^{\prime} = 0, q = 0\,{\text{on }}\eta = 1,} \hfill \\ \end{array} } \right\}$$
(18)

where \(A = v_{l} /v_{w}\).

3 Method of the Solution by HAM

For the HAM solution of Eqs. (16)–(18), base functions followed by [32] because of symmetric properties of channel and upright power series convergence in \(\eta \in \left[ { - 1,1} \right]\) are given by \(\left\{ { \left. {\eta^{2k} } \right| k \ge 0} \right\}\) in the form of

$$F\left( \eta \right) = \mathop \sum \limits_{n = 1}^{\infty } a_{k} \eta^{2k},\quad q\left( \eta \right) = \mathop \sum \limits_{n = 1}^{\infty } b_{k} \eta^{2k}$$
(19)

and initial guesses of \(F\left( \eta \right)\) and \(q\left( \eta \right)\) are expressed as [33, 34]

$$F_{0} \left( \eta \right) = \frac{A - 1}{4}\eta^{3} + \frac{3 - 3A}{4}\eta + \frac{A + 1}{2},$$
(20)
$$q_{0} \left( \eta \right) = \frac{1}{2} \left( {1 - \eta } \right),$$
(21)

while auxiliary linear operators used in this work are

$$l_{1} \left( F \right) = F^{''''} ,$$
(22)
$$l_{2} \left( q \right) = q^{\prime\prime},$$
(23)

which satisfy

$$l_{1} \left( {C_{1} \eta^{3} + C_{2} \eta^{2} + C_{3} \eta + C_{4} } \right) = 0,$$
(24)
$$l_{2} \left( {C_{5} \eta + C_{6} } \right) = 0,$$
(25)

where Ci (i = 1 to 6) are constants.

$$l_{1} \left( {F\left( {\eta ,p} \right) - F_{0} \left( \eta \right)} \right)\left( {1 - p} \right) = phN_{1} \left( {F\left( {\eta ,p} \right)} \right),$$
(26)
$$l_{2} \left( {q\left( {\eta ,p} \right) - q_{0} \left( \eta \right)} \right)\left( {1 - p} \right) = phN_{2} \left( {q\left( {\eta ,p} \right)} \right),$$
(27)

and

$$\left. {\begin{array}{*{20}c} {F\left( {1,p} \right) = 1,^{ } F\left( { - 1,p} \right) = A, } \\ { F^{\prime}\left( {1,p} \right) = 0, F^{'} \left( { - 1,p} \right) = 0, } \\ {q\left( {1,p} \right) = 0 , q\left( { - 1,p} \right) = 1.} \\ \end{array} } \right\}$$
(28)

The nonlinear operators N1 and N2 are defined as

$$\begin{aligned} N_{1} \left( {F\left( {\eta ,p} \right)} \right) & = \left( {1 + \frac{1}{\beta }} \right)\left[ {\left( {1 + \varepsilon (1 - q\left( {\eta ,p} \right)} \right))\frac{{\partial^{4} F\left( {\eta ,p} \right)}}{{\partial \eta^{4} }} - \varepsilon \frac{{\partial^{2} F\left( {\eta ,p} \right)}}{{\partial \eta^{2} }}\frac{{\partial^{2} q\left( {\eta ,p} \right)}}{{\partial \eta^{2} }} - 2\varepsilon \frac{{\partial^{3} F\left( {\eta ,p} \right)}}{{\partial \eta^{3} }}\frac{{\partial q\left( {\eta ,p} \right)}}{\partial \eta }} \right] \\ & \quad + \alpha \left( {\eta \frac{{\partial^{3} F\left( {\eta ,p} \right)}}{{\partial \eta^{3} }} + \frac{{\partial^{2} F\left( {\eta ,p} \right)}}{{\partial \eta^{2} }}} \right) + R\left( {F\left( {\eta ,p} \right)\frac{{\partial^{3} F\left( {\eta ,p} \right)}}{{\partial \eta^{3} }} - \frac{{\partial F\left( {\eta ,p} \right)}}{\partial \eta }\frac{{\partial^{2} F\left( {\eta ,p} \right)}}{{\partial \eta^{2} }}} \right) - M^{2} \frac{{\partial^{2} F\left( {\eta ,p} \right)}}{{\partial \eta^{2} }}, \\ \end{aligned}$$
(29)
$$N_{2} \left( {q\left( {\eta ,p} \right)} \right) = \left( {1 + Nr} \right)\frac{{\partial^{2} q\left( {\eta ,p} \right)}}{{\partial \eta^{2} }} + \Pr \left[ {\left( {\eta q\left( {\eta ,p} \right) + m\frac{{\partial q\left( {\eta ,p} \right)}}{\partial \eta }} \right) - F\left( {\eta ,p} \right)\frac{{\partial q\left( {\eta ,p} \right)}}{\partial \eta } + \frac{{\partial F\left( {\eta ,p} \right)}}{\partial \eta }\frac{{\partial q\left( {\eta ,p} \right)}}{\partial \eta }} \right].$$
(30)

Equations (26) and (27) have resulting solutions for p = 0 and p = 1

$$F\left( {\eta ,0} \right) = F_{0} \left( \eta \right), F\left( {\eta ,1} \right) = F\left( \eta \right)$$
(31)
$$q\left( {\eta ,0} \right) = q_{0} \left( \eta \right),\quad q\left( {\eta ,1} \right) = q\left( \eta \right),$$
(32)

Therefore, one can write through the usage of Taylor’s theorem,

$$\left. {\begin{array}{*{20}c} {F\left( {\eta ,p} \right) = F_{0} \left( \eta \right) + \mathop \sum \limits_{n = 1}^{\infty } F_{n} \left( \eta \right)p^{n} } \\ {F_{n} \left( \eta \right) = \frac{1}{n!}\left. {\frac{{\partial^{n} F\left( {\eta ,p} \right)}}{{\partial \eta^{n} }}} \right|_{p = 0} } \\ \end{array} } \right\},$$
(33)

and

$$\left. {\begin{array}{*{20}c} {q\left( {\eta ,p} \right) = q_{0} \left( \eta \right) + \mathop \sum \limits_{n = 1}^{\infty } q_{n} \left( \eta \right)p^{n} } \\ {q_{n} \left( \eta \right) = \frac{1}{n!}\left. {\frac{{\partial^{n} q\left( {\eta ,p} \right)}}{{\partial \eta^{n} }}} \right|_{p = 0} } \\ \end{array} } \right\}.$$
(34)

A strong convergence can be obtained by depending upon h. We assume that h is selected to be convergent at p = 1. Therefore, we have

$$F = F_{o} \left( \eta \right) + \mathop \sum \limits_{n = 1}^{\infty } F_{n} \left( \eta \right),$$
(35)
$$q = q_{o} \left( \eta \right) + \mathop \sum \limits_{n = 1}^{\infty } q_{n} \left( \eta \right).$$
(36)

For obtaining the nth-order deformation problem, Eqs. (25) and (26) can be differentiated n times with respect to p and finally dividing them by n!, by putting p = 0, we have

$$l_{1} \left( {F\left( \eta \right) - x_{n} F_{n - 1} \left( \eta \right)} \right) = h\chi_{n}^{F} \left( \eta \right),$$
(37)
$$l_{2} \left( {q\left( \eta \right) - x_{n} q_{n - 1} \left( \eta \right)} \right) = h\chi_{n}^{q} \left( \eta \right),$$
(38)
$$F\left( { - 1} \right) = 0, F_{n} \left( 1 \right) = 0, F_{{n^{\prime}}} \left( { - 1} \right) = 0, F_{{n^{\prime}}} \left( 1 \right) = 0,$$
(39)

and

$$q\left( { - 1} \right) = 0, q\left( 1 \right) = 0.$$
(40)

Here,

$$\begin{aligned} \chi_{n}^{F} \left( \eta \right) & = \left( {1 + \frac{1}{\beta }} \right)\left[ {\left( {1 + \varepsilon } \right)F_{n - 1}^{''''} } \right] + \alpha \left( {\eta F_{n - 1}^{'''} + 3F_{n - 1}^{''} } \right) - M^{2} F_{n - 1}^{''} \\ & \quad + \mathop \sum \limits_{k = 0}^{n - 1} q_{n - k - 1} F_{k}^{''''} - \varepsilon q^{'' }_{n - k - 1} F_{k}^{''} + 2\varepsilon q^{' }_{n - k - 1} F_{k}^{'''} + R(F_{n - k - 1} F_{k}^{'''} ) - F_{n - k - 1}^{'} F_{k}^{''} , \\ \end{aligned}$$
(41)
$$\chi_{n}^{q} \left( \eta \right) = \left( {1 + Nr} \right)\theta_{n - 1}^{''} + Pr\left( {m\theta_{n - 1} + \eta \theta_{n - 1}^{''} } \right) - Pr\mathop \sum \limits_{k = 0}^{n - 1} \left( {mq_{k} F_{n - k - 1}^{'} - q_{n - k - 1}^{'} F_{k} } \right),$$
(42)

where

$$x_{n} = \left\{ {\begin{array}{*{20}l} {0,} \hfill & {n \le 1,} \hfill \\ 1 \hfill & {n > 1.} \hfill \\ \end{array} } \right.$$
(43)

In this fashion, the linear non-homogenous Eqs. (37) and (38) can easily be solved for \(n = 1,2, \ldots\) in the order. Further, it is supposed that \(F_{n}^{*} \left( \eta \right)\) and \(q_{n}^{*} \left( \eta \right)\) are taken as the special solutions of Eqs. (26) and (27) and then the expressions for general solutions are given by

$$F_{n} \left( \eta \right) = F_{n}^{*} \left( \eta \right) + C_{1} \eta^{3} + C_{2} \eta^{2} + C_{3} \eta + C_{4} ,\quad q_{n} \left( \eta \right) = q_{n}^{*} \left( \eta \right) + C_{5} \eta + C_{6}$$
(44)

where Ci, (i = to 6) can be determined by using Eqs. (38) and (39) as

$$C_{1} = - \frac{1}{4}\left[ {F_{n}^{*} \left( { - 1} \right) - F_{n}^{*} \left( 1 \right) - F_{n}^{'*} \left( { - 1} \right) - F_{n}^{'*} \left( 1 \right)} \right] , C_{2} = \frac{1}{4}\left[ {F_{n}^{'*} \left( { - 1} \right) - F_{n}^{'*} \left( 1 \right)} \right]$$
$$C_{3} = - \frac{1}{2}\left[ {F_{n}^{*} \left( { - 1} \right) - F_{n}^{*} \left( 1 \right)} \right] - C_{1} ,C_{4} = - \frac{1}{2}\left[ {F_{n}^{*} \left( { - 1} \right) + F_{n}^{*} \left( 1 \right)} \right] - C_{2}$$
$$C_{5} = \frac{1}{2}\left[ {q_{n}^{*} \left( { - 1} \right) - q_{n}^{*} \left( 1 \right)} \right],C_{6} = - \frac{1}{2}\left[ {q_{n}^{*} \left( { - 1} \right) + q_{n}^{*} \left( 1 \right)} \right].$$

4 Results and Discussion

An analysis of the axisymmetric MHD flow of a NN Casson fluid with the assumption of TD viscosity within a porous channel has been carried out analytically using HAM. The flow is caused by pressure variation within the channel.

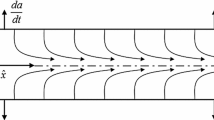
Applying HAM, h-curves are plotted in Fig. 2 to establish the convergence area for various estimations. Admirable approximation range of h changes as the value of A varies. The velocity profile ranges \(- 0.7 \le h \le - 0.1\) when \(A = - 0.2\) and \(- 0.55 \le h \le - 0.1\) when \(A = - 0.6\), while for temperature profile the range is \(- 0.65 \le h \le - 0.2\) when \(A = - 0.2\) and \(- 0.5 \le h \le 0.0\) when \(A = - 0.6.\) The suitable value of \(h = - 0.3\) results in the variation and influence of R and \(\alpha\) on velocity profile \(F\left( \eta \right),F'\left( \eta \right)\) and heat profile \(q\left( \eta \right)\).

Fig. 2
figure 2

Convergence of problem

Full size image

The NN parameter \(\beta\) displays complex rheological characteristics that are helpful to predict the flow of the NN fluids coming across in nature and industrial purposes especially when the viscosity is taken as a function of temperature. The varying response of the flow field with the CF parameter \(\beta\) is presented in Fig. 3 when an injection is applied at the upper wall. The flow becomes asymmetric with increasing \(\beta\) and attains the maximum velocity for NF \(\left( {\beta \to \infty } \right)\).

Fig. 3
figure 3

Velocity behavior for variation of parameter \(\beta\)

Full size image

In Fig. 4, the change in the velocity with different values of wall expansion/contraction ratio is graphically presented. The behavior shows that an increase in wall expansion \((\alpha > 0)\) augments the maximum velocity, whereas the wall contraction \((\alpha < 0)\) results in the reduction in maximum velocity.

Fig. 4
figure 4

Velocity behavior for variation of parameter \(\alpha\)

Full size image

Figure 5 presents the increasing behavior of \(F'\left( \eta \right)\) with an increase in A when the walls are expanding, and injection takes place at the upper wall. Also, the flow becomes symmetric for larger values of A. The effects of Lorentz force on the CF velocity while keeping viscosity as a function of temperature is shown in Fig. 6. The Lorentz force associated with the M is a resistive force that hinders the flow and hence results in the reduction in fluid velocity which can be seen in this figure.

Fig. 5
figure 5

Velocity behavior for variation of parameter A

Full size image
Fig. 6
figure 6

Velocity behavior for variation of parameter M

Full size image

The temperature variation with the change in different parameters A, m, \(\alpha\), Pr, and Nr is shown in Figs. 7, 8, 9, 10, and 11 in the presence of TD viscosity parameter \(\varepsilon\). Moreover, in this article temperature is defined in the form of summation with respect to the wall depending on the power-law index m. Here, in all cases, \(m > 1\) is for shear thickening, \(m < 1\) for shear-thinning, and \(m = 1\) for Newtonian, viscous behavior. From Figs. 7 and 8, it can be seen that the temperature of CF experiences a decrement with the increase in both A and m. It is also clear from Fig. 8 that shear thinning decreases with the increase in power-law index \(0 < m < 1\) and the same for the shear thickness. The impact of the wall expansion/contraction ratio is drawn graphically in Fig. 9, indicating a temperature rise due to wall expansion while a decline in temperature with the decrement contraction ratio \(\alpha\). An increase in the amount of Prandtl number induces a temperature decrease as shown in Fig. 10, suggesting a decline in thermal boundary layer thickness, and hence lower surface temperature within the boundary layer is observed. An increased thermal emission with higher heat intensity results in the disconnection of fluid particles and subsequently fluid temperature changes as shown in Fig. 11. With the rise in thermal radiation, the temperature is rising in this graph.

Fig. 7
figure 7

Temperature behavior for variation of parameter A

Full size image
Fig. 8
figure 8

Temperature behavior for variation of parameter m

Full size image
Fig. 9
figure 9

Temperature behavior for variation of parameter \(\alpha\)

Full size image
Fig. 10
figure 10

Temperature behavior for variation of parameter Pr

Full size image
Fig. 11
figure 11

Temperature behavior for variation of parameter Nr

Full size image

5 Comparison of Results with the Existing Literature

The comparison of the results of the current study with the existing literature is presented to validate the study. A good comparison with the results of [23] is presented in Fig. 12 for NF \(\beta \to \infty\), \(\varepsilon = 0,M = 0\) (bullet curve). The increase in the transport phenomena is due to the increase in temperature and can be restricted by reducing the viscosity across the momentum boundary layer. Due to which the heat transfer rate at the wall is also affected. Consequently, it is necessary that TD viscosity must be taken into account to predict the flow and heat transfer rates of the fluid, accurately. Therefore, a comparison of both Newtonian and NN fluids is also being discussed here by using graphical representation with reference to the TD viscosity parameter. The impact of TD viscosity parameter \(\varepsilon\) on \(F'\left( \eta \right)\) within the channel for \(\beta \to \infty\) (NF) and \(\beta = 0.8\) (NN fluid) is also shown in Fig. 12 with the observation that fluid velocity for the NF is greater than NN fluid. Figure 13 also presents a good comparison with the results of [23] presented for NF \(\beta \to \infty\), \(\varepsilon = 0,M = 0\) (bullet curve). To maintain the laminar flow, Reynolds number is one of the important factors to take into account and whose convergence is necessary to prevent the flow from viscous losses. The change in \(F^{\prime}\left( \eta \right)\) with the Reynolds number R is also plotted in Fig. 13 where A and \(\alpha\) are fixed. The flow field for the NF is asymmetric toward the upper wall, and for NN fluid it shifts toward the lower wall. The figure also shows that with an increment in the suction velocity (R < 0) at the upper wall, the asymmetry of the flow is toward the upper wall; however, it changes to the lower wall with the increasing values of injection velocity (R > 0) at the upper wall. Also, the maximum velocity is achieved near the lower wall for R > 0.

Fig. 12
figure 12

Velocity behavior for variation of parameter \(\varepsilon\)

Full size image
Fig. 13
figure 13

Velocity behavior for variation of R

Full size image

Figure 14 presents an admirable agreement for the comparison of results of [35, 36] and the present study for axial velocity in the case of nonconducting Newtonian fluid without dependence on TD viscosity, i.e., \(\beta \to \infty\), \(\varepsilon = 0, M = 0\).

Fig. 14
figure 14

Comparison of axial velocity for a Newtonian fluid

Full size image

6 Conclusions

The presented investigation deals with the flow of CF with TD viscosity within a porous channel with expansion/contraction in the presence of a velocity slip. The analysis of velocity in the presence of magnetic flux, viscosity as a function of temperature and heat transfer with thermal radiation is also performed. The outcomes from the present investigation are:

  • Viscosity as a function of temperature affects the velocity of the fluid, while the velocity of the fluid is greater for NF as compared to NN fluid.

  • Stream velocity of the fluid is greater for the case of NN fluid as compared to the NF, and due to the increment of Reynolds number the streamwise velocity seems to be shifted toward the wall.

  • CF parameter affects the velocity, becomes gradually increasing and finally at its peak level for NF.

  • The existence of the magnetic field increases the velocity near the lower wall and upper wall but decreases at almost mid of the channel.

  • An increase in Pr causes a decrease in temperature, while the opposite trend is exhibited due to Nr.

  • The expansion ratio due to the wall enhances the temperature of the wall, while the power-law index decreases the temperature.