1 Introduction

With the advancement and application of new technologies and materials, an increased number of long-span bridges have been built, e.g. Tsing Ma Bridge, Runyang Bridge, Jiangyin Bridge, Hong Kong–Zhuhai–Macau Bridge etc. These structures have an obvious deformation influenced by external excitations, such as earthquake, wind, traffic, tidal currents, and their combination. Excessive deformation will lead to structural instability and even destruction. Therefore, a real-time understanding of the structural deformation under external excitations by employing field measurement techniques is an extremely necessary work. At present, accelerometers are widely applied in monitoring the dynamic deformation of long-span bridges in an efficient manner [1, 2]. However, they inevitably result in drift errors when they require a double integral for deriving displacement response of the structure [3, 4]. Subsequently, the advent of global navigation satellite system (GNSS) solves this problem better [5,6,7]. GNSS can measure static, semi-static, and dynamic displacement of bridges for all-weather in real time [8]. Especially, the development of high sampling rate and multi-constellation GNSS (Global Navigation Satellite System) makes this technique acquire a widespread attention [9]. Real-time kinematic (RTK) GNSS technique is an important development to aid dynamic deformation monitoring [10]. Hence, this study adopted high-rate and multi-constellation GNSS-RTK technique to monitor the vibration response of a long-span concrete-filled steel tubular arch bridge.

Besides the aforementioned advantages, GNSS-RTK technique has also two negative factors, i.e. multi-path effect, signals shielding effect. They will seriously affect the measurement accuracy of GNSS-RTK technique. Nowadays, signals shielding effect has been got a significant improvement with the increasing number of visible satellites. However, multi-path effect has not been satisfactorily resolved. It becomes the primary factor to restrict the measurement accuracy of GNSS-RTK technique [11]. Therefore, to realize the effective separation between signal and noise, it is critical to select a proper signal processing method. Empirical mode decomposition (EMD) that was put forth has been widely recognized by academia [12, 13]. It is an efficient means of dealing with nonlinear and non-stationary signals, and decomposes a signal into a series of high- and low-frequency components, called intrinsic mode functions (IMFs). They satisfy two conditions: (1) the numbers of extreme and zero-crossing points must either equal or have a difference of one at most; (2) the decomposition process stops when the last IMF component is monotonous [14]. It is noteworthy that EMD algorithm has a serious problem, i.e. mode mixing. To overcome this problem, an improved approach called ensemble empirical mode decomposition (EEMD) was put forward [15]. This approach alleviates the mode mixing phenomenon via the addition of white noise, however, that brings a new problem. The additional white noise cannot be completely eliminated, which will produce different modes with the interaction of signal and noise. To solve this problem, the complementary ensemble empirical mode decomposition (CEEMD) was proposed [16]. The reconstruction error generated using EEMD is decreased and the computational efficiency is improved by adding white noise in pairs into the raw signal. Following this, CEEMD algorithm has a wide range of applications in signal processing field [17,18,19]. Considering that CEEMD has good denoising performance and adaptability, this method was introduced in this study.

The identification of dynamic characteristic parameters (i.e. natural frequencies, mode shapes and damping ratios) of long-span bridges is a research hotspot in the field of structural health monitoring. It is extremely significant to real-time understand the change of the dynamic parameters of bridges in ensuring safe operation of structures. The traditional parameter identification algorithms, also be called input and output algorithms, need artificial excitation, and are easy to cause the structural damage. In contrast, operational modal identification (OMI) algorithms can realize the dynamic parameter identification of structures only rely on the out-put responses of structures without artificial excitation. Therefore, this method is used more often. At present, there are many OMI algorithms are used in determining dynamic parameters of structures, such as natural excitation technique (NExT) [20, 21], random decrement technique (RDT) [22], Ibrahim time domain (ITD) [23], autoregressive moving average model (ARMA) [24], eigensystem realization algorithm (ERA) [25, 26], stochastic subspace identification (SSI) [27] approach and so on. Among these algorithms, SSI does not need to obtain free decaying signal or cross correlation function via data preprocessing, hence, it has been favored by many researchers [28, 29]. At present, there are mainly two approaches of SSI, i.e. data-driven SSI (DD-SSI) and covariance-driven SSI (CD-SSI) [27]. The recognition accuracy of the two methods is similar. However, DD-SSI avoids computation of covariance matrix, its computational efficiency is better than that of CD-SSI [30]. For this reason, this method was employed in this study.

The present work aims at developing a new combined Chebyshev filter and CEEMD data analysis method (CF-CEEMD) to decrease the interference of GNSS-RTK background noise and acquire the dynamic displacements of long-span bridges. Section 2 introduces the basic principles of the CF-CEEMD and the DD-SSI algorithms. In Sect. 3, a stability test of GNSS-RTK is presented. In Sect. 4, a simulation signal is introduced to verify the effectiveness of CF-CEEMD. Section 5 analyzes the dynamic characteristics of the bridge using CF-CEEMD and DD-SSI approaches based on the field measured data. In addition, the finite element (FE) model of the bridge is established to exam the dynamic characteristic of tested value and followed with discussions. Finally, the concluding remarks are given in Sect. 6.

2 The principles of CF-CEEMD and DATA-SSI algorithms

2.1 CF-CEEMD algorithm

To solve the problem that the white noise added by EEMD cannot be eliminated, a CEEMD algorithm was proposed, which can be expressed as [16]:

  1. 1.

    Add white noise in pairs \(\eta^{ \pm } (t)\) into the original signal \(y(t)\), and form two new signals \(Y(t)\):

    $$\left\{ \begin{aligned} Y^{ + } (t) = y(t) + \eta^{ + } (t) \hfill \\ Y^{ - } (t) = y(t) + \eta^{ - } (t) \hfill \\ \end{aligned} \right..$$
    (1)
  2. 2.

    EMD algorithm [12] is employed to each derived signal to get a series of IMFs.

  3. 3.

    Acquire 2N sets of IMFs for the new signals.

  4. 4.

    Calculate decomposition results via averaging multiple IMFs:

    $${\text{IMF}}_{j} (t) = \frac{1}{2N}\sum\limits_{i = 1}^{2N} {{\text{IMF}}_{ij} }$$
    (2)

    where \({\text{IMF}}_{j}\) is the j-th IMF component of CEEMD decomposition; \({\text{IMF}}_{ij}\) is the j-th IMF of the i-th signal.

With full consideration of the distribution characteristics of GNSS-RTK background noise, this paper put forward a combined method, i.e. CF-CEEMD. Its specific steps are as follows:

  1. 1.

    The low-frequency noise is mainly distributed in the frequency band less than 0.05 Hz based on GNSS-RTK stability test. Hence, a fifth-order type 1 Chebyshev high pass filter is firstly designed to process the GNSS-RTK original data. The pass frequency range over 0.05 Hz and the pass ripple 1 dB.

  2. 2.

    The Chebyshev filtering results were decomposed via using CEEMD. Then a series of IMF components were obtained.

  3. 3.

    Calculate the correlation coefficient \(\rho\) between each IMF component and the Chebyshev filtering signal \(y_{1} (t)\) to be decomposed based on Eq. (3):

    $$\rho_{i} = \frac{{\sum\nolimits_{t = 0}^{\infty } {\text{IMF}_{i} (t)y_{1} (t)} }}{{\left[ {\sum\nolimits_{t = 0}^{\infty } {\text{IMF}_{i}^{2} (t)} \sum\nolimits_{n = 0}^{\infty } {y_{1}^{2} (t)} } \right]^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} }}.$$
    (3)
  4. 4.

    The correlation coefficient is between 0 and 1. The closer its value is to 0, the weaker the correlation of the two sequences is, and the closer its value is to 1, the stronger the correlation of the two sequences is. This study selects 0.1 of the maximum correlation coefficient as the threshold value to determine illusive IMF components. When \(\rho < 0. 1 ,\) the corresponding IMF components are removed, and the remaining IMF components are reconstructed.

It should be noted that the quasi-static displacement of the structure is also removed while the noise is removed using CF-CEEMD method, and only the dynamic displacement is retained.

2.2 DD-SSI algorithm

DD-SSI algorithm is a powerful tool for determining dynamic parameters of long-span bridges under the action of unknown excitation, and several applications are available in literature [31,32,33]. Typically, the discrete time state–space model of a structure can be written as:

$$\left\{ \begin{aligned} {\varvec{x}}_{k + 1} = {\mathbf{A}}_{k} {\varvec{x}}_{k} + {\mathbf{w}}_{k} \hfill \\ {\varvec{y}}_{k} = {\mathbf{C}}_{k} {\varvec{x}}_{k} + {\mathbf{v}}_{k} \hfill \\ \end{aligned} \right.$$
(4)

where \({\varvec{x}}_{k} \in {\mathbb{R}}^{n \times 1}\) is the state vector at time \(k\); \({\varvec{y}}_{k} \in {\mathbb{R}}^{m \times 1}\) is the measurement vector at time \(k\); \({\mathbf{A}}_{k} \in {\mathbb{R}}^{n \times n}\) is the state matrix; \({\mathbf{C}}_{k} \in {\mathbb{R}}^{m \times n}\) is the output matrix; \({\mathbf{w}}_{k} \in {\mathbb{R}}^{n \times 1}\) is the stochastic noise; \({\mathbf{v}}_{k} \in {\mathbb{R}}^{m \times 1}\) is the measurement noise.

In the first step, the block Hankel matrix is constructed as:

$${\mathbf{H}}_{0,2i - 1} = \frac{1}{\sqrt j }\left( {\begin{array}{*{20}c} {{\varvec{y}}_{0} } & {{\varvec{y}}_{1} } & {{\varvec{y}}_{2} } & \cdots & {{\varvec{y}}_{i - 1} } \\ {{\varvec{y}}_{1} } & {{\varvec{y}}_{2} } & {{\varvec{y}}_{3} } & \cdots & {{\varvec{y}}_{i} } \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ {{\varvec{y}}_{i - 1} } & {{\varvec{y}}_{i} } & {{\varvec{y}}_{i + 1} } & \cdots & {{\varvec{y}}_{i + j - 2} } \\ {{\varvec{y}}_{i} } & {{\varvec{y}}_{i + 2} } & {{\varvec{y}}_{i + 3} } & \cdots & {{\varvec{y}}_{i + j - 1} } \\ {{\varvec{y}}_{i + 1} } & {{\varvec{y}}_{i + 2} } & {{\varvec{y}}_{i + 3} } & \cdots & {{\varvec{y}}_{i + j} } \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ {{\varvec{y}}_{2i - 1} } & {{\varvec{y}}_{2i} } & {{\varvec{y}}_{2i + 1} } & \cdots & {{\varvec{y}}_{2i + j - 2} } \\ \end{array} } \right) = \left( {\frac{{{\mathbf{Y}}_{0,i - 1} }}{{{\mathbf{Y}}_{i,2i - 1} }}} \right) = \left( {\frac{{{\mathbf{Y}}_{\text{p}} }}{{{\mathbf{Y}}_{\text{f}} }}} \right)$$
(5)

where \({\mathbf{Y}}_{\text{p}} \in {\mathbb{R}}^{mi \times j}\) and \({\mathbf{Y}}_{\text{f}} \in {\mathbb{R}}^{mi \times j}\) are called the past measurements and the future measurements, respectively.

The second step is QR decomposition of \({\mathbf{H}}_{0,2i - 1}\), which is expressed as:

$${\mathbf{H}}_{0,2i - 1} = \frac{{{\mathbf{Y}}_{\text{p}} }}{{{\mathbf{Y}}_{\text{f}} }} = \varvec{RQ}^{\text{T}} = \left( {\begin{array}{*{20}c} {{\varvec{R}}_{11} } & 0 \\ {{\varvec{R}}_{21} } & {{\varvec{R}}_{22} } \\ \end{array} } \right)\left( \begin{aligned} {\varvec{Q}}_{1}^{T} \hfill \\ {\varvec{Q}}_{2}^{T} \hfill \\ \end{aligned} \right)$$
(6)

where \({\varvec{Q}}\) is the orthogonal matrix, which satisfies \(\varvec{QQ}^{\text{T}} = {\varvec{Q}}^{\text{T}} {\varvec{Q} }= {\mathbf{I}}\); \({\varvec{R}}\) is the lower triangular matrix.

The third step is the calculation of the orthogonal projection matrix \({\boldsymbol{\Pi}}_{i}\). It can be written as:

$${\boldsymbol{\Pi}}_{i} = {\varvec{Y}}_{f} {\varvec{Y}}_{p} \left( {{\varvec{Y}}_{p} {\varvec{Y}}_{p}^{\rm T} } \right)^{\dag } {\varvec{Y}}_{p} = {\varvec{R}}_{21} {\varvec{Q}}_{1}^{\text{T}} .$$
(7)

The singular value decomposition (SVD) is applied on \({\boldsymbol{\Pi}}_{i}\) computed by Eq. (8):

$${\boldsymbol{\Pi}}_{i} = {\varvec{USV}}^{\text{T}} = \left( {{\varvec{U}}_{1} \quad {\varvec{U}}_{2} } \right)\left( \begin{aligned} {\varvec{S}}_{1} \quad 0 \hfill \\ {\kern 1pt} 0\quad {\kern 1pt} \,{\kern 1pt} {\kern 1pt} 0 \hfill \\ \end{aligned} \right)\left( \begin{aligned} \varvec{V}_{1}^{\text{T}} \hfill \\ \varvec{V}_{2}^{\text{T}} \hfill \\ \end{aligned} \right) = {\varvec{U}}_{1} {\varvec{S}}_{1} \varvec{V}_{1}^{\text{T}}$$
(8)

where \({\varvec{U}} \in {\mathbb{R}}^{mi \times mi}\) and \(\varvec{V} \in {\mathbb{R}}^{mi \times mi}\) are the orthogonal matrices of the left and right singular vectors, respectively; \({\varvec{S}}\) is the diagonal matrix of the singular values.

Furthermore, the projection matrix \({\boldsymbol{\Pi}}_{i}\) can be decomposed into an extended observability matrix \({\mathbf{O}}_{i} \in {\mathbb{R}}^{mi \times n}\) and a Kalman filter sequence \(\hat{\varvec{X}}_{i} \in {\mathbb{R}}^{n \times mi}\) as follows:

$${\boldsymbol{\Pi}}_{i} = {\mathbf{O}}_{i} \hat{\varvec{X}}_{i} .$$
(9)

According to Eq. (8), \({\mathbf{O}}_{i}\) and \(\hat{\varvec{X}}_{i}\) can be expressed as:

$$\left\{ \begin{aligned} {\mathbf{O}}_{i} = {\varvec{U}}_{1} {\varvec{S}}_{1}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \hfill \\ \hat{\varvec{X}}_{i} = {\varvec{S}}_{1}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \varvec{V}_{1} \hfill \\ \end{aligned} \right..$$
(10)

In the last step, the system matrices \({\mathbf{A}}\) and \({\mathbf{C}}\) can be derived via using the observability matrix \({\mathbf{O}}_{i}\), as follows:

$$\left\{ {\begin{array}{*{20}l} {{\mathbf{C}} = {\mathbf{O}}_{i} \left( {1:m,\;:} \right)} \hfill \\ {{\mathbf{A}} = {\mathbf{O}}_{i} \left( {1:m\left( {i - 1} \right),\;:} \right)^{\dag } {\mathbf{O}}_{i} \left( {m + 1:mi,\;:} \right)} \hfill \\ \end{array} } \right.$$
(11)

where the symbol \(\left( {\, \cdot \,} \right)^{\dag }\) denotes the pseudoinverse.

Once the system matrices are identified, the natural frequencies and the corresponding damping ratios can be determined by conducting eigenvalue decomposition of the system matrix \({\mathbf{A}}\), and the mode shape coefficients can be obtained via the eigenvectors multiplied by the output matrix \({\mathbf{C}}\).

The eigenvalue decomposition of matrix \({\mathbf{A}}\) is as follows:

$${\mathbf{A}} = {\boldsymbol{\Psi}} {\boldsymbol{\Lambda}} {\boldsymbol{\Psi}}^{ - 1}$$
(12)

where \({\boldsymbol{\Psi}}\) is eigenvector matrix in discrete time. \(\varvec{\Lambda} =\text{diag}(\lambda )\), \(\lambda\) is the eigenvalue in discrete time. It is related to an eigenvalue \(\lambda_{\text{c}}\) in continuous time, with Eq. (13):

$$\lambda_{\text{c}} = \frac{{\text{ln}(\lambda )}}{\Delta t}.$$
(13)

The natural frequency \(f\) and damping ratio \(\xi\) can then be calculated as:

$$f = \frac{{\sqrt {\text{Re}^{2} \left( {\lambda_{\text{c}} } \right) + \text{Im}^{2} \left( {\lambda_{\text{c}} } \right)} }}{2\pi }$$
(14)
$$\xi = - \frac{{\text{Re} \left( {\lambda_{\text{c}} } \right)}}{2\pi f}$$
(15)

The mode shape \(\boldsymbol{\varphi }\) is calculated as:

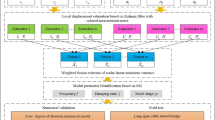
$$\boldsymbol{\varphi} = {\mathbf{C}} \cdot{\boldsymbol{\Psi}}.$$
(16)

The whole computational procedure is summarized in the flowchart given in Fig. 1.

Fig. 1
figure 1

Flow chart of the entire computational procedure

Full size image

3 Stability test of GNSS-RTK

To examine the stability and the measurement accuracy of GNSS sensors under RTK mode, a stability test was carried out. The working principle of RTK can refer to the literature [34,35,36]. In this test, seven H32 multi-constellation GNSS receivers provided by Hi-Target Company were employed. Table 1 provided an accuracy comparison between different brands. All GNSS receivers used in this research can receive signals from GPS, GLONASS and BDS simultaneously, and there are corresponding satellite channels to match them (i.e. BDS:B1, B2, B3; GPS:L1C/A, L1C, L2C, L2E, L5; GLONASS: L1P, L2C/A, L2P, L3). One of them was used as a reference station and the rest as rover stations, as shown in Fig. 2. This experiment lasted for 5 h with a sampling rate of 1 Hz.

Table 1 Accuracy comparison between different brands
Full size table
Fig. 2
figure 2

Schematic figure for stability test

Full size image

The raw observations of GNSS based on RTK mode are primarily addressed via using dedicated post-processing software (i.e. HDS2003 Data Process Software) from Hi-Target Company. The cut-off angle is set to 15°. The height of the antenna from sea level is about 6.21 m. The tropospheric and ionospheric models adopt the improved Hopfield model and the Klobuchar model, respectively. Satellite orbits are mainly affected by two-body gravitation, aspheric perturbation, lunisolar gravitational perturbation, solar radiation pressure perturbation, tidal perturbation, relativistic effect perturbation and other perturbations. Precise satellite orbits via International GNSS Service (IGS) are determined. These orbital data are called IGS precise ephemeris. Position Dilution of Precision (PDOP) is an important indicator for evaluating GNSS measurement accuracy. Given a measurement error, GNSS positioning accuracy is improved with the decrease of PDOP [37]. During the test, the range of visible satellites of multi-constellation GNSS is between 17 and 20, and the range of PDOP values is between 1.6 and 2.0.

Since the vertical vibration is the major form of long-span bridges, this study is only concerned about the vertical vibration of the structure. Assuming that all the sensors are stationary, the monitoring results should be zero. In other words, the result of the stability test was regarded as a background noise. To avoid repetition, one of the monitored points was chosen as an illustrative example. Figure 3 presents the amplitudes of the background noise in the vertical direction of GNSS-RTK and the corresponding power spectral density (PSD) functions. The result depicted that the range of the vertical background noise of GNSS-RTK is between − 0.0162 and 0.0163 m. The corresponding root mean square (RMS) value (i.e. 0.0048 m) was obtained via Eq. (17). Moreover, it can be seen from PSD distribution that the low-frequency component (\(< 0.05\,\text{Hz}\)) of the background noise displays a higher energy, and the high-frequency component (\(> 0.05\,\text{Hz}\)) is close to the white-noise-type spectrum with a lower energy. The influence of low-frequency noise is more significant than that of high-frequency noise. If the fundamental frequency of a long-span bridge is greater than the value of 0.05 Hz, the low-frequency noise can be weakened by setting a proper threshold value based on traditional signal processing methods. In this study, a combined approach of Chebyshev filter and complementary ensemble empirical mode decomposition (CF-CEEMD) was proposed to alleviate the influence of GNSS-RTK background noise:

$${\text{RMS}} = \sqrt {\frac{{\sum\nolimits_{i = 1}^{n} {\left( {x_{i} - \bar{x}} \right)^{2} } }}{n - 1}}$$
(17)

where \(x_{i}\) is the measured sample; \(\bar{x}\) is the mean value of samples; \(n\) is the number of samples.

Fig. 3
figure 3

The amplitudes of background noise and the corresponding PSD functions of GNSS-RTK

Full size image

4 Performance evaluation of CF-CEEMD

To test the performance of CF-CEEMD, we consider the following signal:

$$y\left( t \right) = \underbrace {{A_{1} {\text{e}}^{t} \sin \left( {2\pi f_{1} t} \right) + A_{2} {\text{e}}^{2t} \sin \left( {2\pi f_{2} t} \right)}}_{{y_{1} \left( t \right)}} + y_{2} \left( t \right)$$
(18)

where \(f_{1} = 20\;{\text{Hz}}\), \(f_{2} = 40\;{\text{Hz}}\), \(A_{1} = A_{2} = 0.1\), \(y_{1} \left( t \right)\) is the original signal, \(y_{2} \left( t \right)\) is the noise signal with a SNR of 5 dB. Assume that the unit of vibration amplitude is centimeter (cm). The sample rate is set to 200 Hz and the sampling time is 2 s. Figure 4 shows the time history curves of the original signal \(y_{1} \left( t \right)\) and the signal with additive noise \(y\left( t \right)\). Following this, the frequency range, i.e. 5–60 Hz, is first used for the band-pass Chebyshev filter. Then the first nine IMF components are obtained from the filtered signal using CEEMD, as shown in Fig. 5.

Fig. 4
figure 4

The amplitudes of \(y_{1} \left( t \right)\) and \(y\left( t \right)\)

Full size image
Fig. 5
figure 5

The IMF components from the filtered signal

Full size image

The next step is to calculate the correlation coefficient between each IMF and the Chebyshev filter signal via Eq. (3), which is presented in Table 2. When the correlation coefficient \(\rho\) is less than 0.1, the corresponding IMF components are deemed as the illusive IMF components. Therefore, the IMF6–IMF10 components are removed and the remaining IMF components are reconstructed, as shown in Fig. 6. To evaluate the effect of noise reduction, SNR and root mean square error (RMSE) are introduced. They can be expressed in the following form:

$$\text{SNR} = 10\log_{10} \left\{ {\frac{{\sum\nolimits_{i = 1}^{n} {S_{i}^{2} } }}{{\sum\nolimits_{i = 1}^{n} {\left( {S_{i} - S^{\prime}_{i} } \right)^{2} } }}} \right\}$$
(19)
$$\text{RMSE} = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^{n} {\left( {S_{i} - S^{\prime}_{i} } \right)^{2} } }$$
(20)

where \(S_{i}\) and \(S^{\prime}_{i}\) represent the real signal and the reconstruction signal, respectively, and n is the length of the signal. The maximum SNR and minimum RMSE are better with regard to the effect of noise reduction. In addition, a single CEEMD method was applied to denoise the signal \(y\left( t \right)\), the purpose of which is to make a comparison. Table 3 depicts the statistical results of SNR and RMSE under three different approaches, i.e. CF, CEEMD and CF-CEEMD. It can be seen that the performance of CF-CEEMD is better than the other two approaches. Hence, this approach will be applied to analyze the vibration response of a long-span bridge based on GNSS-RTK measurement.

Table 2 Correlation coefficient between each IMF component and Chebyshev filter signal
Full size table
Fig. 6
figure 6

The amplitudes of the original signal and the reconstruction signal

Full size image
Table 3 Statistical results of SNR and RMSE
Full size table

5 Dynamic monitoring of Tianjin Rainbow Bridge

5.1 Description of the bridge and the FE model

Tianjin Rainbow Bridge is a concrete-filled steel tubular arch bridge in the east part of Tianjin, China. The total length of the bridge is 1215.69 m. The main bridge is a rigid arch system with a simple supported down bearing flexible tie rod with the length of 504 m, as shown in Fig. 7. It consists of three spans with each span of 160 m, and the vector height is 32 m. The total width of the main bridge is 29 m. In June 2010, one longitudinal concrete beam of the main bridge cracked due to the long-term passage of overweight vehicles, and at the same time, two adjacent longitudinal concrete beams were damaged to varying degrees. Subsequently, all longitudinal concrete beams were replaced by combined beams after 4 months of repair.

Fig. 7
figure 7

Panoramic schematic of Tianjin Rainbow Bridge

Full size image

The three-dimensional FE model of the bridge was developed using ANSYS 14.5 software before the field measurement. In this model, there are 1765 nodes and 2727 elements. The longitudinal beams, transverse beams, wind braces, steel pipe and piers were modeled via using BEAM44 elements. The tie bars and the deck of the bridge were modeled via using LINK10 and SHELL63 elements, respectively. Figure 8a–l show the first twelve vertical mode shapes of the structure, and the corresponding modal frequencies are 0.6787, 1.0361, 1.4171, 2.1254, 2.3225, 2.6945, 3.0455, 3.2508, 3.4604, 3.7906, 3.9006, 4.3091 Hz, respectively.

Fig. 8
figure 8

Finite element modal analysis results: a the first-order mode; b the second-order mode; c the third-order mode; d the fourth-order mode; e the fifth-order mode; f the sixth-order mode; g the seventh-order mode; h the eighth-order mode; i the ninth-order mode; g the tenth-order mode; k the 11th-order mode; l the 12th-order mode

Full size image

5.2 Experiment scheme

From Fig. 8, the maximum deformation of the bridge exists at 1/4, 1/2 and 3/4 of each span. The sensors arranged at these positions can effectively reveal the vibration characteristics of the structure. Therefore, this study established a structural health monitoring system based on ten high-rate (50 Hz) GNSS receivers. One GNSS receiver as the reference station was placed on a stable location and nearly 120 m away from the bridge, as shown in Fig. 9a. The other nine GNSS receivers as the rover stations were installed at one side of the bridge, as shown in Fig. 9b. The height of the antenna from sea level is about 18.04 m. Figure 10 depicts the schematic locations with a total of nine monitoring points (i.e. C1–C9).

Fig. 9
figure 9

a The arrangement of GNSS reference station; and b the arrangement of GNSS rover stations

Full size image
Fig. 10
figure 10

The position of GNSS sensors for the bridge

Full size image

5.3 Data processing and results analysis

The vertical vibration experiment on Tianjin Rainbow Bridge was conducted for 9 consecutive hours from 9:00 a.m. to 6:00 p.m. on 10 July 2019. The analysis process of all measuring points is the same. To avoid repetition, only one measuring point, i.e. C5 point, is selected for further study. On the premise that the selected data can fully reflect the dynamic characteristics of the structure and do not contain too many outliers, the time interval of 200 s is chosen. The original signal and the corresponding PSD function of the measured point C5 are shown in Fig. 11. The amplitude of the displacement is between − 0.0349 m and 0.0350 m. Fast Fourier transform (FFT) was adopted to identify the modal frequencies of the bridge. It can be seen that there are three obvious peaks (i.e. 0.6169, 1.096 and 1.3899 Hz) corresponding to the first three vertical modes of the bridge from PSD distribution. Meanwhile, it can also be found that the identified modal frequencies via employing FFT approach coincide with the results of FE analysis with a little difference. In addition, it can be found that GNSS cannot reflect the high-frequency signals with low amplitude. Even with a high sampling rate, only a few low order modes are detected. Subsequently, the proposed CF-CEEMD method was used to reduce the interference of background noise and derive the dynamic displacement of the bridge. Figure 12 presents the Chebyshev filter signal and the corresponding PSD function. It was observed that the amplitude of the displacement (i.e. − 0.0247 to 0.0253 m) was obviously decreased after Chebyshev filter. Figure 13 depicts the obtained 13 IMF components based on CEEMD analysis. It is noteworthy that the de-noising process does not randomly remove some IMF components, which will result in a large error. This study determines the illusive IMF components via calculating the correlation coefficient between each IMF and the Chebyshev filter signal, which is shown in Table 4. It can be found that the correlation coefficients of the IMF10–IMF13 components are less than 0.1; hence, they are deemed as the illusive IMF components and removed. Meanwhile, the remaining IMF components are reconstructed. Figure 14 displays the final de-noising results. The amplitude of the displacement is between − 0.0247 and 0.0248 m. Compared with Fig. 13, the minimum value of the displacement does not change, and the maximum value decreases. Importantly, it can be clearly observed from the PSD distribution of Fig. 14 that the dominant frequency information of the bridge is reserved via CF-CEEMD filter. That is to say, only the background noise and the quasi-static displacement are removed in the filtering process. In addition, the RMS values of the original signal and the final CF-CEEMD filter signal (i.e. 0.0091 and 0.0070 m) are derived via Eq. (17).

Fig. 11
figure 11

The original signal of point C5 and its PSD function

Full size image
Fig. 12
figure 12

The Chebyshev filter signal and its PSD function

Full size image
Fig. 13
figure 13

The IMF components of the Chebyshev filter signal

Full size image
Table 4 Correlation coefficient between each IMF component and Chebyshev filter signal
Full size table
Fig. 14
figure 14

The reconstructed signal and its PSD function

Full size image

Finally, DD-SSI algorithm is applied to identify the damping ratios and the mode shapes of the bridge. The stabilization diagram reveals the functional relationship between the modal parameter and the model order. With the increase of the model order, the number of the extracted modal parameters will gradually increase. However, the real modal parameters will tend to be stable. In general, the stability of modes can be judged based on Eqs. (21)–(23) [38]. As shown in Fig. 15, it was observed that there are three stable modes, and the frequency values were in good agreement with the peaks in the PSD function of the signal. Meanwhile, the corresponding damping ratios were derived (i.e. 1.77, 1.43 and 1.25%). Figure 16 illustrates the identified mode shape. Compared with the results of FE analysis, both agree with each other generally (shown in Table 5). Thus far, all the dynamic parameters of the bridge were successfully derived via using CF-CEEMD and DD-SSI methods:

$$\frac{{f_{i}^{\left( n \right)} - f_{i}^{{\left( {n + 1} \right)}} }}{{f_{i}^{\left( n \right)} }} \le 1\%$$
(21)
$$\frac{{\xi_{i}^{\left( n \right)} - \xi_{i}^{{\left( {n + 1} \right)}} }}{{\xi_{i}^{\left( n \right)} }} \le 5\%$$
(22)
$$1 - \frac{{\left\| {\varphi_{i}^{\left( n \right)} \varphi_{i}^{{\left( {n + 1} \right)}} } \right\|^{2} }}{{\left\| {\varphi_{i}^{\left( n \right)} } \right\|^{2} \left\| {\varphi_{i}^{{\left( {n + 1} \right)}} } \right\|^{2} }} \le 5\%$$
(23)

where \(f_{i}^{\left( n \right)}\), \(\xi_{i}^{\left( n \right)}\) and \(\varphi_{i}^{\left( n \right)}\) are i-th identified natural frequency, damping ratio and mode shape at the system order n, respectively. It should be noted that \(\left\| {\, \cdot \,} \right\|^{2}\) is the 2-norm operator.

Fig. 15
figure 15

Stabilization diagram using DD-SSI

Full size image
Fig. 16
figure 16

The identified mode shapes: a the first-order mode; b the second-order mode; c the third-order mode

Full size image
Table 5 Comparison of field measurement and FE results
Full size table

6 Conclusion

In this study, the dynamic deformation of a long-span bridge is investigated based on high-rate GNSS-RTK technique. A combined data analysis method (i.e. CF-CEEMD) was put forward to derive the dynamic displacement of the bridge. FFT and DD-SSI methods were applied to identify the modal parameters of the bridge. Meanwhile, for the sake of comparing with the identified results, the FE model of the structure is established. The following conclusions are summarized: (1) based on GNSS-RTK measurement, the first three modal parameters of the bridge were successfully derived. This illustrates that high-rate GNSS-RTK technique is an effective tool for monitoring the dynamic responses of long-span bridges. Note that GNSS cannot reflect the high-frequency signals with low amplitude. Even with a high sampling rate, only a few low order modes are detected. (2) Based on the simulation analysis, the proposed CF-CEEMD method performs better than the single CF and CEEMD approaches. It can be used to reduce the interference of GNSS-RTK background noise and derive the dynamic displacement of the structure without distortion. (3) The identified results via DD-SSI method based on the field measurement agree well with the predicted values based on the FE analysis.