1 Introduction

Mechanical, civil, and aerospace engineering communities have already identified structural health monitoring as a challenging problem. The ineffectiveness of visual examination and destructive testing in damage detection has been a major concern for the last few years. The aerospace industry is in need of new low-cost, nondestructive testing techniques for detecting damages in aerospace components. Consequently, in the last few decades, many researchers have reported various nondestructive damage detection methods.

In particular, damage detection based on structural response to vibration has gained popularity in recent years. The basic principle involved in such damage detection methods is to compare the behaviour of structures to vibration in the damaged and undamaged state [1].

Structural damages lead to changes in dynamic characteristics of the structure such as natural frequencies, mode shapes, and modal damping. Since natural frequencies can be easily obtained from vibration response, damage detection by studying the change in natural frequency became a popular way to identifying and quantifying the damages [2]. Pandey, Biswas, and Samman [3] have investigated a parameter called as the curvature mode shape as a possible candidate for locating damage. Later, Artificial Neural Network was used to solve the problem of damage detection [4, 5] and yielded excellent results. Hou, Noori, and Amand [6] developed a wavelet-based approach for structural damage detection, wherein characteristics of the vibration signals under wavelet transformation were examined. Curadelli et al. [7] have extended the use of wavelet transform to detect structural damage by means of the instantaneous damping coefficient identification. Yet, another approach was to minimize an objective function, which is defined in terms of the discrepancy between vibration data identified by modal testing and those computed from analytical model [8,9,10,11]. Giuseppe Quaranta, Biagio Carboni, and Walter Lacarbonara [12] have investigated the numerical issues involved in using modal curvature for damage detection and suggested a more affordable way for detecting damage with modal curvature data.

In this paper, the change in natural frequency of the structure is used to locate and quantify the damage. A sensitivity analysis [13] is performed to compute the change in natural frequencies due to the presence of damage. The sensitivity equation which defines the sensitivity of natural frequencies of the system to small changes in stiffness is used in defining the objective function. The optimization algorithm used is the Cuckoo Search (CS) [14], which is a relatively new optimization algorithm and has shown great potential and simplicity when compared to well-developed algorithms like Genetic Algorithm. Cuckoo Search algorithm is known for its easy implementation and faster convergence rate. The objective function compares the changes in vibration data measured before and after the damage with that of the analytical model. The analytical method used is the Finite-Element Method (FEM). The results are obtained in the form of Stiffness Reduction Factors (SRFs) of different elements of the structure. The results show that the damaged elements can be detected with high accuracy and with relatively shorter computational time.

However, in the case of symmetrical structures, two or more damage sites will be predicted, depending on the degree of geometric and material symmetry [15]. The situation is investigated with the help of a symmetrical fixed–fixed beam. In such cases, to uniquely determine the damage location, displacement measurements or mode shape measurements have to be made. In this paper, in addition to natural frequencies, the structural response (vertical displacements) to a static load is considered to detect the damage in the case of symmetric fixed–fixed beam. Such measurements could be easily made in a real structure such as a Truss bridge where vehicle loads could be considered as a typical static load and displacements could be measured at various points. However, for minor damages, the stiffness reduction will be very low, and hence, change in displacements would be negligible. In such cases, both frequency measurements and displacement measurements have to be used to detect the damage. Two criteria are considered for damage detection, namely, the frequency changes and a combination of frequency changes and displacement changes (or changes in acceleration–time response).

2 Dynamic analysis

2.1 Sensitivity equation

The equation of motion for undamped free vibration of a system can be written in the form of an eigenvalue problem as:

$$\begin{aligned} ({\mathbf {K}_\mathbf {0}}-\lambda _{i0}{\mathbf {M}_\mathbf {0}}){{\varvec{\phi }_\mathbf {i0}}}=0 \quad i=1,2,3,4\ldots n. \end{aligned}$$
(1)

Here, \({\mathbf {K}_\mathbf {0}}\) and \({\mathbf {M}_\mathbf {0}}\) are the stiffness and mass matrices for undamaged structure, respectively. \({{\varvec{\phi }_\mathbf {i0}}}\) represents the mode shape vector for \(\lambda _{i0}\) (eigenvalue) and \(\lambda _{i0}=\omega _{i0}^2\).

If \({\varvec{\delta }\mathbf {K}}\) is the small change in the stiffness matrix due to the damage and \(\delta \lambda _{i0}\) is the change in the eigenvalue, then neglecting the change in mass matrix, Eq. (1) becomes:

$$\begin{aligned}{}[\mathbf {K}_\mathbf {0}+\varvec{\delta }\mathbf {K} -(\lambda _{i0}+\delta \lambda _{i0})\mathbf {M}_\mathbf {0}]({\varvec{\phi }_\mathbf {i0}}+{\varvec{\delta \phi }_\mathbf {i0}})=0. \end{aligned}$$
(2)

Expanding Eq. (2) and neglecting second-order terms yield:

$$\begin{aligned}&\mathbf {K}_\mathbf {0}{\varvec{\phi }_\mathbf {i0}}+\mathbf {K}_\mathbf {0}{\varvec{\delta \phi }_\mathbf {i0}}+\varvec{\delta }\mathbf {K}\mathbf { \phi _{i0}}-\lambda _{i0}\mathbf {M}_\mathbf {0}{\varvec{\phi }_\mathbf {i0}} \nonumber \\&\quad - \delta \lambda _{i0}\mathbf { M_0} {\varvec{\phi }_\mathbf {i0}}-\lambda _{i0}\mathbf {M}_\mathbf {0}{\varvec{\delta \phi }_\mathbf {i0}}= 0 \end{aligned}$$
(3)

Using Eq. (1) in Eq. (3), we get:

$$\begin{aligned} \mathbf {K}_\mathbf {0}{\varvec{\delta \phi }_\mathbf {i0}}+\varvec{\delta }\mathbf {K} {\varvec{\phi }_\mathbf {i0}} -\delta \lambda _{i0} \mathbf {M}_\mathbf {0} {\varvec{\phi }_\mathbf {i0}}-\lambda _{i0}\mathbf {M}_\mathbf {0}{\varvec{\delta \phi }_\mathbf {i0}}=0. \end{aligned}$$
(4)

Multiplying Eq. (4) throughout by \({\varvec{\phi }_\mathbf {i0}^\mathbf {T}}\) gives:

$$\begin{aligned}&{\varvec{\phi }_\mathbf {i0}}^{\text {T}} \varvec{\delta }\mathbf {K} {\varvec{\phi }_\mathbf {i0}}-\delta \lambda _{i0} {\varvec{\phi }_\mathbf {i0}}^{\text {T}} \mathbf {M}_\mathbf {0} {\varvec{\phi }_\mathbf {i0}} \nonumber \\&\quad + ({\varvec{\phi }_\mathbf {i0}}^{\text {T}} \mathbf {K}_\mathbf {0}-\lambda _{i0} {\varvec{\phi }_\mathbf {i0}}^{\text {T}} \mathbf {M}_\mathbf {0}){\varvec{\delta \phi }_\mathbf {i0}}=0. \end{aligned}$$
(5)

The transpose of Eq. (1) gives:

$$\begin{aligned} {\varvec{\phi }_\mathbf {i0}}^{\text {T}}(\mathbf {K}_\mathbf {0}-\lambda _{i0}\mathbf {M}_\mathbf {0})=0. \end{aligned}$$
(6)

Multiplying Eq. (6) by \(\mathbf {\delta \phi _{0i}}\)

$$\begin{aligned} ({\varvec{\phi }_\mathbf {i0}}^{\text {T}}\mathbf {K}_\mathbf {0}-{\varvec{\phi }_\mathbf {i0}}^{\text {T}}\lambda _{i0}\mathbf {M}_\mathbf {0}){\varvec{\delta \phi }_\mathbf {i0}}=0. \end{aligned}$$
(7)

Therefore, Eq. (5) reduces to:

$$\begin{aligned} {\varvec{\phi }_\mathbf {i0}}^{\text {T}}\mathbf { \delta K} {\varvec{\phi }_\mathbf {i0}}-\delta \lambda _{i0} {\varvec{\phi }_\mathbf {i0}}^{\text {T}} \mathbf {M}_\mathbf {0} {\varvec{\phi }_\mathbf {i0}}=0 \end{aligned}$$
(8)

Equation (8) can be rewritten as follows:

$$\begin{aligned} \delta \lambda _{i0}=\frac{{\varvec{\phi }_\mathbf {i0}}^{\text {T}}\times \varvec{\delta }\mathbf {K}\times {\varvec{\phi }_\mathbf {i0}}}{{\varvec{\phi }_\mathbf {i0}}^{\text {T}}\times \mathbf {M}_\mathbf {0} \times {\varvec{\phi }_\mathbf {i0}}}, \end{aligned}$$
(9)

where:

$$\begin{aligned} \varvec{\delta }\mathbf {K}=-\sum _{e=1}^{n} {\delta k_e}\times \mathbf {[K_e]}. \end{aligned}$$
(10)

Here, summation implies assembly. \(\delta k_e\) is defined as the stiffness reduction factor (SRF). \(\mathbf {[K_e]}\) is the element stiffness matrix. From Eq. (9), it is evident that the change in natural frequency of the structure is a function of the change in stiffness of the structure, which by itself is a function of stiffness reduction factors (SRFs) of elements. Hence, the change in natural frequency can be represented as function of SRFs of elements of the structure.

Furthermore, the relative change in the ith eigenvalue as a measure of damage, known as damage index (DI), can be expressed as follows:

$$\begin{aligned} {\text {DI}}=\frac{\lambda _{i}-\lambda _{i0}}{\lambda _{i0}}=\frac{\delta \lambda _{i0}}{\lambda _{i0}}. \end{aligned}$$
(11)

3 Static analysis

As discussed earlier, for symmetric structures, damage site cannot be uniquely determined [15]. In this case, structural response to a static load is considered to accurately detect damage. This is based on the fact that, due to stiffness reduction, the structural response to a given load vector would be more in the damaged state when compared to the undamaged state. In this paper, the vertical displacement measurements are considered to detect the damages.

3.1 Sensitivity equation

In dynamic analysis, a sensitivity equation which defines sensitivity of natural frequency to small change in stiffness was derived. On similar terms, for static analysis, the sensitivity equation describes the sensitivity of displacement vector \(\{x\}\) to a small change in stiffness \(\varvec{\delta }\mathbf {K}\), under the action of a given static load vector \(\mathbf {F}\).

The equilibrium equation in the undamaged state can be written as follows:

$$\begin{aligned} \mathbf {F}=\mathbf {K}_\mathbf {0} \mathbf {x}. \end{aligned}$$
(12)

In the damaged state, under the action of the same load vector \(\mathbf {F}\), Eq. (12) becomes:

$$\begin{aligned} \mathbf {F}=(\mathbf {K}_\mathbf {0}+\varvec{\delta }\mathbf {K})(\mathbf {x}+{\varvec{\delta } \mathbf {x}}). \end{aligned}$$
(13)

Expanding Eq. (13) and using Eq. (12) in Eq. (13), we get:

$$\begin{aligned} \mathbf {K}_\mathbf {0}{\varvec{\delta } \mathbf {x}}+\varvec{\delta }\mathbf {K}\mathbf { x}+\varvec{\delta }\mathbf {K} {\varvec{\delta } \mathbf {x}}=0. \end{aligned}$$
(14)

Rearranging Eq. (14), we get:

$$\begin{aligned} {\varvec{\delta } \mathbf {x}}=-(\mathbf {K}_\mathbf {0}+\varvec{\delta }\mathbf {K})^{-1}\varvec{\delta }\mathbf {K}\mathbf { x}. \end{aligned}$$
(15)

\(\delta x\) is a column vector containing the change in the displacement at various positions in the structure due to the occurrence of a damage. This expression is used in the formulation of objective function based on displacement measurements.

4 Objective function

The objective function defines the error between vibration data obtained from analytical model computations and experimental model testing. Objective function could be defined in three different ways depending on the static and vibration data available.

4.1 Objective function based on frequency measurements

The objective function for the optimisation problem is defined as follows:

$$\begin{aligned} J=\sqrt{\sum _{i=1}^{{\text {nmodes}}} \Bigg (\Big [\frac{\lambda _i-\lambda _{i0}}{\lambda _{i0}}\Big ]^{{\text {AN}}} -\Big [\frac{\lambda _i-\lambda _{i0}}{\lambda _{i0}}\Big ]^{{\text {EX}}}\Bigg )^2}, \end{aligned}$$
(16)

where suffixes ‘AN’ and ‘EX’ represent analytical and experimental values, respectively. The objective function is a global error function which defines the error between the experimentally and analytically obtained frequency changes. The objective function based on relative change was first proposed by Hong Hao and Yong Xia [10]. Here, ‘\(\lambda _i\)’ represents the eigenvalue in the damaged state. In our case, least square error has been considered. The solution of this optimization problem is unique for asymmetric structures [15]. At least two modes of vibration must be considered for formulating the objective function.

Equation (16) can be rewritten as follows:

$$\begin{aligned} J=\sqrt{\sum _{i=1}^{nmodes} \Bigg (\Big [\frac{\delta \lambda _{i0}}{\lambda _{i0}}\Big ]^{AN} -\Big [\frac{\lambda _i-\lambda _{i0}}{\lambda _{i0}}\Big ]^{EX}\Bigg )^2}. \end{aligned}$$
(17)

\(\delta \lambda _{i0}\) is obtained from Eq. (9). From Eqs. (9) and (17), it is evident that J is a function of all the stiffness reduction factors (\(\delta k_e\)). Minimizing J gives the values of all the SRFs. The information contained in the mode shape vectors in the predamaged state is incorporated in the objective function. The analytical values of eigenvalues and mode shape vectors in the predamaged condition are obtained by FEM. The optimisation is carried out using Cuckoo Search algorithm (CSA). The method does not require any accurate analytical modelling to detect damage. The incorporation of sensitivity equation in the objective function has also resulted in relatively lower computational time.

In the present study, numerical experiments are performed with the help of ANSYS. Two examples of cantilever beams with different damage scenario have been considered.

4.2 Objective function based on displacement measurements

Objective function for the optimisation problem based on displacement measurements can be defined in a similar way as follows:

$$\begin{aligned} J=\sqrt{\sum _{i=1}^{{\text {npoints}}} \Bigg (\Big [\frac{\delta x_i}{x_{i0}}\Big ]^{{\text {AN}}} -\Big [\frac{ x_i-x_{i0}}{x_{i0}}\Big ]^{{\text {EX}}}\Bigg )^2}, \end{aligned}$$
(18)

where \(\delta x_i\) represents the change in vertical displacement at the ith position and can be obtained from Eq. (15). The number of points in which displacement measurements has to be made is decided by the investigator. More displacement measurements must be made at those points where damage is suspected. However, the displacement changes tend to be very small in the case of minor damages. In such cases, the accuracy of damage detection might get reduced. In addition, huge static loads have to be applied in such cases. The analytical values of the displacement vector is obtained by FEM. In the previous case, ‘J’ is a function of all SRFs. ‘J’ could be minimized to obtain the SRFs.

4.3 Objective function based on both frequency and displacement measurements

Objective function for the optimization problem based on both displacement and frequency measurements can be defined as \(\sqrt{J}\), where:

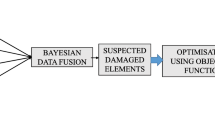
$$\begin{aligned}&J= W_i\sum _{i=1}^{{\text {npoint}}} \Bigg (\Big [\frac{\delta x_i}{x_{i0}}\Big ]^{{\text {AN}}}-\Big [\frac{\delta x_i}{x_{i0}}\Big ]^{{\text {EX}}}\Bigg )^2 \nonumber \\&\quad + W_j\sum _{j=1}^{nmode} \Bigg (\Big [\frac{\delta \lambda _{i0}}{\lambda _{i0}}\Big ]^{AN} - \Big [\frac{\delta \lambda _{i0}}{\lambda _{i0}}\Big ]^{EX}\Bigg )^2. \end{aligned}$$
(19)

The relative accuracy in the measurement of natural frequency and displacement will determine the weights \(W_i\) and \(W_j\). The value of \(W_i\) and \(W_j\) can be chosen between 0 and 1. When the frequency data are more reliable, \(W_j\) is chosen higher than \(W_i\) and closer to 1. In most cases, the relative measurement error of frequency is about 1% [10], whereas the displacement or acceleration measurements are more contaminated with noise and it is customary to add 5–10% white noise to the analytically obtained displacement profile to simulate field measurements [16]. For pursuing the damage detection procedure shown in Fig. 1, the parameters \(W_i\) and \(W_j\) have to be known before hand. This is achieved by developing the finite-element model of the structure to be assessed and simulating a suitable damage scenario. Adequate measurement noise is added to the frequencies and displacements obtained from the numerical model and the weights are determined, so that the damage is located accurately based on the procedure in Fig. 1. The computed weights could be used for assessing the health of the structure based on field measurements. This objective function should be used when dealing with symmetric structures, where frequency measurements alone are not sufficient to guarantee a unique solution to the optimisation problem [15].

4.4 Objective function based on frequency data and acceleration–time history

If accelerometers are used to record the dynamic response of a structure subjected to an arbitrary excitation, the obtained acceleration–time plot could be used to define an objective function as \(\sqrt{J}\), where:

$$\begin{aligned}&J=W_1\sum _{i=1}^{{\text {npoint}}} \sum _{j=1}^{{\text {ntime}}} \Bigg ( \Big [\frac{\delta t_{ij}}{t_{ij}}\Big ]^{{\text {AN}}} -\Big [\frac{\delta t_{ij}}{t_{ij}}\Big ]^{{\text {EX}}}\Bigg )^2\nonumber \\&\quad +W_2\sum _{j=1}^{{\text {nmode}}} \Bigg (\Big [\frac{\delta \lambda _{i0}}{\lambda _{i0}}\Big ]^{{\text {AN}}} - \Big [\frac{\delta \lambda _{i0}}{\lambda _{i0}}\Big ]^{{\text {EX}}}\Bigg )^2, \end{aligned}$$
(20)

where \(t_{ij}\) represents acceleration of ith location at \(j_{th}\) time step. npoint refers to the number of measurement sites. \(W_1\) and \(W_2\) are the weights as discussed previously. The general damage detection procedure is shown in Fig. 1.

Fig. 1
figure 1

Procedure for damage detection

Full size image

5 Overview of Cuckoo Search algorithm

Cuckoo Search is a relatively new metaheuristic optimization algorithm [14, 17]. The algorithm is based on the aggressive breed characteristics of cuckoo birds. This is incorporated in combination with Lévy flight behaviour of certain birds to get a simple and effective optimization algorithm. This is used in minimizing Eqs. (17), (18), (19), and (20).

5.1 Cuckoo breed characteristics

Cuckoos are well known for their breeding strategy. They lay their eggs in the nests of other host birds (particularly crows). If the host bird identifies the cuckoo’s egg, it may throw away the egg or abandon the nest. Some cuckoo species belonging to the ‘Tapera’ genus have evolved, such that female parasitic cuckoos are often found to be extremely specialized in mimicking host eggs. Thus, it becomes very difficult for the host bird to detect the cuckoo’s egg.

5.2 Lévy flight

A Lévy flight is a random walk in which the step lengths have a probability distribution. When defined as walks in space, the steps made are in random directions. However, this direction depends on the current position.

In nature, animals and birds search for food in a random or quasi-random manner. The path in which an animal moves becomes a random walk, because its next step is based on the current location. Hence, the direction that it chooses depends on a probability model which can be modelled mathematically. Thus, it is a type of random walk in which each successive move is chosen randomly and is uninfluenced by any previous moves. For example, consider a drunk person walking on a street. The likelihood of the person taking a step to the right is the same as that of the person taking a step to the left, with no memory of the previous routes. In a Lévy walk, most steps are taken within a small area; however, longer routes may be taken occasionally. A wide variety of animals, such as marine predators, birds, terrestrial mammals, and various insects exhibit Lévy-like patterns. Evidence of Lévy walks has also been found in the ways that people wander freely.

5.3 Cuckoo Search algorithm

For simplicity in defining the CSA, the following idealised rules are considered:

  1. 1.

    Each cuckoo lays one egg at a time and dumps it in a randomly chosen nest.

  2. 2.

    The best nests with high-quality eggs (solutions) will carry over to the next generation.

  3. 3.

    The number of available host nests is fixed, and a host can discover an alien egg with a probability of \(p_a \in [0,1]\). In this case, the host bird can either throw away the egg or build a completely new nest in a completely new location.

For a maximization problem, the fitness or quality of a solution can be taken to be directly proportional to the value of the objective function. For other types of problems, other fitnesses can be defined accordingly. For a minimization problem, for example, the inverse of the function value may be taken as the fitness of the function.

Each egg in a nest is taken to represent a solution. A cuckoo is taken to represent a new solution. The main aim of the program is to discard the old solutions and accept potentially new and improved solutions.

When generating a new solution, \(x^{t+1}\) for a cuckoo i, Lévy flight is performed as:

$$\begin{aligned} x_i^{t+1} = x_i^{t}+\alpha \oplus {\text {Levy}}(\lambda ), \end{aligned}$$
(21)

where \(\alpha > 0\) is the step size, which is related to the scales of the new problem of interest. In most cases, we can use \(\alpha =1\). The product \(\oplus\) means entrywise multiplication.

Based on these steps, the pseudocode for CS algorithm can be written as [14]:

figure a

6 Example 1: cantilever beam (a)

To demonstrate the proposed damage detection technique, a cantilever beam has been used as an example. The example problem is taken from an experimental study reported by Yang et al. [18]. The geometric and material properties of the beam are as follows:

  • Material: Aluminium

  • Length: 495.3 mm

  • Width: 25.4 mm

  • Depth: 6.35 mm

  • Young’s modulus: 7.1 \(\times\)\(10^{10}\) N/m\(^2\)

  • Mass density: 2210 kg/m\(^3\).

Fig. 2
figure 2

Configuration of the cantilever beam [10]

Full size image

The beam was damaged by a saw cut, as shown in Fig. 2b. The beam was modelled using 20 plane frame elements having six degrees of freedom at each node. The natural frequencies of the undamaged beam obtained by eigenvalue analysis are given in Table 1. The damage was induced in the ninth element.

Table 1 Analytical and experimental natural frequencies (Yang et al. 1985)
Full size table

The experimental values of natural frequency in the predamaged and damaged states as obtained by Yang et al. [18] are also provided in Table 1. Only the first six natural frequencies were used for damage detection. Since it is an unsymmetrical structure, natural frequency measurements are sufficient to detect the damage and mode shape measurements are not made.

The objective function was created using the sensitivity equation and the error is minimized using CSA to obtain the SRF’s. For the comparison of results, the objective function defined by Hong and Hao [10] is also minimized using CSA and it was found that the results so obtained agreed well with the reported results in the reference, which was obtained using genetic algorithm.

Fig. 3
figure 3

SRF of the cantilever beam (in %)

Full size image

The results are shown in Fig. 3. The number of nests was set to 25. The probability \(p_a\) is set to 0.35. The process is iterated 65,000 times for good convergence.

The results show that the damage is correctly detected in element 9. Small magnitude of SRF is detected in the 2nd and 12th elements which may be due to noise in the frequency measurements and nonlinearity caused due to severe damage [10]. The use of sensitivity equation in the objective function has improved the accuracy in damage detection. Figure 3 shows that the computed SRF in ninth element is three times the SRF of Element 12. Therefore, it can be concluded with a reasonable level of confidence that the major damage is in element 9. The computational time is also significantly lower compared to the other methods. This is because the time required for eigenvalue analysis is saved in each iteration. The method also has the advantage that it does not require any accurate analytical modelling or finite-element model updating. Algorithm detects very minor damage in element 8 which is adjacent to the actual damage location. This is due to the involvement of mode shape vector in the objective function and very severe damage in element 9 (the section was actually weakened by 93.75% [18]).

6.1 Number of modes and number of finite elements to be used for damage detection

Theoretically, the measurement of frequency changes in one pair of modes will yield a locus of possible damage sites [15]. Only an optimum number of modes are needed to be considered so as to transform the problem into a well-posed one, i.e., for unique determination of the damage location. In the above analysis, it is essential to use the first six natural frequencies to achieve a unique solution to the optimisation problem. Numerical experiment by considering only the first five natural frequencies leads to an ill-posed problem, i.e., a unique solution was not obtained. The noise in the frequency measurement is the major reason that caused the problem to be ill-posed. Since there is practical limit to the range of frequencies that a structure can be tested for, only the first few natural frequencies are used in all the demonstrations.

Fig. 4
figure 4

Effect of number of finite elements on the identified SRF of element containing damage (in %)

Full size image

The effect of number of finite elements used for damage detection is demonstrated in Fig. 4. It can be observed from Fig. 4 that, irrespective of the finite-element mesh used, the damage is accurately detected. However, the magnitude of the detected SRF depends on the proximity of the damage to the adjacent finite element. It is to be understood that, when the number of elements used is 15, 18, 20, 23, or 27, the damage is located approximately in the middle of the finite element which leads to a reasonably good estimate of the damage magnitude as observed in Fig. 4. However, for other cases in Fig. 4, due to the proximity of damage to adjacent element, the damage magnitude gets distributed across elements leading to a lower detected SRF. Numerical experiments by varying the number of elements have to be done for accurately determining the damage magnitude or an objective function defined by Eq. (19) could be used. In the simulations presented here, the number of elements is fixed at 20 to demonstrate that accurate analytical modelling (finer mesh) is not required for efficient damage detection.

7 Example 2: cantilever beam (b)

In this example, a cantilever beam with damages at multiple positions has been considered. The beam is simulated using ANSYS and the modal parameter obtained from ANSYS is used in place of the experimental values. The beam is shown in Fig. 5.

The geometric and material properties of the beam are as follows:

  • Material: Steel

  • Length: 600.0 mm

  • Width: 25.0 mm

  • Depth: 7.00 mm

  • Young’s modulus: 2.0 \(\times\)\(10^{11}\) N/m\(^2\)

  • Mass density: 7850 kg/m\(^3\).

Fig. 5
figure 5

Configuration of the cantilever beam (b)

Full size image

Damage was simulated in the form of a crack of width 5 mm, as shown in Fig. 5. The damage was induced in the 4th and 17th element. 40% and 60% reduction in cross-sectional area was provided in the 4th and 17th elements, respectively.

The values of natural frequency in the predamaged and damaged states as obtained by ANSYS analysis and obtained by analytical modelling are provided in Table 2. The beam was modelled using 20 plane frame elements having six degrees of freedom at each node. The first seven natural frequencies are used for damage detection.

The damage detection procedure was carried out and the results are shown in Fig. 6. The CSA parameters chosen are the same as before. The process is iterated 65,000 times for good convergence of results.

Table 2 Analytical and ANSYS natural frequencies
Full size table
Fig. 6
figure 6

SRF of the cantilever beam with multiple damage location (in %)

Full size image

The results show that the damage is correctly detected in element 4 and element 17. Small magnitude of SRF is detected in the 14th element which may be due to the nonlinearity caused due to severe damage. The algorithm detects SRF of 24.59% and 58.38% in the 4th and 17th elements, respectively. The results show that the algorithm gives a good insight into the relative magnitude of damages at different position.

8 Example 3: fixed–fixed beam

The special case of a symmetrical fixed–fixed beam is considered in this example. In this case, displacement measurements have to be made for effective damage detection. The beam was simulated and analyzed in ANSYS. Both modal analysis and static analysis are done to obtain the natural frequencies and the static displacement values. A uniformly distributed load of magnitude 500 N/m is applied for displacement values. The geometric and material properties of the beam are as follows:

  • Material: Aluminium

  • Length: 600.0 mm

  • Width: 25.0 mm

  • Depth: 6.00 mm

  • Young’s modulus: 7.1 \(\times\)\(10^{10}\) N/m\(^2\)

  • Mass density: 2770 kg/m\(^3\).

Damage was simulated in the form of a saw cut, as shown in Fig. 7. It was induced in the 12th element, the beam being modelled using 20 elements.

Fig. 7
figure 7

Configuration of the fixed–fixed beam

Full size image

The natural frequency values are provided in Table 3. As before, the beam was modelled using plane frame elements. The first six natural frequencies along with displacement values at five points on the beam are used for damage detection.

Table 3 Analytical and ANSYS natural frequencies
Full size table

For damage detection, the objective function defined by Eqs. (17) or (19) can be used. The relative effectiveness of the two objective functions is examined. The CSA parameters are already defined in the previous section and the process is iterated 65,000 times as before.

8.1 Damage detection with frequency measurements

In this case, only the first seven natural frequency values are used for damage detection. Objective function defined by Eq. (17) is minimized in this case. The results are shown in Fig. 8.

Fig. 8
figure 8

Identified SRF with frequency changes (in %)

Full size image

The results show that damage is detected in 12th element and 9th element, whereas the actual damage is in 12th element only. Perfect convergence in solution was not observed in this case. This is because, with symmetric structures, the damage cannot be uniquely located using frequency values [15]. From the observed result, it can be concluded that frequency changes alone are not sufficient to detect the damage.

Damage detection considering only displacement changes is not demonstrated in this example. The procedure requires a large number of displacement measurements, since the displacement changes are negligible for small damages.

8.2 Damage detection with both frequency and displacement measurements

A uniformly distributed load of magnitude 500 N/m is applied on the beam and the vertical displacement at five different positions on the beam (at 90 mm, 210 mm, 330 mm, 450 mm, and 570 mm from left end of the beam) is obtained before and after the damage. The load is chosen so as to obtain a maximum displacement of 5.3 mm, which is of measurable order. The analysis could even be carried out using a suitable concentrated load.

The objective function defined by Eq. (19) is minimized in this case. The weights \(W_i\) and \(W_j\) are set to unity, since both frequencies and displacements are obtained with the same degrees of accuracy. The results are shown in Fig. 9.

Fig. 9
figure 9

Identified SRF with frequency and displacement changes (in %)

Full size image

The figure pinpoints the damage to the 12th element. Thus, by combining frequency and displacement measurements in the analysis, the damage could be detected accurately in the case of symmetric structures. A small damage detected in the fifth element may be due to nonlinearity caused due to the damage. The computational time is reduced by invoking gauss elimination procedure on banded matrix to solve Eq. (15).

In most cases, the displacement changes tend to be very small, and hence, very sophisticated instruments are required for very accurate measurements. In such cases, the investigator is free to choose different weights \(W_i\) and \(W_j\) depending upon the relative accuracy in the measurements of frequencies and displacements.

9 Example 4: space frame model

The damage detection algorithm is applied to a three storey frame model shown in Fig. 10a.

Fig. 10
figure 10

Three storey frame specimen

Full size image

Focus is laid on detecting the storey in which the damage is present rather than identifying the structural element. Lumped mass modelling (LMM) is adopted as the analytical model to compute the natural frequencies and dynamic response. The geometric and material properties of the space frame are as follows:

Column properties

  • Material: Aluminium

  • Shear modulus: 26 \(\times\) 10\(^9\) N/m\(^2\)

  • Young’s modulus: 7.1 \(\times\)\(10^{10}\) N/m\(^2\)

  • Mass density: 2770 kg/m\(^3\)

  • Length of column: 310.0 mm

  • Column-cross section: Trapezoid with dimensions:

  • Longer side: 25 mm

  • Shorter side: 20 mm

  • Thickness: 2.56 mm.

Plate properties

  • Material: Steel

  • Young’s modulus: 2.1 \(\times\)\(10^{11}\) N/m\(^2\)

  • Shear modulus: 77 \(\times\) 10\(^9\) N/m\(^2\)

  • Mass density: 7850 kg/m\(^3\)

  • Dimension of Plate: 250 \(\times\) 200 \(\times\) 10 mm.

The Lumped mass model is shown in Fig. 10b. The model has three degrees of freedom and the shear building model is used to compute the global stiffness and mass matrix. The natural frequencies obtained by eigenvalue analysis are given in Table 4. After constructing the damping matrix, Newmark-beta method is used to obtain the dynamic response to base excitation.

Uni-axial shake table experiment was conducted on the specimen with accelerometers attached at individual storey levels as shown in Fig. 10a. The recorded acceleration–time history and the natural frequency obtained through a sine sweep procedure (Table 4) are used as input to the damage detection algorithm.

Table 4 Analytical and experimental natural frequencies
Full size table

For this particular problem, a two-stage damage detection procedure is carried out. In the first stage, the finite-element model is updated, so that the acceleration–time plot obtained experimentally and analytically has the same character in the undamaged state. The model is updated by applying suitable Stiffness reduction factor (SRF) for each storey. Stiffness reduction of 5%, 62%, and 2% has been obtained for the top, middle, and bottom storey, respectively, by minimizing an objective function based on direct comparison of frequencies in the undamaged state. The flexibility provided by the bolted connection is thus incorporated in the updated model. The updated natural frequency values are provided in Table 4.

Shake table experiment was conducted for sinusoidal wave of frequency 1.6 Hz and amplitude 1 mm. The acceleration–time plot for the damaged and undamaged state is also shown in Figs. 11, 12, and 13. From the plots, it can be inferred that damage has caused a shift in the system’s natural frequency, thereby lagging the response.

The acceleration–time plot obtained after model updating is shown in Fig. 14. The base excitation has a frequency of 1.6 Hz and amplitude 1 mm. 2% damping is considered in the analytical model for computing the response.

Fig. 11
figure 11

Acceleration–time plot for the top storey

Full size image

In the second stage, the updated model is used for damage detection. The objective function defined by Eq. (20) is minimized to obtain the SRF of the three storeys. To control the growth of error, only those time steps for which the acceleration in the intact and damaged state is either both positive or both negative is considered.

Fig. 12
figure 12

Acceleration–time plot for the middle storey

Full size image
Fig. 13
figure 13

Acceleration–time plot for the bottom storey

Full size image
Fig. 14
figure 14

Acceleration–time plot obtained analytically (undamaged state)

Full size image

9.1 Damage identification with changes in acceleration–time response

The acceleration of the three storeys between 2 s and 8 s with a time step of 0.3 s is considered for defining the objective function (npoint = 3). The response becomes steady after 9 s. In this case, \(W_2\) is zero.

The identified SRF are shown in Fig. 15. The figure shows that all the elements are detected as having damages. This may be attributed to the errors in measurement and noise. However, the middle storey is detected as having the most severe damage.

Fig. 15
figure 15

Identified SRF with acceleration changes

Full size image

9.2 Damage identification with both frequency changes and changes in acceleration time response

The frequency changes in the first two modes are also considered in addition to acceleration changes.

The relative contribution of frequency and acceleration to the objective function is considered as unity (\(W_1=1\)) and (\(W_2=\) 1, 0.1, 0.001), respectively.

The obtained SRF are shown in Fig. 16. It can be inferred that the damage is accurately detected in the middle storey when \(W_2=0.01\). Therefore, the relative weights \(W_1\) and \(W_2\) play a very major role in damage detection. In addition, since the error in frequency measurement are relatively less, it is more appropriate to make large number of frequency measurements. The weights have to be chosen based on the relative accuracy in the measurements made. Thus, the proposed algorithm is capable of detecting a minor damage.

Fig. 16
figure 16

Identified SRF considering both frequency changes and acceleration changes with different weights

Full size image

9.3 Effect of damping ratio on damage detection

In the above detection, 2% damping ratio was considered for computing dynamic response. The procedure is repeated for 1.5% and 2.5% damping. Similar results were obtained, indicating that change in damping ratio has negligible effect on damage detection. This may be attributed to the peculiar nature of the objective function defined based on relative error.

9.4 Effect of number of time steps on damage detection

In the above detection procedure, a total of 21 time steps were considered [ntime = 21 in Eq. (20)]. The procedure was repeated for different number of time steps between 2 s and 8s. The results obtained are shown in Fig. 17.

Fig. 17
figure 17

Effect of number of time steps (\({\text {ntime}}\)) on damage detection (\(W_2=0.01\))

Full size image

Figure 17 shows that the damaged storey could be accurately located and is independent of the number of time steps considered. However the magnitude of the detected damage depends on the number of time steps considered. This is due to the error involved in instrumentation and faint noise in the data which causes the problem to be ill-conditioned. This problem may be tackled by including a regularization parameter in the objective function, which stabilizes the ill-conditioned problem [19]. The proposed damage detection technique may find application in the health monitoring of buildings subjected to earthquake. The ground acceleration data could be obtained from an earthquake recording station and the sensors embedded in different structural members of the building could record the acceleration–time response. The initial portion of the response represents the healthy building and the occurrences of damage may be indicated by the jumps in the acceleration–time response. With the base excitation data and acceleration–time response available, one could detect the possible damage sites in a multi-storey building, after the earthquake has subsided.

To detect the exact column containing the damage, a more rigorous analysis is required. The structure may be modelled using space frame element [20]. Accelerometer readings on each of the columns could be used for damage detection. However, the tremendous computational time poses a serious problem for damage detection of large structures. In such cases, frequency and mode shape measurements may be combined to solve the problem. It is theoretically possible to identify the mode shape from acceleration response. It is then possible to define an objective function based on the identified frequencies and mode shapes of the structure. With the damaged storey already identified, the number of parameters to be estimated (SRF) in the objective function and, consequently, the computational time could be significantly reduced. Yet, another way would be to use the obtained mode shape changes to detect the damage based on Modal Strain energy change [21].

The proposed damage identification technique with acceleration response may also find application in the damage detection of bridges. In this case, the vehicle force acts as the forcing function which can by obtained by solving the moving force identification problem [22]. Bridge dynamic response may be obtained from accelerometers attached at specific positions on the bridge. With the above data available and by employing an appropriate finite-element model for the vehicle–bridge interaction, it is possible to detect the damage in the bridge using the proposed technique.

10 Conclusion

A method which detects structural damage accurately is demonstrated in this paper. The method which uses both static and dynamic responses for damage detection has many advantages compared to the existing methods. Based on the analysis done in this paper, the following conclusions can be drawn:

1. The sensitivity equation used in defining the objective function has significantly reduced the computational time when working with frequency data alone as demonstrated in Sect. 6. Cuckoo Search algorithm provided a faster convergence rate compared to other algorithms like genetic algorithm. The method did not require an accurate analytical modelling. Numerical results showed that the damage could be detected with reasonable degree of accuracy.

2. The proposed technique could even quantify the relative magnitude of damages at different positions as demonstrated in Sect. 7.

3. By suitably combining the frequency data with static displacement data, a unique solution (Damage location) to the optimisation problem could be guaranteed as demonstrated in Sect. 8.2.

4. Even a very small damage in one of the columns of a multi-storey frame structure could be detected with reasonable degree of accuracy as demonstrated in Sect. 9.