Introduction

Inverse problems are of particular interest in various scientific and engineering disciplines such as structural health monitoring, seismology, non-destructive evaluation (NDE), medical diagnosis and geophysics/submarine detection. In recent years, many studies have been conducted to develop effective approaches for damage detection in structural components. A significant progress has been achieved in obtaining numerical solutions of these problems during the past years (Kaveh et al. 2014; Kaveh et al. 2019a, b; Kaveh and Zolghadr 2017a, b; Kaveh and Dadras 2018; Kaveh and Mahdavi 2016; Saberi and Kaveh 2015).

Several numerical treatments of inverse problems are categorized as nonlinear. The efforts made over the last decades to overcome these nonlinear mathematical challenges can be categorized into two categories: qualitative methods and iterative algorithms.

Qualitative methods are characterized by an inverse scattering solution. These methods detect the obstacle (damage) from far- and/or near-field measurements of the scattered field which avoids the incorrect model assumption (Cakoni and Colton 2005). These qualitative methods may be classified as topological sensitivity (TS) (Bonnet and Guzina 2004; Gallego and Rus 2004; Guzina and Bonnet 2004), factorization method (FM) (Kirsch 2002), linear sampling method (LSM) (Dehghan Manshadi et al. 2014, 2018; Dehghan Manshadi and Khaji 2014; Khaji and Dehghan Manshadi 2015), the probe method (Potthast 2006) and point source method (Potthast 2001) which seek to determine the geometric properties (i.e., shape and location) of the scattered.

Iterative algorithms deal with the minimization of the error between the responses of a real damaged structure and hypothetical damaged structure. Some of these methods update the structural model during an iterative process (Perera and Fang 2010; Rao et al. 2004; Seyedpoor 2012). The other approaches are based on sensitivity analysis. These methods minimize the objective function to update the finite element model of the structure (Bakir et al. 2007; Li et al. 2016; Teughels and De Roeck 2005; Wu and Li 2006).

In recent years, many optimization techniques have been developed and used in various structural engineering problems, such as designing structures (Akin and Saka 2015; Esfandiari et al. 2018a, b; Esfandiary et al. 2016; Kaveh and Sabzi 2011). For detecting damages in these structures, optimization methods can be implemented using various response parameters. Some researchers used static response parameters such as displacement (Buda and Caddemi 2007; Chou and Ghaboussi 2001) and strain (Wang et al. 2010). Some others used dynamic response parameters such as frequency (Kaveh and Zolghadr 2012, 2015; Khiem and Tran 2014; Lee 2009; Morassi and Rollo 2001; Tabrizian et al. 2013), mode shape (Homaei et al. 2014; Ismail et al. 2006), a combination of frequency and mode shape (Ge and Lui 2005; Kang et al. 2012; Teughels and De Roeck 2005; Yu and Xu 2011), and modal curvatures (Quaranta et al. 2016) and acceleration (Li and Law 2010).

The main objective of this paper is to present a novel and efficient method for damage detection using the Levenberg–Marquardt algorithm. The method uses dynamic response parameters including frequency and mode shape. The formulation of the forward problem is presented first followed by model updating. The damage detection process using the Levenberg–Marquardt algorithm is elaborated followed by results of numerical case studies. The results from this study confirmed the effectiveness of the proposed model in finding damages in variety of structures, which in turn lays the foundation for damage detection in retrofitted beams (Esfandiari et al. 2018a, b, c; Urgessa and Esfandiari 2018).

Forward problem

The well-known dynamic equation of motion for a linear elastic system can be expressed as

$${\varvec{M}}\ddot{\user2{u}} + {\varvec{C}}\dot{\user2{u}} + {\varvec{K}}{\varvec{u}} = {\mathbf{P}}(t)$$
(1)

where M, C and K are the mass, damping and stiffness matrices of the structure, respectively (Chopra 2017). \(\ddot{\user2{u}}\), \(\dot{\user2{u}}\) and \({\varvec{u}}\) are the acceleration, velocity and displacement response vectors of the structure, respectively. P(t) is a vector of applied external forces. Free vibration of un-damped system can be obtained by omitting the damping matrix and applied external forces from Eq. (1):

$${\varvec{M}}\ddot{\user2{u}} + {\varvec{K}}{\varvec{u}} = {\mathbf{0}}$$
(2)

in which 0 is a zero vector. The solution of Eq. (2) can be obtained by solving an eigenvalue problem as shown in Eq. (3).

$${\varvec{K}}{\varvec{\phi}}_{\,\,i} = \omega_{\,\,i}^{2} {\mathbf{M}}{\varvec{\phi}}_{\,\,i}$$
(3)

where \(\omega_{\,i}\) is the natural circular frequency of the ith mode and \({\varvec{\phi}}_{\,\,i}\) is the vibration eigenvector of the ith mode. By assuming that the mass parameter remains unchanged as damage occurs, the eigenvalue equation can be expressed as follows in Eq. (4):

$${\varvec{K}}^{{\text{d}}} {\varvec{\phi}}_{i}^{{\text{d}}} = \left( {\omega_{i}^{{\text{d}}} } \right)^{2} {\mathbf{M}}{\varvec{\phi}}_{i}^{{\text{d}}}$$
(4)

where Kd is the global stiffness matrix of the damaged structure, \(\omega_{i}^{{\text{d}}}\) is the ith circular frequency of the damaged structure and \({\varvec{\phi}}_{i}^{{\text{d}}}\) is the corresponding mode shape. In this paper, damage is defined as perturbation in the stiffness parameter of the structure. Hence, the global stiffness matrix Kd can be defined as

$${\varvec{K}}^{{\text{d}}} = {\mathbf{K}} - \Delta {\mathbf{K}}$$
(5)

Substituting Eq. (5) into Eq. (4) yields:

$$\left( {{\varvec{K}} - \left( {\omega_{i}^{{\text{d}}} } \right)^{2} {\mathbf{M}}} \right){\varvec{\phi}}_{i}^{{\text{d}}} = \Delta {\varvec{K}}{\varvec{\phi}}_{i}^{{\text{d}}}$$
(6)

Model updating

In recent decades, finite element model updating approaches have been widely used for damage detection. In an iterative process, the unknown model parameters (including physical and material properties) are adjusted until the difference between a measured data and an updated finite element model are minimized.

Objective function based on vibration data

Identification of the intensity and position of damage using model updating is similar to detection of unknown parameters in an optimization problem. Hence, the objective function for model updating is defined as minimizing the residual between the dynamic response of a healthy structure and an updated structure. Minimizing the objective function is defined as a nonlinear least square minimization problem that is determined from the sum of squared errors as shown in Eqs. (7) and (8).

$$f({\varvec{X}}) = \frac{1}{2}\sum\limits_{r = 1}^{m} {{\varvec{g}}_{r}^{2} } ({\varvec{X}})$$
(7)
$${\varvec{g}} = {\varvec{R}}^{{{\text{up}}}} ({\varvec{X}}) - {\varvec{R}}^{{\text{d}}} ({\varvec{X}})$$
(8)

where g is the residual matrix function, Rd is the response vector of existing damaged structure, Rup is the response vector of updated model, \({\varvec{X}} = \{ x_{1} ,x_{2} ,...,x_{ne} \}^{{\text{T}}}\) indicates the updated damage vector which consists of updated parameter for all structural elements and the subscript ne is the number of the structural elements. It should be noted that in order to obtain a unique solution, the number of residuals, m, should be greater than the number of updated damage vector, ne.

In this paper, the proposed residual function is based on both natural circular frequency and the corresponding mode shape. It can be expressed as follows

$${\varvec{g}}_{r} = \left( {\omega_{j}^{2} {{\varvec{\Phi}}}_{ij} } \right)^{{{\text{up}}}} - \left( {\omega_{j}^{2} {{\varvec{\Phi}}}_{ij} } \right)^{{\text{d}}} ,\quad j = 1, \ldots ,nm\quad i = 1, \ldots ,nr$$
(9)

where \(\omega_{j}^{{{\text{up}}}}\) is the jth updated natural circular frequency, \(\omega_{j}^{{\text{d}}}\) is the jth circular frequency of the damaged structure, \({{\varvec{\Phi}}}_{ij}^{{{\text{up}}}}\) is the updated modal displacement of the ith receiver of the jth mode shape, \({{\varvec{\Phi}}}_{ij}^{{\text{d}}}\) is the damaged modal displacement of the ith receiver of the jth mode shape, nr is the number of receivers, nm is the number of mode shapes and the subscript r defined as j × i. Substituting Eq. (9) into Eq. (7) yields:

$$f\left( {\varvec{X}} \right) = \frac{1}{2}\mathop \sum \limits_{j = 1}^{nm} \mathop \sum \limits_{i = 1}^{nr} \left( {\left( {\omega_{j}^{2} {{\varvec{\Phi}}}_{ij} } \right)^{{{\text{up}}}} - \left( {\omega_{j}^{2} {{\varvec{\Phi}}}_{ij} } \right)^{{\text{d}}} } \right)^{2}$$
(10)

Updating parameter

The updating parameter is the unknown dimensionless damage severity of the model. In this paper, the damage of the structural elements is modeled as a reduction in Young’s modulus. Thus, the dimensionless updating parameter, for each element, can be defined as

$$x_{e}^{{{\text{up}}}} = - \frac{{E_{e}^{{{\text{up}}}} - E_{e}^{{}} }}{{E_{e}^{{}} }},\quad e = 1,\,2,...,\,ne$$
(11)

where \(E_{e}^{{{\text{up}}}}\) and \(E_{e}^{{}}\) denote the updated modulus of elasticity and its initial value of the ith element, respectively. It is noted that xe ∈ [0, 1] where xe = 0 and xe = 1 denote healthy and completely damaged states, respectively. Based on Eq. (11), the updated stiffness matrix of the eth element in damaged state, Ked, can be defined by Eq. (12).

$${\mathbf{K}}_{e}^{{\text{d}}} = {\mathbf{K}}_{e} (1 - x_{e}^{{{\text{up}}}} )$$
(12)

where the Ke is the initial stiffness matrix of the eth element.

Damage detection using the Levenberg–Marquardt algorithm

Levenberg–Marquardt algorithm

The Gauss–Newton (GN) method is generally used to solve the nonlinear least squares function shown in Eq. (10), which relies on an iterative sensitivity-based optimization approach. The gradient and Hessian matrices of the objective function are defined by Eqs. (14) and (15), respectively.

$$\nabla f({\varvec{X}}) = \sum\limits_{r = 1}^{m} {{\varvec{g}}_{r} ({\varvec{X}})} \nabla {\varvec{g}}_{r} ({\varvec{X}}) = {\mathbf{J}}^{{\text{T}}} ({\varvec{X}}){\varvec{g}}({\varvec{X}})$$
(13)
$${\varvec{H}} = \nabla^{2} f({\varvec{X}}) = {\varvec{J}}^{{\text{T}}} ({\varvec{X}}){\varvec{J}}({\varvec{X}}) + \sum\limits_{r = 1}^{m} {{\varvec{g}}_{r} ({\varvec{X}})} \nabla^{2} {\varvec{g}}_{r} ({\varvec{X}}) \approx \left\| {{\varvec{J}}({\varvec{X}})} \right\|^{2}$$
(14)
$${\varvec{X}}^{k + 1} = {\varvec{X}}^{k} - \left( {{\mathbf{H}}^{k} } \right)^{ - 1} {\mathbf{J}}^{{\text{T}}} ({\varvec{X}}^{k} ){\varvec{g}}({\varvec{X}}^{k} )$$
(15)

where J is the Jacobian matrix containing the first partial derivatives of the residuals gr with respect to X, H denotes the Hessian matrix, the superscript k indicates the iteration number at which the Jacobian and Hessian matrix are computed and Xk+1 is the updated vector of the parameter. The Hessian matrix was improved by Marquardt (1963) in the Levenberg–Marquardt algorithm as shown in Eq. (16).

$${\varvec{H}}^{k} \user2{ = J}^{{\text{T}}} ({\varvec{X}}^{k} ){\varvec{J}}({\varvec{X}}^{k} ) + \lambda \,{\text{diag}}({\varvec{J}}^{{\text{T}}} ({\varvec{X}}^{k} ){\varvec{J}}({\varvec{X}}^{k} ))$$
(16)

where λ is a damping parameter adjusted by the algorithm. The basic strategy behind choosing the damping term depends on the error rate in the updating process. If the error goes down following an update, the algorithm will take a small λ (usually by a constant coefficient) to reduce the influence of gradient descent. On the other hand, if the error goes up, λ is increased by the same factor. Using the Levenberg–Marquardt algorithm, Eq. (15) can be rewritten as shown in Eq. (17):

$${\varvec{X}}^{k + 1} = {\varvec{X}}^{k} - \left[ {{\varvec{J}}^{{\text{T}}} ({\varvec{X}}^{k} ){\varvec{J}}({\varvec{X}}^{k} ) + \lambda \,{\text{diag}}({\varvec{J}}^{{\text{T}}} ({\varvec{X}}^{k} ){\varvec{J}}({\varvec{X}}^{k} ))} \right]^{ - 1} {\mathbf{J}}^{\text{T}} ({\varvec{X}}^{k} ){\varvec{g}}({\varvec{X}}^{k} )$$
(17)

The updating process using the Levenberg–Marquardt algorithm starts out by updating the function and Jacobian values (if necessary) using Eq. (16) and then evaluating the error at the new parameter vector. If the error increases as a result of the update, then retract the step and increase λ in Eq. (16) by a significant constant factor followed by trying the updating process again. If the error has decreased as a result of the update, then accept the step and decrease λ by the same factor.

In the updating process, the Hessian matrix may be severely ill-conditioned. In order to overcome this issue, the Singular Value Decomposition (SVD) method is employed to decompose the Hessian matrix (H) as H = USVT. In this regard, U and V are unitary matrices, VT denotes the transpose of V, and S implies a diagonal matrix whose components are \(S_{ii} = \sigma_{i}\). According to the SVD method, the pseudo-inverse of the Hessian matrix (H) can be calculated as \({\varvec{H}} + = {\varvec{VS}} + {\varvec{U}}^{\user2{*}}\), \(S_{ii}^{ + } = {1 \mathord{\left/ {\vphantom {1 {\sigma_{i} }}} \right. \kern-\nulldelimiterspace} {\sigma_{i} }}\).

The model updating for damage detection is inhibited by challenges associated with structural complexity, large search spaces and the presence of too many variables, amongst other types of constraints. Levenberg–Marquardt algorithm is considered for this study because it is faster to converge than either the gradient descent or the GN. Moreover, it is able to handle models with multiple free parameters and most of the time, it can find an optimal solution despite the initial guess.

Sensitivity matrix

As mentioned earlier, the sensitivity or the Jacobian matrix is defined as the first-order derivative of residual function with respect to vector of updating parameters. The sensitivity matrix can be obtained by forward difference method as shown in Eq. (18).

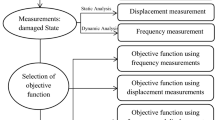
$${\mathbf{J}}_{re} = \frac{{\partial {\varvec{g}}_{r} }}{{\partial {\varvec{X}}_{e} }}$$
(18)

where gr is the rth component of the residual vector and Xe is the eth component of the updating vector. The flowchart of the method presented is shown in Fig. 1.

Fig. 1
figure 1

Flowchart for the algorithm presented

Full size image

Numerical case studies

In this section, the numerical results obtained from the Levenberg–Marquardt (LM) algorithm in conjunction with the finite element method (FEM) is illustrated. In all numerical examples, the damaged structural elements are simulated by using a reduction in the Young’s modulus of the material. All case studies are numerical and where measurement sensor is used in the text, it refers to the place that dynamic responses that used in the algorithm are generated numerically in that place. In these example, the influence of data noise on the quality of the image reconstruction is investigated by considering noisy simulated data of the form uε = ucomp(1 + ηχ) in which χ is a uniformly distributed random number between − 1 and 1.

Thirty one-bar planar truss

In the first case study, a thirty one-bar planar truss shown in Fig. 2 was considered for assessing the efficiency of the proposed method. The truss was previously studied by Seyedpoor (2012). The material properties are assumed to be: Young’s modulus E = 70 GPa and mass density ρ = 2770 kg/m3; and cross-sectional area of the members is 40 cm2. Similar to Seyedpoor (2012), it is assumed that the first five mode shapes of the structure are available. Four different damage cases given in Table 1 are considered. The first three damage cases are similar to Seyedpoor (2012). The measurement sensors are located at nodes numbered 4, 6, 7, 10 and 11. The fourth damage case consists of all damages in previous scenarios at the same time. This scenario was selected to show the efficiency and superiority of the algorithm for detecting several simultaneous damages.

Fig. 2
figure 2

Planar truss having 31 elements

Full size image
Table 1 Four different damage cases induced in 31-bar planar truss
Full size table

Figure 3a–d shows the damage severity with respect to element number for damage cases 1–4, respectively. The results of the LM algorithm are compared with the proposed method reported by Seyedpoor (2012). In fact, the damage detection process in Seyedpoor (2012) is a two-stage method and the responses were recorded in all degrees of freedom. In the first stage, the potentially flawed elements were detected based on modal strain energy and the second stage includes searching in reduced space using particle swarm optimization (PSO). The LM algorithm used in this current study has advantages when compared to Seyedpoor (2012). The proposed LM method was able to detect damaged elements during the one-step process. On the other hand, damaged elements were identified using five sensors (corresponding to the degrees of freedom) accurately. The convergence history of the LM algorithm for various cases is shown in Fig. 4. This figure demonstrates that the convergence speed and accuracy of proposed method is very high.

Fig. 3
figure 3

Damage detection results of the 31-bar planar truss for a case 1, b case 2, c case 3 and d case 4

Full size image
Fig. 4
figure 4

Convergence diagram of the model updating procedure of the 31-bar planar truss for cases 1–4

Full size image

25-Bar truss bridge

The second case study is statically determinate 25-bar truss bridge shown in Fig. 5 (Esfandiari et al. 2009). The truss was previously studied by Kaveh and Maniat (2015). Cross-sectional area of the members for all elements is 10 cm2. The Young’s modulus E and mass density ρ are 200 GPa and 7780 kg/m3, respectively.

Fig. 5
figure 5

A truss with 25 elements

Full size image

Figure 6a–c shows the damage severity with respect to element number for damage cases 1–3, respectively. The convergence history of the LM algorithm for various cases is shown in Fig. 7. As can be seen from the figures, the proposed LM method was able to detect damaged elements during the one-step process and the convergence speed and accuracy of proposed method was very high.

Fig. 6
figure 6

Damage detection results of the 25-bar truss bridge for a case 1, b case 2 and c case 3

Full size image
Fig. 7
figure 7

Convergence diagram of the model updating procedure for 25-bar truss bridge for cases 1–3

Full size image

Two-story two-bay unbraced frame

The two-bay, two-story steel frame shown in Fig. 8 was selected from Tabrizian et al. (2013) as the third case study. The material properties of the frame are as follows: Young’s modulus, Poisson’s ratio and mass density are 207 GPa, 0.30 and 7780 kg/m3, respectively. The cross-sectional area and the moment of inertia of all columns and beams are 0.025 m2, 6.386 × 10–4 m4, 0.0123 m2 and 2.218 × 10–4 m4, respectively. Similar to Tabrizian et al. (2013), three different damage cases given in Table 2 are considered. The measurement sensors are located at nodes numbered 5, 11, 13 and 17. Only the first five mode shapes of the structure are considered. Figure 9 represents the damage states reported by Tabrizian et al. (2013). In Tabrizian et al. (2013), 20 first modes are considered in damage detection for the first and second cases, and 45 first modes for the third case, while the method presented in this study enables us to detect the damaged elements using 5 measurement sensors. The number of sensors used to measure the mode shapes may be limited in the experiments and engineering applications due to cost and other mitigating factors. Therefore, to overcome this drawback, the proposed method in this research can be practical and inexpensive.

Fig. 8
figure 8

Geometry of un-braced plane frame

Full size image
Table 2 Three different damage cases induced in an unbraced planar frame
Full size table
Fig. 9
figure 9

Damage detection results of the 24-element planar frame for a case 1, b case 2 and c case 3

Full size image

Cantilever beam

A 100-element cantilever beam with uniform cross section, which was previously studied by Homaei et al. (2014), was considered as the fourth case study as shown in Fig. 10. The responses of the beam measured by 25 sensors located at select nodes and 10 vibration modes of the beam were available. Damage scenarios for this beam are presented in Table 3. The first damage case is similar to Homaei et al. (2014). In Homaei et al. (2014), damaged elements are identified by the measured first two mode shapes. Figure 11a, b demonstrates that the proposed method in this study provides accurate identification of damaged elements with a limited number of measurement sensors. It is worth mentioning that the proposed method can achieve the actual sizes and locations of damages comparing to the method reported in Homaei et al. (2014).

Fig. 10
figure 10

A cantilever beam with 100 elements

Full size image
Table 3 Two different damage cases induced in cantilever beam
Full size table
Fig. 11
figure 11

Damage detection results of the 100-member planar beam for a case 1 and b case 2

Full size image

Bridge girder with non-prismatic section

The last case study is a three-span continuous steel bridge girder shown in Fig. 12. The bridge has a length of 58.7 m. The finite element model of the bridge includes 100 elements. Two damage case scenarios were induced as shown in Table 4. In the second scenario, six damaged elements were considered, the measurement sensors are located at select nodes. Damage identification results are shown in Fig. 13a, b, respectively. As shown in this figure, the locations and extents of the damaged elements are detected correctly for the two scenarios.

Fig. 12
figure 12

Geometry of the three-span steel bridge girder

Full size image
Table 4 Two different damage scenarios induced the three-span steel bridge girder
Full size table
Fig. 13
figure 13

Damage detection results of the 100-element bridge for a case 1 and b case 2

Full size image

Conclusions

A practical method for detecting the locations and extents of multiple damage in the four different types of structural systems has been presented. This method is based on sensitivity analysis of the structure and provides updating the structural finite element model using the iterative process of Levenberg–Marquardt algorithm. The updating parameter, which is the unknown dimensionless damage severity of the model, is considered as a reduction in Young’s modulus. The method uses dynamic response parameters including frequency and mode shape. The objective function for model updating is defined as minimizing the residual between the dynamic response of a healthy structure and an updated structure. For this purpose, the model uses the nonlinear least square minimization problem that is determined from the sum of squared errors. In order to assess the performance of the proposed method for structural damage detection, the numerical results of the presented method are compared with those available in the literature, including the accuracy and convergence speed of the algorithm. To make a comprehensive assessment, different types of structure including two planar truss, a two-bay unbraced frame, a cantilever beam and a non-prismatic bridge girder were analyzed. According to the high cost of measurement sensors in engineering applications, the number and optimal placement of sensors can play an important role in cost reduction. As such, results of the numerical examples have demonstrated that the proposed method can provide accurate identification of damaged elements with a limited number of measurement sensors and incomplete data.