Abstract
This paper analyzes two incentive schemes available for a closed-loop supply chain (CLSC) in which a manufacturer and a retailer contribute to the return rate dynamics through their investments in green activity programs. Both firms have economic motivations to perform the return rate because customers who return end-of-use goods also repurchase new ones. In addition, the manufacturer exploits the returns’ residual value in operations to increase profits. Because the manufacturer has both operational and marketing motivations to close the loop, he can provide an incentive to the retailer to boost her investments in green activity programs. The incentive can be either state dependent or control dependent. The former assumes that the incentive depends on the fraction of customers who are willing to return end-of-use products; the latter is proportional to the retailer’s green activity programs efforts. Our results show that a state-dependent incentive is profit-Pareto-improving only when the retailer’s environmental effectiveness is large. In contrast, a control-dependent incentive mechanism is profit-Pareto-improving for low incentive values, high retailer’s environmental effectiveness, and customers’ repurchasing intention. In all other cases, players have divergent preferences and neither mechanism coordinates the CLSC.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The recent trend of closed-loop supply chain (CLSC) research has focused substantial attention on coordination, with a particular emphasis on the type of incentive that manufacturers (or remanufacturers) should transfer to other participants to enhance their willingness to close the loop [4]. The engagement of CLSC partners is a prerequisite to succeed in the integration of forward and backward activities into a unique system, as several atypical processes such as product acquisition, reverse logistics, points of use and disposal, testing, sorting, refurbishing, recovery, recycling, re-marketing, and re-selling coexist with the classical management of forward activities [12, 15, 16, 25]. While traditional coordination schemes aim at increasing the economic performance for all chain participants (see [2, 17] for exhaustive reviews), CLSCs mainly use coordination mechanisms to achieve cost savings as well as high return rates and profits [23]. The rationale behind the implementation of a CLSC is that production by means of virgin material is more expensive than production by means of returned products, and thus, cost savings and return rates establish the economic and the environmental benefits of closing the loop [15]. Saving cost targets vary according to the industry, for instance, Kodak reaches cost saving close to 40–60 %, while IBM and Xerox achieve cost saving up to 80 and 65 %, respectively.
Along with these operational reasons to close the loop, additional pressures come from the growing interests of consumers, who are highly concerned about firms’ environmental responsibility. The latter links to the depletion of natural resources, the accumulation of waste products, and the impairment of environmental systems [24]. The need to reacquire end-of-use products and thus protect the environment in the eyes of consumers creates new managerial challenges for manufacturers, who are asked to invest in various green activity programs. These activities may include marketing expenditures (e.g., green advertising, eco-efficiency, green labeling) to increase the customers’ awareness of the end-of-use product return policy [5] as well as operational activities (e.g., collection points, remanufacturing process, recycling capability) to increase remanufacturing efficiency and create a suitable reverse logistics network [21]. In addition, manufacturers actively involve downstream players (retailers) in the collection process as they exert some further motivations to close the loop. Retailers contribute to acquiring end-of-use products through organizing in-store collection and drop-off points, and advertise their environmental initiatives to inform consumers about their environmental commitments [19]. This leads to increasing the number of visits and store preferences and creating a green image for their stores to influence consumers’ purchasing intention and shopping value [27]. Therefore, firms in CLSCs initiate several types of green policies to successfully close the loop, although their decisions are driven by different motivations [25].
This paper investigates pricing and green activity program decisions made in a CLSC by one manufacturer and one retailer to increase profits and enhance environmental performance through the return rate. The latter is modeled as a dynamic equation and represents the fraction of customers who are willing to return end-of use products. Both firms invest in green activity programs to perform the return rate. While the manufacturer invests in green investments to save costs in production, the retailer contributes to the return rate because customers who return end-of-use products also repurchase new ones. A few examples of product categories that fit with this model are cartridges, tires, and cell phones. Therefore, the return rate is also a proxy of consumers’ repurchasing intention. Consequently, firms’ interests for closing the loop are misaligned because the manufacturer benefits from a high return rate in terms of cost savings and higher sales, while the retailer only exploits the return rate as a mean for increasing sales. Under such conditions, incentive alignment is worth investigating.
Incentive alignment in CLSC is meant as the implementation of an agreement (e.g., a contract) to properly engage a firm in the collection process and perform the return rate. An appropriate incentive should be designed for collectors to make all CLSC players economically better off [10]. Incentive alignment in CLSCs has been extensively investigated to properly set out various policies such as outsourcing [8, 21], quality (durability) strategy [9], competition [20, 22], interactions among products’ range [11], innovation [14], and sharing agreements [5, 7]. To reach coordination, most of the literature in CLSC model per-return incentive schemes according to which the collector receives a fixed amount per-product returned (see [3, 7, 8, 13, 21, 22]). Although this incentive scheme is quite intuitive and has been shown to be extremely successful (e.g., [21]), we seek to develop other alternative forms of incentives.
Thus, our study contributes to this research stream by constructing two original incentive mechanisms to support the product acquisition process. Starting from a benchmark model with no incentive, we investigate the effect of incentive schemes on CLSC members’ decisions and profits while departing from the classical per-return incentive assumption. Rather, we establish incentive schemes that depend on players’ strategies and CLSC environmental performance. The incentives are provided by the manufacturer to the retailer—as only the former exploits the return rate for operational and marketing motivations—and can be either a function of the return rate (state-dependent incentive) or a function of the retailer’s GAP efforts (control-dependent incentive). These two forms of incentives have not been explored in the literature. The first incentive scheme is a function of the return rate and thus depends on the CLSC environmental performance. This is the first incentive scheme in the literature that depends on the stock of a state variable, and thus, it aims to reinforce the idea suggested by Savaskan et al. [21] according to which CLSC needs to be studied as a dynamic phenomenon as the product acquisition process refers to the amount of past sold products a firm collects in the future. Although that statement seems to be quite appealing, the literature mainly deals with static games as well as static incentive schemes (e.g., [11, 20–22]). Therefore, this research will contribute to this body of knowledge for which dynamic forms of incentives still need to be explored.
The second scheme implies that only the retailer is responsible for the incentive, which depends on the amount of money the retailer invests to enhance the return rate: The higher the retailer’s GAP efforts, the higher the incentive. This form of incentive has been inspired by the recent debate on supply chain and marketing channel initiated by Cachon [2] and continued by De Giovanni and Roselli [6] on the nature of an incentive. When a firm will know its incentives only after having decided its strategies (e.g., under a revenue sharing contract, the sharing parameter can be endogenous [18]), it will underperform from an economic perspective as compared to the case in which the incentive is common knowledge. Both incentive schemes are demand independent; therefore, retailer’s rewards do not depend on other players’ strategies (e.g., pricing) and demand. Interestingly, while in the control-dependent incentive the retailer exclusively determines the amplitude of the incentive deciding on the GAP efforts, the state-dependent incentive is based on the overall capacity of a CLSC to perform the return rate, which depends on the entire history of players’ contributions to the state. The comparison of strategies and profit functions in the three scenarios allows the identification of changes in players’ strategies and profits when the CLSC moves from a no-incentive to an incentive scenario as well as on the existence of an incentive mechanism that turns out to be profit-Pareto-improving. The findings will therefore be positioned in the literature of CLSC that has investigated similar research questions while looking at classical incentive schemes, such as per-return incentives (e.g., [3, 7, 8, 13, 21, 22]).
The remainder of the paper is organized as follows. Section 2 introduces the models and notations. Section 3 characterizes equilibria in those models and presents some results. Section 4 presents a numerical simulation to compare strategies and profits and discusses some managerial implications. Section 5 provides some concluding remarks and suggestions for the future research.
2 Model Description
In our analysis, a CLSC is composed of a remanufacturer, player \(M\), and a retailer, player \(R\). From this point onward, we will refer to the remanufacturer as he and to the retailer as she. Both players seek to maximize their profits through selling new and remanufactured products to a market in which customers cannot distinguish between products versions. Player \(M\) sells products to \(R\) at a wholesale price, \(\omega \left( t\right) ,\) while \(R\) sells products to the market at a retail price \(p\left( t\right) \). Wholesale and retail price are determined by \(M\) and \(R\), respectively. In addition, \(M\) acquires past sold products from the market and uses these returns to make new products. The return process is characterized as a dynamic equation that expresses the percentage of customers who is willing to return products that reach the end-of-use stage. Both players contribute to that dynamics through their green activity programs (GAPs) strategies, \(A_{i}\left( t\right) ,\,\ i=M,R\). These activities consist of several atypical processes such as product acquisition, reverse logistics, points of use and disposal, testing, sorting, refurbishing, recovery, recycling, re-marketing, and re-selling that coexist with the classical forward activities [12, 15, 16]. For mathematical tractability, we follow the formal convexity assumption for these strategies; thus, GAP efforts will assume the following quadratic cost function:
where \(\kappa _{i}\) is the marginal penalty associated with the profits function of any additional dollar spent in greenness.Footnote 1 Among other targets, GAP strategies contribute to increasing people’s awareness on the benefits in health and quality of life obtainable through their contributions to the return process. The percentage of the overall population who is willing to contribute to the environment changes according to the exposure to some GAP. Therefore, we model that fraction through the dynamic equation:
where \(a>0\) and \(b>0\) represent \(M\)’s and \(R\)’s GAP efforts effectiveness, respectively; these parameters show the contribution that one dollar invested in GAP exercises on the amount of people who are willing to preserve the environment through returning end-of-use products. \(\delta >0\) is the forgetting effect and represents the number of people who have changed their mind or simply forgets to return end-of-use products. The rationale behind the state Eq. (2) is that firms create awareness and push customers to return their end-of-use products to preserve the environment. Several media sources can be used for that reason, such as sustainability reports, green advertising, and green branding [5, 27]. Indeed, firms can have different motivations to sponsor products return. On one hand, manufacturers gain operational benefit since using returned products to producing new ones is cheaper than making new products by means of virgin materials. This is the key assumption for firms to implement a reverse logistics policy. Assume that \(M\) faces a marginal production cost \(c_\mathrm{p}\) when producing by means of raw materials and \(c_\mathrm{e}\) when producing by means of returns. \(M\) faces a marginal production cost that assumes the following form:
This cost function has been used in Savaskan et al. [21], Savaskan and van Wassenhove [22] and De Giovanni and Zaccour [7] and highlights the saving cost that \(M\) has an advantage when \(r\left( t\right) >0,\) because \(c_\mathrm{p}>c_\mathrm{e}\) by construction. When \(r\left( t\right) =0,\,M\) faces a full marginal production cost for all new goods; when \(r\left( t\right) =1,\) all products are manufactured at a lower production cost. \(c_\mathrm{p}-c_\mathrm{e}\) represents the saving costs for \(M\) and then his economic convenience of closing the loop. Because \(c_\mathrm{p}\) and \(c_\mathrm{e}\) are given parameters for our model, we approximate the benefits from reverse logistics as follows:
where \(\varDelta >0\) is the per-return benefit that \(M\) gains. \(\varDelta \) can be interpreted as the average value of a return, which is independent of the number of times a return can be used for remanufacturing activities as well as of its overall conditions. For instance, Kodak can use a batch of parts (e.g., the mechanical parts, the batteries, and the plastic components) of a returned camera to make a new one. \(\varDelta \) is the value of this batch and corresponds to the (saved) expenses that Kodak would have faced if the collection process had not been in place. Finally, through Eq. (4), we investigate remanufacturing as a profit center rather than as a cost center, though the usage of Eq. (3) in our game would not change the overall findings.
Besides operational benefits, all CLSC partners sponsor product return as a mean to increase sales. When a customer returns an end-of-use product, we assume that he needs to purchase a new one to continue satisfying his needs. This assumption is in line with the management of some products categories such as durable and electronic goods, which are replaced by new ones when they reach their end-of-life stage. The Environmental Protection Agency’s (EPA) report shows the shape of sales and returns for some product categories in the US market (www.epa.gov). Using this data, we show that there is a strong correlation between end-of-life returns and new purchases. Table 1 displays the Pearson correlation between purchases and returns for several product categories.
These empirical results support the assumption that customers who return some products need to purchase a new one to continue to satisfy their needs. Therefore, we model a demand function that includes customer’s repurchases and assumes the following form:
where \(\alpha >0\) and \(\beta >0\) represent the market potential and the customers’ sensitivity to price, respectively, and follow the standard assumptions in economics. Further, \(\theta \ge 0\) describes the number of products that customers who returned end-of use products purchase. The latter is the key motivations for CLSC to be in favor of a return policy. Good performance in the product return process translates into higher sales; thus, all suppliers have an economic interest in performing the return rate. In a traditional CLSC, \(M\) retains all economic rewards of closing the loop. \(M\)’s marginal revenue is given by \(\pi _{M}\left( \omega \left( t\right) ,r\left( t\right) \right) =\omega \left( t\right) +\varDelta r\left( t\right) ,\, and R\)’s marginal revenue is given by \(\pi _{R}\left( p\left( t\right) ,\omega \left( t\right) \right) =p\left( t\right) -\omega \left( t\right) \). Therefore, \(M\) diversifies his total revenues through forward and reverse business that are expressed by \(D\left( p\left( t\right) ,r\left( t\right) \right) \omega \left( t\right) \) and \(D\left( p\left( t\right) ,r\left( t\right) \right) r\left( t\right) \varDelta ,\) respectively, though that \( D\left( p\left( t\right) ,r\left( t\right) \right) r\left( t\right) \) is the number of returns. In contrast, \(R\) obtains the total revenues \(D\left( p\left( t\right) ,r\left( t\right) \right) \left( p\left( t\right) -\omega \left( t\right) \right) \) from forward activities only. Table 2 summarizes the notations used throughout the study.
We first introduce the no-incentive model whereby \(M\) does not provide any incentive to \(R\). Players’ objective functions for this game are given by
subject to Eq. (2). \(\rho \) is the discount factor for the game and it is assumed to be equal between the two players. Objective function (6) maximizes the profits of \(M\) through sales as well as remanufacturing activities, while objective function (7) maximizes the profits of \(R\) through sales only. \(R\)’s interest in performing the return rate depends on customers’ repurchasing intention: High return flow translates into higher profits (through sales) even when \(M\) does not supply any specific incentive based on \(r\left( t\right) \). The game is played á la Stackelberg where \(M\) is the leader. The game evolves according to the following moves: \(M\) announces the feedback wholesale price and GAP strategies, \(\omega \left( r\right) \) and \( A_{M}\left( r\right) ;\, R\) sets the feedback pricing and GAP strategies, \( p\left( r\mid \omega ,A_{M}^{{}}\right) \) and \(A_{R}\left( r\mid \omega ,A_{M}^{{}}\right) \) to optimally respond to \(M\)’s announced decisions; \(M\) incorporates \(R\)’s reaction functions into its optimal control problem and solves for the wholesale \(\omega \left( r\right) \) and his GAP strategy \(A_{M}\left( r\right) \). Observe that \(\omega \left( r\right) \) and \(p\left( r\right) \) appear in the integrand but not also in the dynamics of (2). Thus, players can maximize pricing-decision variables as if they solved a static optimization problem. In contrast, GAP strategies affect the evolution of the state. The solution to the no-incentive problem yields the equilibrium feedback strategies \(\omega ^{*}\left( r\right) \) and \(A_{M}^{*}\left( r\right) \) for \(M\). Once we have the solution \(\omega ^{*}\left( r\right) \) and \(A_{M}^{*}\left( r\right) \), we can express \(R\)’s feedback price and GAP strategies as \(p^{*}\left( r\right) =\omega \left( r\mid \omega ^{*},A_{M}^{*}\right) \) and \(A_{R}^{*}\left( r\right) =A_{R}\left( r\mid \omega ^{*},A_{M}^{*}\right) \). Strategies \(p^{*}\left( r\right) ,\omega ^{*}\left( r\right) ,\, A_{M}^{*}\left( r\right) \) and \(A_{R}^{*}\left( r\right) \) constitute a feedback Stackelberg equilibrium, which is time consistent. Using these strategies in Eq. (2), it will result the return rate \(r^{*}\left( t\right) ,t\ge 0,\) and the related decisions will be \(p^{*}\left( r^{*}\right) ,\omega ^{*}\left( r^{*}\right) ,\,A_{M}^{*}\left( r^{*}\right) \) and \(A_{R}^{*}\left( r^{*}\right) \).
After establishing the equilibrium for the no-incentive game that represents a benchmark, we also formulate two incentive problems in which \(M\) supplies an economic premium to \(R\) to encourage the player to better perform the return process. While the literature has deeply investigated several coordination mechanisms that depend on the past demand, we implement coordination mechanisms that depend either on the return rate \(r\left( t\right) \) or on the \(R\)’s GAP efforts \(A_{R}\left( t\right) \); thus, the former depends on the state, while the latter depends on \(R\)’s control. Therefore, the incentive mechanisms will assume the following forms:
where \(\mu >0\) is given and represents the amount that \(M\) transfers to \( R \) as a form of fixed marginal incentive. The state-dependent incentive, \( \varphi ^{S}\left( r\left( t\right) \right) \), possesses an interesting property of being based on the overall CLSC environmental performance, for which both players provide a contribution to the state. Because the incentive is state dependent, \(R\) receives an economic rewards \(\varphi ^{S}\left( r\left( t\right) \right) =\mu r\left( t\right) \) that depends on the fraction of customers who are willing to return end-of-use products. As a counterpart, \(M\) expects \(R\) to enhance the return rate through increasing \(A_{R}\left( t\right) \). Many operational interactions emerge from this problem. Yet, \(M\) faces a trade-off due to the effect of \(r\left( t\right) \) on his objective function: The return rate positively impacts on sales (through customer’s repurchasing intention, \(\theta \)) and profit margins (through the return residual value, \(\varDelta \)) while it negatively affects \( M \)’s profits through the incentive \(\varphi ^{S}\left( r\left( t\right) \right) \). On her side, \(R\) has the advantage of the return rate through its positive effect on sales as well as through the incentive \(\varphi ^{S}\left( r\left( t\right) \right) ,\) and thus, she has a dual benefit from the return policy. Contrary to the literature that reports various forms of incentive schemes that mainly depend on the returns (e.g., [8, 21]), here we focus on the overall environmental performance of a CLSC.
We then formulate a second problem in which the incentive depends on \(R\)’s contribution to the state, \(A_{R}\left( t\right) \). Contrary to the previous incentive mechanism, \(M\) supplies an economic reward that exclusively varies according to \(R\)’s GAP efforts, \(\varphi ^{C}\left( A_{R}\left( t\right) \right) =\mu A_{R}\left( t\right) \). Contrary to the state-dependent case where \(M\) influences the incentive through optimally setting his GAP policy, in this scenario, \(R\) explicitly determines the incentive she will get through setting her optimal GAP efforts. Although \(M\) loses some decisional power (though as the missed possibilities to influence \(\varphi ^{C})\), he will not face any trade-off: The return rate does not negatively influence his payoff function.
Note that we do not consider an incentive game that consists of a combination of control- and state-dependent incentives. Although this option is theoretically doable, it never finds applicability in practice. Firms in CLSC supply incentives according to one feature only. For example, Kodak offers a per-returned-camera incentive [21]; Pitney–Bowes remanufactures off-lease products by offering a trade-in program [10]; Staples supplies a fixed incentive for each cartridge returned (www.staple.com); Expert International GmbH offers a rebate to all stakeholders who return electronic products to be used to repurchase new ones (www.expert-italia.it). This is also confirmed by approaches taken by Savaskan et al. [21], that construct the incentive for collectors only according to the return rate, rather than simultaneously considering return rate, pricing, and green promotion. Similar directions have been taken by other research such as Corbett and DeCroix [3], Corbett and DeCroix [7, 8], Corbett and DeCroix [13] and Savaskan and van Wassenhove [22].
In the incentive games, the players’ objective functions are given by
subject to Eq. (2) where \(\varsigma =S,C.\) As for the benchmark game, \(\rho \) is the discount factor and it is assumed to be equal between the two players and across the incentive games. Objective functions (10) and (11) maximize the players’ profits through sales as well as remanufacturing activities. Note that \(\varphi ^{\varsigma }\) can assume the form introduced in (8) and (9). \(R\)’s interest in performing the return rate depends on customers’ repurchasing intention and incentive: High return rate translates into higher profits even when customers do not repurchase end-of-use products \(\left( \hbox {e.g.,}~\theta =0\right) \). Both incentive games are played \(\acute{a}\, la\, Stackelberg\) where \(M\) is the leader and the nature of the game and the related moves follow the benchmark game structure. The solution to the incentive problems yield the equilibrium feedback strategies \(\omega ^{\varsigma *}\left( r^{\varsigma }\right) \) and \(A_{M}^{\varsigma *}\left( r\right) \) for \(M\). Once we have the solution \(\omega ^{\varsigma *}\left( r^{\varsigma }\right) \) and \(A_{M}^{\varsigma *}\left( r^{\varsigma }\right) \), we can express \(R\)’s feedback price and GAP strategies as \(p^{\varsigma *}\left( r^{\varsigma }\right) =p^{\varsigma }\left( r^{\varsigma }\mid \omega ^{\varsigma *},A_{M}^{\varsigma *}\right) \) and \(A_{R}^{\varsigma *}\left( r\right) =A_{R}^{\varsigma *}\left( r^{j}\mid \omega ^{\varsigma *},A_{M}^{\varsigma *}\right) \). Strategies \(p^{\varsigma *}\left( r\right) ,\omega ^{\varsigma *}\left( r\right) ,\, A_{M}^{\varsigma *}\left( r\right) \) and \(A_{R}^{\varsigma *}\left( r\right) \) constitute a feedback Stackelberg equilibrium, which is time consistent. Using these strategies in Eq. (2), it will result the return rate \( r^{\varsigma *}\left( t\right) ,t\ge 0,\) and the related decisions will be \(p^{\varsigma *}\left( r^{\varsigma *}\right) ,\omega ^{\varsigma *}\left( r^{\varsigma *}\right) ,\, A_{M}^{\varsigma *}\left( r^{\varsigma *}\right) \) and \(A_{R}^{\varsigma *}\left( r^{\varsigma *}\right) \).
3 Analysis
In this section, we optimally solve the games described earlier. We restrict our attention to feedback Stackelberg solutions where the optimal strategies depend on the state. Because the game is played in an infinite time horizon with time-independent parameters, we focus on stationary equilibrium since feedback strategies will not explicitly depend on time \(t\).
3.1 Benchmark: No-Incentive Game
The optimal solution to this problem is given in Proposition 1 where we use the superscript \(B\) to characterize the (Benchmark) no-incentive game.
Proposition 1
Assuming an interior solution, strategies and profit functions in the no-incentive case are as follows:
where \(d_{1},\, d_{2},\, f_{1}\), and \(f_{2}\) are the coefficients of the conjectured value functions
Proof
See the “Appendix 1”.\(\square \)
From Proposition 1, we observe that all strategies are state dependent. While GAP efforts always increase in the return rate, pricing strategies increase in the state only when \(\theta >\varDelta \beta \). Specifically, three cases can be analyzed:
Case 1
\(\theta \le \frac{\varDelta \beta }{3}\). When the customers’ repurchasing intention is low, the advantages of an efficient return process should be transferred to customers who have marginal attitudes toward repurchasing returned products. The return process is a pure operational device that allows firms to benefits from the returns residual value in production while CLSCs should only rely on traditional marketing strategies \(\left( \hbox {e.g.,} \text { pricing}\right) \) to increase sales.
Case 2
\(\theta \in (\frac{\varDelta \beta }{3},\varDelta \beta ]\). When the customers’ repurchasing intention is medium, a CLSC eliminates internal marginalization inefficiencies as the wholesale price decreases in the return rate. Nevertheless, high environmental performance boosts the price that customers will pay. An efficient return process allows the reduction of the first marginalization while it enhances the second marginalization; thus, it only mitigates internal inefficiency.
Case 3
\(\theta >\beta \varDelta \). When the customers’ repurchasing intention is high, an efficient return process implies higher wholesale price and retail price strategies. An environmentally oriented policy penalizes new customers who will pay a higher price when the CLSC successfully performs its return process. In such a case, CLSC members seek to increase profits through customers’ repurchasing intention, in the spirit that firms focus on generating profits through their current customers portfolio rather than looking for new buyers. The chain suffers from a double marginalization effect, as both players charge higher prices at all CLSC levels.
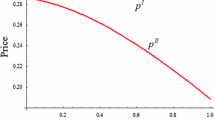
In equilibrium, there is a compensation effect between pricing strategies and GAP efforts: Although sales would decrease due to higher price, customers who repurchase products lead sales to always be positive. This compensation effect mainly depends on customers’ repurchasing intention and exists when \(\theta >0\), (e.g., \(D^{B}\left( r^{B}\right) =\frac{\alpha +r^{B}\left( \theta +\varDelta \beta \right) }{4}\)). Note that when \(\theta =0,\) wholesale and pricing strategies given in Eqs. (14) and (15) decrease in the state and thus \(r^{B}\) contributes to increasing sales through a lower price. It is straightforward to analyze some comparative statics with respect to pricing-decision strategies: \(\omega ^{B}( r^{B}) \) and \(p^{B}( r^{B}) \) increase in the market size \((\hbox {e.g.,}\, \frac{\partial \omega ^{B}( r^{B}) }{\partial \alpha }=\frac{1}{2\beta }>0,\frac{\partial p^{B}( r^{B}) }{\partial \alpha }=\frac{3}{4\beta }>0)\) and in customers’ repurchasing intention \((\hbox {e.g.,}\, \frac{\partial \omega ^{B}( r^{B}) }{\partial \theta }=\frac{r^{B}}{2\beta }>0,\frac{\partial p^{B}( r^{B}) }{\partial \theta }=\frac{3r^{B}}{4\beta }>0)\), while decrease in the customers ’ sensitivity to price \((\hbox {e.g.,}\, \frac{ \partial \omega ^{B}( r^{B}) }{\partial \beta }=-\frac{\alpha +r^{B}\theta }{2\beta ^{2}}<0,\frac{\partial p^{B}( r^{B}) }{ \partial \beta }=-\frac{3( \alpha +r^{B}\theta ) }{4\beta ^{2}} <0)\). In addition, the optimal pricing-decision strategies lead to the margins: \(\pi _{M}^{B}( r^{B}) =\frac{\alpha +r^{B}( \theta +\varDelta \beta ) }{2\beta }\) and \(\pi _{R}^{B}( r^{B}) = \frac{\alpha +r^{B}( \theta +\varDelta \beta ) }{4\beta }\). \(M\) has the advantage of his position of CLSC leader to gain more margins than \(R,\) specifically \(\pi _{M}^{B}( r^{B}) =2\pi _{R}^{B}( r^{B}) \).
Note that because the identified parameters \(d_{1}\) and \(f_{1}\) are coupled (see “Appendix 1”), solving Eqs. (18) and (19) and analyzing \(A_{i}^{B}\left( r^{B}\right) ,V_{i}^{B}\left( r^{B}\right) \) are non-trivial problems. We carried out numerical optimization to obtain insights into the solutions of this problem. First, we numerically solve the set of Riccati equations related to the problem (see “Appendix 1”, Eqs. 48–53) to identify the solution that ensures positive strategies and value functions as well as \( r^{B}\in (0,1]\). We fix the following baseline parameter values: \(\alpha =\beta =1,\, a=.5,b=1,\, \theta =.3,\, \varDelta =.5,\,\delta =.4,\, \rho =.9\).Footnote 2 The system has four solutions but only two of them turn out to be good candidates. If fact, it results that:
-
Solution \({\mathcal {I}},\,d_{1}^{{\mathcal {I}}}=.1016,f_{1}^{{\mathcal {I}} }=.05,\,d_{2}^{{\mathcal {I}}}=.1702,\, f_{2}^{{\mathcal {I}}}=.0834.\)
-
Solution \({\mathcal {II}},\,d_{1}^{{\mathcal {II}}}=1.993,f_{1}^{\mathcal {II }}=0.5607,\,d_{2}^{{\mathcal {II}}}=-1.118,\, f_{2}^{{\mathcal {II}}}=-.2355.\)
-
Solution \({\mathcal {III}},\,d_{1}^{{\mathcal {III}}}=7.067,f_{1}^{\mathcal { III}}=-.0447,\,d_{2}^{{\mathcal {III}}}=2.419,\, f_{2}^{{\mathcal {III}}}=-.1728.\)
-
Solution \({\mathcal {IV}},\,d_{1}^{{\mathcal {IV}}}=-.0954,f_{1}^{\mathcal { IV}}=1.701,\,d_{2}^{{\mathcal {IV}}}=-.465,\, f_{2}^{{\mathcal {IV}}}=0.259.\)
Solutions \({\mathcal {III}}\) and \({\mathcal {IV}}\) are not good candidates because at least one of the previous assumptions is violated. For the purpose of this analysis, it is sufficient to focus on GAP strategies, return rates, and value functions, given the fact that pricing strategies take the same shape of the state. “Appendix 2” displays these violated assumptions in bold. Instead, solutions \({\mathcal {I}}\) and \({\mathcal {II}}\) are good candidates because all positivity assumptions are met, along with admissible values for the return rate at the steady state, specifically, \(r^{B}\in (0,1]\). Second, we check the robustness of solutions \({\mathcal {I}}\) and \({\mathcal {II}}\) to figure out which of them should be used over the research. Therefore, we evaluate the changes of GAP efforts, return rates, and profits when a parameter value is changed, to identify the circumstances under which the assumptions are violated. The full numerical analysis, which is displayed in “Appendix 3”, shows that solution \({\mathcal {I}}\) is more robust than solution \( {\mathcal {II}}\); thus, it is the good solution to be used from now on. Therefore, we will refer to solution \({\mathcal {I}}\) such as \(d_{1}^{*}>0,f_{1}^{*}>0,d_{2}^{*}>0,f_{2}^{*}>0\). Now that we have established a positive sign for \(d_{1}^{*},f_{1}^{*},d_{2}^{*},f_{2}^{*}\), and we can check that all model conditions and assumptions are satisfied in the following Corollary:
Corollary 1
In equilibrium, all players’ strategies are positive in the return rate when \(\theta >\varDelta \beta \). Then
-
1.
The optimal path of the state variable is always monotonous, the steady state \(\left( SS\right) \) of \(r_{ SS }^{B}\in (0,1]\) and \(r^{B}\left( t\right) \in [r_{0},r_{ SS }^{B}]\) if \(r_{0}<r_{ SS }^{B}\) or \( r^{B}\left( t\right) \in [r_{ SS }^{B},r_{0},]\) if \(r_{0}>r_{ SS }^{B};\)
-
2.
\(A_{i}^{B}\left( r_{ SS }^{B}\right) \) is positive and nondecreasing in \(r_{ SS }^{B};\)
-
3.
\(\omega ^{B}\left( r_{ SS }^{B}\right) \) and \(p^{B}\left( r_{ SS }^{B}\right) \) increase in \(r_{ SS }^{B}\) if \(\theta -\varDelta \beta >0;\)
-
4.
\(D^{B}\left( r_{ SS }^{B}\right) \) and \(V_{i}^{B}\left( r_{ SS }^{B}\right) \) are positive and nondecreasing in \(r_{ SS }^{B}.\)
Proof
Substituting Eqs. (12) and (13) in (2) leads to \(\dot{r}^{B}=\, a^{2}d_{2}+b^{2}f_{2}+\left( a^{2}d_{1}+b^{2}f_{1}-\delta \right) r^{B}\left( t\right) ;\)the stability condition requires to have \( a^{2}d_{1}+b^{2}f_{1}-\delta <0.\) The return rate at the steady state is given by \(r_{ SS }^{B}=\frac{a^{2}d_{2}+b^{2}f_{2}}{\delta -a^{2}d_{1}-b^{2}f_{1}}>0.\) The solution \(d_{1}^{*}>0,\,d_{2}^{*}>0, \, f_{1}^{*}>0\) and \(f_{2}^{*}>0\) also satisfies the assumption that \(r_{ SS }^{B}\le 1\) (see the “Appendix 3”) and thus \(r_{ SS }^{B}\in (0,1]\). To check the stability of \(r_{ SS }^{B}\forall t\in [0,\infty ),\) solve Eq. (2) to get \(r^{B}\left( t\right) =( 1-e^{( a^{2}d_{1}+b^{2}f_{1}-\delta ) }) r_{ SS }^{B}+e^{( a^{2}d_{1}+b^{2}f_{1}-\delta ) t}r_{0};\) from this expression, it becomes clear that condition \(a^{2}d_{1}+b^{2}f_{1}- \delta <0\) is needed to ensure that \(r_{{}}^{B}\) monotonously converges from \(r_{0}\) to \(r_{ SS }^{B}\) when the initial value of the return rate is lower than the steady-state value \((r_{0}<r_{ SS }^{B})\) as the time goes to infinite, while \(r^{B}\) monotonously decreases from \(r_{0}\) to \(r_{ SS }^{B}\) when the initial value of the return rate is greater than the steady-state value \((r_{0}>r_{ SS }^{B})\). This solution ensures that \(A_{i}^{B}\left( r_{ SS }^{B}\right) \ge 0,\) with \(i=M,R,\) is stable as well as that \(\frac{ \partial A_{M}^{B}\left( r_{ SS }^{B}\right) }{\partial r_{ SS }^{B}}=ad_{1}>0\) and \(\frac{\partial A_{R}^{B}\left( r_{ SS }^{B}\right) }{\partial r_{ SS }^{B}} =bf_{1}>0\). Previous results on \(r_{ SS }^{B}\) guarantee positive \(\omega ^{B}\left( r_{ SS }^{B}\right) \) and \(p^{B}\left( r_{ SS }^{B}\right) \). \(\theta -\varDelta \beta >0\ \)is a sufficient condition to get pricing-decision strategies increasing in \(r_{ SS }^{B}\) (see the earlier case analysis). Substitute (15) in Eq. (5) to show that \(D^{B}\left( r_{ SS }^{B}\right) =\frac{\alpha +r_{ SS }^{B}\left( \theta +\varDelta \beta \right) }{4}>0\) and then \(\frac{\partial D^{B}\left( r_{ SS }^{B}\right) }{\partial r_{ SS }^{B}}=\frac{\theta +\varDelta \beta }{4}>0\) for all model parameter values. Finally, conditions that ensure \( A_{i}^{B}\left( r_{ SS }^{B}\right) >0\) also guarantee that \(V_{i}^{B}\left( r_{ SS }^{B}\right) >0,\,\frac{\partial V_{M}^{B}\left( r_{ SS }^{B}\right) }{ \partial r_{ SS }^{B}}=d_{1}r_{ SS }^{B}+d_{2}>0\) and \(\frac{\partial V_{R}^{B}\left( r_{ SS }^{B}\right) }{\partial r_{ SS }^{B}} =f_{1}r_{ SS }^{B}+f_{2}>0\). \(\square \)
The game that we analyze in this research carries out some specific properties that make the traditional per-return incentives ineffective. A per-return incentive loses its beneficial effects because both players are able to set their optimal wholesale and pricing strategies by also considering the role of incentives. This mutual adjustment sterilizes the effectiveness of a per-return incentive. This results from De Giovanni and Zaccour [7] who have fixed the wholesale price to gain benefits from remanufacturing. In addition, the missing links between GAP and pricing also nullify the per-return incentive efficiency due to the dynamic return component. In fact, Savaskan et al. [21] and Savanskan and van Wassenhove [22] have demonstrated the value created by a per-return policy in static games, while in dynamic games, several adjustments have been introduced: fix wholesale price [7], interfaces between pricing and GAP [8], and revenue sharing contract agreements [5].
Proposition 2
A per-return incentiveFootnote 3 is an inefficient mechanism to coordinate a dynamic CLSC as it results that \( V_{M}^{P}\left( r_{ SS }^{P}\right) =V_{M}^{B}\left( r_{ SS }^{B}\right) \) and \( V_{R}^{P}\left( r_{ SS }^{P}\right) =V_{R}^{B}\left( r_{ SS }^{B}\right) \).
Proof
See the “Appendix 1”.\(\square \)
The result in Proposition 2 compels us to look into different types of incentive mechanisms to coordinate a dynamic CLSC. Therefore, we have investigated both state- and control-dependent incentives.
3.2 Scenario S: State-Dependent Incentive
As the incentive in the state-dependent problem does not involve players’ policies, all controls assume the same shape as in the no-incentive scenario. Because the incentive \(\varphi ^{S}\left( r\left( t\right) \right) \) is linear in the state, only the linear coefficients will be affected while the optimal solution to this problem is given in Proposition 3.
Proposition 3
Assuming an interior solution, strategies and profit functions in the state-dependent incentive game are as follows:
where \(m_{1},m_{2},n_{1}\), and \(n_{2}\) are the coefficients of the conjectured value functions
Proof
See the “Appendix 1”.\(\square \)
The qualitative analysis of players’ controls and customer demand is somewhat similar to the discussion in benchmark scenario as the analytical solution follows the same structure.
Remark 1
In equilibrium, results in Corollary 1 also apply to the state-incentive scenario, that is:
-
1.
The optimal path of the state variable is always monotonous, \( r_{ SS }^{S}\in (0,1]\) and \(r^{S}\left( t\right) \in [r_{0},r_{ SS }^{S}]\ \) if \(r_{0}<r_{ SS }^{S}\) or \(r^{S}\left( t\right) \in [r_{ SS }^{S},r_{0}]\ \) if \(r_{0}>r_{ SS }^{S};\)
-
2.
\(A_{i}^{S}\left( r_{ SS }^{S}\right) \) is positive and nondecreasing in \( r_{ SS }^{S};\)
-
3.
\(\omega ^{S}\left( r_{ SS }^{S}\right) \) and \(p^{S}\left( r_{ SS }^{S}\right) \) increase in \(r_{ SS }^{S}\) if \(\theta -\varDelta \beta >0;\)
-
4.
\(D^{S}\left( r_{ SS }^{S}\right) \) and \(V_{i}^{S}\left( r_{ SS }^{S}\right) \) are positive and nondecreasing in \(r_{ SS }^{S}.\)
Interestingly, the results in Remark 1 hold because the incentive parameter \( \mu \) does not play any role inside the constants \(m_{1}\) and \(n_{1}\), which have the same structure as the quadratic coefficients in the benchmark scenario [see “Appendix 1”, Eqs. (48), (51), (79), and (82)]. Therefore, it results that \(m_{1}^{*}=d_{1}^{*},\, n_{1}^{*}=f_{1}^{*}\), and then \(\frac{\partial m_{1}^{*}}{\partial \mu }=0\) and \(\frac{\partial n_{1}^{*}}{\partial \mu }=0\). Because \(m_{1}\) and \( n_{1}\) are \(\mu -\hbox {independent},\,m_{2}\) and \(n_{2}\) can be simply derived from the Riccati equations:
(see the “Appendix 1”) where \(B_{1}=a^{2}m_{1}^{*}+b^{2}n_{1}^{*}-\delta -\rho <0\) and \(B_{2}=\alpha \left( \theta +\varDelta \beta \right) >0.\) Analytically, it is easy to derive the sign of \(m_{2}^{*},n_{2}^{*}\) once we have established that \(m_{1}^{*}=d_{1}^{*}>0\) and \(n_{1}^{*}=f_{1}^{*}>0.\)
The solution gives \(m_{2}^{*}=\frac{b^{2}m_{1}^{*}-2\mu -2B_{1}}{ 8\beta \left( B_{1}^{2}-\mu ^{2}-a^{2}b^{2}m_{1}^{*}n_{1}^{*}\right) }B_{2}>0\) and \(n_{2}^{*}=\frac{\mu -B_{1}+2a^{2}n_{1}^{*}}{8\beta \left( B_{1}^{2}-\mu ^{2}-a^{2}b^{2}m_{1}^{*}n_{1}^{*}\right) } B_{2}>0,\) from which we can derive that \(\frac{\partial m_{2}}{\partial \mu } =-\frac{\mu \left( \mu -b^{2}m_{1}^{*}\right) +\left( B_{1}+2\mu \right) B_{1}-a^{2}b^{2}m_{1}^{*}n_{1}^{*}}{4\beta \left( \mu ^{2}-B_{1}^{2}+a^{2}b^{2}m_{1}^{*}n_{1}^{*}\right) ^{2}}B_{2}\le 0\) and \(\frac{\partial n_{2}}{\partial \mu }\,=\frac{2\mu \left( 2a^{2}n_{1}^{*}+\mu -B_{1}\right) +\left[ B_{1}^{2}-\mu ^{2}-a^{2}b^{2}m_{1}^{*}n_{1}^{*}\right] }{8\beta \left( \mu ^{2}-B_{1}^{2}+a^{2}b^{2}m_{1}^{*}n_{1}^{*}\right) ^{2}}B_{2}\ge 0\). Although these results apply in general for all parameter values, a numerical analysis is reported in the Table 3 below, while further simulations are displayed in “Appendix 3” to clarify these signs.
Numerical Example To clarify the results \(\frac{\partial m_{2}}{\partial \mu }\le 0,\frac{\partial n_{2}}{\partial \mu }\ge 0\), we use the baseline parameter values previously fixed. Then, for \(\mu =\left( .025,.05,.2\right) ,\) the solution for \(m_{2},n_{2}\) gives the results displayed in Table 3.
Now that we have established the signs each coefficient of the solution, we substitute Eqs. (20) and (21) in (2) to have \(\dot{r}^{S}\left( t\right) =\, a^{2}m_{2}+b^{2}n_{2}+\left( a^{2}m_{1}+b^{2}n_{1}-\delta \right) r^{S}\left( t\right) ,\) for which the stability condition imposes \( a^{2}m_{1}+b^{2}n_{1}-\delta <0.\) Therefore, \(r_{ SS }^{S}=\frac{ a^{2}m_{2}+b^{2}n_{2}}{\delta -a^{2}m_{1}-b^{2}n_{1}}>0\) and solution \( m_{1}^{*}>0,\,m_{2}^{*}>0,\, n_{1}^{*}>0\ \)and \(n_{2}^{*}>0\) also ensures that \(r_{ SS }^{S}\le 1\) (see the “Appendix 3”). Finally, \( r_{ SS }^{S}\in (0,1]\). The stability of \(r_{ SS }^{S}\forall t\in [0,\infty )\) can be checked by solving Eq. (2) and get \(r^{S}\left( t\right) =\left( 1-e^{\left( a^{2}m_{1}+b^{2}n_{1}-\delta \right) t}\right) r_{ SS }^{S}+e^{\left( a^{2}m_{1}+b^{2}n_{1}-\delta \right) t}r_{0};\) from this expression, it results clear that \(r_{{}}^{S}\) monotonously converges from \(r_{0}\) to \( r_{ SS }^{S}\) when the initial value of the return rate is lower than the steady-state value \((r_{0}<r_{ SS }^{S})\) as the time goes to infinite, while \( r^{S}\) monotonously decreases from \(r_{0}\) to \(r_{ SS }^{S}\) when the initial value of the return rate is greater than the steady-state value \( (r_{0}>r_{ SS }^{S})\). Consequently, \(A_{i}^{S}\left( r_{ SS }^{S}\right) \ge 0\) is also stable \(\forall t\in [0,\infty )\), while \(\frac{\partial A_{M}^{S}\left( r_{ SS }^{S}\right) }{\partial r_{ SS }^{S}}=am_{1}>0\) and \( \frac{\partial A_{R}^{S}\left( r_{ SS }^{S}\right) }{\partial r_{ SS }^{S}} =bn_{1}>0\). Because \(r_{ SS }^{S}\in (0,1]\) ensures positive \(\omega ^{S}\left( r_{ SS }^{S}\right) \) and \(p^{S}\left( r_{ SS }^{S}\right) ,\, D^{S}\left( r_{ SS }^{S}\right) =\frac{\alpha +r_{ SS }^{S}\left( \theta +\varDelta \beta \right) }{4}>0,\,\frac{\partial D^{S}\left( r_{ SS }^{S}\right) }{\partial r_{ SS }^{S}}=\frac{\theta +\varDelta \beta }{4}>0,\) while the impact of \(r_{ SS }^{S}\) on \(\omega ^{S}\left( r_{ SS }^{S}\right) \) and \(p^{S}\left( r_{ SS }^{S}\right) \) is established by the relationships between consumers’ repurchasing intention and sensitivity to price as well as returns’ residual value. Finally, conditions that ensure \(A_{i}^{S}\left( r_{ SS }^{S}\right) >0\) also guarantee that \(V_{i}^{S}\left( r_{ SS }^{S}\right) >0,\,\frac{\partial V_{M}^{S}\left( r_{ SS }^{S}\right) }{\partial r_{ SS }^{S}} =m_{1}r_{ SS }^{S}+m_{2}>0\) and \(\frac{\partial V_{R}^{S}\left( r_{ SS }^{S}\right) }{\partial r_{ SS }^{S}}=n_{1}r_{ SS }^{S}+n_{2}>0.\)
It is now possible to establish the impact of a state-dependent incentive on the return rate through the following proposition:
Proposition 4
In equilibrium, the steady state of return rate \(r_{ SS }^{S}\ \)is positive and nondecreasing in \(\mu \) when \(a^{2}\left| \frac{\partial m_{2}}{ \partial \mu }\right| <b^{2}\frac{\partial n_{2}}{\partial \mu }\).
Proof
Plug (20) and (21) inside (2) and compute the return rate at the steady state as \(r_{ SS }^{S}=\frac{a^{2}m_{2}+b^{2}n_{2}}{ \delta -a^{2}m_{1}-b^{2}n_{1}}>0;\) it results that \(\frac{\partial r_{ SS }^{S} }{\partial \mu }=\frac{1}{\delta -a^{2}m_{1}-b^{2}n_{1}}\left( a^{2}\frac{ \partial m_{2}}{\partial \mu }+b^{2}\frac{\partial n_{2}}{\partial \mu } \right) \ge 0\Leftrightarrow a^{2}\left| \frac{\partial m_{2}}{\partial \mu }\right| <b^{2}\frac{\partial n_{2}}{\partial \mu }.\) When this condition holds, the return rate increases in the incentive \(\mu \). \(\square \)
\(R\)’s GAP effectiveness \(b\) plays a key role in the establishment of conditions to increase the return rate through a state-dependent incentive. Therefore, supplying a state-dependent incentive seems to be a necessary but not also a sufficient condition to perform higher return rates. Intuitively, \(M\)’s willingness to perform the return rate through incentives decreases when \(R\)’s GAP effectiveness is small as \(R\)’s contribution to the state will be marginal even when the incentive is sufficiently high. When these conditions apply, it becomes straightforward to show \(\frac{\partial A_{R}^{S}\left( r_{ SS }^{S}\right) }{ \partial \mu }\ge 0,\) as \(\frac{\partial r_{ SS }^{S}}{\partial \mu }\ge 0\) and \(\frac{\partial n_{2}}{\partial \mu }\ge 0\,;\) thus, \(R\) invests more in GAP when a state-dependent incentive is put in place. Finally, insert \( r_{ SS }^{S}\,\ \)in (21) to obtain \( A_{R}^{S}\left( r_{ SS }^{S}\right) =b\frac{\left( \delta -a^{2}m_{1}\right) n_{2}+a^{2}m_{2}n_{1}}{\delta -a^{2}m_{1}-b^{2}n_{1}}.\) In contrast, the sign of \(\frac{\partial A_{M}^{S}\left( r_{ SS }^{S}\right) }{\partial \mu }\) is not as easy to establish as \(\frac{\partial r_{ SS }^{S}}{\partial \mu } \ge 0\) and \(\frac{\partial m_{2}}{\partial \mu }\le 0\). Note that, \(M\) would invest less in GAP efforts because he has lower economic resources on hand when a state-dependent incentive is supplied. Further, he expects \(R\) to invest more in GAP efforts to perform the return rate and contribute to her profits. A state-dependent incentive determines the conditions under which both players can be economically better off. Plug \(r_{ SS }^{S}\) in (20) and derive \(A_{M}^{S}\left( r_{ SS }^{S}\right) =a\frac{\left( \delta -b^{2}n_{1}\right) m_{2}+b^{2}m_{1}n_{2}}{\delta -a^{2}m_{1}-b^{2}n_{1}}\). Finally, the implementation of a state-dependent incentive leads to higher environmental performance conditionally to \(R\)’s sufficiently large GAP effectiveness.
Finally, in “Appendix 3”, we numerically verify that \(r_{ SS }^{S}\in (0,1]\) as well as positivity of GAP strategies and profits.
Proposition 5
In equilibrium, a state-dependent incentive always leads to higher environmental performance when \(b\ge b^{*}.\)
Proof
Compute the difference between steady state return rates in state-dependent and benchmark scenarios as \(r_{ SS }^{S}-r_{ SS }^{B}=-\frac{B_{1}\left[ 2a^{2}\mu +b^{2}\mu +\left( 2a^{2}-b^{2}\right) B_{1}^{{}}\right] +a^{2}b^{2} \left[ \left( b^{2}-2a^{2}\right) m_{1}^{*}n_{1}^{*}-\left( m_{1}^{*}+\mu n_{1}^{*}\right) \mu \right] }{8\beta \left( a^{2}b^{2}m_{1}^{*}n_{1}^{*}-B_{1}^{2}\right) \left( \mu ^{2}-B_{1}^{2}+a^{2}b^{2}m_{1}^{*}n_{1}^{*}\right) }\mu B_{2}\). There exists a sufficiently large \(b=b^{*}\) for which \( r_{ SS }^{S}>r_{ SS }^{B},\,\forall \mu >0.\) To prove that statement, assume that \(b\) is sufficiently large and results \(b^{2}=2a^{2}\), which implies that \(R\)’s GAP effectiveness is twice \(M\)’s GAP effectiveness; it turns out that \(r_{ SS }^{S}-r_{ SS }^{B}=-\frac{2B_{1}-\left( m_{1}^{*}+\mu n_{1}^{*}\right) a^{2}}{8\beta \left( a^{2}b^{2}m_{1}^{*}n_{1}^{*}-B_{1}^{2}\right) \left( \mu ^{2}-B_{1}^{2}+a^{2}b^{2}m_{1}^{*}n_{1}^{*}\right) }\mu ^{2}b^{2}B_{2}>0 \forall \mu >0\), as \( B_{1}<0\). \(\square \)
While GAP strategies have opposite changes over increasing incentive values, pricing-decision policies would eventually have the same sign. Assume that \( \frac{\partial r_{ SS }^{S}}{\partial \mu }>0,\) relationships among customers’ repurchasing intentions \(\theta \), return residual value \(\varDelta ,\) and customers’ sensitivity to price \(\beta \) establish these signs, specifically, three cases can be identified.
Case 1 \(\theta \le \frac{\varDelta \beta }{3}.\) When the customer’s repurchasing intention is low, high incentive lowers both the wholesale price and the retail price, and thus, it negatively impacts on the first and the second marginalization. When \(M\) supplies a state-dependent incentive, he reduces the first marginalization and charges a lower wholesale price. In these circumstances, a state-dependent incentive also provides an implicit motivation for \(R\) to boost returns while substantially lowering the internal inefficiency. Similarly, \(R\) charges a lower price to customers, for whom a state-dependent mechanism is beneficial—though they will pay a lower price. A state-dependent incentive plays the dual role of performing higher environmental performance (return rate) and higher social performance (customers pay lower prices).
Case 2 \(\theta \in (\frac{\varDelta \beta }{3},\varDelta \beta ].\) When the customer’s repurchasing intention is medium, a higher incentive implies lower wholesale price and higher retail price, and thus, it negatively impacts on the first marginalization, while it positively influences the second marginalization. A state-dependent incentive reduces the first marginalization; therefore, \(M\) will charge a lower wholesale price. In these circumstances, a state-dependent incentive also provides an implicit motivation for \(M\) to boost returns while substantially lowering the internal inefficiency. In contrast, \(R\) charges a higher price to customers, for whom a state-dependent mechanism is not beneficial—though they will pay a higher price.
Case 3 \(\theta >\varDelta \beta \). When the customer’s repurchasing intention is high, an increasing incentive implies higher wholesale price and retail price; therefore, higher quantity purchased by green customers compensates the lower amounts sold to new customers. Increasing fixed incentives penalize the business through boosting the double marginalization effects. Because customers are environmentally conscious, repurchases are less sensitive to price increase; thus, the double marginalization effect does not negatively influence sales.
Because the identified parameters \(m_{2}\) and \(n_{2}\) are both positive, the pair of constants \((m_{3},n_{3})\ \)will always be positive for any model parameter value and their changes in the incentive will depend on \(m_{2}\) and \(n_{2}\) (see the “Appendix 3”). This leads to \( V_{i}^{S}\left( r_{ SS }^{S}\right) \ge 0.\)
3.3 Scenario C: Control-Dependent Incentive
As the incentive in the control-dependent game only involves \(R\)’s GAP efforts, pricing decisions and \(M\)’s GAP efforts assume the structure as in the no-incentive scenario. Because the incentive is linear in \( A_{R}^{C}\left( r^{C}\right) \), only the linear and the constant coefficient of the conjectured value functions will be influenced, whereas the optimal solution to this problem is given in Proposition 6.
Proposition 6
Assuming an interior solution, strategies and profit functions in the control incentive game are as follows:
where \(l_{1},l_{2},k_{1}\), and \(k_{2}\) are the coefficients of the conjectured value functions
Proof
See the “Appendix 1”.\(\square \)
The qualitative analysis of players’ controls and customer demand follows somewhat the discussion in the benchmark scenario as the analytical solution follows the same structure.
Remark 2
In equilibrium, results in Corollary 1 also apply to the control incentive scenario, that is:
-
1.
The optimal path of the state variable is always monotonous, \( r_{ SS }^{C}\in (0,1]\) and \(r^{C}\in (r_{0},r_{ SS }^{C}]\) if \(r_{0}<r_{ SS }^{C}\) or \(r^{C}\in (r_{ SS }^{C},r_{0}]\) if \(r_{0}>r_{ SS }^{C};\)
-
2.
\(A_{i}^{C}\left( r_{ SS }^{C}\right) \) is positive and nondecreasing in \( r_{ SS }^{C};\)
-
3.
\(\omega ^{C}\left( r_{ SS }^{C}\right) \) and \(p^{C}\left( r_{ SS }^{C}\right) \) increase in \(r_{ SS }^{C}\) if \(\theta -\varDelta \beta >0;\)
-
4.
\(D^{C}\left( r_{ SS }^{C}\right) \) and \(V_{i}^{C}\left( r_{ SS }^{C}\right) \) are positive and nondecreasing in \(r_{ SS }^{C}.\)
As for the state-incentive case, the incentive parameter \(\mu \) does not play any role inside the quadratic-state constants \(k_{1}\) and \(l_{1}\). Note that although the incentive is control dependent, it is only a function of \(R\)’s GAP efforts rather than of other strategies. Therefore, the quadratic terms of conjectured value functions take the same structure of previous scenarios [see “Appendix 1”, Eqs. (48), (51), (79), (82), (101), and (104)]. Thus, \(l_{1}^{*}=d_{1}^{*}>0\) and \(k_{1}^{*}=f_{1}^{*}>0\), from which it turns out that \(\frac{\partial l_{1}^{*}}{\partial \mu }=0\) and \(\frac{ \partial k_{1}^{*}}{\partial \mu }=0\). While \(l_{1}\) and \(k_{1}\) are \( \mu \) independent, \(l_{2}\) and \(k_{2}\) are affected by a control-dependent incentive and can be simply derived from the Riccati equations:
(see the “Appendix 1”). The solution gives \(l_{2}=\frac{8b^{3}\beta \mu k_{1}l_{1}+8\mu \beta b\left( B_{1}+a^{2}l_{1}\right) \left( k_{1}-l_{1}\right) -\left( 2B_{1}+\left( 2a^{2}-b^{2}\right) l_{1}\right) B_{2}}{8\beta \left( B_{1}^{2}-a^{2}l_{1}\left( b^{2}k_{1}-B_{1}\right) \right) }>0\) and \(k_{2}=\frac{-B_{2}\left( B_{1}-2a^{2}k_{1}\right) +8b\beta \mu k_{1}\left( a^{2}\left( l_{1}-k_{1}\right) -B_{1}\right) }{8\beta \left( B_{1}^{2}-a^{2}l_{1}\left( b^{2}k_{1}-B_{1}\right) \right) }>0,\) where the denominator \(B_{1}^{2}-a^{2}l_{1}\left( b^{2}k_{1}-B_{1}\right) >0\). The derivatives with respect to the incentive \(\mu \) will be \(\frac{\partial l_{2}}{\partial \mu }=\frac{b\left( B_{1}+a^{2}l_{1}\right) \left( k_{1}-l_{1}\right) +b^{3}k_{1}l_{1}}{ B_{1}^{2}+a^{2}B_{1}l_{1}-a^{2}b^{2}k_{1}l_{1}}\ge 0\) and \(\frac{\partial k_{2}}{\partial \mu }=\frac{a^{2}b\left( l_{1}-k_{1}\right) -bB_{1}}{ B_{1}^{2}+a^{2}B_{1}l_{1}-a^{2}b^{2}k_{1}l_{1}}k_{1}\ge 0.\) The numerical analysis reported in Table 4 as well as the simulations displayed in “Appendix 3” confirm that these results apply in general and independent of the parameter values.
Numerical Example 2 To clarify the results \(\frac{\partial l_{2}}{\partial \mu }\ge 0,\frac{\partial k_{2}}{\partial \mu }\ge 0\), for \(\mu =\left( .025,.05,.2\right) ,\) solutions for \(l_{2},k_{2}\) give the results displayed in Table 4.
After establishing the signs each coefficient of the solution, we substitute Eqs. (28) and (29) in (2) to have \(\dot{r}^{C}\left( t\right) = a^{2}l_{2}+b^{2}k_{2}+\left( a^{2}l_{1}+b^{2}k_{1}-\delta \right) r^{C}\left( t\right) ,\) for which the stability condition imposes \( a^{2}l_{1}+b^{2}k_{1}-\delta <0.\) Therefore, \(r_{ SS }^{C}=\frac{ a^{2}l_{2}+b^{2}k_{2}}{\delta -a^{2}l_{1}-b^{2}k_{1}}>0\) and solution \( l_{1}^{*}>0,\, l_{2}^{*}>0,\, k_{1}^{*}>0\ \)and \(k_{2}^{*}>0\) also ensures that \(r_{ SS }^{C}\le 1\) (see the “Appendix 3”). Finally, \( r_{ SS }^{C}\in (0,1]\). The stability of \(r_{ SS }^{C}\forall t\in [0,\infty )\) can be checked by solving Eq. (2) and get \(r^{C}\left( t\right) =\left( 1-e^{\left( a^{2}l_{1}+b^{2}k_{1}-\delta \right) t}\right) r_{ SS }^{C}+e^{\left( a^{2}l_{1}+b^{2}k_{1}-\delta \right) t}r_{0},\) from which it results that condition \(a^{2}l_{1}+b^{2}k_{1}-\delta <0\) ensures that \(r_{{}}^{C}\) monotonously converges from \(r_{0}\) to \(r_{ SS }^{C}\) when \(r_{0}<r_{ SS }^{C}\), while \(r^{C}\) monotonously decreases from \(r_{0}\) to \(r_{ SS }^{C}\) when \( r_{0}>r_{ SS }^{C}.\) Consequently, \(A_{i}^{C}\left( r_{ SS }^{C}\right) \ge 0\) is also stable \(\forall t\in [0,\infty )\), while \(\frac{\partial A_{M}^{C}\left( r_{ SS }^{C}\right) }{\partial r^{C}}=al_{1}>0\) and \(\frac{\partial A_{R}^{C}\left( r_{ SS }^{C}\right) }{\partial r^{C}}=bk_{1}>0\). Because \(r_{ SS }^{C}\in (0,1]\) ensures positive \(\omega ^{C}\left( r_{ SS }^{C}\right) \) and \(p^{C}\left( r_{ SS }^{C}\right) ,\, D^{C}\left( r_{ SS }^{C}\right) =\frac{\alpha +r_{ SS }^{C}\left( \theta +\varDelta \beta \right) }{4}>0,\,\frac{\partial D^{C}\left( r_{ SS }^{C}\right) }{\partial r_{ SS }^{C}}=\frac{\theta +\varDelta \beta }{4}>0,\) while the impact of \( r_{ SS }^{C}\) on \(\omega ^{C}\left( r_{ SS }^{C}\right) \) and \(p^{C}\left( r_{ SS }^{C}\right) \) depends on the relationships between consumers’ repurchasing, consumers’ sensitivity to price and returns’ residual value. Finally, conditions that ensure \(A_{i}^{C}\left( r_{ SS }^{C}\right) >0\) also guarantee \(V_{i}^{C}\left( r_{ SS }^{C}\right) >0,\,\frac{\partial V_{M}^{C}\left( r_{ SS }^{C}\right) }{\partial r_{ SS }^{C}} =l_{1}r_{ SS }^{C}+l_{2}>0\) and \(\frac{\partial V_{R}^{C}\left( r_{ SS }^{C}\right) }{\partial r_{ SS }^{C}}=k_{1}r_{ SS }^{C}+k_{2}>0.\)
Interestingly, contrary to the state-dependent incentive, a control-dependent incentive pushes both players’ to increase their GAP efforts. It is intuitive that \(R\) increases her GAP efforts. On one hand, she has higher economic resources to boost her profits; on the other hand, she determines the incentive through her GAP efforts decision. In addition, \(M\) contributes more to the return rate dynamics even if he has fewer economic resources to invest in GAP. A control-dependent incentive allows the engagement of \(R\)’s efforts independent of \(A_{M}^{C};\) therefore, enhancing GAP efforts will not directly deteriorate \(M\)’s profits. Rather, \(M\) will spend more in GAP to exploit both the operational and the marketing benefits that the state supplies. It is now easy to establish the impact of a control-dependent incentive inside the return rate, as it is summarized in the following proposition
Proposition 7
In equilibrium, the steady state of return rate \(r_{ SS }^{S}\ \)is positive and nondecreasing in \(\mu \).
Proof
Plug (28) and (29) inside (2) and compute the return rate at the steady state as \(r_{ SS }^{C}=\frac{a^{2}l_{2}+b^{2}k_{2}}{ \delta -a^{2}l_{1}-b^{2}k_{1}}>0;\) because it results that \(\frac{\partial l_{1}}{\partial \mu }=\frac{\partial k_{1}}{\partial \mu }=0,\) it turns out that \(\frac{\partial r_{ SS }^{C}}{\partial \mu }=\frac{1}{\delta -a^{2}l_{1}-b^{2}k_{1}}\left( a^{2}\frac{\partial l_{2}}{\partial \mu }+b^{2} \frac{\partial k_{2}}{\partial \mu }\right) \ge 0\) for all parameter values.
In the control-dependent incentive game, both players’ GAP effectiveness \(a\) and \(b\) establish the conditions under which a CLSC performs better return rates. The implementation of a control-dependent incentive does guarantee higher environmental performance for all model parameter values. Thus, \(M\) always has a high willingness to supply a control-dependent incentive: This result depends on the influence that \(M\) exerts on the incentive itself, which is null as \(R\) is the only one responsible for the incentive she will get. Finally, insert \(r_{ SS }^{C}\) in (28) and (29) to obtain \(A_{M}^{C}\left( r_{ SS }^{C}\right) =a\frac{\left( \delta -b^{2}k_{1}\right) l_{2}+b^{2}k_{2}l_{1}}{\delta -a^{2}l_{1}-b^{2}k_{1}}\) and \(A_{R}^{C}\left( r_{ SS }^{C}\right) =\frac{ bk_{1}\left( a^{2}l_{2}+b^{2}k_{2}\right) +\left( \delta -a^{2}l_{1}-b^{2}k_{1}\right) \left( bk_{2}+\mu \right) }{\delta -a^{2}l_{1}-b^{2}k_{1}}\).
Further, in “Appendix 3”, we numerically verify that \(r_{ SS }^{C}\in (0,1]\) as well as positivity of GAP strategies and profits. As for the previous scenarios, pricing-decision policies are driven by the return rate while the relationships among customers’ repurchasing intentions \(\theta \), return residual value \(\varDelta ,\) and customers’ sensitivity to price \(\beta \) establish the impact of a return process in the first \(\pi _{M}\) and second marginalization \(\pi _{R}\). Note that the qualitative analysis follows the findings in the previous game. Because the identified parameters \(l_{2}\) and \(k_{2}\) are both positive, the pair of constants \((l_{3},k_{3})\ \)will always be positive for any model parameter value as quadratic and linear coefficients are all positive and their changes in the incentive will depend on changes of \(l_{2}\) and \(k_{2}\) (see “Appendix 3”). This ensures that \(V_{i}^{C}\left( r_{ SS }^{C}\right) >0\).
4 Comparison Among Scenarios
In this section, we run a simulation analysis to compare state, strategies, and profits over the three scenarios. In the previous sections, we have analytically characterized the players’ strategies and outcomes and extrapolate some findings. Given the model’s structure, not surprisingly, we obtained the equilibrium wholesale and retail prices have the same structure across all scenarios while their difference mainly depends on the state. This implies that any difference in players’ strategies depends on the influence that an incentive has on the state. As strategies and outcomes cannot be compared analytically, we shall proceed numerically. These features supply relevant managerial insights and their investigation provides new contributions to the literature. We start from a baseline parameters whose values have been taken from the literature: \(\alpha =\beta =1,\, a=0.5,b=1,\,\varDelta =.5,\, \theta =0.3;\delta =.4,\,\rho =.9,\, \mu =.05.\) Then, for the purpose of our research, we investigate how the differences among outcomes change according to all parameter values. Nevertheless, among all parameters, we have put more attention to the marginal incentive \(\mu ,\) customers’ repurchasing intention \(\theta ,\) and \(R\)’s GAP effectiveness \(b,\) whose analysis provides a contribution to the literature.
We start from a comparison of the return rate at the steady state across the three scenarios, which is displayed in Table 5. That table should be read as follows: How an element in the main column changes when one feature in the main row is changed. For instance, \(r^{S}-r^{B}\) in the main column and \( \alpha \) in the main row indicates that the difference between return rates in scenarios \(S\) and \(B\) decreases when the market potential increases.
When the business expands, an incentive mechanism based on the overall CLSC’s environmental performance marginally engages firms as compared to an incentive based on single player’s actions. For instance, a control-dependent incentive leads to better return rates when an expansion of the market \(\alpha \) and an efficient conservation of return residual value \(\varDelta \) occur. In these cases, a CLSC performs the environment either through forward or through reverse activities. In contrast, increasing customers’ sensitivity to price \(\beta \) would suggest the implementation of a state-dependent incentive; both pricing decisions and demand heavily depend on the state; thus, a state-dependent incentive involves the entire CLSC. Similarly, high customers’ repurchasing intention \( \theta \) promotes a control-dependent incentive for performing the return rate because it directly influences the demand. Remember that when \(\theta \le \beta \varDelta \, \left( \hbox {e.g.},\text { }\theta =0\right) \), firms exploit the return rate to charge lower prices and double marginalization rather than expanding their marginal revenues. When firms’ sales are ensured through repurchases, sufficiently high return rates are performed without a state-dependent incentive to which all firms contribute. A similar result is obtained with respect to the marginal fixed incentive \(\mu {:}\) If it is low, engagement of other firms will be difficult and then only possible through a state-dependent incentive. A rapid loss of customers’ willingness to contribute to the environment \(\delta \) pushes a CLSC to the implementation of a state-dependent incentive, while future discounts with high rates \(\rho \) pushes through the adoption of a control-dependent incentive that acts on the players’ contributions to the dynamics.
Interestingly, players’ GAP effectiveness follow different directions. \(M\)’s high GAP effectiveness encourages the adoption of a control-dependent incentive; intuitively, \(M\) does not want to transfer money to \(R\) if he has substantially contributed to the return rate. In contrast, providing an incentive is always environmentally convenient for \(R\)’s sufficiently large GAP effectiveness, \(b\). Finally, a sufficiently large \(R\)’s GAP effectiveness is alone sufficient to guarantee better environmental performance through the adoption of an incentive mechanism. Increasing \(R\)’s GAP effectiveness favors the adoption of a state-dependent incentive as it ensures that both players will substantially contribute to the return rate.
It is worth recalling that pricing and demand are state dependent; thus, the qualitative study developed so far also remains valid for their analysis. Although moving from one incentive to another either deteriorates or ameliorates the trade-off between pricing and demand, firms should aim at maximizing environmental performance: It generates higher sales, although it also increases the prices. Closing the loop through optimal recovery programs also entails other sides of the market, such as the social aspects and implications due to the adoption of an incentive mechanism, which can be captured through the investigation of consumers’ demand [8]. In fact, it is well documented that when firms invest in environment protection and preservation, consumers are more willing to purchase from them (e.g., [1, 27]). The selection of an incentive mechanism can also be seen as a decision to impact the social outcomes, although consumers do not play any active role in the developed games. However, CLSC members should consider both their sensitivity to price as well as repurchasing intentions when deciding the optimal pricing and GAP strategies (check the cases developed earlier) along with the market potential and returns’ residual value (e.g., for all scenarios it results \(D=\frac{\alpha +r\left( \theta \varDelta +\beta \right) }{ 4}\)). The implementation of a control-dependent incentive improves the social outcomes when the market expands and closing the loop is an appealing business, while firms should avoid the adoption of a state-dependent incentive because they show opposite willingness to invest in green programs.
Results in Tables 6 and 7 display how players’ GAP efforts change at the steady state according to the model parameters. Changes in the model parameter values have opposite impacts on the amounts that \(M\) invests in GAP. Compared to the no-incentive scenario, the implementation of a control-dependent incentive pushes \(M\) to invest more in GAP according to increasing market size \(\alpha \), return residual value \(\varDelta \), and customers’ repurchasing intentions \(\theta \). This entails \(M\) to exploit the operational and marketing advantages of closing the loop. In line with these findings, high customers sensitivity to price imposes on firms to reconsider their pricing strategies \(\left( \hbox {e.g.,} \theta \le \beta \varDelta \right) \) rather than using remanufacturing to boost sales through repurchasing behaviors. A different finding results from the marginal incentive \(\mu ,\) for which \(M\) expects \(R\) to invest more in GAP efforts when he offers a control-dependent incentive. In contrast, high forgetting effects \(\delta \) and discount rate \(\rho \) discourage GAP investments as \(M\) expects \(R\) to compensate for these inefficiencies by investing more as a counterpart to receiving an incentive. \(M\) has no advantages to provide an incentive when his GAP substantially influences the state; therefore, he invests less under a control-dependent incentive. In the case of \(R\)’s high GAP contribution to the state, a control-dependent inventive allows \(M\) to use remanufacturing to increase profits, and thus, he invests more in GAP as the incentive directly pushes \(R\) to increase her efforts as well.
Except for \(R\)’s GAP effectiveness, any change in the model parameter values that occurs under a state-dependent incentive has an opposite effect on \(M\) ’s GAP decisions from the change that might eventually occur under a control-dependent incentive: Because \(M\) also contributes to the state he is more reluctant to coordinate the CLSC when the business marginally improves. This implies a large incentive that \(M\) would not eventually transfer. Therefore, increasing market size, return residual value, customer’s repurchasing intention, as well as decreasing discount rate, customers’ willingness to return products and price sensitivity lead \(M\) to invest less efforts in GAP when a state-dependent incentive is offered. Intuitively, a high marginal incentive implies lower availability of monetary resources and thus reduction in \(M\)’s GAP efforts. For high GAP effectiveness, \(M\) invests less under a state-dependent incentive as he expects \(R\) to increase her efforts because he also contributes to the incentive. As in the control-dependent incentive, \(M\) lowers his investments in GAP as \(R\)’s effectiveness improves: Lower \(M\)’s investments in GAP are then compensated by \(R\)’s efforts.
Table 7 displays the comparison of \(R\)’s GAP at the steady state over the three scenarios. Interestingly, a marginal improvement of the CLSC business pushes \(R\) to invest more when an incentive is provided. Then, marginal increase in market size, return residual value, customer’s repurchasing intention, as well as marginal reduction on discount rate, customer’s willingness to return products and price sensitivity lead \(R\) to invest more efforts in GAP independent of the nature of the incentive. This is for the purpose of providing an incentive in a CLSC: Boost \(R\)’s willingness to do more in atypical CLSC activities. For any change in the model parameter values, \(R^{\prime }s\) GAP investments across the three scenarios turn out to be \(A_{R}^{S}>A_{R}^{C}>A_{R}^{B}.\)
Interestingly, the amounts \(A_{M}^{S}-A_{M}^{C}\) in Table 6 and \(A_{R}^{S}-A_{R}^{C}\) in Table 7 change in different directions for any change in the model parameters. Generally speaking, when the business improves \(\left( \hbox {e.g.,}\text { higher market potential}\right) \, M\, \left( R\right) \) invests more \(\left( \text {less}\right) \) when a control-dependent incentive is put in place as the responsibility for the final incentive amount only depends on \(R^{\prime }s\) GAP investments.
\(M\)’s payoffs comparison, as reported in Table 8, follows the earlier discussion for \(M\)’s GAP strategy. That is, when the CLSC business improves through an increase in market size, return residual value, or customers repurchasing intention as well as through a decrease in discount rate, customer’s price sensitivity, and willingness to return end-of-use products, \(M\) will be economically better off through the adoption of a control-dependent incentive. A state–control incentive seems far to be economically sustainable because \(M\) also participates in its formation through optimally deciding on the GAP. In addition, \(M\)’s willingness to supply an incentive decreases according to the fixed incentive amount \(\mu \) and \(M\)’s GAP effectiveness, independent of nature of incentive. \(M\) prefers to exclusively manage the return process when his capability to perform the return rate is sufficiently large, while high fixed term incentives make coordination marginally appealing. In contrast, \( M \) will always be economically better off through coordination when \(R\)’s GAP effectiveness is sufficiently high, independent on the incentive nature. Finally, \(M\) should always optional for a control-dependent over a state-dependent incentive as the business improves and players’ performance enlarges.
Table 9 displays \(R\)’s payoffs comparison at the steady state over the analyzed scenarios. The findings follow the results shown for \(R\)’s GAP strategy as it is displayed in Table 7. When the CLSC business expands, \(R\) will always be economically better off through coordination, independent of the nature of an incentive. \(R^{\prime }s\) willingness to participate in closing the loop increases in the incentive and players’ GAP effectiveness: \( R\) will gain more with coordination independent of the players’ contribution to the state. In comparison with the no-incentive scenario, \(R\) should always optional for a coordinated CLSC. However, she should prefer a control-dependent over a state-dependent incentive as the business improves and players’ performance enlarges. This finding is due to the dependency of an incentive: In a control-dependent incentive, \(M\) does not contribute to the determination of \(R\)’s premium.
From the analysis of Tables 8 and 9, one result emerges: There exists a profit-Pareto-improving region when coordination of CLSC makes both players economically better off. Tables 10 and 11 show the comparison of profits over the three scenarios when changes occur in return residual value, customers’ repurchasing intention, and marginal fixed incentive. These model parameters have been shown to modify the findings for our games. Therefore, we focus the simulation analysis on these three parameters. Other simulations will be supplied upon request. We have used high and low values for the three parameters, in particular \(\mu \left( .025,.05;.2\right) ,\, b\left( .5,1,1.5\right) \), and \(\theta \left( 0,.3,.6\right) \) while other parameters are kept at the benchmark level. Notice that values set for \( \theta \) allow one to explore the cases in which the return rate influences pricing-related strategies, e.g., the return policy has no impact on pricing strategies (e.g., \(\theta \le \frac{\varDelta \beta }{3}),\) or it only mitigates internal CLSC inefficiency on the first marginalization (e.g., \( \theta \in (\frac{\varDelta \beta }{3},\varDelta \beta ]),\) or it entails a higher double marginalization effect (e.g., \(\theta >\frac{\varDelta \beta }{3})\). Interestingly, the profit-Pareto-improving region, which is displayed in bold characters, can be identified in accordance with \(M\)’s improvement space. In fact, \(R\) is always economically better off under CLSC coordination, independent of the supplied incentive.
Table 10 displays the cases in which \(M\) is economically better off under a state-dependent incentive. Independent of the amount \(\mu ,\,M\) is always better off in the case of \(R\)’s sufficiently large GAP effectiveness \(b\) and independent of other model parameter. When this condition does not apply, \(M\) is economically worse off as his contribution to the state is not counterbalanced by sufficient economic rewards. Customers’ repurchasing intention and fixed incentive simply become less important in the identification of a profit-Pareto-improving region. In this case, the CLSC leader opts for a state-dependent incentive according to \(R\)’s operational performance. Notice that when the incentive is not sufficiently high, \(M\) is not economically better off even in case \(R\)’s substantially influences the state. Therefore, the incentive should be properly negotiated before the game starts to ensure that \(M\) can engage \(R\) in closing the loop.
Under a control-dependent incentive, \(M\) has a broader region inside which he is economically better off. Because \(R\) influences the final incentive through the GAP efforts, high marginal rewards \(\mu \) make \(M\) economically worse off. Contrary to a state-dependent incentive, the fixed incentive drives \(M^{\prime }\)s preferences for a control-dependent incentive according to the influence of \(R\)’s GAP effectiveness and customers’ repurchasing intention. Three cases are possible:
-
1.
When \(\mu \) is sufficiently low, coordination through a control-dependent mechanism is possible. A sufficient condition is that either \(R\)’s GAP effectiveness or customers’ repurchasing intention is medium or high: Although both features lead to a profit-Pareto-improving situation, increasing \(b\) enhances profits more than increasing \(\theta \).
-
2.
When \(\mu \) is medium, coordination is reached when \(R\)’s GAP efforts is large, independent of customers’ repurchasing intentions. Nevertheless, a large attitude for repurchasing new products after returning old ones always leads to coordination through a control-dependent incentive mechanism.
-
3.
When \(\mu \) is large, coordination is reached when \(R\)’s GAP efforts is large, while customers’ repurchasing intention is simply less important. Nevertheless, when customers’ repurchasing intention is null, a control-dependent incentive never coordinates the CLSC.
Although \(M\) loses some control on the incentive comparated to the state-dependent scheme, a control-dependent incentive imposes less restrictions in the identification of the profit-Pareto-improving region.
5 Conclusions and Future Research
In this paper, we have characterized optimal wholesale price, retail price, and GAPs strategies for a CLSC with a dynamic return rate that serves to recover the residual value of end-of-use products as well as increase sales through customers’ repurchasing intention. We believe that the latter assumption supplies interesting insights into the coordination game literature in CLSC, as for several product categories, customers who return a product are very likely to repurchase a new one (e.g., cartridges, batteries, cameras, tires). Our work provides the basis to enrich the literature by exploring some coordination mechanisms that depart from the classical per-return-incentive scheme (e.g., [21]). We have demonstrated that a classical per-return incentive never coordinates our chain, and thus, we explored two alternative types of incentives. The first is a state-dependent incentive and implies that a retailer receives an incentive according to the return rate, that is, considering the overall CLSC environmental performance. The second mechanism is a control-dependent incentive and implies that a retailer receives an incentive according to her GAP efforts. While a state-dependent incentive depends on the contribution that all players provide to the return rate, a control-dependent exclusively depends on the amount that the retailer invests in GAP. We compare strategies, profits, and return rates of these incentive games with a benchmark (no-incentive) scenario, in which the retailer does not receive any type of incentive.
We use the return rate as a proxy to check CLSC environmental performance, as it consists of the number of products that have been returned to the manufacturers’ plants to be remanufactured instead of being dispersed in the environment. Our results show that as the business expands (e.g., higher market potential, lower customers’ sensitivity to price), the CLSC should adopt a control-dependent incentive scheme to perform the environment. In this case, all CLSC members invest more in GAP as the retailer is the only one responsible for the incentive amount she receives. A state-dependent incentive discourages a manufacturer from investing more in GAP because the retailer benefits from an incentive that depends on the overall performance of the CLSC, for which all players have contributed. Interestingly, the retailer always invests more in GAP efforts when an incentive is supplied independent of its nature, while the manufacturer is discouraged under a state-dependent incentive. The environmental performance is important to establish changes of wholesale and retail prices as both depend on the return rate. When an incentive mechanism leads to higher return rate, the impact on pricing-related decisions changes according to the customers’ repurchasing intention. When customers’ repurchasing intention is low, performing the environment leads to lower wholesale and retail prices and reduces the double marginalization: Firms focus on attracting new customers through lower pricing. When customers’ repurchasing intention is sufficiently large, higher return rates imply higher prices: Firms focus on increasing profits through selling green products to environmentally conscious established customers rather than attracting new ones. Then, CLSCs perform positive profits even when the double marginalization persists.
We show that when coordination is an option, players’ preferences do not always converge to the implementation of the same incentive mechanism. The manufacturer marginally benefits from a state-dependent incentive because the premium that the retailer receives depends on the CLSC’s environmental performance. Ideally, the retailer will receive an incentive even if she optimally sets GAP efforts at a marginal level. This can substantially penalize the manufacturer who also contributes to the return rate. A sufficiently high retailer’s GAP effectiveness is a necessary condition for a manufacturer to prefer a state-dependent incentive. In fact, when the retailer substantially influences the state even with a marginal GAP investment, the manufacturer will be economically better off independent of other model parameter values such as customers’ repurchasing intention and marginal incentive. The adoption of a control-dependent incentive supplies a greater chance to improve profits to the manufacturer. A necessary condition to better perform profits depends on sufficiently low-fixed incentive. Because the retailer has full control over the incentive premium she gets, large fixed amounts penalize the manufacturer’s profit function. Then, in all cases in which the return rate increases while the fixed incentive is low, the manufacturer is economically better off even if the second marginalization is large. When the fixed incentive is medium, the manufacturer has a preference for a control-dependent incentive when the return rate boosts both the first and the second marginalization and always when the retailer’s GAP effectiveness is sufficiently high. In all cases in which the fixed incentive is too large, high retailer’s GAP effectiveness is a necessary but not a sufficient condition for a manufacturer to be better off through a control-dependent incentive. While the triple incentive, retailer’s GAP effectiveness, and customers’ repurchasing intention drives the manufacturer’s preferences for the adoption of a coordination mechanism, the retailer always prefers coordination independent of the incentive scheme that the CLSC adopts. Therefore, the identification of a profit-Pareto-improving region passes through the analysis of regions inside which the manufacturer is economically better off through coordination.
While our results provide useful insights into this emerging area of coordination in CLSCs, some of our assumptions could be relaxed for wider applicability. For example, a penalty can be added to reflect situations in which firms face some penalty cost per non-returned products. This will lead firms to consider this penalty function when setting their GAP efforts. The deterministic problem presented here could also be extended to the case of return rate presents a random component. Although our research shows the effect of various operational aspects (e.g., returns’ residual value) on the optimal strategies, it might be interesting to include a detailed operations framework to address the direct impact of some decisions such as product durability and perishability. In fact, the return rate is influenced by the performance of products and increases with products’ incapability to perform as customers wish. Competition might be another challenging factor to be considered. Firms’ decisions within a CLSC are influenced by decisions in other CLSCs. CLSCs compete in the collection of end-of-use products; thus, the presence of a competitor might influence strategies and payoffs of firms. In addition, we assumed that returned products are remanufactured and sold as new. In reality, most remanufactured products are sold in a secondary market and enhances the risk of cannibalization. Finally, other forms of coordination can be explored while keeping the same model assumptions, such as a revenue sharing contract and joint profit maximization incentive.
Notes
We assume \(\kappa _{i}=1\) as it will be always possible to evaluate the marginal impact on profits function through the effectiveness that GAP strategies exert inside the state equation.
As it will be demonstrated later, \(M\) is willing to incentivize \(R\) to perform the return rate as long as she shows a larger operational effectiveness.
We use the superscript \(P\) to refer to a per-return incentive.
References
Bhattacharya S, Guide VDR, Van Wassenhove LN (2006) Optimal order quantities with remanufacturing across new product generations. Prod Oper Manag 15(3):421–431
Cachon GP (2003) Supply chain coordination with contracts. In: Graves S, de Kok T (eds) Handbooks in operations research and management science: supply chain management. North-Holland, Amsterdam
Corbett C, DeCroix G (2001) Shared savings contracts in supply chains. Manag Sci 47(7):881–893
Corbett CJ, Savaskan RC (2003) Contracting and coordination in closed-loop supply chains. In: Daniel V, Guide R Jr, Van Wassenhove LN (eds) Business aspects of closed-loop supply chains: exploring the issues. Carnegie Mellon University Press, Pittsburgh, PA
De Giovanni P (2014) Environmental collaboration through a reverse revenue sharing contract. Ann Oper Research 6:1–23
De Giovanni P, Roselli (2012) Overcoming the drawbacks of a revenue sharing contract through a coop program. Ann Oper Research 196(1):201–222
De Giovanni P, Zaccour G (2013) Cost-revenue sharing in a closed loop supply chain. Ann Int Soc Dyn Games 12:395–421
De Giovanni P, Zaccour G (2014) A two period model of closed-loop supply chain. Eur J Oper Res 1(1):22–24
Debo LG, Toktay LB, Van Wassenhove LN (2005) Market segmentation and product technology selection for remanufacturable products. Manag Sci 51(8):1193–1205
Ferguson ME, Toktay LB (2006) The effect of competition on recovery strategies. Prod Oper Manag 15(3):351–368
Ferrer G, Swaminathan JM (2006) Managing new and remanufactured products. Manag Sci 52(1):15–26
Fleischmann M, Krikke HR, Dekker R, Flapper SDP (2000) A characterisation of logistics networks for product. Omega Int J Manag Sci 28(6):653–666
Fleischmann M, van Nunen J, Grave B (2003) Integrating closed-loop supply chains and spare parts in IBM. Interface 33(6):44–56
Geyer R, Van Wassenhove LN, Atasu A (2007) The economics of remanufacturing under limited component durability and finite product life cycles. Manag Sci 53(1):88–10
Guide VDR Jr (2000) Production planning and control for remanufacturing: industry practice and research needs. J Oper Manag 18(4):467–483
Guide VDR, Van Wassenhove LN (2009) The evolution of closed-loop supply chain research. Oper Res 57(1):10–18
Ingene C, Taboubi S, Zaccour G (2012) Game-theoretic coordination mechanisms in distribution channels: integration and extensions for models without competition. J Retail 88(4):476–496
Jørgensen S (2011) Intertemporal contracting in a supply chain. Dyn Games Appl 1(2):280–300
Kang S, Hur WM (2012) Investigating the antecedents of green brand equity: a sustainable development perspective. Corp Soc Responsib Environ Mgmt 1(9):306–316
Majumder P, Groenevelt H (2001) Competition in remanufacturing. Prod Oper Manag 10(2):125–141
Savaskan RC, Bhattacharya S, Van Wassenhove LN (2004) Closed loop supply chain models with product remanufacturing. Manag Sci 50(2):239–252
Savaskan RC, Van Wassenhove LN (2006) Reverse channel design: the case of competing retailers. Manag Sci 52(1):1–14
Scholt A, De Giovanni P, Esposito Vinzi V (2014) Is environmental management an economically sustainable business? J Environ Manag 144(1):73–82
Seitz MA, Peattie K (2004) Meeting the closed-loop challenge: the case of remanufacturing. Calif Manag Rev 46(2):74–89
Souza GC (2013) Closed-loop supply chains: a critical review, and future research. Decis Sci 44(1):7–38
van Hoek RI (1999) From reversed logistics to green supply chains. Supply Chain Manag Int J 4(3):129–134
Yusof JM, Musa R, Rahman SA (2012) The effects of green image of retailers on shopping value and store loyalty. Proc Soc Behav Sci 50:710–721
Websites
Acknowledgments
I wish to thank three anonymous reviewers and Editor Georges Zaccour for very helpful comments. Any remaining errors are the responsibility of the author.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1
Proof of Proposition 1
In the non-coordinated scenario, we search for a pair of bounded and continuously differentiable value functions \( V_{M}^{B}\left( r^{B}\right) ,V_{R}^{B}\left( r^{B}\right) \) for which a unique solution for \(r^{B}\left( t\right) \) does exist, and the Hamilton–Jacobi–Bellman (HJB) equations:
are satisfied for any value of \(r^{B}\in (0,1].\) Maximization of the \(R\)’s HJB gives pricing and \(R\)’s GAP strategies.
Substituting Eqs. (38) and (39) inside \(M\)’s HJB provides:
Maximization of Eq. (40) with respect to \(M\prime s\) GAP strategies and wholesale price gives
Substituting Eq. (42) in (38), pricing results:
Plagging Eqs. (43), (42), (39), and (41) in Eqs. (40) and (37), it provides
We conjecture quadratic value functions \(V_{M}^{B}\left( r^{B}\right) =\frac{ d_{1}}{2}r^{B^{2}}+d_{2}r^{B}+d_{3}\) and \(V_{R}^{B}\left( r^{B}\right) = \frac{f_{1}}{2}r^{B^{2}}+f_{2}r^{B}+f_{3},\) where the pairs \(\left( d_{j},f_{j}\right) ,j=1\ldots 3\) are the constant parameters to be identified. Substituting our conjectures and their derivatives in Eqs. (44) and (45) gives
By identification, the constant parameters can be derived by solving the following set of coupled algebraic Riccati equations:
To derive the coefficients, we can start from Eq. (48) and obtain \(f_{1}\) as a function of \(d_{1}:f_{1}=f\left( d_{1}\right) \) where
with \(B_{3}=\varDelta \beta \left( 2\theta +\varDelta \beta \right) +\theta ^{2}\). Substituting Eq. (54) for Eqs. (49) and (52), we can derive both \(d_{2}\) and \( f_{2} \) as a function of \(d_{1}\)
with \(B_{1}=a^{2}m_{1}^{*}+b^{2}n_{1}^{*}-\delta -\rho <0,\, B_{2}=\alpha \left( \theta +\varDelta \beta \right) >0,\, B_{4}=a^{2}d_{1}+b^{2}\varOmega _{1}-\delta -\rho \). We then substitute Eqs. (55) and (56) in Eqs. (50) and (53) to derive \(d_{3}\) and \(f_{3}\) as a function of \(d_{1}\):
Finally, replacing Eq. (54) into (51) gives a nonlinear equation that we have solved numerically in Mathematica 6.0.\(\square \)
Proof of Proposition 2
To show the inefficiency of a per-return incentive mechanism, we need to search for a pair of bounded and continuously differentiable value functions \(V_{M}^{P}\left( r^{P}\right) ,V_{R}^{P}\left( r^{P}\right) \) for which a unique solution for \(r^{P}\left( t\right) \) exists, and the HJBs are as follows:
Because the coordination game also has a leader–follower structure where \(M\) is the leader, we start from the maximization of \(R\)’s HJB with respect to price and GAP strategies:
Substituting Eqs. (61) and (62) inside \(M\)’s HJB gives
whose maximization with respect to wholesale price and GAP strategies yields:
Plugging Eq. (64) in Eq. (61) leads to
Subsituiting Eqs. (64), (65), (66) and (62) in (63) and (60) gives
from which it turns out that \(V_{M}^{B}\left( r^{B}\right) =V_{M}^{P}\left( r^{P}\right) \) and \(V_{R}^{B}\left( r^{B}\right) =V_{R}^{P}\left( r^{P}\right) ,\) and thus, the implementation of a per-return incentive does not lead to any form of coordination.\(\square \)
Proof of Proposition 3
Here we follow the same steps as in the proof of Proposition 1 to derive the equilibrium strategies under the assumption that the CLSC is coordinated through a state-dependent incentive mechanism. The HJBs for this game are given by
Maximization of \(R\)’s HJB with respect to pricing and GAP strategies gives
These expressions must be satisfied by the pricing and \(R\)’s GAP strategies. Replacing Eqs. (71) and (72) inside Eq. (69), it gives the following expression:
\(M\)’s GAP equilibrium strategy is characterized by
Plugging Eq. (74) inside (71), it gives
Substituting, (72), (74) and (75), (76) inside Eqs. (70), and (73), the HBJ become:
We can conjecture quadratic value functions also in this scenario, specifically: \(V_{M}^{S}\left( r^{S}\right) =\frac{m_{1}}{2} r^{S^{2}}+m_{2}r^{S}+m_{3}\) and \(V_{R}^{S}\left( r^{S}\right) =\frac{n_{1}}{2 }r^{S^{2}}+n_{2}r^{S}+n_{3},\) where the pairs \(\left( m_{j},n_{j}\right) ,j=1\ldots 3\) are the constant parameters to be identified. Substituting the value functions and their derivatives inside Eqs. (77) and (78), the constant parameters can be identified solving the following set of coupled Riccati equations:
The coefficients can be simply derived as \(m_{1}=d_{1}\) and \(n_{1}=f_{1}.\) Thus, we can obtain \(n_{1}\) as a function of \(d_{1}:n_{1}=f_{1}=f\left( d1\right) =\varOmega _{1}\) as it is displayed in Eq. (54). Substituting Eq. (54) for Eqs. (80) and (83), we can derive both \(m_{2}\) and \(n_{2}\) as a function of \(d_{1}\)
We then substitute Eqs. (85) and (86) in Eqs. (81) and (84) to derive \(m_{3}\) and \(n_{3}\) as a function of \(d_{1}\):
See Proof of Proposition 1 to check the solution for \(d_{1}\).\(\square \)
Proof of Proposition 6
This proof follows the proof for Proposition 2, with the difference that the incentive depends on the control \( A_{R}^{C}\left( r^{C}\right) \). The HJB functions should be written as follows:
Maximization of \(R\)’s HJB gives pricing and \(R\)’s GAP strategies:
Substituting these strategies inside Eq. (89) to get
First-order condition for \(M\)’s GAP strategy gives
Plugging Eq. (94) inside (91) gives
Substitute Eqs. (92), (94), (95), (96) in (90) and (93) to get
To obtain a solution for this game, we conjectured quadratic value functions, \(V_{M}^{C}\left( r^{C}\right) =\frac{l_{1}}{2} r^{C^{2}}+l_{2}r^{C}+l_{3}\) and \(V_{R}^{C}\left( r^{C}\right) =\frac{k_{1}}{2 }r^{C^{2}}+k_{2}r^{C}+k_{3},\) where \(\left( l_{j},k_{j}\right) ,j=1\ldots 3,\) are the constant parameters to be identified. Replacing our conjectures and their derivatives into Eqs. (97) and (98), it gives
We identified the constant parameters from the following set of coupled algebraic Riccati equations:
As for the state-dependent case, the coefficients \(l_{i},k_{i},i=1\ldots 3\) can be simply derived as \(l_{1}=d_{1}\) and \(k_{1}=f_{1}\). Thus, we can obtain \( k_{1}\) as a function of \(d_{1}:k_{1}=f_{1}=f\left( d1\right) =\varOmega _{1}\) as it is reported in Eq. (54). Substituting Eq. (54) for Eqs. (102) and (105), we can derive both \(l_{2}\) and \(k_{2}\) as a function of \( d_{1}\)
We then substitute Eqs. (107) and (108) in Eqs. (103) and (106) to derive \(l_{3}\) and \(k_{3}\) as a function of \(d_{1}\):
See Proof of Proposition 1 to check the solution for \(d_{1}\). \(\square \)
Appendix 2
Solution \({\mathcal {I}}\) | Solution \({\mathcal {II}}\) | Solution \({\mathcal {III}}\) | Solution \({\mathcal {IV}}\) | |
|---|---|---|---|---|
\(A_{M}^{B}\left( r_{SS}^{B}\right) \) | .2096 | .4397 | .1098 | \(-\).4544 |
\(A_{R}^{B}\left( r_{SS}^{B}\right) \) | .1028 | .2027 | \(-\).1582 | .0687 |
\(r_{SS}^{B}\) | .3881 | .7816 | \(-\).3268 | \(-\) .1121 |
\(V_{M}^{B}\left( r_{SS}^{B}\right) \) | .192 | .5309 | 1.123 | .0284 |
\(V_{R}^{B}\left( r_{SS}^{B}\right) \) | .0953 | .2008 | \(-\).0509 | .0873 |
Steady-state \((SS)\) value of GAP efforts, return rates, and profits in scenario \(B.\) Bold values highlight the positivity assumptions that solutions \({\mathcal {III}}\) and \({\mathcal {IV}}\) violate
Appendix 3
Parameter values | \(A_{M}^{B}\left( r_{SS}^{B}\right) \ge 0\) | \( A_{R}^{B}\left( r_{SS}^{B}\right) \ge 0\) | \(r_{SS}^{B}\in (0,1]\) | \( V_{M}^{B}\left( r_{SS}^{B}\right) \ge 0\) | \(V_{R}^{B}\left( r_{SS}^{B}\right) \ge 0\) | \(\delta -a^{2}d_{1}-b^{2}f_{1}>0\) |
|---|---|---|---|---|---|---|
\(\alpha \)(1.1;1.2;1.3) | .23;.252;.272 | .11;.12;.134 | .426;.46;.505 | .235;.284;.337 | .115;.138;.134 | .324;.324;.324 |
\(\beta \)(1.1;1.2;1.3) | .204;.2;.197 | .1;.098;.097 | .378;.371;.365 | .176;.163;.152 | .085;.079;.073 | .322;.320;.317 |
\(\varDelta \)(.6;.7;.8) | .261;.329;.426 | .127;.159;.204 | .4812;.604;.777 | .226;.287;.407 | .109;.138;.194 | .3025;.276;.246 |
\(\theta \)(.4;.5;.6) | .261;.329;.426 | .127;.159;.204 | .4812;.604;.777 | .226;.287;.407 | .109;.138;.194 | .3025;.276;.246 |
a(.6;.7;.8) | .22;.234;.253 | .109;.117;.128 | .471;.58;.726 | .211;.24;.289 | .104;.12;.146 | .312;.297;.28 |
b(1.1;.1.2;1.3) | .221;.235;.252 | .107;.113;.12 | .464;.555;.667 | .211;.238;.277 | .101;.113;.13 | .313;.3;.287 |
\(\rho \)(.95;.97;.99) | .199;.195;.191 | .097;.096;.094 | .368;.361;.354 | .177;.172;.167 | .086;.084;.081 | .327;.328;.329 |
\(\delta \)(.5;.6;.7) | .179;.158;.143 | .088;.078;.071 | .265;.196;.152 | .169;.16;.154 | .083;.078;.076 | .433;.54;.646 |
Parameter values | \(A_{M}^{B}\left( r_{SS}^{B}\right) \ge 0\) | \(A_{R}^{B}\left( r_{SS}^{B}\right) \ge 0\) | \(r^{B}\in (0,1]\) | \( V_{M}^{B}\left( r_{SS}^{B}\right) \ge 0\) | \(V_{R}^{B}\left( r_{SS}^{B}\right) \ge 0\) | \(\delta -a^{2}d_{1}-b^{2}f_{1}<0\) |
|---|---|---|---|---|---|---|
\(\alpha \)(1.1;1.2;1.3) | .484;.528;.572 | .223;.243;.263 | .86;.937;1.02 | .559;.568;.551 | .225;.247;.266 | \(-\)1.32;\(-\)1.32;\(-\)1.32 |
\(\beta \)(1.1;1.2;1.3) | .43;.425;.422 | .198;.195;.193 | .76;.754;.747 | 56;.499;.486 | .19;.184;.178 | \(-\)1.322;\(-\)1.323;\(-\)1.324 |
\(\varDelta \)(.6;.7;.8) | .581;.798;1.17 | .363;.354;.514 | 1.022;1.34;2.02 | .433;\(-\) .242;\(-\) 3.6 | .21;.105; \(-\) .626 | \(-\)1.327;\(-\)1.333;\(-\)1.339 |
\(\theta \)(.4;.5;.6) | .581;.798;1.17 | .363;.354;.514 | 1.022;1.34;2.02 | .433;\(-\) .242;\(-\) 3.6 | .21;.105; \(-\) .626 | \(-\)1.327;\(-\)1.333;\(-\)1.339 |
a(.6;.7;.8) | .471;.515;.579 | .225;.257;.302 | .987; 1.27;1.68 | .412;.207;\(-\) .268 | .198;.106;\(-\) .27 | \(-\)1.312;\(-\)1.30;\(-\)1.287 |
b(1.1;.1.2;1.3) | .481;.533;.599 | .215;.23;.25 | .95; 1.16;1.43 | .461;.173;\(-\) .6 | .195;.172;.11 | \(-\)1.33;\(-\)1.34;\(-\)1.35 |
\(\rho \)(.95;.97;.99) | .411;.4;.39 | .19;.186;.181 | .733;.715;.697 | .525;.521;.518 | .19;.188;.18 | \(-\)1.371;\(-\)1.391;\(-\)1.411 |
\(\delta \)(.5;.6;.7) | .369;.327;.298 | .172;.153;.141 | .528;.392;.308 | .471;.388;.327 | .164;.135;.117 | \(-\)1.42;\(-\)1.518;\(-\)1.617 |
Parameter values | \(A_{M}^{B}\left( r_{SS}^{B}\right) \ge 0\) | \(A_{R}^{B}\left( r_{SS}^{B}\right) \ge 0\) | \(r^{B}\in (0,1]\) | \( V_{M}^{B}\left( r_{SS}^{B}\right) \ge 0\) | \(V_{R}^{B}\left( r_{SS}^{B}\right) \ge 0\) | \(\delta -a^{2}d_{1}-b^{2}f_{1}<0\) |
|---|---|---|---|---|---|---|
\(\alpha \)(1.1;1.2;1.3) | .484;.528;.572 | .223;.243;.263 | .86;.937;1.02 | .559;.568;.551 | .225;.247;.266 | \(-\)1.32;\(-\)1.32;\(-\)1.32 |
\(\beta \)(1.1;1.2;1.3) | .43;.425;.422 | .198;.195;.193 | .76;.754;.747 | 56;.499;.486 | .19;.184;.178 | \(-\)1.322;\(-\)1.323;\(-\)1.324 |
\(\varDelta \)(.6;.7;.8) | .581;.798;1.17 | .363;.354;.514 | 1.022;1.34;2.02 | .433;\(-\) .242;\(-\) 3.6 | .21;.105; \(-\) .626 | \(-\)1.327;\(-\)1.333;\(-\)1.339 |
\(\theta \)(.4;.5;.6) | .581;.798;1.17 | .363;.354;.514 | 1.022;1.34;2.02 | .433;\(-\) .242;\(-\) 3.6 | .21;.105; \(-\) .626 | \(-\)1.327;\(-\)1.333;\(-\)1.339 |
a(.6;.7;.8) | .471;.515;.579 | .225;.257;.302 | .987; 1.27;1.68 | .412;.207;\(-\) .268 | .198;.106;\(-\) .27 | \(-\)1.312;\(-\)1.30;\(-\)1.287 |
b(1.1;.1.2;1.3) | .481;.533;.599 | .215;.23;.25 | .95; 1.16;1.43 | .461;.173;\(-\) .6 | .195;.172;.11 | \(-\)1.33;\(-\)1.34;\(-\)1.35 |
\(\rho \)(.95;.97;.99) | .411;.4;.39 | .19;.186;.181 | .733;.715;.697 | .525;.521;.518 | .19;.188;.18 | \(-\)1.371;\(-\)1.391;\(-\)1.411 |
\(\delta \)(.5;.6;.7) | .369;.327;.298 | .172;.153;.141 | .528;.392;.308 | .471;.388;.327 | .164;.135;.117 | \(-\)1.42;\(-\)1.518;\(-\)1.617 |
Parameter values | \(A_{M}^{C}\left( r_{SS}^{C}\right) \ge 0\) | \( A_{R}^{C}\left( r_{SS}^{C}\right) \ge 0\) | \(r^{C}\in (0,1]\) | \( V_{M}^{C}\left( r_{SS}^{C}\right) \ge 0\) | \(V_{R}^{C}\left( r_{SS}^{C}\right) \ge 0\) | \(\delta -a^{2}l_{1}-b^{2}k_{1}>0\) |
|---|---|---|---|---|---|---|
\(\alpha \)(1.1;1.2;1.3) | .23;.25;.275 | .114;.124;.135 | .43;.47;.51 | .214;.265;.321 | .158;.184;.21 | .324;.324;.324 |
\(\beta \)(1.1;1.2;1.3) | .223;.202;.199 | .101;.099;.097 | .383;.375;.369 | .152;.138;.127 | .126;.119;.114 | .322;.320;.317 |
\(\varDelta \)(.6;.7;.8) | .265;.334;.434 | .129;.162;.208 | .488;.614;.791 | .208;.276;.407 | .155;.188;.25 | .3025;.276;.246 |
\(\theta \)(.4;.5;.6) | .265;.334;.434 | .129;.162;.208 | .488;.614;.791 | .208;.276;.407 | .155;.188;.25 | .3025;.276;.246 |
a(.6;.7;.8) | .223;.238;.257 | .11;.12;.129 | .477;.588;.736 | .188;.219;.269 | .146;.163;.191 | .312;.297;.28 |
b(1.1;.1.2;1.3) | .224;.239;.257 | .109;.115;.122 | .47;.564;.678 | .191;.223;.267 | .146;.16;.18 | .313;.3;.287 |
\(\rho \)(.95;.97;.99) | .201;.197;.193 | .099;.097;.095 | .373;.366;.358 | .154;.149;.145 | .125;.122;.118 | .327;.328;.329 |
\(\delta \)(.5;.6;.7) | .18;.16;.144 | .089;.079;.0716 | .268;.198;.154 | .143;.132;.126 | .123;.116;.113 | .433;.54;.646 |
\(\mu \)(.025;.05;.2) | .210;.210;.212 | .1029;.103;.104 | .388;.390;.393 | .194;.195;.168 | .096;.099;.135 | .324;.324;.324 |
Rights and permissions
About this article
Cite this article
De Giovanni, P. State- and Control-Dependent Incentives in a Closed-Loop Supply Chain with Dynamic Returns. Dyn Games Appl 6, 20–54 (2016). https://doi.org/10.1007/s13235-015-0142-6
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13235-015-0142-6