1 Introduction

Recently, the nanoparticles accumulation to the disreputable liquid, the aspects of nanofluids, together with thermo-physical ones, fluctuate in assessment with those of the disreputable liquid without help. Subject to the sort of application, these dissimilarities might show either an optimistic or a destructive part. The reform of nanofluids thermal conductivity is unique and significant optimistic dissimilarities might lead to an enhancement in heat deletion, signifying the opportunity of exhausting nanofluids as coolant in atomic receptacles, that is, protection structures, crucial coolant and austere calamity mitigation policies. Furthermore, the best collective atomic receptacles everywhere in the domain are pressurized water receptacles that are recycled as a coolant. The accumulation of nanoparticles to water can intensify the serious heat fluctuation confines and accelerate reducing heat in the receptacle core. Nanofluids are colloidal diffusion of nanoparticles in a disreputable fluid with magnitude 1–100 nm and retain a capacity of progressive thermal conductivity. These elements, generally a metallic or metallic oxide, exaggerate conduction and convection quantities, leading to different heat transport outside the coolant. Choi [1] established the notion of nanofluids, and reconsidered this study field with their nanoscale nanotube deferral and metallic atoms. For the former two eras, various scientists studied nanofluids as heat transport fluids in several fields [2,3,4,5,6,7,8,9,10,11,12]. The nanofluids have numerous potential benefits resembling high specific area, high diffusion stability, dipping pushing control, dropping particle blockage and flexible possessions, which comprise thermal conductivity and outward wettability. Villarejo et al. [13] analyzed boron nitride nanofluids and discussed the aspects of solar thermal applications. The attained heat transport coefficient was enhanced under the circumstance of turbulent flow up to 18% utilizing nanofluid. Irfan et al. [14] studied numerically the properties of thermal conductivity in Carreau nanofluid. The transport of heat reduces for Brownian and thermophoresis factors. The magnetic dipole and radiation impact on Eyring–Powell nanofluid with activation energy was reported by Waqas et al. [15].

The stagnation point flows dynamically in considerationof how the wide-ranging flow acts. The fluid gesture near the stagnation area at the front of a blunt-nosed frame, occurring on all dense frames stirring in a fluid is characterized as stagnation point flows. The stagnation region comes across the high pressure, the highest heat transfer and rates of mass deposition. Due to their industrial and engineering worth, in the analysis of physiological fluid dynamics, numerous researchers have considered the dynamics of stagnation flow/heat transport under numerous conditions. The cooling of atomic devices in disaster closure, solar dominant phones unprotected to a current of air, hydrodynamic developments, heat exchangers engaged in a low-velocity atmosphere, etc. are some applications of these flows. The use of the similarity conversion to Navier–Stokes terminologies in the stagnation region has been first considered by Hiemenz [16]. Merkin and Pop [17] analyzed the flow initiated by shrinking/stretching surfaces determined by the Arrhenius kinetics in the stagnation region. The stagnation point flow of radiative Maxwell nanofluid caused by a variable thickness with chemical reaction was studied by Khan et al. [18]. They noted that the velocity field declined for higher Deborah number. The combined phenomena of convective and variable conductivity in the stagnation region of unsteady Carreau nanomaterial was established by Khan et al. [19]. They attained dual solutions in the manifestation of MHD and the heat sink/source. They described that for both solutions, the influence of the unsteadiness parameter displays analogous performance on the velocity field. Additionally, the temperature field enhances both solutions for intensifying values of thermal Biot and Prandtl numbers. Latest studies for diverse sorts of fluids over a stagnation region have been elaborated in Refs [20,21,22,23,24].

To scrutinize the properties of chemically reacting flow of Maxwell nanofluid in the stagnation region considering the thermal aspect of convective and radiation, this work has been elaborated. The MHD and heat sink/source are also addressed. Homotopic algorithms are worked for solutions of ODEs. The graphical and tabular study of influential parameters are reported. Furthermore, a study compared with a previous work is presented for validation of current outcomes.

2 Mathematical formulation

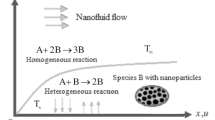
Here, steady 2D chemically reacting Maxwell nanofluid stagnation point flow of stretching cylinder with radius \(R\) has been elaborated. The radiative heat flux, convective heat transport and heat sink/source are also addressed. Furthermore, the mass transport phenomena was reported via chemical reaction. Along the \(z -\) direction, the stretching and free stream velocities of the cylinder are reported to be \(\left( {\tfrac{{U_{0} z}}{l},\,\tfrac{{U_{\infty } z}}{l}} \right),\)where \(l\) is the specific length and \(\left( {U_{0} ,\,U_{\infty } } \right)\) are the reference velocities, respectively. The coordinates of cylindrical surfaces \((z,\,r)\) considered in such an approach are such that \(z - axis\) goes near the axis of the cylinder and \(r - axis\) is restrained along the radial direction. The induced MHD is ignored owing to small Reynolds number and \(B_{0}\) is the length of the magnetic field applied along the \(r -\) direction (as plotted in Fig. 1). Thus, the flow problem under these conditions are [25,26,27]:

$$\frac{\partial u}{{\partial r}} + \frac{u}{r} + \frac{\partial w}{{\partial z}} = 0,$$
(1)
$$u\frac{\partial w}{{\partial r}} + w\frac{\partial w}{{\partial z}} + \lambda \left[ {w^{2} \frac{{\partial^{2} w}}{{\partial z^{2} }} + u^{2} \frac{{\partial^{2} w}}{{\partial r^{2} }} + 2uw\frac{{\partial^{2} w}}{\partial r\partial z}} \right] = W_{e} \frac{{dW_{e} }}{dz} + v\left[ {\frac{{\partial^{2} w}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial w}{{\partial r}}} \right] - \frac{{\sigma B_{0}^{2} }}{{\rho_{f} }}\left( {(W_{e} - w) + \lambda u\frac{\partial w}{{\partial r}}} \right),$$
(2)
$$u\frac{\partial T}{{\partial r}} + w\frac{\partial T}{{\partial z}} = \alpha_{1} \frac{1}{r}\frac{\partial }{\partial r}\left[ {\left( {r\frac{\partial T}{{\partial r}}} \right)} \right] + \tau \left[ {D_{B} \frac{\partial C}{{\partial r}}\frac{\partial T}{{\partial r}} + \frac{{D_{T} }}{{T_{\infty } }}\left( {\frac{\partial T}{{\partial r}}} \right)^{2} } \right] - \frac{1}{{\left( {\rho c} \right)_{f} }}\frac{1}{r}\frac{{\partial \left( {rq_{r} } \right)}}{\partial r} + \frac{{Q_{1} (T - T_{\infty } )}}{{(\rho c)_{f} }}$$
(3)
$$u\frac{\partial C}{{\partial r}} + w\frac{\partial C}{{\partial z}} = D_{B} \frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{\partial C}{{\partial r}}} \right) + \frac{{D_{T} }}{{T_{\infty } }}\frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{\partial T}{{\partial r}}} \right) - K_{r} (C - C_{\infty } ),$$
(4)
$$w(z,\,r) = W(z) = \frac{{U_{0} z}}{l},\, \, u(z,\,r) = 0,\, \, - k_{1} \frac{\partial T}{{\partial r}} = h_{f} \left( {T_{f} - T} \right),\, \, C = C_{w} \, at \, r = R,$$
(5)
$$w \to W_{e} (z) = \frac{{U_{\infty } z}}{l},\, \, T \to T_{\infty } ,\, \, C \to C_{\infty } \, as \, r \to \infty .$$
(6)
Fig.1
figure 1

Schematic diagram

Full size image

The radiative heat flux \(q_{r}\) is defined as

$$q_{r} = \frac{{ - 16\sigma^{ * } }}{{3k^{ * } }}T_{\infty }^{3} \frac{\partial T}{{\partial r}}.$$
(7)

2.1 Appropriate transformations

Letting

$$\begin{aligned} u = - \frac{R}{r}\sqrt {\frac{{U_{0} \nu }}{l}} f(\eta ),\, \, w = \frac{{U_{0} z}}{l}f^{\prime}(\eta ),\, \, \theta (\eta ) = \frac{{T - T_{\infty } }}{{T_{f} - T_{\infty } }}, & \\ \phi (\eta ) = \frac{{C - C_{\infty } }}{{C_{w} - C_{\infty } }},\, \, \eta = \sqrt {\frac{{U_{0} }}{\nu l}} \left( {\frac{{r^{2} - R^{2} }}{2R}} \right). & \\ \end{aligned}$$
(8)

Equations (7) and (8) yeild the following ODEs:

$$(1 + 2\alpha \eta )f^{\prime\prime\prime} + 2\alpha f^{\prime\prime} + ff^{\prime\prime} - f^{\prime 2} + 2\beta ff^{\prime}f^{\prime\prime} - \beta f^{2} f^{\prime\prime\prime} - \frac{\alpha \beta }{{(1 + 2\alpha \eta )}}f^{2} f^{\prime\prime} - M^{2} (f^{\prime} - A - \beta ff^{\prime\prime}) + A^{2} = 0,$$
(9)
$$\left( {1 + \frac{{4R_{d} }}{3}} \right)[(1 + 2\alpha \eta )\theta^{\prime\prime} + 2\alpha \theta^{\prime}] + (1 + 2\alpha \eta )\mathop {\Pr }\limits N_{b} \theta^{\prime}\phi^{\prime} + \mathop {\Pr }\limits f\theta^{\prime} + (1 + 2\alpha \eta )\mathop {\Pr }\limits N_{t} \theta^{\prime 2} + \mathop {\Pr }\limits \delta \theta = 0,$$
(10)
$$(1 + 2\alpha \eta )\phi ^{\prime\prime} + 2\alpha \phi ^{\prime} + Le\mathop {\Pr }\limits f\phi ^{\prime\prime} + (1 + 2\alpha \eta )\left( {\frac{{N_{t} }}{{N_{b} }}} \right)\,\theta^{\prime\prime} + 2\alpha \left( {\frac{{N_{t} }}{{N_{b} }}} \right)\,\theta^{\prime} - Le\mathop {\Pr }\limits C_{R} \phi = 0,$$
(11)
$$f(0) = 0,\, \, f^{\prime}(0) = 1,\, \, \theta^{\prime}\left( 0 \right) = - \gamma \left( {1 - \theta \left( 0 \right)} \right),\,\;\;\;\phi (0) = 1,$$
(12)
$$f^{\prime}(\infty ) = A,\, \, \theta (\infty ) = 0,\, \, \phi (\infty ) = 0.$$
(13)

The dimensionless quantities are

$$\begin{aligned} \alpha \left( { = \frac{1}{R}\sqrt {\frac{\nu l}{{U_{0} }}} } \right),\, \, \beta \left( { = \frac{{\lambda U_{0} }}{l}} \right),\, \, A = \frac{{U_{\infty } }}{{U_{0} }},\, \, M\left( { = \sqrt {\frac{{\sigma B_{0}^{2} l}}{{U_{0} \rho_{f} }}} } \right), & \\ R_{d} \left( {\frac{{4\sigma^{ * } T^{3} }}{{kk^{ * } }}} \right),\, \, N_{b} \left( { = \frac{{\tau D_{B} (C_{w} - C_{\infty } )}}{\nu }} \right),\, \, N_{t} \left( { = \frac{{\tau D_{T} (T_{f} - T_{\infty } )}}{{\nu T_{\infty } }}} \right),\, \, \delta \left( { = \frac{{lQ_{0} }}{{U_{0} (\rho c)_{f} }}} \right), & \\ \gamma = \left( {\frac{{h_{f} }}{{k_{1} }}\sqrt {\frac{\nu l}{{U_{0} }}} } \right),\, \, \mathop {\Pr }\limits \left( { = \frac{\nu }{{\alpha_{1} }}} \right),\, \, Le\left( { = \frac{{\alpha_{1} }}{{D_{B} }}} \right),\, \, C_{R} \left( { = \frac{{K_{r} l}}{{U_{0} }}} \right). & \\ \end{aligned}$$
(14)

3 Physical quantities of interest

The heat–mass transport quantities \((Nu_{z} ,\,Sh_{z} )\) are

$$Nu_{z} = \frac{{ - z\left( {\tfrac{\partial T}{{\partial r}}} \right)_{r = R} }}{{(T_{f} - T_{\infty } )}},\, \, Sh_{z} = \frac{{ - z\left( {\tfrac{\partial C}{{\partial r}}} \right)_{r = R} }}{{(C_{w} - C_{\infty } )}}.$$
(15)

In dimensionless form:

$$Nu_{z} {\text{Re}}_{z}^{{ - \tfrac{1}{2}}} = - \left( {1 + \frac{4}{3}R_{d} } \right)\theta^{\prime}(0),\, \, Sh_{z} {\text{Re}}_{z}^{{ - \tfrac{1}{2}}} = - \phi ^{\prime}\left( 0 \right),$$
(16)

where \({\text{Re}}_{z} = \tfrac{W \left( z \right)z}{\nu }\) depicts the local Reynolds number.

4 Analysis of results

Here, the behavior of radiation, chemical reaction and convective heat transport in the stagnation region for Maxwell nanofluid has been disclosed. For graphical illustrations, the following values of effective parameters are incorporated, i.e., \(C_{r} = 0.2,\) \(\alpha = \beta = \delta = N_{b} = 0.3,\) \(\gamma = N_{t} = 0.4,\) \(M = A = 0.5,\) \(R_{d} = Le = 1.0\) and \(\Pr = 1.5.\) Additionally, the confirmation of the current study is established in Table 1. Here, the important fallouts are noted in Refs [28] and [29].

Table 1 Outcomes of \(- f^{\prime\prime}(0)\) for \(\;\beta\) when \(\alpha = M = A = 0\)
Full size table

4.1 Graphical depiction of \(A\) on \(f^{\prime}(\eta )\)

The properties of stagnation point \(A\) on fluid velocity are disclosed in Fig. 2. It may be noted that \(f^{\prime}(\eta )\) is magnified when \(A\) increases. The differing behavior was documented for both \(A > 1\) and \(A < 1\) and no effect was noted for \(A = 1\). For \(A < 1\) a stretching amount outstrips the free stream quantity and the thickness of boundary layer growths. Conversely, the quantity of free stream velocity is advanced when allied with the quantity of stretching velocity when \(A > 1\), which decays the thickness of boundary layer. Moreover, no progress has been acknowledged when \(A = 1\); this means that free stream and stretching velocities are analogous.

Fig. 2
figure 2

\(f^{\prime}(\eta )\) for \(A < 1,\) \(A = 1\) and \(A > 1\)

Full size image

4.2 Graphical depiction of \(N_{b} ,\) \(N_{t} ,\) \(\gamma\) and \(R_{d}\) on \(\theta (\eta )\).

To portray the characteristics of Brownian \(N_{b}\) and thermophoresis \(N_{t}\) on temperature field, Fig. 3a, b is presented. For \(N_{b}\) and \(N_{t}\), the increase of the temperature field is detected. The increased values of \(N_{b}\) results in greater Brownian diffusion \((D_{B} ),\) which intensifies the nanofluid temperature due to the direct relation of \(N_{b}\) and \(D_{B}\). Furthermore, similar is true for \(N_{t} .\) The liquid elements are transported quickly from warm to cold range and increase the theromophoretic force for \(N_{t}\). Hence,\(\theta (\eta )\) is increased for \(N_{t} .\) Figure  4a, b illustrates the depiction of thermal Biot \(\gamma\) and thermal radiation \(R_{d}\) on \(\theta (\eta ).\) These sketches expose that the temperature increases when \(\gamma\) and \(R_{d}\) increase. The growing values of \(R_{d}\) intensify the surface heat flux which boosts \(\theta (\eta ).\) Furthermore, the mean absorption factor decreases and the thermal thickness of the layer repeatedly increases. Therefore, \(\theta (\eta )\) increases.

Fig. 3
figure 3

a, b \(\theta (\eta )\) for (a) \(N_{b}\) and (b) \(N_{t}\)

Full size image
Fig. 4
figure 4

a, b \(\theta (\eta )\) for (a) γ and (b) Rd

Full size image

4.3 Graphical depiction of \(C_{R} ,\) \(N_{b}\) and \(N_{t}\) on \(\phi (\eta )\)

The effects of chemical reaction parameter \(C_{R}\), i.e., \(C_{R} < 0\) and \(C_{R} > 0\), on concentration scattering are shown in Fig. 5a, b. The differing nature is acknowledged for \(C_{R} < 0\) and \(C_{R} > 0.\) When the values of \(C_{R} < 0\) rise, the concentration field increases; however, the concentration field decays for higher values of \(C_{R} > 0.\) Furthermore, the chemical molecular diffusivity fall-offs for \(C_{R} > 0\) and reverse nature are noted for \(C_{R} < 0.\) The higher values of Brownian \(N_{b}\) and thermophoretic \(N_{t}\) parameters on \(\phi (\eta )\) are plotted as shown in Fig. 6a,b. The concentration fall off for \(N_{b}\) and intensifies for \(N_{t}\) for the Maxwell nanofluid. Physically, \(N_{b}\) increases the unsystematic motion of particles which creates more heat and reduces the Maxwell concentration field. Furthermore, \(\phi (\eta )\) rises for \(N_{t} .\) The thermal conductivity of fluid enhances when \(N_{t}\) increases which enhances \(\phi (\eta )\).

Fig. 5
figure 5

a, b \(\phi (\eta )\) for (a) \(C_{R} < 0\) and (b) \(C_{R} > 0\)

Full size image
Fig. 6
figure 6

a, b \(\phi (\eta )\) for (a) \(N_{b}\) and (b) \(N_{t}\)

Full size image

4.4 Graphical depiction of \(N_{b} ,\,N_{t}\) and \(C_{R}\) i.e., (\(C_{R} < 0\)and \(C_{R} > 0\)) on \(Nu_{z} Re_{z}^{{\tfrac{ - 1}{2}}}\)and \(Sh_{z} Re_{z}^{{\tfrac{ - 1}{2}}}\)

The graphs of \(Nu_{z} Re_{z}^{{\tfrac{ - 1}{2}}}\) and \(Sh_{z} Re_{z}^{{\tfrac{ - 1}{2}}}\) for \(N_{t} ,\) \(N_{b}\) and \(C_{R}\) have been reported in Figs. 7a,b; 8a,b. The influence of \(N_{b} ,\) and \(N_{t}\) on \(\;Nu_{z} Re_{z}^{{\tfrac{ - 1}{2}}}\)causes a decline in performance. The graphs of \(Sh_{z} Re_{z}^{{\tfrac{ - 1}{2}}}\) for the chemical reaction parameter \(C_{R} < 0\) and \(C_{R} > 0\) are noted to be conflicting. The \(Sh_{z} Re_{z}^{{\tfrac{ - 1}{2}}}\) decays for higher \(C_{R} < 0\); however, it enhance for \(C_{R} > 0.\)

Fig. 7
figure 7

a, b \(Nu_{z} Re_{z}^{{\tfrac{ - 1}{2}}}\) for (a) \(N_{b}\) and (b) \(N_{t}\)

Full size image
Fig. 8
figure 8

a, b \(Sh_{z} Re_{z}^{{\tfrac{ - 1}{2}}}\) for (a) \(C_{R} < 0\) and (b) \(C_{R} > 0\)

Full size image

5 Closing remarks

The effect of chemical reaction and radiation on the stagnation point magnetized Maxwell nanofluid is studied. The solution of ODEs via homotpic algorithm (HAM) was exploited. The essential viewpoints are as follows:

  • The Maxwell temperature field enhanced for larger \(N_{b}\) and \(N_{t}\)

  • Thermal Biot \(\gamma\) intensified the temperature field.

  • On concentration field, a relatively opposite performance was noticed for \(N_{b}\) and \(N_{t}\)

  • Local Sherwood number enhanced for \(C_{R} > 0\) and decayed for \(C_{R} < 0.\)