1 Introduction

The only way to overcome the tiredness of the server due to the continuous repair work or inspection of the two identical unit systems either to offer him rest or some refreshment. The idea of offer refreshments to the server whenever needed to make the server more energetic immediately has not been discussed so far in the available literature. Even many researchers like; Devis (1952) threw light on some failure data. Branson and Shah (1971) scrutinized the system reliability when units are comprised of arbitrary repair-time distributions. Osaki and Nakagawa (1971) discussed a redundant system having two-unit standby with repair and preventive maintenance policy. Birolini (1974) explored some uses of stochastic regenerative policy to reliability theory. Kumar and Lal (1979) examined stochastic systems having a two-unit standby policy with contact failure and intermittently available repair facility. Subramanyam and Gopalan (1983) discussed the cost–benefit of two units warm standby system with a single repairman subject to distinct inspection plans. Goyal and Murari (1984) analyzed the cost of the system with a two-unit standby having a single repairman and patience time. Goel et al. (1986) discussed system reliability with preventive maintenance, inspection, and two types of the repair policy. Singh (1987) examined two-unit cold standby stochastic systems. Singh and Srinivasu (1987) discussed two-unit cold standby stochastic systems have preparation time for repair.

Related work: Gupta and Goel (1989) explored the benefit of two unit superiority standby systems having an administrative delay in repair. Chellappa (1989) obtained two-dimensional discrete Gaussian Markov random field models for image processing. Gupta and Goel (1991) examined two-unit cold standby system cost in abnormal weather conditions. Sekhar and Yegnanarayana (1996) evaluated recognition of stop-consonant–vowel (SCV) segments in continuous speech using neural network models. Malik and Barak (2009) analyzed the Reliability and economic of a system operating under different weather conditions. Malik (2013) threw light on a computer system reliability modeling having preventive maintenance and superiority corresponding to maximum operation and repair times. Barak et al. (2014) analyzed the system having a single repairman with inspection corresponding to different weather conditions.

Kumar and Sirohi (2015) analyzed the profit of a two-unit cold standby system with the delayed repair of the partially failed unit and better utilization of units. Kumar and Baweja (2015) analyzed a cold standby system cost with a preventive maintenance policy subject to the arrival time of the repairman. Kumar and Goel (2016) explored the availability and profit measures of a two-unit cold standby system for general distribution. Yadav and Barak (2016) discussed a cold standby stochastic system with a single repairman failure policy.

Barak et al. (2017) explored a redundant system having a refreshment policy subject to inspection with a single repairman. Neeraj et al. (2018) analyzed a two-unit cold standby system model having a single repairman and operating under distinct weather conditions. Gahlot et al. (2018) highlighted the performance assessment of repairable systems in the series configuration under different types of failure and repair policies using copula linguistics. Singh and Poonia (2019) obtained the probabilistic assessment of a two-unit parallel system with correlated lifetime under inspection using the regenerative point technique. Hassan et al. (2019), Gupta et al. (2019), Kadyan et al. (2020) analyzed stochastically a non-identical repairable system of three units with priority for operation and simultaneous working of cold standby units. Gupta et al. (2021b) analyzed the behavior of cooling towers in steam turbine power plants using reliability, availability, maintainability, and dependability. Kumar et al. (2020) evaluated the reliability, availability, and maintainability of the operational performance of soft water treatment and supply plants. Raghav et al. (2020) obtained the probability of a system consisting of two subsystems in the series configuration under the copula repair approach. Singh et al. (2021) analyzed the reliability of a repairable network system of three computer labs connected with a server under 2-out-of-3 G configuration. Verma et al. (2020) highlighted a comparative analysis of data-driven based optimization models for energy-efficient buildings. Gupta et al. (2021a), Gupta and Mittal (2021), Rawat et al. (2021).

Purpose of the study: Keeping in mind, the main role of refreshment to enhance the efficiency of the server to provide him during his job, the model developed as shown in the Fig. 1. In this model, the server inspects the unit before repair or replacement of the unit and refreshment is available to heal up his tiredness or to enhance his capacity.

Fig. 1
figure 1

State transition diagram

Full size image

2 System assumption and notations

Assumptions:

The following are the assumptions for the state transitions diagram.

  1. 1.

    Initially, the whole system is in a good state and one unit is kept as cold standby.

  2. 2.

    The server inspects the unit before repair or replace the unit.

  3. 3.

    Repair of the units is perfect and the unit works as new after repair.

  4. 4.

    Server works with full energy after getting refreshment.

  5. 5.

    All the parameters are statistically independents.

Notations:

\(R\): Set of regenerative states (\( {S_{0},}\, {S_{1},}\, {S_{2},}\,{S_{3},}\, {S_{8}} \)).

\(a/b\): Probability that the cold standby unit of the system is working/not working conditions due to unused of a long time.

\(p/q\): Probability that the cold standby unit is replaced by a new unit/under repair.

\(O/Cs\): The unit of the system is inoperative mode/cold standby mode.

\(Fur/FUR\): The failed unit under repair/ continuous under repairs from the previous stage.

\(Fwr/FWR\): The failed unit waiting for repair/continuously waiting for repair from the previous stage.

\(sut/SUT\): The server is busy in getting refreshment /continuously busy in getting refreshment from the previous state.

\(\lambda /\mu\): The failure rate of the operative unit /rate by which repairman feels the requirement of refreshment.

\(g(t)/G(t)\): Pdf / Cdf of the repair rate of the failed unit.

\(f(t)/F(t)\): Pdf / Cdf of refreshment rate by which the repairman recovers its freshness.

\(q_{rs} (t)/Q_{rs} (t)\): Probability / Continuous density function of direct transition time from \(S_{r} \in R\) to \(S_{s} \in R\) or sth failed state without staying in any \(S_{i} \in R\) in (0,t].

\(q_{ij.k} (t)/Q_{ij.k} (t)\): Pdf/Cdf of first passage time from \(S_{r} \in R\) to \(S_{s} \in R\) or a failed state \(S_{s}\) with visiting state \(S_{k}\) once in (0,t].

\(\begin{gathered} q_{rs.t(u,v)} (t)/ \hfill \\ Q_{rs.t(u,v)} (t) \hfill \\ \end{gathered}\): Pdf/Cdf of first passage time from \(S_{r} \in R\) to or to a failed state \(S_{s}\) with visiting states \(S_{k}\), \(S_{r}\), \(S_{s}\) once in (0,t].

\(m_{ij}\): The unconditional meantime is taken by the system to move from any \(S_{i} \in R\) when it is calculated from an epoch of arrivals into the state \(S_{i}\).

$$ m_{ij} = - q^{\prime *}_{ij} (0) = \int\limits_{0}^{\infty } {td[Q_{ij} (t)]dt} $$

\(\mu_{i}\): Let system failure time is signifying by T and in the state \(S_{i}\) mean sojourn time is

$$ \mu_{i} = \sum\limits_{j} {m_{ij} } = E(t) = \int\limits_{0}^{\infty } {P(T > t)dt} $$

\(M_{r} (t)\): Probability that the system is originally up in the regenerative state \(S_{r} \in R\) up to at the time (t) without passing via any other \(S_{i} \in R\).

\(W_{i} (t)\): Probability that the repairman is busy in the state \(S_{i}\) up to time (t), without making any transition to any other \(S_{i} \in R\) or returning to the same via one or more non- regenerative states.

\(\oplus / \otimes\): Laplace convolution notation/Laplace Stieltjes convolution notation.

\(* / * * /^{\prime}\): Laplace transform notation (LT)/Laplace Stieltjes transform notation (LST)/function’s derivative notation.

3 Transition probabilities

There are the following possible transition probabilities:

$$ \begin{gathered} p_{01} = a,p_{03} = b,p_{31} = p,p_{35} = q,p_{41} = p,p_{45} = q,p_{67} = 1, \hfill \\ p_{10} = \frac{p\psi }{{\lambda + \psi }},p_{12} = \frac{q\psi }{{\lambda + \psi }},p_{14} = \frac{\lambda }{\lambda + \psi },p_{20} = \frac{\phi }{\phi + \mu },p_{28} = \frac{\mu }{\phi + \mu },p_{51} = \frac{\phi }{\phi + \mu }, \hfill \\ p_{56} = \frac{\mu }{\phi + \mu },p_{71} = \frac{\phi }{\phi + \mu },p_{76} = \frac{\mu }{\phi + \mu },p_{82} = \frac{\theta }{\lambda + \theta },p_{86} = \frac{\lambda }{\lambda + \theta } \hfill \\ \end{gathered} $$
(1)

It is simply verified that

$$ \begin{gathered} p_{01} + p_{03} = p_{10} + p_{12} + p_{14} = p_{20} + p_{28} = p_{31} + p_{35} = 1 \hfill \\ p_{41} + p_{45} = p_{51} + p_{56} = p_{71} + p_{76} = p_{82} + p_{86} = 1;\;p_{10} + p_{12} + p_{11.4} + p_{11.(45)} + p_{{11.45(67)^{n} }} = 1 \hfill \\ p_{31} + p_{31.5} + p_{{35.1(67)^{n} }} = 1,p_{82} + p_{{81.(67)^{n} }} = 1 \hfill \\ \end{gathered} $$
(2)

4 Mean sojourn time

Let system failure time is signifying by ‘T’ and in the state Si the mean sojourn time is:

$$ \mu_{i} = \sum\limits_{j} {m_{ij} } = E(t) = \int\limits_{0}^{\infty } {P(T > t)dt} $$
$$ \begin{aligned} \mu_{{0}} &= m_{01} + m_{03} = \frac{1}{\lambda }, \quad \mu_{{1}} = m_{10} + m_{12} + m_{14} = \frac{1}{\lambda + \psi }, \\ \mu_{{2}} &= m_{20} + m_{28} = \frac{1}{\varphi + \mu }\quad \mu_{{3}} = m_{31} + m_{35} = \frac{1}{\psi }, \\ \mu_{{4}} &= m_{41} + m_{45} = \frac{1}{\psi }, \quad \mu_{5} = m_{51} + m_{56} = \frac{1}{\varphi + \mu }, \quad \mu_{6} = m_{67} = \frac{1}{\varphi } \\ \mu_{7} &= m_{71} + m_{76} = \frac{1}{\varphi + \mu }, \quad \mu_{8} = m_{82} + m_{86} = \frac{1}{\theta + \lambda } \\ \mu^{\prime}_{1} &= m_{10} + m_{12} + m_{11.4} + m_{11.(45)} + m_{{11.45(67)^{n} }} = \frac{\theta \varphi (\lambda + \psi ) + q\lambda \psi (\theta + \mu )}{{\theta \varphi \psi (\lambda + \psi )}}\\ \mu^{\prime}_{3} &= m_{31} + m_{31.5} + m_{{31.5(67)^{n} }} = \frac{(\theta + \mu )}{{\theta \varphi }}, \\ \mu^{\prime}_{8} &= m_{82} + m_{{81.(67)^{n} }} = \frac{\theta \varphi + \lambda (\theta + \varphi )}{{\theta \varphi (\theta + \lambda )}} \end{aligned} $$
(3)

5 Meantime to system failure (MTSF)

Let \(\phi_{i} (t)\) is the continuous density function of the first passage time from \(S_{i} \in R\) to a failed state. Treating the failed states as trapping states, then upcoming recursive interface for \(\phi_{i} (t)\) is:

$$ \begin{gathered} \phi_{0} (t) = Q_{03} (t) + Q_{01} (t) \otimes \phi_{1} (t);\;\phi_{1} (t) = Q_{14} (t) + Q_{10} (t) \otimes \phi_{0} (t) + Q_{12} (t) \otimes \phi_{2} (t) \hfill \\ \phi_{2} (t) = Q_{20} (t) \otimes \phi_{0} (t) + Q_{28} (t) \otimes \phi_{8} (t);\;\phi_{8} (t) = Q_{86} (t) + Q_{82} (t) \otimes \phi_{2} (t) \hfill \\ \end{gathered} $$
(4)

Now taking LST of the above relations (4) and solving for \(\phi_{0}^{**} (s)\), we have

$$ M^{*} \left( s \right) = \frac{{1 - \phi_{0}^{**} (s)}}{s} $$
(5)

Now, the reliability of the system model can be obtained by using inverse LT of Eq. (5), we have

$$ MTSF = \lim_{s \to 0} \frac{{1 - \phi_{0}^{**} (s)}}{s} = \frac{{p_{01} p_{12} \left( {\mu_{2} + p_{28} \mu_{8} } \right) + \left[ {1 - p_{28} p_{82} } \right]\left( {\mu_{0} + p_{01} \mu_{1} } \right)}}{{\left[ {1 - p_{28} p_{82} } \right]\left( {1 - p_{01} p_{10} } \right) - p_{01} p_{12} p_{20} }} $$
(6)

6 Steady-state availability

Let \(A_{i} (t)\) is the probability that the system is in up-state at a moment ‘t’ specified that the system arrives at the regenerative-state \(S_{i}\) at t = 0. Then upcoming recursive relation for \(A_{i} (t)\) is:

$$ \begin{aligned} A_{0} (t) &= q_{01} (t) \oplus A_{1} (t) + q_{03} (t) \oplus A_{3} (t) + M_{0} (t) \hfill \\ A_{1} (t) &= q_{10} (t) \oplus A_{0} (t) + q_{12} (t) \oplus A_{2} (t) + [q_{11.4} (t) + q_{11.(45)} (t) + q_{{11.45(67)^{n} }} (t)] \oplus A_{1} (t) + M_{1} (t) \hfill \\ A_{2} (t) &= q_{20} (t) \oplus A_{0} (t) + q_{28} (t) \oplus A_{8} (t) + M_{2} (t);A_{3} (t) = [q_{31} (t) + q_{31.5} (t) + q_{{31.5(67)^{n} }} (t)] \oplus A_{1} (t) \\ A_{8} (t) &= q_{{81.(67)^{n} }} (t) \oplus A_{1} (t) + q_{82} (t) \oplus A_{2} (t) + M_{8} (t) \end{aligned} $$
(7)

where, \(M_{0} (t) = e^{ - \lambda t}\), \(M_{1} (t) = \overline{H(t)} \,e^{ - \lambda t}\), \(M_{2} (t) = \overline{G(t)} \,e^{ - \mu t}\), \(M_{8} (t) = \overline{F(t)} \,e^{ - \lambda t}\).

Now taking LT of above relation (7) and solving for \(A_{0}^{*} (s)\), the steady-state availability is given by

$$ A_{0} = \lim_{s \to 0} sA_{0}^{*} (s) = \frac{{N_{A} }}{{D^{\prime}}} $$
(8)

where,

$$ N_{A} = \mu_{0} [(1 - p_{28} p_{82} )p_{10} + p_{12} p_{20} ] + \mu_{1} (1 - p_{28} p_{82} ) + \mu_{2} p_{12} + \mu_{8} p_{12} p_{28} $$
$$ D^{\prime} = \left[ \begin{gathered} \mu_{0} [(1 - p_{28} p_{82} )p_{10} + p_{12} p_{20} ] \hfill \\ + \mu^{\prime}_{1} (1 - p_{28} p_{82} ) + \mu_{2} p_{12} + \mu^{\prime}_{3} p_{03} [(1 - p_{28} p_{82} )p_{10} + p_{12} p_{20} ] + \mu^{\prime}_{8} p_{12} p_{28} \hfill \\ \end{gathered} \right] $$
(9)

6.1 Busy period of the server due to the inspection of the failed unit

Let \(B_{i}^{I} (t)\) is the probability that the repairman is busy due to the inspection of the failed unit at a moment ‘t’ specified that the system arrives at the regenerative state \(S_{i}\) at t = 0. The upcoming recursive interface for \(B_{i} (t)\) is:

$$ \begin{gathered} B_{0}^{I} (t) = q_{01} (t) \oplus B_{1}^{I} (t) + q_{03} (t) \oplus B_{3}^{I} (t) \hfill \\ B_{1}^{I} (t) = q_{10} (t) \oplus B_{0}^{I} (t) + q_{12} (t) \oplus B_{2}^{I} (t) + [q_{11.4} (t) + q_{11.(45)} (t) + q_{{11.45(67)^{n} }} (t)] \oplus B_{1}^{I} (t) + W_{1} (t) \hfill \\ B_{2}^{I} (t) = q_{20} (t) \oplus B_{0}^{I} (t) + q_{28} (t) \oplus B_{8}^{I} (t);B_{3}^{I} (t) = [q_{31} (t) + q_{31.5} (t) + q_{{31.5(67)^{n} }} (t)] \oplus B_{1}^{I} (t) + W_{3} (t) \hfill \\ B_{8}^{I} (t) = q_{{81.(67)^{n} }} (t) \oplus B_{1}^{I} (t) + q_{82} (t) \oplus B_{2}^{I} (t) \hfill \\ \end{gathered} $$
(10)

where, \(W_{1} (t) = \overline{H(t)} \,e^{ - \lambda t} + \overline{H(t)} \,\lambda e^{ - \lambda t} \oplus \overline{H(t)}\), \(W_{3} (t) = \overline{H(t)}\).

Now taking LT of above relation (10) solving for \(B_{0}^{I*} (s)\), the time for which server is busy due to repair is given by

$$ B_{0}^{I} = \lim_{s \to 0} sB_{0}^{I*} (s) = \frac{{N_{B}^{I} }}{{D^{\prime}}} $$
(11)

where

$$ N_{B}^{I} = W_{1}^{*} (0)(1 - p_{28} p_{82} ) + W_{3}^{*} (0)p_{03} [(1 - p_{28} p_{82} )p_{10} + p_{12} p_{20} ] $$
(12)

and \(D^{\prime}\) is earlier defined by Eq. (9).

6.2 Busy period of the server due to repair of the failed unit

Let \(B_{i}^{R} (t)\) is the probability that the repairman is busy due to repair at a moment ‘t’ specified that the system arrives at the regenerative state \(S_{i}\) at t = 0. The upcoming recursive interface for \(B_{i} (t)\) is:

$$ \begin{gathered} B_{0}^{R} (t) = q_{01} (t) \oplus B_{1}^{R} (t) + q_{03} (t) \oplus B_{3}^{R} (t) \hfill \\ B_{1}^{R} (t) = q_{10} (t) \oplus B_{0}^{R} (t) + q_{12} (t) \oplus B_{2}^{R} (t) + [q_{11.4} (t) + q_{11.(45)} (t) + q_{{11.45(67)^{n} }} (t)] \oplus B_{1}^{R} (t) \hfill \\ B_{2}^{R} (t) = W_{2} + q_{20} (t) \oplus B_{0}^{R} (t) + q_{28} (t) \oplus B_{8}^{R} (t);B_{3}^{R} (t) = [q_{31} (t) + q_{31.5} (t) + q_{{31.5(67)^{n} }} (t)] \oplus B_{1}^{R} (t) \hfill \\ B_{8}^{R} (t) = W_{8} (t) + q_{{81.(67)^{n} }} (t) \oplus B_{1}^{R} (t) + q_{82} (t) \oplus B_{2}^{R} (t) \hfill \\ \end{gathered} $$
(13)

where,\(W_{2} (t) = \overline{G(t)} \,e^{ - \mu t}\), and \( W_{8} (t) = \overline{F(t)} \,\lambda e^{ - \lambda t} \oplus f(t) \oplus \overline{G(t)} \,e^{ - \mu t} + \overline{F(t)} \,\lambda e^{ - \lambda t} \oplus f(t) \oplus \overline{G(t)} \mu \,e^{ - \mu t} \oplus f(t) \oplus \overline{G(t)} \,e^{ - \mu t} + \cdots \)

Now taking LT of above relation (13) solving for \(B_{0}^{R*} (s)\), the time for which server is busy due to repair is given by

$$ B_{0}^{R} = \lim_{s \to 0} sB_{0}^{R*} (s) = \frac{{N_{B}^{R} }}{{D^{\prime}}} $$
(14)

where

$$ N_{B}^{R} = W_{2}^{*} (0)p_{12} + W_{8}^{*} (0)p_{12} p_{28} $$
(15)

and \(D^{\prime}\) is earlier defined by Eq. (9).

7 Expected numbers of visits by the server due to repair of the failed unit

Let \(V_{i} (t)\) is the estimated no. of visits by the repairman for repair in (0, t] specified that the system arrives at the regenerative state \(S_{i}\) at t = 0. The upcoming recursive interface for \(V_{i} (t)\) is:

$$ \begin{gathered} V_{0} (t) = Q_{01} (t) \otimes [1 + V_{1} (t)] + Q_{03} (t) \otimes [1 + V_{3} (t)] \hfill \\ V_{1} (t) = Q_{10} (t) \otimes V_{0} (t) + Q_{12} (t) \otimes V_{2} (t) + [Q_{11.4} (t) + Q_{11.(45)} (t) + Q_{{11.45(67)^{n} }} (t)] \otimes V_{1} (t) \hfill \\ V_{2} (t) = Q_{20} (t) \otimes V_{0} (t) + Q_{28} (t) \otimes V_{8} (t);V_{3} (t) = [Q_{31} (t) + Q_{31.5} (t) + Q_{{31.5(67)^{n} }} (t)] \otimes V_{1} (t) \hfill \\ V_{8} (t) = Q_{{81.(67)^{n} }} (t) \otimes V_{1} (t) + Q_{82} (t) \otimes V_{2} (t) \hfill \\ \end{gathered} $$
(16)

Now taking LST of above relation (16) and solving for \(R_{0}^{**} (s)\). The expected no. of visits of the server can be obtained as:

$$ V_{0} = \lim_{s \to 0} sV_{0}^{**} (s) = \frac{{V_{r} }}{{D^{\prime}}} $$

where

$$ V_{r} = \left( {1 - p_{28} p_{82} } \right)p_{10} + p_{12} p_{20} $$
(17)

and \(D^{\prime}\) is earlier defined by Eq. (9).

8 Expected number of refreshments given to the server

Let \(T_{i} (t)\) is the estimated no. of refreshment offered to the repairman for repair in (0, t] specified.

that the system arrives at the regenerative state \(S_{i}\) at t = 0. The upcoming recursive interface for \(T_{i} (t)\) is:

$$ \begin{gathered} T_{0} (t) = Q_{01} (t) \otimes T_{1} (t) + Q_{03} (t) \otimes T_{3} (t) \hfill \\ T_{1} (t) = Q_{10} (t) \otimes T_{0} (t) + Q_{12} (t) \otimes T_{2} (t) + [Q_{11.4} (t) + Q_{11.(45)} (t) + Q_{{11.45(67)^{n} }} (t)] \otimes T_{1} (t) \hfill \\ T_{2} (t) = Q_{20} (t) \otimes T_{0} (t) + Q_{28} (t) \otimes \left[ {1 + T_{8} (t)} \right];T_{3} (t) = [Q_{31} (t) + Q_{31.5} (t)] \otimes T_{1} (t) + Q_{{31.5(67)^{n} }} (t) \otimes \left[ {1 + T_{1} (t)} \right] \hfill \\ T_{8} (t) = Q_{{81.(67)^{n} }} (t) \otimes \left[ {1 + T_{1} (t)} \right] + Q_{82} (t) \otimes T_{2} (t) \hfill \\ \end{gathered} $$
(18)

Now taking LST of above relation (17) and solving for \(T_{0}^{**} (s)\). The expected no of visits of the server can be obtained as:

$$ T_{0} = \lim_{s \to 0} sT_{0}^{**} (s),N_{0} = \frac{{T_{rf} }}{{D^{\prime}}} $$

where,

$$ T_{rf} = p_{{11.45(67)^{n} }} \left( {1 - p_{28} p_{82} } \right) + p_{{31.5(67)^{n} }} \left[ {p_{03} \left( {1 - p_{28} p_{82} } \right)p_{10} + p_{12} p_{20} } \right] + p_{{81.(67)^{n} }} p_{12} p_{28} $$
(19)

and \(D^{\prime}\) is earlier defined by Eq. (9).

9 Particular cases

Suppose that \(f(t) = \theta e^{ - \theta t}\), \(g(t) = \varphi e^{ - \varphi t}\),\(h(t) = \psi e^{ - \psi t}\)

$$ \begin{gathered} p_{11.4} = \frac{\lambda \varphi }{{(\varphi + \mu + \lambda )(\varphi + \mu )}},p_{{11.(45)^{n} }} = \frac{\lambda \mu }{{(\varphi + \mu + \lambda )(\varphi + \mu )}},p_{21.(76)} = \frac{\lambda }{(\theta + \lambda )},p_{{31.(54)^{n} }} = \frac{\mu }{(\varphi + \mu )} \hfill \\ p_{{81.(67)^{n} }} = \frac{\lambda }{(\theta + \lambda )},M_{0} = \frac{1}{\lambda } = \mu_{0} ,M_{1} = \frac{1}{(\lambda + \psi )} = \mu_{1} ,M_{2} = \frac{1}{(\varphi + \mu )} = \mu_{2} ,M_{8} = \frac{1}{(\lambda + \theta )} = \mu_{8} \hfill \\ W_{1} (t) = \mu^{\prime}_{1} ,W_{2} (t) = \mu_{2} ,W_{3} (t) = \mu^{\prime}_{3} ,W_{8} (t) = \mu^{\prime}_{8} \hfill \\ \end{gathered} $$
$$ MTSF = \frac{{\left[ {\theta \varphi + \lambda (\varphi + \mu )} \right]\,\left( {\lambda + \psi + a\lambda } \right) + aq\psi \lambda + a\lambda^{2} \left( {\lambda + \theta + \mu } \right)}}{{\lambda \left[ {\{ \theta \varphi + \lambda (\varphi + \mu )\} \left( {\lambda + \psi - ap\psi } \right) - aq\psi \varphi \left( {\lambda + \theta } \right)} \right]}} $$
(20)
$$ (A_{0} ) = \frac{{\theta \varphi \psi (\lambda + \psi )\left[ {\left\{ {\theta \varphi + \lambda (\varphi + \mu )} \right\}(\lambda + \psi ) + q\lambda \psi (\lambda + \theta )} \right]}}{{\left[ {D_{0} } \right]}} $$
(21)
$$ D_{0} = \left[ \begin{gathered} \left( {\theta \varphi + \lambda (\varphi + \mu )} \right)\,\left[ \begin{gathered} p\theta \varphi \psi^{2} + bp\psi \lambda \left\{ {\theta \varphi + q\psi (\theta + \mu )} \right\} \hfill \\ + \lambda \left\{ {\theta \varphi (\psi + \lambda ) + q\lambda \psi (\theta + \mu )} \right\} \hfill \\ \end{gathered} \right] \hfill \\ + q\theta \varphi \psi^{2} (\lambda + \theta ) + q\psi \lambda \,\left[ \begin{gathered} b\varphi (\lambda + \theta )\left\{ {\theta \varphi + (\lambda + \psi ) + q\lambda \psi (\theta + \mu )} \right\} \hfill \\ + \left\{ {\theta \varphi + \lambda (\theta + \mu + \varphi )} \right\}\mu \psi \hfill \\ \end{gathered} \right] \hfill \\ \end{gathered} \right] $$
(22)
$$ (B_{0}^{R} ) = \frac{{q\lambda \psi^{2} \left[ {\theta \varphi (\lambda + \mu ) + \theta (\theta \varphi + \lambda \mu ) + \lambda \mu (\mu + \varphi )} \right]}}{{\left[ {D_{0} } \right]}} $$
(23)
$$ (B_{0}^{I} ) = \frac{{\lambda \left[ \begin{gathered} \left\{ {\theta \varphi + \lambda (\varphi + \mu )} \right\}\left[ {\theta \varphi (\psi + \lambda + p\psi ) + q\psi (\theta + \mu )(\lambda + p\psi )} \right] \hfill \\ + q\psi \varphi \left[ {\theta \varphi + q\psi (\theta + \mu )} \right](\lambda + \theta ) \hfill \\ \end{gathered} \right]}}{{\left[ {D_{0} } \right]}} $$
(24)
$$ (N_{0} ) = \frac{{\lambda \theta \varphi^{2} \left[ {\varphi \psi (\lambda + \theta ) + p\lambda \psi \mu } \right]}}{{\left[ {D_{0} } \right]}} $$
(25)
$$ (T_{0} ) = \frac{{\lambda \theta \varphi \psi \left[ \begin{gathered} \left[ {\theta \varphi + \lambda (\varphi + \mu )} \right]\left\{ {q\mu (\lambda + bp\psi )} \right\} \hfill \\ + q\psi \left\{ {q\mu \varphi (\lambda + \theta ) + \lambda \mu (\varphi + \mu )} \right\} \hfill \\ \end{gathered} \right]}}{{(\varphi + \mu )[D_{0} ]}} $$
(26)

10 Profit analysis

The profit analysis of the system can be done by using the profit function;

$$ P = C_{0} A_{0} - C_{1} B_{0}^{I} - C_{2} B_{0}^{R} - C_{3} V_{0} - C_{4} T_{0} $$
(27)

where, \(C_{0} =\) 15,000 (Revenue per unit uptime of the system is available).

\(C_{1} =\) 600 (Cost per unit time for which server is busy due to inspection).

\(C_{2} =\) 800 (Cost per unit time for which server is busy due to repair).

\(C_{3} =\) 500 (Cost per unit visit by the server).

\(C_{4} =\) 200 (Cost per unit time treatment given to the server).

11 Discussion

Figure 2 represents the pictorial behavior of MTSF having an increasing trend corresponding to refreshment rate (\(\theta\)). In this graph, the values of parameters \(\mu = 0.4\),\(\varphi = 0.65\),\(\psi = 0.8\) refresh-ment request (or server failure) rate, treatment rate, and the inspection rate respectively taken as constant for simplicity. When \(\lambda\) the failure rate of the operative unit changing from 0.3 to 0.35 then MTSF declined but having increasing trends and when \(\psi\) changing from 0.5 to 0.6 then MTSF spontaneously increase its value with the same increasing trends, and when \(\varphi\) changing from 0.6 to 0.7 then MTSF slightly increased the value. Figure 2, reflects the increasing trend of the MTSF corresponding to the increasing values of refreshment rate.

Fig. 2
figure 2

MTSF vs. Refreshment rate (θ)

Full size image

Figure 3 represents the pictorial behavior of availability having an increasing trend corresponding to refreshment rate (\(\theta\)) increases from 0.1 to 1.0. In this graph, the values of parameters \(\mu = 0.4\),\(\varphi = 0.65\),\(\psi = 0.8\) refreshment request (or server failure) rate, treatment rate, and the inspection rate respectively taken as constant for simplicity. When \(\lambda\) changing from 0.3 to 0.35 then availability declined but having an increasing trend corresponding to the increasing value of the refreshment rate and when \(\psi\) changing from 0.5 to 0.6 then system is available for use more than the previous time, and when \(\varphi\) changing from 0.6 to 0.7 then availability enhanced. This graph also reveals that as the rate of refreshment \(\theta\) changing from 0.1 to 1.0 then availability having an increasing trend.

Fig. 3
figure 3

Availability vs. refreshment rate (θ)

Full size image

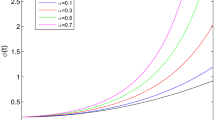
The main objective of any system that manages the system that profit enhances, as well as quality of the product, should not be degraded. Figure 4 depicts the behavior of the profit of the system having an increasing trend corresponding to refreshment rate (\(\theta\)). In this graph, the values of parameters \(\mu = 0.4\),\(\varphi = 0.65\),\(\psi = 0.8\) refreshment request (or server failure) rate, treatment rate, and inspection rate respectively taken as constant for simplicity. This graph shows that the profit of the system always in an increasing manner corresponding to the increasing refreshment rate from 0.1 to 1.0 and at the highest value when \(\varphi\) varies from 0.6 to 0.7. Hence, offering refreshment to the server always enhance the system toward more benefit.

Fig. 4
figure 4

Profit vs. refreshment rate (θ)

Full size image

12 Conclusion

The main finding of the above study is that the idea to provide refreshment to the repairman during his job plays an important role to enhance the capacity of the server. The novelty of the study that the refreshment increases the efficiency of the repairman and it is very valuable and economical for the effective functioning of the system. From Figs. 3 and 4, it is clear that the availability and profit of the system increase corresponding to an increased refreshment rate.

12.1 Future scope

Hence, refreshment to provide the server always enhances the performance of the server, availability of the system, and profit of the system.