A new repair model and its optimization for cold standby system

Abstract

In this paper, we propose a new repair model for a cold standby system, which consists of two components and one repairman. It is assumed that the consecutive working time follows decreasing geometric process after repair, and the repair time interval is a constant for component 1. For component 2 (standby component), the failure process during working time follows Generalized Polya Process, which is a generalized version of the nonhomogeneous Poisson process. Component 2 is rectified by Generalized Polya Process repair when it fails. The repair time of component 2 is assumed to be negligible. Component 1 is assumed to have priority in use. The long-run average cost rate function of the system is deduced based on the failure number of component 1. Moreover, the optimal replacement policy of model is established by minimizing the long-run average cost rate function theoretically, which proves the existence and uniqueness of the optimal replacement policy. Numerical examples are provided to verify the effectiveness of the proposed approaches. Sensitivity analysis are conducted to illustrate the influence of parameters under the optimal replacement policy.

1 Introduction

Geometric process (GP) repair model is first introduced into the reliability areas and maintenance problems by Lam (1988a, b). It is a model that has been widely used in optimisation of maintenance policies. The GP was first discussed by Smith and Leadbetter (1963). In Lam’s model, two univariate replacement policies are discussed. One is based on the working age T of a system and another is based on the failure number N of the system. Stadje and Zuckerman (1990) generalized Lam’s work and introduced a general monotone process repair model. Finkelstein (1993) studied a general repair model based on a scale transformation. Zhang (1994) applied the GP in maintenance policy optimisation, in which Zhang generalized Lam’s work, proposed the bivariate replacement policy (T, N) and proved that the bivariate optimal policy $(T,N)^*$ is better than univariate optimal policy $N^*$ and $T^*$. In bivariate policy case, the system is replaced at the working age T or at the Nth failure of the system which occurs first. Lam (1988b), Stadje and Zuckerman (1990) proved that optimal replacement policy $N^*$ is better than the optimal policy $T^*$ under some conditions. The different variants of the GP model is still researched. Braun et al. (2005) studied the $\alpha$ series process. Chan et al. (2006) proposed threshold GP. Wu and Wang (2017) studied the Semi-GP. Wu (2018) studied the doubly GP. Furthermore, Zhang and Wang (2009) proposed a new repair model based on the reliability and failure number of a system. Zhao and Nakagawa (2012) proposed age and periodic replacement last models with working cycles, and comparisons between such a replacement last and the conventional replacement first are made in detail. Zhao et al. (2015) proposed several approximate models in maintenance theory. Sheu et al. (2016) studied an operating system subject to shock occurring as a non-homogeneous pure birth process. Zhang and Wang (2016) proposed the extended GP repairable model. Lim et al. (2016) studied an age replacement model based on imperfect repair with random probability. Berrade et al. (2017) proposed a new postponed delay time model. Ito et al. (2017) studied the reliability and preventive replacement problems for a K-out-of-n system, where K is a stochastic parameter provided. Zhao et al. (2017a) summarized some perspectives and method in age replacement models. Levitin et al. (2018) studied heterogeneous 1-out-of-N warm standby systems when all components can experience internal failures whereas operating components are exposed to the external shocks as well. The expression for the instantaneous availability is derived and the original numerical algorithm for its evaluation is suggested. In recent years, many extensions works have been studied. More generalized studies can be obtained from Tsai et al. (2017), Zhao et al. (2017b), Cha and Finkelstein (2018), Chen et al. (2019), Levitin and Finkelstein (2019) and so on.

Cold standby systems are widely used in some engineering fields. Using standby component can improve the reliability performance of the system and reduce the cost. In a nuclear plant, to reduce the risk of the ‘scram’ of a reactor in case of a coolant pipe breaking or some other failure happening, a standby diesel generator should be installed. In a hospital or a steel manufacturing complex, if the power supply suddenly suspends when required, the consequences might be catastrophic, such as a patient may die in an operating room. In this case, a storage generator is usually equipped to provide electric power. Then the electric power and the storage generator form a cold standby power system. Usually, it is reasonable to assume that the storage generator is the standby component of the cold standby system. In the operating theater of a hospital, an operation have to be discontinued as soon as the power source is cut (i.e. power station failures). Usually, there is a standby power station (i.e. a storage battery) in the operating theater. Therefore, the power station (component 1) and the storage battery (component 2) form a cold standby repairable system. Obviously, it is reasonable to assume that the storage battery is as good as new after repair, since its used time is shorter than the power station, and the repair time of the storage battery is also short, while the repair time of power stations is long, due to the complexity of the power stations equipment. Besides the electric power system in a hospital, some similar examples can be found from Lam (2007), Zhang and Wang (2007), Wang and Zhang (2011). Zhang and Wang (2007) studied a cold standby repairable system. It is assumed that component 1 has priority in use when two components are all good. Wang and Zhang (2011) studied the optimal replacement policy for a cold standby system with preventive repair. Wang and Zhang (2016) studied a cold standby system and assumed that the failure process of standby component is nonhomogeneous Poisson process (NHPP).

Many researchers considered the failure system with the minimal repair, in which the failure intensity function of the system does not change. Barlow and Hunter (1960) concluded that the minimal repair does not have effect on the failure rate function of the system. Brown and Proschan (1983) studied the imperfect repair model, in which the system is replaced with probability p and minimal repair with probability $1-p$. Later, Nakagawa (1986) studied the minimal repair in preventive maintenance model. Many other works on minimal repair have been developed, such as Jaturonnateeaba (2006), Avenab (2008), Sheu and Li (2012). Although minimal repair has numerous advantages in model development and maintenance optimization, it has practical limitations. In minimal repair system, NHPP is a usually used to describe the failure event process of the repairable system. However, NHPP has the property of an independent increment, i.e., the imminent failure process does not dependent on the failure history. In fact, it can be too restrictive to describe most of the real life problems. For example, in engineering maintenance problem, many systems are deteriorating gradually with the increasing of failure number. A system’s susceptibility to shocks (failure) increases with the failure number experienced previously. Thus a minor failure or even a negligible failure that had occurred during the initial lifetime period can become harmful and even catastrophic with time. Namely most failure process of repairable systems are depending on the failure history and accumulative wear. NHPP is not a natural assumption for repairable models. More detailed research on the property of independent increment can be found in the Cha and Finkelstein (2009, 2011). However, in the paper of Wang and Zhang (2016), the failure number of component 2 follows NHPP.

Inspired by the above consideration, the main objective is to study the optimal replacement policy of cold standby system. Assuming that the failure process of component 2 follows the Generalized Polya Process (GPP) in each periodic working time, which is the generalized NHPP. The working time of component 1 follows GP and component 2 adopts GPP repair. A GPP repair restores the system to its operating status just prior to failure, and the failure intensity function after repair is the same as that just before failure. We derive the long-run average cost rate (ACR) function of the system based on the failure number of component 1 and investigate the optimal replacement policy both theoretically and numerically. The main contributions of this paper are twofold. On one hand, a more general and reasonable GGP maintenance model for a two components cold standby system is studied; on the other hand, the existence and uniqueness of the optimal replacement policy is proved.

The rest of the paper is organized as follows. In Sect. 2, definitions of GP and GPP are introduced, and a new repair model for cold standby system with two components is proposed. In Sect. 3, we derive the long-run ACR function of the system and analyze the optimal replacement policy $N^*$ theoretically. Simulation studies are concluded to verify the effectiveness of the theoretical analysis in Sect. 4. Section 5 gives conclusions of this work.

2 Definitions and model assumptions

2.1 Definitions

For convenient purpose, we give the definitions of the GP and GPP as follows.

Definition 1

Assume that $\left\{ X_n,n=1,2,\ldots \right\}$ is a sequence independent non-negative random variables. If the cumulative distribution function (CDF) of $X_n$ is $F_{n}(t) = F(a^{n-1}t)$, for $n=1,2,\ldots$, and a is a positive constant, then $\left\{ X_n,n=1,2,\ldots \right\}$ is called a GP (Lam 1988a), and a is the ratio of the GP.

Obviously, if $a>1$, $\left\{ X_n,n=1,2,\ldots \right\}$ is stochastically decreasing; if $0<a<1$, $\left\{ X_n,n=1,2,\ldots \right\}$ is stochastically increasing; if $a=1$, $\left\{ X_n, n=1, 2, \ldots \right\}$ is a renewal process.

Let $\left\{ N(t), t\ge 0 \right\}$ be the point process, $N({t-})=\left\{ N(u), 0\le u< t \right\}$ be the history of the point process, and $T_i$ be the time from 0 until the arrival of the ith event in [0, t). Then the point process is described by stochastic intensity $\lambda (t)$, which is described as Lee and Cha (2016).

$$\begin{aligned} \lambda (t)= \lim _{\varDelta t \rightarrow 0} \frac{ P \left[ (N(t,t+\varDelta t)=1)| N({t-}) \right] }{\varDelta t} = \lim _{\varDelta t \rightarrow 0} \frac{ E \left[ N(t,t+\varDelta t) | N({t-}) \right] }{\varDelta t}, \end{aligned}$$

(1)

where $N(t_1, t_2)$ denotes the number of events in time interval $[t_1, t_2)$, $t_1<t_2$.

Definition 2

Generalized Polya Process (GPP) (Cha 2014)

A counting process $\left\{ N(t), t\ge 0 \right\}$ is called the GPP with the set of parameters $(\lambda (t), \alpha , \beta )$, $\alpha \ge 0$, $\beta >0$, if

• (i) $N(0)=0$;

• (ii) $\lambda _t= \left( \alpha N(t-) +\beta \right) \lambda (t)$.

When $\alpha =0$, $\beta =1$, then $\lambda _t=\lambda (t)$, the GPP is NHPP, which has intensity function $\lambda (t)$.

Some property of GPP is given as follows. The proof is provided in Cha (2014).

Proposition 1

Suppose that a counting process $\left\{ N(t), t\ge 0 \right\}$ is the GPP with the set of parameters $(\lambda (t), \alpha , \beta )$, $\alpha \ge 0$, $\beta >0$. Then the distribution of N(t) is

$$\begin{aligned} P \left( N(t) = n \right) = \frac{\varGamma \left( \frac{\beta }{\alpha }+ n \right) }{\varGamma \left( \frac{\beta }{\alpha } \right) n! } \left( 1- \exp \left\{ -\alpha \varLambda (t) \right\} \right) ^n \times \left( \exp \left\{ - \alpha \varLambda (t) \right\} \right) ^{\frac{\beta }{\alpha }},\quad {n=0,1,2, \ldots , } \end{aligned}$$

(2)

and

$$\begin{aligned} E[N(t)]=\frac{\beta }{\alpha } \left( \exp \left\{ \alpha \varLambda (t) \right\} - 1 \right) , \end{aligned}$$

(3)

where $\varLambda (t)=\int _0^t \lambda (s) {{\,\mathrm{d\!}\,}}s$.

Based on the definition of GPP, GPP repair is given as follows.

Definition 3

GPP repair (Lee and Cha 2016)

For an item with failure rate $\lambda (t)$, a repair type is called the ‘GPP repair’ with parameter $\alpha$ if $\left\{ N(t), t\ge 0 \right\}$ is the GPP with parameter set $(\lambda (t),\alpha ,1)$. The GPP repair was defined via three parameters $(\lambda (t),\alpha , \beta )$. Under the GPP repair process, the corresponding stochastic intensity is specified as

$$\begin{aligned} \lambda _{t}=(\alpha (N(t-)+1)\lambda (t). \end{aligned}$$

Remark 1

:

• (i) $\alpha$ determines the degree of repair, which means bigger $\alpha$ accelerates the deterioration, and smaller $\alpha$ decelerates it. Furthermore, as $\alpha$ increases, the corresponding repair becomes worse and worse.

According to the Definition 3, the GPP repair has one parameter $\alpha$. Now we interpret the effect of the parameter $\alpha$ from the modeling point of view. For this, the failure intensity function $\phi (t)$ is defined as follows:

$$\begin{aligned} \phi (t)=\lim _{\varDelta t \rightarrow 0} \frac{ E \left[ N(t,t+\varDelta t) \right] }{\varDelta t}=\frac{ {{\,\mathrm{d\!}\,}}E[N(t)]}{ {{\,\mathrm{d\!}\,}}t}, \end{aligned}$$

which represents the mean number of failures per unit time at time t. According to Proposition 1 and Definition 3, $\phi (t)$ can be written as

$$\begin{aligned} \phi (t)=\lambda (t) \exp \left\{ \alpha \varLambda (t) \right\} , t \ge 0. \end{aligned}$$

When $\lambda (t)=0.02t^2+0.2$, $\phi (t)$ was plotted for different $\alpha$ in Fig. 1. According to Fig. 1, it is easy to see that the parameter $\alpha$ determines the degree of the deterioration. And bigger $\alpha$ accelerates the deterioration of the system, whereas smaller $\alpha$ decelerates it.

Fig. 1

The failure intensity function $\phi (t)$ for different $\alpha$

2.2 Model assumptions

Now, a new repair model for a two components cold standby system based on two types of repairs is proposed. Some assumptions are given as follows.

Assumption 1

Component 1 is in a working state, and component 2 is in cold standby state at the same time.

Assumption 2

The successive working time interval of component 1 after repair forms a decreasing GP, which is denoted by $\{ X_n, n=1,2,\ldots \}$. The CDF of $X_n$ is denoted by

$$\begin{aligned} F_n(t)=F(a^{n-1}t), \end{aligned}$$

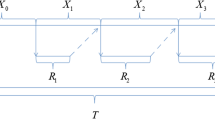
where $t>0$, $a>1$ is the ratio of the GP. The repair time interval of component 1 is denoted by T, and $E(X_1)=\lambda$.

Assumption 3

When component 2 fails, GPP repair is carried out. The failure process during repair time interval T follows the GPP with parameters set $\left( \lambda \left( \left( i - 1 \right) T + t \right) , \alpha , 1 \right) , i=1,2, \ldots$, where $\lambda \left( (i-1) T \right)$ denotes the failure intensity function after the ith repair of component 2. Similar to minimal repair. The durations of the GPP repair is negligible.

Assumption 4

The replacement policy N based on the failure number of component 1. Namely, the system is replaced at the Nth failure of component 1.

Assumption 5

The replacement time of the system is negligible.

The time interval between completion of the $(i-1)$th repair and completion of the ith repair of component 1 is called the ith cycle. A working process of the cold standby system is illustrated in Fig. 2. Component 1 has two states, which is working or down. Component 2 is in working status when component 1 is being repaired. Component 2 would be repaired right away if it fails and its repair time is minimal and ignorable. After repair, component 2 will be ready to work instantaneously.

Fig. 2

A possible working process of a cold standby system

3 Optimal replacement policy $N^*$

Let $C_1$ be the repair cost of component 1. $C_2$ be the GPP repair cost of component 2 and $C_0$ be the replacement cost of the system. Let $\tau _n, n=1, 2, \ldots$ be the time between the $(n-1)$th replacement and the nth replacement of the system, where $\tau _1$ is the first replacement time of the system. Obviously, $\{\tau _n, n=1, 2, \ldots \}$ is a renewal process. Let C(N) be the long-run ACR function of the system under the policy of N. According to the renewal reward theorem (Ross 1996), we have

$$\begin{aligned} C(N)=\lim \limits _{t \rightarrow +\infty } \frac{E[R(t)]}{t}, \end{aligned}$$

where the R(t) denotes the profit within interval [0, t].

Let L and S denote the total working time and total repair time of the system in a renewal cycle respectively. According to the assumptions 1-5, $L=X_1 + X_2 + \cdots + X_N + (N-1)T$, $S=(N-1)T$. The length of the renewal cycle is L. Using $N_{GP}$ denotes the total GPP repair number of component 2 in the renewal cycle. According to the Eq. (3) of Proposition 1 in part 2, the expected failure number of GPP repair in the ith working period of component 2 is given by

$$\begin{aligned} \frac{1}{\alpha } \left( \exp \left\{ \alpha \int _0^T \lambda ((i-1)T+t) {{\,\mathrm{d\!}\,}}t \right\} -1 \right) , \ i=1, 2, \ldots , N. \end{aligned}$$

By applying the renewal reward theorem Ross (1996), the long-run ACR function C(N) is expressed as follows:

$$\begin{aligned} C(N)&= \frac{ C_1(N-1)T + C_2 E[N_{GP}] + C_0}{ E \left[ \sum \nolimits _{i=1}^N X_i \right] + (N-1) T } \nonumber \\&= \frac{ C_1(N-1)T + C_2 \left[ \sum \nolimits _{i=1}^N \frac{1}{\alpha } \left( \exp \left\{ \alpha \int _0^{T} \lambda ((i-1)T + t) {{\,\mathrm{d\!}\,}}t \right\} -1 \right) \right] + C_0 }{\sum \nolimits _{i=1}^N \lambda _i + (N-1)T }, \end{aligned}$$

(4)

where $\lambda _i= E(X_i)= \frac{\lambda }{b^{i-1}}$.

Remark 2

:

• (i) When the failure number of component 2 follows NHPP with intensity function $\lambda (t)$ in the time interval [0, t]. Then, the long-run ACR function is

  $$\begin{aligned} C(N)=\frac{ C_1(N-1)T + C_2 (N-1) \int _0^{T} \lambda (t) {{\,\mathrm{d\!}\,}}t + C_0}{\sum \nolimits _{i=1}^N \lambda _i + (N-1) T}. \end{aligned}$$

• (ii) If the failure number of component 2 forms a homogeneous Poisson process with intensity r. The failure number of component 2 in a renewal cycle is $(N-1)Tr$. Then, the long-run ACR function becomes

  $$\begin{aligned} C(N)=\frac{ C_1(N-1)T + C_2 (N-1)Tr + C_0}{\sum \nolimits _{i=1}^N \lambda _i + (N-1)T}. \end{aligned}$$

• (iii) If $N=1$, the long-run ACR function of the system is

  $$\begin{aligned} C(1)=\frac{ \frac{C_2}{\alpha} \left( \exp \left\{ \alpha \int _0^{T} \lambda (t) {{\,\mathrm{d\!}\,}}t \right\} - 1 \right) + C_0}{\lambda _1}, \end{aligned}$$

  this case is studied by Lee and Cha (2016).

Now, the optimal replacement policy $N^*$ of the system by minimizing the long-run ACR function is discussed theoretically. The optimal $N^*$ is analyzed under some conditions in Theorem 1.

Firstly, we compute the difference between $C(N+1)$ and C(N) as follows

$$\begin{aligned}&C(N+1)-C(N) \nonumber \\&\quad = \frac{ C_1 NT + C_2 \left[ \sum \nolimits _{i=1}^{N+1} \frac{1}{\alpha } \left( \exp \left\{ \alpha \int _0^{T} \lambda ((i-1)T+t) {{\,\mathrm{d\!}\,}}t \right\} -1 \right) \right] + C_0 }{\sum \nolimits _{i=1}^{N+1} \lambda _i + NT} \nonumber \\&\qquad - \frac{C_1(N-1)T + C_2 \left[ \sum \nolimits _{i=2}^N \frac{1}{\alpha } \left( \exp \left\{ \alpha \int _0^{T} \lambda ((i-1)T+t) {{\,\mathrm{d\!}\,}}t \right\} -1 \right) \right] + C_0 }{\sum \nolimits _{i=1}^N \lambda _i + (N-1)T} \nonumber \\&\quad = \frac{\varPsi (N)}{ \left( \sum \nolimits _{i=1}^{N+1} \lambda _i + NT \right) \left( \sum \nolimits _{i=1}^N \lambda _i + (N-1)T \right) }, \end{aligned}$$

(5)

where

$$\begin{aligned} \varPsi (N)=\varPsi _1(N)+\varPsi _2(N), \end{aligned}$$

and

$$\begin{aligned} \varPsi _1(N)& = {} C_1 T \left[ \sum _{i=1}^N \lambda _i - (N-1)\lambda _{N+1} \right] - C \left( \lambda _{N+1} + T \right) ,\\ \varPsi _2(N)& = {} C_2 \left[ \sum _{i=1}^N \lambda _i + (N-1)T \right] \frac{1}{\alpha } \left( \exp \left\{ \alpha \int _0^{T} \lambda ((N-1)T+t) {{\,\mathrm{d\!}\,}}t \right\} -1 \right) \\&-C_2 \left( \lambda _{N+1} + T \right) \left[ \sum _{i=1}^{N-1} \frac{1}{\alpha } \left( \exp \left\{ \alpha \int _0^{T} \lambda ((i-1)T + t) {{\,\mathrm{d\!}\,}}t \right\} -1 \right) \right] . \end{aligned}$$

The denominator of Eq. (5) is positive. So the sign of $C(N+1)-C(N)$ is depend on the sign of numerator $\varPsi (N)$ in Eq. (5). It is easy to get $C(N+1)-C(N)>0$ if and only if $\varPsi (N)>0$.

Next, the property of the function $\varPsi (N)$ is given as follows.

Lemma 1

: If the failure rate function $\lambda (t)$ is increasing with t, then function $\varPsi (N)$ is increasing with N.

The proof will be divided into two parts.

Proof

(i) First we show $\varPsi _1(N)$ is increasing with N. This can be easily see by the following:

$$\begin{aligned} \varPsi _1(N+1)-\varPsi _1(N)&= C_1 T \left[ \sum _{i=1}^{N+1} \lambda _i - N \lambda _{N+2} \right] - C_0 (\lambda _{N+2} + T) \nonumber \\&\quad -\, C_1 T \left[ \sum _{i=1}^N \lambda _i - (N-1)\lambda _{N+1} \right] + C_0 (\lambda _{N+1} + T) \nonumber \\&= (\lambda _{N+1}- \lambda _{N+2})(C_1NT + C_0)>0. \end{aligned}$$

(6)

(ii) The difference of the $\varPsi _2(N+1)-\varPsi _2(N)$ is

$$\begin{aligned}&\varPsi _2(N+1) - \varPsi _2(N) \nonumber \\&\quad = f(N) + C_2 (\lambda _{N+1} - \lambda _{N+2}) \left[ \sum _{i=1}^{N-1} \frac{1}{\alpha } \left( \exp \left\{ \alpha \int _0^{T} \lambda ((i-1)T + t) {{\,\mathrm{d\!}\,}}t \right\} -1 \right) \right] , \end{aligned}$$

(7)

where

$$\begin{aligned} f(N)&= C_2 \left[ \sum _{i=1}^{N+1} \lambda _i + NT \right] \frac{1}{\alpha } \left( \exp \left\{ \alpha \int _0^{T} \lambda ({N}T+t) {{\,\mathrm{d\!}\,}}t \right\} -1 \right) \nonumber \\&\quad -\, C_2 \left[ \sum _{i=1}^N \lambda _i +\lambda _{N+2}+NT \right] \frac{1}{\alpha } \left( \exp \left\{ \alpha \int _0^{T} \lambda ((N-1)T+t) {{\,\mathrm{d\!}\,}}t \right\} -1 \right) . \end{aligned}$$

(8)

By differentiating f(N) with respect to T, we have

$$\begin{aligned} f'(N)&= C_2 N \frac{1}{\alpha } \left( \exp \left\{ \alpha \int _0^{T} \lambda (NT+t) {{\,\mathrm{d\!}\,}}t \right\} - \exp \left\{ \alpha _0 \int _0^{T} \lambda ((N-1)T+t) {{\,\mathrm{d\!}\,}}t \right\} \right) \nonumber \\&\quad +\, C_2 \left[ \sum _{i=1}^{N+1} \lambda _i + NT \right] \times \left( \lambda (({N+1})T) + \int _0^{T} N \lambda '(NT + t) {{\,\mathrm{d\!}\,}}t \right) \nonumber \\&\quad \times \, \left( \exp \left\{ \alpha \int _0^{T} \lambda (NT+t) {{\,\mathrm{d\!}\,}}t \right\} -1 \right) - C_2 \left[ \sum _{i=1}^N \lambda _i + \lambda _{N+2} + NT \right] \nonumber \\&\quad \times \, \left( \lambda (NT) + \int _0^{T} (N-1) \lambda '((N-1)T + t) {{\,\mathrm{d\!}\,}}t \right) \nonumber \\&\quad \times \, \left( \exp \left\{ \alpha \int _0^{T} \lambda ((N-1)T+t) {{\,\mathrm{d\!}\,}}t \right\} -1 \right) \nonumber \\ \ge&C_2 N \frac{1}{\alpha } \left( \exp \left\{ \alpha \int _0^{T} \lambda ( NT+t) {{\,\mathrm{d\!}\,}}t \right\} - \exp \left\{ \alpha \int _0^{T} \lambda ((N-1)T+t) {{\,\mathrm{d\!}\,}}t \right\} \right) \nonumber \\&\quad +\, C_2 \left[ \sum _{i=1}^{N+1} \lambda _i + NT \right] \times \left( \lambda (({N+1})T) + \int _0^{T} N \lambda '( NT + t) {{\,\mathrm{d\!}\,}}t \right) \nonumber \\&\quad \times \, \left( \exp \left\{ \alpha \int _0^{T} \lambda (NT+t) {{\,\mathrm{d\!}\,}}t \right\} -1 \right) - C_2 \left[ \sum _{i=1}^N \lambda _i + \lambda _{N+1} + NT \right] \nonumber \\&\quad \times \, \left( \lambda (NT) + \int _0^{T} (N-1) \lambda '((N-1)T + t) {{\,\mathrm{d\!}\,}}t \right) \nonumber \\&\quad \times \, \left( \exp \left\{ \alpha \int _0^{T} \lambda ( (N-1)T+t) {{\,\mathrm{d\!}\,}}t \right\} -1 \right) \nonumber \\&= C_2 N \frac{1}{\alpha } \left( \exp \left\{ \alpha \int _0^{T} \lambda ( NT+t) {{\,\mathrm{d\!}\,}}t \right\} - \exp \left\{ \alpha \int _0^{T} \lambda ((N-1)T+t) {{\,\mathrm{d\!}\,}}t \right\} \right) \nonumber \\&\quad +\, C_2 \left[ \sum _{i=1}^{N+1} \lambda _i + NT \right] \times \left( \exp \left\{ \alpha \int _0^{T} \lambda (NT+t) {{\,\mathrm{d\!}\,}}t \right\} -1 \right) \nonumber \\&\quad \times \Big ( \lambda (({N+1})T) - \lambda (NT) + \int _0^{T} N \lambda '(NT + t) {{\,\mathrm{d\!}\,}}t \nonumber \\&\quad -\, \int _0^{T} (N-1) \lambda '((N-1)T + t) {{\,\mathrm{d\!}\,}}t \Big ), \end{aligned}$$

(9)

since $\lambda (t)$ is increasing with t, then

$$\begin{aligned} \lambda ((N+1)T)> & {} \lambda (NT),\\ \exp \left\{ \alpha \int _0^{T} \lambda (NT+t) {{\,\mathrm{d\!}\,}}t \right\}\ge & {} \exp \left\{ \alpha \int _0^{T} \lambda ((N-1)T+t) {{\,\mathrm{d\!}\,}}t \right\} . \end{aligned}$$

Meanwhile $\lambda '(t)>0$, which implies

$$\begin{aligned} \int _{0}^T N \lambda '( NT+t) {{\,\mathrm{d\!}\,}}t < \int _{0}^T (N+1) \lambda '(NT+t) {{\,\mathrm{d\!}\,}}t. \end{aligned}$$

Therefore $f'(N)>0$, i.e., the function of f(N) is increasing with N. $f(N)>0$ because $\exp \left\{ \alpha \int _0^{T} \lambda ((i-1)T + t) {{\,\mathrm{d\!}\,}}t \right\} -1 >0, i=1,2, \ldots N$.

Thus, $\varPsi _2(N+1)-\varPsi _2(N)>0$. i.e., the $\varPsi _2 (N)$ is increasing with N for any fixed $T>0$. According to the above (i) and (ii), the function $\varPsi (N)$ is increasing with N. $\square$

Lemma 2

: Assume the failure rate function $\lambda (t)$ is strictly increasing, then $\varPsi (\infty )=\lim \limits _{N \rightarrow +\infty } \varPsi (N)=\infty$.

Proof

(i) Since $\lim \limits _{N \rightarrow +\infty } \lambda _{N}=0$, $\lim \limits _{N \rightarrow +\infty } (N-1) \lambda _{N+1}=\frac{N-1}{b^N}\lambda =0$,

$\lim \limits _{N \rightarrow +\infty } \sum \limits _{i=1}^N \lambda _i=\frac{b \lambda }{b-1}$,

hence

$$\begin{aligned} \lim \limits _{N \rightarrow +\infty } \varPsi _1(N)&= \lim _{N \rightarrow + \infty } \left\{ C_1 T \left[ \sum _{i=1}^{N} \lambda _i -(N-1) \lambda _{N+1} \right] - C_0 (\lambda _{N+1} + T) \right\} \nonumber \\&= \lim _{N \rightarrow +\infty } \left\{ C_1 T \sum _{i=1}^{N} \lambda _i - C_0 T \right\} \nonumber \\&= C_1 T \frac{b \lambda }{b-1} - C_0 T. \end{aligned}$$

(10)

(ii) $\varPsi _2(N)$ can be also expressed as

$$\begin{aligned} \varPsi _2(N)=\varPhi _1(N)+ \varPhi _2(N), \end{aligned}$$

(11)

where

$$\begin{aligned} \varPhi _1(N)&= C_2 T \Bigg \{ (N-1)\sum _{i=1}^N \frac{1}{\alpha } \left( \exp \left\{ \alpha \int _0^{T} \lambda ((i-1)T + t) {{\,\mathrm{d\!}\,}}t \right\} -1 \right) \nonumber \\&\quad -\, N \sum _{i=1}^{N-1} \frac{1}{\alpha } \left( \exp \left\{ \alpha \int _0^{T} \lambda ((i-1)T+t) {{\,\mathrm{d\!}\,}}t \right\} -1 \right) \Bigg \}, \end{aligned}$$

(12)

and

$$\begin{aligned} \varPhi _2(N)&= C_2 \Bigg \{ \sum _{i=1}^N \frac{1}{\alpha } \left( \exp \left\{ \alpha \int _0^{T} \lambda ((i-1)T+t) {{\,\mathrm{d\!}\,}}t \right\} -1 \right) \sum _{i=1}^{N} \lambda _i \\&\quad -\, \sum _{i=1}^{N-1} \frac{1}{\alpha } \left( \exp \left\{ \alpha \int _0^{T} \lambda ((i-1)T+t) {{\,\mathrm{d\!}\,}}t \right\} -1 \right) \sum _{i=1}^{N+1} \lambda _i \Bigg \}. \end{aligned}$$

(13)

$$\begin{aligned} \varPhi _1(N)&= C_2 T \Bigg \{ (N-1)\sum _{i=1}^N \frac{1}{\alpha } \left( \exp \left\{ \alpha \int _0^{T} \lambda ((i-1)T+t) {{\,\mathrm{d\!}\,}}t \right\} -1 \right) \nonumber \\&\quad -\, N \sum _{i=1}^{N-1} \frac{1}{\alpha } \left( \exp \left\{ \alpha \int _0^{T} \lambda ((i-1)T+t) {{\,\mathrm{d\!}\,}}t \right\} -1 \right) \Bigg \}\nonumber \\&= C_2 T \Bigg \{ N \sum _{i=1}^N \frac{1}{\alpha } \left( \exp \left\{ \alpha \int _0^{T} \lambda ((i-1)T+t) {{\,\mathrm{d\!}\,}}t \right\} -1 \right) \nonumber \\&\quad -\, N \sum _{i=1}^{N-1} \frac{1}{\alpha } \left( \exp \left\{ \alpha \int _0^{T} \lambda ((i-1)T+t) {{\,\mathrm{d\!}\,}}t \right\} -1 \right) \Bigg \} \nonumber \\&\quad -\, \sum _{i=1}^N \frac{1}{\alpha } \left( \exp \left\{ \alpha \int _0^{T} \lambda ((i-1)T+t) {{\,\mathrm{d\!}\,}}t \right\} -1 \right) \nonumber \\&= C_2 T \Bigg [ \frac{1}{\alpha} \left( \exp \left\{ \alpha \int _0^{T} \lambda ((N-1)T+t) {{\,\mathrm{d\!}\,}}t \right\} -1 \right) \nonumber \\&\quad -\, \sum _{i=1}^N \frac{1}{\alpha } \left( \exp \left\{ \alpha \int _0^{T} \lambda ((i-1)T+t) {{\,\mathrm{d\!}\,}}t \right\} -1 \right) \Bigg ] \ge 0. \end{aligned}$$

(14)

$$\begin{aligned} \varPhi _2(N)&= C_2 \Bigg \{ \sum _{i=1}^N \frac{1}{\alpha } \left( \exp \left\{ \alpha \int _0^{T} \lambda ((i-1)T+t) {{\,\mathrm{d\!}\,}}t \right\} -1 \right) \sum _{i=1}^{N} \lambda _i \nonumber \\&\quad -\, \sum _{i=1}^{N-1} \frac{1}{\alpha } \left( \exp \left\{ \alpha \int _0^{T} \lambda ((i-1)T+t) {{\,\mathrm{d\!}\,}}t \right\} -1 \right) \sum _{i=1}^{N+1} \lambda _i \Bigg \} \nonumber \\ \ge&\frac{C_2}{\alpha }\Big ( \exp \left\{ \alpha \int _0^{T} \lambda ((N-1)T+t) {{\,\mathrm{d\!}\,}}t \right\} -1 \Big ) \sum _{i=1}^{N} \lambda _i\nonumber \\&\quad -\, \frac{C_2}{\alpha } (N-1) \left( \exp \left\{ \alpha \int _0^{T} \lambda ((N-1)T+t) {{\,\mathrm{d\!}\,}}t \right\} -1 \right) \lambda _{N+1} \nonumber \\&= \frac{C_2}{\alpha } \left( \exp \left\{ \alpha \int _0^{T} \lambda ((N-1)T+t) {{\,\mathrm{d\!}\,}}t \right\} -1 \right) \left[ \sum _{i=1}^{N+1} \lambda _i -(N-1) \lambda _{N+1} \right] . \end{aligned}$$

(15)

Since $\lambda (t)$ is increasing up to $\infty$, we have

$$\begin{aligned}&\lim _{N \rightarrow +\infty } \left( \exp \left\{ \alpha \int _0^{T} \lambda ((N-1)T+t) {{\,\mathrm{d\!}\,}}t \right\} -1 \right) = \infty , \end{aligned}$$

(16)

$$\begin{aligned}&\lim _{N \rightarrow +\infty } \left[ \sum _{i=1}^{N+1} \lambda _i -(N-1) \lambda _{N+1} \right] = \frac{b \lambda }{b-1}, \end{aligned}$$

(17)

hence

$$\begin{aligned} \lim _{N \rightarrow +\infty } \varPhi _2(N)= \infty , \end{aligned}$$

(18)

and

$$\begin{aligned} \lim _{N \rightarrow +\infty } \varPsi _2(N)= \infty , \end{aligned}$$

(19)

according to the Eqs. (11)–(19)

$$\begin{aligned} \lim _{N \rightarrow +\infty } \varPsi (N)= \infty . \end{aligned}$$

(20)

$\square$

When $N=1$, $\varPsi (1)= C_1 T \lambda - C_0 \left( \frac{\lambda }{b} + T \right) + C_2 \frac{\lambda }{\alpha} \left( \exp \left\{ \alpha \int _0^{T} \lambda (t) {{\,\mathrm{d\!}\,}}t \right\} -1 \right)$ and $\varPsi (1)>0$ $\Longleftrightarrow$ $C(2)>C(1)$, namely the long-run ACR function is minimized by $N=1$, therefore the optimal policy is $N^*=1$.

According to the above Lemmas 1 and 2, we obtain the following Theorem 1.

Theorem 1

Assume that r(t) is increasing. The following results hold.

• (i) If $C_1 T \lambda + C_2 \frac{\lambda }{\alpha} \left( \exp \left\{ \alpha \int _0^{T} \lambda (t) {{\,\mathrm{d\!}\,}}t \right\} -1 \right) > C_0 \left( \frac{\lambda }{b}+ T \right)$, the optimal $N^*=1$.

• (ii) If r(t) is increasing, and $r(\infty )=\infty$, $\varPsi (\infty )=\infty$, then there exists an unique optimal policy $N^*$ such that

  $$\begin{aligned} N^* = min \left\{ \; N \;| \; \varPsi (N) \ge 0 \right\} . \end{aligned}$$

  (21)

Table 1 The optimal replacement policy $N^*$ and corresponding $C(N^*)$ for different values of $C_0$, $C_1$ and $\alpha$ when $T=3$, $C_2=5$

4 Numerical examples

In this section, numerical examples for illustrating the effectiveness of our model and optimal replacement policy are provided.

• (1) Let the failure rate function of the component 2 as $\lambda (t)=0.01t^2$ with parameter $b=1.15$, $\lambda =50$, $T=3$. The condition of Theorem 1 is thus satisfied. The optimal replacement policy $N^*$ and $C(N^*)$ for different values of $C_0$, $C_1$ and $\alpha$ are shown in Table 1 when $C_2=5$, $T=3$. For example, when $C_1=50$, $C_2=5$, $C_0=4000$, $\alpha =0.5$, the optimal replacement policy $N^*=6$. It is easy to see that the optimal replacement policy $N^*$ is decreasing with the increasing of $\alpha$, however the optimal $C(N^*)$ is increasing with $\alpha$ increasing.

• (2) Let $b=1.15$, $\lambda =50$, $C_1=50$, $C_2=5$, $C_0=2000$, $\alpha =0.3$, $T=3$. The experimental results show that the optimal replacement policy $N^*=7$ and the corresponding $C(7)=12.19$. The curve of C(N) is plotted in Fig. 3 and the curve of $\varPsi (N)$ is plotted in Fig. 4. According to Fig. 4, the optimal $N^*$ is the minimal N satisfying $\varPsi (N)>0$.

• (3) Assume that $\lambda =50$, $C_1=50$, $C_2=5$, $C_0=2000$, $\alpha =0.3$, $T=3$. The long-run ACR function C(N) for different values of b is shown in Fig. 5. We can see that the long-run ACR function becomes bigger when b increases.

• (4) Furthermore, assume that $\lambda =50$, $C_1=50$, $C_2=5$, $C_0=2000$, $b=1.2$, $T=3$, the long-run ACR function C(N) for different values of $\alpha$ is plotted in Fig. 6. The long-run ACR function becomes bigger and bigger when $\alpha$ increases. The trend of growth is obvious especially when $\alpha =0.9$.

Fig. 3

The long-run ACR function C(N)

Fig. 4

The function $\varPsi (N)$ against N

Fig. 5

The long-run ACR function C(N) for different values of b

Fig. 6

The long-run ACR function C(N) for different values of $\alpha$

5 Conclusions and future work

In this paper, a repair model for a cold standby system based on two types of failure repairs is proposed. Therefore, it is general model and will have a great potential in application. The long-run ACR function of the system is derived. Moreover, the existence and uniqueness of the optimal replacement policy is proved. Numerical examples were conducted to illustrate the theoretical results. From our experience, we can believe that an optimal replacement policy will exist. Sensitivity analysis were performed to study the effect of parameters on the optimal replacement policy.

In the future, we will consider the time needed for repair and replacement in the system and study the optimal maintenance policies for repair systems with one working state and multiple failure state models. This is more realistic and challenging.