Inference for an Inverted Exponentiated Pareto Distribution Under Progressive Censoring

Abstract

In this paper, estimation of unknown parameters of an inverted exponentiated Pareto distribution is considered under progressive Type-II censoring. Maximum likelihood estimates are obtained from the expectation–maximization algorithm. We also compute the observed Fisher information matrix. In the sequel, asymptotic and bootstrap-p intervals are constructed. Bayes estimates are derived using the importance sampling procedure with respect to symmetric and asymmetric loss functions. Highest posterior density intervals of unknown parameters are constructed as well. The problem of one- and two-sample prediction is discussed in Bayesian framework. Optimal plans are obtained with respect to two information measure criteria. We assess the behavior of suggested estimation and prediction methods using a simulation study. A real dataset is also analyzed for illustration purposes. Finally, we present some concluding remarks.

1 Introduction

In many reliability and life-testing experiments, one of the primary objectives is to establish a framework for an empirical analysis of various physical phenomena. The framework is often formulated on the basis of observations with a view of deriving predictive inference in a coherent manner. Traditionally, several practical fields of study require adequate inferential analysis of various lifetime data. In such investigations, one of the important features is to identify the underlying distribution that can adequately be used to describe the phenomenon under consideration. In the literature, several distributions with flexible shape characteristics have been proposed and studied in details. One may refer to Johnson et al. [14] for a review of interesting applications of different distributions based on reliability data. Recently, Ghitany et al. [12] proposed and studied an inverse exponentiated class of distributions. The basic idea here stems from the exponentiated class of models with density function given by

$$\begin{aligned} f_Y\left( y\right) = \alpha \beta \, H'\left( y\right) \left( 1-e^{-\beta H\left( y\right) }\right) ^{\alpha -1}\, e^{-\beta H\left( y\right) },\quad y>0,\, \alpha ,\, \beta >0, \end{aligned}$$

(1)

where $H(\cdot )$ is an increasing function satisfying $H(0)=0$ and $H(\infty )=\infty$. Also $\alpha$ and $\beta$ denote model parameters. This class of distributions includes some known models like exponentiated exponential distribution, exponentiated Rayleigh distribution and exponentiated Pareto distribution. Several researchers have analyzed these distributions under constrained and unconstrained observations. The corresponding class of inverse exponentiated distributions has the density function of the type

$$\begin{aligned} f_{X}\left( x\right) =\alpha \beta \frac{H'\left( \frac{1}{x}\right) }{x^{2}}e^{-\beta H\left( \frac{1}{x}\right) }\left( 1-e^{-\beta H\left( \frac{1}{x}\right) }\right) ^{\alpha -1},\quad x>0,\; \alpha ,\; \beta >0. \end{aligned}$$

(2)

This family of distributions includes some useful models from the literature. Among others, inverted exponentiated exponential distribution, inverted Burr X distribution and inverted exponentiated Pareto distribution belong to this class of distributions. Abouammoh and Alshingiti [1] considered estimation of unknown parameters and reliability function of a generalized inverted exponential distribution under the complete sampling situation. Authors used maximum likelihood and least square estimation methods to derive the desired estimates of unknown quantities. They analyzed different datasets and concluded that studied distribution can be used to model various reliability data. Recently, Rastogi and Tripathi [27] derived different point and interval estimates of unknown parameters, reliability and hazard functions of an inverted Burr X distribution from classical and Bayesian viewpoints using progressively censored data. Authors conducted a simulation study to compare proposed methods and also analyzed a real dataset for illustration purposes. The case $H\left( \frac{1}{x}\right) =\log (1 + \frac{1}{x})$ in (2) corresponds to the inverted exponentiated Pareto (IEP) distribution. The corresponding probability density and cumulative distribution functions are given by, respectively,

$$\begin{aligned} f_{X}\left( x\right)= & {} \alpha \, \beta \,x^{\beta -1} \left( 1+x\right) ^{-\left( \beta + 1\right) }\left[ 1-\left( \frac{1+x}{x}\right) ^{-\beta }\right] ^{\alpha -1},\quad x>0, \end{aligned}$$

(3)

$$\begin{aligned} F_{X}\left( x\right)= & {} 1-\left[ 1-\left( \frac{1+x}{x}\right) ^{-\beta }\right] ^{\alpha },\quad x>0, \end{aligned}$$

(4)

where $\alpha >0$ and $\beta >0$ denote unknown parameters. The reliability function is given by

$$\begin{aligned} R\left( t\right) =\left[ 1-\left( \frac{1+t}{t}\right) ^{-\beta }\right] ^{\alpha },\quad t>0, \end{aligned}$$

and the hazard function is of the form

$$\begin{aligned} h\left( t\right) =\alpha \, \beta \,t^{\beta -1} \left( 1+t\right) ^{-\left( \beta +1\right) }\left[ 1-\left( \frac{1+t}{t}\right) ^{-\beta }\right] ^{-1},\quad t>0. \end{aligned}$$

Fig. 1

Hazard function for different values of $\alpha$ and $\beta$

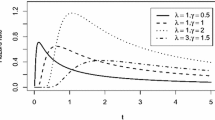
In Fig. 1, we have displayed hazard function of the IEP distribution for some arbitrarily selected parameter values. Visual inspection suggests that hazard function decreases rapidly with time when both the shape parameters take values less than one. It is also seen that the behavior can be non-monotone in nature. This suggests that the IEP distribution may adequately fit datasets which indicate decreasing or non-monotone hazard behavior. Thus, potential applications of an IEP distribution include several fields of studies like mortality data analysis, working conditions of mechanical or electrical components, degradation experiments, fatigue failure. Thus, this distribution can have wide applications in reliability and lifetime studies, similar to some other common models like inverted exponential Rayleigh, exponentiated moment exponential, generalized exponential, (see [24]). Not much work has been done on the family of distributions proposed by Ghitany et al. [12]. In fact, authors derived maximum likelihood estimates of unknown model parameters under progressive censoring and analyzed a real dataset for illustration purposes. For the sake of completeness, we now briefly describe the progressive Type-II censoring. Suppose that a total of n test items is subjected to a life test and a progressively censored sample of size $m\, (\le n)$ is to be observed. This happens in m stages of the experiment using a prefixed censoring scheme $\left( r_1, \ldots , r_m\right)$. At the time of the first failure $X_{1}$, the $r_{1}$ number of live units is removed randomly from the experiment. Similarly, at second failure $X_{2}$, the $r_{2}$ number of live units is removed from the test. When mth failure occurs, the test stops and the remaining surviving units $r_{m}= n-m-r_{1}-r_{2}-\cdots -r_{m-1}$ are removed from the test. The complete sampling corresponds to the case $r_{1}=r_{2}=\ldots =r_{m-1}=r_{m}=0$. We refer to Balakrishnan and Aggarwala [3] and Balakrishnan and Cramer [6] for a detailed review of work done on progressive censoring. The literature on this censoring methodology is quite broad, and one may further refer to Huang and Wu [13], Singh et al. [29], Dey et al. [10], Rastogi et al. [26], Rastogi and Tripathi [27], Maurya et al. [20] and Asgharzadeh [2] for some interesting applications of this censoring in reliability and lifetime analysis.

In this work, we study an inverted exponentiated Pareto distribution under progressive Type-II censoring. This distribution can be used to analyze lifetime data arising from various life-testing experiments such as clinical trials, industrial experiments and mortality analysis. Among others, one may refer to Ghitany et al. [12] for some useful applications of the IEP distribution in reliability experiments. Motivation of this paper is threefold. We first obtain point and interval estimates of unknown parameters of the IEP distribution using classical and Bayesian approaches when it is known that samples are progressively Type-II censored. In particular, we obtain maximum likelihood estimators (MLEs) of parameters and then derive Fisher information matrix of these estimates. In the sequel, asymptotic and bootstrap intervals are constructed. For comparison purposes, we also compute Bayes estimates of parameters against symmetric and asymmetric loss functions assuming different prior distributions. The highest posterior density intervals of unknown parameters are obtained from the importance sampling procedure. The second aim of this paper is to obtain prediction estimates and prediction intervals of censored observation under the given censoring scheme. The problem of predicting censored observations arises quite naturally in many industrial and engineering applications. Finally, we establish optimal censoring plans with respect to different performance measure criteria. We have provided algorithm required for numerical computation of these optimal plans.

In Sect. 2, we discuss maximum likelihood estimation of unknown parameters and also compute Fisher information matrix. Asymptotic and bootstrap intervals are constructed as well. In Sect. 3, we derive Bayes estimates of parameters with respect to different loss functions and also obtain highest posterior density intervals. Prediction of future observations is studied in Sect. 4 under one- and two-sample schemes. We establish optimal censoring schemes using two different criteria in Sect. 5. We conduct a simulation study and analyze a real dataset in Sect. 6. Finally, a conclusion is given in Sect. 7.

2 Maximum Likelihood Estimation

In this section, we derive maximum likelihood estimators of unknown parameters $\alpha$ and $\beta$ of the IEP distribution as defined in (3). We derive these estimates based on a progressive Type-II censored sample $X =\left( X_{1:m:n}, \ldots , X_{m:m:n}\right)$ obtained under a prescribed censoring scheme $r=\left( r_{1}, \ldots , r_{m}\right)$. The likelihood function of $\alpha$ and $\beta$ is given by (see [3])

$$\begin{aligned} L\left( \alpha , \beta \right) \propto \alpha ^{m}\beta ^{m}\prod _{i=1}^m x_{i:m:n}^{\beta -1}\left( 1+x_{i:m:n}\right) ^{-\left( \beta +1\right) }\left[ 1-\left( \psi (x_{i:m:n})\right) ^{-\beta }\right] ^{\alpha (r_{i}+1)-1} \end{aligned}$$

(5)

where $\psi \left( x\right) = \left( \frac{1+x}{x}\right)$. The corresponding log-likelihood function is of the following form

$$\begin{aligned} \log L\left( \alpha , \beta \right)\propto & {}\; m\log \alpha +m\log \beta +\left( \beta -1\right) \sum _{i=1}^{m}\log x_{i:m:n}-\left( \beta +1\right) \sum _{i=1}^{m}\log \left( 1+x_{i:m:n}\right) \\&+ \sum _{i=1}^{m}\left( \alpha \left( r_{i}+1\right) -1\right) \log \left[ 1-\left( \psi \left( x_{i:m:n}\right) \right) ^{-\beta }\right] . \end{aligned}$$

(6)

The respective maximum likelihood estimates $\hat{\alpha }$ and $\hat{\beta }$ of parameters $\alpha$ and $\beta$ can be obtained by solving following likelihood equations:

$$\begin{aligned} \frac{\partial \log L}{\partial \alpha }=\frac{m}{\alpha }+\sum _{i=1}^m (r_{i}+1)\log \left[ 1-\left( \psi (x_{i:m:n})\right) ^{-\beta }\right] = 0, \end{aligned}$$

(7)

and

$$ \frac{\partial \log L}{\partial \beta }= \frac{m}{\beta }- \sum _{i=1}^{m}\log \left( \psi (x_{i:m:n})\right) +\sum _{i=1}^{m}(\alpha (r_{i}+1)-1)\frac{\left( \psi (x_{i:m:n})\right) ^{-\beta } \log \left( \psi (x_{i:m:n})\right) }{\left[ 1-\left( \psi (x_{i:m:n})\right) ^{-\beta }\right] }=0. $$

(8)

From (7) and (8), we obtain

$$\begin{aligned} \hat{\alpha }(\beta )=-\frac{m}{\sum _{i=1}^{m}(r_i+1)\log \left[ 1-\left( \psi \left( x_{i:m:n}\right) \right) ^{-\beta }\right] }, \end{aligned}$$

and $\hat{\beta }$ can be obtained by solving nonlinear equation $G(\beta )=\beta$, where

$$\begin{aligned} G(\beta )= & {} \bigg [\frac{1}{m} \sum _{i=1}^{m} \log \left( \psi \left( x_{i:m:n}\right) \right) + \frac{\sum \nolimits _{i=1}^{m}(r_i+1)\frac{\left( \psi \left( x_{i:m:n}\right) \right) ^{-\beta } \log \left( \psi \left( x_{i:m:n}\right) \right) }{\left[ 1-\left( \psi \left( x_{i:m:n}\right) \right) ^{-\beta } \right] } }{\sum _{i=1}^{m}(r_i+1) \log \left[ 1-\left( \psi \left( x_{i:m:n}\right) \right) ^{-\beta } \right] }\\&+\frac{1}{m}\sum _{i=1}^{m}\frac{\left( \psi \left( x_{i:m:n}\right) \right) ^{-\beta } \log \left( \psi \left( x_{i:m:n}\right) \right) }{\left[ 1-\left( \psi \left( x_{i:m:n}\right) \right) ^{-\beta } \right] }\bigg ]^{-1}. \end{aligned}$$

Since the equation $G(\beta )=\beta$ cannot be solved analytically, some numerical technique such as Newton–Raphson method can be employed to obtain the MLE $\hat{\beta }$ of $\beta$. Subsequently, the corresponding estimate of $\alpha$ can be computed. In the next section, we suggest to use the expectation–maximization (EM) algorithm for computing MLEs of unknown parameters.

2.1 EM Algorithm

The expectation–maximization algorithm is a powerful numerical tool for deriving maximum likelihood estimates of parameters in situations where data are censored in nature. This method was originally discussed by Dempster et al. [9] in the literature. The method as such is very general and commonly used in various estimation problems. At each iteration of this algorithm, we need to implement two steps, namely the expectation-step and the maximization-step. The maximization-step maximizes the likelihood function under consideration which is updated by the expectation-step during iteration. In sequel and for further consideration, we assume that $X = \left( X_{1}, \ldots , X_{m}\right)$ and $Z = \left( Z_1, \ldots , Z_{m}\right)$ denote observed and censored data, respectively, where $Z_i$ represents a $1\times r_i$ vector with $Z_i = \left( Z_{i1}, \ldots , Z_{ir_{i}}\right) ,\, i=1, 2, \ldots , m$. The complete dataset is now given as $W = (X, Z)$. The log-likelihood function of this complete data is then obtained as

$$\begin{aligned} \log L_c\left( \alpha , \beta \right)& {}= n\log \alpha +n\log \beta +\left( \beta -1\right) \sum _{i=1}^{m}\log x_{i:m:n}-\left( \beta +1\right) \sum _{i=1}^{m}\log \left( 1+x_{i:m:n}\right) \\&+\left( \alpha -1\right) \sum _{i=1}^{m}\log \left[ 1-\left( \psi \left( x_{i:m:n}\right) \right) ^{-\beta }\right] +\left( \beta -1\right) \sum _{i=1}^{m}\sum _{k=1}^{r_{i}}\log Z_{ik} \\&-\left( \beta +1\right) \sum _{i=1}^{m}\sum _{k=1}^{r_{i}}\log \left( 1+ Z_{ik}\right) +\left( \alpha -1\right) \sum _{i=1}^{m}\sum _{k=1}^{r_{i}}\log \left[ 1-\left( \psi (Z_{ik})\right) ^{-\beta }\right] . \end{aligned}$$

(9)

In E-step, we take the expectation of this function with respect to the distribution of $Z_i$ conditional on $X_i = x_{i}$ which turns out to be

$$\begin{aligned} L_s\left( \alpha , \beta \right)& {}= n\log \alpha +n\log \beta +\left( \beta -1\right) \sum _{i=1}^{m}\log x_{i:m:n}-\left( \beta +1\right) \sum _{i=1}^{m}\log \left( 1+x_{i:m:n}\right) \\&\quad +\left( \alpha -1\right) \sum _{i=1}^{m}\log \left[ 1-\left( \psi (x_{i:m:n})\right) ^{-\beta }\right] +\left( \beta -1\right) \sum _{i=1}^{m}\sum _{k=1}^{r_{i}}E\left( \log Z_{ik}|Z_{ik}>x_{i}\right) \\&\quad -\left( \beta +1\right) \sum _{i=1}^{m}\sum _{k=1}^{r_{i}}E\left( \log (1+ Z_{ik}) \mid Z_{ik}>x_{i}\right) \\&\quad +(\alpha -1)\sum _{i=1}^{m}\sum _{k=1}^{r_{i}}E\left( \log \left[ 1-\left( \psi \left( Z_{ik}\right) \right) ^{-\beta }\right] \mid Z_{ik}>x_{i}\right) . \end{aligned}$$

(10)

We have computed required expectations of Eq. (10) in Appendix 1. In M-step, the maximization of (10) is performed with respect to $\alpha$ and $\beta$. Suppose $(\alpha ^{(k)},\, \beta ^{(k)})$ denotes the base estimate of $(\alpha , \beta )$. Then, the corresponding updated estimate $(\alpha ^{(k+1)},\, \beta ^{(k+1)})$ is computed by maximizing the equation

$$\begin{aligned} g(\alpha ,\, \beta )=\,& {} n\log \alpha + n\log \beta +(\beta -1)\sum _{i=1}^{m}\log x_{i:m:n}-(\beta +1)\sum _{i=1}^{m}\log (1+x_{i:m:n}) \\&+(\alpha -1)\sum _{i=1}^{m}\log \left[ 1-\left( \psi (x_{i:m:n})\right) ^{-\beta }\right] +(\beta -1)\sum _{j=1}^m r_{j}\,A(x_j, \alpha ^{(k)}, \beta ^{(k)}) \\&-(\beta +1)\sum _{j=1}^m r_{j}\,B(x_{j}, \alpha ^{(k)}, \beta ^{(k)})+(\alpha -1)\sum _{j=1}^m r_{j}\,C(x_{j}, \alpha ^{(k)}, \beta ^{(k)}), \end{aligned}$$

(11)

where $A(x_{j}, \alpha ^{(k)}, \beta ^{(k)})$, $B(x_{j}, \alpha ^{(k)}, \beta ^{(k)})$ and $C(x_{j}, \alpha ^{(k)}, \beta ^{(k)})$ are obtained in Appendix 1. We next apply the method as discussed in Pradhan and Kundu [24] to first obtain the estimate $\beta ^{(k+1)}$. We solve the following fixed point-type equation

$$\begin{aligned} h\left( \beta \right) =\beta \end{aligned}$$

(12)

where

$$\begin{aligned} h\left( \beta \right) = \left[ \frac{\frac{{\left( \hat{\alpha }\left( \beta \right) -1\right) }}{n}\sum _{i=1}^m \left( \psi \left( x_{i:m:n}\right) \right) ^{-\beta }\log \left( \psi (x_{i:m:n})\right) }{\left[ 1-\left( \psi (x_{i:m:n})\right) ^{-\beta } \right] }+\frac{1}{n} \sum _{i=1}^{m}\log \left( \psi (x_{i:m:n})\right) -\frac{\tilde{A}}{n} +\frac{\tilde{B}}{n} \right] ^{-1} , \end{aligned}$$

and

$$\begin{aligned} \hat{\alpha }(\beta ) = -\frac{n}{\sum _{i=1}^m \left[ 1-\left( \psi (x_{i:m:n})\right) ^{-\beta } \right] +\tilde{C}}, \end{aligned}$$

(13)

with $\tilde{A}=\sum _{j=1}^m r_{j}\,A\left( x_j, \alpha ^{\left( k\right) }, \beta ^{\left( k\right) }\right)$,    $\tilde{B}=\sum _{j=1}^m r_{j}\,B\left( x_j,\alpha ^{\left( k\right) },\beta ^{\left( k\right) }\right)$ and $\tilde{C}=\sum _{j=1}^m r_{j}\,C\left( x_j, \alpha ^{\left( k\right) }, \beta ^{\left( k\right) }\right)$. Note that using the updated estimate of $\beta$ we can derive the corresponding updated estimate $\alpha ^{\left( k+1\right) }$ of $\alpha$ as $\alpha ^{\left( k+1\right) } = \hat{\alpha } \left( \beta ^{\left( k+1\right) }\right)$. This iterative process is repeated till the desired convergence is achieved. In the next section, we obtain Fisher information matrix.

2.2 Fisher Information Matrix

In this section, we compute the asymptotic variance–covariance matrix of MLEs of unknown parameters which we further use to construct asymptotic confidence intervals. We make use of the Louis [19] method (see also [31]) to compute the observed Fisher information matrix. According to this method

$$\begin{aligned} \hbox {Observed}\; \hbox {information} = \hbox {Complete} \; \hbox {information} - \hbox {Missing} \; \hbox {information}. \end{aligned}$$

Now using notations $\theta = \left( \alpha , \beta \right)$, X = observed data, W = complete data, $I{_{W}\left( \theta \right) }$ = complete information, $I{_{X}\left( \theta \right) }$ = observed information and $I{_{W\mid X}(\theta )}$ = missing information, we find that we have

$$\begin{aligned} I_{X}\left( \theta \right) = I_{W}\left( \theta \right) - I_{W\mid X}\left( \theta \right) . \end{aligned}$$

(14)

The complete information is now given by

$$\begin{aligned} I_{W}\left( \theta \right) = - E\Big [\frac{\partial ^2L_{c}\left( W; \theta \right) }{\partial \theta ^2}\Big ]. \end{aligned}$$

(15)

For the missing information, note that the Fisher information in a single observation censored at jth failure time $x_{j}$ is given by

$$\begin{aligned} I^{\left( j\right) }_{W\mid X}\left( \theta \right) =E_{Z_{j}\mid X_{j}}\Big [\frac{\partial ^2\log {f_{Z_{j}}(z_{j}\mid X_{j}, \theta )}}{\partial \theta ^2}\Big ], \end{aligned}$$

and so the total missing information turns out to be

$$\begin{aligned} I{_{W\mid X}\left( \theta \right) }=\sum _{j=1}^{m} r_{j}I^{j}_{W\mid X}{\left( \theta \right) }. \end{aligned}$$

(16)

We have computed the element of both the matrices $I_{W}\left( \theta \right)$ and $I{_{W\mid X}\left( \theta \right) }$ in Appendix 2. Accordingly, the Fisher information matrix can be computed from Eq. (14). The asymptotic variance–covariance matrix of $\hat{\alpha }$ and $\hat{\beta }$ is then obtained as $\left[ I{_{X}\left( \theta \right) }\right] ^{-1}$. Next proceeding in a manner similar to Kohansal [16], we are able to observe that asymptotic distribution of $(\hat{\alpha }, \hat{\beta })$ bivariate normal, that is, $\left[ \left( \hat{\alpha }-\alpha \right) , ( \hat{\beta }- \beta )\right] ^{T}\xrightarrow {D}N\left( 0, I^{-1}\left( \alpha , \beta \right) \right)$ where $I^{-1}(\alpha , \beta )$ denotes the variance–covariance matrix. The symmetric $100(1-\xi )\%$ asymptotic confidence interval of the parameters $\alpha$ and $\beta$ is now obtained as $\hat{\theta }\pm z_{\frac{\xi }{2}}\sqrt{Var(\hat{\theta } )}$ where $z_{\frac{\xi }{2}}$ denotes the upper $\frac{\xi }{2}$th percentile of the standard normal distribution.

In the next section, we obtain Bayes estimates of unknown parameters.

3 Bayes Estimation

In this section, we derive Bayes estimators of unknown parameters $\alpha$ and $\beta$ of the IEP distribution against different symmetric and asymmetric loss functions. In general, squared error loss function is taken into consideration to compute Bayes estimates of unknown parameters. In this case, overestimation and underestimation are equally penalized. However, in reliability and life-testing experiments overestimation is often considered more serious than underestimation. In this regard, different asymmetric loss functions such as linex and entropy are introduced in the literature. We compute Bayes estimates of unknown parameters of the IEP distribution using squared error, linex and entropy loss functions. The squared error loss is defined as

$$\begin{aligned} L_s\left( \mu , \hat{\mu }\right) =(\hat{\mu }-\mu )^2, \end{aligned}$$

where $\hat{\mu }$ denotes an estimate of the unknown parameter $\mu$. The corresponding Bayes estimator $\hat{\mu }_s$ of $\mu$ is then obtained as the posterior mean of $\mu$. The linex loss function is given by

$$\begin{aligned} L_l \left( \mu , \hat{\mu } \right) = e^{h\left( \hat{\mu } - \mu \right) }-h\left( \hat{\mu }-\mu \right) -1,\, h\ne 0, \end{aligned}$$

where h is the loss parameter. Following Zellner [33], we observe that underestimation is more serious for the case h is negative and overestimation is more serious when h is positive. In this case, the Bayes estimator of $\mu$ is obtained as $\hat{\mu }_L = -\frac{1}{h}\log \left( E_\mu \left( e^{-h \mu } \mid X\right) \right)$. Finally, we define the entropy loss function as

$$ L_e\left( \mu , \hat{\mu }\right) = \left( \frac{\hat{\mu }}{\mu }\right) ^{\omega } - \omega \log \left( \frac{\hat{\mu }}{\mu }\right) - 1, \quad \omega \ne 0. $$

In this case, Bayes estimator of $\mu$ is obtained as $\hat{\mu }_E = E_\mu \left( \mu ^{-\omega }\mid X\right) ^{\frac{1}{\omega }}$. Let $X =\left( X_{1:m:n}, \ldots , X_{m:m:n}\right)$ denote a progressive Type-II censored sample taken from the distribution as defined in (3) using the censoring scheme $\left( r_1, \ldots , r_m\right)$. It is relatively difficult to construct a bivariate prior distribution for $(\alpha , \beta )$ when both the parameters of IEP distribution are unknown. So, we have assumed that $\alpha$ and $\beta$ are a priori distributed as independent gamma $G\left( a, b\right)$ and $G\left( c, d\right)$ distributions. Such kind of prior distribution is quite flexible in nature and includes noninformative case as well. One may refer to Sinha [28] and Kundu and Pradhan [18] for further details in this regard. The joint prior distribution is given by

$$ \pi \left( \alpha , \beta \right) \propto \alpha ^{a-1} e^{-b\alpha } \beta ^{c-1} e^{-d\beta } \quad\,\alpha>0,\quad\beta>0,\; a>0,\; b>0,\; c>0,\; d>0, $$

(17)

and the corresponding posterior distribution is obtained as

$$\begin{aligned} \pi \left( \alpha , \beta \mid x\right) \propto \frac{\alpha ^{m+a-1} \beta ^{m+c-1}}{k} e^{-b\alpha } e^{-d\beta } \prod _{i=1}^{m} x_{i:m:n}^{\beta -1}\left( 1+x_{i:m:n}\right) ^{-\left( \beta +1\right) }\left[ 1-\left( \psi (x_{i:m:n})\right) ^{-\beta }\right] ^{\alpha \left( r_{i}+1\right) -1}. \end{aligned}$$

(18)

Bayes estimators of both the unknown parameters can be obtained using this posterior distribution. We note that these estimators appear as the ratio of two integrals which are difficult to simplify analytically. To overcome this situation, we propose to use the importance sampling technique which is discussed next.

3.1 Importance Sampling Method

In this section, we use the importance sampling technique to compute Bayes estimators of unknown parameters $\alpha$ and $\beta$ under different loss functions. The posterior distribution of $\alpha$ and $\beta$ given data is of the form

$$\begin{aligned}\pi \left( \alpha , \beta \mid X = x\right) & \propto G_{\alpha \mid \beta }\left( m+a,\,b-\sum _{i=1}^{m}(r_{i}+1)\log \left[ 1-\left( \psi (x_{i:m:n})\right) ^{-\beta } \right] \right) \\&\quad \times G_{\beta }\left( m+c,\,d+\sum _{i=1}^m\log \left( \psi (x_{i:m:n})\right) \right) K\left( \alpha , \beta \right) , \end{aligned}$$

where

$$\begin{aligned} K\left( \alpha , \beta \right) = \left( b-\sum _{i=1}^{m}\left( r_{i}+1\right) \log \left[ 1-\left( \psi \left( x_{i:m:n}\right) \right) ^{-\beta } \right] \right) ^{-\left( m+a\right) } e^{-\sum _{i=1}^{m}\log \left[ 1-\left( \psi (x_{i:m:n})\right) ^{-\beta } \right] }. \end{aligned}$$

The following steps are required for computation purposes.

Step 1::

Generate $\beta _1$ from $G_{\beta }\left( ., .\right)$,   $\alpha _1$ from $G_{\alpha \mid \beta }\left( ., .\right)$.

Step 2::

Repeat Step 1, M times to obtain $\left( \alpha _1, \beta _1\right) , \ldots , \left( \alpha _M, \beta _M\right)$.

Step 3::

Now, Bayes estimates of $u\left( \alpha , \beta \right)$ under $L_{s}, L_{l}$ and $L_{e}$ losses are given by, respectively,

$$\begin{aligned} \hat{u}_{BS}= & {} \frac{\sum \nolimits _{i=1}^M u\left( \alpha _i, \beta _i\right) \,K\left( \alpha _i, \beta _i\right) }{\sum _{i=1}^M K\left( \alpha _i, \beta _i\right) },\\ \hat{u}_{BL}= & {} -\frac{1}{h}\log \left( \frac{\sum \nolimits _{i=1}^M e^{-h u\left( \alpha _i, \beta _i\right) }\; K\left( \alpha _i, \beta _i\right) }{\sum _{i=1}^M K\left( \alpha _i, \beta _i\right) } \right) ,\,\, {\text {and}}\\ \hat{u}_{BE}= & {} \left( \frac{\sum \nolimits _{i=1}^M u(\alpha _i, \beta _i)^{- \omega }\,K(\alpha _i, \beta _i)}{\sum _{i=1}^M K(\alpha _i, \beta _i)}\right) ^{-\frac{1}{\omega }}. \end{aligned}$$

We further construct HPD intervals of unknown parameters using samples generated from the importance sampling procedure. We have applied the method of Chen and Shao [8] for this purpose. Performance of point and interval estimates proposed in this section is discussed via numerical comparisons.

4 Prediction of Future Observations

In this section, we derive prediction estimates of future observations and also construct corresponding prediction intervals. The problem of predicting future observations arises quite naturally in reliability and lifetime analysis and one may refer to Huang and Wu [13], Kayal et al. [15] for some recent applications. Here, we obtain Bayes predictors with respect to gamma prior distributions under one- and two-sample frameworks.

4.1 One-Sample Prediction

Suppose that n test units following an IEP distribution are subjected to a life test and a progressive censored sample $x=\left( x_{1:m:n}, \ldots , x_{m:m:n}\right)$ is observed under a prescribed censoring scheme $\left( r_1, \ldots , r_m\right)$. Recall that at jth failure $x_{j}$ the $r_{j}$ number of live test units is removed from the experiment. Now, let $y_{jk}$ denote lifetime of kth censored unit where $j = 1, \ldots , m$ and $k=1, \ldots , r_{j}$. The density of $y_{jk}$ conditional on observed data is given by (see [23])

$$\begin{aligned} f_{1}\left( {y_{jk} \mid x,\alpha , \beta }\right) =k{r_{j} \atopwithdelims ()k}\frac{\left( F\left( y_{jk}\right) -F({x_{j})}\right) ^{k-1}\left( 1-F(y_{jk})\right) ^{r_{j}-k}f(y_{jk})}{\left( 1-F(x_{j})\right) ^{r_{j}}},\,\,y_{jk} > x_j. \end{aligned}$$

(19)

Note that a priori predictive survival function is given by

$$\begin{aligned} R_{1}\left( t \mid x, \alpha , \beta \right)= & {} \frac{P(y_{jk}> t \mid x, \alpha , \beta )}{P(y_{jk} > x_{j} \mid x, \alpha , \beta )} = \frac{\int _{t}^{\infty }f_{1}(y_{jk} \mid x, \alpha , \beta ) {\hbox {d}} y_{jk}}{\int _{x_{j}}^{\infty }f_{1}(y_{jk} \mid x, \alpha , \beta ) {\hbox {d}} y_{jk}}, \end{aligned}$$

where  $\int _{t}^{\infty }f_{1}(y_{jk} \mid x, \alpha , \beta ) {\hbox {d}} y_{jk} = k {r_{j} \atopwithdelims ()k} \sum _{i=0}^{k-1} {k-1 \atopwithdelims ()i} (-1)^{k-1-i} (1-F(x_{j}))^{i-r_{j}} \frac{(1-F(t))^{r_{j}-i}}{r_{j}-i},$ and $\int _{x_{j}}^{\infty }f_{1}(y_{jk} \mid x, \alpha , \beta ) {\hbox {d}} y_{jk} = k {r_{j}\atopwithdelims ()k} \sum _{i=0}^{k-1} {k-1\atopwithdelims ()i} (-1)^{k-1-i} \frac{1}{r_{j}-i}.$

As a consequence, posterior predictive density and posterior predictive survival functions are obtained as

$$\begin{aligned} f_{1}^{*}(y_{jk}\mid x)= & {} \int _{0}^{\infty }\int _{0}^{\infty } f_{1}(y_{jk} \mid x, \alpha , \beta ) \pi (\alpha , \beta \mid x) {\hbox {d}}\alpha {\hbox {d}}\beta \\ R_{1}^{*}(t \mid x)= & {} \int _{0}^{\infty }\int _{0}^{\infty } R_{1}(t \mid x, \alpha , \beta ) \pi (\alpha , \beta \mid x) {\hbox {d}}\alpha {\hbox {d}}\beta . \end{aligned}$$

Thus, the Bayes predictor of the censored observation $y_{jk}$ can be computed as

$$\begin{aligned} {\hat{y}_{jk}}= & {} \int _{x_{j}}^{\infty } y_{jk}f_{1}^{*}(y_{jk}\mid x)\,{\hbox {d}} y_{jk} \\= & {} \int _{0}^{\infty }\int _{0}^{\infty } I_{1}(\alpha , \beta ) \pi (\alpha , \beta \mid x){\hbox {d}}\alpha {\hbox {d}}\beta , \end{aligned}$$

(20)

where  $I_{1}(\alpha , \beta )=\int _{x_{j}}^{\infty } y_{jk} f_{1}(y_{jk}\mid {x})\,{\hbox {d}} y_{jk}.$

We use importance samples $\left\{ (\alpha _{i}, \beta _{i}); i=1, \ldots , M \right\}$ to simplify the integral (20). The corresponding predictive estimate is given by

$$\begin{aligned} {\hat{y}_{jk}}=\frac{\sum \nolimits _{i=1}^{M}I_{1}(\alpha _{i}, \beta _{i})K(\alpha _{i}, \beta _{i})}{\sum _{i=1}^{M}K(\alpha _{i}, \beta _{i})}. \end{aligned}$$

(21)

The HPD prediction interval $(L_1, U_1)$ of censored observation $y_{jk}$ is obtained by solving the following equations simultaneously:

$$ \int _{L_1}^{U_1} f_{1}^{\star }(y_{jk}|x) {\hbox {d}}y_{jk}=(1-\xi ) \,\,{\text {and}}\quad f_{1}^{\star }(L_{1}|x)=f_{1}^{\star }(U_{1}|x). $$

(22)

Further, the corresponding $100(1-\xi )\%$ equal-tail prediction interval $(L_1, U_1)$ can be constructed by simultaneously solving the following nonlinear equations:

$$\begin{aligned} R_{1}^{*}(L_1 \mid x)= & {} \frac{\xi }{2} \text{ and } R_{1}^{*}(U_1 \mid x) = 1- \frac{\xi }{2}. \end{aligned}$$

(23)

Two-sample prediction is discussed next.

4.2 Two-Sample Prediction

In this section, we discuss two-sample prediction problem. We obtain prediction estimates and prediction intervals of future observable under progressive Type-II censoring. Let $x =\left( x_{1:m:n}, \ldots , x_{m:m:n}\right)$ denote a base sample obtained using the censoring scheme $\left( r_1, \ldots , r_m\right)$. Further, let $T_{1}<\cdots < T_{l}$ be the lifetimes of a future sample of size l which is taken from an IEP distribution and is independent of the base sample. We wish to predict the qth observation $(1\le q \le l)$ of future sample on the basis of observed progressive Type-II censored data (see [11]). The density function of a qth order statistic is given by

$$\begin{aligned} f_{2}(t_{q}\mid \alpha , \beta )=\frac{l!}{(q-1)!(l-q)!}\left[ F(t_{q}) \right] ^{q-1}\left[ 1-F(t_{q}) \right] ^{l-q} f(t_{q}\mid \alpha , \beta ),\,t_q > 0. \end{aligned}$$

(24)

As earlier, the two-sample posterior predictive density and the posterior predictive distribution function are, respectively, obtained as

$$\begin{aligned} f_{2}^{*}(t_{q}\mid x)= & {} \int _{0}^{\infty }\int _{0}^{\infty } f_{2}(t_{q} \mid x, \alpha , \beta ) \pi (\alpha , \beta \mid x) {\hbox {d}}\alpha {\hbox {d}}\beta ,\\ F_{2}^{*}(t \mid x)= & {} \int _{0}^{\infty }\int _{0}^{\infty } F_{2}(t \mid x, \alpha , \beta ) \pi (\alpha , \beta \mid x) {\hbox {d}}\alpha {\hbox {d}}\beta . \end{aligned}$$

The two-sample Bayes predictive estimate of the qth future observation is now given by

$$\begin{aligned} \hat{t_{q}}=\int _{0}^{\infty }\int _{0}^{\infty } I_{2}\left( \alpha , \beta \right) \pi \left( \alpha , \beta \mid x\right) {\hbox {d}}\alpha {\hbox {d}}\beta \end{aligned}$$

(25)

where  $I_{2}\left( \alpha , \beta \right) =\int _{0}^{\infty }t_{q}\, f\left( t_{q}\mid x\right) \,{\hbox {d}} t_{q}.$

Observe that (25) cannot be simplified as the corresponding posterior distribution is analytically intractable. So, we use importance samples $\left\{ (\alpha _{i}, \beta _{i});i=1, \ldots , M \right\}$ to simplify the corresponding posterior expectation. The prediction estimate of future observable $t_q$ is then obtained as

$$\begin{aligned} \hat{t_{q}}=\frac{\sum \nolimits _{i=1}^{M}I_{2}\left( \alpha _{i}, \beta _{i}\right) K\left( \alpha _{i}, \beta _{i}\right) }{\sum _{i=1}^{M}K\left( \alpha _{i}, \beta _{i}\right) }. \end{aligned}$$

(26)

The $100\left( 1-\xi \right) \%$ HPD predictive interval of qth future observation is given by $\left( L_2, U_2\right)$ where $L_2$ and $U_2$ satisfy the following equations:

$$\begin{aligned} \int _{L_2}^{U_2}f_{2}^{\star } \left( t_{q}\mid x\right) \,{\hbox {d}} t_{q}=\left( 1-\xi \right) \,\,{\text {and}}\,\, f_{2}^{\star }\left( L_2 \mid x\right) = f_{2}^{\star }\left( U_2\mid x\right) . \end{aligned}$$

(27)

Also, the $100\left( 1-\xi \right) \%$ equal-tail predictive interval $(L_2,\, U_2)$ can be obtained by solving the following equations:

$$\begin{aligned} F_{2}^{*}\left( L_2 \mid x\right)= & {} \frac{\xi }{2} \text{ and } F_{2}^{*}\left( U_2 \mid x\right) = 1- \frac{\xi }{2}. \end{aligned}$$

(28)

In the next section, optimal censoring is discussed.

5 Optimal Censoring

In previous sections, we discussed problems of estimation and prediction for the IEP distribution based on progressive Type-II censored samples obtained using prefixed censoring schemes. In many situations, it is of interest to establish optimal plans from a class of prescribed censoring schemes; that is, for a given parent sample of size n and a progressive Type-II censored sample of size m, an experimenter requires to select a censoring scheme $r_i,\, i=1, \ldots , m,$ which provides maximum information on unknown parameters of interest. The problem of establishing optimal plans has received some attention in the literature, among others, one may refer to Ng et al. [22], Kundu [17], Pradhan and Kundu [24] for some interesting results on this topic. Here, we make use of two criteria, namely Fisher information and entropy measure for establishing desired optimum plans.

5.1 Fisher Information Criterion

In this case, our objective is to minimize the trace of a variance–covariance matrix with respect to progressive Type-II censored data. The Fisher information matrix, for the vector parameter $\theta$, is given by

$$\begin{aligned} I(\theta )=-E\left[ \frac{\partial ^2{ \log L(\theta )} }{\partial \theta \, \partial \theta '} \right] . \end{aligned}$$

Equivalently, we have (see [7, 34])

$$\begin{aligned} I\left( \theta \right) =\int _{0}^{\infty }\left\langle \frac{\partial }{\partial \theta } \log h_{\theta }\left( x\right) \right\rangle \sum _{i=1}^{m} f_{i:m:n}\left( x, \theta \right) \, {\hbox {d}}x, \end{aligned}$$

(29)

where $h_{\theta }(x)$ denotes hazard function, $\frac{\partial }{\partial \theta } \log h_\theta (x)$ is the vector given as $\left( \frac{\partial }{\partial \theta _1}\log h_{\theta _{1}}(x), \ldots , \frac{\partial }{\partial \theta _p}\log h_{\theta _{p}}(x) \right)$ with $\theta =(\theta _1, \ldots , \theta _p)$ and $\left\langle b \right\rangle$ is defined as a matrix $b\, b'$, for $b\in {\mathbb {R}}^{p}$. Also $f_{i:m:n}(x, \theta )$ is the density function of $X_{i:m:n}$ where (see [4]))

$$\begin{aligned} f_{i:m:n}\left( x,\theta \right)& {}= \sigma _{i-1}\sum _{k=1}^{i}a_{k, i}\left( 1-F_{X}\left( x,\theta \right) \right) ^{\gamma _{k}-1}f_{X}\left( x,\theta \right) \\& {}= \sigma _{i-1}\sum _{k=1}^{i}a_{k, i}\left[ 1-\left( \psi \left( x\right) \right) ^{-\beta }\right] ^{\alpha \left( \gamma _{k}-1\right) } \alpha \beta x^{\beta -1} \left( 1+x\right) ^{-\left( \beta +1\right) }\left[ 1-\left( \psi \left( x\right) \right) ^{-\beta }\right] ^{\alpha -1}\\& {}= \sigma _{i-1}\sum _{k=1}^{i}a_{k, i}\left( \alpha \beta x^{\beta -1} (1+x)^{-(\beta +1)}\right) \left[ 1-\left( \psi (x)\right) ^{-\beta }\right] ^{(\alpha \gamma _{k}-1)}. \end{aligned}$$

We further note that $\gamma _{i}=m-i+1+\sum _{k=i}^{m} r_{k}$, $\sigma _{i-1}=\prod _{k=1}^{i} \gamma _{k},\,1\le i \le m$ and $a_{k, i}=\prod _{\begin{array}{c} j=1\\ j\ne k \end{array}}^{i} \frac{1}{\gamma _{j}-\gamma _{k}},\,1\le k\le i \le m$. Elements of the Fisher information matrix $I(\theta )$ are obtained in Appendix 3. Thus, the asymptotic variance–covariance matrix finally turns out to be $I^{-1}(\hat{\theta })$. We wish to minimize the trace of this variance–covariance matrix. The optimum solutions and corresponding optimum censoring schemes are presented in Table 5. We have used the partitions package in R software for determining optimal schemes. We first generated all feasible solutions, and then we made use of the complete search technique to obtain optimum scheme among all possible solutions.

The following steps are required to implement the complete search algorithm:

• Assign values of n and m.

• Compute $k ={{n-1} \atopwithdelims (){m-1}}$.

• Generate all possible combinations of the censoring scheme $\left\{ \left( r_1,\ldots , r_m\right) \mid \sum _{i=1}^{m} r_i = n-m\right\}$ using the partitions package in R statistical software.

• Compute trace of the variance–covariance matrix for all k using the corresponding censoring scheme as given in the previous step.

• The minimum trace of the variance–covariance matrix corresponds to the optimum censoring scheme.

5.2 Entropy Measure

Now, we establish optimal plans based on entropy measure. Shannon [30] introduced joint differential entropy as information measure. It measures the uncertainty present in a data. In this case, one of the primary objectives is to optimize uncertainty in the system and select the plan which provides reasonably efficient estimates of unknown parameters. One may also refer to Balakrishnan et al. [5] in this regard. The entropy function under progressive Type-II censoring is given by

$$\begin{aligned} H^{\mathrm{min}\mid \mathrm{max}}=-\log C +m-\int _{0}^{\infty }\sum _{i=1}^{m}f_{i:m:n}(x, \theta )\log h_{\theta }(x){\hbox {d}}x, \end{aligned}$$

(30)

where

$$\begin{aligned} C=n(n-r_{1}-1)(n-(r_{1}+r_{2})-2)\ldots \left( n-\sum _{i=1}^{m-1}r_{i}-(m-1)\right) . \end{aligned}$$

Here, we consider both maximum and minimum entropy plans. Note that maximum entropy criterion under progressive Type-II censoring measures the maximum uncertainty present in a data and such optimal plans carry important information about the model under consideration. Plans based on minimum entropy can also be used to derive better estimates for unknown quantities of interest. We have solved the corresponding optimization problem using the complete search technique. In Table 5, we have presented minimum and maximum entropy values along with optimum plans. We obtained desired results for the objective function defined in (30) using the previous algorithm.

Remark

We would like to mention that in this work we have computed the optimum censoring scheme from all possible choices $R = \left\{ (r_1, \ldots , r_m)\mid \sum _{i=1}^{m} r_i = n - m\right\}$ by solving integer programming problem. We have considered moderate choices of n, m and used a complete enumeration search technique to determine the optimum scheme. Pradhan and Kundu [24] suggested that for given n and m the number of sampling schemes is although finite but this number can be quite large as a total of $\left( {\begin{array}{c}n-1\\ m-1\end{array}}\right)$ possible censoring schemes is available. For example, if $n=20$ and $m=10$ then total number of possible sampling schemes is 92,378. So far one does not have any efficient algorithm to search the optimal schemes from all possible progressive censoring schemes. Because of computational limitations, it is practically infeasible to apply enumeration search technique for relatively large values of n and m. In such cases, one can use meta heuristic algorithm to find near-optimum solutions within a reasonable time period. Optimum censoring schemes can be established by prefixing n and m values as well. However, in practice n and m both may vary. Therefore, finding optimum schemes $(n, m,(r_1, \ldots , r_m))$ from the meta heuristic algorithm may turn out to be a useful approach.

6 Simulation Study and Data Analysis

In this section, we assess the behavior of proposed methods using a Monte Carlo simulation study. A real dataset is also analyzed for illustration purposes.

6.1 Simulation Study

We compare the performance of suggested methods of estimation and prediction based on a simulation study under the assumption that samples are progressive Type-II censored. The comparison between different estimates is made on the basis of bias and mean square error (MSE) values using 5000 replications. These estimates are computed for different combinations of sample size (n, m) and censoring schemes. The true values of parameters are arbitrarily taken as $\alpha =1.5$ and $\beta =1$. The maximum likelihood estimates of unknown parameters of the prescribed model are numerically computed using the expectation–maximization algorithm. We mention that all simulations are performed on the statistical software R and we have used nleqslv, rootSolve and partitions packages for different computation purposes. We compute Bayes estimates of unknown parameters against gamma prior distributions with respect to squared error, linex and entropy loss functions. We use importance sampling procedure for computing Bayes estimates and in process, the vector hyperparameter (a, b, c, d) is considered as (15, 10, 6, 6). Selection of hyperparameters against a prior distribution can sometimes be made on the basis a priori data. Let M number of such samples be available from the model under consideration with MLEs $(\hat{\alpha _{j}}, \hat{\beta _{j}})$ where $j=1, \ldots , M$. Then, hyperparameters can be estimated on equating mean and variance of these MLEs with the corresponding prior mean and prior variance. For example, consider a prior distribution $\pi (\delta ) \propto \delta ^{z_{1}-1}e^{-z_{2}\delta }$ where $z_1$ and $z_2$ denote hyperparameters. We can estimate these unknowns from equations

$$\begin{aligned} \frac{1}{M}\sum _{j=1}^{M}\hat{\delta }_{j} = \frac{z_{1}}{z_{2}}, \quad \text{ and }\quad \frac{1}{M-1}\sum _{j=1}^{M}\Big (\hat{\delta }_{j} - \frac{1}{M}\sum _{i=1}^{M}\hat{\delta }_{i}\Big )^{2} = \frac{z_{1}}{z^2_{2}}. \end{aligned}$$

We have estimated hyperparameters based on one thousand past data. In Table 1, we present MLEs of unknown parameters of $\alpha$ and $\beta$ along with MSE values for different sampling situations. Bayes estimates of $\alpha$ and $\beta$ are also given in this table. Note that $\tilde{\alpha }_{BS}$ and $\tilde{\beta }_{BS}$ represent respective Bayes estimates of parameters $\alpha$ and $\beta$ when the loss function is squared error. Similar notations are used for the other two loss functions. We mention that these estimates, under linex and entropy losses, are computed for different h and $\omega$ values like − 0.25, 0.5 and 1. For each scheme, the first two values denote estimate and corresponding MSE for the parameter $\alpha$. The last two values represent similar estimates for the parameter $\beta$. Tabulated estimates indicate that MLEs of both the unknown parameters compete quite good with corresponding Bayes estimates as far as bias and mean square errors are concerned. However, Bayes estimates seem to be more efficient than their counterpart MLEs. In particular, squared error Bayes estimates of $\alpha$ and $\beta$ perform better than respective MLEs. In case estimation is carried out under linex loss function, the choice − 0.25 of the corresponding loss parameter h produces better estimates for both the unknown parameters. Similar observations hold true for the entropy loss function. Proposed estimation methods tend to produce more efficient estimates with the increase in effective sample size. In Table 2, we present asymptotic confidence intervals (ACI), bootstrap intervals and HPD intervals of both the unknown parameters $\alpha$ and $\beta$ for different censoring schemes under 95% confidence level. In fact, we provide average interval length (AIL) and corresponding coverage probabilities (CPs) for each interval estimate. Bootstrap-p and asymptotic intervals compete quite good with each other. Overall, the highest posterior density intervals perform better than the other two intervals as far as average interval length is concerned. All the tabulated intervals provide good coverage probabilities, and in general, they remain quite close to the nominal level. In Table 3, we present one-sample prediction estimates along with equal-tail (EQT) and HPD prediction intervals of observations censored at different stages of the experiment. We have derived prediction estimates and corresponding intervals for the first four observations which are censored at different stages of the test. In general, equal-tail prediction intervals are wider compared to corresponding HPD intervals. This holds for all the presented censoring schemes. The corresponding two-sample predictive estimates and prediction intervals of the first four observable are presented in Table 4 where future sample size is 5. We observed a similar pattern in this case as well. Here also, we predict lifetimes upto the first four units. A similar conclusion can be drawn from these tables as well. Finally, optimum censoring plans and optimum values are given in Table 5 for different combinations of (n, m, r) under two different optimal criteria. From this table, we observe that trace of the variance–covariance matrix and the entropy decrease with an increase in values of n and m, as expected.

Table 1 Average and MSEs values of all estimates of $\alpha$ and $\beta$ for different choices of n, m

Table 2 Confidence intervals of $\alpha$ and $\beta$ for different choices of n, m

Table 3 Prediction estimates and prediction intervals in one-sample case

Table 4 Prediction estimates and prediction intervals in two-sample case

Table 5 Optimal censoring schemes

6.2 Real Data Analysis

In this section, we present analysis of a real dataset to illustrate prediction and estimation methods discussed in preceding sections. The dataset describes failure times of 84 aircraft windshield as discussed in Murthy et al. [21] (see also [25]). The failure times of these aircraft windshields are listed below as

$$\begin{aligned} \begin{array}{l} {\texttt {0.040}} \;\;{\texttt {0.301}} \;\;{\texttt {0.309}} \;\;{\texttt {0.557}} \;\;{\texttt {0.943}} \;\;{\texttt {1.070}} \;\;{\texttt {1.124}} \;\;{\texttt {1.248}} \;\;{\texttt {1.281}} \;\;{\texttt {1.281}}\\ {\texttt {1.303}} \;\;{\texttt {1.432}} \;\;{\texttt {1.480}} \;\;{\texttt {1.505}} \;\;{\texttt {1.506}} \;\;{\texttt {1.568}} \;\;{\texttt {1.615}} \;\;{\texttt {1.619}} \;\;{\texttt {1.652}} \;\;{\texttt {1.652}}\\ {\texttt {1.757}} \;\;{\texttt {1.866}} \;\;{\texttt {1.876}} \;\;{\texttt {1.899}} \;\;{\texttt {1.911}} \;\;{\texttt {1.912}} \;\;{\texttt {1.914}} \;\;{\texttt {1.981}} \;\;{\texttt {2.010}} \;\;{\texttt {2.038}}\\ {\texttt {2.085}} \;\;{\texttt {2.089}} \;\;{\texttt {2.097}} \;\;{\texttt {2.135}} \;\;{\texttt {2.154}} \;\;{\texttt {2.190}} \;\;{\texttt {2.194}} \;\;{\texttt {2.223}} \;\;{\texttt {2.224}} \;\;{\texttt {2.229}}\\ {\texttt {2.300}} \;\;{\texttt {2.324}} \;\;{\texttt {2.385}} \;\;{\texttt {2.481}} \;\;{\texttt {2.610}} \;\;{\texttt {2.625}} \;\;{\texttt {2.632}} \;\;{\texttt {2.646}} \;\;{\texttt {2.661}} \;\;{\texttt {2.688}}\\ {\texttt {2.823}} \;\;{\texttt {2.890}} \;\;{\texttt {2.902}} \;\;{\texttt {2.934}} \;\;{\texttt {2.962}} \;\;{\texttt {2.964}} \;\;{\texttt {3.000}} \;\;{\texttt {3.103}} \;\;{\texttt {3.114}} \;\;{\texttt {3.117}}\\ {\texttt {3.166}} \;\;{\texttt {3.344}} \;\;{\texttt {3.376}} \;\;{\texttt {3.443}} \;\;{\texttt {3.467}} \;\;{\texttt {3.478}} \;\;{\texttt {3.578}} \;\;{\texttt {3.595}} \;\;{\texttt {3.699}} \;\;{\texttt {3.779}}\\ {\texttt {3.924}} \;\;{\texttt {4.035}} \;\;{\texttt {4.121}} \;\;{\texttt {4.167}} \;\;{\texttt {4.240}} \;\;{\texttt {4.255}} \;\;{\texttt {4.278}} \;\;{\texttt {4.305}} \;\;{\texttt {4.376}} \;\;{\texttt {4.449}}\\ {\texttt {4.485}} \;\;{\texttt {4.570}} \;\;{\texttt {4.602}} \;\;{\texttt {4.663}} \end{array} \end{aligned}$$

and corresponding observed data for different censoring schemes are reported in Table 6.

Table 6 Progressively censored data

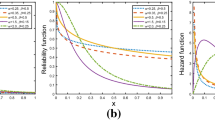
Before we make any inference on the basis of this dataset, we first verify whether an inverted exponentiated Pareto (IEP) distribution can be used to fit this dataset. For comparison purpose, we also fit generalized inverted exponentiated exponential (GIE) distribution and inverted exponentiated Rayleigh (IER) distributions. In Table 7, we present maximum likelihood estimates of all model parameters along with estimated values of negative log-likelihood criterion (NLC), Akaike’s information criterion (AIC), corrected Akaike’s information criterion (AICc), Bayesian information criterion (BIC). From this table, we observe that the inverted exponentiated Pareto distribution fits this dataset reasonably good compared to the other competing models. So, we derive point and interval estimates based on this dataset for different censoring schemes. In Table 8, we have presented maximum likelihood and Bayes estimates of unknown parameters. Bayes estimates are computed with respect to a noninformative prior distribution when loss parameters take values − 0.25, 0.5 and 1. It is seen that tabulated estimates of both the parameters remain reasonably close to each other. The corresponding asymptotic, bootstrap-p and noninformative HPD intervals are constructed for both the unknown parameters in Table 9 under different censoring schemes. One-sample prediction estimates of the first two observations censored at different stages are presented in Table 10 along with corresponding equal-tail and noninformative HPD intervals. It is seen that prediction intervals tend to become wider for higher ordered future observable. In Table 11, we present two-sample prediction estimates and corresponding prediction intervals for the first two observations when future sample is of size 5.

Table 7 Goodness of fit for real data

Table 8 MLEs and Bayes estimates for real data

Table 9 Interval estimates for real data

Table 10 One-sample predictive estimates for real data

Table 11 Two-sample predictive estimates for real data

7 Conclusion

In this paper, we have considered point and interval estimation of unknown parameters of the IEP distribution under the assumption that samples are progressively Type-II censored. We observed that maximum likelihood estimates of parameters cannot be obtained analytically, and so we applied the EM algorithm to compute these estimates. We further obtained Bayes estimates of parameters under different loss functions using the importance sampling procedure. Asymptotic and HPD intervals of IEP parameters are also constructed. Another aim of this work is to derive prediction estimates and prediction intervals of censored observations in one- and two-sample situations. We compared performance of different methods using Monte Carlo simulations and observed that Bayes method gives better estimates of unknown parameters provided proper prior information on unknown parameters is available. An illustrative example is also discussed in support of the proposed methods. An interesting problem can be to estimate unknown parameters of IEP distribution using the modified censored moment method under progressive Type-II censoring, as suggested by an anonymous reviewer. Wang et al. [32] have discussed this procedure for the two-parameter Birnbaum–Saunders distribution. Till now, we have not succeeded in finding such estimates for our problem. We would like to work on this in near future. We have also used two different optimality criteria for comparing various censoring schemes. We could report results on optimal plans for reasonably moderate values of n and m using the complete search algorithm technique. It is of interest to determine optimal plans for effectively large sample sizes as well. To the best of our knowledge, metaheuristic algorithms can be a potential method for such cases. More work is required in this direction as well.

Appendices

Appendix 1

We compute required expectations as

$$\begin{aligned} A\left( c, \alpha , \beta \right)& {}= E\left( \log \left( Z_{ik}\right) \mid Z_{ik}>c\right) \\& {}= \frac{\alpha \beta }{1-F(c, \alpha , \beta )}\int _{c}^{\infty } x^{\beta -1}\left( 1+x\right) ^{-\left( \beta +1\right) }\left[ 1-\left( \psi \left( x\right) \right) ^{-\beta }\right] ^{\alpha -1}\log x\, {\hbox {d}}x\,\,\, \\& {}= \frac{1}{1-F\left( c, \alpha , \beta \right) }\int _{0}^{1-F\left( c\right) } \log \left[ \frac{1}{\left( 1-u^{\frac{1}{\alpha }}\right) ^{-\frac{1}{\beta }}-1} \right] \, {\hbox {d}}u,\\ B\left( c, \alpha , \beta \right)& {}= E\left( \log (1+Z_{ik})\mid Z_{ik}>c\right) \\& {}= \frac{\alpha \beta }{1-F\left( c, \alpha , \beta \right) }\int _{c}^{\infty } x^{\beta -1}(1+x)^{-\left( \beta +1\right) }\left[ 1-\left( \psi (x)\right) ^{-\beta }\right] ^{\alpha -1} \log \left( 1+x\right) \,{\hbox {d}}x\\& {}= \frac{1}{1-F\left( c, \alpha , \beta \right) }\int _{0}^{1-F\left( c\right) } \log \left[ \frac{\left( 1-u^{\frac{1}{\alpha }}\right) ^{-\frac{1}{\beta }}}{\left( 1-u^{\frac{1}{\alpha }}\right) ^{-\frac{1}{\beta }}-1} \right] \, {\hbox {d}}u, \end{aligned}$$

and

$$\begin{aligned} C(c, \alpha , \beta )& {}= E\left( \log \left[ 1-\left( \psi (Z_{ik})\right) ^{-\beta }\right] \left| {} \right. Z_{ik}>c\right) \\& {}= \frac{\alpha \beta }{1-F(c, \alpha , \beta )}\int _{c}^{\infty } x^{\beta -1}(1+x)^{-(\beta +1)}\left[ 1-\left( \psi (x)\right) ^{-\beta }\right] ^{\alpha -1} \log \left[ 1-\left( \psi (x)\right) ^{-\beta }\right] \,{\text {d}}x\\& {}= \frac{1}{1-F(c, \alpha , \beta )}\int _{0}^{1-F(c)} \log (u^{\frac{1}{\alpha }})\, {\text {d}}u, \end{aligned}$$

where $c=x_{i}$.

Appendix 2

We provide elements of matrices $I_{W}\left( \theta \right)$ and $I_{W\mid X}\left( \theta \right)$. Let $a_{ij}\left( \alpha , \beta \right)$ denote $\left( i, j\right)$th, $i, j = 1, 2,$ element of $I_{W}\left( \theta \right)$. Then, we have

$$\begin{aligned} a_{11}=\frac{n}{\alpha ^2},\,\,a_{12}=a_{21}=\frac{n\alpha }{\beta }\int _{0}^{1}u^{\alpha -3} \left( 1-u\right) \left( \log \left( 1-u\right) \right) ^{2} \, {\hbox {d}}u, \end{aligned}$$

and

$$\begin{aligned} a_{22}=\frac{n }{\beta ^2}+ \frac{n\left( \alpha -1\right) \alpha ^{2}}{\beta }\int _{0}^{1}\left( 1-u\right) u^{\alpha -3} \left( \log \left( 1-u\right) \right) ^{2}\, {\hbox {d}}u. \end{aligned}$$

Next, we have

$$\begin{aligned} I^{(j)}_{W\mid X}(\theta )=\begin{bmatrix} c_{11}&c_{12} \\ c_{21}&c_{22} \end{bmatrix} \end{aligned}$$

where

$$\begin{aligned} c_{11}& {}= \frac{1}{\alpha ^2},\\ c_{12}& {}= c_{21}=\frac{\left( \psi \left( x_{j}\right) \right) ^{-\beta }\log \left( \psi \left( x_{j}\right) \right) }{\left[ 1-\left( \psi (x_{j}\right) ^{-\beta }\right] } +\frac{\alpha }{\beta \left[ 1-\left( \psi (x_{j}\right) ^{-\beta }\right] ^{\alpha }}\int _{0}^{1-\left( \psi (x_{j})\right) ^{-\beta }} \left( 1-u\right) u^{\alpha -2} \log \left( 1-u\right) \,{\hbox {d}}u, \end{aligned}$$

and

$$\begin{aligned} c_{22}=\frac{1}{\beta ^{2}}-\alpha \frac{\left( \psi \left( x_{j}\right) \right) ^{-\beta }\left( \log \psi \left( x_{j}\right) \right) ^{2} }{\left[ 1-\left( \psi \left( x_{j})\right) \right) ^{-\beta }\right] ^{2}}+\frac{\left( \alpha -1\right) \alpha }{\beta ^{2} \left[ 1-\left( \psi \left( x_{j}\right) \right) ^{-\beta }\right] ^{\alpha }}\int _{0}^{1-\left( \psi (x_{j})\right) ^{-\beta }} \left( 1-u\right) u^{\alpha -3} \left( \log \left( 1-u\right) \right) ^{2}\,{\hbox {d}}u. \end{aligned}$$

Appendix 3

$$\begin{aligned} I_{11}& {}= \frac{1}{\alpha ^2} \sum _{i=1}^{m}\sigma _{i-1}\sum _{k=1}^{i}a_{k, i}\int _{0}^{\infty }\left[ 1-F_{X}(x, \theta ) \right] ^{\gamma _{k}-1} f_{X}(x, \theta ){\hbox {d}}x \\& {}= \frac{1}{\alpha ^2} \sum _{i=1}^{m}\sigma _{i-1}\sum _{k=1}^{i}\frac{a_{k, i}}{\gamma _{k}}, \\ I_{22}& {}= \sum _{i=1}^{m} \int _{0}^{\infty }\frac{1}{\beta ^{2}}\left[ 1+\frac{\log (1-(1+F_{X}(x, \theta ))^{\frac{1}{\alpha }})}{(1-F_{X}(x, \theta ))^{\frac{1}{\alpha }}} \right] \sigma _{i-1}\sum _{k=1}^{i}a_{k, i}(1-F_{X}(x, \theta ))^{\gamma _{k}-1} f_X(x, \theta ){\hbox {d}}x \\& {}= \frac{1}{\beta ^2} \sum _{i=1}^{m}\sigma _{i-1}\sum _{k=1}^{i}a_{k,i}\int _{0}^{1}\left( 1+\frac{\log (1-z^{\frac{1}{\alpha }})}{z^\frac{1}{\alpha }} \right) z^{\gamma _{k}-1}dz, \\ I_{12}& {}= I_{21}=\frac{1}{\alpha \beta } \sum _{i=1}^{m}\sigma _{i-1}\sum _{k=1}^{i}a_{k, i}\int _{0}^{1}\left( 1+\frac{\log (1-z^{\frac{1}{\alpha }})}{z^\frac{1}{\alpha }} \right) z^{\gamma _{k}-1}dz. \end{aligned}$$