Stochastic analysis of a complex repairable system comprises two subsystems in series configuration via multi-repair strategy

Abstract

The present paper study of the complex repairable system in combination with subsystems in series configuration each having four identical units and work policy as; the 2-out-of-4: G scheme. The entire system embraces exponential failure rates and variable repair rates. The system performance was evaluated employing a supplementary variable approach for different types of failure and two types of repairs under the concept of joint probability distribution Gumbel-Hougaard family copula. The traditional reliability measures have been computed with the implication of Maple 17 software. Tables and Graphs predict the behavior of the system for different values of the time variable.

1 Introduction

The design of complex engineering systems, particularly in the manufacturing industry, lacks the research community for the prospect of developing new models and designing uninterruptible systems capable of attaining high-level standards of availability and reliability. Any enhancement in system reliability is often tracked by the imposed cost; the improvement in trustworthiness is defensible to the degree that the cost of system non-approachability is greater than that of the standard service rendered. Customer satisfaction is also a prime consideration, in combination with the financial dimension to preserve the truthfulness of every establishment. In maintaining integrity and customer loyalty, reliability controls for the program play a crucial role. Redundancy is a stratagem that is commonly used to boost measures of device solidity and benefit sustained. In addition, redundancy is particularly beneficial in maintaining a certain degree of system reliability. A special type of configuration in which k units are necessary to be operative is known as the k-out-of-n: G type of configuration. To explore some examples of such a designed structure, a four-transmitter telecommunications system can be modeled as a 2-out-of-4: a G system, an aircraft having four engines with successful operation with at least two engines can me present a system of 2-out-of-4: G system, an oil transferring system from one station to another station in which the k-stations out of n pumping stations are essential to be proper supply is the system of k-out-of-n. G, digital car parking system, etc. are good examples of presenting the effectiveness of the such type of configuration. In system reliability theory, a conclusively k-out-of-n system plays a very crucial role in proper system operation. The warm standby system model k-out-of-n has found numerous applications in real-world phenomena, especially in the fields of reliability including reduction system monitoring, network design, power generation, telecommunication systems, manufacturing systems, transmission systems, industrial systems, etc.

Initially, authors Kullstam (1981) and Zhao (1994) have made comprehensive efforts over the past decades to formulate and solve the reliability characteristics of k-out-of-n systems, such as availability, MTSF, and MTTR for a repairable system. Malinowski (2016) studied the efficiency of a series–parallel-reducible network of flows. Levitin et al. (2013) evacuation reliability of mixed configured series–parallel systems with propagation time for spontaneous failures. Liang et al. (2010) have demonstrated the exact reliability formula for consecutive repairable k-out-of-n: type operating systems. Sharma and Kumar (2017) used standby with several working holidays to calculate the availability and other reliability measures of the successive k-out-of-n machining method. Eryilmaz (2010), developed formulas for a consecutive k-out-of-n: F system using lifetime distribution, reliability, and k-out-of-n system properties with arbitrarily dependent components and mixture representations to ensure the reliability of consecutive k-out-of-n: G/F systems. Kumar and Gupta (2007) evaluated the reliability characteristics of a 1-out-of-2 warm standby system consisting of the main unit with a supporting unit, including a general repair facility. Cha et al. (2014) introduced a competing risk model for evaluating the reliability of the device that is subject to both deterioration and catastrophic failures. They contrasted deterioration with catastrophic failure and demonstrated a more serious catastrophic failure as the device could not perform its function once a catastrophic failure occurs. Authors Chander and Bhardwaj (2007) presented reliability and cost–benefit analysis of a system of 2-out-of-3 redundant systems under a general repair and waiting time strategy. Munjal and Singh (2014) analyzed a complex system composed of two 2-out-of-3: G subsystems in parallel configuration by use of a supplementary variable approach. It was noteworthy in this paper that both of the subsystems namely subsystems L& M were configured n units in parallel configuration but the special case was discussed for the 2-out-of- 3: G system. The authors Singh et al. (2021) examine some reliability measures of the repairable network system connecting three computer labs to a server in a 2-out-of-3: G arrangement. Singh and Poonia (2019) have under inspection using regenerative point technique premeditated the system of two units under associated lifetimes. A system with (M + N) units under k-out-of-(M + N): G system was analyzed by Zhang et al. (2006), in which the M units were inactive in warm standby mode. Rawal et al. (2013) analyzed an Internet data center (IDC) model of a redundant server of main mail service trickling various forms of failure and two types of copula distribution in repair. Confirming the various operational possibilities in the network, some crucial research was performed to determine the network's different reliability features. Singh et al. (2013) under the principle of k-out-of-n, studied the cost analysis of an engineering system involving two subsystems in a series configuration with controllers and human failure: under the k-out-of-n: G operational directives. Remarkably, one can employ general repair if the device is in service and operating with a minor or major partial failure mode. Since the system is inoperable due to a complete shutdown mode, it must be repaired immediately. For this purpose, the copula repair, specifically [Gumbel-Hougaard family copula], must be implemented to restore the failed system by Copula, R. B. Nelson (2006). Singh et al. (2013), Gulati et al. (2016), Ibrahim et al. (2017), Jia et al. (2016), and Kumar et al. (2017), among others, studied the reliability measures of systems comprising subsystems in series configurations and k-out-of-n: G/F policy with implications of a joint probability distribution copula repair approach. Gokdere et al. (2016) developed a new technique for computing the reliability of consecutive k-out-of-n: F systems using a logical approach with computing several reliability measures. Authors Ram Niwas and Harish Garg (2018) have analyzed the reliability and profit function of the industrial system by the assumption of cost-free repair during warranty policy under the Markov method and supplementary variable methodology. Singh et al. (2020) examined a complex system with two subsystems in a series configuration with an imperfect switching device and concluded that copula repair predicts superior performance to general repair. Recently, authors Poonia (2021), and Poonia et al. (2021) have examined system performances of complex repairable systems consisting of subsystems in series configuration employing supplementary variable and copula repair strategy and examined system performances of computer lab networking systems via evaluating availability, reliability, MTSF, sensitivity and profit function. The Exact reliability formula for the n-client’s computer network with catastrophic failure and copula repair have deliberated by P. K. Poonia (2022a). Authors P. K. Poonia, (2022b) have performed a sensitivity analysis of a system of computer lab networking system with copula repair and consideration of one important type of failure as a catastrophic failure.

2 Model description and notations

2.1 System description

Conferring to the mentioned reviewed literature in the introduction anyone among authors has not analyzed the system consisting of the k-out-of-n: G/F type operational policy with switching device and human failure which is usually needed to be considered as the important failures. To bridge this gap, we examined the performance of a repairable warm standby system with two subsystems in a series configuration working under the 2-out-of-4: G scheme in which both important types of failure have been treated as a cause of complete failure. The units of both subsystems are associated with switching devices to auto-changing load. If an operating unit fails, it is replaced by a standby unit right at once using the switch of the failed unit of the subsystem to balance k units as an operative. Furthermore, the system may face precipitate human failure due to the wrong operation. There may be four types of possible states for the system operation: perfect state, minor degraded state, major degraded state, and complete failure. Failure rates of both operational and standby units are constant and assumed to have negative exponential distributions. The repair in the system abundant two distributions general and Gumbel- Hougaard (GH) family copula distribution. The repair rate of each unit in subsystem-1 and subsystem-2 is preserved as alike, but different for each subsystem.

The paper is organized as follows is as described below. In Sect. 1, we examined the relevant research presented in several articles. Section 2 provides an overview of the system description along with assumptions and notations; Sect. 3 provides a state description, and Sect. 4 presents the system configuration and transition diagram. In Sect. 5, mathematical modeling using differential equations is presented. Analytical results of system performance such as reliability, availability, mean time to failure (MTTF), and expected profit are presented in Sect. 6. We provided an overview of our findings in Sect. 7. With the aid of MAPLE, explicit expressions for reliability characteristics are obtained (software). Table 1 describes the investigated system's state, and Fig. 1 depicts the system's transitional state.

Table 1 State Description

Fig. 1

(a) System configuration

2.2 Assumptions

The following assumptions are made in this paper:

• 1. The subsystem-1 / subsystem-2 works successfully until at least two units are in good working condition, i.e., $\text{2-out-of-4: G}\text{ operation }{\text{policy}}$ is satisfied.

• 2. Both the subsystems have a switching device, and switch failure is treated as the complete damage state.

• 3. Human failure may occur at any time due to mishandling and human failure is also tracked as a completed failed state.

• 4. The entire system has four types of states: Good, minor partially failed, major partially failed, and utterly failed.

• 5. The units in both the subsystems are in active mode as a hot standby mode which is always ready to start within a slight time after the failure of any unit in the subsystems.

• 6. The repairman is available full-time and ready to restore minor and major faults.

• 7. All failure rates are constant and follow the negative exponential distribution.

• 8. In a complete failed situation system restore using a joint probability distribution copula.

• 9. The repaired unit is trickled as new and it is ready to perform the task as required.

2.3 Notations

$s/t$: Laplace transforms / Time scale variable.

${\lambda }_{1}/{\lambda }_{2}$: The failure rate of each unit in subsystem-1/subsystem-2.

${\lambda }_{{s}_{1}}/{\lambda }_{{s}_{2}}$: The failure rate of a switch for subsystem-1/subsystem-2.

${\lambda }_{h}$: Human failure due to mishandling or wrongly acting by the operator.

${\varphi }_{1}\left(x\right)/{\varphi }_{2}\left(x\right):$ Repair rate of units in subsystem-1/subsystem-2.

$P\left(t\right)$/$\overline{P }\left(s\right):$ State transition probability/ Laplace transform of state transition probability.

${P}_{i}\left(x,t\right)$: The probability that the system is in the state $S_{i}$ for i = 1, 2, …8 and the system is under repair with elapsed repair time is $(x,t)$ where x is a repaired variable and t is the time variable.

${E}_{p}\left(t\right):$ Expected profit in the interval [0, t).

${K}_{1}/{ K}_{2}:$ Revenue generation/ service cost per unit time, respectively.

${\mu }_{0}\left(x\right)$: An expression of the joint probability from failed state S_i to good state S₀ according to the Gumbel-Hougaard family copula is given as

$${ \mu }_{0}\left(x\right)={C}_{\theta }\left\{{u}_{1}\left(x\right),{u}_{2}\left(x\right)\right\}={\mathit{exp}\left[{x}^{\theta }+{\left\{\mathit{log}\varphi \left(x\right)\right\}}^{\theta }\right]}^{\frac{1}{\theta }}$$

here.

${u}_{1}\left(x\right)=\varphi \left(x\right)$ and ${u}_{2}\left(x\right)={e}^{\lambda x}$ here $\theta$ is the parameter $1<\theta <\infty$.

3 System configuration and state transition diagram

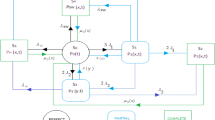
The system configuration is shown in Fig. 1a while the state transition diagram is in Fig. 1b. In the transition diagram, S₀ is the perfect state, S₁ and S₄ are minor partially failed, S₂ and S₅ are major partially failed, and S₃, S₆, S₇, and S₈are failed states. Due to the failure of a maximum of one unit from subsystem-1 or 2, the transitions approach minors partially failed states S₁ and S₄, and if two units failed in subsystem-1 or 2, the transitions approach to major partially failed states S₂ and S₅. The state S₃ is a complete failed state due to the failure of any three units in either of the subsystems. The states S₆, S₇, and S₈ are completely failed states due to controllers or catastrophic failure.

3.1 State description

The state explanation of the model is that S₀ is a state where both the subsystems are in good working condition. S₁ and S₄ are the states where the system is in minor partially failure mode, while S₂ and S₅ are indicating that the system is in major partially failure mode, and the repair is employed, states S₃, S₆, S₇ and S₈ are the total failure mode. Repair is being employed using the Gumbel-Hougaard (GH)family copula.

4 Formulation of the mathematical model

By a probability of considerations and permanency stochastic theory arguments, one can obtain the undermentioned set of differential equations allied with the present mathematical model.

$$\left[\frac{\partial }{\partial t}+4{\lambda }_{1}+4{\lambda }_{2}+{\lambda }_{{s}_{1}}+{\lambda }_{{s}_{2}}+{\lambda }_{h}\right]{P}_{0}\left(t\right)=\left[{P}_{1}\left(x,t\right)dx+{\int }_{0}^{\infty }{\varphi }_{2}\left(x\right){P}_{4}\left(x,t\right)dx \quad + {\int }_{0}^{\infty }{\mu }_{0}\left(x\right){P}_{j}\left(x,t\right)dx\right], j=\mathrm{3,6},\mathrm{7,8},9$$

(1)

$$\left[\frac{\partial }{\partial t}+\frac{\partial }{\partial x}+3{\lambda }_{1}+{\lambda }_{{s}_{1}}++{\varphi }_{1}\left(x\right)\right]{P}_{1}\left(x,t\right)=0$$

(2)

$$\left[\frac{\partial }{\partial t}+\frac{\partial }{\partial x}+2{\lambda }_{1}+{\lambda }_{{s}_{1}}+{\lambda }_{h}+{\varphi }_{1}\left(x\right)\right]{P}_{2}\left(x,t\right)=0$$

(3)

$$\left[\frac{\partial }{\partial t}+\frac{\partial }{\partial x}+{\mu }_{0}(x)\right]{P}_{3}\left(x,t\right)=0$$

(4)

$$\left[\frac{\partial }{\partial t}+\frac{\partial }{\partial x}+3{\lambda }_{2}+{\lambda }_{{s}_{2}}+{\lambda }_{h}+{\varphi }_{2}\left(x\right)\right]{P}_{4}\left(x,t\right)=0$$

(5)

$$\left[\frac{\partial }{\partial t}+\frac{\partial }{\partial x}+2{\lambda }_{2}+{\lambda }_{{s}_{2}}+{\lambda }_{h}+{\varphi }_{2}\left(x\right)\right]{P}_{5}\left(x,t\right)=0$$

(6)

$$\left[\frac{\partial }{\partial t}+\frac{\partial }{\partial x}+{\mu }_{0}\left(x\right)\right]{P}_{6}\left(x,t\right)=0$$

(7)

$$\left[\frac{\partial }{\partial t}+\frac{\partial }{\partial x}+{\mu }_{0}\left(x\right)\right]{P}_{7}\left(x,t\right)=0$$

(8)

$$\left[\frac{\partial }{\partial t}+\frac{\partial }{\partial x}+{\mu }_{0}\left(x\right)\right]{P}_{8}\left(x,t\right)=0$$

(9)

$$\left[\frac{\partial }{\partial t}+\frac{\partial }{\partial x}+{\mu }_{0}\left(x\right)\right]{P}_{9}\left(x,t\right)=0$$

(10)

Boundary conditions

$${P}_{1}\left(0,t\right)=4{\lambda }_{1}{P}_{0}\left(t\right)$$

(11)

$${P}_{2}\left(0,t\right)=3{\lambda }_{1}{P}_{1}\left(0,t\right)=12{\lambda }_{1}^{2}{P}_{0}\left(t\right)$$

(12)

$${P}_{3}\left(0,t\right)=24{\lambda }_{1}^{3}{P}_{0}\left(t\right)$$

(13)

$${P}_{4}\left(0,t\right)=4{\lambda }_{2}{P}_{0}\left(t\right)$$

(14)

$${P}_{5}\left(0,t\right)=12{\lambda }_{2}^{2}{P}_{0}\left(t\right)$$

(15)

$${P}_{6}\left(0,t\right)=24{\lambda }_{2}^{3}{P}_{0}\left(t\right)$$

(16)

$${P}_{7}\left(0,t\right)={\lambda }_{h}\left[{P}_{0}\left(t\right)+{P}_{1}\left(0,t\right)+{P}_{4}\left(0,t\right)+{P}_{2}\left(0,t\right)+{P}_{5}\left(0,t\right)\right]$$

(17)

$${P}_{8}\left(0,t\right)={\lambda }_{{s}_{1}}\left[{P}_{0}\left(t\right)+{P}_{1}\left(0,t\right)+{P}_{2}\left(0,t\right)\right]$$

(18)

$${P}_{9}\left(0,t\right)={\lambda }_{{s}_{2}}\left[{P}_{0}\left(t\right)+{P}_{1}\left(0,t\right)+{P}_{2}\left(0,t\right)\right]$$

(19)

Initials conditions.

$${P}_{0}\left(0\right)=1, \mathrm{and} {P}_{j}\left(x,0\right)=o, i=\mathrm{1,2},\mathrm{3,4}\dots 9$$

(20)

Laplace transformation of Eqs. (1) to (17) and using Eq. (18), one may obtain

$$\left[s+4{\lambda }_{1}+4{\lambda }_{2}+{\lambda }_{{s}_{1}}+{\lambda }_{{s}_{2}}+{\lambda }_{h}\right]{\bar{P}}_{0}\left(s\right)=1+{\int }_{0}^{\infty }{\varphi }_{1}\left(x\right){\bar{P}}_{1}\left(x,s\right)dx+{\int }_{0}^{\infty }{\varphi }_{2}\left(x\right){\bar{P}}_{4}\left(x,s\right)dx+$$

$${\int }_{0}^{\infty }{\mu }_{0}\left(x\right){\bar{P}}_{j}\left(x,s\right)dx, j=\mathrm{3,6}, 7, 8, 9$$

(21)

$$\left[s+\frac{\partial }{\partial x}+3{\lambda }_{1}+{\lambda }_{{s}_{1}}+{\lambda }_{h}+{\varphi }_{1}\left(x\right)\right]{\overline{P} }_{1}\left(x,s\right)=0$$

(22)

$$\left[s+\frac{\partial }{\partial x}+2{\lambda }_{1}+{\lambda }_{{s}_{1}}+{\lambda }_{h}+{\varphi }_{1}\left(x\right)\right]{\overline{P} }_{2}\left(x,s\right)=0$$

(23)

$$\left[s+\frac{\partial }{\partial x}+{\mu }_{0}(x)\right]{\overline{P} }_{3}\left(x,s\right)=0$$

(24)

$$\left[s+\frac{\partial }{\partial x}+3{\lambda }_{2}+{\lambda }_{{s}_{2}}+{\lambda }_{h}+{\varphi }_{2}\left(x\right)\right]{\overline{P} }_{4}\left(x,s\right)=0$$

(25)

$$\left[s+\frac{\partial }{\partial x}+2{\lambda }_{2}+{\lambda }_{{s}_{2}}+{\lambda }_{h}+{\varphi }_{2}\left(x\right)\right]{\overline{P} }_{5}\left(x,s\right)=0$$

(26)

$$\left[s+\frac{\partial }{\partial x}+{\mu }_{0}\left(x\right)\right]{\overline{P} }_{6}\left(x,s\right)=0$$

(27)

$$\left[s+\frac{\partial }{\partial x}+{\mu }_{0}\left(x\right)\right]{\overline{P} }_{7}\left(x,s\right)=0$$

(28)

$$\left[s+\frac{\partial }{\partial x}+{\mu }_{0}\left(x\right)\right]{\overline{P} }_{8}\left(x,s\right)=0$$

(29)

$$\left[s+\frac{\partial }{\partial x}+{\mu }_{0}\left(x\right)\right]{\overline{P} }_{9}\left(x,s\right)=0$$

(30)

Laplace Transform of Boundary conditions:

$${\overline{P} }_{1}\left(0,s\right)=4{\lambda }_{1}{\overline{P} }_{0}\left(s\right)$$

(31)

$${\overline{P} }_{2}\left(0,s\right)=12{\lambda }_{1}^{2}{\overline{P} }_{0}\left(s\right)$$

(32)

$${\overline{P} }_{3}\left(0,s\right)=24{\lambda }_{1}^{3}{\overline{P} }_{0}\left(s\right)$$

(33)

$${\overline{P} }_{4}\left(0,s\right)=4{\lambda }_{2}{\overline{P} }_{0}\left(s\right)$$

(34)

$${\overline{P} }_{5}\left(0,s\right)=12{\lambda }_{2}^{2}{\overline{P} }_{0}\left(s\right)$$

(35)

$${\overline{P} }_{6}\left(0,s\right)=24{\lambda }_{2}^{3}{\overline{P} }_{0}\left(s\right)$$

(36)

$${\overline{P} }_{7}\left(0,s\right)={\lambda }_{h}\left[{\overline{P} }_{0}\left(s\right)+{\overline{P} }_{1}\left(0,s\right)+{\overline{P} }_{4}\left(0,s\right)+{\overline{P} }_{5}\left(0,s\right)+{\overline{P} }_{2}\left(0,s\right)\right]$$

(37)

$${\overline{P} }_{8}\left(0,s\right)={\lambda }_{{s}_{1}}\left[{\overline{P} }_{0}\left(s\right)+{\overline{P} }_{1}\left(0,s\right)+{\overline{P} }_{2}\left(0,s\right)\right]$$

(38)

$${\overline{P} }_{9}\left(0,s\right)={\lambda }_{{s}_{2}}\left[{\overline{P} }_{0}\left(s\right)+{\overline{P} }_{1}\left(0,s\right)+{\overline{P} }_{2}\left(0,s\right)\right]$$

(39)

Initials conditions

$${\overline{P} }_{0}\left(0\right)=1, \mathrm{and} {\overline{P} }_{j}\left(x,0\right)=0, j=\mathrm{1,2},\mathrm{3,4}\dots 9$$

Now solving the Eqs. (19) (27) with the boundary conditions, (28)- (35) one may get the solution of Eq. (21) as; $D\left(s\right){\overline{P} }_{0}\left(s\right)=1$, and consequently, the solutions of successive equations are given as;

$${\bar{P}}_{0}\left(s\right)=\frac{1}{D\left(s\right)}$$

(40)

$${\bar{P}}_{1}\left(s\right)=\frac{4{\lambda }_{1}}{D\left(s\right)}\frac{1}{\left(s+3{\lambda }_{1}+{\lambda }_{{s}_{1}}+{\lambda }_{h}+{\varnothing }_{1}\right)}$$

(41)

$${\bar{P}}_{2}\left(s\right)=\frac{12{\lambda }_{1}^{2}}{D\left(s\right)}\frac{1}{\left(s+2{\lambda }_{1}+{\lambda }_{{s}_{1}}+{\lambda }_{h}+{\varnothing }_{1}\right)}$$

(42)

$${\bar{P}}_{3}\left(s\right)=\frac{24{\lambda }_{1}^{3}}{D\left(s\right)}\frac{1}{s+{\mu }_{0}}$$

(43)

$${\bar{P}}_{4}\left(s\right)=\frac{4{\lambda }_{2}}{D\left(s\right)}\frac{1}{\left(s+3{\lambda }_{2}+{\lambda }_{{s}_{2}}+{\lambda }_{h}+{\varphi }_{2}\right)}$$

(40)

$${\bar{P}}_{5}\left(s\right)=\frac{12{\lambda }_{2}^{2}}{D\left(s\right)}\frac{1}{\left(s+2{\lambda }_{2}+{\lambda }_{{s}_{2}}+{\lambda }_{h}+{\varphi }_{2}\right)}$$

(41)

$${\bar{P}}_{6}\left(s\right)=\frac{24{\lambda }_{2}^{3}}{D\left(s\right)}\frac{1}{s+{\mu }_{0}}$$

(42)

$${\bar{P}}_{7}\left(s\right)=\frac{{\lambda }_{h}(1+4{(\lambda }_{1}+{\lambda }_{2)+}12({\lambda }_{1}^{2}+{\lambda }_{2}^{2}))}{D\left(s\right)}$$

(43)

$${\bar{P}}_{8}\left(s\right)=\frac{{\lambda }_{{s}_{1}}(1+4{\lambda }_{1}+12{\lambda }_{1}^{2})}{D\left(s\right)}$$

(44)

$${\bar{P}}_{9}\left(s\right)=\frac{{\lambda }_{{s}_{2}}(1+4{\lambda }_{1}+12{\lambda }_{1}^{2})}{D\left(s\right)}$$

(45)

Here,

$$D\left(s\right)=s+4{\lambda }_{1}+4{\lambda }_{2}+{\lambda }_{{s}_{1}}+{\lambda }_{{s}_{2}}+{\lambda }_{h}-4{\lambda }_{1}P-4{\lambda }_{2}Q-{\lambda }_{{s}_{1}}\left(1+ 4{\lambda }_{1}+12{\lambda }_{1}^{2}\right)R+{\lambda }_{{s}_{2}}\left(1+ 4{\lambda }_{2}+12{\lambda }_{2}^{2}\right)R+{\lambda }_{h}(1+ 4({\lambda }_{1}+{\lambda }_{2})+12{(\lambda }_{1}^{2}+{\lambda }_{2}))R$$

$P=\frac{{\varphi }_{1}}{s+3{\lambda }_{1}+{\lambda }_{{s}_{1}}+{\lambda }_{h}+{\varphi }_{1}}$, $Q=\frac{{\varphi }_{2}}{s+{3\lambda }_{2}+{\lambda }_{{s}_{2}}+{\lambda }_{h}+{\varphi }_{2}} ,$   $R=\frac{{\mu }_{0}}{s+{\mu }_{0}}$The Sum of Laplace transformations of the state transitions, for operative states and failed states at any time, is given as.

$${\bar{P}}_{up}\left(s\right)={\bar{P}}_{0}\left(s\right)+{\bar{P}}_{1}\left(s\right)+{\bar{P}}_{2}\left(s\right)+{\bar{P}}_{4}\left(s\right)+{\bar{P}}_{5}\left(s\right)$$

(46)

5 Analytical study

5.1 System availability analysis for copula repair approach

1. Repair follows two types of distributions general and (GH) family copula distribution, we have

${\bar{S}}_{{\mu }_{0}}\left(s\right)=\frac{{\mu }_{0}}{s+{\mu }_{0}}$, ${\bar{S}}_{\varphi i}\left(s\right)=\frac{\varphi i}{s+\varphi i}, i=1, 2$

Setting the failure and repair rates as the specific values ${\lambda }_{1}=0.02{, \lambda }_{2}=0.02,{\lambda }_{{s}_{1}}=0.03,{\lambda }_{{s}_{2}}=0.025,{\lambda }_{h}=0.04,\theta =1,x=1,{\varphi }_{i}=1, i=1, 2$ in (46), for performance outcomes of the repairable system and computing inverse Laplace transform, with Maple 17 software one can obtain the following availability expression of the system. Here we have considered the following particular cases:

Case I: System availability for given set of failure rates,

$${\lambda }_{1}=0.02{, \lambda }_{2}=0.02,{\lambda }_{{s}_{1}}=0.03,{\lambda }_{{s}_{2}}=0.025,{\lambda }_{h}=0.04, \theta =1,{\varphi }_{i}(x)=1,i=\mathrm{1,2}$$

$$\left(a\right):{P}_{up}\left(t\right)=-o.00058464798{e}^{-1.1050000t}+0.03637264{e}^{-2.8227094t}-0.0249363528{e}^{-1.262571253t}- 0.0000204294{e}^{-1.127459589t}+0.98963260{e}^{-o.01555974t}-0.000463817{e}^{-1.1100000t}$$

(47a)

Case II: System availability expression for failure rates,

$${\lambda }_{1}=0.02{, \lambda }_{2}=0.02,{\lambda }_{{s}_{1}}=0.03,{\lambda }_{{s}_{2}}=0.025,{\lambda }_{h}=0, \theta =1,{\varphi }_{i}(x)=1,i=\mathrm{1,2}$$

$$(b:){P}_{up}\left(t\right)=0.0215065444{e}^{-2.77884738t}-0.019770593{e}^{-1.2308643t}-0.0000176710{e}^{-1.087462347t} +0.999338522{e}^{-0.01112595t}-0.00058964950{e}^{-1.06500000t}-0.00046696982{e}^{-1.0700000t}$$

(47b)

Case III: Availability function for system parameters;

$${\lambda }_{1}=0.02{, \lambda }_{2}=0.02,{\lambda }_{{s}_{1}}=0.03, {\lambda }_{{s}_{2}}=0,{\lambda }_{h}=0.04, \theta =1,{\varphi }_{i}(x)=1,i=\mathrm{1,2}$$

$${\left(c\right):P}_{up}\left(t\right)=0.02714588327{e}^{-2.7953333t}-0.0226415899{e}^{-1.255114724t}-0.0020210092{e}^{-1.11360291t}+0.9966486380{e}^{-0.014248853t}-0.00073102249{e}^{-1.0800000t}+0.0015991002{e}^{-1.110000t}$$

(47c)

Case IV: Availability function for given set of parameters,

$${\lambda }_{1}=0.02{, \lambda }_{2}=0.02,{\lambda }_{{s}_{1}}=0,{\lambda }_{{s}_{2}}=0.025,{\lambda }_{h}=0.04, \theta =1,{\varphi }_{i}(x)=1,i=\mathrm{1,2}$$

$$\left(\mathrm{d}\right):{P}_{up}\left(t\right)=-0.0009411773{e}^{-1.3300000t}-0.000887660{e}^{-1.0800000t}+0.101231084{e}^{-3.03421041t}-0.026974992{e}^{-1.41119842t}-0.0069049887{e}^{-1.149925006t}+0.934477735{e}^{-0.022966108t}$$

(47d)

For different values of time variable $t=\mathrm{0,1}, 2, 3, 4, 5, 6, 7, 8, 9\text{, and }10$ units of time, one may get different values ${P}_{up}\left(t\right)$ with the help of (47a-47d), as presented in Table 2 and the corresponding Fig. 2.

Table 2 Computation of MTTF corresponding to the failure rates

Fig. 2

(b) State transition diagram of the model

5.2 System availability analysis for general repair approach

1. Repair follows two types of distributions general distribution, we have

$${\bar{S}}_{{\mu }_{0}}\left(s\right)=\frac{{\mu }_{0}}{s+{\mu }_{0}}, {\bar{S}}_{\varphi i}\left(s\right)=\frac{\varphi i}{s+\varphi i}, i=1, 2$$

Setting the failure and repair rates as the specific values ${\lambda }_{1}=0.02{, \lambda }_{2}=0.02,{\lambda }_{{s}_{1}}=0.03,{\lambda }_{{s}_{2}}=0.025,{\lambda }_{h}=0.04,\theta =1,x=1,{\varphi }_{i}={\mu }_{0}=1,$ in (46), for performance outcomes of the repairable system and computing inverse Laplace transform, with Maple 17 software one can obtain the following availability expression of the system. Here we have considered the following particular cases:

Case I: System availability for given set of failure rates,

$${\lambda }_{1}=0.02{, \lambda }_{2}=0.02,{\lambda }_{{s}_{1}}=0.03,{\lambda }_{{s}_{2}}=0.025,{\lambda }_{h}=0.04, {\varphi }_{i}(x)=1,i=\mathrm{1,2}$$

$${\left(a\right):P}_{up}\left(t\right)=-00051476204{e}^{-1.1100000t}+0.029347910{e}^{-1.330541744t}+0.00001503048{e}^{-1.12749503t}+ 0.032553559{e}^{-1.03718134t}+0.93927004{e}^{-0.014781891t}-0.00067177607{e}^{-1.05000000t}+$$

(48a)

Case II: System availability expression for failure rates,

$${\lambda }_{1}=0.02{, \lambda }_{2}=0.02,{\lambda }_{{s}_{1}}=0.03,{\lambda }_{{s}_{2}}=0.025,{\lambda }_{h}=0,{\varphi }_{i}(x)=1,i=\mathrm{1,2}$$

$$\left(b\right):{P}_{up}\left(t\right)=-0.00066631073{e}^{-1.0650000t}+0.0150362399{e}^{-1.2739677323t}+0.01672525504{e}^{-1.087490475t} +0.96940483{e}^{-0.01079707t}-0.000510496{e}^{-1.0700000t}$$

(48b)

Case III: Availability function for system parameters;

$${\lambda }_{1}=0.02{, \lambda }_{2}=0.02,{\lambda }_{{s}_{1}}=0.03,{\lambda }_{{s}_{2}}=0,{\lambda }_{h}=0.04,{\varphi }_{i}(x)=1,i=\mathrm{1,2}$$

$$\left(c\right):{P}_{up}\left(t\right)=0.0012778316{e}^{-1.1100000t}+0.017289155{e}^{-1.305302694t}-0.0006296254{e}^{-1.11461512t}+0.024258108{e}^{-1.026367342t}+0.958665517{e}^{-0.013714847t}-0.0008609865{e}^{-1.0800000t}$$

(48c)

Case IV: Availability function for given set of parameters,

$${\lambda }_{1}=0.02{, \lambda }_{2}=0.02,{\lambda }_{{s}_{1}}=0,{\lambda }_{{s}_{2}}=0.025,{\lambda }_{h}=0.04, {\varphi }_{i}(x)=1,i=\mathrm{1,2}$$

$$\left(d\right):{P}_{up}\left(t\right)=-0.0013138497{e}^{-1.330000t}-0.0036886295{e}^{-1.0800000t}+0.090899984{e}^{-1.55116394t}+0.07727621563{e}^{-1.25535526t}+0.298658745{e}^{-1.073581672t}+0.8069604050{e}^{-0.019899121t}$$

(48d)

For different values of time variable $t=\mathrm{0,1}, 2, 3, 4, 5, 6, 7, 8, 9\text{, and }10$ units of time, one may get different values P_up(t) for general repair with the help of (48a-48d), as presented in Table 3 and the corresponding Fig. 3.

Table 3 availability variation with respect to time

Fig. 3

Availability as a function of time

5.3 System reliability analysis

Reliability is the probabilistic measure of a non-repairable system. Therefore, by treating all repair rates equal to zero and obtaining the inverse Laplace transform in (45), we get an expression for the reliability of the system after taking the failure rates as ${\lambda }_{1}=0.02,{\lambda }_{2}=0.03,{\lambda }_{{s}_{1}}=0.03,{\lambda }_{{s}_{2}}=0.025, {\lambda }_{\mathrm{h}}=0.04$ considered the same cases like availability, we have.

Case I: Reliability function when the failure rates fixed as; ${\lambda }_{1}=0.02,{\lambda }_{2}=0.03,{\lambda }_{{s}_{1}}=0.03,{\lambda }_{{s}_{2}}=0.025, {\lambda }_{\mathrm{h}}=0.04$ one can obtain,

$$\left(a\right): R\left(t\right)=0.03310344828{e}^{-0.1100000t}+0.6400000{e}^{-0.1300000t}+0.6153846154{e}^{-0.12500000t}+0.032000{e}^{-0.1050000t}-0.32488063{e}^{-0.25500000t}$$

(49a)

Case II: Reliability function when the failure rates fixed as; ${\lambda }_{1}=0.02,{\lambda }_{2}=0.03,{\lambda }_{{s}_{1}}=0.03,{\lambda }_{{s}_{2}}=0.025, {\lambda }_{\mathrm{h}}=0$ one can obtain,

$$\left(b\right):R\left(t\right)=0.64000000{e}^{-0.09000000t}+0.0320000{e}^{-0.06500000t}- 0.320488063{e}^{-0.21500000t}+0.615384615{e}^{-0.0850000t}+ 0.033103448{e}^{-0.0700000t}$$

(49b)

Case III: Reliability function when the failure rates fixed as; ${\lambda }_{1}=0.02,{\lambda }_{2}=0.03,{\lambda }_{{s}_{1}}=0.03,{\lambda }_{{s}_{2}}=0, {\lambda }_{\mathrm{h}}=0.04$, we obtain.

$$\left(\mathrm{c}\right):R\left(t\right)=\,0.0400000{e}^{-0.1100000t}+0.03200000{e}^{-0.080000t}+0.80000000{e}^{-0.1300000t}+ 0.615384615{e}^{-0.1000000t}-04873846154{e}^{-0.2300000t}$$

(49c)

Case IV: Reliability expression for given failure rates ${\lambda }_{1}=0.02,{\lambda }_{2}=0.03,{\lambda }_{{s}_{1}}=0,{\lambda }_{{s}_{2}}=0.025, {\lambda }_{\mathrm{h}}=0.04$ obtain as;

$${\left(d\right):R}_{i}\left(t\right)=0.03310344828{e}^{-0.080000t}+0.800000{e}^{-0.1250000t}+0.6400000{e}^{-0.100000t}-0.5131034483{e}^{-0.22500000t}+0.0400000{e}^{-0.10500000t}$$

(54)

For different values of time variable $t=\mathrm{0,1}, 2, 3, 4, 5, 6, 7, 8, 9\text{, and }10$ units of time, one may get different values of reliability $R(t)$ with the help of (49a-49d), as shown in Table 4 and the corresponding Fig. 4.

Table 4 availability variation with respect to time

Fig. 4

Availability variation as a function of time for the general repair strategy

5.4 Mean time to failure (MTTF)

Taking all repair rates to zero and the limit as s tends to zero in (46) for the exponential distribution; we can obtain the MTTF as:

$$MTTF=\frac{1}{A}\left[1+\frac{4{\lambda }_{1}}{3{\lambda }_{1}+{\lambda }_{{s}_{1}+{\lambda }_{h}}}+\frac{12{\lambda }_{1}^{2}}{2{\lambda }_{1}+{\lambda }_{{s}_{1}+{\lambda }_{h}}}+\frac{4{\lambda }_{2}}{3{\lambda }_{2}+{\lambda }_{{s}_{2}+{\lambda }_{h}}}+\frac{12{\lambda }_{2}^{2}}{2{\lambda }_{2}+{\lambda }_{{s}_{2}+{\lambda }_{h}}}\right]$$

(50)

where $A=4{\lambda }_{1}+4{\lambda }_{2}+{\lambda }_{{s}_{1}}+{\lambda }_{{s}_{2}}+{\lambda }_{h}$

Now taking the values of different parameters as ${\lambda }_{1}=0.02,{\lambda }_{2}=0.02,{\lambda }_{{s}_{1}}=0.03,{\lambda }_{{s}_{2}}=0.025\text{, and }{\lambda }_{h}=0.04$ and varying ${\lambda }_{1},{\lambda }_{2},{\lambda }_{{s}_{1}},{\lambda }_{{s}_{2}}\text{ and }{\lambda }_{h}$ one by one respectively as $0.01,0.02,0.03,0.04,0.05,0.06,$$0.07,0.08,0.09,0.10$ in (50), the variation of MTTF, for failure rates, can be obtained as given Table 2 and Fig. 5.

Fig. 5

Reliability as a function of time

5.5 Cost analysis

Let the service facility be always available, then the expected profit during the interval [0, t) is

$${E}_{p}\left(t\right)={K}_{1}{\int }_{0}^{t}{P}_{up}\left(t\right)dt-{K}_{2}t$$

(51)

For the same set of parameters defined in (46), one can obtain (52) (Table 5).

Table 5 Computed values of reliability corresponding to the different cases

Therefore

$${E}_{p}\left(t\right)={K}_{1}\left\{0.00065935177{e}^{-1.080000t}-0.0090586482{e}^{-2.789849966t}+0.01773655598{e}^{-1.25292472t}+0.00076159421{e}^{-1.111532685t}-71.32848258{e}^{-0.0139926289t}-0.0003945233{e}^{-1.105000t}+71.319\right\}-{K}_{2}t$$

(52)

Setting ${K}_{1}=1$ and ${K}_{2}=\mathrm{0.3,0.4,0.5,0.6}$ respectively, and varying t = 0,1,2,3…0.10 units of time, the results for expected profit can be obtained as per Table 6 and Fig. 6.

Table 6 Profit computation for different values of time

Fig. 6

MTTF as a function of failure rates

6 Conclusion via result analysis

The probabilistic measures of a repairable system with two subsystems in series, switching, and human failure are investigated in this study. Each subsystem is composed of the following identical units which run simultaneously and follow the 2-out-of-4: G strategy. Copula repair is a better and more performable repair policy, according to the model's analysis with the help of supplementary variables. The following conclusions have been drawn from the research presented in this paper:

• 1. Table 2 and Fig. 2 show a study of the system's availability in four different scenarios (Gumbel-Houggard family copula and general repair strategy). It is evident that as time t increases, the availability decreases. When a copula repair approach is used, system performance improves (see Table 3, Fig. 2 and Table 4, Fig. 3 for evidence).

• 2. Table 5 and Fig. 4 show the system's reliability at various time intervals. The graph showed lower reliability and performance values when comparing availability for the same time variables. Four different study situations have been highlighted as examples of similar availability analyses.

• 3. Table 5 and Fig. 5 yield the MTTF of the system concerning variation ${\lambda }_{1},{\lambda }_{2},{\lambda }_{{s}_{1}},{\lambda }_{{s}_{2}}\text{, and }{\lambda }_{h}$. It can see that the MTTF of the system reduces with the increasing values of all the failure rates. MTTF was found to be the highest for ${\lambda }_{{s}_{2}}$ but the deviation rate is very high for others. The MTTF corresponding failure rate ${\lambda }_{1}$ is lower than others but the tendency of MTTF concerning failure rate ${\lambda }_{{s}_{1}}$ is growing. The MTTF of the system for failure rates ${\lambda }_{{s}_{1}}\&{\lambda }_{{s}_{2}}$ become the same at failure rates 0.07, 0.08].

• 4. A detailed analysis in Table 6 and Fig. 6 reveals that forecasted profit increases when service cost K₂ decreases, while revenue cost per unit time remains constant at K₁ = 1. K₂ = 0.3 has the highest expected profit, while K₂ = 0.6 has the lowest. Over time, we notice that as service costs reduce, profit rises. In general, the predicted profit is high with the high service cost for low service charges.

• 5. The model created in this research was proven to be quite useful in proper maintenance analysis, decision-making, and performance evaluation. Another possible future project is to assess the researched system's maximum dependability and availability (Fig. 7).

Fig. 7

Expected profit as a function of time