Incremental approaches to knowledge reduction based on characteristic matrices

Abstract

Knowledge reduction is complicated with the dynamic change of the object set in applications. In this paper, we propose incremental approaches to computing the type-1 and type-2 characteristic matrices of coverings with respect to variation of objects. Also we present two incremental algorithms of calculating the second and sixth lower and upper approximations of sets when adding and deleting more objects in dynamic covering approximation spaces. Subsequently, we employ experiments to validate that the incremental approaches are more effective and efficient to construct approximations of sets in dynamic covering information systems. Finally, we preform knowledge reduction of dynamic covering decision information systems by using the incremental approaches.

1 Introduction

Covering-based rough set theory, as an extension of Pawlak’s model [35] to deal with covering information systems [5, 7, 8, 11, 19, 31, 41, 52, 63], has been successfully applied to many fields. To our best knowledge, researchers [1, 6, 10, 12, 15, 16, 18, 28, 32–34, 36, 40, 42, 46, 47, 49–51, 56–62] have presented various kinds of lower and upper approximation operators and investigated knowledge reduction of information systems.

Recently, Wang et al. [45] transformed the computation of approximations into products of the characteristic matrices and the characteristic function of the set. The work provides a new view to the covering-based rough sets by using the boolean matrices. However, Wang et al. paid little attention to approaches to calculating the characteristic matrices in computing approximations of concepts. In practice, covering approximation spaces always vary with the time, and the non-incremental approach to constructing the characteristic matrices of coverings is often very costly. No work on constructions of characteristic matrices has been reported for computing approximations of sets thus far. Therefore, an efficient approach to calculating the characteristic matrices is truly desirable in covering approximation spaces.

Previously, dynamic information systems [2–4, 9, 13–15, 17, 20–22, 24–27, 29, 30, 37–39, 43, 44, 53–55] have attracted a great deal of attention. For example, Chen et al. [2–4] constructed approximations of sets under dynamic maintenance environments. Fan et al. [9] investigated rule induction based on an incremental rough set. Huang et al. [13] proposed alternative rule induction methods based on incremental object by using rough set theory. Jiang et al. [14] introduced an incremental decision tree algorithm based on rough sets. Ju et al. [15] investigated dynamic updating multigranulation fuzzy rough set. Lang et al. [17] presented an incremental approach to attribute reduction of dynamic set-valued information systems. Li et al. [22] provided incremental approaches to computing approximations in dominance-based rough sets approach under the variation of attribute set. Li et al. [20] focused on the dynamic attribute generalization based on the characteristic relation. Li et al. [21] presented incremental approaches to inducing decision rules with rough set under characteristic relation. Liang et al. [24] developed a group incremental approach to feature selection applying rough set technique. Liu et al. [25–27] induced knowledge from dynamic information systems. Luo et al. [29, 30] studied dynamic maintenance of approximations in set-valued ordered information systems. Shan et al. [37] introduced data-based acquisition and incremental modification of classification rules. Shu et al. [38, 39] performed attribute reduction in dynamic incomplete information systems. Wang et al. [43, 44] proposed attribute reduction algorithms for data sets with dynamically varying data values and a dimension incremental strategy for attribute reduction. Yang et al. [48] updated multigranulation rough approximations with increasing of granular structures. Zhang et al. [54] provided incremental approaches to updating rough set approximations based on relation matrices. Zhang et al. [53, 55] also investigated neighborhood rough sets and composite rough sets for dynamic data mining. These works demonstrate that the incremental approaches are effective for knowledge reduction in dynamic information systems. It motivates us to apply an incremental updating scheme to maintain the characteristic matrices of coverings dynamically for knowledge reduction in dynamic covering decision information systems.

The purpose of this paper is to perform knowledge reduction in dynamic covering decision information systems. First, we introduce incremental approaches to computing type-1 and type-2 characteristic matrices in dynamic covering approximation spaces. We mainly focus on two situations: the immigration and emigration of more objects. We also consider the immigration and emigration of more objects simultaneously. Second, we propose incremental algorithms of constructing characteristic matrices-based approximations of sets in dynamic covering approximation spaces. Several examples are employed to illustrate that the process of calculating the characteristic matrices-based approximations of sets is simplified greatly by utilizing the incremental approach. Third, we perform experiments on six dynamic covering approximation spaces. The experimental results illustrate that the incremental algorithms are more effective to calculate approximations of sets with respect to the variation of objects. Fourth, we perform knowledge reduction with the incremental approaches in dynamic covering decision information systems.

The rest of this paper is organized as follows: Sect. 2 briefly reviews the basic concepts of covering-based rough set theory. In Sect. 3, we introduce incremental algorithms of calculating the second and sixth lower and upper approximations of sets by using the characteristic matrices. In Sect. 4, several experiments are employed to show that the incremental approaches are more effective to compute approximations of sets. Section 5 is devoted to knowledge reduction by using the incremental approaches in dynamic covering decision information systems. We conclude the paper in Sect. 6.

2 Preliminaries

In this section, we review some concepts of covering-based rough set theory.

Definition 2.1

[52] Let $U$ be a finite universe of discourse, and $\fancyscript{C}$ a family of subsets of $U$. If none of elements of $\fancyscript{C}$ is empty and $\bigcup \{C|C\in \fancyscript{C}\}=U$, then $(U,\fancyscript{C})$ is called a covering approximation space.

By Definition 2.1, $\fancyscript{C}$ is referred to as a covering of $U$, and $MD(\fancyscript{C}, x)=\{K\in \fancyscript{C}|x\in K \wedge (\forall S\in \fancyscript{C} \wedge x\in S \wedge K\subseteq S )\Rightarrow K=S\}$ is called the maximal description of $x\in U$.

Definition 2.2

[45] Let $U=\{x_{1},x_{2},...,x_{n}\}$ be a finite universe, and $\fancyscript{C}=\{C_{1},C_{2},...,C_{m}\}$ a covering of $U$. For any $X\subseteq U$, the second, fifth and sixth upper and lower approximations of $X$ with respect to $\fancyscript{C}$ are defined as follows:

• (1) $SH_{\fancyscript{C}}(X)=\bigcup \{C\in \fancyscript{C}|C\cap X\ne \emptyset \}$, $SL_{\fancyscript{C}}(X)=[SH_{\fancyscript{C}}(X^{c})]^{c}$;

• (2) $IH_{\fancyscript{C}}(X)=\bigcup \{N(x)|x\in X\}$, $IL_{\fancyscript{C}}(X)=\{x\in U|N(x)\subseteq X\}$;

• (3) $XH_{\fancyscript{C}}(X)=\{x\in U|N(x)\cap X\ne \emptyset \}$, $XL_{\fancyscript{C}}(X)=\{x\in U|N(x)\subseteq X\}$, where $N(x)=\bigcap \{C_{i}|x\in C_{i}\in \fancyscript{C}\}$.

By Definitions 2.1 and 2.2, $SH_{\fancyscript{C}}(X)=\bigcup \{C\in \fancyscript{C}|C\cap X\ne \emptyset \}=\bigcup \{C\in \fancyscript{X}_{\fancyscript{C}}|C\cap X\ne \emptyset \}$, where $\fancyscript{X}_{\fancyscript{C}}=\bigcup \{MD(\fancyscript{C}, x)|x\in U\}$. Furthermore, since $IL$ and $XH$ are dual operators, we obtain $IL_{\fancyscript{C}}(X)$ by using $XH_{\fancyscript{C}}(X^{c})$ for any $X\subseteq U$ easily. In what follows, we omit $\fancyscript{C}$ in the description of approximation operators for simplicity.

Recently, Wang et al. presented a matrice representation of a covering for constructing approximations of sets.

Definition 2.3

[45] Let $U=\{x_{1},x_{2},...,x_{n}\}$ be a finite universe, $\fancyscript{C}=\{C_{1}, C_{2}, ..., C_{m}\}$ a covering of $U$, and $M_{\fancyscript{C}}=(a_{ij})_{n\times m}$, where $a_{ij}=\left\{ \begin{array}{ll} 1,& x_{i}\in C_{j}\\ 0,&x_{i}\notin C_{j}. \end{array} \right.$ Then $M_{\fancyscript{C}}$ is called a matrice representation of $\fancyscript{C}$.

By Definition 2.3, Wang et al. provided concepts of the type-1 and type-2 characteristic matrices of coverings.

Definition 2.4

[45] Let $U=\{x_{1},x_{2},...,x_{n}\}$ be a finite universe, $\fancyscript{C}=\{C_{1}, C_{2}, ..., C_{m}\}$ a covering of $U$, and $M_{\fancyscript{C}}=(a_{ij})_{n\times m}$ the matrice representation of $\fancyscript{C}$. Then $M_{\fancyscript{C}}\cdot M_{\fancyscript{C}}^{T}=(b_{ij})_{n\times n}$ is called the type-1 characteristic matrice of $\fancyscript{C}$, where $a_{ij}=\left\{ \begin{array}{ccc} 1,&{}\mathrm{}&{} x_{i}\in C_{j};\\ 0,&{}\mathrm{}&{} x_{i}\notin C_{j}. \end{array} \right.$ and $b_{ij}=\bigvee ^{m}_{k=1}(a_{ik}\cdot a_{jk})$.

For convenience, we denote $M_{\fancyscript{C}}\cdot M_{\fancyscript{C}}^{T}$ as $\Gamma (\fancyscript{C})$. Actually, $M_{\fancyscript{C}}\cdot M_{\fancyscript{C}}^{T}$ is the boolean product of $M_{\fancyscript{C}}$ and its transpose $M_{\fancyscript{C}}^{T}$. In addition, we obtain the characteristic function $\mathcal {X}_{X} =\left[ \begin{array}{cccccc} a_{1}&{}a_{2}&{}.&{}.&{}. &{} a_{n} \\ \end{array} \right] ^{T}$ of $X\subseteq U$, where $a_{i}=\left\{ \begin{array}{ccc} 1,&{}\mathrm{}&{} x_{i}\in X;\\ 0,&{}\mathrm{}&{} x_{i}\notin X. \end{array} \right.$

Definition 2.5

[45] Let $A=(a_{ij})_{n\times m}$ and $B=(b_{ij})_{m\times p}$ be two boolean matrices, $C=A\odot B=(c_{ij})_{n\times p}$, where $c_{ij}=\bigwedge ^{m}_{k=1}(b_{kj}-a_{ik}+1).$ If $\fancyscript{C}$ is a covering of the universe $U$, then $M_{\fancyscript{C}}\odot M_{\fancyscript{C}}^{T}$, denoted as $\prod (\fancyscript{C})$, is called the type-2 characteristic matrice of $\fancyscript{C}$.

By using the type-1 and type-2 characteristic matrices, Wang et al. axiomatized the second and sixth lower and upper approximation operators equivalently.

Definition 2.6

[45] Let $U=\{x_{1},x_{2},...,x_{n}\}$ be a finite universe, $\fancyscript{C}=\{C_{1},C_{2},...,C_{m}\}$ a covering of $U$, and $\mathcal {X}_{X}$ the characteristic function of $X$ in $U$. Then

• (1) $\mathcal {X}_{SH(X)}=\Gamma (\fancyscript{C})\cdot \mathcal {X}_{X}$, $\mathcal {X}_{SL(X)}=\Gamma (\fancyscript{C})\odot \mathcal {X}_{X}$;

• (2) $\mathcal {X}_{XH(X)}=\prod (\fancyscript{C})\cdot \mathcal {X}_{X}$, $\mathcal {X}_{XL(X)}=\prod (\fancyscript{C})\odot \mathcal {X}_{X}$.

By Definitions 2.2 and 2.6, we have $\mathcal {X}_{SH(X)}=\Gamma (\fancyscript{X}_{\fancyscript{C}})\cdot \mathcal {X}_{X}$ and $\mathcal {X}_{SL(X)}=\Gamma (\fancyscript{X}_{\fancyscript{C}})\odot \mathcal {X}_{X}$.

3 Incremental approaches to computing approximations of sets

In this section, we present incremental approaches to computing the second and sixth lower and upper approximations of sets by using the type-1 and type-2 characteristic matrices, respectively.

Definition 3.1

Let $(U,\fancyscript{C})$ and $(U^{+},\fancyscript{C}^{+})$ be covering approximation spaces, where $U=\{x_{1},x_{2},...,x_{n}\}$, $U^{+}=U\cup U^{*},$ $U^{*}=\{x_{i}|n+1\le i\le n+t, t\ge 2\}$, $\fancyscript{C}=\{C_{1},C_{2},...,C_{m}\}$, $\fancyscript{C}^{+}=\{C^{+}_{1},C^{+}_{2},...,C^{+}_{m}\}$, where $C^{+}_{i}=C_{i}\cup \Delta C_{i}$ and $\Delta C_{i}\subseteq U^{*}$. Then $(U^{+},\fancyscript{C}^{+})$ is called a AOS-covering approximation space.

In Definition 3.1, we get $C^{+}_{i}$ when adding some objects of $U^{*}$ into $C_{i}$, and $\fancyscript{C}^{+}$ is called a AOS-covering. In addition, it is time-consuming to compute the type-1 and type-2 characteristic matrices of AOS-coverings by Definitions 2.4 and 2.5, respectively. So there is a need to present an effective approach to constructing the characteristic matrices.

Remark

In practice, there are two aspects: $|\fancyscript{C}^{+}|=|\fancyscript{C}|$ and $|\fancyscript{C}^{+}|>|\fancyscript{C}|$ when adding more objects, where $|\bullet |$ denotes the cardinality of $\bullet$. Furthermore, the incremental approaches are proposed for knowledge reduction of dynamic information systems which vary with the time. The cardinality of the object set in the original information system is very large in general. In other words, $t$ is far less than $n$. If $n$ is far less than $t$, then the incremental approaches are not more efficient than the non-incremental approaches. For convenience, we only discuss the AOS-covering approximation space when $|\fancyscript{C}^{+}|=|\fancyscript{C}|$ and $t$ is far less than $n$ in this work. In our future work, we will discuss the situation $|\fancyscript{C}^{+}|>|\fancyscript{C}|$ when adding more objects.

Below, we discuss the relationship between $\Gamma (\fancyscript{C})$ and $\Gamma (\fancyscript{C}^{+})$. For convenience, we denote $M_{\fancyscript{C}}=(a_{ij})_{n\times m}$, $M_{\fancyscript{C}^{+}}=(a_{ij})_{(n+t)\times m}$, $\Gamma (\fancyscript{C})=(b_{ij})_{n\times n}$ and $\Gamma (\fancyscript{C}^{+})=(c_{ij})_{(n+t)\times (n+t)}$.

Theorem 3.2

Let $(U^{+},\fancyscript{C}^{+})$ be a AOS-covering approximation space of $(U,\fancyscript{C})$, $\Gamma (\fancyscript{C})$ and $\Gamma (\fancyscript{C}^{+})$ the type-1 characteristic matrices of $\fancyscript{C}$ and $\fancyscript{C}^{+}$, respectively. Then

$$\begin{aligned} \Gamma (\fancyscript{C}^{+})=\left[ \begin{array}{ll} \Gamma (\fancyscript{C}) &{} (\triangle _{1}\Gamma (\fancyscript{C}))^{T} \\ \triangle _{1}\Gamma (\fancyscript{C}) &{} \triangle _{2}\Gamma (\fancyscript{C}) \\ \end{array} \right] , \end{aligned}$$

where

$$\begin{aligned} \triangle _{1}\Gamma (\fancyscript{C})&= \left[ \begin{array}{cccccc} a_{(n+1)1}&{}a_{(n+1)2}&{}.&{}.&{}. &{} a_{(n+1)m} \\ a_{(n+2)1}&{}a_{(n+2)2}&{}.&{}.&{}. &{} a_{(n+2)m} \\ .&{}.&{}.&{}.&{}. &{} . \\ .&{}.&{}.&{}.&{}. &{} . \\ .&{}.&{}.&{}.&{}. &{} . \\ a_{(n+t)1}&{}a_{(n+t)2}&{}.&{}.&{}. &{} a_{(n+t)m} \\ \end{array} \right] \cdot M^{T}_{\fancyscript{C}};\\ \triangle _{2}\Gamma (\fancyscript{C})&= \left[ \begin{array}{cccccc} a_{(n+1)1}&{}a_{(n+1)2}&{}.&{}.&{}. &{} a_{(n+1)m} \\ a_{(n+2)1}&{}a_{(n+2)2}&{}.&{}.&{}. &{} a_{(n+2)m} \\ .&{}.&{}.&{}.&{}. &{} . \\ .&{}.&{}.&{}.&{}. &{} . \\ .&{}.&{}.&{}.&{}. &{} . \\ a_{(n+t)1}&{}a_{(n+t)2}&{}.&{}.&{}. &{} a_{(n+t)m} \\ \end{array} \right] \cdot \left[ \begin{array}{cccccc} a_{(n+1)1}&{}a_{(n+1)2}&{}.&{}.&{}. &{} a_{(n+1)m} \\ a_{(n+2)1}&{}a_{(n+2)2}&{}.&{}.&{}. &{} a_{(n+2)m} \\ .&{}.&{}.&{}.&{}. &{} . \\ .&{}.&{}.&{}.&{}. &{} . \\ .&{}.&{}.&{}.&{}. &{} . \\ a_{(n+t)1}&{}a_{(n+t)2}&{}.&{}.&{}. &{} a_{(n+t)m} \\ \end{array} \right] ^{T}. \end{aligned}$$

Proof

In the sense of the type-1 characteristic matrice, we have $\Gamma (\fancyscript{C})$ and $\Gamma (\fancyscript{C}^{+})$ as follows:

$$\begin{aligned} \Gamma (\fancyscript{C})&= M_{\fancyscript{C}}\cdot M_{\fancyscript{C}}^{T}\\ {}&= \left[ \begin{array}{cccccc} a_{11} &{} a_{12} &{} . &{} . &{} . &{} a_{1m} \\ a_{21} &{} a_{22} &{} . &{} . &{} . &{} a_{2m} \\ . &{} . &{} . &{} . &{} . &{} . \\ . &{} . &{} . &{} . &{} . &{} . \\ . &{} . &{} . &{} . &{} . &{} . \\ a_{n1} &{} a_{n2} &{} . &{} . &{} . &{} a_{nm} \\ \end{array} \right] \cdot \left[ \begin{array}{cccccc} a_{11} &{} a_{12} &{} . &{} . &{} . &{} a_{1m} \\ a_{21} &{} a_{22} &{} . &{} . &{} . &{} a_{2m} \\ . &{} . &{} . &{} . &{} . &{} . \\ . &{} . &{} . &{} . &{} . &{} . \\ . &{} . &{} . &{} . &{} . &{} . \\ a_{n1} &{} a_{n2} &{} . &{} . &{} . &{} a_{nm} \\ \end{array} \right] ^{T} \\&= \left[ \begin{array}{cccccc} b_{11} &{} b_{12} &{} . &{} . &{} . &{} b_{1n} \\ b_{21} &{} b_{22} &{} . &{} . &{} . &{} b_{2n} \\ . &{} . &{} . &{} . &{} . &{} . \\ . &{} . &{} . &{} . &{} . &{} . \\ . &{} . &{} . &{} . &{} . &{} . \\ b_{n1} &{} b_{n2} &{} . &{} . &{} . &{} b_{nn} \\ \end{array} \right] ; \end{aligned}$$

$$\begin{aligned} \Gamma (\fancyscript{C}^{+})&= M_{\fancyscript{C}^{+}}\cdot M_{\fancyscript{C}^{+}}^{T}\\&= \left[ \begin{array}{cccccc} a_{11} &{} a_{12} &{} . &{} . &{} . &{} a_{1m} \\ a_{21} &{} a_{22} &{} . &{} . &{} . &{} a_{2m} \\ . &{} . &{} . &{} . &{} . &{} . \\ . &{} . &{} . &{} . &{} . &{} . \\ . &{} . &{} . &{} . &{} . &{} . \\ a_{n1} &{} a_{n2} &{} . &{} . &{} . &{} a_{nm} \\ a_{(n+1)1} &{} a_{(n+1)2} &{} . &{} . &{} . &{} a_{(n+1)m} \\ . &{} . &{} . &{} . &{} . &{} . \\ . &{} . &{} . &{} . &{} . &{} . \\ . &{} . &{} . &{} . &{} . &{} . \\ a_{(n+t)1} &{} a_{(n+t)2} &{} . &{} . &{} . &{} a_{(n+t)m} \\ \end{array} \right] \cdot \left[ \begin{array}{cccccc} a_{11} &{} a_{12} &{} . &{} . &{} . &{} a_{1m} \\ a_{21} &{} a_{22} &{} . &{} . &{} . &{} a_{2m} \\ . &{} . &{} . &{} . &{} . &{} . \\ . &{} . &{} . &{} . &{} . &{} . \\ . &{} . &{} . &{} . &{} . &{} . \\ a_{n1} &{} a_{n2} &{} . &{} . &{} . &{} a_{nm} \\ a_{(n+1)1} &{} a_{(n+1)2} &{} . &{} . &{} . &{} a_{(n+1)m} \\ . &{} . &{} . &{} . &{} . &{} . \\ . &{} . &{} . &{} . &{} . &{} . \\ . &{} . &{} . &{} . &{} . &{} . \\ a_{(n+t)1} &{} a_{(n+t)2} &{} . &{} . &{} . &{} a_{(n+t)m} \\ \end{array} \right] ^{T} \\ {}&= \left[ \begin{array}{ccccccccccc} c_{11} &{} c_{12} &{} . &{} . &{} . &{} c_{1n}&{} c_{1(n+1)}&{}.&{}.&{}.&{} c_{1(n+t)} \\ c_{21} &{} c_{22} &{} . &{} . &{} . &{} c_{2n}&{} c_{2(n+1)}&{}.&{}.&{}.&{} c_{2(n+t)} \\ . &{} . &{} . &{} . &{} . &{} . &{} . &{} . &{} . &{} . &{} .\\ . &{} . &{} . &{} . &{} . &{} . &{} . &{} . &{} . &{} . &{} .\\ . &{} . &{} . &{} . &{} . &{} . &{} . &{} . &{} . &{} . &{} .\\ c_{n1} &{} c_{n2} &{} . &{} . &{} .&{} c_{nn}&{} c_{n(n+1)}&{}.&{}.&{}. &{} c_{n(n+t)} \\ c_{(n+1)1} &{} c_{(n+1)2} &{} . &{} . &{} . &{} c_{(n+1)n}&{} c_{(n+1)(n+1)}&{}.&{}.&{}.&{} c_{(n+1)(n+t)} \\ . &{} . &{} . &{} . &{} . &{} . &{} . &{} . &{} . &{} . &{} .\\ . &{} . &{} . &{} . &{} . &{} . &{} . &{} . &{} . &{} . &{} .\\ . &{} . &{} . &{} . &{} . &{} . &{} . &{} . &{} . &{} . &{} .\\ c_{(n+t)1} &{} c_{(n+t)2} &{} . &{} . &{} . &{} c_{(n+t)n}&{} c_{(n+t)(n+1)}&{}.&{}.&{}.&{} c_{(n+t)(n+t)} \\ \end{array} \right] . \end{aligned}$$

By Definition 2.1, we see that $b_{ij}=c_{ij}$ for $1\le i,j\le n$. To obtain $\Gamma (\fancyscript{C}^{+})$ on the basis of $\Gamma (\fancyscript{C})$, we only need to compute $\triangle _{1}\Gamma (\fancyscript{C})=(c_{(n+i)j})_{(1\le i \le t, 1\le j\le n)}$ and $\triangle _{2}\Gamma (\fancyscript{C})=(c_{(n+i)(n+j)})_{(1\le i, j\le t)}$, where

$$\begin{aligned} \triangle _{1}\Gamma (\fancyscript{C})&= \left[ \begin{array}{cccccc} c_{(n+1)1} &{} c_{(n+1)2} &{} . &{} . &{} . &{} c_{(n+1)n}\\ c_{(n+2)1} &{} c_{(n+2)2} &{} . &{} . &{} . &{} c_{(n+2)n} \\ . &{} . &{} . &{} . &{} . &{} . \\ . &{} . &{} . &{} . &{} . &{} . \\ . &{} . &{} . &{} . &{} . &{} . \\ c_{(n+t)1} &{} c_{(n+t)2} &{} . &{} . &{} . &{} c_{(n+t)n}\\ \end{array} \right] \\&= \left[ \begin{array}{cccccc} a_{(n+1)1} &{} a_{(n+1)2} &{} . &{} . &{} . &{} a_{(n+1)m} \\ a_{(n+2)1} &{} a_{(n+2)2} &{} . &{} . &{} . &{} a_{(n+2)m} \\ . &{} . &{} . &{} . &{} . &{} . \\ . &{} . &{} . &{} . &{} . &{} . \\ . &{} . &{} . &{} . &{} . &{} . \\ a_{(n+t)1} &{} a_{(n+t)2} &{} . &{} . &{} . &{} a_{(n+t)m} \\ \end{array} \right] \cdot \left[ \begin{array}{cccccc} a_{11} &{} a_{12} &{} . &{} . &{} . &{} a_{1m} \\ a_{21} &{} a_{22} &{} . &{} . &{} . &{} a_{2m} \\ . &{} . &{} . &{} . &{} . &{} . \\ . &{} . &{} . &{} . &{} . &{} . \\ . &{} . &{} . &{} . &{} . &{} . \\ a_{n1} &{} a_{n2} &{} . &{} . &{} . &{} a_{nm} \\ \end{array} \right] ^{T};\\ \triangle _{2}\Gamma (\fancyscript{C})&= \left[ \begin{array}{ccccccccccc} c_{(n+1)(n+1)}&{}.&{}.&{}.&{} c_{(n+1)(n+t)} \\ c_{(n+2)(n+1)}&{}.&{}.&{}.&{} c_{(n+2)(n+t)} \\ . &{} . &{} . &{} . &{} .\\ . &{} . &{} . &{} . &{} .\\ . &{} . &{} . &{} . &{} .\\ c_{(n+t)(n+1)}&{}.&{}.&{}.&{} c_{(n+t)(n+t)} \\ \end{array} \right] \\&= \left[ \begin{array}{cccccc} a_{(n+1)1} &{} a_{(n+1)2} &{} . &{} . &{} . &{} a_{(n+1)m} \\ a_{(n+2)1} &{} a_{(n+2)2} &{} . &{} . &{} . &{} a_{(n+2)m} \\ . &{} . &{} . &{} . &{} . &{} . \\ . &{} . &{} . &{} . &{} . &{} . \\ . &{} . &{} . &{} . &{} . &{} . \\ a_{(n+t)1} &{} a_{(n+t)2} &{} . &{} . &{} . &{} a_{(n+t)m} \\ \end{array} \right] \cdot \left[ \begin{array}{cccccc} a_{(n+1)1} &{} a_{(n+1)2} &{} . &{} . &{} . &{} a_{(n+1)m} \\ a_{(n+2)1} &{} a_{(n+2)2} &{} . &{} . &{} . &{} a_{(n+2)m} \\ . &{} . &{} . &{} . &{} . &{} . \\ . &{} . &{} . &{} . &{} . &{} . \\ . &{} . &{} . &{} . &{} . &{} . \\ a_{(n+t)1} &{} a_{(n+t)2} &{} . &{} . &{} . &{} a_{(n+t)m} \\ \end{array} \right] ^{T}. \end{aligned}$$

Therefore,

$$\begin{aligned}\Gamma (\fancyscript{C}^{+})=\left[ \begin{array}{ll} \Gamma (\fancyscript{C}) &{} (\triangle _{1}\Gamma (\fancyscript{C}))^{T} \\ \triangle _{1}\Gamma (\fancyscript{C}) &{} \triangle _{2}\Gamma (\fancyscript{C}) \\ \end{array} \right] . \end{aligned}$$

$\square$

By Theorem 3.2, we present an incremental algorithm of computing the second lower and upper approximations of sets.

Algorithm 3.3

Input: $(U,\fancyscript{C})$, $(U^{+},\fancyscript{C}^{+})$ and $X\subseteq U^{+}$.

Output: $\mathcal {X}_{SH(X)}$ and $\mathcal {X}_{SL(X)}.$

• Step 1: Constructing $M_{\fancyscript{C}}$ based on $\fancyscript{C}$.

• Step 2: Calculating $\Gamma (\fancyscript{C})$, where $\Gamma (\fancyscript{C})=M_{\fancyscript{C}}\cdot M^{T}_{\fancyscript{C}}.$

• Step 3: Computing $M_{\fancyscript{C}^{+}}$, where

  $$\begin{aligned} M_{\fancyscript{C}^{+}}=\left[ \begin{array}{c} M_{\fancyscript{C}}\\ \Delta M_{\fancyscript{C}} \end{array} \right] , \,\, \Delta M_{\fancyscript{C}}=\left[ \begin{array}{cccccc} a_{(n+1)1} &{} a_{(n+1)2}&{} .&{}.&{}. &{} a_{(n+1)m} \\ a_{(n+2)1} &{} a_{(n+2)2}&{} .&{}.&{}. &{} a_{(n+2)m} \\ . &{} .&{} .&{}.&{}. &{} . \\ . &{} .&{} .&{}.&{}. &{} . \\ . &{} .&{} .&{}.&{}. &{} . \\ a_{(n+t)1} &{} a_{(n+t)2}&{} .&{}.&{}. &{} a_{(n+t)m} \\ \end{array} \right] . \end{aligned}$$

• Step 4: Getting $\triangle _{1}\Gamma (\fancyscript{C})$ and $\triangle _{2}\Gamma (\fancyscript{C})$, where

  $$\begin{aligned} \triangle _{1}\Gamma (\fancyscript{C})=\Delta M_{\fancyscript{C}}\cdot (M_{\fancyscript{C}})^{T}, \triangle _{2}\Gamma (\fancyscript{C}) = \Delta M_{\fancyscript{C}}\cdot (\Delta M_{\fancyscript{C}})^{T}. \end{aligned}$$

• Step 5: Computing $\Gamma (\fancyscript{C}^{+})$, where

  $$\begin{aligned} \Gamma (\fancyscript{C}^{+})&= \left[ \begin{array}{cc} \Gamma (\fancyscript{C}) &{} (\triangle _{1}\Gamma (\fancyscript{C}))^{T} \\ \triangle _{1}\Gamma (\fancyscript{C}) &{} \triangle _{2}\Gamma (\fancyscript{C}) \\ \end{array} \right] . \end{aligned}$$

• Step 6: Obtaining $\mathcal {X}_{SH(X)}$ and $\mathcal {X}_{SL(X)}$, where

  $$\begin{aligned} \mathcal {X}_{SH(X)}=\Gamma (\fancyscript{C}^{+})\cdot \mathcal {X}_{X}, \mathcal {X}_{SL(X)}=\Gamma (\fancyscript{C}^{+})\odot \mathcal {X}_{X}. \end{aligned}$$

By analyzing Algorithm 3.3, we see that the time of the incremental algorithm for computing the second lower and upper approximations of sets is less than that of the non-incremental algorithm. In other words, the incremental algorithm is more effective than the non-incremental algorithm when computing the second lower and upper approximations of sets in dynamic covering approximation spaces.

Remark

Since $SH$ and $SL$ are dual operators, we simplify the calculus of approximations of concepts. For example, for any $X\subseteq U$, we have

$$\begin{aligned} \mathcal {X}_{SH(X)}&= \mathcal {X}_{U}-\Gamma (\fancyscript{C}^{+})\odot \mathcal {X}_{X^{c}}=\mathcal {X}_{U}-\mathcal {X}_{SL(X^{c})};\\ \mathcal {X}_{SL(X)}&= \mathcal {X}_{U}-\Gamma (\fancyscript{C}^{+})\cdot \mathcal {X}_{X^{c}} =\mathcal {X}_{U}-\mathcal {X}_{SH(X^{c})}. \end{aligned}$$

In other words, we have $\mathcal {X}_{SH(X)}$ and $\mathcal {X}_{SL(X)}$ based on $\mathcal {X}_{SL(X^{c})}$ and $\mathcal {X}_{SH(X^{c})}$ for any $X\subseteq U$, respectively.

The following example is employed to show the process of constructing approximations of sets by using Algorithm 3.3.

Example 3.4

Let $U=\{x_{1},x_{2},x_{3},x_{4}\}$, $U^{+}=U\cup \{x_{5},x_{6}\}$, $\fancyscript{C}=\{C_{1},C_{2},C_{3}\}$, $\fancyscript{C}^{+}=\{C^{+}_{1},C^{+}_{2},C^{+}_{3}\}$, where $C_{1}=\{x_{1},x_{4}\}$, $C_{2}=\{x_{1},x_{2},x_{4}\}$, $C_{3}=\{x_{3},x_{4}\}$, $C^{+}_{1}=\{x_{1},x_{4},x_{5}\}$, $C^{+}_{2}=\{x_{1},x_{2},x_{4},x_{5},x_{6}\}$, $C^{+}_{3}=\{x_{3},x_{4},x_{6}\}$, and $X=\{x_{3},x_{4},x_{5},x_{6}\}$. By Definition 2.4, we first have that

$$\begin{aligned} \Gamma (\fancyscript{C})&= M_{\fancyscript{C}}\cdot M_{\fancyscript{C}}^{T}=\left[ \begin{array}{cccc} 1 &{} 1 &{} 0 \\ 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 \\ 1 &{} 1 &{} 1 \\ \end{array} \right] \cdot \left[ \begin{array}{cccc} 1 &{} 1 &{} 0 \\ 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 \\ 1 &{} 1 &{} 1 \\ \end{array} \right] ^{T} =\left[ \begin{array}{cccc} 1 &{} 1 &{} 0 &{} 1 \\ 1 &{} 1 &{} 0 &{} 1 \\ 0 &{} 0 &{} 1 &{} 1 \\ 1 &{} 1 &{} 1 &{} 1 \\ \end{array} \right] . \end{aligned}$$

On the other hand, $\fancyscript{X}_{\fancyscript{C}}=\bigcup \{MD(\fancyscript{C}, x_{i})|x_{i}\in U\}=\{C_{2},C_{3}\}$. In the sense of the maximal description, we have

$$\begin{aligned} \Gamma (\fancyscript{C})&= \Gamma (\fancyscript{X}_{\fancyscript{C}})=M_{\fancyscript{X}_{\fancyscript{C}}}\cdot M_{\fancyscript{X}_{\fancyscript{C}}}^{T}=\left[ \begin{array}{ccc} 1 &{} 0 \\ 1 &{} 0 \\ 0 &{} 1 \\ 1 &{} 1 \\ \end{array} \right] \cdot \left[ \begin{array}{ccc} 1 &{} 0 \\ 1 &{} 0 \\ 0 &{} 1 \\ 1 &{} 1 \\ \end{array} \right] ^{T} =\left[ \begin{array}{cccc} 1 &{} 1 &{} 0 &{} 1 \\ 1 &{} 1 &{} 0 &{} 1 \\ 0 &{} 0 &{} 1 &{} 1 \\ 1 &{} 1 &{} 1 &{} 1 \\ \end{array} \right] . \end{aligned}$$

Second, by Theorem 3.2, we get that

$$\begin{aligned} \triangle _{1}\Gamma (\fancyscript{C})&= \left[ \begin{array}{ccc} 1 &{} 1 &{} 0 \\ 0 &{} 1 &{} 1 \\ \end{array} \right] \cdot \left[ \begin{array}{cccc} \begin{array}{cccc} 1 &{} 0 &{} 0 &{} 1 \\ 1 &{} 1 &{} 0 &{} 1 \\ 0 &{} 0 &{} 1 &{} 1 \\ \end{array} \end{array} \right] =\left[ \begin{array}{cccc} 1 &{} 1 &{} 0 &{} 1 \\ 1 &{} 1 &{} 1 &{} 1 \\ \end{array} \right] ;\\ \triangle _{2}\Gamma (\fancyscript{C})&= \left[ \begin{array}{ccc} 1 &{} 1 &{} 0 \\ 0 &{} 1 &{} 1 \\ \end{array} \right] \cdot \left[ \begin{array}{cccc} 1 &{} 1 &{} 0 \\ 0 &{} 1 &{} 1 \\ \end{array} \right] ^{T}=\left[ \begin{array}{cc} 1 &{}1\\ 1 &{}1\\ \end{array} \right] . \end{aligned}$$

Thus, we obtain that

$$\begin{aligned} \Gamma (\fancyscript{C}^{+})&= \left[ \begin{array}{cc} \Gamma (\fancyscript{C}) &{} (\triangle _{1}\Gamma (\fancyscript{C}))^{T} \\ \triangle _{1}\Gamma (\fancyscript{C}) &{} \triangle _{2}\Gamma (\fancyscript{C}) \\ \end{array} \right] =\left[ \begin{array}{cccccc} 1 &{} 1 &{} 0 &{} 1 &{}1 &{} 1\\ 1 &{} 1 &{} 0 &{} 1 &{}1 &{} 1\\ 0 &{} 0 &{} 1 &{} 1 &{}0 &{} 1\\ 1 &{} 1 &{} 1 &{} 1 &{}1 &{} 1\\ 1 &{} 1 &{} 0 &{} 1 &{}1 &{} 1\\ 1 &{} 1 &{} 1 &{} 1 &{}1 &{} 1\\ \end{array} \right] . \end{aligned}$$

By Definition 2.6, we have that

$$\begin{aligned} \mathcal {X}_{SH(X)}&= \Gamma (\fancyscript{C}^{+})\cdot \mathcal {X}_{X} =\left[ \begin{array}{cccccc} 1 &{} 1 &{} 0 &{} 1 &{}1 &{} 1\\ 1 &{} 1 &{} 0 &{} 1 &{}1 &{} 1\\ 0 &{} 0 &{} 1 &{} 1 &{}0 &{} 1\\ 1 &{} 1 &{} 1 &{} 1 &{}1 &{} 1\\ 1 &{} 1 &{} 0 &{} 1 &{}1 &{} 1\\ 1 &{} 1 &{} 1 &{} 1 &{}1 &{} 1\\ \end{array} \right] \cdot \left[ \begin{array}{c} 0 \\ 0 \\ 1 \\ 1 \\ 1 \\ 1 \\ \end{array} \right] =\left[ \begin{array}{cccccc} 1 &{} 1 &{} 1 &{} 1 &{} 1 &{} 1 \\ \end{array} \right] ^{T};\\ \mathcal {X}_{SL(X)}&= \Gamma (\fancyscript{C}^{+})\odot \mathcal {X}_{X} =\left[ \begin{array}{cccccc} 1 &{} 1 &{} 0 &{} 1 &{}1 &{} 1\\ 1 &{} 1 &{} 0 &{} 1 &{}1 &{} 1\\ 0 &{} 0 &{} 1 &{} 1 &{}0 &{} 1\\ 1 &{} 1 &{} 1 &{} 1 &{}1 &{} 1\\ 1 &{} 1 &{} 0 &{} 1 &{}1 &{} 1\\ 1 &{} 1 &{} 1 &{} 1 &{}1 &{} 1\\ \end{array} \right] \odot \left[ \begin{array}{c} 0 \\ 0 \\ 1 \\ 1 \\ 1 \\ 1 \\ \end{array} \right] =\left[ \begin{array}{cccccc} 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0 \\ \end{array} \right] ^{T};\\ \mathcal {X}_{SH(X^{c})}&= \left[ \begin{array}{cccccc} 1 &{} 1 &{} 1 &{} 1 &{}1 &{} 1\\ \end{array} \right] ^{T}-\mathcal {X}_{SL(X)} =\left[ \begin{array}{cccccc} 1 &{} 1 &{} 0 &{} 1 &{} 1 &{} 1 \\ \end{array} \right] ^{T};\\ \mathcal {X}_{SL(X^{c})}&= \left[ \begin{array}{cccccc} 1 &{} 1 &{} 1 &{} 1 &{}1 &{} 1\\ \end{array} \right] ^{T}-\mathcal {X}_{SH(X)} =\left[ \begin{array}{cccccc} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \end{array} \right] ^{T}. \end{aligned}$$

Therefore, we have $SH(X)=\{x_{1},x_{2},x_{3},x_{4},x_{5},x_{6}\}$, $SL(X)=\{x_{3}\}$, $SH(X^{c})=\{x_{1},x_{2},x_{4},x_{5},x_{6}\}$ and $SL(X^{c})=\emptyset$.

In Example 3.4, there is a need to compute all elements in $\Gamma (\fancyscript{C}^{+})$ by Definition 2.4. By Theorem 3.2, we only need to calculate elements in $\triangle _{1}\Gamma (\fancyscript{C})$ and $\triangle _{2}\Gamma (\fancyscript{C})$. Thereby, the incremental algorithm is more effective to compute approximations of sets in dynamic covering approximation spaces.

Subsequently, we construct $\prod (\fancyscript{C}^{+})$ based on $\prod (\fancyscript{C})$. For convenience, we denote $\prod (\fancyscript{C})=(d_{ij})_{n\times n}$ and $\prod (\fancyscript{C}^{+})=(e_{ij})_{(n+t)\times (n+t)}$.

Theorem 3.5

Let $(U^{+},\fancyscript{C}^{+})$ be a AOS-covering approximation space of $(U,\fancyscript{C})$, $\prod (\fancyscript{C})$ and $\prod (\fancyscript{C}^{+})$ the type-2 characteristic matrices of $\fancyscript{C}$ and $\fancyscript{C}^{+}$, respectively. Then

$$\begin{aligned} \prod (\fancyscript{C}^{+})=\left[ \begin{array}{ll} \prod (\fancyscript{C}) &{} \triangle _{2}\prod (\fancyscript{C}) \\ \triangle _{1}\prod (\fancyscript{C}) &{} \triangle _{3}\prod (\fancyscript{C}) \\ \end{array} \right] , \end{aligned}$$

where

$$\begin{aligned} \triangle _{1}\prod (\fancyscript{C})&= \Delta M_{\fancyscript{C}}\odot M^{T}_{\fancyscript{C}}; \triangle _{2}\prod (\fancyscript{C})=M_{\fancyscript{C}}\odot (\Delta M_{\fancyscript{C}})^{T};\\ \triangle _{3}\prod (\fancyscript{C})&= \Delta M_{\fancyscript{C}}\odot (\Delta M_{\fancyscript{C}})^{T}; \Delta M_{\fancyscript{C}}= \left[ \begin{array}{cccccc} a_{(n+1)1} &{} a_{(n+1)2} &{} .&{}.&{}. &{} a_{(n+1)m} \\ a_{(n+2)1} &{} a_{(n+2)2} &{} .&{}.&{}. &{} a_{(n+2)m} \\ . &{} . &{} .&{}.&{}. &{} . \\ . &{} . &{} .&{}.&{}. &{} . \\ . &{} . &{} .&{}.&{}. &{} . \\ a_{(n+t)1} &{} a_{(n+t)2} &{} .&{}.&{}. &{} a_{(n+t)m} \\ \end{array} \right] . \end{aligned}$$

Proof

By Definition 2.5, we have the type-2 characteristic matrices of $\fancyscript{C}$ and $\fancyscript{C}^{+}$ as follows:

$$\begin{aligned} \prod (\fancyscript{C})&= M_{\fancyscript{C}}\odot M_{\fancyscript{C}}^{T}\\&= \left[ \begin{array}{cccccc} a_{11} &{} a_{12} &{} . &{} . &{} . &{} a_{1m} \\ a_{21} &{} a_{22} &{} . &{} . &{} . &{} a_{2m} \\ . &{} . &{} . &{} . &{} . &{} . \\ . &{} . &{} . &{} . &{} . &{} . \\ . &{} . &{} . &{} . &{} . &{} . \\ a_{n1} &{} a_{n2} &{} . &{} . &{} . &{} a_{nm} \\ \end{array} \right] \odot \left[ \begin{array}{cccccc} a_{11} &{} a_{12} &{} . &{} . &{} . &{} a_{1m} \\ a_{21} &{} a_{22} &{} . &{} . &{} . &{} a_{2m} \\ . &{} . &{} . &{} . &{} . &{} . \\ . &{} . &{} . &{} . &{} . &{} . \\ . &{} . &{} . &{} . &{} . &{} . \\ a_{n1} &{} a_{n2} &{} . &{} . &{} . &{} a_{nm} \\ \end{array} \right] ^{T}\\&= \left[ \begin{array}{cccccc} d_{11} &{} d_{12} &{} . &{} . &{} . &{} d_{1n} \\ d_{21} &{} d_{22} &{} . &{} . &{} . &{} d_{2n} \\ . &{} . &{} . &{} . &{} . &{} . \\ . &{} . &{} . &{} . &{} . &{} . \\ . &{} . &{} . &{} . &{} . &{} . \\ d_{n1} &{} d_{n2} &{} . &{} . &{} . &{} d_{nn} \\ \end{array} \right] ;\\ \prod (\fancyscript{C}^{+})&= M_{\fancyscript{C}^{+}}\odot M_{\fancyscript{C}^{+}}^{T}\\ {}&= \left[ \begin{array}{cccccc} a_{11} &{} a_{12} &{} . &{} . &{} . &{} a_{1m} \\ a_{21} &{} a_{22} &{} . &{} . &{} . &{} a_{2m} \\ . &{} . &{} . &{} . &{} . &{} . \\ . &{} . &{} . &{} . &{} . &{} . \\ . &{} . &{} . &{} . &{} . &{} . \\ a_{n1} &{} a_{n2} &{} . &{} . &{} . &{} a_{nm} \\ a_{(n+1)1} &{} a_{(n+1)2} &{} . &{} . &{} . &{} a_{(n+1)m} \\ . &{} . &{} . &{} . &{} . &{} . \\ . &{} . &{} . &{} . &{} . &{} . \\ . &{} . &{} . &{} . &{} . &{} . \\ a_{(n+t)1} &{} a_{(n+t)2} &{} . &{} . &{} . &{} a_{(n+t)m} \\ \end{array} \right] \odot \left[ \begin{array}{cccccc} a_{11} &{} a_{12} &{} . &{} . &{} . &{} a_{1m} \\ a_{21} &{} a_{22} &{} . &{} . &{} . &{} a_{2m} \\ . &{} . &{} . &{} . &{} . &{} . \\ . &{} . &{} . &{} . &{} . &{} . \\ . &{} . &{} . &{} . &{} . &{} . \\ a_{n1} &{} a_{n2} &{} . &{} . &{} . &{} a_{nm} \\ a_{(n+1)1} &{} a_{(n+1)2} &{} . &{} . &{} . &{} a_{(n+1)m} \\ . &{} . &{} . &{} . &{} . &{} . \\ . &{} . &{} . &{} . &{} . &{} . \\ . &{} . &{} . &{} . &{} . &{} . \\ a_{(n+t)1} &{} a_{(n+t)2} &{} . &{} . &{} . &{} a_{(n+t)m} \\ \end{array} \right] ^{T} \end{aligned}$$

$$\begin{aligned}&= \left[ \begin{array}{ccccccccccc} e_{11} &{} e_{12} &{} . &{} . &{} . &{} e_{1n}&{} e_{1(n+1)}&{}.&{}.&{}.&{} e_{1(n+t)} \\ e_{21} &{} e_{22} &{} . &{} . &{} . &{} e_{2n}&{} e_{2(n+1)}&{}.&{}.&{}.&{} e_{2(n+t)} \\ . &{} . &{} . &{} . &{} . &{} . &{} . &{} . &{} . &{} . &{} .\\ . &{} . &{} . &{} . &{} . &{} . &{} . &{} . &{} . &{} . &{} .\\ . &{} . &{} . &{} . &{} . &{} . &{} . &{} . &{} . &{} . &{} .\\ e_{n1} &{} e_{n2} &{} . &{} . &{} .&{} e_{nn}&{} e_{n(n+1)}&{}.&{}.&{}. &{} e_{n(n+t)} \\ e_{(n+1)1} &{} e_{(n+1)2} &{} . &{} . &{} . &{} e_{(n+1)n}&{} e_{(n+1)(n+1)}&{}.&{}.&{}.&{} e_{(n+1)(n+t)} \\ . &{} . &{} . &{} . &{} . &{} . &{} . &{} . &{} . &{} . &{} .\\ . &{} . &{} . &{} . &{} . &{} . &{} . &{} . &{} . &{} . &{} .\\ . &{} . &{} . &{} . &{} . &{} . &{} . &{} . &{} . &{} . &{} .\\ e_{(n+t)1} &{} e_{(n+t)2} &{} . &{} . &{} . &{} e_{(n+t)n}&{} e_{(n+t)(n+1)}&{}.&{}.&{}.&{} e_{(n+t)(n+t)} \\ \end{array} \right] . \end{aligned}$$

In the sense of the type-2 characteristic matrices, we observe that $d_{ij}=e_{ij}$ for $1\le i,j\le n$. To obtain $\prod (\fancyscript{C}^{+})$ based on $\prod (\fancyscript{C})$, we need to compute $\triangle _{1}\prod (\fancyscript{C})=(e_{(n+i)j})_{(1\le i \le t,1\le j\le m)}$, $\triangle _{2}\prod (\fancyscript{C})=(e_{i(n+j)})_{(1\le i \le n,1\le j\le t)}$ and $\triangle _{3}\prod (\fancyscript{C})=(e_{(n+i)(n+j)})_{(1\le i, j\le t)}$, where

$$\begin{aligned} \triangle _{1}\prod (\fancyscript{C})&= \left[ \begin{array}{cccccc} e_{(n+1)1} &{} e_{(n+1)2} &{} . &{} . &{} . &{} e_{(n+1)n}\\ e_{(n+2)1} &{} e_{(n+2)2} &{} . &{} . &{} . &{} e_{(n+2)n}\\ . &{} . &{} . &{} . &{} . &{} . \\ . &{} . &{} . &{} . &{} . &{} . \\ . &{} . &{} . &{} . &{} . &{} . \\ e_{(n+t)1} &{} e_{(n+t)2} &{} . &{} . &{} . &{} e_{(n+t)n} \\ \end{array} \right] \\&= \left[ \begin{array}{cccccc} a_{(n+1)1} &{} a_{(n+1)2} &{} . &{} . &{} . &{} a_{(n+1)m} \\ a_{(n+2)1} &{} a_{(n+2)2} &{} . &{} . &{} . &{} a_{(n+2)m} \\ . &{} . &{} . &{} . &{} . &{} . \\ . &{} . &{} . &{} . &{} . &{} . \\ . &{} . &{} . &{} . &{} . &{} . \\ a_{(n+t)1} &{} a_{(n+t)2} &{} . &{} . &{} . &{} a_{(n+t)m} \\ \end{array} \right] \odot \left[ \begin{array}{cccccc} a_{11} &{} a_{12} &{} . &{} . &{} . &{} a_{1m} \\ a_{21} &{} a_{22} &{} . &{} . &{} . &{} a_{2m} \\ . &{} . &{} . &{} . &{} . &{} . \\ . &{} . &{} . &{} . &{} . &{} . \\ . &{} . &{} . &{} . &{} . &{} . \\ a_{n1} &{} a_{n2} &{} . &{} . &{} . &{} a_{nm} \\ \end{array} \right] ^{T};\\ \triangle _{2}\prod (\fancyscript{C})&= \left[ \begin{array}{ccccccccccc} e_{1(n+1)} &{} e_{1(n+2)} &{} . &{} . &{} . &{} e_{1(n+t)}\\ e_{2(n+1)} &{} e_{2(n+2)} &{} . &{} . &{} . &{} e_{2(n+t)}\\ . &{} . &{} . &{} . &{} . &{} .\\ . &{} . &{} . &{} . &{} . &{} .\\ . &{} . &{} . &{} . &{} . &{} .\\ e_{n(n+1)} &{} e_{n(n+2)} &{} . &{} . &{} . &{} e_{n(n+t)}\\ \end{array} \right] \\&= \left[ \begin{array}{cccccc} a_{11} &{} a_{12} &{} . &{} . &{} . &{} a_{1m} \\ a_{21} &{} a_{22} &{} . &{} . &{} . &{} a_{2m} \\ . &{} . &{} . &{} . &{} . &{} . \\ . &{} . &{} . &{} . &{} . &{} . \\ . &{} . &{} . &{} . &{} . &{} . \\ a_{n1} &{} a_{n2} &{} . &{} . &{} . &{} a_{nm} \\ \end{array} \right] \odot \left[ \begin{array}{cccccc} a_{(n+1)1} &{} a_{(n+1)2} &{} . &{} . &{} . &{} a_{(n+1)m} \\ a_{(n+2)1} &{} a_{(n+2)2} &{} . &{} . &{} . &{} a_{(n+2)m} \\ . &{} . &{} . &{} . &{} . &{} . \\ . &{} . &{} . &{} . &{} . &{} . \\ . &{} . &{} . &{} . &{} . &{} . \\ a_{(n+t)1} &{} a_{(n+t)2} &{} . &{} . &{} . &{} a_{(n+t)m} \\ \end{array} \right] ^{T};\\ \triangle _{3}\prod (\fancyscript{C})&= \left[ \begin{array}{cccccccccccc} e_{(n+1)(n+1)}&{}e_{(n+1)(n+2)}&{}.&{}.&{}.&{} e_{(n+1)(n+t)} \\ e_{(n+1)(n+1)}&{}e_{(n+2)(n+2)}&{}.&{}.&{}.&{} e_{(n+2)(n+t)} \\ . &{}. &{} . &{} . &{} . &{} . \\ . &{}. &{} . &{} . &{} . &{} . \\ . &{}. &{} . &{} . &{} . &{} . \\ e_{(n+1)(n+1)}&{}e_{(n+t)(n+2)}&{}.&{}.&{}.&{} e_{(n+t)(n+t)} \\ \end{array} \right] \\&= \left[ \begin{array}{cccccc} a_{(n+1)1} &{} a_{(n+1)2} &{} . &{} . &{} . &{} a_{(n+1)m} \\ a_{(n+2)1} &{} a_{(n+2)2} &{} . &{} . &{} . &{} a_{(n+2)m} \\ . &{} . &{} . &{} . &{} . &{} . \\ . &{} . &{} . &{} . &{} . &{} . \\ . &{} . &{} . &{} . &{} . &{} . \\ a_{(n+t)1} &{} a_{(n+t)2} &{} . &{} . &{} . &{} a_{(n+t)m} \\ \end{array} \right] \odot \left[ \begin{array}{cccccc} a_{(n+1)1} &{} a_{(n+1)2} &{} . &{} . &{} . &{} a_{(n+1)m} \\ a_{(n+2)1} &{} a_{(n+2)2} &{} . &{} . &{} . &{} a_{(n+2)m} \\ . &{} . &{} . &{} . &{} . &{} . \\ . &{} . &{} . &{} . &{} . &{} . \\ . &{} . &{} . &{} . &{} . &{} . \\ a_{(n+t)1} &{} a_{(n+t)2} &{} . &{} . &{} . &{} a_{(n+t)m} \\ \end{array} \right] ^{T}. \end{aligned}$$

Therefore,

$$\begin{aligned}\prod (\fancyscript{C}^{+})=\left[ \begin{array}{cc} \prod (\fancyscript{C}) &{} \triangle _{2}\prod (\fancyscript{C}) \\ \triangle _{1}\prod (\fancyscript{C}) &{} \triangle _{3}\prod (\fancyscript{C}) \\ \end{array} \right] . \end{aligned}$$

$\square$

By Theorem 3.5, we provide an incremental algorithm of calculating the sixth lower and upper approximations of sets below.

Algorithm 3.6

• Input: $(U,\fancyscript{C})$, $(U^{+},\fancyscript{C}^{+})$ and $X\subseteq U^{+}$.

• Output: $\mathcal {X}_{XH(X)}$ and $\mathcal {X}_{XL(X)}$.

• Step 1: Constructing $M_{\fancyscript{C}}$ based on $\fancyscript{C}$.

• Step 2: Calculating $\prod (\fancyscript{C})$, where $\prod (\fancyscript{C})=M_{\fancyscript{C}}\odot M^{T}_{\fancyscript{C}}.$

• Step 3: Getting $M_{\fancyscript{C}^{+}}$, where

  $$\begin{aligned} M_{\fancyscript{C}^{+}}=\left[ \begin{array}{c} M_{\fancyscript{C}}\\ \Delta M_{\fancyscript{C}} \end{array} \right] , \,\, \Delta M_{\fancyscript{C}}=\left[ \begin{array}{cccccc} a_{(n+1)1} &{} a_{(n+1)2}&{} .&{}.&{}. &{} a_{(n+1)m} \\ a_{(n+2)1} &{} a_{(n+2)2}&{} .&{}.&{}. &{} a_{(n+2)m} \\ . &{} .&{} .&{}.&{}. &{} . \\ . &{} .&{} .&{}.&{}. &{} . \\ . &{} .&{} .&{}.&{}. &{} . \\ a_{(n+t)1} &{} a_{(n+t)2}&{} .&{}.&{}. &{} a_{(n+t)m} \\ \end{array} \right] . \end{aligned}$$

• Step 4: Computing $\triangle _{1}\prod (\fancyscript{C})$, $\triangle _{2}\prod (\fancyscript{C})$ and $\triangle _{3}\prod (\fancyscript{C})$, where

  $$\begin{aligned} \triangle _{1}\prod (\fancyscript{C})= \Delta M_{\fancyscript{C}}\odot M^{T}_{\fancyscript{C}}, \triangle _{2}\prod (\fancyscript{C})=M_{\fancyscript{C}}\odot (\Delta M_{\fancyscript{C}})^{T}, \triangle _{3}\prod (\fancyscript{C})=\Delta M_{\fancyscript{C}}\odot (\Delta M_{\fancyscript{C}})^{T}. \end{aligned}$$

• Step 5: Constructing $\prod (\fancyscript{C}^{+})$, where

  $$\begin{aligned} \prod (\fancyscript{C}^{+})&= \left[ \begin{array}{cc} \prod (\fancyscript{C}) &{} \triangle _{2}\prod (\fancyscript{C}) \\ \triangle _{1}\prod (\fancyscript{C}) &{} \triangle _{3}\prod (\fancyscript{C}) \\ \end{array} \right] . \end{aligned}$$

• Steps 6: Obtaining $\mathcal {X}_{XH(X)}$ and $\mathcal {X}_{XL(X)}$, where

  $$\begin{aligned} \mathcal {X}_{XH(X)}=\prod (\fancyscript{C}^{+})\cdot \mathcal {X}_{X}, \mathcal {X}_{XL(X)}=\prod (\fancyscript{C}^{+})\odot \mathcal {X}_{X}. \end{aligned}$$

By analyzing Algorithm 3.6, we see that the time of the incremental algorithm for computing the sixth lower and upper approximations of sets is less than that of the non-incremental algorithm. In other words, the incremental algorithm is more effective than the non-incremental algorithm when computing the sixth lower and upper approximations of sets in dynamic covering approximation spaces.

The following example is employed to illustrate that how to compute the sixth lower and upper approximations of set with Algorithm 3.6.

Example 3.7

(Continuation of Example 3.4) By Definition 3.1, $\fancyscript{C}^{+}$ is a AOS-covering of $\fancyscript{C}$. Then we obtain that

$$\begin{aligned} \prod (\fancyscript{C})&= M_{\fancyscript{C}}\odot M_{\fancyscript{C}}^{T} =\left[ \begin{array}{cccc} 1 &{} 1 &{} 0 \\ 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 \\ 1 &{} 1 &{} 1 \\ \end{array} \right] \odot \left[ \begin{array}{cccc} 1 &{} 1 &{} 0 \\ 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 \\ 1 &{} 1 &{} 1 \\ \end{array} \right] ^{T} =\left[ \begin{array}{cccc} 1 &{} 0 &{} 0 &{} 1 \\ 1 &{} 1 &{} 0 &{} 1 \\ 0 &{} 0 &{} 1 &{} 1 \\ 0 &{} 0 &{} 0 &{} 1 \\ \end{array} \right] . \end{aligned}$$

By Theorem 3.5, we have that

$$\begin{aligned} \triangle _{1}\prod (\fancyscript{C})&= \left[ \begin{array}{ccc} 1 &{} 1 &{} 0 \\ 0 &{} 1 &{} 1 \\ \end{array} \right] \odot \left[ \begin{array}{cccc} 1 &{} 0 &{} 0 &{} 1 \\ 1 &{} 1 &{} 0 &{} 1 \\ 0 &{} 0 &{} 1 &{} 1 \\ \end{array} \right] =\left[ \begin{array}{cccc} 1 &{} 0 &{} 0 &{} 1 \\ 0 &{} 0 &{} 0 &{} 1 \\ \end{array} \right] ;\\ \triangle _{2}\prod (\fancyscript{C})&= \left[ \begin{array}{ccc} 1 &{} 1 &{} 0 \\ 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 \\ 1 &{} 1 &{} 1 \\ \end{array} \right] \odot \left[ \begin{array}{cc} 1 &{} 0 \\ 1 &{} 1 \\ 0 &{} 1 \\ \end{array} \right] =\left[ \begin{array}{cccccc} 1 &{} 0 \\ 1 &{} 1 \\ 0 &{} 1 \\ 0 &{} 0 \\ \end{array} \right] ;\\ \triangle _{3}\prod (\fancyscript{C})&= \left[ \begin{array}{ccc} 1 &{} 1 &{} 0 \\ 0 &{} 1 &{} 1 \\ \end{array} \right] \odot \left[ \begin{array}{cccccc} 1 &{}0\\ 1 &{}1\\ 0 &{}1\\ \end{array} \right] =\left[ \begin{array}{cccccc} 1 &{}0\\ 0 &{}1\\ \end{array} \right] . \end{aligned}$$

Thus, we have that $\prod (\fancyscript{C}^{+})=\left[ \begin{array}{cccccc} 1 &{} 0 &{} 0 &{} 1 &{} 1 &{} 0\\ 1 &{} 1 &{} 0 &{} 1 &{} 1 &{} 1\\ 0 &{} 0 &{} 1 &{} 1 &{} 0 &{} 1\\ 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0\\ 1 &{} 0 &{} 0 &{} 1 &{} 1 &{} 0\\ 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 1\\ \end{array} \right] .$

By Definition 2.6, we obtain

$$\begin{aligned} \mathcal {X}_{XH(X)}&= \prod (\fancyscript{C}^{+})\cdot \mathcal {X}_{X} =\left[ \begin{array}{cccccc} 1 &{} 0 &{} 0 &{} 1 &{} 1 &{} 0\\ 1 &{} 1 &{} 0 &{} 1 &{} 1 &{} 1\\ 0 &{} 0 &{} 1 &{} 1 &{} 0 &{} 1\\ 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0\\ 1 &{} 0 &{} 0 &{} 1 &{} 1 &{} 0\\ 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 1\\ \end{array} \right] \cdot \left[ \begin{array}{c} 0 \\ 0 \\ 1 \\ 1 \\ 1 \\ 1 \\ \end{array} \right] =\left[ \begin{array}{cccccc} 1 &{} 1 &{} 1 &{} 1 &{} 1 &{} 1 \\ \end{array} \right] ^{T};\\ \mathcal {X}_{XL(X)}&= \prod (\fancyscript{C}^{+})\odot \mathcal {X}_{X}=\left[ \begin{array}{cccccc} 1 &{} 0 &{} 0 &{} 1 &{} 1 &{} 0\\ 1 &{} 1 &{} 0 &{} 1 &{} 1 &{} 1\\ 0 &{} 0 &{} 1 &{} 1 &{} 0 &{} 1\\ 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0\\ 1 &{} 0 &{} 0 &{} 1 &{} 1 &{} 0\\ 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 1\\ \end{array} \right] \odot \left[ \begin{array}{c} 0 \\ 0 \\ 1 \\ 1 \\ 1 \\ 1 \\ \end{array} \right] =\left[ \begin{array}{cccccc} 0 &{} 0 &{} 1 &{} 1 &{} 0 &{} 1 \\ \end{array} \right] ^{T};\\ \mathcal {X}_{XH(X^{c})}&= \left[ \begin{array}{cccccc} 1 &{} 1 &{} 1 &{} 1 &{} 1 &{} 1\\ \end{array} \right] -\mathcal {X}_{IL(X)}=\left[ \begin{array}{cccccc} 1 &{} 1 &{} 0 &{} 0 &{} 1 &{} 0 \\ \end{array} \right] ^{T};\\ \mathcal {X}_{IL(X^{c})}&= \left[ \begin{array}{cccccc} 1 &{} 1 &{} 1 &{} 1 &{} 1 &{} 1\\ \end{array} \right] -\mathcal {X}_{XH(X)}=\left[ \begin{array}{cccccc} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \end{array} \right] ^{T}. \end{aligned}$$

Therefore, $XH(X)=\{x_{1},x_{2},x_{3},x_{4},x_{5},x_{6}\}$, $XL(X)=\{x_{3},x_{4},x_{6}\}$, $XH(X^{c})=\{x_{1},x_{2},x_{5}\}$ and $IL(X^{c})=\emptyset$.

In Example 3.7, we obtain $\prod (\fancyscript{C}^{+})$ by Definition 2.5. Obviously, all elements in $\prod (\fancyscript{C}^{+})$ need to be computed. By Theorem 3.5, we only need to calculate elements in $\triangle _{1}\prod (\fancyscript{C})$, $\triangle _{2}\prod (\fancyscript{C})$ and $\triangle _{3}\prod (\fancyscript{C})$. Thereby, the incremental algorithm is more effective to compute approximations of sets in dynamic covering approximation spaces.

Subsequently, we construct the type-1 and type-2 characteristic matrices of coverings when deleting more objects.

Definition 3.8

Let $(U,\fancyscript{C})$ be a covering approximation space, where $U=\{x_{1},x_{2},...,x_{n}\}$, $\fancyscript{C}=\{C_{1},C_{2},...,C_{m}\}$, $U^{*}\subseteq U$, $U^{-}=U-U^{*},$ $\fancyscript{C}^{-}=\{C^{-}_{1},C^{-}_{2},...,C^{-}_{m}\}$, where $|U^{*}|\ge 2$, $C^{-}_{i}=C_{i}-\Delta C_{i}$ and $\Delta C_{i}\subseteq U^{*}$. Then $(U^{-},\fancyscript{C}^{-})$ is called a DOS-covering approximation space.

In Definition 3.8, $\fancyscript{C}^{-}$ is called a DOS-covering, and it is time-consuming to compute the type-1 and type-2 characteristic matrices of DOS-coverings by Definitions 2.4 and 2.5, respectively.

By Definition 3.8, we present the process of computing $\Gamma (\fancyscript{C}^{-})$ and $\prod (\fancyscript{C}^{-})$ based on $\Gamma (\fancyscript{C})$ and $\prod (\fancyscript{C})$, respectively. Suppose that we have obtained $\Gamma (\fancyscript{C})=(b_{ij})_{n\times n}$ and $\prod (\fancyscript{C})=(d_{ij})_{n\times n}$ and deleted $\{x_{i_{k}}|1\le k \le N\}$, we get $\Gamma (\fancyscript{C}^{-})$ and $\prod (\fancyscript{C}^{-})$ by deleting $\{b_{i_{k}j}\}$, $\{b_{ji_{k}}\}$, $\{d_{i_{k}j}\}$ and $\{d_{ji_{k}}\}$ $(1\le j \le n, 1\le k\le N)$ in $\Gamma (\fancyscript{C})$ and $\prod (\fancyscript{C})$, respectively.

An example is employed to show that how to get the type-1 and type-2 characteristic matrices of DOS-coverings.

Example 3.9

(Continuation of Examples 3.4 and 3.7) By deleting $x_{2}$ and $x_{4}$, we obtain $U^{-}=\{x_{1},x_{3}\}$ and $\fancyscript{C}^{-}=\{C^{-}_{1},C^{-}_{2},C^{-}_{4}\}$, where $C^{-}_{1}=\{x_{1}\}$, $C^{-}_{2}=\{x_{1}\}$ and $C^{-}_{3}=\{x_{3}\}$. To delete $b_{21},b_{22},b_{23},b_{24},b_{12},b_{22},b_{32},b_{41}, b_{42},b_{43},b_{44},b_{14},b_{24},b_{34}$ in $\Gamma (\fancyscript{C})=(b_{ij})_{4\times 4}$ shown in Example 3.4 and $d_{21},d_{22},d_{23},d_{24},d_{12},d_{32},d_{41},d_{42},d_{43}, d_{44},d_{14},d_{34}$ in $\prod (\fancyscript{C})=(d_{ij})_{4\times 4}$ shown in Example 3.7, we have that

$$\begin{aligned} \Gamma (\fancyscript{C}^{-})=\left[ \begin{array}{cc} 1 &{} 0 \\ 0 &{} 1 \\ \end{array} \right] , \prod (\fancyscript{C}^{-})=\left[ \begin{array}{cc} 1 &{} 0 \\ 0 &{} 1 \\ \end{array} \right] . \end{aligned}$$

Taking $X=\{x_{1}\}$, we have that

$$\begin{aligned} \mathcal {X}_{SH(X)}&= \Gamma (\fancyscript{C}^{-})\cdot \mathcal {X}_{X} =\left[ \begin{array}{cc} 1 &{} 0 \\ 0 &{} 1 \\ \end{array} \right] \cdot \left[ \begin{array}{c} 1 \\ 0 \\ \end{array} \right] =\left[ \begin{array}{cc} 1 &{} 0 \\ \end{array} \right] ^{T};\\ \mathcal {X}_{SL(X)}&= \Gamma (\fancyscript{C}^{-})\odot \mathcal {X}_{X}=\left[ \begin{array}{cc} 1 &{} 0 \\ 0 &{} 1 \\ \end{array} \right] \odot \left[ \begin{array}{c} 1 \\ 0 \\ \end{array} \right] =\left[ \begin{array}{cc} 1 &{} 0 \\ \end{array} \right] ^{T};\\ \mathcal {X}_{XH(X)}&= \prod (\fancyscript{C}^{-})\cdot \mathcal {X}_{X} =\left[ \begin{array}{cc} 1 &{} 0 \\ 0 &{} 1 \\ \end{array} \right] \cdot \left[ \begin{array}{c} 1 \\ 0 \\ \end{array} \right] =\left[ \begin{array}{cc} 1 &{} 0 \\ \end{array} \right] ^{T};\\ \mathcal {X}_{XL(X)}&= \prod (\fancyscript{C}^{+})\odot \mathcal {X}_{X}=\left[ \begin{array}{cccccc} 1 &{} 0 \\ 0 &{} 1 \\ \end{array} \right] \odot \left[ \begin{array}{c} 1 \\ 0 \\ \end{array} \right] =\left[ \begin{array}{cc} 1 &{} 0 \\ \end{array} \right] ^{T}. \end{aligned}$$

Therefore, $SH(X)=\{x_{1}\}$, $SL(X)=\{x_{1}\}$, $XH(X)=\{x_{1}\}$ and $XL(X)=\{x_{1}\}$.

In practice, some objects enter the covering approximation space while some ones go out. We provide concepts of ADOS-covering and DAOS-covering approximation spaces as follows.

Definition 3.10

Let $(U,\fancyscript{C})$ and $(U^{+-},\fancyscript{C}^{+-})$ be covering approximation spaces, where $U=\{x_{1},x_{2},...,x_{n}\}$, $U^{+-}=(U\cup U^{*+})-U^{*-},$ $U^{*+}=\{x_{i}|n+1\le i\le n+s, s\ge 2\}, U^{*-}=\{x_{ki}|2\le i\le t\}\subseteq U, U^{*+}\cap U^{*-}=\emptyset$, $\fancyscript{C}=\{C_{1},C_{2},...,C_{m}\}$, $\fancyscript{C}^{+-}=\{C^{+-}_{1},C^{+-}_{2},...,C^{+-}_{m}\}$, where $C^{+-}_{i}=(C_{i}\cup \Delta C^{+}_{i})- \Delta C^{-}_{i}$, $\Delta C^{+}_{i}\subseteq U^{*+}$ and $\Delta C^{-}_{i}\subseteq U^{*-}$. Then $(U^{+-},\fancyscript{C}^{+-})$ is called a ADOS-covering approximation space.

In Definition 3.10, $\fancyscript{C}^{+-}$ is called a ADOS-covering. Furthermore, we denote $U^{-+}=(U-U^{*-})\cup U^{*+}, \fancyscript{C}^{-+}=\{C^{-+}_{1},C^{-+}_{2},...,C^{-+}_{m}\}$ and $C^{-+}_{i}=(C_{i}-\Delta C^{-}_{i})\cup \Delta C^{+}_{i}$. Then $(U^{-+},\fancyscript{C}^{-+})$ and $\fancyscript{C}^{-+}$ are called a DAOS-covering approximation space and a DAOS-covering, respectively. By Definition 3.10, we have $U^{-+}=U^{+-}$ and $\fancyscript{C}^{-+}=\fancyscript{C}^{+-}$ since $U^{*+}\cap U^{*-}=\emptyset$.

Following, we present incremental approaches to computing the type-1 and type-2 characteristic matrices of $\fancyscript{C}^{+-}$ when considering the immigration and emigration of more objects simultaneously.

Approach 1: (1) Constructing $M_{\fancyscript{C}}$ based on $\fancyscript{C}$. (2) Calculating $\Gamma (\fancyscript{C})$ and $\prod (\fancyscript{C})$, where $\Gamma (\fancyscript{C})=M_{\fancyscript{C}}\cdot M^{T}_{\fancyscript{C}}$ and $\prod (\fancyscript{C})=M_{\fancyscript{C}}\odot M^{T}_{\fancyscript{C}}$. (3) Computing $\Gamma (\fancyscript{C}^{+})$ and $\prod (\fancyscript{C}^{+})$ by Algorithms 3.3 and 3.6, respectively, where $\fancyscript{C}^{+}=\{C^{+}_{1},C^{+}_{2},...,C^{+}_{m}\}$, $C^{+}_{i}=C_{i}\cup \Delta C^{+}_{i}$ and $\Delta C^{+}_{i}\subseteq U^{*+}$. (4) Constructing $\Gamma (\fancyscript{C}^{+-})$ and $\prod (\fancyscript{C}^{+-})$ as Example 3.9, where $\fancyscript{C}^{+-}=\{C^{+-}_{1},C^{+-}_{2},...,C^{+-}_{m}\}$, $C^{+-}_{i}=C^{+}_{i}-\Delta C^{-}_{i}$ and $\Delta C^{-}_{i}\subseteq U^{*-}$.

Approach 2: (1) Constructing $M_{\fancyscript{C}}$ based on $\fancyscript{C}$. (2) Calculating $\Gamma (\fancyscript{C})$ and $\prod (\fancyscript{C})$, where $\Gamma (\fancyscript{C})=M_{\fancyscript{C}}\cdot M^{T}_{\fancyscript{C}}$ and $\prod (\fancyscript{C})=M_{\fancyscript{C}}\odot M^{T}_{\fancyscript{C}}$. (3) Calculating $\Gamma (\fancyscript{C}^{-})$ and $\prod (\fancyscript{C}^{-})$ as Example 3.9. (4) Constructing $\Gamma (\fancyscript{C}^{-+})$ and $\prod (\fancyscript{C}^{-+})$ by Algorithms 3.3 and 3.6, respectively, where $\fancyscript{C}^{-+}=\{C^{-+}_{1},C^{-+}_{2},...,C^{-+}_{m}\}$, $C^{-+}_{i}=C^{-}_{i}\cup \Delta C^{+}_{i}$, $\Delta C^{+}_{i}\subseteq U^{*+}$, $C^{-}_{i}=C_{i}-\Delta C^{-}_{i}$ and $\Delta C^{-}_{i}\subseteq U^{*-}$.

The following examples are employed to show the process of constructing approximations of sets with the incremental approaches.

Example 3.11

Let $U=\{x_{1},x_{2},x_{3},x_{4}\}$, $U^{+-}=(U\cup \{x_{5},x_{6}\})-\{x_{1},x_{2}\}$, $\fancyscript{C}=\{C_{1},C_{2},C_{3}\}$, $\fancyscript{C}^{+-}=\{C^{+-}_{1},C^{+-}_{2},C^{+-}_{3}\}$, where $C_{1}=\{x_{1},x_{4}\}$, $C_{2}=\{x_{1},x_{2},x_{4}\}$, $C_{3}=\{x_{3},x_{4}\}$, $C^{+-}_{1}=\{x_{4},x_{5}\}$, $C^{+-}_{2}=\{x_{4},x_{5},x_{6}\}$, $C^{+-}_{3}=\{x_{3},x_{4},x_{6}\}$, and $X=\{x_{3},x_{4},x_{5}\}$. By Definitions 2.4 and 2.5, we first have

$$\begin{aligned} \Gamma (\fancyscript{C})&= M_{\fancyscript{C}}\cdot M_{\fancyscript{C}}^{T}=\left[ \begin{array}{cccc} 1 &{} 1 &{} 0 \\ 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 \\ 1 &{} 1 &{} 1 \\ \end{array} \right] \cdot \left[ \begin{array}{cccc} 1 &{} 1 &{} 0 \\ 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 \\ 1 &{} 1 &{} 1 \\ \end{array} \right] ^{T} =\left[ \begin{array}{cccc} 1 &{} 1 &{} 0 &{} 1 \\ 1 &{} 1 &{} 0 &{} 1 \\ 0 &{} 0 &{} 1 &{} 1 \\ 1 &{} 1 &{} 1 &{} 1 \\ \end{array} \right] ;\\ \prod (\fancyscript{C})&= M_{\fancyscript{C}}\odot M_{\fancyscript{C}}^{T} =\left[ \begin{array}{cccc} 1 &{} 1 &{} 0 \\ 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 \\ 1 &{} 1 &{} 1 \\ \end{array} \right] \odot \left[ \begin{array}{cccc} 1 &{} 1 &{} 0 \\ 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 \\ 1 &{} 1 &{} 1 \\ \end{array} \right] ^{T}=\left[ \begin{array}{cccc} 1 &{} 0 &{} 0 &{} 1 \\ 1 &{} 1 &{} 0 &{} 1 \\ 0 &{} 0 &{} 1 &{} 1 \\ 0 &{} 0 &{} 0 &{} 1 \\ \end{array} \right] . \end{aligned}$$

Second, by Theorems 3.2 and 3.5, we get

$$\begin{aligned} \Gamma (\fancyscript{C}^{+})=\left[ \begin{array}{cccccc} 1 &{} 1 &{} 0 &{} 1 &{}1 &{} 1\\ 1 &{} 1 &{} 0 &{} 1 &{}1 &{} 1\\ 0 &{} 0 &{} 1 &{} 1 &{}0 &{} 1\\ 1 &{} 1 &{} 1 &{} 1 &{}1 &{} 1\\ 1 &{} 1 &{} 0 &{} 1 &{}1 &{} 1\\ 1 &{} 1 &{} 1 &{} 1 &{}1 &{} 1\\ \end{array} \right],\quad \prod (\fancyscript{C}^{+})=\left[ \begin{array}{cccccc} 1 &{} 0 &{} 0 &{} 1 &{} 1 &{} 0\\ 1 &{} 1 &{} 0 &{} 1 &{} 1 &{} 1\\ 0 &{} 0 &{} 1 &{} 1 &{} 0 &{} 1\\ 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0\\ 1 &{} 0 &{} 0 &{} 1 &{} 1 &{} 0\\ 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 1\\ \end{array} \right] . \end{aligned}$$

Third, as Example 3.9, we have

$$\begin{aligned} \Gamma (\fancyscript{C}^{+-})=\left[ \begin{array}{cccc} 1 &{} 1 &{}0 &{} 1\\ 1 &{} 1 &{}1 &{} 1\\ 0 &{} 1 &{}1 &{} 1\\ 1 &{} 1 &{}1 &{} 1\\ \end{array} \right] , \,\, \prod (\fancyscript{C}^{+-})=\left[ \begin{array}{cccc} 1 &{} 1 &{} 0 &{} 1\\ 0 &{} 1 &{} 0 &{} 0\\ 0 &{} 1 &{} 1 &{} 0\\ 0 &{} 1 &{} 0 &{} 1\\ \end{array} \right] . \end{aligned}$$

By Definition 2.6, we get

$$\begin{aligned} \mathcal {X}_{SH(X)}&= \Gamma (\fancyscript{C}^{+-})\cdot \mathcal {X}_{X}=\left[ \begin{array}{cccc} 1 &{} 1 &{}0 &{} 1\\ 1 &{} 1 &{}1 &{} 1\\ 0 &{} 1 &{}1 &{} 1\\ 1 &{} 1 &{}1 &{} 1\\ \end{array} \right] \cdot \left[ \begin{array}{c} 1 \\ 1 \\ 1 \\ 0 \\ \end{array} \right] =\left[ \begin{array}{cccc} 1 &{} 1 &{} 1 &{} 1 \\ \end{array} \right] ^{T};\\ \mathcal {X}_{SL(X)}&= \Gamma (\fancyscript{C}^{+-})\odot \mathcal {X}_{X}=\left[ \begin{array}{cccc} 1 &{} 1 &{}0 &{} 1\\ 1 &{} 1 &{}1 &{} 1\\ 0 &{} 1 &{}1 &{} 1\\ 1 &{} 1 &{}1 &{} 1\\ \end{array} \right] \odot \left[ \begin{array}{c} 1 \\ 1 \\ 1 \\ 0 \\ \end{array} \right] =\left[ \begin{array}{cccc} 0 &{} 0 &{} 0 &{} 0 \\ \end{array} \right] ^{T}; \end{aligned}$$

$$\begin{aligned} \mathcal {X}_{XH(X)}&= \prod (\fancyscript{C}^{+-})\cdot \mathcal {X}_{X}=\left[ \begin{array}{cccc} 1 &{} 1 &{} 0 &{} 1\\ 0 &{} 1 &{} 0 &{} 0\\ 0 &{} 1 &{} 1 &{} 0\\ 0 &{} 1 &{} 0 &{} 1\\ \end{array} \right] \cdot \left[ \begin{array}{c} 1 \\ 1 \\ 1 \\ 0 \\ \end{array} \right] =\left[ \begin{array}{cccc} 1 &{} 1 &{} 1 &{} 1 \\ \end{array} \right] ^{T};\\ \mathcal {X}_{XL(X)}&= \prod (\fancyscript{C}^{+-})\odot \mathcal {X}_{X}=\left[ \begin{array}{cccc} 1 &{} 1 &{} 0 &{} 1\\ 0 &{} 1 &{} 0 &{} 0\\ 0 &{} 1 &{} 1 &{} 0\\ 0 &{} 1 &{} 0 &{} 1\\ \end{array} \right] \odot \left[ \begin{array}{c} 1 \\ 1 \\ 1 \\ 0 \\ \end{array} \right] =\left[ \begin{array}{cccc} 0 &{} 1 &{} 1 &{} 0 \\ \end{array} \right] ^{T}. \end{aligned}$$

Therefore, $SH(X)=\{x_{3},x_{4},x_{5},x_{6}\}$, $SL(X)=\emptyset$, $XH(X)=\{x_{3},x_{4},x_{5},x_{6}\}$ and $XL(X)=\{x_{4},x_{5}\}$.

Example 3.12

(Continuation of Example 3.11) As Example 3.9, we first have

$$\begin{aligned} \Gamma (\fancyscript{C}^{-})=\left[ \begin{array}{cc} 1 &{} 1 \\ 1 &{} 1 \\ \end{array} \right] ; \,\, \prod (\fancyscript{C}^{-})=\left[ \begin{array}{cc} 1 &{} 1 \\ 0 &{} 1 \\ \end{array} \right] . \end{aligned}$$

Second, by Theorems 3.2 and 3.5, we have

$$\begin{aligned} \Gamma (\fancyscript{C}^{-+})=\left[ \begin{array}{cccc} 1 &{} 1 &{}0 &{} 1\\ 1 &{} 1 &{}1 &{} 1\\ 0 &{} 1 &{}1 &{} 1\\ 1 &{} 1 &{}1 &{} 1\\ \end{array} \right] ; \,\, \prod (\fancyscript{C}^{-+})=\left[ \begin{array}{cccc} 1 &{} 1 &{} 0 &{} 1\\ 0 &{} 1 &{} 0 &{} 0\\ 0 &{} 1 &{} 1 &{} 0\\ 0 &{} 1 &{} 0 &{} 1\\ \end{array} \right] . \end{aligned}$$

By Definition 2.6, we get

$$\begin{aligned} \mathcal {X}_{SH(X)}&= \Gamma (\fancyscript{C}^{-+})\cdot \mathcal {X}_{X}=\left[ \begin{array}{cccc} 1 &{} 1 &{}0 &{} 1\\ 1 &{} 1 &{}1 &{} 1\\ 0 &{} 1 &{}1 &{} 1\\ 1 &{} 1 &{}1 &{} 1\\ \end{array} \right] \cdot \left[ \begin{array}{c} 1 \\ 1 \\ 1 \\ 0 \\ \end{array} \right] =\left[ \begin{array}{cccc} 1 &{} 1 &{} 1 &{} 1 \\ \end{array} \right] ^{T};\\ \mathcal {X}_{SL(X)}&= \Gamma (\fancyscript{C}^{-+})\odot \mathcal {X}_{X} =\left[ \begin{array}{cccc} 1 &{} 1 &{}0 &{} 1\\ 1 &{} 1 &{}1 &{} 1\\ 0 &{} 1 &{}1 &{} 1\\ 1 &{} 1 &{}1 &{} 1\\ \end{array} \right] \odot \left[ \begin{array}{c} 1 \\ 1 \\ 1 \\ 0 \\ \end{array} \right] =\left[ \begin{array}{cccc} 0 &{} 0 &{} 0 &{} 0 \\ \end{array} \right] ^{T};\\ \mathcal {X}_{XH(X)}&= \prod (\fancyscript{C}^{-+})\cdot \mathcal {X}_{X}=\left[ \begin{array}{cccc} 1 &{} 1 &{} 0 &{} 1\\ 0 &{} 1 &{} 0 &{} 0\\ 0 &{} 1 &{} 1 &{} 0\\ 0 &{} 1 &{} 0 &{} 1\\ \end{array} \right] \cdot \left[ \begin{array}{c} 1 \\ 1 \\ 1 \\ 0 \\ \end{array} \right] =\left[ \begin{array}{cccc} 1 &{} 1 &{} 1 &{} 1 \\ \end{array} \right] ^{T};\\ \mathcal {X}_{XL(X)}&= \prod (\fancyscript{C}^{-+})\odot \mathcal {X}_{X}=\left[ \begin{array}{cccc} 1 &{} 1 &{} 0 &{} 1\\ 0 &{} 1 &{} 0 &{} 0\\ 0 &{} 1 &{} 1 &{} 0\\ 0 &{} 1 &{} 0 &{} 1\\ \end{array} \right] \odot \left[ \begin{array}{c} 1 \\ 1 \\ 1 \\ 0 \\ \end{array} \right] =\left[ \begin{array}{cccc} 0 &{} 1 &{} 1 &{} 0 \\ \end{array} \right] ^{T}. \end{aligned}$$

Therefore, $SH(X)=\{x_{3},x_{4},x_{5},x_{6}\}$, $SL(X)=\emptyset$, $XH(X)=\{x_{3},x_{4},x_{5},x_{6}\}$ and $XL(X)=\{x_{4},x_{5}\}$.

4 Experiments

In this section, we compute the second and sixth lower and upper approximations of sets by using Algorithms 3.3 and 3.6 in dynamic covering approximation spaces, respectively. To test the incremental algorithms, we generate randomly six covering approximation spaces outlined in Table 1, where $|U_{i}|$ means the number of objects in $U_{i}$; $|\fancyscript{C}_{i}|$ denotes the cardinality of $\fancyscript{C}_{i}$; $|U^{*}_{i}|$ stands for the number of objects added into $U_{i}$. All experiments are conducted on a PC with Windows 7 and Interl(R) Core(TM) i5 CPU 650@3.20 GHZ and 4.00GB memory and Matlab R2010a.

Table 1 Description of experimental covering approximation spaces

In what follows, we apply Algorithms 3.3 and 3.6 to the covering approximation space $A:(U_{1},\fancyscript{C}_{1})$, where $|U_{1}|=600$ and $|\fancyscript{C}_{1}|=60$. Concretely, $U_{1}=\{x_{1},x_{2},...,x_{600}\}$, $\fancyscript{C}_{1}=\{C_{1},C_{2},...,C_{60}\}$ and $U^{*}_{1}=\{x_{601},x_{602},...,x_{610}\}$.

First, we calculate $\Gamma (\fancyscript{C}_{1})$ and $\prod (\fancyscript{C}_{1})$ by Definitions 2.4 and 2.5, respectively. Also we obtain the AOS-covering approximation space $A^{+}:(U_{1}^{+},\fancyscript{C}^{+}_{1})$ when adding $U_{1}^{*}=\{x_{601},x_{602},...,x_{610}\}$ into $U_{1}$, where $U_{1}^{+}=U_{1}\cup U_{1}^{*}$, $C^{+}_{i}=C_{i} \text { or } C_{i}\cup \Delta C_{i}(1\le i\le 60)$, where $\Delta C_{i}\subseteq U_{1}^{*}$.

Second, we get $\Gamma (\fancyscript{C}^{+}_{1})$ and $\prod (\fancyscript{C}^{+}_{1})$ by Definitions 2.4 and 2.5, respectively. Then $SH(X)$, $SL(X)$, $XH(X)$ and $XL(X)$ are calculated based on $\Gamma (\fancyscript{C}^{+}_{1})$ and $\prod (\fancyscript{C}^{+}_{1})$ for $X\subseteq U_{1}^{+}$, respectively. We show the time of computing $SH(X)$, $SL(X)$, $XH(X)$ and $XL(X)$ in Table 2. Concretely, $NT_{S}$ $(\text {respectively, } NT_{X})$ stands for the time of constructing $SH(X)$ and $SL(X)$ $(\text {respectively, } XH(X)$ and $XL(X))$ by using the non-incremental algorithm in Table 2.

Table 2 Computing times using IA and NIA in $A^{+}:(U^{+}_{1},\fancyscript{C}^{+}_{1})$

Fig. 1

Times of computing SH(X), SL(X), XH(X) and XL(X) in $A^{+}$

Third, we obtain $\Gamma (\fancyscript{C}^{+}_{1})$ and $\prod (\fancyscript{C}^{+}_{1})$ by Algorithms 3.3 and 3.6, respectively. Then we show the time of computing $SH(X)$, $SL(X)$, $XH(X)$ and $XL(X)$ for $X\subseteq U_{1}^{+}$ in Table 2. Concretely, $IT_{S}$ $(\text {respectively, } IT_{X})$ means the time of calculating $SH(X)$ and $SL(X)$ $(\text {respectively, } XH(X)$ and $XL(X))$ by using the incremental algorithm in Table 2.

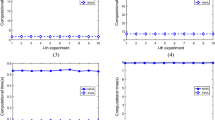
Fourth, we perform this experiment ten times and show the results in Table 2 and Fig. 1. The experimental results illustrate that all algorithms are stable to compute approximations of sets. For example, the times of computing approximations by using the same algorithm are almost the same in Table 2. Consequently, we see that the times of computing approximations of sets by using incremental algorithms are much smaller than those of the non-incremental algorithms. In Fig. 1, we also observe that the computing times of the incremental algorithms are far less than those of the non-incremental algorithms. Therefore, the incremental algorithms are more effective to construct approximations of sets in the AOS-covering approximation space $A^{+}:(U^{+}_{1},\fancyscript{C}^{+}_{1})$.

Remark

In Table 2, $t(s)$ denotes that the measure of time is in seconds; $AT$ indicates the average time of the corresponding algorithm in the experiment; IA and NIA mean the incremental and non-incremental algorithms, respectively. In Figs. 1, 2, 3, 4, 5 and 6, $i$ stands for the experimental number in $X$ Axis; In Fig. 7, $i$ refers to as the number of objects in $X$ Axis; In Figs. 1, 2, 3, 4, 5, 6 and 7, $i$ is the computing time in $Y$ Axis.

Subsequently, we generate covering approximation spaces $B, C, D, E$ and $F$ randomly. For instance, we create $B:(U_{2},\fancyscript{C}_{2})$, where $|U_{2}|=1500$ and $|\fancyscript{C}_{2}|=50$. Then we perform the above process on these covering approximation spaces. We show all the results in Tables 3, 4, 5, 6 and 7. Obviously, the computing times of the incremental algorithms when adding ten objects are much smaller than those of the non-incremental algorithms. Furthermore, all experimental results are shown by Figs. 2, 3, 4, 5 and 6.

Table 3 Computing times using IA and NIA in $B^{+}:(U^{+}_{2},\fancyscript{C}^{+}_{2})$

Fig. 2

Times of computing SH(X), SL(X), XH(X) and XL(X) in $B^{+}$

Table 4 Computing times using IA and NIA in $C^{+}:(U^{+}_{3},\fancyscript{C}^{+}_{3})$

Fig. 3

Times of computing SH(X), SL(X), XH(X) and XL(X) in $C^{+}$

Table 5 Computing times using IA and NIA in $D^{+}:(U^{+}_{4},\fancyscript{C}^{+}_{4})$

Fig. 4

Times of computing SH(X), SL(X), XH(X) and XL(X) in $D^{+}$

Table 6 Computing times using IA and NIA in $E^{+}:(U^{+}_{5},\fancyscript{C}^{+}_{5})$

Fig. 5

Times of computing SH(X), SL(X), XH(X) and XL(X) in $E^{+}$

Table 7 Computing times using IA and NIA in $F^{+}:(U^{+}_{6},\fancyscript{C}^{+}_{6})$

Fig. 6

Times of computing SH(X), SL(X), XH(X) and XL(X) in $F^{+}$

Fig. 7

The average times of computing SH(X), SL(X), XH(X) and XL(X) with IA and NIA

In Fig. 7, we observe that the average times of the incremental and non-incremental algorithms rise monotonically with the increase of the number of objects. Obviously, the incremental algorithms when adding ten objects perform always faster than the non-incremental algorithms in the experiment, and the average times of the incremental algorithms by adding ten objects are much smaller than those of the non-incremental algorithms. Moreover, with the increasing cardinality of the object set, the speed-up ratios of times by using the non-incremental algorithms are higher than the incremental algorithms.

All the experimental results illustrate that the incremental algorithms are more effective to construct approximations of sets in AOS-covering approximation spaces. We should point out that the computing times by using each algorithm are not absolutely consistent with each other in the same type of covering approximation spaces because of the system delay. Furthermore, we run the proposed algorithms on six relatively small covering approximation spaces due to the limitations such as hardware. In the future, we will test the performance of the incremental algorithms on large-scale covering approximation spaces without these limitations.

5 Knowledge reduction in dynamic covering decision information systems

In this section, we perform knowledge reduction of dynamic covering decision information systems with the incremental approaches. In what follows, we present concepts of type-1 and type-2 reducts in covering decision information systems.

Definition 5.1

Let $(U,\fancyscript{D}\cup U/d)$ be a covering decision information system, where $\fancyscript{D}=\{\fancyscript{C}_{i}|i\in I\}$, $U/d=\{D_{i}|i\in J\}$, I and J are index sets. Then

• (1) $\fancyscript{P}\subseteq \fancyscript{D}$ is called a type-1 reduct of $(U,\fancyscript{D}\cup U/d)$ if it satisfies: $(a)$ $SH_{\fancyscript{D}}(D_{i})=SH_{\fancyscript{P}}(D_{i})$, $SL_{\fancyscript{D}}(D_{i})=SL_{\fancyscript{P}}(D_{i}), \, \forall i\in J;$ $(b)$ $SH_{\fancyscript{D}}(D_{i})\ne SH_{\fancyscript{P^{'}}}(D_{i})$, $SL_{\fancyscript{D}}(D_{i})\ne SL_{\fancyscript{P^{'}}}(D_{i}), \, \forall \fancyscript{P^{'}}\subset \fancyscript{P};$

• (2) $\fancyscript{P}\subseteq \fancyscript{D}$ is called a type-2 reduct of $(U,\fancyscript{D}\cup U/d)$ if it satisfies: $(a)$ $XH_{\fancyscript{D}}(D_{i})=XH_{\fancyscript{P}}(D_{i})$, $XL_{\fancyscript{D}}(D_{i})=XL_{\fancyscript{P}}(D_{i}),\, \forall i\in J;$ $(b)\, XH_{\fancyscript{D}}(D_{i})\ne XH_{\fancyscript{P^{'}}}(D_{i})$, $XL_{\fancyscript{D}}(D_{i})\ne XL_{\fancyscript{P^{'}}}(D_{i}),\, \forall \fancyscript{P^{'}}\subset \fancyscript{P}.$

By Definition 5.1, the type-1 and type-2 reducts are the minimal attribute sets which keep the second and sixth lower and upper approximations of equivalence classes with respect to the decision attribute, respectively. Generally speaking, a type-1 reduct is not a type-2 reduct, and vice versa.

Theorem 5.2

Let $(U,\fancyscript{D}\cup U/d)$ be a covering decision information system, where $\fancyscript{D}=\{\fancyscript{C}_{i}|i\in I\}$, $U/d=\{D_{i}|i\in J\}$, I and J are index sets.

• (1) If $\fancyscript{P}\subseteq \fancyscript{D}$ is a type-1 reduct of $(U,\fancyscript{D}\cup U/d)$. Then we have: $(a)$ $\Gamma (\fancyscript{D})\cdot \mathcal {X}_{D_{i}}=\Gamma (\fancyscript{P})\cdot \mathcal {X}_{D_{i}}, \Gamma (\fancyscript{D})\odot \mathcal {X}_{D_{i}}=\Gamma (\fancyscript{P})\odot \mathcal {X}_{D_{i}}, \forall i\in J;$ $(b)$ $\Gamma (\fancyscript{D})\cdot \mathcal {X}_{D_{i}}\ne \Gamma (\fancyscript{P^{'}})\cdot \mathcal {X}_{D_{i}}, \Gamma (\fancyscript{D})\odot \mathcal {X}_{D_{i}}\ne \Gamma (\fancyscript{P^{'}})\odot \mathcal {X}_{D_{i}}, \forall \fancyscript{P^{'}}\subset \fancyscript{P};$

• (2) If $\fancyscript{P}\subseteq \fancyscript{D}$ is a type-2 reduct of $(U,\fancyscript{D}\cup U/d)$. Then we have: $(a)$ $\prod (\fancyscript{D})\cdot \mathcal {X}_{D_{i}}=\prod (\fancyscript{P})\cdot \mathcal {X}_{D_{i}}, \prod (\fancyscript{D})\odot \mathcal {X}_{D_{i}}=\prod (\fancyscript{P})\odot \mathcal {X}_{D_{i}}, \forall i\in J;$ $(b)$ $\prod (\fancyscript{D})\cdot \mathcal {X}_{D_{i}}\ne \prod (\fancyscript{P^{'}})\cdot \mathcal {X}_{D_{i}}, \prod (\fancyscript{D})\odot \mathcal {X}_{D_{i}}\ne \prod (\fancyscript{P^{'}})\odot \mathcal {X}_{D_{i}}, \forall \fancyscript{P^{'}}\subset \fancyscript{P}.$

Proof

(1),(2) By Definitions 2.4, 2.5 and 5.1, the proof is straightforward. $\square$

Proposition 5.3

Let $(U,\fancyscript{D}\cup U/d)$ be a covering decision information system, where $\fancyscript{D}=\{\fancyscript{C}_{i}|i\in I\}$, $U/d=\{D_{i}|i\in J\}$, I and J are index sets.

• (1) If $\Gamma (\fancyscript{D})=\Gamma (\fancyscript{P})$ for $\fancyscript{P}\subseteq \fancyscript{D}$, then $\Gamma (\fancyscript{D})\cdot \mathcal {X}_{D_{i}}=\Gamma (\fancyscript{P})\cdot \mathcal {X}_{D_{i}}$ and $\Gamma (\fancyscript{D})\odot \mathcal {X}_{D_{i}}=\Gamma (\fancyscript{P})\odot \mathcal {X}_{D_{i}}$ for any $i\in J.$ But the converse doesn’t hold necessarily;

• (2) If $\prod (\fancyscript{D})=\prod (\fancyscript{P})$ for $\fancyscript{P}\subseteq \fancyscript{D}$, then $\prod (\fancyscript{D})\cdot \mathcal {X}_{D_{i}}=\prod (\fancyscript{P})\cdot \mathcal {X}_{D_{i}}$ and $\prod (\fancyscript{D})\odot \mathcal {X}_{D_{i}}=\prod (\fancyscript{P})\odot \mathcal {X}_{D_{i}}$ for any $i\in J.$ But the converse doesn’t hold necessarily.

Proof

By Theorem 5.2, the proof is straightforward. $\square$

The following examples are employed to illustrate that how to compute type-1 reducts of covering decision information systems and dynamic covering decision information systems.

Example 5.4

Let $(U,\fancyscript{D}\cup U/d)$ be a covering decision information system, where $\fancyscript{D}=\{\fancyscript{C}_{1},\fancyscript{C}_{2},\fancyscript{C}_{3}$, $\fancyscript{C}_{1}=\{\{x_{1},x_{2},x_{3},x_{4}\},\{x_{5},x_{6}\}\}$, $\fancyscript{C}_{2}=\{\{x_{1},x_{2}\},\{x_{3},x_{4}\},\{x_{5},x_{6}\}\}$, $\fancyscript{C}_{3}=\{\{x_{1},x_{2},x_{5},x_{6}\},\{x_{3},x_{4}\}\}$, $U/d=\{D_{1},D_{2}\}=\{\{x_{1},x_{2}\},\{x_{3},x_{4},x_{5},x_{6}\}\}$. By Definitions 2.4 and 2.6(1), we obtain

$$\begin{aligned} \Gamma (\fancyscript{D})&= \left[ \begin{array}{ccccccc} 1 &{} 1 &{} 1 &{} 1 &{}1&{}1 \\ 1 &{} 1 &{} 1 &{} 1 &{}1&{}1 \\ 1 &{} 1 &{} 1 &{} 1 &{}0&{}0 \\ 1 &{} 1 &{} 1 &{} 1 &{}0&{}0 \\ 1 &{} 1 &{} 0 &{} 0 &{}1&{}1 \\ 1 &{} 1 &{} 0 &{} 0 &{}1&{}1 \\ \end{array} \right] ;\\ \mathcal {X}_{SH(D_{1})}&= \Gamma (\fancyscript{D})\cdot \mathcal {X}_{D_{1}}=\left[ \begin{array}{ccccccc} 1&1&1&1&1&1 \end{array} \right] ;\\ \mathcal {X}_{SL(D_{1})}&= \Gamma (\fancyscript{D})\odot \mathcal {X}_{D_{1}}=\left[ \begin{array}{ccccccc} 0&0&0&0&0&0 \end{array} \right] ;\\ \mathcal {X}_{SH(D_{2})}&= \Gamma (\fancyscript{D})\cdot \mathcal {X}_{D_{2}}=\left[ \begin{array}{ccccccc} 1&1&1&1&1&1 \end{array} \right] ;\\ \mathcal {X}_{SL(D_{2})}&= \Gamma (\fancyscript{D})\odot \mathcal {X}_{D_{2}}=\left[ \begin{array}{ccccccc} 0&0&0&0&0&0 \end{array} \right] . \end{aligned}$$

Moreover, we have that

$$\begin{aligned} &\Gamma (\fancyscript{D}/\fancyscript{C}_{2})\cdot \mathcal {X}_{D_{1}}= \mathcal {X}_{SH(D_{1})};\\ &\Gamma (\fancyscript{D}/\fancyscript{C}_{2})\odot \mathcal {X}_{D_{1}}= \mathcal {X}_{SL(D_{1})}; \\ &\Gamma (\fancyscript{D}/\fancyscript{C}_{2})\cdot \mathcal {X}_{D_{2}}= \mathcal {X}_{SH(D_{2})}; \end{aligned}$$

$$\begin{aligned} &\Gamma (\fancyscript{D}/\fancyscript{C}_{2})\odot \mathcal {X}_{D_{2}}= \mathcal {X}_{SL(D_{2})};\\ &\Gamma (\fancyscript{D}/\{\fancyscript{C}_{1},\fancyscript{C}_{2}\})\cdot \mathcal {X}_{D_{1}}\ne \mathcal {X}_{SH(D_{1})};\\ &\Gamma (\fancyscript{D}/\{\fancyscript{C}_{1},\fancyscript{C}_{2}\})\odot \mathcal {X}_{D_{1}}\ne \mathcal {X}_{SL(D_{1})};\\ &\Gamma (\fancyscript{D}/\{\fancyscript{C}_{1},\fancyscript{C}_{2}\})\cdot \mathcal {X}_{D_{2}}\ne \mathcal {X}_{SH(D_{2})};\\ &\Gamma (\fancyscript{D}/\{\fancyscript{C}_{1},\fancyscript{C}_{2}\})\odot \mathcal {X}_{D_{2}}\ne \mathcal {X}_{SL(D_{2})};\\ &\Gamma (\fancyscript{D}/\{\fancyscript{C}_{2},\fancyscript{C}_{3}\})\cdot \mathcal {X}_{D_{1}}\ne \mathcal {X}_{SH(D_{1})};\\ &\Gamma (\fancyscript{D}/\{\fancyscript{C}_{2},\fancyscript{C}_{3}\})\odot \mathcal {X}_{D_{1}}\ne \mathcal {X}_{SL(D_{1})};\\ &\Gamma (\fancyscript{D}/\{\fancyscript{C}_{2},\fancyscript{C}_{3}\})\cdot \mathcal {X}_{D_{2}}\ne \mathcal {X}_{SH(D_{2})};\\ &\Gamma (\fancyscript{D}/\{\fancyscript{C}_{2},\fancyscript{C}_{3}\})\odot \mathcal {X}_{D_{2}}\ne \mathcal {X}_{SL(D_{2})}. \end{aligned}$$

Therefore, we have that $\{\fancyscript{C}_{1},\fancyscript{C}_{3}\}$ is a type-1 reduct of $(U,\fancyscript{D}\cup U/d)$.

Example 5.5

(Continuation of Example 5.4) Let $(U^{+},\fancyscript{D}^{+}\cup U^{+}/d)$ be a dynamic covering decision information system of $(U,\fancyscript{D}\cup U/d)$, where $\fancyscript{D}^{+}=\{\fancyscript{C}^{+}_{1},\fancyscript{C}^{+}_{2},\fancyscript{C}^{+}_{3}\}$, $\fancyscript{C}^{+}_{1}=\{\{x_{1},x_{2},x_{3},x_{4},x_{7}\},\{x_{5},x_{6},x_{8}\}\}$, $\fancyscript{C}^{+}_{2}=\{\{x_{1},x_{2},x_{7}\},\{x_{3},x_{4}\},\{x_{5},x_{6},x_{8}\}\}$, $\fancyscript{C}^{+}_{3}=\{\{x_{1},x_{2},x_{5},x_{6},x_{7},x_{8}\},\{x_{3},x_{4}\}\}$, $U^{+}/d=\{D^{+}_{1},D^{+}_{2}\}=\{\{x_{1},x_{2},x_{7}\},\{x_{3},x_{4},x_{5},x_{6},x_{8}\}\}$. By Theorem 3.2 and Definition 2.6(1), we have that

$$\begin{aligned} \Gamma (\fancyscript{D}^{+})&= \left[ \begin{array}{ccccccccc} 1 &{} 1 &{} 1 &{} 1 &{}1 &{} 1 &{} 1 &{} 1\\ 1 &{} 1 &{} 1 &{} 1 &{}1 &{} 1 &{} 1 &{} 1\\ 1 &{} 1 &{} 1 &{} 1 &{}0 &{} 0 &{} 1 &{} 0\\ 1 &{} 1 &{} 1 &{} 1 &{}0 &{} 0 &{} 1 &{} 0\\ 1 &{} 1 &{} 0 &{} 0 &{}1 &{} 1 &{} 1 &{} 1\\ 1 &{} 1 &{} 0 &{} 0 &{}1 &{} 1 &{} 1 &{} 1\\ 1 &{} 1 &{} 1 &{} 1 &{}1 &{} 1 &{} 1 &{} 1\\ 1 &{} 1 &{} 0 &{} 0 &{}1 &{} 1 &{} 1 &{} 1\\ \end{array} \right] ;\\ \mathcal {X}_{SH(D^{+}_{1})}&= \Gamma (\fancyscript{D}^{+})\cdot \mathcal {X}_{D^{+}_{1}}=\left[ \begin{array}{ccccccccc} 1&1&1&1&1&1&1&1 \end{array} \right] ; \\ \mathcal {X}_{SL(D^{+}_{1})}&= \Gamma (\fancyscript{D}^{+})\odot \mathcal {X}_{D^{+}_{1}}=\left[ \begin{array}{ccccccccc} 0&0&0&0&0&0&0&0 \end{array} \right] ;\\ \mathcal {X}_{SH(D^{+}_{2})}&= \Gamma (\fancyscript{D}^{+})\cdot \mathcal {X}_{D^{+}_{2}}=\left[ \begin{array}{ccccccccc} 1&1&1&1&1&1&1&1 \end{array} \right] ;\\ \mathcal {X}_{SL(D^{+}_{2})}&= \Gamma (\fancyscript{D}^{+})\odot \mathcal {X}_{D^{+}_{2}}=\left[ \begin{array}{ccccccccc} 0&0&0&0&0&0&0&0 \end{array} \right] . \end{aligned}$$

Furthermore, we obtain

$$\begin{aligned} &\Gamma (\fancyscript{D}^{+}/\fancyscript{C}^{+}_{2})\cdot \mathcal {X}_{D^{+}_{1}}= \mathcal {X}_{SH(D^{+}_{1})};\\ &\Gamma (\fancyscript{D}^{+}/\fancyscript{C}^{+}_{2})\odot \mathcal {X}_{D^{+}_{1}}= \mathcal {X}_{SL(D^{+}_{1})};\\ &\Gamma (\fancyscript{D}^{+}/\fancyscript{C}^{+}_{2})\cdot \mathcal {X}_{D^{+}_{2}}= \mathcal {X}_{SH(D^{+}_{2})};\\ &\Gamma (\fancyscript{D}^{+}/\fancyscript{C}^{+}_{2})\odot \mathcal {X}_{D^{+}_{2}}= \mathcal {X}_{SL(D^{+}_{2})};\\ &\Gamma (\fancyscript{D}^{+}/\{\fancyscript{C}^{+}_{1},\fancyscript{C}^{+}_{2}\})\cdot \mathcal {X}_{D^{+}_{1}}\ne \mathcal {X}_{SH(D^{+}_{1})};\\ &\Gamma (\fancyscript{D}^{+}/\{\fancyscript{C}^{+}_{1},\fancyscript{C}^{+}_{2}\})\odot \mathcal {X}_{D^{+}_{1}}\ne \mathcal {X}_{SL(D^{+}_{1})}; \end{aligned}$$

$$\begin{aligned} &\Gamma (\fancyscript{D}^{+}/\{\fancyscript{C}^{+}_{1},\fancyscript{C}^{+}_{2}\})\cdot \mathcal {X}_{D^{+}_{2}}\ne \mathcal {X}_{SH(D^{+}_{2})};\\ &\Gamma (\fancyscript{D}^{+}/\{\fancyscript{C}^{+}_{1},\fancyscript{C}^{+}_{2}\})\odot \mathcal {X}_{D^{+}_{2}}\ne \mathcal {X}_{SL(D^{+}_{2})};\\ &\Gamma (\fancyscript{D}^{+}/\{\fancyscript{C}^{+}_{2},\fancyscript{C}^{+}_{3}\})\cdot \mathcal {X}_{D^{+}_{1}}\ne \mathcal {X}_{SH(D^{+}_{1})};\\ &\Gamma (\fancyscript{D}^{+}/\{\fancyscript{C}^{+}_{2},\fancyscript{C}^{+}_{3}\})\odot \mathcal {X}_{D^{+}_{1}}\ne \mathcal {X}_{SL(D^{+}_{1})};\\ &\Gamma (\fancyscript{D}^{+}/\{\fancyscript{C}^{+}_{2},\fancyscript{C}^{+}_{3}\})\cdot \mathcal {X}_{D^{+}_{2}}\ne \mathcal {X}_{SH(D^{+}_{2})};\\ &\Gamma (\fancyscript{D}^{+}/\{\fancyscript{C}^{+}_{2},\fancyscript{C}^{+}_{3}\})\odot \mathcal {X}_{D^{+}_{2}}\ne \mathcal {X}_{SL(D^{+}_{2})}. \end{aligned}$$

Thereby, we have that $\{\fancyscript{C}^{+}_{1},\fancyscript{C}^{+}_{3}\}$ is a type-1 reduct of $(U^{+},\fancyscript{D}^{+}\cup U^{+}/d)$.

In Example 5.5, the computation complexities of constructing type-1 characteristic matrices are lower on the basis of results in Example 5.4, and the incremental algorithms are more effective to perform knowledge reduction in dynamic covering decision information systems. Furthermore, we can construct type-2 reducts of $(U,\fancyscript{D}\cup U/d)$ and $(U^{+},\fancyscript{D}^{+}\cup U^{+}/d)$ by Definition 2.4 and Theorem 3.5. For simplicity, we do not present the process of computing type-2 reducts of covering decision information systems and dynamic covering decision information systems in this section.

6 Conclusions

Many researchers have focused on dynamic information systems. In this paper, we have provided two incremental algorithms of constructing approximations of concepts in dynamic covering approximation spaces. Concretely, we have constructed the type-1 and type-2 characteristic matrices of coverings with the incremental approaches. We have constructed the second and sixth lower and upper approximations of sets on the basis of dynamic type-1 and type-2 characteristic matrices. Furthermore, we have employed experiments to illustrate that the time of computing approximations of sets could be reduced greatly by using the incremental approaches. Finally, we have performed knowledge reduction of dynamic covering decision information systems with the incremental approaches.

There are still many interesting topics deserving further investigations on dynamic information systems. For example, the cardinality of $\fancyscript{C}^+$ is not equal to the cardinality of $\fancyscript{C}$ when objects are coming sometimes, it is of interest to study this type of dynamic covering decision information system. In the future, we will present more effective approaches for knowledge discovery of dynamic covering decision information systems.