Retailer’s ordering policies for time-varying deteriorating items with partial backlogging and permissible delay in payments in a two-warehouse environment

Abstract

With the convergence of innovation, technology, and supply chain, the world has been shrinking, and the retail industry is one of the largest spread across the globe in the past few decades. Consumer expectations are on priority for the retailers. Most of the retail sector deals with the items whose usefulness declines with time and reaches the expiration date, resulting in a decrease in sales and eventually diminishing revenues for the retailers. In such cases, effective replenishment decisions and ordering policies may yield a significant increase in revenues. Further, with emerging retail trends, providing trade credit is considered a price reduction tool and an alternative to price discounts. Motivated by this, an inventory model developed and analyzed for items exhibiting time-varying deterioration with partially backlogged shortages and permissible delay in payment in the two-warehouse environment. The primary objective is to obtain the optimal ordering and backlogging policies for the retailer by minimizing the relevant cost. The optimal solution is obtained, solved analytically, and the inventory model validated with the help of numerical illustrations. The sensitivity analysis of the optimal solution with respect to key parameters and the managerial implications are also provided. The model is applicable to perishable items such as baked products, fruits, vegetables, groceries, meat, and seafood, where the deterioration is time-dependent and is perceived by its expiration date.

1 Introduction and research motivation

Globalization has led businesses to source and distribute raw materials, semi-finished goods, and finished goods across the world. With the dynamic behavior of the business enterprises, cut-throat competition in the retail industry, and sprouting technologies, the companies are facing a challenge in determining the optimal order quantity under demand uncertainty. The advent of e-businesses has added to the problem of retailers since the customer has spread its wings across the globe, shifting the focus from product to customer-centric. Thus, efficient inventory management, planning, and scheduling have become the target of companies to achieve strategic goals. Optimization models have been developed to answer the questions of how much and when to replenish the inventory to minimize the inherent costs associated with the management of stocks.

The study of inventory management plays a significant role when dealing with items exhibiting time-varying deterioration (e.g., perishable products, expiring inventories) depending on their category and storage facilities. Products such as pharmaceuticals, chemicals, blood banks, foodstuffs, vegetables, and even electronic gadgets have an expiration date or decline over time. They start deteriorating once they land on the shelf and, with time, lose their usefulness and original value. The primary concern of the customers while purchasing the grocery products is to buy one with the farther expiry date so that it can be stored for a longer time. Thus for maintaining inventories, researchers have been analyzing the impact of time-varying deterioration, which influences the purchase decision of the customers.

Further, trade credit policies have been practiced in developing countries for the past few decades because it is benefitting both vendors and buyers. Trade credit allows the retailer flexibility and feasibility in stocking the items and reducing the inventory carrying cost. Thus, to avail the opportunity of trade credit and to survive in the volatile market, a significant amount of stock is ordered, which creates the need for an additional warehouse to store the stock. Thus, the retailer is forced to rent an additional warehouse to store the excess amount of items. In many realistic inventory management systems, stock-outs are also considered; in such cases, demand may be back-ordered when the order replenished in the system, or it may be lost depending on the utility and availability of the product to the customer. The novelty of the paper is that it amalgamates the above-mentioned realistic scenarios such as expiring inventories, trade credit policy provided by the supplier to the retailer, and partially backlogged shortages when the retailer has two storage facilities. The numerical in the study illustrates deterioration rate firstly with expiration rate for products such as pharmaceuticals, bread cakes, etc., and secondly following Weibull distribution deterioration rate. Weibull distribution is a versatile distribution that can be used to model the increasing or decreasing rate of deterioration depending on the choice of the parameters. Thus, increasing the efficacy of the model in the retail sector. The coordination of the factors mentioned above has been the motivation behind the development of the inventory model for time-varying deteriorating products exhibiting deterioration with the expiry date and Weibull distribution deterioration rate with two storage facilities.

2 Literature review

2.1 Deteriorating inventories

Nowadays, customers are more conscious about the quality of the product due to which the demand for fresh products and packaged goods have intensely increased in current years. Freshness is a key element of the products as consumers pay more attention to the expiry date. Stock management of time-varying deteriorating items has been kept on top priority by the retailers considering the associated cost due to deterioration. Expiring inventories such as fruits, vegetables, pharmaceuticals, volatile liquids, electronic goods, etc. result in a shrinkage in stock due to several reasons such as evaporation, spoilage, obsolescence, etc., as once deteriorated an item cannot be sold. Ghare and Schrader (1963) were the first to propose an EOQ inventory model by assuming the deterioration rate follows an exponential distribution. Then Covert and Philip (1973) generalized the constant exponential deterioration rate to a two-parameter Weibull distribution. Goswami and Chaudhuri (1991) built an EOQ inventory model for deteriorating items considering the linear trend in demand. Further, many researchers have done tremendous work in this field, which are summarized by Raafat (1991), Goyal and Giri (2001), and Bakker et al. (2012). Effective management of expiring inventories has been the primary objective of recent studies. If not handled efficiently, it may add to waste and thus have a detrimental impact on the global environment. Jaggi et al. (2017a, b), Soni et al. investigated an inventory model for a non-instantaneous deteriorating item with partial backlogging; demand depends on price and promotional effort and shortage. Li and Teng (2018) studied a deterministic inventory model with the selling price and reference price, product freshness linked to the expiration date, and displayed stock level. Mishra et al. (2018) investigated trade credit financing for items with a preservation-dependent deterioration rate. Numerous researches have been done in this area, such as: Chen and Teng (2015), Kaya and Polat (2017), Tavakoli and Taleizadeh (2017), Taleizadeh et al. (2020).

2.2 Trade credit

The retail industry has been operating within the dynamic and highly competitive environment; most of the businesses have no pricing force and operate on a small profit margin. In order to upsurge the sales, mostly three different types of payment strategies are employed, which are (1) cash on delivery (COD), (2) delayed payment or credit payment and (3) prepayment. To dodge lasting price competition and to motivate the buyers to buy more and to promote their products, businesses mainly apply delayed payment or credit payment schemes as part of their pricing strategy. Trade credit is the credit extended to a company or customers by vendors who allow them to “buy now and pay later”. Goyal (1985) was the first to develop an economic order quantity (EOQ) model for the buyer when the vendor offers a fixed permissible delay period. Aggarwal and Jaggi (1995) developed an ordering policy for deteriorating items. Teng (2002) amended Goyal’s model by considering the difference between the unit price and unit cost. Teng et al. (2013) considered an inventory model for increasing demand in a supply chain with an upstream trade credit linked to order quantity. Wu et al. (2014) made the credit period and lot size decisions for deteriorating items with expiration dates under two-level trade credit financing. Chen et al. (2014) determined the economic order quantity when the supplier offers conditional permissible delay in payments linked to order quantity. Tiwari et al. (2018a, b) developed an inventory model for deteriorating items considering various trade credit financing policies, namely: order-size dependent trade credit and two-level partial trade credit, respectively. Cárdenas-Barrón et al. (2018) proposed an algorithm for an EOQ inventory model with nonlinear stock-dependent holding cost, nonlinear stock-dependent demand, and trade credit by relaxing the terminal condition. Lin et al. (2019) established an integrated inventory model for two-stage deterioration under trade credit and variable capacity utilization. Chang et al. (2019) presented a manufacturer’s pricing and lot-sizing decisions for perishable goods under various payment terms by a discounted cash flow analysis. Shi et al. (2019) build a sustainable inventory model for the retailer under upstream advance, cash, credit payment schemes. The literature is replete with papers on trade credit such as Jaggi et al. (2016, 2017a, b, 2018, 2019), Tiwari et al. (2016), Wu et al. (2014, 2016), Tsao et al., Shaikh et al. (2020a, b), Khakzad and Gholamian (2020), Khan et al. (2020).

2.3 Two warehouse environment

The classical Economic Order Quantity (EOQ) model is often based on the assumption of the single warehouse (OW) with unlimited capacity. However, there could be many reasons such as the discounted price of goods offered by the supplier, revenue (acquisition price) being higher than the holding cost in RW or evading high inflation rates that may lead to purchasing an amount of units that may exceed the capacity of OW, resulting in the excessive units being stored in an additional rented warehouse (RW), which is assumed to be of an ample capacity. Hsieh et al., Yang (2004, 2006, 2012), Banerjee and Agrawal (2008), Yang and Chang (2013), and Agrawal et al. (2013) are worth mentioning work in the area of two-warehouse. Most recently, Tiwari et al. (2016, 2017) developed two warehouse inventory models for non-instantaneous deteriorating items under trade credit policy. Tiwari et al. (2018c) optimized the pricing and inventory control problem for deteriorating items in an SC with limited storage capacity.

Since the past few decades, researchers have been developing inventory models suitable for enterprises to strive in various situations to increase sales and profits. For instance, it may be beneficial for a system to allow shortages when demand exists. In the area of logistics and supply, chain shortages may generate different impacts depending on the utility of the item for the customer. It may either result in backorders or lost sales. Alternatively, the case may be only a few customers wait for backorders and rest switch to other sellers to fulfill their demand; such a case of partial backlogging is close to the practical scenario and has been considered in this study. Inventory models assuming partial backlogging developed by several researchers are compiled by Pentico and Drake (2011).

From the literature search, it is observed that there is a research scope in inventory management for items exhibiting time-varying deterioration. Thus, to fill this gap, an inventory model is developed for such items considering trade credit under a two-warehouse environment. Moreover, in order to move closer towards a realistic scenario, shortages are allowed and are partially backlogged.

This paper is structured as follows. Section 3 sets the assumptions and notation used. Section 4 provides the inventory model formulation. Section 5 proposes some theoretical results for the optimal solutions. Sections 6 and 7 validate the inventory model through numerical experimentation and illustrates the robustness of the proposed model through sensitivity analysis, respectively. Finally, Sect. 8 concludes with some future research directions.

3 Assumptions and notation

The following assumptions and notations have been used in developing the model.

3.1 Hypothesis of the inventory system

The proposed inventory model has been developed under the following assumptions. The replenishment cycle length is constant and unknown. The order is instantaneously replenished, and the lead-time is negligible. The inventory system shows continuously repeated behavior; thus, the planning horizon of the inventory system is infinite. The demand rate is deterministic at a rate of D quantity units per unit of time. The own warehouse (OW) has a predetermined capacity of W units, and the rented warehouse (RW) has a limitless capacity. The unit inventory holding cost per unit time in RW is higher than that in OW. The deterioration rate in RW is less than that in OW because of better preservation facilities available at RW; thus, it is economical to consume the goods from RW before OW. Shortages, if any, are allowed, and unsatisfied demand is partially backlogged that is, will be fulfilled from the next replenishment. The fraction of shortages backlogged denoted by $\delta (t)$ is a differentiable and decreasing function of time t. The partial backlogging rate for the negative inventory is defined as $e^{ - \delta (T - t)}$; where $\delta ( > 0)$ denotes the backlogging parameter and $(T - t)$ is the waiting time up to the next replenishment. The retailer is offered fixed credit period M by the supplier, beyond which the retailer begins to pay the interest charges for the items in stock at rate I_p. The retailer can use the sales revenue generated before the settlement of the replenishment account to earn interest at an annual rate I_e, where I_p ≥ I_e. A deteriorating item deteriorates continuously and cannot be sold after its expiration or maximum lifetime date. Hence, its deterioration rate is 100% close to its expiration date. There exist several real-life products that exhibit time-varying deterioration, such as bakery products, pharmaceuticals, fruits, vegetables, fish, dairy products, etc. Thus, it is assumed that the deterioration rate $\theta (t)\;{\text{at}}\;{\text{time}}\;{\text{t}},\;0 \le t \le k$, where k is expiration time, satisfies the following conditions: $0 \le \theta (t) \le 1, \, \theta^{\prime}(t) \ge 0,\;{\text{and}}\;\theta (k) = 1$.

Notation

Parameters
W	The storage capacity of OW (units)
D	Demand rate (units/ time unit)
S	The maximum stock level at the beginning of the cycle (units)
Q	Order quantity per cycle (units)
c	The purchase cost per item ($/unit)
p	Unit selling price per item ($/ unit)
B	The maximum amount of backlogged demand
cb	Backlogging cost per unit per unit time ($/unit)
co	Unit opportunity cost due to a lost sale ($/unit)
A	The fixed cost of placing an order ($/order)
H, F	Unit holding cost per unit per unit time at OW and RW respectively, (F > H)
M	The retailer’s trade credit period offered by the supplier (time unit)
Ie	Interest earned per dollar per unit time per year by the retailer (%)
Ip	Interest paid per dollar per unit in stock per year by the retailer (%)
tw	Time at which the inventory level reaches zero in OW (time unit)
k	Maximum lifetime or expiration time in years
Decision variables
tr	Time at which the inventory level reaches zero in RW (time unit)
T	The length of the replenishment cycle (time unit)
Functions
Qo(t)	Inventory level of OW at time t (units)
Qr(t)	Inventory level of RW at time t (units)
B(t)	Backlogged level at time t (units)
L(t)	Number of lost sales at time t (units)
TCi(tr, T)	Total relevant cost per unit time for case i = 1, 2 and 3 ($/time unit)

3.2 Mathematical model formulation

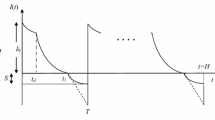
Given the above notations and assumptions, in this section mathematical formulation of two warehouse inventory model for deteriorating items with expiration date and partially backlogged shortages is derived. The behavior of the model is shown graphically in Fig. 1. Initially, a lot size Q enters the system; after satisfying the backorders of the previous cycle, initial inventory left is S. Out of these S units W units are stocked in OW, whereas remaining $(S - W)$ units are stored in RW. During the interval, $[0,\;t_{r} ]$ the demand is fulfilled through RW; thus, the inventory level is depleted by demand and deterioration.

Fig. 1

Graphical representation of the inventory system

3.3 Inventory levels

The inventory levels are governed by the following differential equation:

$$ \frac{{dQ_{r} (t)}}{dt} + \theta_{r} (t)Q_{r} (t) = - D\quad 0 \le t \le t_{r} $$

(1)

with the boundary condition $Q_{r} (0) = S - W,\;{\text{and}}\; \, Q_{r} (t_{r} ) = 0$, the solution of the differential equation is obtained as:

$$ Q_{r} (t) = De^{{ - Z_{r} (t)}} \int\limits_{t}^{{t_{r} }} {e^{{Z_{r} (u)}} du} \quad 0 \le t \le t_{r} $$

(2)

where

$$ Z_{r} (t) = \int\limits_{0}^{t} {\theta_{r} (u)du} $$

(3)

Also using initial boundary condition $Q_{r} (0) = S - W$, gives

$$ S = W + D\int\limits_{0}^{{t_{r} }} {e^{{Z_{r} (u)}} du} $$

(4)

During the time interval $[0,\;t_{r} ]$ inventory in OW reduces only due to deterioration. At t_r the stock at RW is exhausted and the demand is satisfied from OW. Thus, during the time interval $[t_{r} ,\;t_{w} ]$ inventory in OW depletes due to demand as well as deterioration. the differential equations that describe the inventory level in OW over the period $[0,\;t_{r} ]$ and $[t_{r} ,\;t_{w} ]$ are given by:

$$ \frac{{dQ_{0} (t)}}{dt} + \theta_{0} (t)Q_{0} (t) = 0;\quad 0 \le t \le t_{r} $$

(5)

with the boundary condition $Q_{0} (0) = W$, the solution of the differential equation is obtained as:

$$ Q_{0} (t) = We^{{ - Z_{0} (t)}} \quad 0 \le t \le t_{r} $$

(6)

where

$$ Z_{o} (t) = \int\limits_{0}^{t} {\theta_{o} (u)du} $$

(7)

Also,

$$ \frac{{dQ_{0} (t)}}{dt} + \theta_{0} (t)Q_{0} (t) = - D;\quad t_{r} < t \le t_{w} $$

(8)

Using boundary condition $Q_{0} (t_{w} ) = 0$, the solution of differential equation is

$$ Q_{0} (t) = e^{{ - Z_{0} (t)}} D\int\limits_{t}^{{t_{w} }} {e^{{Z_{0} (u)}} du} \quad t_{r} < t \le t_{w} $$

(9)

Using continuity of $Q_{0} (t)$ at $t = t_{r}$, it follows that

$$ We^{{ - Z_{0} \left( {t_{r} } \right)}} = e^{{ - Z_{0} \left( {t_{r} } \right)}} D\int\limits_{{t_{r} }}^{{t_{w} }} {e^{{Z_{0} \left( u \right)}} du} $$

(10)

$$ W = D\int\limits_{{t_{r} }}^{{t_{w} }} {e^{{Z_{0} (u)}} du} $$

(11)

During the time interval $[t_{w} ,\;T]$, the demand is partially backlogged, and the differential equation is given by:

$$ \frac{dB(t)}{{dt}} = De^{ - \delta (T - t)} \quad t_{w} \le t \le T $$

(12)

Using the boundary condition $B(t_{w} ) = 0$, we have

$$ B(t) = \frac{D}{\delta }\left( {e^{ - \delta (T - t)} - e^{{ - \delta (T - t_{w} )}} \, } \right)\quad t_{w} \le t \le T $$

(13)

The amount of lost sales at time t is

$$ L(t) = \int\limits_{{t_{w} }}^{t} D \left( {1 - e^{ - \delta (T - t)} } \right)dt\quad t_{w} \le t \le T $$

(14)

$$ L(t) = D\left\{ {(t - t_{w} ) - \frac{1}{\delta }\left( {e^{ - \delta (T - t)} - e^{{ - \delta (T - t_{w} )}} \, } \right)} \right\}\quad t_{w} \le t \le T $$

(15)

The maximum amount of demand backlogged per cycle is

$$ B(T) = \frac{D}{\delta }\left( {1 - e^{{ - \delta (T - t_{w} )}} } \right) $$

(16)

Thus, the order quantity for the replenishment cycle is obtained as

$$ Q = S + B(T) = W + D\int\limits_{0}^{{t_{r} }} {e^{{Z_{r} (u)}} du} + \frac{D}{\delta }\left( {1 - e^{{ - \delta (T - t_{w} )}} } \right) $$

(17)

3.4 Retailer’s cost components

Based on the above-obtained inventory levels, the inventory related costs per cycle are obtained as follows:

• The replenishment cost is A

• The inventory holding cost in RW

  $$ HC_{rw} = FD\int\limits_{0}^{{t_{r} }} {e^{{ - Z_{r} (t)}} } \int\limits_{t}^{{t_{r} }} {e^{{Z_{r} (u)}} du} dt $$

  (18)

• The inventory holding cost in OW

  $$ \begin{gathered} HC_{ow} = H\left[ {\int\limits_{0}^{{t_{r} }} {Q_{0} (t)dt} + \int\limits_{{t_{r} }}^{{t_{w} }} {Q_{0} (t)dt} } \right] \hfill \\ HC_{ow} = H\left[ {W\int\limits_{0}^{{t_{r} }} {e^{{ - Z_{0} (t)}} dt} + D\int\limits_{{t_{r} }}^{{t_{w} }} {e^{{ - Z_{0} \left( t \right)}} \int\limits_{t}^{{t_{w} }} {e^{{Z_{0} (u)}} du} dt} } \right] \hfill \\ \end{gathered} $$

  (19)

• The backlogging cost is

  $$ \begin{gathered} BC = c_{b} \int\limits_{{t_{w} }}^{T} B (t)dt \hfill \\ BC = \frac{{c_{b} D}}{{\delta^{2} }}\left[ {1 - e^{{ - \delta (T - t_{w} )}} \left\{ {1 + \delta (T - t_{w} )} \right\}} \right] \hfill \\ \end{gathered} $$

  (20)

• The opportunity cost due to lost sales

  $$ \begin{gathered} LC = c_{o} D\int\limits_{{t_{w} }}^{T} {\left( {1 - e^{ - \delta (T - t)} } \right)} dt \hfill \\ LC = \frac{{c_{o} D}}{\delta }\left[ {\delta (T - t_{w} ) - \left( {1 - e^{{ - \delta (T - t_{w} )}} } \right)} \right] \hfill \\ \end{gathered} $$

  (21)

• The purchasing cost $PC = cQ$

  $$ PC = c\left\{ {W + D\int\limits_{0}^{{t_{r} }} {e^{{Z_{r} (u)}} du} + \frac{D}{\delta }\left( {1 - e^{{ - \delta (T - t_{w} )}} } \right)} \right\} $$

  (22)

3.5 Interest earned, and interest paid

In addition, the supplier offers permissible delay in payment to the retailer. The interest earned, interest paid, and cost functions for distinct cases are computed as follows:

Case 1 $0 < M \le t_{r}$.

In addition to the interest earned by fulfilling the demand of the current cycle for the time period 0 to M the retailer also earns interest on the revenue generated by satisfying shortages of the previous cycle. After the payment of the account at M, the retailer must finance the unsold items for the time period [M, T]. The interest earned is calculated as:

$$ \begin{gathered} {\text{Interest earned}}\quad IE_{1} = \frac{1}{2}pI_{e} DM^{2} + pI_{e} \int\limits_{0}^{M} B (T)dt \hfill \\ IE_{1} = \frac{1}{2}pI_{e} DM^{2} + pI_{e} \frac{D}{\delta }M\left( {1 - e^{{ - \delta (T - t_{w} )}} } \right) \hfill \\ \end{gathered} $$

(23)

$$ \begin{gathered} {\text{Interest}}\;{\text{paid}}\quad IP_{1} = cI_{p} \left[ {\int\limits_{M}^{{t_{r} }} {Q_{r} (t)dt} + \int\limits_{M}^{{t_{r} }} {Q_{0} (t)dt} + \int\limits_{{t_{r} }}^{{t_{w} }} {Q_{0} (t)dt} } \right] \hfill \\ IP_{1} = cI_{p} \left[ {\int\limits_{M}^{{t_{r} }} {De^{{ - Z_{r} (t)}} \int\limits_{t}^{{t_{r} }} {e^{{Z_{r} (u)}} du} dt} + \int\limits_{M}^{{t_{r} }} {We^{{ - Z_{0} (t)}} dt} + \int\limits_{{t_{r} }}^{{t_{w} }} {e^{{ - Z_{0} (t)}} D\int\limits_{t}^{{t_{w} }} {e^{{Z_{0} (u)}} du} dt} } \right] \hfill \\ \end{gathered} $$

(24)

Case 2 $t_{r} < M \le t_{w}$.

In this case, also the retailer earns interest on the sales revenue generated during the time period 0 to M. Account is settled at M, and the payment for the remaining stock is to be done for the time period [M, T].

$$ \begin{gathered} {\text{Interest earned}}\quad IE_{2} = \frac{1}{2}pI_{e} DM^{2} + pI_{e} \int\limits_{0}^{M} B (T)dt \hfill \\ IE_{2} = \frac{1}{2}pI_{e} DM^{2} + pI_{e} \frac{D}{\delta }M\left( {1 - e^{{ - \delta (T - t_{w} )}} } \right) \hfill \\ \end{gathered} $$

(25)

$$ \begin{gathered} {\text{Interest}}\;{\text{paid}}\quad IP_{2} = cI_{p} \int\limits_{M}^{{t_{w} }} {Q_{0} (t)dt} \hfill \\ IP_{2} = cI_{p} D\int\limits_{M}^{{t_{w} }} {e^{{ - Z_{0} (t)}} \int\limits_{t}^{{t_{w} }} {e^{{Z_{0} (u)}} du} dt} \hfill \\ \end{gathered} $$

(26)

Case 3 $t_{w} < M \le T$.

In this case, the complete stock bought on credit by the retailer from the supplier is sold. Hence the interest paid is zero. In addition to the interest earned on sold items up to M the retailer also earns additional interest on inventory from M to T.

$$ {\text{Interest }}\;{\text{earned}}\;IE_{3} = \frac{1}{2}pI_{e} Dt_{w}^{2} + pI_{e} D(M - t_{w} )t_{w} + pI_{e} \frac{D}{\delta }M\left( {1 - e^{{ - \delta (T - t_{w} )}} } \right) $$

(27)

4 Retailer’s total cost function

Therefore, the total cost per unit time during the cycle time (0, T) is determined as:

$$ TC_{i} (t_{r} ,\;T) = \frac{1}{T}\left[ {A + HC_{rw} + HC_{ow} + BC + LC + PC - IE_{i} + IP_{i} } \right],\quad \, i = 1,2,3 $$

$$ TC(t_{r} ,\;T) = \biggl\{ \begin{gathered} TC_{1} (t_{r} ,\;T)\quad {\text{if}}\; \, 0 < M \le t_{r} \hfill \\ TC_{2} (t_{r} ,\;T)\quad {\text{if}}\; \, t_{r} < M \le t_{w} \hfill \\ TC_{3} (t_{r} ,\;T)\quad {\text{if}}\; \, t_{w} < M \le T \, \;{\text{or}}\; \, T < M \hfill \\ \end{gathered} $$

(28)

$$ TC_{1} (t_{r} ,\;T) = \frac{1}{T}\left[ \begin{gathered} A + c\left\{ {W + D\int\limits_{0}^{{t_{r} }} {e^{{Z_{r} (u)}} du} + \frac{D}{\delta }\left( {1 - e^{{ - \delta (T - t_{w} )}} } \right)} \right\} + FD\int\limits_{0}^{{t_{r} }} {e^{{ - Z_{r} (t)}} } \int\limits_{t}^{{t_{r} }} {e^{{Z_{r} (u)}} du} dt \hfill \\ + H\left\{ {W\int\limits_{0}^{{t_{r} }} {e^{{ - Z_{0} (t)}} dt} + D\int\limits_{{t_{r} }}^{{t_{w} }} {e^{{ - Z_{0} (t)}} \int\limits_{t}^{{t_{w} }} {e^{{Z_{0} (u)}} du} dt} } \right\} + \frac{{c_{b} D}}{{\delta^{2} }}\left\{ {1 - e^{{ - \delta (T - t_{w} )}} \left\{ {1 + \delta (T - t_{w} )} \right\}} \right\} \hfill \\ + \frac{{c_{o} D}}{\delta }\left\{ {\delta (T - t_{w} ) - \left( {1 - e^{{ - \delta (T - t_{w} )}} } \right)} \right\} - \left\{ {\frac{1}{2}pI_{e} DM^{2} + pI_{e} \frac{D}{\delta }M\left( {1 - e^{{ - \delta (T - t_{w} )}} } \right)} \right\} \hfill \\ + cI_{p} \left\{ {\int\limits_{M}^{{t_{r} }} {De^{{ - Z_{r} (t)}} \int\limits_{t}^{{t_{r} }} {e^{{Z_{r} (u)}} du} dt} + \int\limits_{M}^{{t_{r} }} {We^{{ - Z_{0} (t)}} dt} + \int\limits_{{t_{r} }}^{{t_{w} }} {e^{{ - Z_{0} (t)}} D\int\limits_{t}^{{t_{w} }} {e^{{Z_{0} (u)}} (u)du} dt} } \right\} \hfill \\ \end{gathered} \right];\quad 0 < M \le t_{r} $$

(29)

$$ TC_{2} (t_{r} ,\;T) = \frac{1}{T}\left[ \begin{gathered} A + c\left\{ {W + D\int\limits_{0}^{{t_{r} }} {e^{{Z_{r} (u)}} du} + \frac{D}{\delta }\left( {1 - e^{{ - \delta (T - t_{w} )}} } \right)} \right\} + FD\int\limits_{0}^{{t_{r} }} {e^{{ - Z_{r} (t)}} } \int\limits_{t}^{{t_{r} }} {e^{{Z_{r} (u)}} du} dt \hfill \\ + H\left\{ {W\int\limits_{0}^{{t_{r} }} {e^{{ - Z_{0} (t)}} dt} + D\int\limits_{{t_{r} }}^{{t_{w} }} {e^{{ - Z_{0} (t)}} \int\limits_{t}^{{t_{w} }} {e^{{Z_{0} (u)}} du} dt} } \right\} \hfill \\ + \frac{{c_{b} D}}{{\delta^{2} }}\left\{ {1 - e^{{ - \delta (T - t_{w} )}} \left\{ {1 + \delta (T - t_{w} )} \right\}} \right\} + \frac{{c_{o} D}}{\delta }\left\{ {\delta (T - t_{w} ) - \left( {1 - e^{{ - \delta (T - t_{w} )}} } \right)} \right\} \hfill \\ - \left\{ {\frac{1}{2}pI_{e} DM^{2} + pI_{e} \frac{D}{\delta }M\left( {1 - e^{{ - \delta (T - t_{w} )}} } \right)} \right\} + cI_{p} D\int\limits_{M}^{{t_{w} }} {e^{{ - Z_{0} (t)}} \int\limits_{t}^{{t_{w} }} {e^{{Z_{0} (u)}} du} dt} \hfill \\ \end{gathered} \right];\quad t_{r} < M \le t_{w} $$

(30)

$$ TC_{3} (t_{r} ,\;T) = \frac{1}{T}\left[ \begin{gathered} A + c\left\{ {W + D\int\limits_{0}^{{t_{r} }} {e^{{Z_{r} (u)}} du} + \frac{D}{\delta }\left( {1 - e^{{ - \delta (T - t_{w} )}} } \right)} \right\} + FD\int\limits_{0}^{{t_{r} }} {e^{{ - Z_{r} (t)}} } \int\limits_{t}^{{t_{r} }} {e^{{Z_{r} (u)}} du} dt \hfill \\ + H\left\{ {W\int\limits_{0}^{{t_{r} }} {e^{{ - Z_{0} (t)}} dt} + D\int\limits_{{t_{r} }}^{{t_{w} }} {e^{{ - Z_{0} (t)}} \int\limits_{t}^{{t_{w} }} {e^{{Z_{0} (u)}} du} dt} } \right\} \hfill \\ + \frac{{c_{b} D}}{{\delta^{2} }}\left\{ {1 - e^{{ - \delta (T - t_{w} )}} \left\{ {1 + \delta (T - t_{w} )} \right\}} \right\} + \frac{{c_{o} D}}{\delta }\left\{ {\delta (T - t_{w} ) - \left( {1 - e^{{ - \delta (T - t_{w} )}} } \right)} \right\} \hfill \\ - \left\{ {\frac{1}{2}pI_{e} Dt_{w}^{2} + pI_{e} D(M - t_{w} )t_{w} + pI_{e} \frac{D}{\delta }M\left( {1 - e^{{ - \delta (T - t_{w} )}} } \right)} \right\} \hfill \\ \end{gathered} \right];\quad t_{w} < M \le T \, or \, T < M $$

(31)

5 Theoretical theorems and results

In this section, the retailer's optimal solution and the optimal replenishment cycle time is determined. Now the problem is to minimize the total cost function:

$$ \begin{aligned} {\text{Minimize}} & \quad TC(t_{r} ,\;T) \\ {\text{s.t.}} & \quad 0 < t_{r} < t_{w} , \, \;\;S \ge W \\ \end{aligned} $$

According to Theorems 3.2.9 and 3.2.10 in Cambini and Martein (2009), the real-valued function

$$ q(x) = \frac{g(x)}{{h(x)}} $$

(32)

is (strictly) pseudo-convex, if g(x) is non-negative, differentiable and (strictly) convex, and h(x) is positive, differentiable, and concave. Let

$$ J = \left\{ {c_{o} + c + pI_{e} M + c_{b} - c_{b} (T - t_{w} )} \right\}D\delta e^{{ - \delta (T - t_{w} )}} $$

(33)

Without any loss of generality, it can be assumed that $J > 0$. Given $t_{r}$, and using Eq. (32) it can be proved that the retailer's total cost $TC(t_{r} ,\;T)$ in Eq. (28) is strictly pseudo-convex in T if $J > 0$. Consequently, there exists a unique global optimal solution $T^{*}$ such that $TC(t_{r} ,\;T)$ is minimized.

Theorem 1

Given the time when the stock level of RW reaches zero, if $J > 0$ then $TC(t_{r} ,\;T)$ in Eq. (28) is a strictly pseudo-convex function in T, and there exists a unique minimum solution T^*.

Proof

See Appendix 1.

Given the time when the stock level of RW reaches zero, applying Theorem 1, taking the first-order derivative of $TC_{1} (t_{r} ,\;T)$ with respect to T and equating to zero, the necessary and sufficient conditions for the optimal replenishment cycle time T^* are obtained as follows:

$$ \begin{aligned} & \left[ {\left\{ {c_{b} \delta (T - t_{w} ) - c_{o} - c - pI_{e} M} \right\}De^{{ - \delta (T - t_{w} )}} + c_{o} D} \right]T \\ & \quad = A + c\left\{ {W + D\int\limits_{0}^{{t_{r} }} {e^{{Z_{r} (u)}} du} + \frac{D}{\delta }\left( {1 - e^{{ - \delta (T - t_{w} )}} } \right)} \right\} + FD\int\limits_{0}^{{t_{r} }} {e^{{ - Z_{r} (t)}} } \int\limits_{t}^{{t_{r} }} {e^{{Z_{r} (u)}} du} dt \\ & \quad \quad + H\left\{ {W\int\limits_{0}^{{t_{r} }} {e^{{ - Z_{0} (t)}} dt} + D\int\limits_{{t_{r} }}^{{t_{w} }} {e^{{ - Z_{0} (t)}} \int\limits_{t}^{{t_{w} }} {e^{{Z_{0} (u)}} du} dt} } \right\} + \frac{{c_{b} D}}{{\delta^{2} }}\left\{ {1 - e^{{ - \delta (T - t_{w} )}} \left\{ {1 + \delta (T - t_{w} )} \right\}} \right\} \\ & \quad \quad + \frac{{c_{o} D}}{\delta }\left\{ {\delta (T - t_{w} ) - \left( {1 - e^{{ - \delta (T - t_{w} )}} } \right)} \right\} - \left\{ {\frac{1}{2}pI_{e} DM^{2} + pI_{e} \frac{D}{\delta }M\left( {1 - e^{{ - \delta (T - t_{w} )}} } \right)} \right\} \\ & \quad \quad + cI_{p} \left\{ {\int\limits_{M}^{{t_{r} }} {De^{{ - Z_{r} (t)}} \int\limits_{t}^{{t_{r} }} {e^{{Z_{r} (u)}} du} dt} + \int\limits_{M}^{{t_{r} }} {We^{{ - Z_{0} (t)}} dt} + \int\limits_{{t_{r} }}^{{t_{w} }} {e^{{ - Z_{0} (t)}} D\int\limits_{t}^{{t_{w} }} {e^{{Z_{0} (u)}} du} dt} } \right\} \\ \end{aligned} $$

(34)

The detailed derivation of Case 2 and Case 3 are provided in Appendix 2.

Similarly, for given replenishment cycle time T it can be further proved that $TC(t_{r} ,\;T)$ in Eq. (28) is a strictly convex function in $t_{r}$. Let

$$ \left( {c_{o} - c_{b} (T - t_{w} ) - c} \right) = L $$

(35)

Without any loss of generality, it can be assumed that $L > 0$. Thus, the following result is obtained.

Theorem 2

For given replenishment cycle time T, if $L > 0$, then $TC(t_{r} ,\;T)$ in Eq. (28) is a strictly convex function of $t_{r}$ and hence there exists a unique optimal solution $t_{r}^{*}$.

Proof

See Appendix 3.

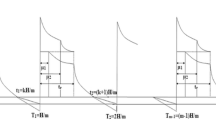
6 Numerical examples

To illustrate the proposed model, two numerical examples have been considered.

In the first numerical example, the newly adopted deterioration rate $\theta (t) = 1/(1 + k - t)\;{\text{with}}\;t \le k$ is used to incorporate the fact that the deterioration rate is $100\%$ near to its expiration date. In the second example, the most commonly known Weibull non-decreasing deterioration rate $\theta (t) = \alpha \beta t^{\beta - 1} ,\;\;0 < \alpha < 1,\; \, \beta \ge 1,\;{\text{ and}}\; \, t \ge 0$ is used.

To demonstrate numerically the proposed system, the following data set is taken:

A = $1000 per order, D = 1000 units per year, W = 200 units, H = $ 0.5 per unit per year, F = $0.7 per unit per year, c = $1.0 per unit, p = $3.0 per unit, c_b = $0.8 per unit, c_o = $2 per unit, δ = 0.9, M = 0.25 or 0.50 years, I_e = 0.12 per dollar per year, I_p = 0.15 per dollar per year.

Example 1

For $\theta_{i} (t) = 1/(1 + k_{i} - t) \, \;{\text{with}}\; \, t \le k_{i} ,\;\;i = r,\;o$, let k_r = 1 year, k_o = 1 year. The optimal solution to M = 0.25 and 0.50 is obtained for each case as shown in Table 1.

Table 1 Impact of credit period M, when $\theta (t) = 1/(1 + k - t)\;{\text{with}}\; \, t \le k$

Table 1 reveals that a higher value of the trade credit period diminishes the total relevant cost. Although the order quantity and the cycle length remain unaffected but the extended credit terms for payments to the supplier reduces costs incurred by the retailer.

Example 2

Using the same data set as in Example 1 except for M = 0.30 years, an optimal solution obtained for k_r = k_o = 1 year and 2 years for each case is shown in Table 2.

Table 2 Impact of a maximum lifetime, when $\theta (t) = 1/(1 + k - t)\;{\text{with}}\;t \le k$

It is observed from Table 2 that if the maximum lifetime k is high, order quantity increases, which eventually results in declining total relevant cost. This pattern of change suggests that if the maximum lifetime k is high, then the retailer can reduce the total cost by increasing the order quantity, thereby balancing the cost due to deterioration.

Example 3

Considering the Weibull deterioration rate $\theta_{i} (t) = \alpha_{i} \beta_{i} t^{{\beta_{i} - 1}} , \, \;\;i = r,\;o$, where $\alpha_{o} = 0.05,\;\beta_{o} = 1.8,\;\alpha_{r} = 0.02,\;\beta_{r} = 1.8$, the optimal solution obtained for M = 0.25 and 0.50 for each case is presented in Table 3.

Table 3 Impact of credit period M, when $\theta (t) = \alpha \beta t^{\beta - 1} ,\; \, 0 < \alpha < 1, \, \;\beta \ge 1, \, \;{\text{and}}\; \, t \ge 0$

Table 3 shows that the increase in trade credit period slightly lowers the order quantity and the cycle length and eventually reduces the retailer’s total relevant cost.

Example 4

Considering Weibull deterioration rate $\theta_{i} (t) = \alpha_{i} \beta_{i} t^{{\beta_{i} - 1}} , \, \;\;i = r,\;o$ the optimal solution obtained for different values of α and β at M = 0.30 is presented in Table 4.

Table 4 Impact of α and β, when $\theta \left( t \right) = \alpha \beta t^{\beta - 1} , \, 0 < \alpha < 1, \, \beta \ge 1,{\text{ and }}t \ge 0$

The total relevant cost it quite sensitive to the parameter of the deterioration rate α_o and α_r. When α_o and α_r increases, the order quantity declines, which eventually results in higher costs. Whereas, the total cost is not so sensitive to the shape parameters of the deterioration rate β_o and β_r.

7 Sensitivity analysis and managerial insights

In this section, some managerial implications based on the sensitivity analysis of the parameters are displayed. Further sensitivity analysis is performed on the two different time-varying deterioration rates, but both show similar results with the change in significant parameters of the model. Thus, to avoid unnecessary repetitions, computational results of sensitivity analysis performed on maximum lifetime data set based on Example 1 are presented in Table 5.

Table 5 Sensitivity analysis on parameters

The sensitivity analysis reveals the following managerial insights:

7.1 Impact of deterioration distribution parameters

It has been demonstrated from a sensitivity analysis that the maximum lifetime or deterioration distribution parameters of the product are of prime considerations in decision making by the retailer. The time to the expiration date is of utmost importance while dealing with deteriorating items, especially in decisions regarding optimal cycle time. Also, as can be observed, the total relevant cost decreases as the maximum lifetime increases, thus, to achieve the optimal total cost managing the order quantity and the cycle time in the presence of maximum lifetime and deterioration distribution parameters is essential.

7.2 Impact of selling price and purchase cost

Similar to the common practice increase in purchase cost results in an increase in total relevant cost. Retailers have been taking benefit of this result through bulk purchases or engaging in discounting strategies that provide a lesser unit cost of the product. Also, the increase in selling price results in decreasing the total relevant cost.

7.3 Impact of cost parameters

The increment in the cost parameters H, F, A results in an increase in total relevant cost. The order quantity declines with increment in H, F since the retailer is forced to procure less when the deterioration cost incremented, which eventually results in increased total cost. Whereas, the order quantity increases with a decrement in A, thus resulting in lesser total cost.

Traditionally, the supplier offers trade credit to the retailer in order to stimulate the retailer's order quantity. Whereas, in the numerical examples, it is observed that there is a marginal change in order quantity as the credit period rises. This variation suggests that as the credit period increases, it results in higher opportunity costs for the supplier and lower opportunity cost of capital for the retailer. Thus, to obtain the minimum cost, there is no substantial deviation in order quantity and hence the cycle length.

8 Conclusion and further research

In this paper, the following essential factors are captured: (1) stock management of expiring inventories is essential for emerging retail outlets and plays a vital role in effective decision making, thus in contrast to a constant decay rate it is assumed that perishable products have a fixed lifetime, (2) trade credit has a substantial impact on retailers' inventory policies, (3) additional warehouse helps to cope with uncertainties of demand in business settings, and (4) consideration of partial backlogging provides a real-life scenario of the retail sector where the customer is free to look for substitutes of the unavailable product, and the backlogged rate depends on the waiting time up to the next replenishment. Several theoretical results are also established to characterize the existence and uniqueness of the optimal solution of the proposed model. Sensitivity analysis is performed to investigate the impact of the crucial model parameter on the total relevant cost. Several managerial insights have been obtained, such as considering the deterioration distribution, or expiration dates of the items is beneficial for inventory management, and accordingly, the decision strategies can be employed. By implementing the policies and considering the factors mentioned in the proposed model, the manager can retard the total cost. The model is practical for fruits, vegetables, medicine, grains, electronic products, and other goods that deteriorate or decline over time. Retailers want to sell such products before their expiry date else, they lose their invested amount. Thus the model reflects the pragmatic views by considering the time-dependent deterioration with maximum lifetime, trade credit, two warehouse, and partial backlogging.

It would be interesting to extend the model by considering advance payment and other trade credit options. Deterministic demand can also be replaced by stochastic demand or price-dependent demand. Future extensions for research can be including multi-items in an integrated supply chain, inflation, and quantity discount effects, two-stage trade credit financing, different demand forms such as stock-dependent demand, credit-linked demand, or promotion dependent demand.

Appendices

Appendix 1

Proof of Theorem 1 Let $g_{1} (T) = A + HC_{rw} + HC_{ow} + BC + LC + PC - IE_{1} + IP_{1}$ and $h\left( T \right) = T > 0$.

Therefore,

$$ q_{1} (T) = \frac{{g_{1} (T)}}{h(T)} = TC_{1} (t_{r} ,\;T) $$

For the given value of $t_{r}$, the first order derivative of $g_{1} (T)$ is obtained as

$$ g_{1}^{^{\prime}} (T) = \left\{ {c_{b} \delta (T - t_{w} ) - c_{o} - c - pI_{e} M} \right\}De^{{ - \delta (T - t_{w} )}} + c_{o} D $$

(36)

A derivative of (36) is further obtained as,

$$ g_{1}^{^{\prime\prime}} (T) = \left\{ {c_{o} + c + pI_{e} M + c_{b} - c_{b} (T - t_{w} )} \right\}D\delta e^{{ - \delta (T - t_{w} )}} $$

This implies, if $J > 0$, then $g_{1}^{^{\prime\prime}} (T) > 0$ and hence $g_{1} (T)$ is non-negative, differentiable and strictly convex.

It has been calculated and verified that $g_{2}^{^{\prime}} (T)$ and $g_{3}^{^{\prime}} (T)$ is the same as $g_{1}^{^{\prime}} (T)$, where

$$ g_{2} (T) = A + HC_{rw} + HC_{ow} + BC + LC + PC - IE_{2} + IP_{2} $$

$$ g_{3} (T) = A + HC_{rw} + HC_{ow} + BC + LC + PC - IE_{3} $$

Thus, if $J > 0$ then the total cost $TC(t_{r} ,\;T)$ in Eq. (28) is a strictly pseudo-convex function in T, and there exists a unique optimal solution.

Appendix 2

It is observed that $\frac{{g_{i} (T)}}{h(T)} = TC_{i} (t_{r} ,\;T),\;\;i = 1,2,3$. Hence given $t_{r}$, taking the first order derivative of $TC_{1} (t_{r} ,\;T)$ with respect to T, and setting the result to zero, the necessary and sufficient condition to find $T^{*}$, is obtained as follows:

$$ \begin{aligned} & \frac{{dTC_{1} (t_{r} ,\;T)}}{dT} = \frac{{g_{1}^{^{\prime}} (T)}}{T} - \frac{{g_{1} (T)}}{{T^{2} }} = 0 \\ & \quad \Rightarrow g_{1}^{^{\prime}} (T)T - g_{1} (T) = 0 \\ \end{aligned} $$

Thus from Eqs. (29) and (36), if $J > 0$ then the necessary and sufficient condition for $T^{*}$ is

$$ \begin{aligned} & \left[ {\left\{ {c_{b} \delta \left( {T - t_{w} } \right) - c_{o} - c - pI_{e} M} \right\}De^{{ - \delta \left( {T - t_{w} } \right)}} + c_{o} D} \right]T \\ & \quad = A + c\left\{ {W + D\int\limits_{0}^{{t_{r} }} {e^{{Z_{r} \left( u \right)}} du} + \frac{D}{\delta }\left( {1 - e^{{ - \delta \left( {T - t_{w} } \right)}} } \right)} \right\} + FD\int\limits_{0}^{{t_{r} }} {e^{{ - Z_{r} \left( t \right)}} } \int\limits_{t}^{{t_{r} }} {e^{{Z_{r} \left( u \right)}} du} dt \\ & \quad \quad + H\left\{ {W\int\limits_{0}^{{t_{r} }} {e^{{ - Z_{0} \left( t \right)}} dt} + D\int\limits_{{t_{r} }}^{{t_{w} }} {e^{{ - Z_{0} \left( t \right)}} \int\limits_{t}^{{t_{w} }} {e^{{Z_{0} \left( u \right)}} du} dt} } \right\} + \frac{{c_{b} D}}{{\delta^{2} }}\left\{ {1 - e^{{ - \delta \left( {T - t_{w} } \right)}} \left\{ {1 + \delta \left( {T - t_{w} } \right)} \right\}} \right\}\quad \quad 0 < M \le t_{r} \\ & \quad \quad + \frac{{c_{o} D}}{\delta }\left\{ {\delta \left( {T - t_{w} } \right) - \left( {1 - e^{{ - \delta \left( {T - t_{w} } \right)}} } \right)} \right\} - \left\{ {\frac{1}{2}pI_{e} DM^{2} + pI_{e} \frac{D}{\delta }M\left( {1 - e^{{ - \delta \left( {T - t_{w} } \right)}} } \right)} \right\} \\ & \quad \quad + cI_{p} \left\{ {\int\limits_{M}^{{t_{r} }} {De^{{ - Z_{r} \left( t \right)}} \int\limits_{t}^{{t_{r} }} {e^{{Z_{r} \left( u \right)}} du} dt} + \int\limits_{M}^{{t_{r} }} {We^{{ - Z_{0} \left( t \right)}} dt} + \int\limits_{{t_{r} }}^{{t_{w} }} {e^{{ - Z_{0} \left( t \right)}} D\int\limits_{t}^{{t_{w} }} {e^{{Z_{0} \left( u \right)}} du} dt} } \right\} \\ \end{aligned} $$

Similarly, the necessary and sufficient conditions for $TC_{2} \left( {t_{r} ,T} \right)$, $TC_{3} \left( {t_{r} ,T} \right)$ with respect to T are obtained as follows:

$$ \begin{aligned} & \left[ {\left\{ {c_{b} \delta \left( {T - t_{w} } \right) - c_{o} - c - pI_{e} M} \right\}De^{{ - \delta \left( {T - t_{w} } \right)}} + c_{o} D} \right]T \\ & \quad = A + c\left\{ {W + D\int\limits_{0}^{{t_{r} }} {e^{{Z_{r} \left( u \right)}} du} + \frac{D}{\delta }\left( {1 - e^{{ - \delta \left( {T - t_{w} } \right)}} } \right)} \right\} + FD\int\limits_{0}^{{t_{r} }} {e^{{ - Z_{r} \left( t \right)}} } \int\limits_{t}^{{t_{r} }} {e^{{Z_{r} \left( u \right)}} du} dt \\ & \quad \quad + H\left\{ {W\int\limits_{0}^{{t_{r} }} {e^{{ - Z_{0} \left( t \right)}} dt} + D\int\limits_{{t_{r} }}^{{t_{w} }} {e^{{ - Z_{0} \left( t \right)}} \int\limits_{t}^{{t_{w} }} {e^{{Z_{0} \left( u \right)}} du} dt} } \right\} \\ & \quad \quad + \frac{{c_{b} D}}{{\delta^{2} }}\left\{ {1 - e^{{ - \delta \left( {T - t_{w} } \right)}} \left\{ {1 + \delta \left( {T - t_{w} } \right)} \right\}} \right\} + \frac{{c_{o} D}}{\delta }\left\{ {\delta \left( {T - t_{w} } \right) - \left( {1 - e^{{ - \delta \left( {T - t_{w} } \right)}} } \right)} \right\} \\ & \quad \quad - \left\{ {\frac{1}{2}pI_{e} DM^{2} + pI_{e} \frac{D}{\delta }M\left( {1 - e^{{ - \delta \left( {T - t_{w} } \right)}} } \right)} \right\} + cI_{p} D\int\limits_{M}^{{t_{w} }} {e^{{ - Z_{0} \left( t \right)}} \int\limits_{t}^{{t_{w} }} {e^{{Z_{0} \left( u \right)}} du} dt} \\ & \quad \quad t_{r} < M \le t_{w} \\ \end{aligned} $$

$$ \begin{aligned} & \left[ {\left\{ {c_{b} \delta \left( {T - t_{w} } \right) - c_{o} - c - pI_{e} M} \right\}De^{{ - \delta \left( {T - t_{w} } \right)}} + c_{o} D} \right]T \\ & \quad = A + c\left\{ {W + D\int\limits_{0}^{{t_{r} }} {e^{{Z_{r} \left( u \right)}} du} + \frac{D}{\delta }\left( {1 - e^{{ - \delta \left( {T - t_{w} } \right)}} } \right)} \right\} + FD\int\limits_{0}^{{t_{r} }} {e^{{ - Z_{r} \left( t \right)}} } \int\limits_{t}^{{t_{r} }} {e^{{Z_{r} \left( u \right)}} du} dt \\ & \quad \quad + H\left\{ {W\int\limits_{0}^{{t_{r} }} {e^{{ - Z_{0} \left( t \right)}} dt} + D\int\limits_{{t_{r} }}^{{t_{w} }} {e^{{ - Z_{0} \left( t \right)}} \int\limits_{t}^{{t_{w} }} {e^{{Z_{0} \left( u \right)}} du} dt} } \right\}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \begin{array}{*{20}c} {t_{w} < M \le T} \\ {{\text{or }}T < M} \\ \end{array} \\ & \quad \quad + \frac{{c_{b} D}}{{\delta^{2} }}\left\{ {1 - e^{{ - \delta \left( {T - t_{w} } \right)}} \left\{ {1 + \delta \left( {T - t_{w} } \right)} \right\}} \right\} + \frac{{c_{o} D}}{\delta }\left\{ {\delta \left( {T - t_{w} } \right) - \left( {1 - e^{{ - \delta \left( {T - t_{w} } \right)}} } \right)} \right\} \\ & \quad \quad - \left\{ {\frac{1}{2}pI_{e} Dt_{w}^{2} + pI_{e} D\left( {M - t_{w} } \right)t_{w} + pI_{e} \frac{D}{\delta }M\left( {1 - e^{{ - \delta \left( {T - t_{w} } \right)}} } \right)} \right\} \\ \end{aligned} $$

Appendix 3

Proof of Theorem 2 For any given T, the first and second order derivatives of $TC_{1} \left( {t_{r} ,T} \right)$ with respect to $t_{r}$ are obtained as:

$$ \frac{{dTC_{1} \left( {t_{r} ,T} \right)}}{dt} = \frac{1}{T}\left[ \begin{gathered} FDe^{{Z_{r} \left( {t_{r} } \right)}} \int\limits_{0}^{{t_{r} }} {e^{{ - Z_{r} \left( t \right)}} } dt + cDe^{{Z_{r} \left( {t_{r} } \right)}} + cI_{p} De^{{Z_{r} \left( {t_{r} } \right)}} \int\limits_{M}^{{t_{r} }} {e^{{ - Z_{r} \left( t \right)}} } dt \hfill \\ + \left\{ \begin{gathered} \left( {H + cI_{p} } \right)De^{{Z_{0} \left( {t_{w} } \right)}} \int\limits_{{t_{r} }}^{{t_{w} }} {e^{{ - Z_{0} \left( t \right)}} dt} - c_{b} De^{{ - \delta \left( {T - t_{w} } \right)}} \left( {T - t_{w} } \right) \hfill \\ + c_{o} D\left( {e^{{ - \delta \left( {T - t_{w} } \right)}} - 1} \right) - cDe^{{ - \delta \left( {T - t_{w} } \right)}} + pI_{e} DMe^{{ - \delta \left( {T - t_{w} } \right)}} \hfill \\ \end{gathered} \right\}\frac{{dt_{w} }}{{dt_{r} }} \hfill \\ \end{gathered} \right];\quad 0 < M \le t_{r} $$

$$ \frac{{d^{2} TC_{1} \left( {t_{r} ,T} \right)}}{{dt^{2} }} = \frac{1}{T}\left[ \begin{gathered} FD\left\{ {e^{{Z_{r} \left( {t_{r} } \right)}} \theta_{r} \left( {t_{r} } \right)\int\limits_{0}^{{t_{r} }} {e^{{ - Z_{r} \left( t \right)}} } dt + 1} \right\} + cDe^{{Z_{r} \left( {t_{r} } \right)}} \theta_{r} \left( {t_{r} } \right) + cI_{p} De^{{Z_{r} \left( {t_{r} } \right)}} \theta_{r} \left( {t_{r} } \right)\int\limits_{M}^{{t_{r} }} {e^{{ - Z_{r} \left( t \right)}} } dt \hfill \\ + \left\{ {HDe^{{Z_{0} \left( {t_{w} } \right)}} \int\limits_{{t_{r} }}^{{t_{w} }} {e^{{ - Z_{0} \left( t \right)}} dt} + \left( {c_{o} - c_{b} \left( {T - t_{w} } \right) - c} \right)De^{{ - \delta \left( {T - t_{w} } \right)}} - c_{o} D} \right\}\frac{{d^{2} t_{w} }}{{dt_{r}^{2} }} \hfill \\ + \left\{ {HDe^{{Z_{0} \left( {t_{w} } \right)}} \theta_{o} \left( {t_{w} } \right)\int\limits_{{t_{r} }}^{{t_{w} }} {e^{{ - Z_{0} \left( t \right)}} dt} + \left( {c_{o} - c_{b} \left( {T - t_{w} } \right) - c} \right)D\delta e^{{ - \delta \left( {T - t_{w} } \right)}} + c_{b} De^{{ - \delta \left( {T - t_{w} } \right)}} } \right\}\left( {\frac{{dt_{w} }}{{dt_{r} }}} \right)^{2} \hfill \\ cI_{p} D\left\{ {\left( {e^{{Z_{0} \left( {t_{w} } \right)}} \theta_{o} \left( {t_{w} } \right)\int\limits_{{t_{r} }}^{{t_{w} }} {e^{{ - Z_{0} \left( t \right)}} dt} + 1} \right)\left( {\frac{{dt_{w} }}{{dt_{r} }}} \right)^{2} - 1 + e^{{Z_{0} \left( {t_{w} } \right)}} \int\limits_{{t_{r} }}^{{t_{w} }} {e^{{ - Z_{0} \left( t \right)}} dt} \frac{{d^{2} t_{w} }}{{dt_{r}^{2} }}} \right\} \hfill \\ + pI_{e} DMe^{{ - \delta \left( {T - t_{w} } \right)}} \left\{ {\delta \left( {\frac{{dt_{w} }}{{dt_{r} }}} \right)^{2} + \frac{{d^{2} t_{w} }}{{dt_{r}^{2} }}} \right\}^{2} \hfill \\ \end{gathered} \right];\quad 0 < M \le t_{r} $$

$$ \frac{{dTC_{2} \left( {t_{r} ,T} \right)}}{dt} = \frac{1}{T}\left[ \begin{gathered} FDe^{{Z_{r} \left( {t_{r} } \right)}} \int\limits_{0}^{{t_{r} }} {e^{{ - Z_{r} \left( t \right)}} } dt + cDe^{{Z_{r} \left( {t_{r} } \right)}} + \hfill \\ + \left\{ \begin{gathered} HDe^{{Z_{0} \left( {t_{w} } \right)}} \int\limits_{{t_{r} }}^{{t_{w} }} {e^{{ - Z_{0} \left( t \right)}} dt} - c_{b} De^{{ - \delta \left( {T - t_{w} } \right)}} \left( {T - t_{w} } \right) \hfill \\ + c_{o} D\left( {e^{{ - \delta \left( {T - t_{w} } \right)}} - 1} \right) - cDe^{{ - \delta \left( {T - t_{w} } \right)}} + pI_{e} DMe^{{ - \delta \left( {T - t_{w} } \right)}} \hfill \\ + cI_{p} De^{{Z_{0} \left( {t_{w} } \right)}} \int\limits_{M}^{{t_{w} }} {e^{{ - Z_{0} \left( t \right)}} dt} \hfill \\ \end{gathered} \right\}\frac{{dt_{w} }}{{dt_{r} }} \hfill \\ \end{gathered} \right];\quad t_{r} < M \le t_{w} $$

$$ \frac{{d^{2} TC_{2} \left( {t_{r} ,T} \right)}}{{dt^{2} }} = \frac{1}{T}\left[ \begin{gathered} FD\left\{ {e^{{Z_{r} \left( {t_{r} } \right)}} \theta_{r} \left( {t_{r} } \right)\int\limits_{0}^{{t_{r} }} {e^{{ - Z_{r} \left( t \right)}} } dt + 1} \right\} + cDe^{{Z_{r} \left( {t_{r} } \right)}} \theta_{r} \left( {t_{r} } \right) \hfill \\ + \left\{ {HDe^{{Z_{0} \left( {t_{w} } \right)}} \int\limits_{{t_{r} }}^{{t_{w} }} {e^{{ - Z_{0} \left( t \right)}} dt} + \left( {c_{o} - c_{b} \left( {T - t_{w} } \right) - c} \right)De^{{ - \delta \left( {T - t_{w} } \right)}} - c_{o} D} \right\}\frac{{d^{2} t_{w} }}{{dt_{r}^{2} }} \hfill \\ + \left\{ {HDe^{{Z_{0} \left( {t_{w} } \right)}} \theta_{o} \left( {t_{w} } \right)\int\limits_{{t_{r} }}^{{t_{w} }} {e^{{ - Z_{0} \left( t \right)}} dt} + D\delta e^{{ - \delta \left( {T - t_{w} } \right)}} \left( {c_{o} - c_{b} \left( {T - t_{w} } \right) - c} \right) + c_{b} De^{{ - \delta \left( {T - t_{w} } \right)}} } \right\}\left( {\frac{{dt_{w} }}{{dt_{r} }}} \right)^{2} \hfill \\ cI_{p} D\left\{ {\left( {e^{{Z_{0} \left( {t_{w} } \right)}} \theta_{o} \left( {t_{w} } \right)\int\limits_{M}^{{t_{w} }} {e^{{ - Z_{0} \left( t \right)}} dt} + 1} \right)\left( {\frac{{dt_{w} }}{{dt_{r} }}} \right)^{2} + e^{{Z_{0} \left( {t_{w} } \right)}} \int\limits_{M}^{{t_{w} }} {e^{{ - Z_{0} \left( t \right)}} dt} \frac{{d^{2} t_{w} }}{{dt_{r}^{2} }}} \right\} \hfill \\ + pI_{e} DMe^{{ - \delta \left( {T - t_{w} } \right)}} \left\{ {\delta \left( {\frac{{dt_{w} }}{{dt_{r} }}} \right)^{2} + \frac{{d^{2} t_{w} }}{{dt_{r}^{2} }}} \right\}^{2} \hfill \\ \end{gathered} \right]; \, \quad \, t_{r} < M \le t_{w} $$

$$ \frac{{dTC_{3} \left( {t_{r} ,T} \right)}}{dt} = \frac{1}{T}\left[ \begin{gathered} FDe^{{Z_{r} \left( {t_{r} } \right)}} \int\limits_{0}^{{t_{r} }} {e^{{ - Z_{r} \left( t \right)}} } dt + cDe^{{Z_{r} \left( {t_{r} } \right)}} + \hfill \\ + \left\{ \begin{gathered} HDe^{{Z_{0} \left( {t_{w} } \right)}} \int\limits_{{t_{r} }}^{{t_{w} }} {e^{{ - Z_{0} \left( t \right)}} dt} - c_{b} De^{{ - \delta \left( {T - t_{w} } \right)}} \left( {T - t_{w} } \right) \hfill \\ + c_{o} D\left( {e^{{ - \delta \left( {T - t_{w} } \right)}} - 1} \right) - cDe^{{ - \delta \left( {T - t_{w} } \right)}} \hfill \\ + pI_{e} D\left( {M - t_{w} - Me^{{ - \delta \left( {T - t_{w} } \right)}} } \right) \hfill \\ \end{gathered} \right\}\frac{{dt_{w} }}{{dt_{r} }} \hfill \\ \end{gathered} \right]; \, \quad \, t_{w} < M \le T\;{\text{ or}}\; \, T < M $$

$$ \frac{{d^{2} TC_{3} \left( {t_{r} ,T} \right)}}{{dt^{2} }} = \frac{1}{T}\left[ \begin{gathered} FD\left\{ {e^{{Z_{r} \left( {t_{r} } \right)}} \theta_{r} \left( {t_{r} } \right)\int\limits_{0}^{{t_{r} }} {e^{{ - Z_{r} \left( t \right)}} } dt + 1} \right\} + cDe^{{Z_{r} \left( {t_{r} } \right)}} \theta_{r} \left( {t_{r} } \right) \hfill \\ + \left\{ {HDe^{{Z_{0} \left( {t_{w} } \right)}} \int\limits_{{t_{r} }}^{{t_{w} }} {e^{{ - Z_{0} \left( t \right)}} dt} + \left( {c_{o} - c_{b} \left( {T - t_{w} } \right) - c} \right)De^{{ - \delta \left( {T - t_{w} } \right)}} - c_{o} D} \right\}\frac{{d^{2} t_{w} }}{{dt_{r}^{2} }} \hfill \\ + \left\{ {HDe^{{Z_{0} \left( {t_{w} } \right)}} \theta_{o} \left( {t_{w} } \right)\int\limits_{{t_{r} }}^{{t_{w} }} {e^{{ - Z_{0} \left( t \right)}} dt} + D\delta e^{{ - \delta \left( {T - t_{w} } \right)}} \left( {c_{o} - c_{b} \left( {T - t_{w} } \right) - c} \right) + c_{b} De^{{ - \delta \left( {T - t_{w} } \right)}} } \right\}\left( {\frac{{dt_{w} }}{{dt_{r} }}} \right)^{2} \hfill \\ + pI_{e} D\left\{ {\left( {M\delta e^{{ - \delta \left( {T - t_{w} } \right)}} + 1} \right)\left( {\frac{{dt_{w} }}{{dt_{r} }}} \right)^{2} + \left( {M\left( {e^{{ - \delta \left( {T - t_{w} } \right)}} - 1} \right) + t_{w} } \right)\frac{{d^{2} t_{w} }}{{dt_{r}^{2} }}} \right\} \hfill \\ \end{gathered} \right];\quad t_{w} < M \le T \, \;{\text{or }}\;T < M $$

Let $(c_{o} - c_{b} (T - t_{w} ) - c) = L$, then for any given T, if $L > 0$, then $TC_{1} (t_{r} ,\;T)$, $TC_{2} (t_{r} ,\;T)$ and $TC_{3} (t_{r} ,\;T)$ given in Eqs. (29), (30) and (31) respectively are a strictly convex function of $t_{r}$. Consequently, there exists a unique optimal solution for a total cost $TC(t_{r} ,\;T)$ in Eq. (28).