Fuzzy neural control of uncertain chaotic systems with backlash nonlinearity

Abstract

In this paper, a class of uncertain chaotic systems preceded by unknown backlash nonlinearity is investigated. Combining backstepping technique with fuzzy neural network identifying, an adaptive backstepping fuzzy neural controller (ABFNC) for uncertain chaotic systems with unknown backlash is proposed. The proposed ABFNC system is comprised of a fuzzy neural network identifier (FNNI) and a robust controller. The FNNI is the principal controller utilized for online estimation of the unknown nonlinear function. The robust controller is used to attenuate the effects of the approximation error so that the stability and control performance of the closed-loop adaptive system is achieved always. Finally, simulation results show that the ABFNC can achieve favorable tracking performances.

1 Introduction

The study of chaotic systems has been rapidly expanded during the last two decades. Many fundamental characteristics can be found in a chaotic system, such as excessive sensitivity to initial conditions, broad spectrums of Fourier Transform, and fractal properties of the motion in phase space. Controlling chaotic systems has attracted a great deal of attention within the engineering society, in which different techniques have been proposed. For instance, linear state space feedback [1], Lyapunov function methods [2], adaptive control [3], and bang–bang control [4], among many others [5].

In recent years, adaptive control for uncertain nonlinear systems has received much attention based on universal function approximation, such as neural networks (NNs) or fuzzy logic systems [6–13]. Also, the application of neural networks and fuzzy logic controllers to chaotic systems has been proposed [14–18], which appears to be quite promising.

Recently, the concept of incorporation fuzzy logic into a neural network has grown into a popular research topic [19]. The integrated fuzzy neural network (FNN) system possesses the merits of both fuzzy systems [20] and neural networks [21]. In this way, one can bring the low-level learning and computational power of neural networks into fuzzy systems and also high-level humanlike IF-THEN rule thinking and reasoning of fuzzy systems into neural networks. Moreover, adaptive control schemes of chaotic systems that incorporate the techniques of FNN have also grown rapidly [22–24]. However, the results motivated above in [1–24] did not consider the affection of unknown backlash nonlinearity.

Backlash is one of the most important non-smooth nonlinearities in a wide range of physical systems and devices, such as biology optics, electro-magnetism, mechanical actuators, electronic relay circuits and other areas. The development of control techniques to mitigate effects of unknown backlash has been studied for a long time. To handle with systems with unknown backlash, several adaptive control schemes have recently been proposed, see for examples [25–29]. In [26–28], an adaptive inverse cascaded with the plant was employed to cancel the effects of nonlinearity. In [25], a dynamic backlash model is defined to pattern a backlash rather than constructing an inverse model to mitigate the effects of the backlash. However in [25], the term multiplying the control and the uncertain parameters of the system must be within known intervals and the ‘disturbance-like’ term must be bounded by a known bound. Projection was used to handle the ‘disturbance-like’ term and unknown parameters. System stability was established and the tracking error was shown to converge to a residual. In [29], the backstepping adaptive control schemes for uncertain nonlinear systems with unknown backlash nonlinearity were proposed. However, this result in [29] required the nonlinear functions of systems are known.

In this paper, an adaptive backstepping fuzzy neural controller (ABFNC) is proposed for a class of uncertain chaotic systems with unknown nonlinear functions and backlash nonlinearity. The unknown nonlinear functions are approximated by the FNN. In the design, the term multiplying the control and the system parameters are not assumed to be within known intervals. The bound of the ‘disturbance-like’ term is not required. To handle such a term, an estimator is used to estimate its bound. Based on the Lyapunov stability theory, the adaptive control law is derived. The global stability of the chaotic system is achieved. Finally, simulation results are presented to demonstrate the effectiveness of the proposed control scheme.

2 Problem statement

The controlled system consists of a chaos system preceded by a backlash-like hysteresis actuator, that is, the hysteresis is present as an input of the chaos system. It is a challenging task of major practical interests to develop a control scheme for unknown backlash-like hysteresis. The development of such a control scheme will now be pursued.

A backlash-like hysteresis nonlinearity can be denoted as an operator as follows:

$$ u(t) = P(v(t)), $$

(1)

with $v(t)$ as input and $u(t)$ as output. The operator $P(v(t))$ will be discussed in detail in the next section. The uncertain chaos system being preceded by the above hysteresis is described in the canonical form

$$ \left\{ \begin{aligned} \dot{x}_{1} & = x_{2} \\ \dot{x}_{2} & = x_{3} \\ \vdots \\ \dot{x}_{n} & = f\left( \varvec{X} \right) + u\left( t \right) + \bar{d}(t) \\ \end{aligned} \right., $$

(2)

where $\varvec{X} = \left[ {x_{1} ,\dot{x}_{1} , \ldots ,x_{1}^{{\left( {n - 1} \right)}} } \right]^{\text{T}} = \left[ {x_{1} ,x_{2} , \ldots ,x_{n} } \right]^{\text{T}} \in \varvec{R}^{n}$ is the state vector, $f\left( \varvec{X} \right)$ is unknown nonlinear bounded function, $\bar{d}\left( t \right)$ denotes bounded external disturbances. The control objective is to design a control law for $v(t)$ in Eq. (1), to force the uncertain chaotic system (2) state vector to follow a specified desired trajectory, $\varvec{X}_{d} = \left[ {x_{d} ,\dot{x}_{d} , \cdots x_{d}^{(n - 1)} } \right]^{\text{T}}$, i.e., $\varvec{X} \to \varvec{X}_{d}$ as $t \to \infty$.

Remark:

A class of chaos systems can be described by the nonlinear system (2), such as Duffing chaotic system, Van der Pol chaotic system, Jerk systems and so on.

3 Backlash-like hysteresis model and its properties

Traditionally, a backlash hysteresis nonlinearity can be described by

$$ \begin{aligned} u(t) & = P(v(t)) \\ \, & = \left\{ \begin{gathered} c(v(t) - B),\;{\text{if}}\;\dot{v}(t) > 0{\text{ and }}u(t) = c(v(t) - B) \hfill \\ c(v(t) + B),\;{\text{if}}\;\dot{v}(t) < 0{\text{ and }}u(t) = c(v(t) + B) \hfill \\ u(t_{ - } ),{\text{ otherwise}} \hfill \\ \end{gathered} \right., \\ \end{aligned} $$

(3)

where $c > 0$ is the slope of the lines and $B > 0$ is the backlash distance, $u(t_{ - } )$is delay input. This mode is itself discontinuous and may not be amenable to controller design for the chaotic systems (2).

Instead of using the above model, in this paper we use a continuous-time dynamic model to describe a class of backlash-like hysteresis [25], as given by

$$ \frac{du}{dt} = \alpha \left| \frac{dv}{dt} \right|\left( {cv - u} \right) + B_{1} \frac{dv}{dt}, $$

(4)

where $\alpha > 0$ is the switch rate, $B_{1} > 0$ is the backlash distance, $c > 0$ is the slope of the lines satisfying $c > B_{1}$.

Remark:

This backlash-like hysteresis mode is reported by Ref. [25], to read conveniently, we give the main results that from Ref. [25].

Equation (4) can be solved explicitly for $v$ piecewise monotone,

$$ u\left( t \right) = cv\left( t \right) + d_{1} \left( v \right), $$

(5)

With $d_{1} \left( v \right) = \left[ {u_{0} - cv_{0} } \right]e^{{ - \alpha \left( {v - v_{0} } \right){\text{sign}}\left( {\dot{v}} \right)}} + e^{{ - \alpha v{\text{sign}}\left( {\dot{v}} \right)}} \int_{{v_{0} }}^{v} {\left[ {B_{1} - c} \right]} e^{{\alpha \xi {\text{sign}}\left( {\dot{v}} \right)}} d\xi ,$ for $\dot{v}$ constant and $u\left( {v_{0} } \right) = u_{0}$. Analyzing Eq. (5), we see that it is composed of a line with the slop $c$, together with a term $d_{1} \left( v \right)$. For $d_{1} \left( v \right)$, it can be easily shown that if $u\left( {v;v_{0} ,u_{0} } \right)$ is the solution of Eq. (5) with initial values $\left( {v_{0} ,u_{0} } \right)$, then, if $\dot{v} > 0(\dot{v} < 0)$ and $v \to + \infty \left( { - \infty } \right)$, one has

$$ \mathop {\lim }\limits_{v \to \infty } d_{1} \left( v \right) = \mathop {\lim }\limits_{v \to \infty } \left[ {u\left( {v;v_{0} ,u_{0} } \right) - g\left( v \right)} \right] = - \frac{{c - B_{1} }}{\alpha } , $$

(6)

$$ \mathop {\lim }\limits_{v \to - \infty } d_{1} \left( v \right) = \mathop {\lim }\limits_{v \to - \infty } \left[ {u\left( {v;v_{0} ,u_{0} } \right) - g\left( v \right)} \right] = \frac{{c - B_{1} }}{\alpha } , $$

(7)

where $g(v) = cv(t)$. It should be noted that the above convergence is exponential at the rate of $\alpha$. Solution (5) and properties (6) and (7) show that $u(t)$ eventually satisfied the first and the second conditions of (3). Furthermore, setting $\dot{v} = 0$ results in $\dot{u} = 0$ which satisfied the last condition of (3). This implies that the dynamic Equation (4) can be used to model a class of backlash-like hysteresis and is an approximation of backlash hysteresis (3).Let us use an example for specified initial data to show the switching mechanism for the dynamic model (4) when $\dot{v}$ changes direction. We note that when $\dot{v} > 0$ on $u(0) = 0$ and $v(0) = 0$, Eq. (5) gives

$$ \begin{gathered} u(t) = cv(t) - \frac{{c - B_{1} }}{\alpha }\left( {1 - e^{ - \alpha v(t)} } \right) \hfill \\ {\text{ for }}v(t) \ge 0{\text{ and }}\dot{v} > 0 \hfill \\ \end{gathered} . $$

(8)

Let $v_{s}$ be a positive value of $v$ and consider now a specimen such that $v$ is increasing along the initial curve (8) until a time $t_{s}$ at which $v$ reaches the level $v_{s}$. Suppose now that from the time $t_{s}$, the signal $v$ is decreased. In this case, $u$ is given by

$$ u(t) = cv(t) + \frac{{c - B_{1} }}{\alpha }\left[ {1 - \left( {2e^{{ - \alpha v_{s} }} - e^{{ - 2\alpha v_{s} }} } \right)e^{\alpha v(t)} } \right]{\text{ for }}\dot{v} < 0 , $$

(9)

where $v < v_{s}$. Eqs. (8) and (9) indeed show that $u$ switches exponentially from the line $cv(t) - ({{(c - B_{1} )} \mathord{\left/ {\vphantom {{(c - B_{1} )} \alpha }} \right. \kern-0pt} \alpha })$ to $cv(t) + ({{(c - B_{1} )} \mathord{\left/ {\vphantom {{(c - B_{1} )} \alpha }} \right. \kern-0pt} \alpha })$ to generate backlash-like hysteresis curves.

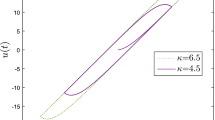
To confirm the above analysis, the solutions of Eq. (4) can be obtained by numerical integration with $v$ as the independent variable. Figures 1, 2 shows that model (4) indeed generates backlash-like hysteresis curves, which confirms the above analysis. The details are described in the section of simulation studies. It should be mentioned that the parameter $\alpha$ determines the rate at which $u(t)$ switches between $- ({{(c - B_{1} )} \mathord{\left/ {\vphantom {{(c - B_{1} )} \alpha }} \right. \kern-0pt} \alpha })$ and $({{(c - B_{1} )} \mathord{\left/ {\vphantom {{(c - B_{1} )} \alpha }} \right. \kern-0pt} \alpha })$. The larger the parameter $\alpha$ is, the faster the transition in $u(t)$ is going to be. However, the backlash distance is determined by $({{(c - B_{1} )} \mathord{\left/ {\vphantom {{(c - B_{1} )} \alpha }} \right. \kern-0pt} \alpha })$ and the parameter must satisfy $c > B_{1}$. Therefore, the parameter $\alpha$ cannot be chosen freely. A compromise should be made in choosing a suitable parameter set $\left\{ {\alpha ,c,B_{1} } \right\}$ to model the required shape of backlash-like hysteresis.

Fig. 1

Hysteresis curves given by (4) with $\alpha = 1$, $c = 3.1635$, and $B_{1} = 0.345$ for $v\left( t \right) = k{ \sin }\left( {2.3t} \right)$ with $k = 2.5,\;3.5,\;4.5,\;5.5,\;{\text{and}}\; 6. 5$

Fig. 2

Fuzzy partitions of two-dimensional input space. a Grid-type partitioning. b If-then rules based on grid-type partitioning. c Clustering-type partitioning. d If-then rules based on clustering-type partitioning

4 Fuzzy neural network

According to the method of input space partition, fuzzy neural networks are divided into two categories: grid-based partitioning and clustering-based partitioning [30]. In this paper, the grid-based partitioning FNN is used to identify the unknown nonlinear function $f\left( \varvec{X} \right)$. The structure of the FNN has four layers of neural network: the input, the membership function, the rule and the output layers. The interactions for those layers are given as follows.

Layer 1: For every node $i$, in this layer, the net input and the net output are represented as

$$ net_{i}^{1} = x_{i}^{1} , $$

(10)

$$ y_{i}^{1} = f_{i}^{1} \left( {net_{i}^{1} } \right) = net_{i}^{1} \, (i = 1,2, \ldots ,L) , $$

(11)

where $x_{i}^{1}$ represents the ith input to the node of layer 1, and $L$ is the total number of input variables.

Layer 2: In this layer, each node performs a membership function and acts as a unit of memory. The Gaussian function is adopted as the membership function. For the ith input, the corresponding net input and output of the jth node can be expressed as

$$ net_{ij}^{2} = - \frac{{\left( {x_{i}^{2} - m_{ij}^{2} } \right)^{2} }}{{\left( {\sigma_{ij}^{2} } \right)^{2} }} , $$

(12)

$$ y_{ij}^{2} = f_{ij}^{2} \left( {net_{ij}^{2} } \right) = \exp \left( {net_{ij}^{2} } \right) \, (j = 1,2, \ldots ,M) , $$

(13)

where $m_{ij}^{2}$ is the mean, $\sigma_{ij}^{2}$ is the standard deviation and $M$ is the total number of membership functions with respect to the respective input node.

Layer 3: The links in this layer are used to implement the antecedent matching. The matching operation or the fuzzy AND aggregation operation is chosen as the simple PRODUCT operation instead of the MIN operation. Then, for the kth rule node

$$ net_{k}^{3} = x_{i}^{3} \cdot x_{j}^{3} , $$

(14)

$$ y_{k}^{3} = f_{k}^{3} \left( {net_{k}^{3} } \right) = \frac{{net_{k}^{3} }}{{\sum\nolimits_{k} {net_{k}^{3} } }} \, (k = 1,2, \ldots ,N) , $$

(15)

where $x_{i}^{3}$ and $x_{j}^{3}$ represent the i, jth input to the kth node of layer 3 respectively, and $N$ is the total number of fuzzy rules.

Layer 4: Since the overall net output is a linear combination of the consequences of all rules, the net input and output are simply defined by

$$ net_{o}^{4} = \sum\limits_{k} {w_{k}^{4} x_{k}^{4} } , $$

(16)

$$ y_{o}^{4} = f_{o}^{4} \left( {net_{o}^{4} } \right) = net_{o}^{4} , $$

(17)

where $w_{k}^{4}$ is the output action strength of the output associated with the kth rule, $x_{k}^{4}$ represents the kth input to the node of layer 4 and $y_{o}^{4}$ is the output of SFNN.

According to the gradient descent method [31], we will give the learning law for each layer in the feedbackward direction. The derivation is the same as that of the back-propagation learning law. To describe the algorithm more clearly, we consider two inputs and one output.

Layer 4: If the cost function to be minimized is defined as

$$ E = \frac{1}{2}(d - y_{o}^{4} )^{2} , $$

(18)

where $d$ is the desired output and $y_{o}^{4}$ is the current output of FNN, the error term to be propagated is given by

$$ \delta^{4} = d - y_{o}^{4} . $$

(19)

Then, the weight $w_{k}^{4}$ is updated by the amount

$$ \varDelta w_{k}^{4} = \delta^{4} y_{k}^{3} \;(k = 1, \ldots ,N) , $$

(20)

where $y_{k}^{3}$ denote the output of layer 3, and N is the total number of fuzzy rules.

Layer 3: Since the weights in this layer are unity, none of them is to be modified. Only the error term needs to be calculated and propagated.

$$ \delta_{k}^{3} = \delta^{4} w_{k}^{4} \;(k = 1, \ldots ,N) . $$

(21)

Layer 2: The multiplication operation is done in this layer. The adaptive rule for $m_{ij}$ and $\sigma_{ij}$ are as follows. First, the error term is computed,

$$ \left\{ \begin{aligned} \delta_{1j}^{2} & = \left( {\sum\limits_{i = 1}^{M} {\delta_{k}^{3} y_{2i}^{2} } } \right)y_{1j}^{2} \;(j = 1, \ldots ,M) \\ \delta_{2j}^{2} & = \left( {\sum\limits_{i = 1}^{M} {\delta_{k}^{3} y_{1i}^{2} } } \right)y_{2j}^{2} \;(j = 1, \ldots ,M) \\ \end{aligned} \right. , $$

(22)

where the subscript k denotes the rule node in connection with the ith node in Layer 2, $y_{1}^{2}$ denote the membership of first input, and $y_{2}^{2}$ denote the membership of second input. Then, the adaptive rule of $m_{ij}$ is

$$ \varDelta m_{ij} = \delta_{ij}^{2} \frac{{2(y_{i}^{1} - m_{ij} )}}{{\sigma_{ij}^{2} }}\;(i = 1,2;\;j = 1, \ldots ,M) , $$

(23)

and the adaptive rule of $\sigma_{ij}$ is

$$ \varDelta \sigma_{ij} = \delta_{ij}^{2} \frac{{2(y_{i}^{1} - m_{ij} )^{2} }}{{\sigma_{ij}^{3} }}(i = 1,2;j = 1, \ldots ,M) . $$

(24)

Remark:

This fuzzy neural network is reported by Refs. [30, 31]. The interesting readers are referred to Refs. [30, 31] for a more detailed explanation of the network.

5 The ABFNC design and stability analysis

From the solution structure (5) of the model (4) we see that the signal $u(t)$ is expressed as a linear function of input signal $v(t)$ plus a bounded term. Using the solution expression (5), system (2) becomes

$$ \left\{ \begin{aligned} \dot{x}_{1} & = x_{2} \\ \dot{x}_{2} & = x_{3} \\ \vdots \\ \dot{x}_{n} & = f\left( \varvec{X} \right) + cv\left( t \right) + d(t) \\ \end{aligned} \right. , $$

(25)

where $d\left( t \right) = d_{1} \left( {v\left( t \right)} \right) + \bar{d}\left( t \right)$. The effect of $d\left( t \right)$ is due to both external disturbances and $d_{1} \left( {v\left( t \right)} \right)$. We call $d\left( t \right)$ a ‘disturbance-like’ term for simplicity of presentation. The uncertain parameter $c$ is not assumed inside known intervals, also the bound $D$ for $d\left( t \right)$ is not assumed to be known and it will be estimated by our adaptive controllers. Furthermore, fuzzy neural adaptive control techniques can be utilized for the controller design. In this section, we shall utilize backstepping technique with fuzzy neural network identifying, and design the adaptive backstepping fuzzy neural controller (ABFNC) for uncertain chaotic systems with unknown backlash.

For the development of control laws, the following assumption is made.

Assumption 1

The desired trajectory $\varvec{X}_{d} \left( t \right)$ and its nth order derivatives are known and bounded.

Before presenting the adaptive fuzzy neural controller design using the backstepping technique to achieve the desired control objectives, the following change of coordinates is made.

$$ e_{1} = x_{1} - x_{d} , $$

(26)

$$ e_{i} = x_{i} - x_{d}^{{\left( {i - 1} \right)}} - \beta_{i - 1} ,\quad i = 2,3, \ldots ,n , $$

(27)

where $\beta_{i - 1}$ is the virtual control at the ith step and will be determined in later discussion. To illustrate the backstepping procedures, only the last step of the design, i.e. step n below, is elaborated in details.

Step 1: For $i = 2$, it follows from Eqs. (25), (26) and (27) that

$$ \dot{e}_{1} = e_{2} + \beta_{1} . $$

(28)

We design the virtual control law $\beta_{1}$ as

$$ \beta_{1} = - a_{1} e_{1} , $$

(29)

where $a_{1}$ is a positive design parameter. From Eqs. (28) and (29) we have

$$ e_{1} \dot{e}_{1} = - a_{1} e_{1}^{2} + e_{1} e_{2} . $$

(30)

Step i (i = 2,…,n − 1): Choose virtual control law $\beta_{i}$ as

$$ \beta_{i} = - a_{i} e_{i} - e_{i - 1} + \dot{\beta }_{i - 1} \left( {x_{1} , \ldots ,x_{i - 1} ,x_{d} , \ldots ,x_{d}^{{\left( {i - 1} \right)}} } \right) , $$

(31)

where $a_{i} ,i = 2, \ldots ,n - 1$ are positive design parameters. From Eqs. (27) and (31) we obtain

$$ e_{i} \dot{e}_{i} = - e_{i - 1} e_{i} - a_{i} e_{i}^{2} + e_{i} e_{i + 1} . $$

(32)

Step n: From Eqs. (25) and (27) we obtain

$$ \dot{e}_{n} = cv\left( t \right) + f\left( \varvec{X} \right) + d\left( t \right) - x_{d}^{\left( n \right)} - \dot{\beta }_{n - 1} . $$

(33)

In this paper, we use FNN to identify the unknown function $f\left( \varvec{X} \right)$. Now consider the following optimal parameter vectors

$$ \varvec{W}^{4*} = { \arg }\;\hbox{min} \left[ {{ \sup }\left| {\hat{f}\left( {\left. \varvec{X} \right|\hat{\varvec{W}}^{4} } \right) - f\left( \varvec{X} \right)} \right|} \right], $$

(34)

where $\varvec{\xi}(\varvec{X})$ denote the layer 4 input vector, $\varvec{W}^{4}$ is the link weight vector between layer 3 and layer 4; $\hat{f}\left( {\left. \varvec{X} \right|\hat{\varvec{W}}^{4} } \right) = (\hat{\varvec{W}}^{ 4} \text{)}^{\text{T}}\varvec{\xi}\text{(}\varvec{X}\text{)}$ is the output of FNN, which is used to estimate the unknown nonlinear function $f\left( \varvec{X} \right)$ in system (25). Defining the minimum approximation error as

$$ \varepsilon = \varepsilon \left( {\varvec{X},\varvec{W}^{4} } \right) = \hat{f}\left( {\left. \varvec{X} \right|\varvec{W}^{4*} } \right) - f\left( \varvec{X} \right), $$

(35)

and $\left| \varepsilon \right| \le \bar{\varepsilon }$, where $\bar{\varepsilon }$ is positive constant.

We design the adaptive fuzzy neural controller $v$ as follows:

$$ v = \hat{C}\bar{v}, $$

(36)

with$\bar{v} = - a_{n} e_{n} - e_{n - 1} - (\hat{\varvec{W}}^{4} )^{\text{T}}\varvec{\xi}\left( \varvec{X} \right) - {\text{sign}}\left( {e_{n} } \right)\hat{D} + x_{d}^{\left( n \right)} + \dot{\beta }_{n - 1} + v_{s} ,$where sign() denote signal function, $v_{s} = - {\text{sign}}(e_{n} )\bar{\varepsilon }$, the robust controller $v_{s}$ is used to attenuate the effects of the approximation error so that the stability and control performance of the closed-loop adaptive system is achieved always. The parameter adaptive laws are given by

$$ \varvec{\dot{\hat{W}}}^{4} =\varvec{\xi}\left( \varvec{X} \right)e_{n} , $$

(37)

$$ \dot{\hat{C}} = - \gamma \bar{v}e_{n} , $$

(38)

$$ \dot{\hat{D}} = \eta \left| {e_{n} } \right|, $$

(39)

where $a_{n}$, $\gamma$ and $\eta$ are three positive design parameters, $\hat{C}$, $\hat{\varvec{W}}^{4}$ and $\hat{D}$ are estimates of ${1 \mathord{\left/ {\vphantom {1 c}} \right. \kern-0pt} c}$, $\varvec{W}^{4*}$ and $D$. Let $\tilde{C} = C - \hat{C}$, $\tilde{\varvec{W}}^{4} = \varvec{W}^{4*} \varvec{ - \hat{W}}^{4}$ and $\tilde{D} = D - \hat{D}$. Note that $cv\left( t \right)$ in Eq. (33) can be expressed as

$$ cv = c\hat{C}\bar{v} = \bar{v} - c\tilde{C}\bar{v} . $$

(40)

From Eqs. (33), (35), (37) and (40) we obtain

$$ \dot{e}_{n} = - a_{n} e_{n} - e_{n - 1} + \text{(}\tilde{\varvec{W}}^{4} )^{\text{T}}\varvec{\xi}\left( \varvec{X} \right) - {\text{sign}}\left( {e_{n} } \right)\hat{D} + d\left( t \right) - c\tilde{C}\bar{v} + \varepsilon - {\text{sign}}\left( {e_{n} } \right)\bar{\varepsilon } $$

(41)

Let Lyapunov function as

$$ V = \sum\limits_{i = 1}^{n} \frac{1}{2} e_{i}^{2} + \frac{1}{2}(\tilde{\varvec{W}}^{4} )^{\text{T}} \tilde{\varvec{W}}^{4} + \frac{c}{2\gamma }\tilde{C}^{2} + \frac{1}{2\eta }\tilde{D}^{2} $$

(42)

Then the derivative of $V$ along with Eqs. (25) and (36)-(39) is given by

$$ \begin{aligned} \dot{V} & = \sum\limits_{i = 1}^{n} {e_{i} \dot{e}_{i} + (\tilde{\varvec{W}}^{4} )^{\text{T}} \varvec{\dot{\tilde{W}}}^{4} } + \frac{c}{\gamma }\tilde{C}\dot{\tilde{C}} + \frac{1}{\eta }\tilde{D}\dot{\tilde{D}} \\ & = - \sum\limits_{i = 1}^{n} {a_{i} e_{i}^{2} } + (\tilde{\varvec{W}}^{4} )^{\text{T}}\varvec{\xi}\left( \varvec{X} \right)e_{n} - \left| {e_{n} } \right|\hat{D} + d\left( t \right)e_{n} - c\tilde{C}\bar{v}e_{n} - (\tilde{\varvec{W}}^{4} )^{\text{T}} \varvec{\dot{\hat{W}}}^{4} \\ & \quad - \frac{c}{\gamma }\tilde{C}\dot{\hat{C}} - \frac{1}{\eta }\tilde{D}\dot{\hat{D}} - e_{n} {\text{sign}}\left( {e_{n} } \right)\bar{\varepsilon } + e_{n} \varepsilon \\ & \quad \le - \sum\limits_{i = 1}^{n} {a_{i} e_{i}^{2} } + (\tilde{\varvec{W}}^{4} )^{\text{T}} \left[ {\varvec{\xi}\left( \varvec{X} \right)e_{n} - \varvec{\dot{\hat{W}}}^{4} } \right] - \frac{c}{\gamma }\tilde{C}\left( {\gamma \bar{v}e_{n} + \dot{\hat{C}}} \right) + \frac{1}{\eta }\tilde{D}\left( {\eta \left| {e_{n} } \right| - \dot{\hat{D}}} \right) - \left| {e_{n} } \right|\bar{\varepsilon } + \left| {e_{n} } \right|\bar{\varepsilon } \\ & = - \sum\limits_{i = 1}^{n} {a_{i} e_{i}^{2} } \\ \end{aligned} , $$

(43)

where we have used Eqs. (30), (32), (41) and $e_{n} d\left( t \right) \le \left| {e_{n} } \right|D$ to obtain Eq. (43).

We have the following stability theorem based on this scheme.

Theorem 1

Consider the uncertain chaotic system (25) satisfying Assumptions 1. With the application of controller (36), the link weight of FNN update law (37) and parameter update laws (38) and (39), the following statements hold:

(i) The resulting closed loop system is globally stable.(ii) The asymptotic tracking is achieved, i.e. $\mathop {\lim }\limits_{t \to \infty } \left[ {\varvec{X}\left( t \right) - \varvec{X}_{d} \left( t \right)} \right] = 0$.

Proof:

From Eq. (43) we established that $V$ is non-increasing. Hence, $e_{i} ,\;i = 1, \ldots ,n$, $\hat{C}$, $\hat{\varvec{W}}^{4}$, $\hat{D}$ are bounded. By applying the LaSalle-Yoshizawa theorem to Eq. (43), it further follows that$e_{i} \left( t \right) \to 0,\;i = 1, \ldots ,n\;{\text{as}}\;t \to \infty$, which implies that $\mathop {\lim }\limits_{t \to \infty } \left[ {\varvec{X}\left( t \right) - \varvec{X}_{d} \left( t \right)} \right] = 0$. This proof completed. □

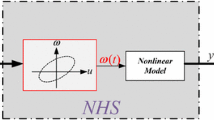
The control scheme is shown in Fig. 3.

Fig. 3

Block of diagram of ABFNC system

6 Simulation studies

In this section, we use the proposed ABFNC to control Van der Pol chaotic system states $\varvec{X} = \left[ {x_{1} ,x_{2} } \right]$ to follow Duffing chaotic system states $\varvec{X}_{d} = \left[ {x_{d1} ,x_{d2} } \right]$. Duffing chaotic system is given by

$$ \begin{aligned} \dot{x}_{d1} & = x_{d2} \\ \dot{x}_{d2} & = - 0.15x_{d2} + x_{d1} - (x_{d1} )^{3} + 1.75\cos \left( {\frac{2}{3}t} \right) \\ \end{aligned} . $$

(44)

According to Eq. (25), Van der Pol chaotic system with backlash is described as follows:

$$ \begin{aligned} \dot{x}_{1} & = x_{2} \\ \dot{x}_{2} & = - 0.1(1 - x_{1} )x_{2} - x_{1}^{3} + 0.3\cos \left( t \right) + cv\left( t \right) + d\left( t \right) \\ \end{aligned} , $$

(45)

where $f\left( X \right) = - 0.1(1 - x_{1} )x_{2} - x_{1}^{3} + 0.3\cos \left( t \right)$ is unknown, $c = 3.1635$, $B_{1} = 0.345$, and $\alpha = 1$.

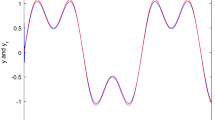
In the simulation, the adaptive control laws (36)–(39) were used, taking $a_{1} = a_{2} = 1$, $\gamma = \eta = 0.4$, $\bar{\varepsilon } = 0.05$. The initial values are chosen to $\hat{C}\left( 0 \right) = 0.5$, $\hat{D}\left( 0 \right) = 2$, $\varvec{X}\left( 0 \right) = \left[ {1,1} \right]$, $\varvec{Y}\left( 0 \right) = \left[ {0.1,0.1} \right]$ and $v\left( 0 \right) = 0$. In this paper, we use a FNN to estimate the unknown function $f(\varvec{X})$. The structure of FNN is 2-6-9-1, i.e. two nodes in layer 1, six nodes in layer 2, nine nodes in layer 3, one node in layer 4. The initial FNN parameters are chosen as $\varvec{W}^{4} = \left[ { 0. 6 ,\,\text{ - } 3 ,\, 6. 6 ,\,\text{ - } 8 ,\, 3. 8 ,\, 5. 8 ,\, 6 ,\,\text{ - } 7 ,\, 5. 8 0 2 6} \right]$, $\varvec{m}_{1} = \left[ {\text{ - } 0. 6 ,\,\text{ - } 0. 5 8 ,\,\text{ - } 0. 5} \right]$, $\varvec{m}_{2} = [ 1. 9 ,\, 1. 8 8 ,\, 2]$ $\varvec{\sigma}_{1} =\varvec{\sigma}_{2} = \left[ {1,\,1,\,1} \right]$. Here, $\varvec{W}^{4}$ represent the link weigh vector, and $\varvec{m}_{1}$ represents the mean vector of the Gaussian membership functions of $x_{1}$, and $\varvec{m}_{2}$ represents the mean vector of the Gaussian membership functions of $x_{2}$;$\varvec{\sigma}_{1}$ represents the variance vectors of the Gaussian membership functions of $x_{1}$, $\varvec{\sigma}_{2}$ represents the variance vectors of the Gaussian membership functions of $x_{2}$. The simulation results are shown in Figs. 4, 5, 6, 7 and 8. From Figs 4 and 5, we can see that $X \to X_{d}$ completely. From Figs. 6 and 7, we can see that the tracking errors are very small, and the identifying errors are shown in Fig. 8. The effectiveness of ABFNC scheme is demonstrated by the fact that the tracking error is reduced to zero after transient process. To further illustrate the effectiveness of ABFNC scheme, we make illustration, and compare with FSMC scheme in Ref. [16]. The tracking performance is shown in Fig. 9, and we define average errors as $AE = {{\left( {\left| {e_{1} } \right| + \left| {e_{2} } \right|} \right)} \mathord{\left/ {\vphantom {{\left( {\left| {e_{1} } \right| + \left| {e_{2} } \right|} \right)} 2}} \right. \kern-0pt} 2}$. From Fig. 9, we can see that the proposed ABFNC scheme is more effectively than FSMC scheme.

Fig. 4

Trajectories of x₁, xd₁

Fig. 5

Trajectories of x₂, xd₂

Fig. 6

Tracking error

Fig. 7

Identifying results

Fig. 8

Identifying error

Fig. 9

The average errors of ABFNC and FSMC

7 Conclusions

In this paper, we have developed an ABFNC scheme for a class of uncertain chaotic systems with unknown backlash nonlinearity. The developed control system does not require the model parameters with known intervals and the knowledge on the bound of ‘disturbance-like’ term is not required. In addition, the online tuning parameters include the weighting factors in the consequent part, and the means and variances of the Gaussian membership functions in the antecedent part of fuzzy implications.

Finally, this method has been applied to control Van der Pol chaotic system states to track Duffing chaotic system states. The computer simulation results show that the ABFNC can perform successful control and achieved desired performance.