1 Introduction

In mechanical systems, hysteresis and dead zone are two kinds of input nonsmooth nonlinearities which will degrade the performance of the systems. These nonlinear phenomena exist in many physical systems and materials, such as ferroelectric and ferromagnetic materials, mechanical actuators, electronic throttles, and other related fields [1–7]. Although hysteresis and dead zone commonly coexist, they have different nonlinear properties, actually. Hence, in this paper, we only discuss the hysteretic nonlinearities. In fact, different types of hysteresis have totally different nonlinear properties. Thus, we focus mainly on the hysteresis model called “backlash-like hysteresis.” Backlash-like hysteresis is usually found in the mechanical systems, which causes a delay between the input force and output response. To control the systems with unknown backlash-like hysteresis is quite important but typically challenging. Incidentally, conventional control methods are insufficient to deal with the nonlinear systems with these non-smooth nonlinearities [8]. For simplicity, the hysteresis is sometimes ignored in the controller design. However, ignorance of nonlinear hysteresis will lead to the obvious steady-state error, oscillation, and even instability. Hence, the development of alternate effective approaches is required and urging.

For research purpose, the foremost task is to find a model to describe the hysteretic nonlinearities, which helps us to design a proper controller. Until now, the research on mathematical models for unknown hysteresis is still an on-going topic. Thus, there are various models being proposed in past decades, and different hysteresis models will affect the effectiveness of the control algorithms. Generally, the existing hysteresis model can be roughly categorized into two types [9]: operator-based hysteresis models and differential equation-based hysteresis models. The operator-based models use integral equations which contain numerous hysteresis operators and can describe the shapes of hysteresis curves accurately. The popular operator-based models are Preisach model [10], Prandtl-Ishlinskii (PI) model [11], etc. For differential equation-based models, they have finite dimensions and can be extend to continuous inputs using approximation [9], which can reduce the computational complexity effectively. The models like Bouc-Wen model [12], Duhem model [9], and Backlash-like model [13] are used widely in the controller design for hysteretic problems. For nonlinear hysteretic properties in our benchmark problems, the backlash-like model proposed in [13] is adopted with a little modification throughout this paper to model our problems.

Based on the mathematical models, several alternate approaches have been proposed in [13–21] in past decades. The above methods used the adaptive control schemes to mitigate the nonlinear effects of hysteresis. In [14–16], an adaptive inverse operator was constructed to cancel the backlash nonlinearity, but the strict initial conditions were required. In [21], a smooth inverse function combined with the backstepping technique was utilized to compensate the nonlinear effects of the backlash. Using the intelligent control schemes like fuzzy logic control (FLC) or neural network (NN) has been depicted in [17–19]. Those intelligent control methods have the advantage of excellent nonlinearity approximation, which can eliminate the inversion error [17–19]. Some experimental applications showed that backlash inverters would degrade the system control performance [22, 23]. Hence, a controller design scheme without constructing the inverse operator has been proposed in [13, 18, 20]. In [18] and [13], a continuous dynamic backlash-like hysteresis model was defined. However, the backlash-like term multiplying the control in [18] and [13] must be bounded, and the uncertain parameters must also be within known intervals. The adaptive backstepping control methods proposed in [20] strived to eliminate the above restrictions. Some more complex problems and methods can be found in [24–26].

A new indirect adaptive fuzzy controller (IAFC) using “feedback + feed-forward” scheme is proposed to mitigate the hysteretic phenomenon without the above restrictions, Besides, a dynamic backlash-like hysteresis model is utilized in the nonlinear systems with unknown nonlinear control gain which is more general than that in [13]. The existence of the IAFC for the unknown hysteretic system is first shown in Theorem 2. The adaptive laws of IAFC are constructed based on the Lyapunov stability theory, and the IAFC control law guarantees that all the signals of the closed-loop system are stable. Finally, the proposed IAFC is compared with the adaptive backstepping control method, and the results demonstrate that our proposed IAFC has better effectiveness and excellent tracking performance.

This paper is organized as follows: Sect. 2 states the problem of this paper, where the nonlinear backlash-like model is introduced. In Sect. 3, the proposed IAFC scheme is presented. In Sect. 4, the simulation results are presented. Finally, in Sect. 5, conclusions are drawn.

2 Problem Formulation

2.1 System Model

We consider the following nth-order SISO nonlinear system described by the differential equations which are more general than that in [13] and [20]:

$$ \left\{ {\begin{array}{*{20}l} {\dot{x}_{i} \,= x_{i + 1} \, , \, i = 1, \cdots ,n - 1 \, } \\ {\dot{x}_{n}= F({\text{\bf x}}) + g({\text{\bf x}})\omega (u) \, } \\ {y\,\,= x_{1} \, } \\ \end{array} } \right. \, , $$
(1)

where \( {\text{\bf x}} = [x_{1} ,x_{2} , \cdots ,x_{n} ]^{T} = [x,\dot{x}, \cdots ,x^{(n - 1)} ]^{T} \in {\mathbb{R}}^{n} \) is the measurable state vector; \( u \in {\mathbb{R}} \) and \( y \in {\mathbb{R}} \) are the input and the output of the system, respectively; \( F({\text{\bf x}}) = - \sum\nolimits_{i = 1}^{r} {a_{i} f_{i} ({\text{\bf x}})} \); and parameters a i are unknown but bounded constants f i (x) and control gain g(x) are unknown nonlinear functions. (1) has to be controllable so we require that the control gain g(x) ≠ 0. Besides, without losing generality, it is assumed that g(x) > 0. In [13], the control gain g is simply an unknown constant, and functions f i have to be known linear or nonlinear functions. The function ω(u) is the output of the nonlinear hysteresis. Incorporating this hysteretic function into our system model, a nonlinear hysteretic system is formed and the system schematic diagram is shown in Fig. 1.

Fig. 1
figure 1

Representation of the nonlinear hysteretic system

Full size image

The control objective is to design a control law for u(t) in (1) and an adaptive law for adjusting the parameter vector, such that the system output x can track the reference signal y m . Note that the reference signal y m is assumed to be (n−1)th differentiable.

2.2 Backlash-like Model and Its Characteristics

A continuous dynamic model to simulate the hysteretic phenomenon defined by [13] can be described by

$$ \frac{{\text{d}\omega }}{{\text{d}t}} = \alpha \left| {\frac{{\text{d}u}}{{\text{d}t}}} \right|(cu - \omega ) + B\frac{{\text{d}u}}{{\text{d}t}}, $$
(2)

where α, B, c are constants and c > B > 0; u(t) is the input of ω(u) and also the control signal to the plant in this paper. Actually, the backlash-like model is just an extension of the Duhem model [9]. Thus, the solution of (2) can be solved explicitly:

$$ \omega (u(t)) = cu(t) + \text{d}(u) $$
(3)

and

$$ \begin{gathered} \text{d}(u) = \left[ {\omega_{0} - {cu_{0}} } \right]\text{e}^{{ - \alpha (u - {u_{0}} ){\text{sgn}} ( {\dot{u}} )}} \hfill \\ \, +\, \text{e}^{{ - \alpha u{\text{sgn}} ( {\dot{u}} )}} \int_{{{u_{0}} }}^{u} {\left[ {B - c} \right]\text{e}^{{\alpha \zeta {\text{sgn}} ( {\dot{u}} )}} } \text{d}\zeta , \hfill \\ \end{gathered} $$
(4)

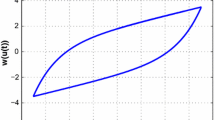
where \( u_{0} \) and \( \omega_{0} = \omega (u_{0} ) \) are initial conditions which are defined as \( u_{0} \; = \omega_{0} \; = \;0 \) (initial rest) in this paper; \( \text{sgn} ( \cdot ) \) represents the sign (or signum) function. The relationship between ω and u is illustrated in Fig. 2. In Fig. 2, the sign of α in (4) determines the direction of the curves. When α > 0, the hysteresis loop will be in counterclockwise direction. Similarly, when α < 0, the hysteresis loop will be in clockwise direction. In this paper, we only take α > 0 into consideration.

Fig. 2
figure 2

The hysteretic illustrations: a α > 0; b α < 0

Full size image

In addition, solving for (3) and (4), we can get an explicit solution of backlash-like hysteretic function \( \omega (u) \) as follows:

when \( \dot{u} \ge 0 \),

$$ \begin{gathered} \omega (u) = cu(t) + \left( {\omega_{0} - cu_{0} } \right)\text{e}^{{ - \alpha (u(t) - u_{0} )}} \hfill \\ \quad\quad\quad+ \frac{(B - c)}{\alpha }\left[ {1 - (2\text{e}^{{ - \left| \alpha \right|u_{s} }} - \text{e}^{{ - 2\left| \alpha \right|u_{s} }} )\text{e}^{{\alpha \left( {u_{0} - u(t)} \right)}} } \right] \hfill \\ \end{gathered} $$
(5)

and when \( \dot{u} < 0 \),

$$ \begin{gathered} \omega (u) = cu(t) + \left( {\omega_{0} - cu_{0} } \right)\text{e}^{{\alpha (u(t) - u_{0} )}} \hfill \\ \quad\quad\quad+\,\frac{(c - B)}{\alpha }\left[ {1 - (2\text{e}^{{ - \left| \alpha \right|u_{s} }} - \text{e}^{{ - 2\left| \alpha \right|u_{s} }} )\text{e}^{{\alpha \left( {u(t) - u_{0} } \right)}} } \right], \hfill \\ \end{gathered} $$
(6)

where \( u_{s} > 0 \) is the upper bound (also lower bound) of the hysteretic input u(t), i.e., \( \left| u \right| \le u_{s} \). As mentioned previously, \( u_{0} \) and \( \omega_{0} \) are set to zero; thus (5) and (6) can be simplified as follows:

when \( \dot{u}\; \ge \;0 \),

$$ \omega (u) = cu(t) + \frac{(B - c)}{\alpha }\left[ {1 - (2\text{e}^{{ - \left| \alpha \right|u_{s} }} - \text{e}^{{ - 2\left| \alpha \right|u_{s} }} )\text{e}^{ - \alpha u(t)} } \right] $$
(7)

and when \( \dot{u} < 0 \),

$$ \omega (u) = cu(t) + \frac{(c - B)}{\alpha }\left[ {1 - (2\text{e}^{{ - \left| \alpha \right|u_{s} }} - \text{e}^{{ - 2\left| \alpha \right|u_{s} }} )\text{e}^{\alpha u(t)} } \right]. $$
(8)

3 Design of Indirect Adaptive Fuzzy Controller

To properly control the nonlinear systems with hysteretic phenomena, a “feedback plus feed-forward” closed loop configuration which is used widely in numerous industrial applications is presented. The control strategy is shown in Fig. 3.

Fig. 3
figure 3

The control strategy to handle the nonlinear hysteretic system

Full size image

In Fig. 3, y m is the input signal to the system, and, in this paper, the feed-forward controller is simply a transducer to convert the reference signal to our control signal, i.e., \( u_{{\text{forward}}} = \beta y_{m} \), where β is a unit constant gain (β = 1). Then, the feedback controller is the proposed IAFC which is presented step by step as below.

3.1 Ideal Hysteresis Controller

Before presenting the IAFC, the following assumptions and lemma must be discussed:

Assumption 1

For all \( x \in {\mathbb{R}}^{n} \), there exist unknown bound functions \( \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{g} (\text{\bf{x}}) \) and \( \bar{g}(\text{\bf{x}}) \) such that \( 0 \,<\, \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{g} (\text{\bf{x}})\, \le\, g(\text{\bf{x}}) \,\le \bar{g}(\text{\bf{x}}) \).

Lemma 1

In (3) and (4), the hysteretic displacement d(u) is bounded, i.e., d(u) ≤ ρ, where ρ is a constant.

Proof

By (7) and (8), the hysteretic displacement can be simplified as

$$ \text{d}(u) = {\text{sgn}} (\dot{u})\frac{(B - c)}{\alpha }\left[ {1 - \left( {2{\text{e}}^{{ - \left| \alpha \right|u_{s} }} - {\text{e}}^{{ - 2\left| \alpha \right|u_{s} }} } \right)\text{e}^{{ - {\text{sgn}} (\dot{u})\alpha u(t)}} } \right]. $$

Obviously, if \( \alpha > 0 \) and \( \dot{u} > 0 \), then

$$ \mathop {\lim }\limits_{u \to \infty } \text{d}(u) = \frac{B - c}{\alpha }. $$
(9)

Similarly, if α > 0 and \( \dot{u}\, <\, 0 \), then

$$ \mathop {\lim }\limits_{u \to - \infty } \text{d}(u) = \frac{c - B}{\alpha }. $$
(10)

From (9) and (10), we can imply that there is a uniform bound ρ such that \( \left| {\text{d}(u)} \right| \le \rho \).

For the development of the control law, the following further Assumption 2 is made.

Assumption 2

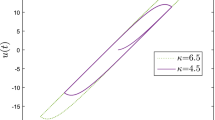
Based on some observations and the decent choose of the parameters, we can find that because the term \( \left( {2{\text{e}}^{{ - \left| \alpha \right|u_{s} }} - {\text{e}}^{{ - 2\left| \alpha \right|u_{s} }} } \right){\text{e}}^{{ - {\text{sgn}} (\dot{u})\alpha u(t)}} \) in d(u) is steady, d(u) varies slightly, which can be asserted by the experimental results shown in Fig. 4. In Fig. 4, the parameters are chosen as B = 0.345, c = 1.345, u = 10sin(2.5t), and α differs as shown in the figure.

Fig. 4
figure 4

The values of hysteretic displacement under different conditions

Full size image

Observing the behaviors of d(u) in Fig. 4, we can find that the hysteretic displacement almost equals to the bound value\( \rho = \text{sgn} (\dot{u})\frac{B - c}{\alpha } \). Hence, we can assume that d(u) is not only a uniform bounded function but also a constant, i.e., \( \text{d}(u) = - \text{sgn} (\dot{u})\text{d} \), where d is a positive constant. Replace (3) with \( \text{d}(u) = - \text{sgn} (\dot{u})\text{d} \), and the following equation can be derived:

$$ \omega (u) = cu(t) - \text{sgn} (\dot{u})\text{d}. $$
(11)

With Lemma 1, Assumption 1, and Assumption 2, the following Theorem 1 can be presented:

Theorem 1

Consider the system in (1) with hysteretic functions (5) and (6). There exists an ideal controller \( u_{{\text{ideal}}} \) such that the system output x 1 can track the reference signal y m as close as possible.

Proof

Let \( y = \left[ {y,\dot{y}, \cdots ,y^{(n - 1)} } \right]^{T} \) denotes the output vector, and \( y_{m} = \left[ {y_{m} ,\dot{y}_{m} , \cdots ,y_{m}^{(n - 1)} } \right]^{T} \) denotes a bounded reference input which has the nth-order derivative.

Define the output tracking error as \( \text{\bf{e}} = {\text{\bf{y}}}_{m} \bf{-} {\text{\bf{y}}} \) and the error vector as \( {\text{\bf{e}}} = {\text{\bf{y}}}_{\text{\bf{m}}} \;{ - }\;{\text{\bf{y}}} \, = \left[ {\text{e}_{1} ,\text{e}_{2} , \cdots ,\text{e}_{n} } \right]^{T} = \left[ {\text{e},{\dot{e}}, \cdots ,\text{e}^{(n - 1)} } \right]^{T} \). Choose a vector \( {\text{\bf{k}}} = \left[ {k_{n} , \cdots ,k_{1} } \right] \) such that all roots of the polynomial \( s^{n} + k_{1} s^{n - 1} + \cdots + k_{n} \) are in the left-half complex plane, and the polynomial is called Hurwitz polynomial [27, 28].

Then, apply (11) into (1), and we can get the following equation:

$$ x^{(n)} = F({\text{\bf x}}) + g({\text{\bf x}})(cu(t) - \text{sgn} (\dot{u})\text{d}). $$
(12)

From (12), if F(x) and g(x) are known, we can assume that there exists an ideal controller as given below:

$$ u_{{\text{ideal}}} = \frac{1}{{cg({\text{\bf x}})}}\left[ { - F({\text{\bf x}}) + y_{m}^{(n)} + {\text{\bf{k}}}^{T} {\text{\bf{e}}}} \right] + \text{sgn} (\dot{u}_{{\text{ideal}}} )\frac{\text{d}}{c}. $$
(13)

Then, we have to prove that (13) can control the output x 1 to track the reference signal y m. Substituting (13) into (12), we can obtain the closed-loop system as

$$ x^{(n)} - y_{m}^{(n)} = {\text{\bf{k}}}^{T} {\text{\bf{e}}} $$
(14)
$$ \Rightarrow \text{e}^{(n)} + k_{1} \text{e}^{(n - 1)} + \cdots + k_{n} \text{e} = 0. $$
(15)

With the Routh-Hurwitz stability criterion, via choosing the vector k properly, we can acquire that \( \mathop {\lim }\limits_{t \to \infty } \text{e}(t) = 0 \), which proves the theorem.

3.2 Indirect Adaptive Fuzzy Controller

Although we can prove the existence of the ideal hysteresis controller, F(x) and g(x) are usually unknown; hence, we cannot actually derive the ideal controller. In order to overcome this problem, utilizing the control strategy mentioned in Fig. 3, the ideal controller can be approximated by an IAFC.

For the design of the IAFC, firstly, we have to construct the fuzzy logic system which can be expressed through singleton fuzzifier, center average defuzzifier, and product inference [27, 28]:

$$y({\text{\bf x}}) = \frac{{\sum\nolimits_{{l = 1}}^{M} {\bar{y}^{l} \left( {\prod\nolimits_{{i = 1}}^{n} {\mu _{{A_{i}^{l} }} (x_{i} )} } \right)} }}{{\sum\nolimits_{{l = 1}}^{M} {\left( {\prod\nolimits_{{i = 1}}^{n} {\mu _{{A_{i}^{l} }} (x_{i} )} } \right)} }} = {\varvec{\uptheta }}^{T} \xi ({\text{\bf x}}), $$
(16)

where \( \mu_{{A_{i}^{l} }} (x_{i} ) \) are the fuzzy input membership functions, \( \bar{y}^{l} \) is the maximum point (or called center) of the output membership function \( \mu_{{B^{l} }} (y) \), and, without loss of generality, we assume that \( \mu_{{B^{l} }} (\bar{y}^{l} ) = 1 \). \( {\varvec{\uptheta}} = \left[ {\bar{y}^{l} , \cdots ,\bar{y}^{M} } \right]^{T} \) is an adaptive parameter vector, and \( \xi ({\text{\bf x}}) = \left[ {\xi^{1} ({\text{\bf x}}), \cdots ,\xi^{M} ({\text{\bf x}})} \right]^{T} \) is an input fuzzy basis function, where \( \xi^{l} ({\text{\bf x}}) \) can be defined as

$$ \xi^{l} ({\text{\bf x}}) = \frac{{\prod\nolimits_{i = 1}^{n} {\mu_{{A_{i}^{l} }} (x_{i} )} }}{{\sum\nolimits_{l = 1}^{M} {\left( {\prod\nolimits_{i = 1}^{n} {\mu_{{A_{i}^{l} }} (x_{i} )} } \right)} }}. $$
(17)

Since F(x) and g(x) are unknown, utilizing the fuzzy control logic system, we can approximate them by \( \hat{f}(x|{\uptheta}_{f} ) \) and \( \hat{g}({x}|{\uptheta}_{g} ) \), respectively: For variable x i , define fuzzy sets \( F_{i}^{{l_{i} }} \) and \( G_{i}^{{r_{i} }} \), where \( i = 1,2, \cdots ,n \); \( l_{i} = 1,2, \cdots ,p_{i} \) and \( r_{i} = 1,2, \cdots ,q_{i} \). Then, we obtain

$$ \hat{f}(x|{\varvec{\uptheta}}_{f} ) = \frac{{\sum\nolimits_{{l_{1} = 1}}^{{p_{1} }} { \cdots \sum\nolimits_{{l_{n} = 1}}^{{p_{n} }} {\bar{y}_{f}^{{l_{1} \cdots l_{n} }} } } \left( {\prod\nolimits_{i = 1}^{n} {\mu_{{F_{i}^{{l_{i} }} }} (x_{i} )} } \right)}}{{\sum\nolimits_{{l_{1} = 1}}^{{p_{1} }} { \cdots \sum\nolimits_{{l_{n} = 1}}^{{p_{n} }} {\left( {\prod\nolimits_{i = 1}^{n} {\mu_{{F_{i}^{{l_{i} }} }} (x_{i} )} } \right)} } }} = {\varvec{\uptheta}}_{f}^{T} \xi ({\text{\bf x}}) $$
(18)
$$ \hat{g}(x|{\varvec{\uptheta }}_{g} ) = \frac{{\sum\nolimits_{{r_{1} = 1}}^{{q_{1} }} { \cdots \sum\nolimits_{{r_{n} = 1}}^{{q_{n} }} {\bar{y}_{g}^{{l_{1} \cdots l_{n} }} } } \left( {\prod\nolimits_{i = 1}^{n} {\mu_{{G_{i}^{{l_{i} }} }} (x_{i} )} } \right)}}{{\sum\nolimits_{{r_{1} = 1}}^{{q_{1} }} { \cdots \sum\nolimits_{{r_{n} = 1}}^{{q_{n} }} {\left( {\prod\nolimits_{i = 1}^{n} {\mu_{{G_{i}^{{l_{i} }} }} (x_{i} )} } \right)} } }} = {\uptheta }_{g}^{T} \eta ({\text{\bf x}}), $$
(19)

where \( \bar{y}_{f}^{{l_{1} \cdots l_{n} }} \) and \( \bar{y}_{g}^{{l_{1} \cdots l_{n} }} \) are free parameters which can be chosen randomly or by some certain structures. Then, the resulting control law is

$$ u_{{\text{IAFC}}} = \frac{1}{{c\hat{g}({\text{\bf x}}|{\varvec{\uptheta }}_{g} )}}\left[ { - \hat{f}({\text{\bf x}}|{\varvec{\uptheta }}_{f} ) + y_{m}^{(n)} + {\text{\bf{k}}}^{T} {\text{\bf{e}}}} \right] - \frac{{\text{d}}(u)}{c}. $$
(20)

However, for industrial applications, a feed-forward controller is incorporated into our control scheme to enhance the steady-state error and improve the rise and settling time. The complete control strategy has been presented in Fig. 3, and the overall control signal can be as given below:

$$ u = u_{{\text{IAFC}}} + \beta y_{m} . $$
(21)

Applying (21) to (1), we can obtain the error equation in the vector form [28]

$$ {\dot{\text{\bf{e}}}} = {\bf{\Lambda}} {\text{\bf{e}}}\,+\,{\text{\bf{b}}}\left\{ {\left[ {\hat{f}({\text{\bf x}}|{\varvec{\uptheta} }_{f} ) - F({\text{\bf x}})} \right] + \left[ {\hat{g}({\text{\bf x}}|{\varvec{\uptheta }}_{g} ) - g({\text{\bf x}})} \right]\left( cu + \text{d}(u) \right) \, } \right\} $$
(22)

where \( \Lambda = \left[ {\begin{array}{*{20}c} 0 & 1 & 0 & 0 & \cdots & 0 & 0 \\ 0 & 0 & 1 & 0 & \cdots & 0 & 0 \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ 0 & 0 & 0 & 0 & \cdots & 0 & 1 \\ { - k_{n} } & { - k_{n - 1} } & \cdots & \cdots & \cdots & \cdots & { - k_{1} } \\ \end{array} } \right] \) and \( {\text{\bf{b}}} = \left[ {\begin{array}{*{20}c} 0 & 0 & \cdots & 1 \\ \end{array} } \right]^{T} \).

In [28], the optimal parameters \( {\varvec{\uptheta }}_{f}^{*} \) and \( {\varvec{\uptheta }}_{g}^{*} \) are defined, and the minimum approximation error can be defined as

$$ E = \left[ {\hat{f}({\text{\bf x}}|{\varvec{\uptheta }}_{f}^{*} ) - F({\text{\bf x}})} \right] + \left[ {\hat{g}({\text{\bf x}}|{\varvec{\uptheta }}_{g}^{*} ) - g({\text{\bf x}})} \right]\left( {cu + \text{d}(u)} \right). $$
(23)

Substituting (23) into (22), we can rewrite (22) as

$$ \begin{gathered} {\dot{\text{\bf{e}}}} = {\bf{\Lambda}} {\text{\bf{e}}} + {\text{\bf{b}}}\left\{ {\left[ {\hat{f}({\text{\bf x}}|{\varvec{\uptheta }}_{f} ) - \hat{f}({\text{\bf x}}|{\varvec{\uptheta }}_{f}^{*} )} \right] + \left[ {\hat{g}({\text{\bf x}}|{\varvec{\uptheta }}_{g} ) - \hat{g}({\text{\bf x}}|{\varvec{\uptheta }}_{g}^{*} )} \right]\left( {cu + \text{d}(u)} \right) + E} \right\}, \hfill \\ \hfill \\ \end{gathered} $$
(24)

which is equivalent to

$$ \begin{gathered} {\dot{\text{\bf{e}}}} = {\bf\Lambda} {\text{\bf{e}}} + {\text{\bf{b}}}\left\{ {\left[ {\varvec{\uptheta }}_{f} - {\varvec{\uptheta }}_{f}^{*} \right]^{T} \xi ({\text{\bf x}}) + \left[ {\varvec{\uptheta }}_{g} - {\varvec{\uptheta }}_{g}^{*} \right]^{T}\eta ({\text{\bf x}}) \left( {cu + \text{d}(u)} \right) + E} \right\}, \hfill \\ \hfill \\ \end{gathered} $$
(25)

Finally, the adaptive laws are defined to minimize the tracking error e, \( {\varvec{\uptheta }}_{f} - {\varvec{\uptheta }}_{f}^{*} \), and \( {\varvec{\uptheta }}_{g} - {\varvec{\uptheta }}_{g}^{*} \). The adaptive laws are presented in Theorem 2.

Theorem 2

Consider the backlash-like system (1) satisfying Assumptions 1 and 2. The control law is designed in (20), and the adaptive laws are

$$ {\dot{\varvec{\uptheta }}}_{f} = - \gamma_{1} {\text{\bf{e}}}^{T} {\text{\bf{Pb}}}\xi ({\text{\bf x}}) $$
(26)
$$ {\dot{\varvec{\uptheta }}}_{g} = - \gamma_{2} \text{\bf{e}}^{T} {\text{\bf{Pb}}}\eta ({\text{\bf x}})(cu_{\text{IAFC}} + c\beta y_{m} - \text{sgn} (\dot{u}_{\text{IAFC}} ){d}), $$
(27)

where γ 1 and γ 2 are the learning rate, and P and Q are positive definite matrix satisfying the following Lyapunov Matrix Equation:

$$ {\bf\Lambda }^{T} {\text{\bf{P}}} + {\text{\bf{P}}}{\bf\Lambda } = - {\text{\bf{Q}}}. $$
(28)

Proof

Choose a candidate Lyapunov equation

$$ V = \frac{1}{2}{\text{\bf{e}}}^{T} {\text{\bf{Pe}}} + \frac{1}{{2\gamma_{1} }}\left( {{\varvec{\uptheta }}_{f} - {\varvec{\uptheta }}_{f}^{*} } \right)^{T} \left( {{\varvec{\uptheta }}_{f} - {\varvec{\uptheta }}_{f}^{*} } \right) + \frac{1}{{2\gamma_{2} }}\left( {{\varvec{\uptheta }}_{g} - {\varvec{\uptheta }}_{g}^{*} } \right)^{T} \left({{\varvec{\uptheta }}_{g} - {\varvec{\uptheta }}_{g}^{*}} \right). $$
(29)

Then, differentiate Eq. (29), and we can get

$$ \begin{gathered} \dot{V} = - \frac{1}{2}{\text{\bf{e}}}^{T} Q{\text{\bf{e}}} + {\text{\bf{e}}}^{T} {\text{\bf{Pb}}}E \hfill \\ \quad+ \frac{1}{{\gamma_{1} }}\left( {{\varvec{\uptheta }}_{f} - {\varvec{\uptheta }}_{f}^{*} } \right)^{T} \left[ {{\dot{\varvec{\uptheta }}}_{f} + \gamma_{1} {\text{\bf{e}}}^{T} {\text{\bf{Pb}}}\xi ({\text{\bf x}})} \right] \hfill \\ \quad+ \frac{1}{{\gamma_{2} }}\left( {{\varvec{\uptheta }}_{g} - {\varvec{\uptheta }}_{g}^{*} } \right)^{T} \left[ {{\dot{\varvec{\uptheta }}}_{g} + \gamma_{2} {\text{e}}^{T} {\text{\bf{Pb}}}\eta ({\text{\bf x}})\left({cu_{{\text{IAFC}}}} + c\beta y_{m} - \text{sgn} (\dot{u}_{\text{IAFC}})d \right)} \right] \hfill \\ \end{gathered} $$
(30)

In order to minimize the three terms e, \( {\varvec{\uptheta }}_{f} - {\varvec{\uptheta }}_{f}^{*} \), and \( {\varvec{\uptheta }}_{g} - {\varvec{\uptheta }}_{g}^{*} \), we have to make \( \dot{V} < 0 \). \( \dot{V} \) consists of four terms as below:

  1. 1.

    \( - \frac{1}{2}{\text{\bf{e}}}^{T} Q{\text{\bf{e}}} < 0 \) is obvious because Q is a positive definite symmetric matrix.

  2. 2.

    \( {\text{\bf{e}}}^{T} {\text{\bf{Pb}}}E \) can be small enough: when the fuzzy logic system is adequate, the minimum approximation error will become a small value or even zero.

  3. 3.

    \( \frac{1}{{\gamma_{1} }}\left( {{\varvec{\uptheta }}_{f} - {\varvec{\uptheta }}_{f}^{*} } \right)^{T} \left[ {{\dot{\varvec{\uptheta }}}_{f} + \gamma_{1} {\text{\bf{e}}}^{T} {\text{\bf{Pb}}}\xi ({\text{\bf x}})} \right] \) becomes zero when we choose \( {\dot{\varvec{\uptheta }}}_{f} = - \gamma_{1} {\text{\bf{e}}}^{T} {\text{\bf{Pb}}}\xi ({\text{\bf x}}) \).

  4. 4.

    \( \frac{1}{{\gamma_{2} }}\left( {{\varvec{\uptheta }}_{g} - {\varvec{\uptheta }}_{g}^{*} } \right)^{T} \left[ {{\dot{\varvec{\uptheta }}}_{g} + \gamma_{2} {\text{e}}^{T} {\text{\bf{Pb}}}\eta ({\text{\bf x}})\left( {cu_{{\text{IAFC}}} + c\beta y_{m} - \text{sgn} (\dot{u}_{{\text{IAFC}}} )\text{d}} \right)} \right] \) can also become to zero when we choose \( {\dot{\varvec{\uptheta }}}_{g} = \; - \gamma_{2} {\text{\bf{e}}}^{T} {\text{\bf{Pb}}}\eta ({\text{\bf x}})(cu_{{\text{IAFC}}} + c\beta y_{m} - \text{sgn} (\dot{u}_{{\text{IAFC}}} )\text{d}) . \)

The sum of the above four terms is negative, and this completes the proof.

4 Simulation Studies

In this section, three benchmark hysteretic examples controlled by the proposed IAFC are presented and compared to the adaptive backstepping control (ABC) method in [20]. Example 1 uses the hysteresis example in [13, 18, 20–22] with a little modification: the control gain in Example 1 is an unknown nonlinear function; however, the control gain in [13, 18, 20–22] is just an unknown constant. Example 2 is an Inverted Pendulum System (IPS) [27] with hysteresis, which is a standard benchmark used in numerous researches. Example 3 is a single-link robotic manipulator problem stated in [29]. This problem already exists a frictional model, and we impose the hysteretic function into this example. These three examples, which are simulated based on MATALB simulation platform, can fully examine the effectiveness of the proposed novel IAFC. The details and the results of the problem are shown below:

Example 1

Consider the following second-order nonlinear backlash-like hysteresis system:

$$ \left\{ {\begin{aligned} &{\dot{x}_{1} = x_{2} \, } \\ &{\dot{x}_{2} = a\frac{{1 - \text{e}^{{ - x_{2} }} }}{{1 + \text{e}^{{ - x_{2} }} }} + g(x_{1} ,x_{2} )\omega (u)} \\ & {y = x_{1} \, } \\ \end{aligned} } \right., $$
(31)

where \( \omega \) represents the output of the hysteresis nonlinearity as in (7) and (8); the actual parameter \( a = 1 \) and, for simulation purpose, \( g(x_{1} ,x_{2} )\; = 2 + \sin (x_{1} x_{2} ) > 0 \).

The control objective is to control the system output \( y = x_{1} \) with initial state \( x_{0} = \left[ {0.3,\;0} \right] \) to follow a desired trajectory \( y_{m} = 0.5\sin \left( {2.3t} \right) \). The backlash-like hysteresis model is described by (7) and (8) with parameters \( \alpha = 1,B = 0.345,c = 3.1635, \, \text{and} \, u_{s} = 10 \). The initial 25 values of vector \( \theta_{f} (0) \) and the initial 9 values of vector \( \theta_{g} (0) \) can be randomly chosen in \( \left[ {\begin{array}{*{20}c} 0 & 1 \\ \end{array} } \right] \).

Construct the IAFC for the nonlinear system:

Step 1: Select the design parameters: the learning rates\( \text{ }\gamma_{1} = 35 \) and \( \gamma_{2} = 1 \) for (26) and (27), respectively; control parameters \( {\user2{k}} = [k_{1} ,k_{2} ]^{T} = [\begin{array}{*{20}c} {10} \quad 1 \\ \end{array} ]^{T} \), positive definite matrix \( {\user2{P}} = \left[ {\begin{array}{*{20}c} {255} & {25} \\ {25} & 5 \\ \end{array} } \right] \), and \( {\user2{b}} = [\begin{array}{*{20}c} 0 & 0 & \cdots & 1 \\ \end{array} ]^{T} \).

Step 2: The adaptive fuzzy membership function can be defined as Gaussian functions as follows:

$$ \mu_{{F_{i}^{l} }} \left( {x_{i} } \right) = \text{e}^{{\left( { - \frac{{(x_{i} - c_{fl} )^{2} }}{2}} \right)}} \text{ },\quad \text{for} \text{ }i = 1,2;\;\;l = 1,2, \cdots ,5 $$
(32)
$$ \mu_{{G_{i}^{m} }} \left( {x_{i} } \right) = \text{e}^{{\left( { - \frac{{(x_{i} - c_{gl} )^{2} }}{2}} \right)}} ,\quad \text{for}\text{ }i = 1,2;\;\;m = 1,2,3 $$
(33)

where \( [c_{f1} ,c_{f2} ,c_{f3} ,c_{f4} ,c_{f5} ] = [ - 10, - 5,0,5,10] \) and \( [c_{g1} ,c_{g2} ,c_{g3} ] = [1,\text{ }1.5,\text{ }3] \). Then, compute the fuzzy basis functions.

Step 3: Compute the adaptive laws in (26), (27) and control law in (20), and then obtain the control signal in (21).

The parameters of the adaptive backstepping method in [20] are chosen as \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{c}_{1} = 15 \), \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\gamma } = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\varGamma } = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\eta } = 0.5 \).

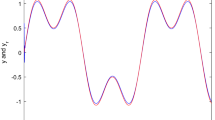
The simulation results are shown in Figs. 5, 6 and 7. The system output x1 tracks the desired reference signal \( y_{m} \) as shown in Fig. 5. The control input \( u(t) \) is shown in Fig. 6, and tracking error \( e_{1} (t) \) is shown in Fig. 7.

Fig. 5
figure 5

Output y tracks the reference signal y m

Full size image
Fig. 6
figure 6

Control input u(t)

Full size image
Fig. 7
figure 7

Tracking error e 1 (t)

Full size image

In Fig. 5, we can find that these two approaches can handle this hysteretic problem appropriately. In Fig. 7, the system reaches the steady state at about 1 s using these two methods. In order to evaluate the effectiveness of these two controllers, the Mean Square Error (MSE) is adopted and given as follows:

$$ \text{MSE} = \frac{1}{n}\sum\limits_{i = 1}^{n} {\left( {y_{m} - y_{i} } \right)^{2} } = \frac{1}{n}\sum\limits_{i = 1}^{n} {\text{e}_{i}^{2} } , $$
(34)

where i is the index of the n points over which the MSE is computed.

The mean square errors of IAFC and ABC are shown in Table 1: the MSE of the proposed IAFC is smaller than ABC. Besides, in Fig. 6, the control input of ABC has more severe chattering effects than the proposed method.

Table 1 Mean square errors of ABC and IAFC
Full size table

Example 2

Consider a second-order IPS with hysteresis, which is shown below:

$$ \left\{ {\begin{aligned} & {\dot{x}_{1} = x_{2} \, \text{ }} \\ & {\dot{x}_{2} = \frac{{g\sin x_{1} - \frac{{mlx_{2}^{2} \cos x_{1} \sin x_{1} }}{{M_{c} + m}}}}{{l\left( {\frac{4}{3} - \frac{{m(\cos x_{1} )^{2} }}{{M_{c} + m}}} \right)}}} \\ & {y = x_{1} \text{ }} \\ \end{aligned} } \right. + \frac{{\frac{{\cos x_{1} }}{{M_{c} + m}}}}{{l\left( {\frac{4}{3} - \frac{{m(\cos x_{1} )^{2} }}{{M_{c} + m}}} \right)}}\omega (u), $$
(35)

where x 1 is the angular position of the pendulum, x 2 is the angular velocity of the pendulum, g = 9.8 m/s2 is the gravitational acceleration, m c  = 1 kg is the mass of the cart, m = 0.1 kg is the mass of the pole, and l = 0.5 m is the half-length of the pendulum. The control objective is to ensure the system output x 1 with initial state \( x_{0} = [{\pi \mathord{\left/ {\vphantom {\pi {12}}} \right. \kern-0pt} {12}},\;0] \) which can track the desired reference signal \( y_{m} = \left( {{\pi \mathord{\left/ {\vphantom {\pi {30}}} \right. \kern-0pt} {30}}} \right)\sin (t) \). The backlash-like hysteresis parameters are the same as the previous example.

The initial values of θ f (0) and θ g (0) are shown in Table 2, 3.

Table 2 Initial value of θ f (0)
Full size table
Table 3 Initial value of θ g (0)
Full size table

Construct the IAFC for the nonlinear system:

Step 1: Select the design parameters: the learning rates γ 1 = 50 and γ 2 = 0.1 for (26) and (27), respectively; control parameters are the same as in the previous example.

Step 2: Compute the fuzzy basis functions with the adaptive fuzzy membership function as below:

$$ \mu_{{F_{i}^{l} }} \left( {x_{i} } \right) = \mu_{{G_{i}^{l} }} \left( {x_{i} } \right) = \text{e}^{{\left( { - \frac{{(x_{i} - c_{l} )^{2} }}{2}} \right)}} ,\quad \text{for} \text{ }i = 1,2;\;\;l = 1,2, \cdots ,5 $$

where \( [c_{1} ,c_{2} ,c_{3} ,c_{4} ,c_{5} ] = \left[ { - \frac{\pi }{6}, - \frac{\pi }{12},0,\frac{\pi }{12},\frac{\pi }{6}} \right] \).

Step 3: Compute the adaptive laws in (26), (27) and control law in (20), and then obtain the control signal in (21).

The parameters of the adaptive backstepping method in [20] are chosen as \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{c}_{1} = 35 \), \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\gamma } = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\varGamma } = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\eta } = 0.6 \).

The simulation results are shown in Figs. 8 and 9. The system output x 1 tracks the desired reference signal y m as shown in Fig. 8. The tracking error e 1(t) is shown in Fig. 9. Besides, the mean square errors of the two approaches are shown in Table 4. As we can see, with faster rise time and smaller steady-state error, the proposed IAFC outperforms the adaptive backstepping controller.

Fig. 8
figure 8

Output y tracks reference signal y m

Full size image
Fig. 9
figure 9

Tracking error e 1 (t)

Full size image
Table 4 Mean square errors of ABC and IAFC
Full size table

Example 3

Consider a single-link manipulator with the following dynamic equation [29]:

$$ \left\{ {\begin{array}{*{20}l}{\dot{x}_{1} = x_{2} \, } \\ {\dot{x}_{2} = - (d_{r} x_{2} + m_{r} g_{v} l_{r} \cos (x_{1} ))/J + \left( {{1 \mathord{\left/ {\vphantom {1 J}} \right. \kern-0pt} J}} \right)\omega + \text{d}(t)} \\ {y \,\,= x_{1} \, } \\ \end{array} } \right., $$
(36)

where x 1 is the angular position of the manipulator and x 2 is the angular velocity of the manipulator. m r is the mass of the payload, l r is the length of the manipulator, J is the inertia coefficient, and d r is the damping factor. d(t) is the external disturbance, which is a frictional model as given below:

$$ \text{d}(t) = \frac{{ - \left( {\text{sgn}} \left( {x_{2} (t)} \right)c_{r} + v_{r} x_{2} (t) \right)}}{J}, $$
(37)

where c r is the Coulomb friction torque, and v r is the dynamic friction coefficient. The parameters are chosen as m r  = 5 + 4sin(t), l r  = 0.25 m, d r  = 2 kg m2/s, v r  = 0.3, c r  = 1.5, J = 1.33m r l 2 r , and x(0) = [π/6, 0].

The control objective is to ensure that the system output x 1 can track the desired reference signal y m  = sin(t). The backlash-like hysteresis parameters are the same as Example 1 and Example 2.

Construct the IAFC for the hysteretic robotic manipulator problem:

Step 1: Select the design parameters: the learning rate γ 1 = 50 and γ 1 = 1 for (26) and (27), respectively; control parameters are identical to Example 1.

Step 2: Compute the fuzzy basis functions with the adaptive fuzzy membership function as below:

$$ \mu_{{F_{i}^{l} }} (x_{i} ) = \mu_{{G_{i}^{m} }} (x_{i} ) = \text{e}^{{\left( { - \frac{{(x_{i} - c_{i} )^{2} }}{2}} \right)}} , \quad \text{for} \, i = 1,2; \, l = 1,2, \cdots ,5 $$

where \( \left[ {c_{1} ,c_{2} ,c_{3} ,c_{4} ,c_{5} } \right] = \left[ { - \frac{\pi }{6}, - \frac{\pi }{12},0,\frac{\pi }{12},\frac{\pi }{6}} \right] \).

Step 3: Compute the adaptive laws in (26) and (27) and control law in (20), and then obtain the control signal in (21). The initial values of θ f (0) and θ g (0) are set to zero vectors.

The parameters of the adaptive backstepping method in [20] are chosen as \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{c}_{1} = 35 \), \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\gamma } = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\varGamma } = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\eta } = 0.7 \).

The simulation results are shown in Figs. 10 and 11. The system output x 1 tracks the desired reference signal y m as shown in Fig. 10. The tracking error e 1(t) is shown in Fig. 11. Besides, the mean square errors of the two approaches are shown in Table 5. In this more complex hysteretic system, both of the approaches can reach good performance. However, referring to the MSE, the proposed IAFC can achieve better performance than the adaptive backstepping method.

Fig. 10
figure 10

Output y tracks reference signal y m

Full size image
Fig. 11
figure 11

Tracking error e 1 (t)

Full size image
Table 5 Mean square errors of ABC and IAFC
Full size table

5 Conclusions

In this paper, a new “feedback + feed-forward” control strategy for real applications is presented to deal with nonlinear hysteretic problems. However, ideal controller cannot be derived directly; hence, an IAFC is proposed to approximate the ideal controller. Then, using Lyapunov theory, the stability of the closed-loop system and the tracking performance can be guaranteed. Finally, the simulation results demonstrated that the proposed approach can achieve excellent tracking performance for the hysteretic IPS with unknown nonlinear gain, which cannot be handled by previous approach. Further studies would focus on real industrial applications to verify the effectiveness of our proposed approach. Besides, we will extend our proposed IAFC to deal with different kinds of hysteretic problems in this research area.