Efficient matching of very complex time series

Abstract

We propose a novel method (FANSEA) that performs very complex time series matching. The matching here includes comparison and alignment of time series, for diverse needs: diagnosis, clustering, retrieval, mining, etc. The complexity stands in the fact that the method is able to match quasi-periodic time series, that are eventually phase shifted, of different lengths, composed of different number of periods, characterized by local morphological changes and that might be shifted/scaled on the time/magnitude axis. This is the most complex case that can occur in time series matching. The efficiency stands in the fact that the newly developed FANSEA method produces alignments that are comparable to those of the previously published SEA method. However and as a result of data reduction, FANSEA consumes much less time and data; hence, allowing for faster matching and lower storage space. Basically, FANSEA is composed of two main steps: Data reduction by curve simplification of the time series traces and matching through exchange of extracted signatures between the time series under process. Due to the quasi-periodic nature of the electrocardiogram (ECG), the tests were conducted on records selected from the Massachusetts Institute of Technology-Beth Israel Hospital database (MIT-BIH). Numerically, the new method data reduction was up to 80 % and the time reduction was up to 95 %. Accordingly and among many possible applications, the new method is very suitable for searching, querying and mining of large time series databases.

1 Introduction

Modeling, analysis and exploration of time series are important applications in many fields of science and technology. They are particularly useful in knowledge discovery, machine learning and in diagnosis of systems generating these time series. Domains for such applications include economy, e.g., financial data [1], physiology, e.g., [2–4], data retrieval by content, e.g., music retrieval by humming [5–7] and fault/anomaly/novelty detection in industrial systems [8–11]. One basic operation that many time series analysis and exploration systems use is comparison of two given time series based on their shapes. That is, given two time series, the comparison operation consists in establishing a way to tell whether their traces are similar enough. One of the two time series stands in general for the reference (known behavior), whereas the second for the target (the unknown behavior). Some typical examples are illustrated in Fig. 1I–III, where the reference-target time series are (a, b), (c, d) and (e, f).

Fig. 1

Illustration of some typical situations of similar time series to compare. (I) illustrates two similar time series (a and b) with local morphology change. In (II), time series (d) is significantly shifted to the right (time axis) and to the bottom (magnitude axis), with respect to time series (c). In (III), time series (f) is a down-scaled version of time series (e). In all situations, the challenge of comparing/aligning the time series is to overcome these obstacles and declare the appropriate time series similar

Many techniques have been developed for time series comparison. Yet, the dynamic time warping (DTW) [12] is recognized by many researchers as the most accurate comparison technique. The main advantage of the DTW is its great ability in taking into account the time axis shift (Fig. 1II) and/or scaling problems (Fig. 1III). It can also align time series of different lengths. The main problem with DTW is its high computational complexity. In addition and from our point of view, DTW can only deal with the simplest case of time series matching: 1-period time series with no phase-shift (e.g., Fig. 1I–III). In [13], we developed a novel time series matching technique, SEA, that can also match time series with time/magnitude axis shift and/or scaling and that might be of different lengths. In other words, SEA can do the same job as the DTW technique. However, the SEA method can also perform more complex matchings. These include: 1-period phase-shifted time series (e.g., Fig. 2I) and multiple-periods time series containing different number of periods each (Fig. 2II). These are the most complex time series matching that we have encountered. The SEA method was also shown to be more accurate and less memory and time consuming than DTW. In this study, we propose an even more efficient method for time series comparison (acronym: FANSEA). The efficiency of FANSEA stands in the fact that it consumes much less time than SEA and uses only a small fraction of the original time series samples for comparable quality of matching with respect to SEA.

Fig. 2

Very complex time series matching situations. I 1-period time series, with one phase-shifted with respect to the other. Here, S1 and S2 are 1-period instances of a quasi-periodic time series. From this perspective, they are similar. II Many-periods time series containing different number of periods each. Here, S3 and S4 are instances of a quasi periodic time series, with 2 and 3 periods respectively. These are also similar time series

Basically, the proposed FANSEA is an accelerated and enhanced version of the SEA method. Whereas the SEA method performs the alignment on the whole data sets of the two time series to match, FANSEA proceeds first to extraction of as few significant points as possible from the two time series curves, on which the matching is performed. Accordingly, the FANSEA technique is composed of two main phases. In the first phase, there is dominant points (DPs) extraction from the two time series (e.g., Fig. 3). This objective is realized through a variant of the FAN line simplification algorithm [14]. In the second phase, the SEA matching method is applied to the two sets of extracted DPs. To show the effectiveness and efficiency of the new method, we compare it to the SEA method. We specifically use electrocardiogram (ECG) data, since this type of time series is basically a quasi-periodic signal that is characterized by high variability and noise (See Sect. 4). Obtained results show that the new method uses less than 20 % of the original samples and that it is much less time consuming than SEA, for comparable alignments.

Fig. 3

A time series and 15 computed dominant points (DPs) on its curve. Dominant points are perceptually attractive points on the time series curve. They constitute a kind of abstraction (compression) of the time series, while preserving most of the time series shape (discontinuous line)

The rest of this paper is organized as follows. In Sect. 2, there is review of existing time series comparison methods, including our own and new classification of these techniques. In Sect. 3, the proposed FANSEA method is presented. In Sect. 4, applications on the FANSEA and the SEA methods are performed. In Sect. 5, obtained results are discussed. At last, in Sect. 6, a general conclusion is dressed.

2 Time series comparison: what methods and what data?

In this section, the emphasis is on existing time series comparison techniques. In sub-Sect. 2.1, we review the main existing methods, in terms of the nature of the used algorithms and techniques. In sub-Sect. 2.2, we present our personal and new categorization of time series comparison methods, in terms of the nature of the used data.

2.1 Algorithm nature: comparison or alignment?

There should be distinction between two classes of time series matching techniques: Comparison methods and alignment methods. Let X = (x_i), i = 1:n and Y = (y_j), j = 1:m, be two given time series to be matched. Comparison methods render a distance that reflects the degree of dissimilarity between X and Y; whereas alignment methods perform a mapping between the points of X and those of Y. Of course, alignment methods render also a distance measure. The Euclidian distance (Eq. 1) seems to be the first used time series comparison. This is basically due to its simplicity, but, also to its interesting linear temporal and spatial complexities. One of the drawbacks of the Euclidian distance is that it works on equal lengths time series. It is also reported to be very sensitive to the time axis shift and/or scaling and to local noise. A discrete fourier transform (DFT) based method was proposed by Agrawal et al [15]. In this method, the two time series are mapped from the time domain to the frequency domain through the DFT. Then, the first most significant k coefficients of the DFT in each series are used in the comparison through the Euclidian distance. To all evidence, this technique compares the two time series, but does not align them. Shatkay and Zdonic [16] proposed also a comparison method. Their technique consists in transforming first the raw data into characters defined over a limited alphabet and then in applying string matching techniques. However, this method effectiveness is limited since data reduction by quantification of time series leads to important data distortion. A histogram based comparison method was proposed by Chen and O¨zsu [17]. Since histograms ignore the temporal dimension of the data sequences, this category of methods is capable of rendering only a global similarity measure. However, no alignment at the point-to-point level is possible in such methods. Another comparison method was proposed by Bozkaya et al [18] and is referred to by longest common sub-sequence (LCSS). This method is based on a modified version of the Edit distance [19]. This method allows non-linear mapping between the two time series. However, the threshold on the edit distance is very difficult to be set.

The other category of methods performs alignment between the two time series. That is, in this class of methods, there is a mapping between the points of the two time series to match. The famous DTW [12] leads this class and has been intensively used by many researchers in resolving many technological and scientific problems in numerous fields. As examples of DTW applications, we cite speech recognition [20], music retrieval [21], ECG recognition [22] and general time series mining [23]. As mentioned above, the main advantage of the DTW is its remarkable ability in taking into account the time axis shift and/or scaling problems (e.g., Fig. 4). However, the DTW main problem resides in its high temporal complexity. SEA [13] is another alignment method that was recently proposed for time series matching. It was shown to be more effective than DTW in the precision of matching. It also consumes less memory and less time than DTW.

$$ Euclidian\;(X,\;Y) = \sqrt {\sum\limits_{i = 1}^{i = n} {(x_{i} - y_{i} )^{2} } } \;. $$

(1)

Fig. 4

Alignment of two time series S1 and S2 by the DTW method. In this case, S2 is shifted to the right (time axis). Note that DTW performs a non-uniform alignment to achieve such a remarkable result. Note also that S1 and S2 are of different lengths

2.2 Data nature: periodic or not-periodic?

From another point of view, we classify time series comparison methods according to the nature of the data it can process. Basically, our analysis of existing time series comparison methods shows three main classes in terms of the nature of the data it can match. We report these classes in ascending order of complexity of the data: (a) non-periodic or 1-period-no-phase-shift (e.g., Fig. 1I–III), (b) one-period-with-phase-shift (e.g., Fig. 2I) and (c) periodic-many-periods (e.g., Fig. 2II). Note that this classification is organized also in order of inclusion. In other words, methods in (c) can treat data (a), (b) and (c), methods in (b) can treat data (a) and (b), and methods in (a) can treat data (a) only. This situation is illustrated in Fig. 5.

Fig. 5

Classification of time series comparison methods from the point of view of the data it can match. a Non-periodic or 1-period-no-phase-shift (e.g., Fig. 1 I–III), b one-period-with-phase-shift (e.g., Fig. 2 I) and (c) periodic-many-periods (e.g., Fig. 2 II). Note that methods in (c) can treat data (a), (b) and (c), methods in (b) can treat data (a), (b) and methods in (a) can treat data (a) only

2.2.1 Non-periodic or 1-period-no-phase-shift

This type of data is treated by all existing methods with more or less satisfactory results, including comparison and alignment techniques. To report some, the DFT [15] and the DTW [12] belong to this class. The types of data that can be treated by this class are time series that are non-periodic (e.g., Fig. 1I–III) and also (about) 1-period of periodic time series, with the condition that none of the two time series is significantly phase shifted with respect to the other.

2.2.2 1-Period of phase-shifted time series

This type of data is present in periodic time series (e.g., Fig. 2I), but also and specifically in some techniques of shape recognition/retrieval using object contour time series. For the case in Fig. 2I, the two time series are instances of one period of the same (or similar) quasi-periodic time series. However, each time series is phase-shifted with respect to the other. In the case of shape recognition/retrieval using object contour time series, the mapping contour → time series leads generally to phase-shifted time series due to object rotation, among many other complications. Except SEA and its derivatives, none of the above mentioned techniques can correctly match this type of time series, including DTW. However, Keogh et. al. [24] proposed a modified version of DTW they called Phase independent DTW (PI-DTW) that can deal with phase shifted 1-period time series. They successfully used it to match shapes based on their contours. If PI-DTW can match (a) and (b) time series, it is unable to match time series of type (c).

2.2.3 Periodic-many-periods time series

This kind of data is of course present in periodic time series (e.g. Fig. 2II). In this case, the two time series to compare/align must contain many periods each, but not necessarily the same number of periods. Indeed, time series that contain many periods but the same number of periods brings the data to type (a) if there is no (significant) phase shift and to (b) if there is (significant) phase shift. Thus, the types of data specific to this class are time series that are phase-shifted, in addition to being composed of a different number of periods each. This is the most complex comparison/alignment case that one can face. More, this is a problem that is naturally encountered in many applications: clustering, pattern recognition, summarizing etc. of quasi-periodic time series. Methods that can match such types of data should consider the repetitive (patterns) as redundant information. Thus, with this principle in mind, no matter the number of periods in each time series, the two time series should be appropriately aligned and a distance or a similarity measure that reflects the degree of resemblance rendered. To the best of our knowledge and except SEA and its derivatives, none of the above mentioned techniques can align this type of time series. This analysis and comparison is further summarized in Table 1.

Table 1 Summary of the comparative study on existing time series comparison methods

Through this study, we show that, like SEA, the proposed new time series matching method (FANSEA) can align this last category of time series, but with more efficiency. The efficiency stands in two aspects: time reduction and used data reduction, for nearly the same precision of matching with respect to SEA. If the aspect of speed is clearly admitted as an advantage, the aspect of data reduction may need some clarification. In addition to the fact that data reduction speeds up the matching process, it also gives the opportunity to efficiently represent the time series in memory. To all evidence, this is another important advantage when it comes to represent and explore large or even very large databases (VLDB).

3 The proposed method

As stated above, the proposed method is composed of two main steps: data reduction and Matching.

3.1 Data reduction: the FAN method

The data reduction step is performed through curve simplification of the two time series. This approach can briefly be defined as follows. Let P = (p_i), i = 1…N, where p_i = (x1⁽ⁱ⁾, x2⁽ⁱ⁾), be a given polyline (discrete curve), with x1⁽ⁱ⁾ being the horizontal (temporal) coordinate and x2⁽ⁱ⁾ being the vertical (magnitude) coordinate of point p_i. The simplification of P to a given precision ε, ε > 0, a preset threshold on the tolerance of the approximation, consists in computing another polyline Q = (q_j), j = 1…K, satisfying the following conditions [25]:

• (a) K < N; (data reduction rule)

• (b) q₁ = p₁ and q_K = p_N; (endpoints must coincide)

• (c) Let ||.,.|| be a distance defined on discrete curves. Then ||P, Q|| < ε.

We use the FAN [14] line simplification algorithm for the points of Q determination. This algorithm uses a sequential selection strategy, reducing gradually the distance between P and Q by the maximal possible amount under norm ||.,.|| at each selection. The FAN main steps are as follows.

• (a) The first point of the curve is selected as the first DP: (Q = [p₁]).

• (b) At each following step, let q_i be the current selected dominant point. The next selected point, say q_i+1, is computed as the furthest point from q_i (Max(|X1^qi − X1^qi+1|)) that satisfies the tolerance error (|X2^q − X2^r|) < ε) for all the points q lying between q_i and q_i+1, where r is the vertical projection of point q on the line joining q_i and q_i+1. Figure 6 illustrates the selection of the fifth DP q₅ in a 150 samples time series.

  Fig. 6

  

  Curve simplification of a 150 samples time series (red color) with eight DPs (green squares) using the FAN method. The red color time series represents here the input polyline P and the set of DPs represents the reduced form Q to the tolerance error ε . The data reduction in this case is DR (P, Q) = (1 − 2 × 16/150) × 100 % ≈ 78.7 %. It can be seen that the eight DPs by themselves bear most of the time series shape (blue, discontinuous curve). Thus, comparisons based on the eight DPs instead of the 150 original points will potentially be much faster than and nearly as precise as comparisons using the whole data. In addition, one can use the eight DPs (16 values only, instead of 150) to store the time series. Note that the red time series is a true portion of electrocardiogram data (see Sect. 4). The selection of DP q₅, as an example, is such that q₅ is the furthest possible point from the last selected DP q₄ (Max (|X1^q4 − X1^q5|)) that satisfies the tolerance error (|X2^q − X2^r|) < ε), for all the points q lying between q₄ and q₅, where r is the vertical projection of point q on the line joining q₄ and q₅ (color figure online)

• (c) The process is repeated for the remaining sub-curve beginning at q_i+1 and ending at p_N, until the right endpoint is selected.

Following the simplification process, we compute the data reduction (in terms of samples reduction) by Eq. 2.

$$ DR\;(P,\;Q) = \left( {1 - 2\frac{|Q|}{|P|}} \right) \times 100\% $$

(2)

The 2 factor in Eq. 2 is due to the fact that, upon simplification, the time indexes of the selected DPs are no longer implicit as in the case of the original samples. Therefore, both the magnitude and the time indexes are stored.

3.2 Matching

3.2.1 Step 1

Data reduction: both time series to align X and Y are passed through the FAN procedure, described in sub-Sect. 3.1. The outcome of processing a time series with the FAN procedure is a set of (perceptually) significant points on the time series curve. Let Xs be the reduced set of points for X and Ys that of Y. For the need of the method, we report here that each element of Xs coordinates are as follows. Temporal-index: Xs₁; magnitude-value: Xs₂. (respectively, Ys₁ and Ys₂ for Y_S).

3.2.2 Step 2

Signature establishment: time series Xs = (Xs₁, Xs₂)_i, i = 1:k, which is initially ordered on the temporal value (Xs₁) is reordered on the magnitude value Xs₂. The obtained trace is referred to in this study as signature (Xs). This operation is performed for both Xs and Ys. The obtained signature (Xs) and signature (Ys) will be used for the matching of X and Y through Xs and Ys alignment. The comparison is explained in the next step.

3.2.3 Step 3

Magnitude exchange and comparison: in the third step of FANSEA, there is exchange of the magnitudes between the two time series Xs and Ys. That is, time series Xs will ‘wear’ the magnitude of time series Ys and vice versa. Upon the exchange operation, the resulting two time series are put in natural (temporal) order. This specific action is designed herein by reconstruction. The comparison is then performed for each time series (e.g., Xs) with its reconstructed correspondent resulting from the exchange step (e.g., Xs_Rec), using the correlation factor, corr (Eq. 3) as an objective criterion and visual inspection as a subjective criterion. Note here that the method handles time series of different lengths since the effective alignments and computed correlations are performed on equal lengths series (Xs, Xs_rec) and (Ys, Ys_rec). An illustrative example is presented in Fig. 7. The illustration is performed on two ECG time series taken from two different records (see Sect. 4 for a brief presentation of ECG). Plot 1-up shows respectively: time series X (600 samples, two periods) and Y (700 samples, three periods). Plot 1-middle shows the reconstructed time series by FANSEA upon exchange of the magnitudes between X and Y, using only the computed DPs (circles). Plot 1-lower shows the local difference (X-Xrec, Y-Yrec). Plot II shows the sorted magnitudes (signatures) of the computed DPs for X (red) and Y (blue). This step is used for the exchange operation by linear mapping.

Fig. 7

I Upper-subplot: shows the time series X (600 samples, two periods, red) and Y (700 samples, three periods, blue). Middle sub-plot: shows the reconstructed Xrec (using DPs of X temporal index and DPs of Y magnitudes) versus the computed DPs of X for comparison (left) and vice-versa (right). Lower sub-plot: shows the local distance (point to point difference) between the originals and the reconstructed time series (left X-Xrec, right Y-Yrec). II Sorted magnitudes of the DPs (Signatures). Note that, in this case, X and Y are both portions of ECG taken from two different records. It may be noticed the ability of FANSEA to correctly align these time series and report the local difference in magnitude using only 35 and 43 DPs out of 600 and 700 samples (11.7 and 12.3 %). The correlation factors in this case are: corr (X, Xrec) = 0.9731; corr (Y, Yrec) = 0.9827 (color figure online)

$$ Corr\;(X,\;Y) = \frac{{cov\;(X,\;Y)^{2} }}{var\;(X) \times var\;(Y)} $$

(3)

In the following, we present the FANSEA method in a more formal way.

3.3 The FANSEA algorithm

Let X = (X ⁽ⁱ⁾₁ , X ⁽ⁱ⁾₂ ), i = 1…n, and Y = (Y ^(j)₁ , Y ^(j)₂ ), j = 1…m, be the original time series to match, where: X₁ is the temporal index of time series X, X₂ is the magnitude index of time series X, Y₁ is the temporal index of time series Y, Y₂ is the magnitude index of time series Y.

Let also sort-on-magnitude-value be a procedure that sorts any input time series on the magnitude coordinate; and sort-on-temporal-index the inverse procedure of sort-on-magnitude-value.

Let also FAN (X, ε) → Xs be the procedure that performs samples reduction on the given time series X curve by extraction of perceptually most significant points Xs to a given precision ε (sub-Sect. 3.1).

The FANSEA algorithm is then as follows:

• (a) Data reduction:

  • FAN (X, ε) → Xs;

  • FAN (Y, ε) → Ys

• (b) Sorting on Magnitude:

  • X′s = (X′s₁, X′s₂) ← sort-on-magnitude-value (Xs); where X′s₁ is the temporal-index (X′s), and X′s₂ is the magnitude-value (X′s).

  • Y′s = (Y′s₁, Y′s₂) ← sort-on-magnitude-value (Ys); where Y′s₁ is the temporal-index (Y’s), and Y’s₂ is the magnitude-Value (Y′s).

• (c) Normalization: If n ≠ m, then X′s₂ and Y′s₂ are normalized as described in step e.

• (d) Signature exchange: there is exchange of the magnitudes between the two reduced time series.

  • X′′ ← (X′s₁, Y′s₂): X′′ uses magnitudes of Y′s and time indexes of X′s.

  • Y′′ ← (Y′s₁, X′s₂): Y′′ uses magnitudes of X′s and time indexes of Y′s.

• (e) Reconstruction and matching: let Xs_Rec (resp. Ys_Rec) be the reconstructed time series as a result of reordering X′′ and Y′′ on their respective temporal index. Formally:

  • Xs_rec ← sort-on-temporal-index (X′′): The reconstructed time series of Xs;

  • Ys_rec ← sort-on-temporal-index (Y′′): The reconstructed time series of Ys;

  note here that since |Xs_rec| < |X| and |Ys_rec| < |Y|, the gaps between the DPs are filled by linear interpolation between successive such DPs.

• (f) Times series of different lengths: using the same notations above, and assuming that |X| = n ≠ |Y| = m, the comparison is performed by first applying a linear mapping between the two signatures X′s₂ and Y′s₂.

4 Applications

We apply the newly developed FANSEA method and the SEA method on electro-cardiogram (ECG) time series. Briefly, the ECG is a series of measurements taken at regular times that reflect the heart activity. A normal ECG is composed of three complexes in this order: P wave, QRS complex and T wave (Fig. 8). Comparison of this kind of data is a very complex problem since the ECG is a quasi-periodic signal intensively subject to local (physiological) variabilities and also to different kinds of noise. In all our applications, we used time series taken from the MIT-BIH ECG database. This is a public collection of records sampled at 360 Hz.

Fig. 8

Two ECG time series. Examples of P-wave, QRS complex and T-wave are indicated. These are the clinically significant basic patterns. Likewise, examples of periods in each time series are indicated. Physiologically, each period corresponds to one heart beat cycle

4.1 Application 1

This application illustrates the ability of FANSEA to match very complex similar time series much faster than SEA and using much less samples. Figure 9 Uppper shows two similar time series taken from the same record of MIT-BIH database (X at the very beginning; Y at the very end of record Rec. 102 of MIT-BIH database) and processed by SEA. Figure 9 Middle shows the plots of the original time series versus the respective reconstructed ones (X vs. Xrec and Y vs. Yrec). Notice that in both cases, the reconstructed time series are almost identical to the original ones, which demonstrates the ability of SEA to match similar time series, even with local variabilities and noise. Figure 9 Lower shows the local differences between the original time series and their respective reconstructed ones (X–Xrec and Y–Yrec). Notice here also that the differences are very small. In other words, using the SEA method, similar patterns allow near perfect alignments and render very small differences. This property could be exploited to recognize similar patterns of time series for different practical needs.

Fig. 9

Matching two similar time series (X, Y) using SEA. Results: mean correlation 0.995; processing time 1.22 s. Each reconstructed time series bear the color of the other time series to recall the exchange operation. So is the case for the local difference

On the numerical level, the processing time for SEA was 1.22 s and the mean correlation 0.995. Note that the correlation factor is very close to the perfect one value. This is a sign of the resemblance between X and Y. The correlation factor also could be used to consolidate the recognition problem of similar time series.

The next figure (Fig. 10) shows the processing of the same two time series of Fig. 9 using the FANSEA method. The plots are shown in the same fashion as in Fig. 9, except that in the middle subplot the original series were replaced by the dominant points extracted by the FAN method. The plots show almost the same alignments as in Fig. 9. That is, using FANSEA, similar patterns are also very well aligned and render small differences.

Fig. 10

Matching of the same time series in Fig. 9 using FANSEA. Results: mean correlation 0.987; mean data reduction 82.8 %; execution time 0.875 s. The DPs are plotted as small dots in the same color of the time series it belongs to. Each reconstructed time series bear the color of the other time series to recall the exchange operation. So is the case for the local difference

On the numerical level, the processing time was 0.875 s; the mean correlation was 0.989. Note here also that the correlation factor is very close to the one perfect value and the time used by FANSEA is roughly half that of SEA. On the other hand, the mean data reduction was 82.8 %. That is the data used by FANSEA to perform nearly as good as SEA is less than 20 % that used by SEA (100 %).

4.2 Application 2

This application illustrates the ability of FANSEA to discriminate between very complex non-similar time series in much less time and using a small percent of the original samples with respect to SEA. It is illustrated in Figs. 11, 12, where X = Rec. 102 and Y = Rec. 103 (hence, two different ECGs belonging to two different persons). Figure 11 shows results of processing these records with the SEA method. The middle plots clearly show severe reconstruction distortions (dashed plots), which reflects important mismatches between the two time series. The differences are plotted in the bottom subplots and confirm the mismatch. That is, using SEA, non-similar patterns align poorly and render important differences.

Fig. 11

Matching two different time series (X = rec. 102, Y = Rec. 103) using SEA. Results: processing time 1.532 s; mean correlation factor 0.950

Fig. 12

Matching the same two series in Fig. 11 with FANSEA. Results: processing time 0.765 s; mean correlation factor 0.871; mean data reduction 83.7 %

Numerically, the processing time was 1.532 s and the mean correlation factor was 0.950.

Figure 12 shows the processing of the same records in Fig. 11 using FANSEA. The plots are in the same fashion of Fig. 11 and are basically comparable to those in Fig. 11 (SEA results). In other words, the plots of Fig. 12 also reflect the mismatch between X and Y. That is, using FANSEA, non-similar patterns align poorly and render important differences.

On the numerical level, the processing time was 0.765 s; the mean correlation factor was 0.871 and the mean data reduction was 83.7 %. That is here also, FANSEA used less than 20 % of the original samples and roughly half the time of SEA to do comparable work.

4.3 Application 3

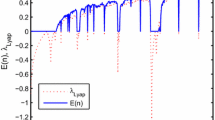
The aim of this application is to show the effect of the time series length on the numerical results of the two methods. For this purpose, record 102 of the MIT-BIH database has been chosen. The two methods (SEA and FANSEA) have then been applied to segments of lengths ranging from 500 samples to 50,000 samples (X at very beginning; Y at very end of record 102). The correlation factor, execution time for SEA and FANSEA and the data reduction for the FANSEA have been determined. These results are shown in Figs. 13, 14, 15. Figure 13 shows the correlation factor of FANSEA versus that of SEA. The figure shows that FANSEA performs practically as well as SEA in terms of the correlation factor. Figure 14 shows the execution time of FANSEA versus that of SEA in seconds. The figure clearly shows that FANSEA consumes much less time than SEA as the time series get longer. Figure 15 shows both the data reduction (squares) and the time reduction (stars) recorded for FANSEA with respect to SEA. This plot shows that the data reduction is always beyond 80 % and that the time reduction ranges from 35 % for short time series to 95 % for very long time series. Particularly, this application shows also the ability of FANSEA to match very long time series. Indeed, except SEA and its derivatives, existing time series matching techniques deal only with short (few hundred samples) to moderately long time series (few thousands of samples). The application shows the ability of FANSEA (and SEA) to match very long time series (tens of thousands of samples).

Fig. 13

Correlation factor as a function of time series length (samples) for SEA (squares) and FANSEA (stars)

Fig. 14

Execution time as a function of time series length (samples) for SEA (squares) and FANSEA (stars)

Fig. 15

Percentage of data reduction (squares) and time reduction (stars) recorded by FANSEA with respect to SEA as a function of time series length (samples)

Note that all experiments were performed on a machine with 2.4 GHz processor and 256 Mega Byte main memory, under MatLab7 programming environment.

5 Discussion

The different applications show globally the ability of the proposed FANSEA to match very complex time series (class c). They also show the ability of FANSEA to deal with very long time series, which in the author’s believe is another distinctive power that must be reported. Needless is to say that, the SEA method is also characterized by these two last abilities, since FANSEA is an enhancement to the SEA method. Indeed, in all applications, the qualitative results (plots) and numerical results (correlation factor) show that the FANSEA method performs practically as good as the SEA method. Precisely, like SEA, it is able to correctly align very complex time series and give the opportunity to ‘recognize’ those that are similar and the opportunity to ‘discriminate’ between those that are different. However, FANSEA is much faster. It consumes much less time than SEA to do the same work. In addition, FANSEA uses globally speaking less than 20 % of the original samples to do the same job of the SEA method. These last two properties grant the FANSEA method the efficiency that enables it to be a much better candidate for searching, querying and mining of large scale time series databases, where data reduction and speed of process are a must. In general, it is useful in applications where there is need for searching/recognizing specific time series based on their shapes. For instance, economic, medical and industrial signals are typical data where such need is expressed by experts in their respective fields.

Quantifying the complexity of the match by a metric is also an interesting problem to mention. For this purpose, we suggest the edit-distance measure [19] as a metric to render the degree of complexity of matching time series s1 and s2. In other words, the complexity of the case to match would be handled as a string to string correction problem. As well known, the edit-distance between two strings s1 and s2 is defined as the minimal number of (weighted) operations among the set {insertion, deletion, substitution} that are necessary to transform s1 into s2. If we consider the two time series as two strings s1 and s2 defined over an appropriate alphabet, the metric we propose would be: edit-distance (s1, s2). This metric is capable of handling the following decisive information regarding the match (s1, s2):

• (a) Difference in the number of periods: there is more effort needed to transform s1 into s2 in case the two time series have a different number of periods (there are more deletions/insertions/substitutions than in the case where the number of periods is the same).

• (b) Difference in length of the two time series: there is also more effort needed to transform s1 into s2 in case the two time series have different lengths (there are also more deletions/insertions/substitutions than in the case where the lengths are equal).

• (c) The amount of phase-shift between the two time series to match: the more the two time series are shifted one with respect to the other, the more there is effort to transform s1 into s2.

• (d) The degree of variability: here also, the more there are variations within the periods, the more effort is needed to transform s1 into s2.

It might also be of interest to mention that ASEAL [26] is another accelerated version of SEA that was previously published. A thorough comparison of FANSEA to ASEAL is, evidently, an important and interesting issue. However, this study is focused on the promotion of FANSEA as an accelerated version of SEA. But globally, and according to the findings in [26], the ASEAL method attained data savings up to 90 %, and time savings up to 97 %. For FANSEA, the savings in data were up to 80 % and the time reductions up to 95 %. ASEAL seems then to be slightly more efficient than FANSEA. However, this conclusion must be considered with caution, since the two methods should be directly and intensively compared using the same data. Furthermore, the experimentation data has to be significantly rich and representing the most usual situations. This can only be performed in a separate study.

6 Conclusion

We have proposed a new time series matching technique (FANSEA) that is based on combination of a data reduction technique (FAN) with the previously published time series matching method SEA. The combination objectives were to obtain an enhanced time series matching method with the same abilities of SEA in recognizing similar time series and discriminating between non-similar time series and that would consume less data and time. The illustrations clearly show that our objectives were attained. As well known, processes acceleration can be achieved, mainly, through hardware and algorithmic (complexity reduction). The study clearly showed that data reduction can also be a very good acceleration paradigm.

A distinctive quality of the method is that it targets specifically very complex time series (quasi periodic, phase-shifted, with different number of periods, different lengths and possibly with time/magnitude axis shift/scaling). The study illustrated the complexity property of the matching through qualitative descriptions. Quantitative measures, like the edit-distance, should be studied in future works to better express and handle the complexity aspect of the time series to match.

For future works, we plan also to explore possibilities of integrating the novel method in specific application platforms. Other data reduction techniques could also be considered for possible combination with SEA and perhaps with other time series alignment methods. The aim is to propose always much more efficient time series matching methods for different applications and needs.