Keywords

1 Introduction

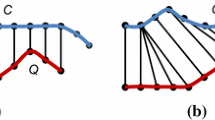
Joining two time series on subsequence correlation is considered as a basic problem in time series data mining and appears in many practical applications such as entertainment, meteorology, economy, finance, medicine, and engineering [2]. Assume that we have two time series representing the runoffs at the two measurement stations in Mekong River, Vietnam as in Fig. 1. Meteorologists may concern about in what periods the runoffs of these two stations (in pink curve and dotted curve in Fig. 1) are similar. Subsequence join can bring out some useful information about the runoffs at different stations in the same river by finding subsequences which are most correlated based on some distance function (see the red (bold) subsequence in Fig. 1). Moreover, this approach can be extended easily to find all pairs of subsequences from the two time series that are considered similar. Thanks to these resultant subsequences, meteorologists can predict about the runoff of the river in future.

Fig. 1.
figure 1

Two time series of the runoff at the two stations in Mekong River, Vietnam. (Color figure online)

Full size image

The subsequence join over time series can be viewed in different aspects. The first view is joining two time series based on their timestamps [8]. This approach does not carry out any similarity comparison because it just concerns about the high availability of timestamps and ignores the content of time series data. The second view of subsequence join is based on a nested-loop algorithm and some distance functions like Euclidian distance or Dynamic Time Warping [6, 7]. This joining approach returns all pairs of subsequences drawn from two time series that satisfy a given similarity threshold. This approach has some disadvantages such as time consumption because distance function is called many times over a lot of iterations. Moreover, the threshold for determining the resulting sets needs to be given by user. To reduce the runtime for nested-loop algorithm, some works tend to approximately estimate the similarity between two time series by dividing time series into segments. In this approach, Y. Lin et al. [6] introduced solutions for joining two time series based on a non-uniform segmentation and a similarity function over a feature-set. Their method is not only difficult to implement but also requires high computational complexity, especially for large time series data. To avoid these drawbacks, the work in [7] proposed joining based on important extreme points to segment time series. And then, the authors applied Dynamic Time Warping function to calculate the distance between two subsequences. The resulting sets are determined based on a threshold given from user. Although this method executes very fast, it may suffer some false dismissals because it ignores some data points when shifting the sliding window several data points at a time.

A recent work on subsequence join proposed by Mueen et al. in 2014 [2] can find the exact correlated subsequence. Mueen et al. introduced an exhaustive searching method, JOCOR, for discovering the most correlated subsequence based on maximizing Pearson’s correlation coefficient in two given time series. Although the authors incorporated several speeding-up techniques to reduce the complexity from O(n 4) to O(n 2 lgn), where n is the length of two time series, the runtime of JOCOR is still unacceptable even for many time series datasets with moderate size. For example, running JOCOR on the input time series with length of 40000 data points will take more than 12 days to find the resulting subsequence. Furthermore, in [2], Mueen et al. also proposed an approximate method, α-approximate-JOCOR. This algorithm finds the nearly exact correlation subsequence by assigning the step size a value greater than one in each iteration depending on datasets. A natural question arises as to what reasonable value for step size. This is like a blind search.

To improve the time efficiency of JOCOR algorithm, in this work, our proposed method combines PAA dimensionality reduction, SAX discretization and an efficient Longest Common Substring algorithm to find the candidates of the most correlated subsequence before applying the JOCOR algorithm to post-process the candidates. The preprocessing helps to speed-up the process of finding the most correlated subsequence without causing any false dismissals. The experiment results demonstrate that our proposed method not only is more accurate than α-approximate-JOCOR but also achieves the high accuracy, even 100%, when being compared to exact JOCOR while the time efficiency is much better.

2 Background

2.1 Basic Concepts

Definition 1.

A time series T = t 1 , t 2 ,…, t n is a sequence of n data points measured at equal periods, where n is the length of the time series. For most applications, each data point is usually represented by a real value.

Definition 2.

Given a time series T = t 1 , t 2 ,…, t n of length n, a subsequence T[i: i + m−1] = t i , t i+1 ,…, t i+m−1 is a continuous subsequence of T, starting at position i and length m (m ≤ n).

This work aims to approximately join two time series T 1 and T 2 of length n 1 and n 2 , respectively. The problem of time series join was defined by Mueen et al. [2] which is described as follows.

Problem 1.

(Max-Correlation Join ): Given two time series T 1 and T 2 of length n 1 and n 2 , respectively (assume n 1 ≥ n 2 ), find the most correlated subsequences of T 1 and T 2 with length ≥ minlength.

The definition for Problem 1 can be extended to find α-Approximate join.

Problem 2.

(α-Approximate Join ): Given two time series T 1 and T 2 of length n 1 and n 2 , respectively, find the subsequences of T 1 and T 2 with length ≥ minlength such that the correlation between the subsequences is within α of the most correlated segments.

When joining two time series, we refer to finding the most correlated subsequence by calculating Pearson’s correlation coefficient. The correlation coefficient is defined as follows.

$$ C(x,y) = \frac{1}{n}\sum\limits_{i = 0}^{n - 1} {\left( {\frac{{x_{i} - \mu_{x} }}{{\sigma_{x} }}} \right)} \left( {\frac{{y_{i} - \mu_{y} }}{{\sigma_{y} }}} \right) $$
(1)

where x and y are two given time series of equal length n, with average values μ x and μ y , and standard deviations σ x and σ y , respectively.

The value of Pearson’s correlation coefficient ranges in [−1, 1]. Besides, the z-normalized Euclidean distance is also a commonly used measure in time series data mining. The distance between two time series X = x 1 , x 2 ,…, x n and Y = y 1 , y 2 ,…, y n with the same length n is calculated by:

$$ d(x,y) = \sqrt {\sum\limits_{i = 1}^{n} {(\hat{x}_{i} - \hat{y}_{i} )^{2} } } $$
(2)

where \( \hat{x}_{i} = \frac{1}{{\sigma_{x} }}(x_{i} - \mu_{x} ) \) and \( \hat{y}_{i} = \frac{1}{{\sigma_{y} }}(y_{i} - \mu_{y} ) \)

Because we just pay attention to maximizing positive correlations and ignore the negatively correlated subsequences, we can take advantage of the relationship between Euclidian distance and positive correlation as follows.

$$ C(x,y) = 1 - \frac{{dist^{2} (x,y)}}{2n} $$
(3)

In this work, we will take advantage of statistics for computing correlation coefficient as follows.

$$ C(x,y) = \frac{{\sum {xy - n\mu_{x} \mu_{y} } }}{{n\sigma_{x} \sigma_{y} }} $$
(4)
$$ d(x,y) = \sqrt {2n(1 - C(x,y))} $$
(5)

This approach brings us two benefits. Firstly, the algorithm just takes one pass to compute all of these statistic variables. Secondly, it enables us to reuse computations and reduce the amortized time complexity to constant instead of linear [2]. In this paper, the above formulas will be used for computing correlation coefficient and z-normalized Euclidian distance between two subsequences.

2.2 Symbolic Aggregate Approximation (SAX)

A time series T = t 1…. t n of length n can be represented in a reduced w-dimensional space as another time series D = d 1…d w by segmenting T into w equally-sized segments and then replacing each segment by its mean value d i . This dimensionality reduction technique is called Piecewise Aggregate Approximation (PAA) [4]. After this step, the time series D is transformed into a symbolic sequence A = a 1…a w in which each real value d i is mapped to a symbol a i through a table look-up. The lookup table contains the breakpoints that divide a Gaussian distribution in an arbitrary number (from 3 to 10) of equi-probable regions. This discretization is called Symbolic Aggregate Approximation (SAX) [5] which is based on the assumption that the reduced time series have a Gaussian distribution.

Given two time series Q and C of the same length n, we transform the original time series into PAA representations, \( Q^{\prime} \) and \( C^{\prime} \), we can define lower bounding approximation of the Euclidean distance between the original time series by:

$$ DR\left( {Q^{\prime}, \, C^{\prime}} \right) = \sqrt {\frac{n}{w}} \sqrt {\sum\limits_{i = 1}^{w} {\mathop {(q^{\prime}_{i} - c^{\prime}_{i} )}\nolimits^{2} } } $$
(6)

When we transform further the data into SAX representations, i.e. two symbolic strings \( Q^{\prime\prime} \) and \( C^{\prime\prime} \), we can define a MINDIST function that returns the minimum distance between the original time series of two words:

$$ MINDIST(Q^{\prime\prime},C^{\prime\prime}) = \sqrt {\frac{n}{w}} \sqrt {\sum\limits_{i = 1}^{w} {(dist(q_{i}^{\prime\prime} ,c_{i}^{\prime\prime} )^{2} } } $$
(7)

The dist() function can be implemented using a table lookup as shown in Table 1. This table is for an alphabet a = 4. The distance between two symbols can be read off by examining the corresponding row and column. For example, dist(a, b) = 0 and dist(a, c) = 0.67.

Table 1. A look-up table used by the MINDIST function.
Full size table

3 The Proposed Method

In Fig. 2 we presents our proposed method for joining two time series based on the Pearson’s correlation coefficients of their subsequences. The process of time series join consists of two main phases: (1) reducing the dimensionality of the two time series, discretizing the reduced time series and (2) joining the discretized time series based on a Longest Common Substring (LCS) algorithm. We will explain these two main phases.

Fig. 2.
figure 2

Outline of LCS-JOCOR.

Full size image

3.1 Phase 1: Reducing the Dimensionality and Discretizing the Time Series

This phase consists of the following steps.

Step 1: :

Two original time series will be normalized by z-normalization. This normalization has two advantages. It helps our proposed method minimize the effect of noise and makes the whole dataset to fluctuate around x-axis while reserving the shape of time series.

Step 2: :

After being normalized, the time series will be dimensionally reduced by Piecewise Aggregate Approximation (PAA) transformation. PAA is chosen in this work since it is an effective and very simple dimensionality reduction technique for time series. In this work, the PAA compression rate will range from 1/20 to 1/5 depending on each type of datasets.

Step 3: :

The z-normalized PAA representations of the two time series are mapped into two strings of characters by applying Symbolic Aggregate Approximation (SAX) discretization. Thus, we have transformed our original problem of joining two long time series based on their most correlated subsequence into the problem of finding the Longest Common Substring (LCS) of two given strings.

In the next subsection, we will describe how to find the LCS of two strings efficiently.

3.2 Phase 2: Joining Two Time Series based on LCS Algorithm

This phase consists of the following steps.

Step 1: :

After discretizing two original time series, we get two strings, S 1 corresponding to time series T 1 and S 2 corresponding to time series T 2 . We apply the algorithm of finding the Longest Common Substring (LCS) of the two strings S 1 and S 2 . Our LCS algorithm is an iterative approach which is based on a level-wise search. The main idea of our LCS algorithm is that the k-character common substrings are used to explore (k + 1)-character common substrings. The algorithm is described as follows:

  1. (i)

    Find all unique single character strings in the first string S 1 .

  2. (ii)

    Find the positions of each of these single character strings in the second string S 2 .

  3. (iii)

    Then check if we can extend any of these single characters into two (or longer) character strings that are in common between the two strings. Find the positions of all these common strings in the second string S2.

    Repeat (iii) until we can not find any longer common substrings in the two strings.

Note that in the above algorithm, we introduce two versions of finding LCS: exact matching and approximate matching. Exact matching simply considers the operator ‘=’ between two characters. In contrast, approximate matching checks whether two compared characters equal or not depending on MINDIST(.) function introduced at Subsect. 2.2.

Step 2: :

After executing the LCS algorithm successfully, we will have two resulting substrings, one for exact matching and one for approximate matching. These longest common substrings will be mapped back to get the corresponding subsequences in the original time series. These subsequences are potentially the most correlated subsequences when compared to other ones in the whole time series.

Step 3: :

At the final step, we will apply JOCOR algorithm to calculate the Pearson’s correlation coefficient and find the most correlated subsequence among the candidate subsequences found in Step 2. The main idea of JOCOR is to reuse the sufficient statistics for overlapping correlation computation and then prune unnecessary correlation computation admissibly. The JOCOR algorithm is described in details in [3].

4 Experimental Evaluation

We implemented all the methods in MATLAB and carried out the experiments on an Intel(R) Core(TM) i7-4790, 3.6 GHz, 8 GB RAM PC. We will conduct two experiments. First, we compare the performance of our proposed method to that of exact JOCOR on three measurements: the correlation coefficient of resulting subsequence, the runtime of algorithm and the length of the resulting subsequence. Second, we compare the performance of our proposed method to that of α-approximate-JOCOR also on the three above measurements.

4.1 Datasets

Our experiments were conducted over the datasets from the UCR Time Series Data Mining archive [1] and from [2]. There are 10 datasets used in these experiments. The names and lengths of 10 datasets are as following: Power (29,931 data points), Koski-ECG (144,002 data points), Chromosome (999,541 data points), Stock (2,119,415 data points), EEG (10,957,312 data points), Random Walks (RW2 - 1,600,002 data points), Ratbp (1,296,000 data points), LFS6 (180,214 data points), LightCurve (8,192,002 data points), and Temperature (2,324,134 data points). The datasets may be categorized into two types. The first type is that two long time series are from same source. In this case, we divide the time series into two equal halves. The first subseries will be T 1 . The second one will be T 2 . The second type is that two time series are from different sources. In this case, time series data downloaded from UCR will be T 1 . Basing on T 1 , we randomly generate the synthetic dataset T 2 by applying the following rule:

$$ x_{i} = x_{i - 1} \pm |x_{i - 1} - \varepsilon |\;\;\;\;\;{\text{ where}}\;\varepsilon = \frac{{\sum\nolimits_{i = 1}^{6} {x_{i} } }}{6} $$

In the above formula, + or – is determined by a random process. Time series data T 2 is generated after the correspondent dataset has been normalized; therefore, there is no effect of noise in T 2 .

4.2 LCS-JOCOR Versus Exact JOCOR

When operating some task on very long time series, the response time is one of the most challenging factors for researchers. In this experiment, we plan to compare the performance of our proposed method with that of exact JOCOR. The performance of each method is evaluated by three measurements: the maximum correlation coefficient of resulting subsequence, the runtime of the method, and the length of the resulting subsequence. Because the lengths of the resulting subsequences of the two methods are nearly similar, we exclude them from our comparison.

From Table 2, with datasets Stock, Koski-ECG and Chromosome, our LCS-JOCOR produced the same maximum correlation values as the exact JOCOR. In average of all experiments, our maximum correlation coefficients reach 95% of JOCOR’s results. Regarding the runtime, our method outperforms JOCOR for eight out of ten datasets. Especially, with RW2 dataset, in the experiment with 15,000 data points, the runtime of our method was more than 15,000 times faster than that of JOCOR. The differences between the two runtimes of LCS-JOCOR and JOCOR are wider when the length of the datasets increases. Nevertheless, with Stock and LightCurve datasets, JOCOR runs slightly faster than our method. This is because the time series are undergone several transformations without being really preprocessed.

Table 2. Experimental results of LCS-JOCOR and JOCOR over 7 datasets (RT: runtime in secs; MC: maximum correlation).
Full size table

4.3 LCS-JOCOR Versus α-approximate-JOCOR

In this experiment, we compare the performances of LCS-JOCOR to that of α-approximate-JOCOR introduced in [2]. We recorded three measurements: the length of the resulting subsequence (Length), the runtime of algorithm (RT), and the maximum correlation coefficient (MC). Firstly, we examined the performances on 8,000 data points with the same setting as in [2]. For α-approximate-JOCOR, we conducted the experiments at different α values (2, 8, 16, 32, 64), and then we took average of each parameter. Table 3 presents experimental results for comparison.

Table 3. Experimental results of LCS-JOCOR and α-approximate-JOCOR over 7 datasets.
Full size table

With Power and Lightcurve datasets, LCS-JOCOR outperformed α-approximate-JOCOR in all three measures, especially the runtime of LCS-JOCOR is remarkably smaller. With datasets RW2, RATBP, and EEG, our method achieved the results approximately equivalent to α-approximate-JOCOR. Our method did not perform well on Chromosome and Stock datasets where we obtained the same MC but with greater runtime and shorter length; however, the differences are insignificant.

In general, the results show that the runtime of LCS-JOCOR is smaller than that of α-approximate-JOCOR for most datasets, the length of resulting subsequence and the value of Pearson’s correlation coefficient is nearly equivalent. This is because LCS-JOCOR exploits dimensionality reduction and discretization to preprocess the two time series before applying the efficient LCS algorithm to find the candidates of the most correlated subsequence between the two time series while α-approximate-JOCOR jumps k data points in each iteration without considering the characteristic features of the two time series.

5 Conclusion and Future works

Subsequence join provides useful information about the synchronization of the time series. Solving method to the problem can be used as an analysis tool for several domains. In this paper, we proposed a new method, called LCS-JOCOR, to find approximate correlated subsequence of two time series with acceptable time efficiency. The experimental results show that our method runs faster than JOCOR and α-approximate-JOCOR while the accuracy of our approach is nearly the same as that of exact JOCOR, and higher than that of the α-approximate-JOCOR. We attribute the high performance of our method to the use of PAA to reduce the dimensionality of the two time series and the LCS algorithm to speed up the finding of the most correlated subsequence. As for future work, we intend to apply some more efficient LCS algorithm which is based on suffix tree [9] to our LCS-JOCOR in order to improve further its time efficiency.