1 Introduction

Clustering analysis is an important tool for image processing, remote sensing, data mining, biology, and pattern recognition [1, 2]. The idea of ensemble can be found in many fields [3–5]. Cluster ensembles have been introduced as a more accurate alternative to individual clustering algorithms [6].

Two major themes in ensembles are combination rules of the ensemble votes and the diversity of clusterers. Firstly, we consider how to build diverse yet accurate individual clusterers, or to select clustering algorithms for the ensemble. Various methods have been proposed for getting the diversity of clusterers, such as random initialization of the clustering algorithm, resampling the data [7, 8], resampling the features of the data [8], etc. Finally, we need to know how to combine the outputs of multiple clusterers, or to construct a consensus function. There are several approaches for constructing consensus functions, such as the relabeling method [7–10], the feature-based approach [11, 12], the hyper-graph approach [8] and others.

In [12], a consensus function based on quadratic mutual information (QMI) was presented and reduced to the k-means clustering in the space of specially transformed cluster labels. Here we focus on these label attributes instead of some transformed partition attributes.

In this paper, a framework for cascaded cluster ensembles is proposed, in which there are two layers of clustering. The first layer deals with the diversity of clustering, and generates different partitions. In doing so, the samples in input space are mapped into labeled samples in a label attribute space whose dimensionality equals the ensemble size. In the second layer clustering, we choose a clustering algorithm as the consensus function. In other words, a combined partition is given by using the clustering algorithm on these labeled samples instead of input samples. We also give some reduced clustering algorithms, e.g., k-means, spectral, and hierarchical single-linkage, for the second layer clustering. We have two main contributions. One is that a framework of cascaded cluster ensembles is presented. The other is that some traditional clustering algorithms are reduced and adapted for re-clustering.

The rest of this paper is organized as follows. In Sect. 2, we review the related work on consensus functions, such as relabeling methods and hypergraph methods. Section 3 presents the framework for cascaded cluster ensembles. We also discuss reduced clustering algorithms, such as k-means, spectral, hierarchical single-linkage algorithms, for the second layer clustering. We apply cascaded cluster ensembles to toy and UCI data sets in Sect. 4 and conclude our paper in Sect. 5.

2 Related work

Notation. Let the set of N unlabeled samples be \(\mathcal{X}=\{{\bf x}_{1},\ldots,{\bf x}_{N}\},\) where \({\mathcal{X}\in \mathbb{R}^d, }\) and d is the dimensionality of sample space. Assume that there are L partitions \(\mathcal{P}=\{P_{1},\ldots,P_{L}\}\) for \(\mathcal {X}, \) where L is the ensemble size or the number of clusterers, and \({P_{i}\in \mathbb{R}^N}\) is the label vector of \(\mathcal{X}\) obtained by the i-th individual clusterer. Labels take value from 1 to k, where k is the number of clusters. L clusterers give a set of labels for each sample \({\bf x}_{i}, i=1,\ldots,N\)

$$ {\mathbf x}_{i}\rightarrow {\mathbf y}_{i}=\{P_{1}({\mathbf x}_{i}),\ldots,P_{L}({\mathbf x}_{i})\} $$
(1)

where P j (x i ) denotes a label assigned to x i by the j-th clusterer, and y i called labeled samples corresponding to \({\mathbf x}_{i}\) is all L labels assigned to \({\mathbf x}_{i}\) by all individual clusterers. Denote \(\mathcal{Y}=\{{\mathbf y}_{1},\ldots,{\mathbf y}_{N}\}\) be a set of labeled samples in a label attribute space \({\mathbb{Y}. }\)

We want to give \({\mathbf x}_{i}\) an optimal label y * i or \(P^*({\mathbf x}_{i}). \) The goal is to find a combined partition P * by using a consensus function. There are many consensus functions available, which are briefly described as follows.

2.1 Relabeling methods

These methods are also called direct approaches or voting approaches, such as two bagged clustering procedures in [10], path based clustering in [9], bagging-based selective cluster ensemble (BBSCE) in [7].

Assume that the set of L partitions \(\mathcal{P}\) is generated. Since no assumption is made about the correspondence between the labels produced by individual clusterers, the label \(P_{j}({\mathbf x}_{i})\) maybe differs from \(P_{l}({\mathbf x}_{i}). \) Relabeling method is firstly to relabel partitions according to a fixed reference partition which can be selected from these partitions. The complexity of relabeling two partitions is O(k 3) if the Hungarian method is employed. The total complexity of relabeling process should be O((L − 1)k 3). Finally relabeling method is to find the best partition P* by some combination rules such as the voting rule.

In [7], the selective weighted voting rule is presented for getting the best partition. The mutual information between the reference partition and other partitions is taken as the weights of these partitions. If the weights are larger than the average weight, the corresponding partitions are used to determine a single consensus clustering.

2.2 Hypergraph methods

These methods are to construct a hypergraph representing partitions from the clusterers and cutting the redundant edges. A hypergraph contains of vertices and hyperedges. Vertices denote samples in \(\mathcal{X}\) and each hyperedge describes a set of samples belonging to the same cluster. Here, the cluster ensemble problem is casted into an optimization problem of finding the k-way minimum-cut of a hypergraph.

Strehl and Ghosh [8] proposed three different consensus functions for ensembles. The cluster-based similarity partitioning algorithm (CSPA) generates a graph from a similarity matrix and reclusters it using the similarity-based clustering algorithms. The hypergraph partitioning algorithm (HGPA) represents each cluster by a hyperedge in a graph and uses minimal cut algorithms to find good hypergraph partitions. The meta-clustering algorithm (MCLA) is to group and collapse related hyperedges and assign each sample to the collapsed hyperedge in which it shares most strongly. By doing so, MCLA can determine soft cluster-membership values for each sample. By using CSPA and MCLA as consensus functions, a new selective clustering ensemble algorithm was proposed in [13].

The computational complexity of CSPA, HGPA and MCLA are O(kN 2 L), O(kNL) and O(k 2 NL 2), respectively.

2.3 Feature-based methods

A unified representation of multiple clusterings was given in [11] and [12]. The outputs from the multiple clusterers are treated as L new features. The next problem is how to get a clustering by using these new features. A probabilistic model consensus using a finite mixture of multinominal distribution was proposed in [11] and [12]. The consensus problem is casted into the maximum-likelihood problem which is solved by the EM algorithm. A consensus function based on quadratic mutual information (QMI) was also presented and reduced to the k-means clustering in the space of specially transformed cluster labels.

2.4 Pairwise methods

In pairwise methods, consensus functions operate on the co-association matrix which can be taken as a similarity matrix for the data points. A voting-k-means algorithm was proposed in [14] where the combination of partitions is performed by transforming data partitions into a co-association matrix. The data points should be linked into a clusters if their corresponding co-association values exceed a given threshold. Fred and Jain [15] adopted a hierarchical clustering to the co-association matrix instead of a fixed threshold.

3 Cascaded cluster ensembles

In this section, we discuss cascaded cluster ensembles. Here are two main contributions. One is to give a framework of cascaded cluster ensembles. The other is to propose reduced versions for some traditional clustering algorithms and apply them to re-clustering.

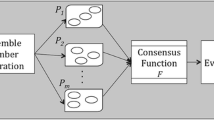
Figure 1 gives the framework of cascaded cluster ensembles. There are L individual clusterers in the first layer clustering. The goal of the first layer is to generate different partitions, or \(P_1,P_2,\ldots,P_L. \) In the second layer clustering, different partitions are combined to an optimal partition by using some clustering algorithm, such as k-means.

Fig. 1
figure 1

Framework of cascaded ensembles

Full size image

3.1 First layer clustering

In this layer, we consider about the diversity of clustering, or generating different partitions. There are several methods available for getting diverse partitions:

  1. 1.

    Using different clustering algorithms such as k-means, fuzzy k-means, mixture of Gaussian, graph partitioning based, statistical mechanics based, etc., [8].

  2. 2.

    Using randomness or different parameters of some algorithms, e.g., initialization and various values of k for k-means clustering algorithm [6, 15, 16].

  3. 3.

    Using different data subsets, such as bootstrap samples [7, 8], and feature subsets [8, 17, 18].

The only constraint in our frame is that k is fixed to a constant. \(\mathcal{X}_{1}, \mathcal{X}_{2}, \ldots,\mathcal{X}_{L}, \) the inputs of the first layer can be different data subsets if the same type of individual clusterers are used, and be the same data set if the different types of individual clusterers are exploited. The outputs of the first layer are different partitions \(P_1, P_2, \ldots, P_L. \)

3.2 Second layer clustering

From Fig. 1, we can see that the inputs of the second layer clustering are \(P_1, P_2, \ldots, P_L\) which are called partition attributes. For a sample \({\mathbf x}_i, \) its original attributes is itself \({\mathbf x}_i, \) and its label attributes \({\mathbf y}_i\) can be expressed as (1). Note that the label attributes are all represented by integers, say \(1, \ldots, k. \) An optimal partition P* can be obtained by using any clustering algorithm on these labeled samples. Here the consensus function is a clusterer.

In the label attribute space, we can use different clustering algorithm to handle the second layer clustering problem, including k-means, fuzzy k-means, spectral, hierarchical clustering, and so on.

Firstly, we illustrate why we consider a clustering algorithm as the consensus function by using a simple example. Suppose that there are seven points belonging to three classes. Three individual clusterers are used to generate three different partitions shown in the left hand of Table 1. Inspection of these label attributes for seven samples reveals that the label attributes of \({\mathbf x}_{1}, {\mathbf x}_{2}\) and \({\mathbf x}_{3}\) are identical, \({\mathbf x}_{4}\) and \({\mathbf x}_{5}\) are also identical, and \({\mathbf x}_{6}\) and \({\mathbf x}_{7}\) are some different. Given that centers of three classes be (2, 3, 1)T, (1, 2, 3)T and (3, 1, 2)T, respectively, the right hand of Table 1 shows the Hamming distance between samples to these centers. In information theory, the Hamming distance between two strings (or vector) of equal length is the number of positions for which the corresponding symbols (or figures) are different. By simply observing these Hamming distances, we can sure that \({\mathbf x}_{1}, \) \({\mathbf x}_{2}\) and \({\mathbf x}_{3}\) belong to the same cluster, \({\mathbf x}_{4}\) and \({\mathbf x}_{5}\) belong to another cluster, and \({\mathbf x}_{6}\) and \({\mathbf x}_{7}\) are in the same cluster.

Table 1 Illustrative example problem with k = 3, l = 7, L = 3
Full size table

From the example, we can see that there still exist similarities in points belonging to the same cluster even if \(P_{1}, P_{2}, \ldots, P_L\) are different partitions generated by L individual clusterers. Therefore, we can directly adopt this information to combine L partitions using a clusterer. Although [12] uses the k-means clustering algorithm, the data clustered locate in a transformed spaces instead of the label attribute space.

Next we discuss how to use these clustering algorithms in the second layer clustering. Note that most of label attributes are identical, such as \({\mathbf y}_1, {\mathbf{y}}_2\) and \({\mathbf{y}}_3\) in our example. Hence, we do not need process all labeled samples. So the first step that we need do is to select all distinct labeled samples from the set \(\mathcal{Y}.\) Let \(\overline{\mathcal{Y}}=\left\{\overline{{\mathbf y}}_j\right\}_{i=1}^{n}\) be the set of distinct labeled samples, where n < N. The Hamming distance between \(\overline{\mathbf{y}}_i\) and \(\overline{\bf{y}}_j\) is at least 1. In the following, some detail clustering algorithms are discussed.

3.2.1 Reduced k-means algorithm

In the label space, k-means clustering algorithm with the Hamming distance metric is one simple choice. It is well known, the k-means clustering algorithm is sensitive to initialization, which could be used in the first layer clustering for increasing diversity but should be avoided in the second layer clustering. Thus it is necessary to consider the selection of initial centers for k-means algorithm. Now \(\overline{\mathcal{Y}}\) is the candidate set for selecting the initial centers \(\{{\mathbf c}_i\}_{i=1}^{k}. \) After we get these centers, we can directly compute the Hamming distance between a labeled sample y j to those centers. Once we find that the minimal Hamming distance is that between \({\mathbf{c}}_m\) and \({\mathbf{y}}_j, \) the corresponding label m should be assigned to the sample \({\mathbf{x}}_j.\) The reduced k-means clustering used in the second layer clustering is shown in Algorithm 1.

3.2.2 Reduced spectral clustering

Remember that all attributes of labeled samples are only expressed by positive integers. We compute the Hamming distance matrix H between these distinct labeled samples. Namely,

$$ {\mathbf{H}}_{ij}=h({\overline{\mathbf{y}}}_i,{\overline{{\mathbf y}}}_j),\quad i, j=1,\ldots,n $$
(2)

where \(h(\cdot,\cdot)\) denotes the Hamming distance function, and \({\mathbf H}\) is a symmetrical matrix and can be taken as a dissimilarity matrix. Return to the above example, Table 2 shows the Hamming distances between four distinct labeled samples. We can see that the maximum Hamming distance is three which equals the ensemble size. The reduced spectral clustering used in the second layer clustering is shown in Algorithm 2.

Table 2 Illustrative example problem with k = 3, ℓ = 7, L = 3
Full size table

3.2.3 Reduced hierarchical clustering

Hierarchical clustering creates a hierarchy of clusters for which may be represented in a tree structure called a dendrogram. The root of the tree consists of a single cluster containing all samples, and the leaves correspond to individual samples. According to the definition of the distance between one cluster and another cluster, there have three different hierarchical clustering algorithms, such as single-linkage, complete-linkage and average-linkage clustering. Here we take the single-linkage clustering as an example, and show its reduced version in Algorithm 3.

4 Simulation

In order to validate the performance of cascaded cluster ensembles, we perform experiments on two toy [12] and seven UCI data sets [19] described in Table 3, where true natural clusters are known, and compare them with five other methods for cluster ensembles.

Table 3 Description of data sets used in experiments
Full size table

The performance criterion is the same as [12]. The performance of all methods is evaluated by matching the optimal partition P* with the known partitions of data sets and expressed as the clustering error. Table 3 also gives the average clustering errors of these data sets, which are obtained by running 30 k-means clustering algorithms independently.

All numerical experiments were performed on the personal computer with a 1.8 GHz Pentium III and 1 G bytes of memory. This computer runs on Windows XP, with Matlab 7.1 installed.

4.1 Selection of algorithms and their parameters

The k-means clustering is used to generate the different partitions in the first layer clustering. The diversity of the partitions is obtained by using different data subsets, including bootstrap samples and feature subsets. The following parameters for the first layer are especially important.

  • k: the number of clusters. We set it as the same as the true class number.

  • L: the ensemble size or the number of individual clusterers. Its value varies in the set \([5,10,15,\ldots,50]. \)

  • r: the bootstrap sampling ratio (the ratio of the bootstrap sample number to the total sample number N), or the feature sampling ratio (the ratio of the feature number of subset to the whole feature number d). r takes only three values, or 25, 50 and 75%.

After we get different partitions, five other consensus functions besides clusterer consensus functions in cascaded cluster ensembles are adopted, including BBSCE, CSPA, MCLA, the EM and QMI algorithms. BBSCE in [7] is a relabeling method. The code of CSPA and MCLA in [8] is available at http://www.strehl.co. The code of the EM and QMI algorithms was provided by Dr. A. Topchy. In cascaded cluster ensembles, we choose the k-means, spectral, and hierarchical single-linkage (H-single) and complete-linkage (H-complete) clusterers as consensus functions, respectively. Thus there are nine consensus functions. In the second layer clustering, k takes the same value as that in the first layer clustering.

4.2 Experiments with bootstrap sampling method

In this part, the diversity of the partitions in the first layer clustering is obtained by using the bootstrap sampling method which are obtained by randomly sampling with replacement from the original data set. Here r denotes the bootstrap sampling ratio. The number of samples with whole features for individual clusterers in the first layer clustering takes value from \(\left\{\lceil N\times 0.25\rceil,\lceil N\times 0.5\rceil,\lceil N\times 0.75\rceil\right\}, \) where \(\lceil \cdot \rceil\) rounds \(\cdot\) to the nearest integers towards infinity. For each data set, we perform 30 independent runs. Only the average errors on 30 runs are reported.

4.2.1 Toy data sets

Two artificial data sets, Half-rings and two-spirals shown in Fig. 2, are traditionally difficult for any centroid-based clustering algorithm [12]. Table 4 shows the average clustering error rate (%) for the Half-rings data set with 25, 50 and 75% bootstrap sampling ratio, respectively. The average clustering error rate in bold type in each column of Table 4 is the best one of the corresponding algorithm with different bootstrap sampling ratio.

Fig. 2
figure 2

Two toy data sets

Full size image
Table 4 Average clustering error rate (%) for the "Half-rings" data set with bootstrap samples
Full size table

For different bootstrap sampling ratio, most methods obtain the similar results, except for BBSCE. In a nutshell about the Half-rings data set H-single gets the best performance 19.83%, followed by spectral clustering 20.65%.

For the two-spirals data sets, we only report the best performance of all algorithms under different bootstrap sample ratios, and the corresponding ensemble size in Table 5 due to space limitations. The average clustering error rate in bold type in each column of Table 5 is the best one under the same bootstrap sampling ratio. Under different bootstrap sample ratios, spectral clusterer, QMI, and k-means get the best performance 38.35, 38.62 and 38.07%, respectively.

Table 5 Results for the "two-spiral" data set with bootstrap samples
Full size table

Thus in both toy data sets, the bootstrap sample ratio plays a little role on the performance of mostly algorithms. Moreover ensembles of very large size are less important.

4.2.2 UCI data sets

Due to space limitation, Table 6 only reports the average best results of all algorithms on UCI data sets with different bootstrap sample ratios and different ensemble sizes, where the error in bold type in each row is the best one for the corresponding data set. From this table, we can see that H-single is better than other methods. BBSCE has the best accuracy on the Wdbc data set, which is only 0.2% higher than the next highest H-Complete consensus function (see the first and ninth columns of Table 6). MCLA achieves the best accuracies on the Vote data set, but its advantage is very slight. The k-means consensus function has about 3% higher in accuracy than the next highest CSPA (see the second and the seventh columns of Table 6) on the Soy data set. The advantage of spectral consensus function on the Musk data set is not so obvious, only 0.3% higher than the H-Single clusterer. The H-Single consensus function performs well on the Glass, Liver and Wpbd data sets. It achieves almost 10% higher in accuracy than the next highest spectral consensus function (see the seventh and eighth columns of Table 6) on the Wpbc data set.

Table 6 Average clustering error rate (%) for seven UCI data sets with bootstrap samples
Full size table

4.3 Experiments with feature subset method

Here, the diversity of the partitions in the first layer clustering is assured by using the feature subset method which are obtained by randomly sampling with replacement from the original data feature set. Here r denotes the feature sampling ratio. The number of samples with a part of features for individual clusterers in the first layer clustering is N, while the dimensionality of feature subset takes value from \(\left\{\lceil d\times 0.25\rceil,\lceil d\times 0.5\rceil,\lceil d\times 0.75\rceil\right\}. \) For each data set, we also perform 30 independent runs and only report the average clustering errors on 30 runs.

Table 7 summarizes the average best results of all algorithms on UCI data sets with different feature sampling ratios and different ensemble sizes, where the error in bold type in each row is the best one for the corresponding data set. From this table, we can see that H-single is better than other methods. MCLA achieves the best accuracies on the Vote data set, but its advantage is very slight. The k-means consensus function also achieves 0.94% higher in accuracy than the next highest CSPA (see the second and the seventh columns of Table 7) on the Soy data set. On the Glass data set, the spectral consensus function gets the best accuracy which is 1.4% higher than the next highest k-mean clusterer. The H-Single consensus function performs well on the Liver, Musk, and Wpbd data sets, which is 0.41, 1.1 and 5.32% than the next corresponding highest consensus function, respectively.

Table 7 Average clustering error rate (%) for seven UCI data sets with feature subset
Full size table

From all experimental results, we have a conclusion that the framework of cascaded cluster ensembles is feasible and promising. But which clustering algorithm should we exploit in the second layer clustering? It is difficult to answer it. From the result analysis, we know the reduced hierarchical single-linkage has good performance in our experiments. As is known, however, each clustering algorithm has its own drawback and could not perform well on all types of data. In the reduced k-means clustering, the selected k centers may be not the optimal ones. The spectral clustering does not get the best performance, which does not mean that it is bad one. Here we used the standard k-means clustering in the spectral clustering, which may be one reason for explaining its results.

5 Conclusions

A framework for cascaded cluster ensembles is proposed, in which there are two layer clustering. The goal of the first layer is to generate different partitions. The first layer is a necessary step for all cluster ensembles. Various methods (consensus functions) were proposed to combine these different partitions to an optimal partition. Here we focus on taking clustering algorithms as consensus functions, which actually is the second layer clustering. In the view of mapping, the first layer could map the samples in the input space into a label attribute space spanned by labeled samples whose dimensionality equals the ensemble size. Some clustering algorithm is performed on these labeled samples instead of input samples. The clustering problem in the second layer can be solved by existing clustering algorithms, such as k-means, fuzzy k-means, spectral, hierarchical clustering, and so on. We also give some reduced clustering algorithms, e.g., k-means, spectral, and hierarchical single-linkage, for the second layer clustering. An experimental comparison with other consensus functions shows that clusterer consensus functions have compared performance, where the reduced hierarchical single-linkage clustering methods perform well in our experiments.

In the second layer, we just use the reduced traditional clustering algorithms. There provide some new clustering algorithms, such as algorithms in [20–22]. Thus, we try to use some new stable clustering algorithm in the second layer in the future.