1 Introduction

Numerous real-world issues are resolved by utilizing extremely beneficial straightforward machine learning models (Nejatian et al. 2019; Pirbonyeh et al. 2019; Hosseinpoor et al. 2019; Partabian et al. 2020; Shabaniyan et al. 2019; Szetoa et al. 2020; Moradi et al. 2018; Jenghara et al. 2018a; Parvin et al. 2018; Alishvandi et al. 2016; Omidvar et al. 2018; Yasrebi et al. 2018). Nevertheless, since understandable machine learning models encounter difficulties in challenging issues (Nejatian et al. 2018; Jamalinia et al. 2018; Jenghara et al. 2018b), ensemble models have emerged as a new option in regard with the machine learning classification tasks (Rashidi et al. Aug. 2019; Mojarad et al. 2019a,b; Nazari et al. 2019; Bagherinia et al. 2019).

To find a partition with the goal of assigning data points within identical groups is a prominent and complicated matter which has been employed in many real-world problems such as knowledge extraction and pattern recognition. According to no free lunch (NFL), there is no dominant algorithm among many algorithms for solving a problem (Huang et al. 2016b; Fred and Jain 2005). Therefore, we know that there is a dominant algorithm depending on the at-hand data set. However, lack of knowledge on distributions, structures and natures of the clusters in the at-hand data set results in some problems which prevent us from detection of the most suitable clustering algorithm to our specific application (Roth et al. 2002).

Cluster ensembles have attracted enormous interest in result of several successful applications of ensemble learning in supervised fields such as (Freund and Schapire 1995; Ho 1995; Friedman 2001; Soto et al. 2014; Yu et al. 2015,2016a,2017). Many classification applications have shown a tendency towards hybrid methods in the past few years (Faceli et al. 2006) similar to every sub-field of the supervised pattern detection. Generally, several fields including data mining (Hong et al. 2008; Zhang et al. 2012; Yu et al. 2012,2016b; Naldi et al. 2013; Franek and Jiang 2014; Jiang et al. 2015; Huang et al. 2017; Yousefnezhad et al. 2018), multimedia (Rafiee et al. 2013) and bio-informatics (Yu et al. 2011,2013; Hanczar and Nadif 2012) have used various cluster ensemble approaches which have intended to clarify innovative partitions because they are stronger than simple clustering algorithms (Ayad and Kamel 2008). Using ensembles as a group of primary partitions to devise a consensus partitions is the objective of the ensemble clustering (Domeniconi and Al-Razgan 2009; Ghosh and Acharya 2011; Ghaemi et al. 2011). Consensus ensemble uses every primary partition within the ensemble in construction of the consensus partition, and the consensus partition enhances a specific objective function.

Cluster ensemble consists of two stages. First stage is to generate a pool of primary partitions. These primary partitions usually are the moderate or low-quality ones (Topchy et al. 2003). Actually, they should be low-quality but not without-quality. It is widely acceptable to generate these primary partitions through a simple clusterer method (usually k-means) on a number of dissimilar parameters (Topchy et al. 2005), on a number of dissimilar initializations, on a number of dissimilar data subspaces (Ayad and Kamel 2008), or on a number of dissimilar data subsamples (Minaei-Bidgoli et al. 2004). The proposed method has used all of the mentioned approaches.

In second step, we aim at finding a consensus partition that has maximum similarity to the primary partitions in our ensemble generated in the first step. Evidence accumulation clustering (EAC) is proposed in Fred and Jain (2002) as an ideal consensus function in which the ensemble is initially transformed into a co-association matrix (CAM), and then, the consensus partition is found by employing a single linkage hierarchical clusterer algorithm.

Normalized mutual information (NMI) measure is proposed in Fred and Jain (2005) to assess a cluster which has numerous deficiencies described in Alizadeh et al. (2011a). MAX is an edition of the normalized mutual information measure which has also some flaws. Therefore, Alizadeh–Parvin–Moshki–Minaei (APMM) measure has been introduced in Alizadeh et al. (2011b) as a metric to enhance the MAX. All of mentioned metrics, i.e. NMI, MAX, and APMM, are weak in dealing with complement cluster effect.

In this paper, an innovative cluster–cluster similarity measure is introduced. Then, we extend it to EAC. MLCC is inspired by dual-similarity clustering ensemble (DSCE) method (Alqurashi and Wang 2014,2015). DSCE and MLCC have three differences. First, MLCC has less sensitivity to the usage of the real number of clusters in primary partitions. Second, the MLCC method has less parameters than DSCE. Third, MLCC is a CAM-based consensus clustering, but DSCE is a voting-based consensus clustering that is an important consensus function clustering (Strehl and Ghosh 2000; Fern and Brodley 2003; Breiman 1996; Alizadeh et al. 2015; Iam-On et al. 2010,2012; Gionis et al. 2007; Yi et al. 2012; Mirzaei and Rahmati 2010; Akbari et al. 2015).

This article has been continued as follows. In Sect. 2, the clustering ensemble problem of the paper is defined. In Sect. 3, the related works are presented. Section 4 has explained the proposed method. Section 5 presents the experimental results, and the paper conclusions will be presented in Sect. 6.

2 Related work

Encapsulating ensemble information into a CAM and application of a hierarchical clusterer algorithm on the obtained CAM are needed for extracting the consensus partition in an approach that is based on CAM (Fred and Jain 2002). These types of clustering ensembles take the advantage of bypassing the need for a relabeling phase. As an instance, consensus partition was achieved in Fred and Jain (2005) through applying an average linkage hierarchical clusterer which we have named CO–AL as a slow and CAM-based method. A new CAM which considers the between cluster relations was introduced in Iam-On et al. (2008) where the implemented approach was named SRS which can be considered to be a slow method. It was based on CAM and used link similarity. After that, it was extended it into WCT method (Iam-On et al. 2011).

Instead of an object–object similarity CAM, a cluster–cluster similarity matrix was introduced in Mimaroglu and Aksehirli (2012) where a method named DICLENS was offered as a CAM-based, slow, and robust approach. An object-neighbourhood-based similarity matrix was introduced in where a new cluster–cluster similarity matrix was obtained by neighbourhood and real relation between objects. This method that was named ONCE–AL together with its extension DSCE method introduced in Alqurashi and Wang (2015), can be considered to be a heuristic, fast, and parameter-sensitive approach. The mentioned method later extended (Huang et al. 2016b). An extended version of the DSCE was also proposed in Huang et al. (2015) which introduces WEAC and GPMGLA as a pair of two cluster weighting, CAM-based, slow and robust clustering ensemble methods.

CSEAC was proposed in Alizadeh et al. (2014a) as a CAM-based, very slow robust clustering ensemble method, and also Wisdom of Crowds Ensemble (WCE) was introduced in Alizadeh et al. (2015) as a CAM-based, slow, robust and flexible ensemble method. Another related work is ECSEAC which is a cluster selection-based ensemble clustering algorithm proposed in Parvin and Minaei-Bidgoli (2015) as a cluster weighting, CAM-based, slow and robust approach. TME is also an ensemble method which was proposed in Zhong et al. (2015) as a cluster weighting and CAM-based one; it is widely considered to be a very slow and robust method.

Clustering ensemble has been reformulated as a linear binary programming problem by Huang et al. (2016). This approach was also extended and used for categorical data set by Zhao et al. (2017).

A cluster ensemble was introduced through sampling by Yang and Jiang (2016) which was inspired by bagging and boosting theory. Also, information theory as a suitable tool for data clustering was used to introduce a cluster ensemble method by Bai et al. (2017).

Consensus partition was extracted by Strehl and Ghosh (2003) by partitioning a hyper-graph which is constructed on a CAM so that each row and each column in the CAM are, respectively, assumed to be a node and a hyper-edge. The hyper-graph partitioning algorithm used in the mentioned work could be HMETIS (Dimitriadou et al. 2002). This algorithm is named cluster-based similarity partitioning algorithm (CSPA). Hyper-graph partitioning algorithm (HGPA) and meta-clustering algorithm (MCLA) are some other examples of the methods in which each cluster is considered to be a hyper-edge and each data as a node. CSPA has been extended by Fren and Brodley (2004) as a hybrid bi-partite graph formulation (HBGF) which outperforms HGPA, MCLA and CSPA.

A cluster ensemble method was proposed in Rashidi et al. (2019) which did not need the original features of data set and also did not consider any distribution in the data set. Moreover, it used assessment of the clusters’ undependability and the weighting mechanism to suggest a clustering ensemble. In addition, diversity was defined in cluster level. During consensus function process, quality of the clusters and their diversity were used in order to improve the consensus partition. Any clusters' dependability was computed based on its undependability which itself was calculated according to the entropy in the labels of its data points throughout all the ensemble partitions. Also, an innovational cluster-wise weighing CAM was suggested according to measuring the clusters’ reliability and then emphasizing those with higher reliability in the ensemble. Furthermore, a cluster-wise weighting bi-partite graph was suggested to offer the ensemble based on the related cluster-wise weighing co-association matrix. Finally, the consensus partition was extracted using two mechanisms including application of a simple hierarchical clustering algorithm for cluster-wise weighing of the co-association matrix as a similarity matrix and cluster-wise weighting bi-partite graph partitioning into a certain number of parts.

The idea proposed in Alizadeh et al. (2014a) is to find a subset of primary clusters which performs better in the ensemble, and through participating the clusters with more quality in consensus function process, the consensus partition performance was improved. In this regard, many clusters are first gained by specific generation of primary results. Then, a goodness function is used to evaluate and also to sort the achieved clusters. After that, with the goal of finding more efficient clusters for participating in the ensemble, a specific subset of primary clusters is offered for each class of datasets. The selected clusters are then combined to extract the final clusters which is followed by a post-processing.

A supreme consensus partition was produced in Alizadeh et al. (2013) by combination of spurious clustering results where the objective function was inspired by proposed immature formulation in which simultaneous maximization of the agreement between the ensemble members and minimization of the disagreement was implemented. They improve a nonlinear binary goal function which was introduced to propose a constrained nonlinear fuzzy objective function. The genetic algorithm was also used to solve the proposed model and while any other optimizer could be used to solve the model.

In the clustering ensemble proposed in Minaei-Bidgoli et al. (2014), a simple adaptive attitude was suggested for generating primary partitions. It uses the clustering history. Since it is supposed in the clustering that the ground truth is not achievable in the class labels form, it is needed to use an alternative performance measure for an ensemble of partitions throughout process of the clustering. To determine clustering consistency of data points, a history of cluster assignments was evaluated in the generated sequence of the partitions for each data point which could adapt the data sampling during the partition generation to the current state of an ensemble that improves the confidence in cluster assignments.

By extending the previous clustering frameworks, ensemble and swarm concepts in the clustering field were suggested in Parvin et al. (2012) where an unprecedented clustering ensemble learning method was introduced according to the ant colony clustering algorithm. Since diversity of the ensemble is very important and swarm intelligence is inherently related to random processes, a new dataset space was introduced by diverse partitions of the acquired results from different runs of the ant colony clustering algorithm with different initializations on a data set and they were aggregated into a consensus partition by a simple clusterer algorithm. The contribution of swarm intelligence in reaching better results was also measured.

Benefits of the ensemble diversity together with quality of the fuzzy clustering-level were used to select a subset of fuzzy base-clusterings in Bagherinia et al. (2019). Integrating diversity of the base-clusterings and quality of the clustering level was resulted into enhancement of the final clustering quality. It first calculated a new fuzzy normalized mutual information (FNMI) and then calculated the diversity of each fuzzy base-clustering in relation to other fuzzy base-clusterings. After that, the calculated diversity was used to cluster all the base-clusterings which resulted in clusters of base-clusterings named base-clusterings-clusters. In subsequence, a base-clusterings-cluster is selected which satisfies the quality measure. Final clustering was achieved by using a novel consensus method derived by graph portioning algorithm named FCBGP algorithm or by forming extended fuzzy co-association matrix (EFCo) which is finally considered as similarity matrix.

Because of lower information or higher variances some features of under-consideration data set have more information than the others in that data set, weighted locally adaptive clustering (WLAC) algorithm was proposed in Parvin and Minaei-Bidgoli (2013) as a weighted clustering algorithm which could encounter the imbalanced clustering. WLAC algorithm is very sensitive to the two parameters which was resulted in proposing a simple clustering ensemble framework and an elite cluster ensemble framework to manage those two control parameters. It was later extended into a fuzzy version, i.e. Fuzzy WLAC (FWLAC) algorithm (Parvin and Minaei-Bidgoli 2015).

A novel approach for clustering ensemble was also suggested in Abbasi and Nejatian (2019). It uses a subset of primary clusters. It proposed to evaluate the cluster quality by suggesting stab as a new validity measure so that the clusters that satisfy a stab threshold are qualified to be used in construction of the consensus partition. A set of methods for consensus function such as co-association based ones were used to combine the chosen clusters. Extended evidence accumulation clustering (EEAC) was used for co-association matrix construction from the selected clusters because it was not possible for evidence accumulation clustering (EAC) method to use a subset of clusters in construction of co-association matrix. Other class of consensus functions was also used based on hyper-graph partitioning algorithms. In another one, the chosen clusters were considered to be a new feature space and the consensus partition was extracted by using a simple clusterer algorithm.

Averaged Alizadeh–Parvin–Moshki–Minaei (AAPMM) criterion was introduced in Alizadeh et al. (2014b) for assessing a cluster quality. It was proposed to use AAPMM for obtaining quality of clusters. Then, in their clustering ensemble method, the clusters satisfying an AAPMM value threshold participate in constructing the co-association matrix. In addition, EEAC was proposed as a new method for matrix establishment. Finally, consensus partition extraction was performed by application of a hierarchical clusterer method over the obtained co-association matrix.

A primary partitions' generator was suggested in Parvin et al. (2013). It could be considered to be a boosting mechanism in clustering. As true labels are needed for each cluster to be available in weight updating of boosting, the clustering needs an alternative performance metric for an ensemble of partitions to update the probability sampling vector. This study has determined the clustering consistency of data points was determined to assess a cluster assignment history for every data point in the generated partitions of ensemble. In order to have a suitable data sampling, determination of the clustering consistency for produced partitions was performed during the partition generation. The adaptation concentrated the sampling distribution on problematic regions of the feature space to modify the confidence in cluster assignments. Accordingly, better approximation of the inter-cluster boundaries was performed by concentrating the notice on the data points which have the minimum consistent clustering assignments.

3 Clustering ensemble

3.1 Clustering ensemble definition

Let’s assume a set of data points be denoted by \({\mathcal{X}}\). In the data set \({\mathcal{X}}\), \(i\) th feature of all data points is denoted by data set \({\mathcal{X}}_{:,i}\) and \(j\) th data point is denoted by \({\mathcal{X}}_{j,:}\). The number of data points in the data set \({\mathcal{X}}\) is denoted by \(\left| {{\mathcal{X}}_{:,1} } \right|\). The number of features in the data set \({\mathcal{X}}\) is denoted by \(\left| {{\mathcal{X}}_{1,:} } \right|\). A partition on the data set \({\mathcal{X}}\) is denoted by \(\pi_{{\mathcal{X}}}\) (also, \(\pi_{{\mathcal{X}}}^{k}\) is \(k\) th partition on the data set \({\mathcal{X}}\) where \(k\) is an integer value indicating the index of partition). The partition \(\pi_{{\mathcal{X}}}\) contains a \(\left| {\pi_{{{\mathcal{X}},:}} } \right|\) subsets of \(\left\{ {1,2, \ldots ,\left| {{\mathcal{X}}_{:,1} } \right|} \right\}\). Let’s denote \(p\) th subset of partition \(\pi_{{\mathcal{X}}}\) by \(\pi_{{{\mathcal{X}},p}}\). To name \(\pi_{{\mathcal{X}}}\) a non-overlapping partition, we must have

$$ \forall p_{1} ,p_{2} \in \left\{ {1,2, \ldots ,\left| {\pi_{{{\mathcal{X}},:}} } \right|} \right\}\bullet \pi_{{{\mathcal{X}},p_{1} }} \cap \pi_{{{\mathcal{X}},p_{2} }} = \emptyset $$
(1)

If the Eq. 1 holds for a partition, we name it a non-overlapping partition. From now on, without loss of generality, we assume all of the partitions, discussed in the paper, are non-overlapping. Any member of a partition, i.e. \(\pi_{{{\mathcal{X}},p}}\), is considered to be a cluster. If the union of all clusters in a partition is \(\left\{ {1,2, \ldots ,\left| {{\mathcal{X}}_{:,1} } \right|} \right\}\), then the partition is named a complete partition. It means the Eq. 2 must be correct for a partition \(\pi_{{\mathcal{X}}}\) to name it a complete partition.

$$ \bigcup\limits_{p = 1}^{{\pi_{{\mathcal{X}}} }} {\pi_{{{\mathcal{X}},p}} = \left\{ {1,2, \ldots ,\left| {{\mathcal{X}}_{:,1} } \right|} \right\}} $$
(2)

Let’s assume a data set \({\mathcal{X}}\) has a desired clustering similar to its ground-truth labels denoted by \(\pi_{{\mathcal{X}}}^{ + }\). Note that we have not assumed that any of \(\left| {\pi_{{{\mathcal{X}},:}}^{k} } \right|\) should be equal to \(\left| {\pi_{{{\mathcal{X}},:}}^{ + } } \right|\). Each cluster, say \(\pi_{{{\mathcal{X}},p}}\), has a central point denoted by \(C^{{\pi_{{{\mathcal{X}},p}} }}\) defined according to Eq. 3.

$$ C^{{\pi_{{{\mathcal{X}},p}} }} = \frac{1}{{\left| {\pi_{{{\mathcal{X}},p}} } \right|}}\mathop \sum \limits_{{j \in \pi_{{{\mathcal{X}},p}} }} {\mathcal{X}}_{j,:} $$
(3)

We denote the complete version of partition \(\pi_{{\mathcal{X}}}\) by \(\dot{\pi }_{{\mathcal{X}}}\) whose \(p\) th cluster is defined according to Eq. 4.

$$ \dot{\pi }_{{{\mathcal{X}},p}} = \left\{ {\forall j \in \left\{ {1 \ldots \left| {{\mathcal{X}}_{:,1} } \right|} \right\}\bullet \left[ {\forall p_{1} \in \left\{ {1 \ldots \left| {\pi_{{{\mathcal{X}},:}} } \right|} \right\}\bullet \left| {C^{{\pi_{{{\mathcal{X}},p}} }} - {\mathcal{X}}_{j,:} } \right| \le \left| {C^{{\pi_{{{\mathcal{X}},p_{1} }} }} - {\mathcal{X}}_{j,:} } \right|} \right]|j} \right\} $$
(4)

We consider all of the partitions \(\pi_{{\mathcal{X}}}^{k}\) to be an ensemble (denoted by \({\varvec{\pi}}_{{\mathcal{X}}}\)) with the ensemble size \(\left| {{\varvec{\pi}}_{{\mathcal{X}}}^{:} } \right|\). Our aim is to combine them to extract a consensus partition denoted by \(\pi_{{\mathcal{X}}}^{*}\) in such a way that it is as much robust and high-quality as possible. Formally, the ensemble clustering intends to find a better consensus partition by integrating the information of the primary partitions in the ensemble.

Clustering ensemble domain has examined the creation of an ensemble and also the consensus function construction which both have highly influenced the outcomes of the final clustering. Since variety of the results from the base learners is a crucial factor to make a successful ensemble, the diversity could be extended into the clustering ensemble field in regard to classifier ensemble.

3.2 Ensemble creation

First of all, the ensemble members should be created in clustering ensemble framework. To find various data substructures and also to enhance the potential performance of consensus partition, we must use at least one of the clustering generation methods that guarantee to produce an ensemble of partitions where any of them has a minimum quality and all of them have a minimum diversity.

Many problem-specific ensemble generation methods have been introduced. Subspace clustering has been done on different projections of data set by Strehl and Ghosh (2000). Along to feature subset selection, a subsampling (or instance subset selection) is also used for generating each partition. Almost the same approach was proposed by Fern and Brodley (2003). Breiman (1996) first presents subsampling in machine learning, and later, it was extended by Minaei-Bidgoli et al. (2004).

An alternative to the prior methods including a subset of primary members within the ensemble was used by Alizadeh et al. (2011a,2011b). They used a subsampling for generating each primary partition. Each partition is attained by running a randomly initialized k-means clustering algorithm. Then, a subset of primary partitions that has maximum diversity is selected as final ensemble. A similar study was also conducted by Nazari et al. (2019).

Since k-means clusterer algorithm is an easy and efficient clusterer algorithm (Minaei-Bidgoli et al. 2004), it is considered to be the most suitable clusterer algorithm in ensemble generation. Thus, for each base clustering, k-means clusterer method was used in Alizadeh et al. (2015) with two random elements: randomly initialized seed points and randomly selected number of clusters. These random sources cause to produce a diverse ensemble. It is widely recommended to select an integer value randomly in \(\left[ {2;\sqrt {\left| {{\mathcal{X}}_{:,1} } \right|} } \right]\) as the number of clusters (Iam-On et al. 2010,2012) during generating the ensemble. Different clusterer algorithms can be also a source for generating a diverse ensemble (Gionis et al. 2007; Yi et al. 2012; Mirzaei and Rahmati 2010; Akbari et al. 2015).

For ensemble creation, Wisdom of Crowds (WOC) was proposed in Alizadeh et al. (2015) as a concept in social sciences field that provides suitable criteria for group behaviour. Meeting these criteria could result in favourable ensembles. Therefore, WOC cluster ensemble (WOCCE) has been proposed. It was later extended in Yousefnezhad et al. (2018).

3.3 Ensemble combiner

In the literature, researchers pay more attention to ensemble combiner. It can be viewed as a function with two inputs: (a) ensemble members or partitions and (b) the number of clusters, i.e. \(\left| {\pi_{{{\mathcal{X}},:}}^{ + } } \right|\). It returns an output, widely referred to as consensus or aggregated partition, i.e. \(\pi_{{{\mathbf{\mathcal{X}}},:}}^{*}\).

As there are some widely accepted approaches for ensemble combiner, we will present a brief summarization on them here. Any ensemble combiner is in one category of the following ones: (a) category of CAM based ensemble combiners, (b) category of median partition based ensemble combiners, (c) category of graph partitioning based ensemble combiners, (d) category of voting based ensemble combiners, and (e) category of intermediate space based ensemble combiners.

The methods in the first category transform information of ensemble partitions into a similarity matrix, named CAM, and then, they apply a second clustering, widely a hierarchical one, to find the consensus partition. The methods in the second category transform the finding of consensus partition into an optimization problem, and then, they solve it through an optimizer. The methods in the third category transform the finding of consensus partition into a graph clustering problem, and then, they solve it through a graph partitioning algorithm. The methods in the fourth category first make a relabeling between all of the partitions, and then, they find consensus partition by a voting or averaging mechanism. The methods in the fifth category assume the clusters of data points as new intermediate features, and then, they apply a secondary simple clusterer algorithm on the new intermediate data set to find consensus partition.

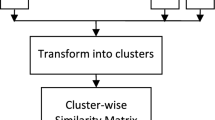
Figure 1 depicts framework of the proposed framework. In the proposed framework, the initial data set is subsampled several times and then by applying a k-means clusterer method on each of them to partition them into a random number of clusters, an ensemble of \(\left|{{\varvec{\pi}}}_{\mathcal{X}}^{:}\right|\) partitions denoted by \({\pi }_{\mathcal{X}}^{q}\) will be generated, where \(q=\left\{1,\dots ,\left|{\pi }_{\mathcal{X}}^{:}\right|\right\}\). After that, each partition is extended to its complete version, i.e. \({\dot{\pi }}_{\mathcal{X}}^{q}\). After that, the ensemble is converted into a cluster representation, and then, a similarity matrix is created to determine the similarities of the clusters. In the next step, a CAM boosted cluster similarity matrix is obtained. Finally, a merging mechanism (a hierarchical clusterer algorithm) and post-processing are used to determine the consensus partition.

Fig. 1
figure 1

Framework of our ensemble clustering

Full size image

4 Proposed consensus function

Ensemble combiner or consensus function is the main part in a clustering ensemble framework. It must be appropriately designed so as to maximally extract ensemble information. We first create a graph according to Eq. 5 for our clustering ensemble \({\varvec{\pi}}_{{\mathcal{X}}}\).

$$ {\mathcal{G}}\left( {{\varvec{\pi}}_{{\mathcal{X}}} } \right) = \left( {{\mathcal{V}}\left( {{\varvec{\pi}}_{{\mathcal{X}}} } \right),{\mathcal{E}}\left( {{\varvec{\pi}}_{{\mathcal{X}}} } \right)} \right) $$
(5)

In Eq. 5, \({\mathcal{V}}\left( {{\varvec{\pi}}_{{\mathcal{X}}} } \right)\) is set of indices of all the data clusters that are in the ensemble, i.e. \(\left\{ {1,2, \ldots ,\left| {{\varvec{\pi}}_{{{\mathcal{X}},:}} } \right|} \right\}\) where \(\left| {{\varvec{\pi}}_{{{\mathcal{X}},:}} } \right|\) denotes the number of clusters in ensemble \({\varvec{\pi}}_{{\mathcal{X}}}\) and \({\mathcal{E}}\left( {{\varvec{\pi}}_{{\mathcal{X}}} } \right)\) is set of edge weights for graph \({\mathcal{G}}\left( {{\varvec{\pi}}_{{\mathcal{X}}} } \right)\). The term \(\left| {{\varvec{\pi}}_{{{\mathcal{X}},:}} } \right|\) is defined according to Eq. 6.

$$ \left| {{\varvec{\pi}}_{{{\mathcal{X}},:}} } \right| = \mathop \sum \limits_{k = 1}^{{\left| {{\varvec{\pi}}_{{\mathcal{X}}}^{:} } \right|}} \left| {\pi_{{{\mathcal{X}},:}}^{k} } \right| $$
(6)

In Eq. 5, \({\mathcal{E}}\left( {{\varvec{\pi}}_{{\mathcal{X}}} } \right)\) is defined according to Eq. 7.

$$ {\mathcal{E}}\left( {{\varvec{\pi}}_{{\mathcal{X}}} } \right) = \left\{ {\forall j_{1} ,j_{2} \in {\mathcal{V}}\left( {{\varvec{\pi}}_{{\mathcal{X}}} } \right) \bullet w_{{{\varvec{\pi}}_{{\mathcal{X}}} }} \left( {j_{1} ,j_{2} } \right) \ne 0|\left( {j_{1} ,j_{2} ,w_{{{\varvec{\pi}}_{{\mathcal{X}}} }} \left( {j_{1} ,j_{2} } \right)} \right)} \right\} $$
(7)

where \(w_{{{\varvec{\pi}}_{{\mathcal{X}}} }} \left( {j_{1} ,j_{2} } \right)\) is defined according to Eq. 8.

$$ w_{{{\varvec{\pi}}_{{\mathcal{X}}} }} \left( {j_{1} ,j_{2} } \right) = \left\{ {\begin{array}{*{20}l} 0 & {} & {j_{1} = j_{2} } \\ {SCCS_{{{\varvec{\pi}}_{{\mathcal{X}}} }} \left( {\dot{\pi }_{{{\mathcal{X}},p_{{j_{1} ,{\varvec{\pi}}_{{\mathcal{X}}} }} }}^{{k_{{j_{1} ,{\varvec{\pi}}_{{\mathcal{X}}} }} }} ,\dot{\pi }_{{{\mathcal{X}},p_{{j_{2} ,{\varvec{\pi}}_{{\mathcal{X}}} }} }}^{{k_{{j_{2} ,{\varvec{\pi}}_{{\mathcal{X}}} }} }} } \right)} & {} & {j_{1} \ne j_{2} } \\ \end{array} } \right. $$
(8)

where \(k_{{j,{\varvec{\pi}}_{{\mathcal{X}}} }}\) and \(p_{{j,{\varvec{\pi}}_{{\mathcal{X}}} }}\) are, respectively, defined according to Eqs. 8 and 9.

$$ k_{{j,{\varvec{\pi}}_{{\mathcal{X}}} }} = arg\mathop {\max }\limits_{K} \mathop \sum \limits_{k = 1}^{K} \left| {\pi_{{{\mathcal{X}},:}}^{k} } \right| \le j $$
(9)
$$ p_{{j,{\varvec{\pi}}_{{\mathcal{X}}} }} = j - k_{{j,{\varvec{\pi}}_{{\mathcal{X}}} }} $$
(10)

In Eq. 8, \(SCCS_{{{\varvec{\pi}}_{{\mathcal{X}}} }} \left( {A,B} \right)\) stands for a simple cluster–cluster similarity function. It is the corrected version of the set correlation ratio. The set correlation first emerged in (Houle, 2008). It is defined according to Eq. 11.

$$ SCCS_{{{\varvec{\pi}}_{{\mathcal{X}}} }} \left( {\pi_{{{\mathcal{X}},a}}^{{k_{1} }} ,\pi_{{{\mathcal{X}},b}}^{{k_{2} }} } \right) = 0.5 + \frac{{\left| {\pi_{{{\mathcal{X}},a}}^{{k_{1} }} \cap \pi_{{{\mathcal{X}},b}}^{{k_{2} }} } \right| \times \left| {{\mathcal{X}}_{:,1} } \right| - \left| {\pi_{{{\mathcal{X}},a}}^{{k_{1} }} } \right| \times \left| {\pi_{{{\mathcal{X}},b}}^{{k_{2} }} } \right|}}{{2 \times \sqrt {\left| {\pi_{{{\mathcal{X}},a}}^{{k_{1} }} } \right| \times \left| {\pi_{{{\mathcal{X}},b}}^{{k_{2} }} } \right| \times \left( {\left| {{\mathcal{X}}_{:,1} } \right| - \left| {\pi_{{{\mathcal{X}},a}}^{{k_{1} }} } \right|} \right) \times \left( {\left| {{\mathcal{X}}_{:,1} } \right| - \left| {\pi_{{{\mathcal{X}},b}}^{{k_{2} }} } \right|} \right)} }} $$
(11)

It can be proven that \(SCCS_{{{\varvec{\pi}}_{{\mathcal{X}}} }} \left( {A,B} \right)\) is less than or equal to one and greater than or equal to zero. If the cluster A and cluster B have maximum similarity, it will return one. If the cluster \(A\) and cluster \(B\) have minimum similarity, it will return zero (Vinh and Houle 2010). It can be proven that \(w_{{{\varvec{\pi}}_{{\mathcal{X}}} }}\) is reflexive. Now, assuming we are at the \(j_{1}\) th cluster, i.e. \(\dot{\pi }_{{{\mathcal{X}},p_{{j_{1} ,{\varvec{\pi}}_{{\mathcal{X}}} }} }}^{{k_{{j_{1} ,{\varvec{\pi}}_{{\mathcal{X}}} }} }}\), we intend to define a transition probability to cluster the \(j_{2}\) th cluster, i.e. \(\dot{\pi }_{{{\mathcal{X}},p_{{j_{2} ,{\varvec{\pi}}_{{\mathcal{X}}} }} }}^{{k_{{j_{2} ,{\varvec{\pi}}_{{\mathcal{X}}} }} }}\) after \(r\) steps denoted by \(TP_{{{\varvec{\pi}}_{{\mathcal{X}}} }}^{r} \left( {j_{1} ,j_{2} } \right)\). For \(r = 1\), it is defined according to Eq. 12.

$$ {\text{TP}}_{{{\varvec{\pi}}_{{\mathcal{X}}} }}^{1} \left( {j_{1} ,j_{2} } \right) = \left\{ {\begin{array}{*{20}c} 0 & {} & {j_{1} = j_{2} } \\ {\frac{{w_{{{\varvec{\pi}}_{{\mathcal{X}}} }} \left( {j_{1} ,j_{2} } \right)}}{{\mathop \sum \nolimits_{j = 1}^{{\left| {{\varvec{\pi}}_{{{\mathcal{X}},:}} } \right|}} w_{{{\varvec{\pi}}_{{\mathcal{X}}} }} \left( {j_{1} ,j} \right)}}} & {} & {j_{1} \ne j_{2} } \\ \end{array} } \right. $$
(12)

Now, we have the matrix \({\varvec{TP}}_{{{\varvec{\pi}}_{{\mathcal{X}}} }}\) whose \(\left( {i,j} \right)\) th entry shows the probability that a traveller that is currently at the \(i\) th cluster will be at the \(j\) th cluster in the next step.

To compute the probability that a traveller that is currently at the \(i\) th cluster will be at the \(j\) th cluster in the next two steps, we should compute it by Eq. 13.

$$ TP_{{{\varvec{\pi}}_{{\mathcal{X}}} }}^{2} \left( {j_{1} ,j_{2} } \right) = \mathop \sum \limits_{j = 1}^{{\left| {{\varvec{\pi}}_{{{\mathcal{X}},:}} } \right|}} TP_{{{\varvec{\pi}}_{{\mathcal{X}}} }}^{1} \left( {j_{1} ,j} \right) \times TP_{{{\varvec{\pi}}_{{\mathcal{X}}} }}^{1} \left( {j,j_{2} } \right) $$
(13)

Therefore, it is easy to prove that \({\varvec{TP}}_{{{\varvec{\pi}}_{{\mathcal{X}}} }}^{2} = {\varvec{TP}}_{{{\varvec{\pi}}_{{\mathcal{X}}} }}^{1} \times {\varvec{TP}}_{{{\varvec{\pi}}_{{\mathcal{X}}} }}^{1}\). Also, it is easy to show the transition probability matrix after \(r\) steps, i.e. \({\varvec{TP}}_{{{\varvec{\pi}}_{{\mathcal{X}}} }}^{r}\), is computed according to Eq. 14.

$$ {\varvec{TP}}_{{{\varvec{\pi}}_{{\mathcal{X}}} }}^{r} = \mathop \prod \limits_{k = 1}^{r} {\varvec{TP}}_{{{\varvec{\pi}}_{{\mathcal{X}}} }}^{1} $$
(14)

Now, we introduce a new feature space for clusters of the ensemble, denoted by \({\varvec{NF}}_{{{\varvec{\pi}}_{{\mathcal{X}}} }}^{r}\), as follows in Eq. 15.

$$ {\varvec{NF}}_{{{\varvec{\pi}}_{{\mathcal{X}}} }}^{r} = \left[ {{\varvec{TP}}_{{{\varvec{\pi}}_{{\mathcal{X}}} }}^{1} {\varvec{TP}}_{{{\varvec{\pi}}_{{\mathcal{X}}} }}^{2} \ldots {\varvec{TP}}_{{{\varvec{\pi}}_{{\mathcal{X}}} }}^{r} } \right] $$
(15)

Note that each row corresponds to a cluster and each column corresponds to a feature in our new feature space. Therefore, we have \(\left| {{\varvec{\pi}}_{{{\mathcal{X}},:}} } \right|\) rows and \(\left| {{\varvec{\pi}}_{{{\mathcal{X}},:}} } \right| \times r\) defined features. According to a distance metric (here, we use Euclidian distance), the distances between pairs of the ensemble clusters are computed. The mentioned distances for all pairs of clusters in the ensemble are stored in a distance matrix denoted by \({\varvec{EuclidianDis}}_{{{\varvec{\pi}}_{{\mathcal{X}}} }}^{r}\) and defined based on Eq. 16.

$$ EuclidianDis_{{{\varvec{\pi}}_{{\mathcal{X}}} }}^{r} \left( {j_{1} ,j_{2} } \right) = \left( {\mathop \sum \limits_{j = 1}^{{\left| {{\varvec{\pi}}_{{{\mathcal{X}},:}} } \right|}} \frac{{\left( {NF_{{{\varvec{\pi}}_{{\mathcal{X}}} }}^{r} \left( {j_{1} ,j} \right) - NF_{{{\varvec{\pi}}_{{\mathcal{X}}} }}^{r} \left( {j_{2} ,j} \right)} \right)^{2} }}{{\left| {{\varvec{\pi}}_{{{\mathcal{X}},:}} } \right|}}} \right)^{0.5} $$
(16)

Correspondingly, a distance matrix can be denoted by \({\varvec{CosineDis}}_{{{\varvec{\pi}}_{{\mathcal{X}}} }}^{r}\) and defined based on Eq. 17 if we use Cosine distance.

$$ CosineDis_{{{\varvec{\pi}}_{{\mathcal{X}}} }}^{r} \left( {j_{1} ,j_{2} } \right) = 1 - \left( {\frac{{\mathop \sum \nolimits_{j = 1}^{{\left| {{\varvec{\pi}}_{{{\mathcal{X}},:}} } \right|}} \left( {NF_{{{\varvec{\pi}}_{{\mathcal{X}}} }}^{r} \left( {j_{1} ,j} \right) \times NF_{{{\varvec{\pi}}_{{\mathcal{X}}} }}^{r} \left( {j_{2} ,j} \right)} \right)}}{{\left( {\mathop \sum \nolimits_{j = 1}^{{\left| {{\varvec{\pi}}_{{{\mathcal{X}},:}} } \right|}} \left( {NF_{{{\varvec{\pi}}_{{\mathcal{X}}} }}^{r} \left( {j_{1} ,j} \right)} \right)^{2} } \right)^{0.5} \times \left( {\mathop \sum \nolimits_{j = 1}^{{\left| {{\varvec{\pi}}_{{{\mathcal{X}},:}} } \right|}} \left( {NF_{{{\varvec{\pi}}_{{\mathcal{X}}} }}^{r} \left( {j_{2} ,j} \right)} \right)^{2} } \right)^{0.5} }}} \right)^{0.5} $$
(17)

According to Eq. 18, the cluster–cluster similarity matrix, denoted by \({\varvec{CCS}}_{{{\varvec{\pi}}_{{\mathcal{X}}} }}^{r}\), is computed.

$$ {\varvec{CCS}}_{{{\varvec{\pi}}_{{\mathcal{X}}} }}^{r} = \left\{ {\begin{array}{*{20}c} {1 - {\varvec{EuclidianDis}}_{{{\varvec{\pi}}_{{\mathcal{X}}} }}^{r} } & {} & {measure = Euclidian} \\ {1 - {\varvec{CosineDis}}_{{{\varvec{\pi}}_{{\mathcal{X}}} }}^{r} } & {} & {measure = Cosine} \\ \end{array} } \right. $$
(18)

Now, we define a point–point similarity matrix, denoted by \({\varvec{PPS}}_{{{\varvec{\pi}}_{{\mathcal{X}}} }}^{r}\), according to Eq. 19.

$$ PPS_{{{\varvec{\pi}}_{{\mathcal{X}}} }}^{r} \left( {j_{1} ,j_{2} } \right) = \frac{{\mathop \sum \nolimits_{b = 1}^{{\left| {{\varvec{\pi}}_{{\mathcal{X}}} } \right|}} CCS_{{{\varvec{\pi}}_{{\mathcal{X}}} }}^{r} \left( {CI_{{{\varvec{\pi}}_{{\mathcal{X}}} }} \left( {{\mathcal{X}}_{{j_{1} ,:}} ,b} \right),CI\left( {{\mathcal{X}}_{{j_{2} ,:}} ,b} \right)} \right)}}{{\left| {{\varvec{\pi}}_{{\mathcal{X}}} } \right|}} $$
(19)

where \(CI_{{{\varvec{\pi}}_{{\mathcal{X}}} }} \left( {{\mathcal{X}}_{j,:} ,b} \right)\) is the index of the cluster to which the \(j\) th data point belongs in the \(b\) th partition (note the index is computed among all clusters of ensemble). It is computed according to Eq. 20.

$$ CI_{{{\varvec{\pi}}_{{\mathcal{X}}} }} \left( {{\mathcal{X}}_{j,:} ,b} \right) = \mathop \sum \limits_{i = 1}^{b - 1} \left| {\pi_{{{\mathcal{X}},:}}^{i} } \right| + \mathop {\arg }\limits_{p} \left[ {{\mathcal{X}}_{{j_{1} ,:}} \in \dot{\pi }_{{{\mathcal{X}},p}}^{b} } \right] $$
(20)

It is worthy to be mentioned that the matrix \({\varvec{PPS}}_{{{\varvec{\pi}}_{{\mathcal{X}}} }}^{r}\) is symmetric, i.e. \(PPS_{{{\varvec{\pi}}_{{\mathcal{X}}} }}^{r} \left( {j_{1} ,j_{2} } \right) = PPS_{{{\varvec{\pi}}_{{\mathcal{X}}} }}^{r} \left( {j_{2} ,j_{1} } \right)\), just like \(w_{{{\varvec{\pi}}_{{\mathcal{X}}} }}\). Therefore, we propose to apply an agglomerative hierarchical complete linkage clustering algorithm on the attained point–point similarity matrix, i.e. \({\varvec{PPS}}_{{{\varvec{\pi}}_{{\mathcal{X}}} }}^{r}\), to cluster data points into a set of \(\left| {\pi_{{{\mathcal{X}},:}}^{ + } } \right|\) clusters. The mentioned obtained set of \(\left| {\pi_{{{\mathcal{X}},:}}^{ + } } \right|\) clusters is considered to be consensus partition.

Toy Example: We have assumed a dataset with 13 instances and three clusters. Let’s assume we want to generate an ensemble of size 5 using k-means clusterer algorithm. We have considered k-means clusterer algorithm running 5 times on our dataset to partition them into 2, 2, 3, 3 and 3 clusters, respectively. Let’s assume we have obtained an ensemble of size 5 on 13 instances. The assumptive ensemble is considered to be presented by Fig. 2. Therefore, we have ensemble \({\varvec{\pi}}_{{\mathbf{\mathcal{X}}}} = \left\{ {\pi_{{{\mathbf{\mathcal{X}}},1}} ,\pi_{{{\mathbf{\mathcal{X}}},2}} ,\pi_{{{\mathbf{\mathcal{X}}},3}} ,\pi_{{{\mathbf{\mathcal{X}}},4}} ,\pi_{{{\mathbf{\mathcal{X}}},5}} } \right\}\) where first partition is as follows \(\pi_{{{\mathbf{\mathcal{X}}},1}} = \left\{ {\pi_{{{\mathbf{\mathcal{X}}},1}}^{1} ,\pi_{{{\mathbf{\mathcal{X}}},1}}^{2} } \right\}\), second partition is as follows \(\pi_{{{\mathbf{\mathcal{X}}},2}} = \left\{ {\pi_{{{\mathbf{\mathcal{X}}},2}}^{1} ,\pi_{{{\mathbf{\mathcal{X}}},2}}^{2} } \right\}\), third partition is as follows \(\pi_{{{\mathbf{\mathcal{X}}},3}} = \left\{ {\pi_{{{\mathbf{\mathcal{X}}},3}}^{1} ,\pi_{{{\mathbf{\mathcal{X}}},3}}^{2} ,\pi_{{{\mathbf{\mathcal{X}}},3}}^{3} } \right\}\), fourth partition is as follows \(\pi_{{{\mathbf{\mathcal{X}}},4}} = \left\{ {\pi_{{{\mathbf{\mathcal{X}}},4}}^{1} ,\pi_{{{\mathbf{\mathcal{X}}},4}}^{2} ,\pi_{{{\mathbf{\mathcal{X}}},4}}^{3} } \right\}\), and fifth partition is as follows \(\pi_{{{\mathbf{\mathcal{X}}},5}} = \left\{ {\pi_{{{\mathbf{\mathcal{X}}},5}}^{1} ,\pi_{{{\mathbf{\mathcal{X}}},5}}^{2} ,\pi_{{{\mathbf{\mathcal{X}}},5}}^{3} } \right\}\).

Fig. 2
figure 2

A clustering ensemble with four base partitions

Full size image

Also, clusters of first partition are as follows: \(\pi_{{{\mathbf{\mathcal{X}}},1}}^{1}\) is equal to \(\left\{ {{\mathcal{X}}_{1,:} ,{\mathcal{X}}_{2,:} ,{\mathcal{X}}_{3,:} ,{\mathcal{X}}_{4,:} ,{\mathcal{X}}_{6,:} ,{\mathcal{X}}_{7,:} ,{\mathcal{X}}_{11,:} } \right\}\), and \(\pi_{{{\mathbf{\mathcal{X}}},1}}^{2}\) is equal to \(\left\{ {{\mathcal{X}}_{5,:} ,{\mathcal{X}}_{8,:} ,{\mathcal{X}}_{9,:} ,{\mathcal{X}}_{10,:} ,{\mathcal{X}}_{12,:} ,{\mathcal{X}}_{13,:} } \right\}\). Clusters of second partition are as follows: \(\pi_{{{\mathbf{\mathcal{X}}},2}}^{1}\) is equal to \(\left\{ {{\mathcal{X}}_{1,:} ,{\mathcal{X}}_{4,:} ,{\mathcal{X}}_{7,:} ,{\mathcal{X}}_{8,:} ,{\mathcal{X}}_{9,:} ,{\mathcal{X}}_{11,:} ,{\mathcal{X}}_{12,:} } \right\}\), \(\pi_{{{\mathbf{\mathcal{X}}},2}}^{2}\) is equal to \(\left\{ {{\mathcal{X}}_{2,:} ,{\mathcal{X}}_{3,:} ,{\mathcal{X}}_{5,:} ,{\mathcal{X}}_{6,:} ,{\mathcal{X}}_{10,:} ,{\mathcal{X}}_{13,:} } \right\}\). Clusters of third partition are as follows: \(\pi_{{{\mathbf{\mathcal{X}}},2}}^{2}\) \(\pi_{{{\mathbf{\mathcal{X}}},3}}^{1}\) is equal to \(\left\{ {{\mathcal{X}}_{1,:} ,{\mathcal{X}}_{2,:} ,{\mathcal{X}}_{3,:} ,{\mathcal{X}}_{4,:} ,{\mathcal{X}}_{11,:} ,{\mathcal{X}}_{12,:} } \right\}\), \(\pi_{{{\mathbf{\mathcal{X}}},3}}^{2}\) is equal to \(\left\{ {{\mathcal{X}}_{8,:} ,{\mathcal{X}}_{9,:} } \right\}\), \(\pi_{{{\mathbf{\mathcal{X}}},3}}^{3}\) is equal to \(\left\{ {{\mathcal{X}}_{5,:} ,{\mathcal{X}}_{6,:} ,{\mathcal{X}}_{7,:} ,{\mathcal{X}}_{10,:} ,{\mathcal{X}}_{13,:} } \right\}\). Clusters of fourth partition are as follows: \(\pi_{{{\mathbf{\mathcal{X}}},4}}^{1}\) is equal to \(\left\{ {{\mathcal{X}}_{3,:} ,{\mathcal{X}}_{5,:} ,{\mathcal{X}}_{6,:} ,{\mathcal{X}}_{9,:} } \right\}\), \(\pi_{{{\mathbf{\mathcal{X}}},4}}^{2}\) is equal to \(\left\{ {{\mathcal{X}}_{10,:} ,{\mathcal{X}}_{11,:} ,{\mathcal{X}}_{12,:} ,{\mathcal{X}}_{13,:} } \right\}\), \(\pi_{{{\mathbf{\mathcal{X}}},4}}^{3}\) is equal to \(\left\{ {{\mathcal{X}}_{1,:} ,{\mathcal{X}}_{2,:} ,{\mathcal{X}}_{4,:} ,{\mathcal{X}}_{7,:} ,{\mathcal{X}}_{8,:} } \right\}\). Finally, clusters of last partition are as follows: \(\pi_{{{\mathbf{\mathcal{X}}},5}}^{1}\) is equal to \(\left\{ {{\mathcal{X}}_{9,:} ,{\mathcal{X}}_{10,:} ,{\mathcal{X}}_{11,:} ,{\mathcal{X}}_{12,:} ,{\mathcal{X}}_{13,:} } \right\}\), \(\pi_{{{\mathbf{\mathcal{X}}},5}}^{2}\) is equal to \(\left\{ {{\mathcal{X}}_{3,:} ,{\mathcal{X}}_{5,:} ,{\mathcal{X}}_{6,:} } \right\}\), \(\pi_{{{\mathbf{\mathcal{X}}},5}}^{3}\) is equal to \(\left\{ {{\mathcal{X}}_{1,:} ,{\mathcal{X}}_{2,:} ,{\mathcal{X}}_{4,:} ,{\mathcal{X}}_{7,:} ,{\mathcal{X}}_{8,:} } \right\}\).

\({\varvec{SCCS}}_{{{\varvec{\pi}}_{{\mathcal{X}}} }}\) for the ensemble presented in Fig. 2 is depicted in Fig. 3. Now, we have a graph \({\mathcal{G}}\left( {{\varvec{\pi}}_{{\mathcal{X}}} } \right)\) where set of its vertices, i.e. \({\mathcal{V}}\left( {{\varvec{\pi}}_{{\mathcal{X}}} } \right)\), is \(\left\{ {1,2,3,4,5,6,7,8,9,10,11,12,13} \right\}\) and set of its edges, i.e. \({\mathcal{E}}\left( {{\varvec{\pi}}_{{\mathcal{X}}} } \right)\), is presented in Fig. 4. Figure 5 depicts cluster–cluster similarity matrix, i.e. \({\varvec{CCS}}_{{{\varvec{\pi}}_{{\mathcal{X}}} }}^{2}\), when (a) Euclidian distance, i.e. \({\varvec{EuclidianDis}}_{{{\varvec{\pi}}_{{\mathcal{X}}} }}^{2}\), or (b) Cosine distance, i.e. \({\varvec{CosineDis}}_{{{\varvec{\pi}}_{{\mathcal{X}}} }}^{2}\) is used for our toy ensemble. Finally, Fig. 6 depicts point–point similarity matrix, i.e. \({\varvec{PPS}}_{{{\varvec{\pi}}_{{\mathcal{X}}} }}^{2}\), when (a) Euclidian distance, i.e. \({\varvec{EuclidianDis}}_{{{\varvec{\pi}}_{{\mathcal{X}}} }}^{2}\), or (b) Cosine distance, i.e. \({\varvec{CosineDis}}_{{{\varvec{\pi}}_{{\mathcal{X}}} }}^{2}\) is used for our toy ensemble.

Fig. 3
figure 3

The \({\varvec{SCCS}}_{{{\varvec{\pi}}_{{\mathcal{X}}} }}\) for the ensemble presented in Fig. 2

Full size image
Fig. 4
figure 4

The edges of the transition graph, i.e. \({\mathcal{E}}\left( {{\varvec{\pi}}_{{\mathcal{X}}} } \right)\), for the ensemble presented in Fig. 2

Full size image
Fig. 5
figure 5

Cluster–cluster similarity matrix, i.e. \({\varvec{CCS}}_{{{\varvec{\pi}}_{{\mathcal{X}}} }}^{2}\), when (a) Euclidian distance, i.e. \({\varvec{EuclidianDis}}_{{{\varvec{\pi}}_{{\mathcal{X}}} }}^{2}\), or (b) Cosine distance, i.e. \({\varvec{CosineDis}}_{{{\varvec{\pi}}_{{\mathcal{X}}} }}^{2}\) is used for the ensemble presented in Fig. 2

Full size image
Fig. 6
figure 6

Point–point similarity matrix, i.e. \({\varvec{PPS}}_{{{\varvec{\pi}}_{{\mathcal{X}}} }}^{2}\), when (a) Euclidian distance, i.e. \({\varvec{EuclidianDis}}_{{{\varvec{\pi}}_{{\mathcal{X}}} }}^{2}\), or (b) Cosine distance, i.e. \({\varvec{CosineDis}}_{{{\varvec{\pi}}_{{\mathcal{X}}} }}^{2}\) is used for the ensemble presented in Fig. 2

Full size image

5 Experimental study

5.1 Datasets

Many real-world and synthetic data sets are here employed for assessment. The real-world data sets are as follows: Bupa, Breast-cancer, Glass, Galaxy, Ionosphere, Iris, ISOLET, Landsat-satellite, Letter-Recognition, SAHeart, Wine, and Yeast from UCI machine learning repository (Newman et al. 1998) together with an auxiliary real data set of USPS (Dueck 2009). Bupa, Breast-cancer, Glass, Galaxy, Ionosphere, Iris, ISOLET, Landsat-satellite, Letter-Recognition, SAHeart, USPS, Wine, and Yeast data sets have 345, 683, 214, 323, 351, 150, 7,797, 6,435, 20,000, 462, 11,000, 178, and 1,484 data samples, respectively; they also have 6, 9, 9, 4, 34, 4, 617, 36, 16, 9, 256, 13, and 8 features and 2, 2, 6, 7, 2, 3, 26, 6, 26, 2, 10, 3, and 10 clusters, respectively.

Our benchmark includes two dimensions synthetic data sets including \({Artificial}_{1}\), \({Artificial}_{2}\), \({Artificial}_{3}\), and Halfring. Halfring data set contains two clusters and 400 instances, while other three data sets contain three clusters and 300 instances. The scatter plots of these synthetic data sets are depicted in Fig. 7. We have standardized all of our mentioned data sets so that in all datasets, each feature is transformed into a new range with distribution of \(N\left(\mathrm{0,1}\right)\) and the features with missed values are removed from the data sets.

Fig. 7.
figure 7

4 artificial benchmark datasets

Full size image

5.2 Parameters

The ensemble generation has been accomplished according to the technique introduced in Ren et al. (2013). The k-means clustering algorithm was employed for 50 different subsets of a given data set to generate ensemble of size 50. The sampling ratio employed in this paper is 0.8.

The following recent clustering ensembles have been employed as a benchmark to this paper: HBGF (Fern and Brodley 2004), CO–AL (Fred and Jain 2005), SRS (Iam-On et al. 2008), WCT (Iam-On et al. 2011), DICLENS (Mimaroglu and Aksehirli 2012) , ONCE –AL (Alqurashi and Wang 2014), CSEAC (Alizadeh et al. 2014a), DSCE (Alqurashi and Wang 2015), WEAC (Huang et al. 2015), GPMGLA (Huang et al. 2015), WCE (Alizadeh et al. 2015) ECSEAC (Parvin and Minaei-Bidgoli 2015) and TME (Zhong et al. 2015).

For a given clustering ensemble, its initialization is performed according to its corresponding paper. The results of the paper are provided after averaging on 30 independent runs, while all methods are considered with the ensemble size of 100.

5.3 Evaluation metrics

Internal measures such as silhouette or sum of square errors (SSE) computed without caring about the ground-truth labels of the data could be used to assess a clustering result on a given data set. External measures computed considering the ground-truth labels of the data are other set of the measures to assess a resultant partition on a given data set. Note that the ground-truth labels of the data are only used for assessment after obtaining the resultant partition, and they are not used during the clustering task. Although both the internal and external sets of the measures are popular, we have only used four external measures of adjust rand index (ARI), normalized mutual information (NMI) and accuracy (ACC) rate and F-measure (FM). Given the ground-truth labels \({\pi }_{\mathcal{X}}^{+}\), adjust rand index of a resultant partition \({\pi }_{\mathcal{X}}^{*}\) is achieved using the following equation

$$ARI\left({\pi }_{\mathcal{X}}^{*},{\pi }_{\mathcal{X}}^{+}\right)=\frac{\sum_{i=1}^{\left|{\pi }_{\mathcal{X},:}^{*}\right|}\sum_{j=1}^{\left|{\pi }_{\mathcal{X},:}^{+}\right|}\left(\begin{array}{c}\left|{\pi }_{\mathcal{X},i}^{*}\cap {\pi }_{\mathcal{X},j}^{+}\right|\\ 2\end{array}\right)-\frac{\sum_{i=1}^{\left|{\pi }_{\mathcal{X},:}^{*}\right|}\left(\begin{array}{c}\left|{\pi }_{\mathcal{X},i}^{*}\right|\\ 2\end{array}\right)\times \sum_{i=1}^{\left|{\pi }_{\mathcal{X},:}^{+}\right|}\left(\begin{array}{c}\left|{\pi }_{\mathcal{X},i}^{+}\right|\\ 2\end{array}\right)}{\left(\begin{array}{c}\left|{\mathcal{X}}_{:,1}\right|\\ 2\end{array}\right)}}{\frac{\sum_{i=1}^{\left|{\pi }_{\mathcal{X},:}^{*}\right|}\left(\begin{array}{c}\left|{\pi }_{\mathcal{X},i}^{*}\right|\\ 2\end{array}\right)+\sum_{i=1}^{\left|{\pi }_{\mathcal{X},:}^{+}\right|}\left(\begin{array}{c}\left|{\pi }_{\mathcal{X},i}^{+}\right|\\ 2\end{array}\right)}{\left(\begin{array}{c}\left|{\mathcal{X}}_{:,1}\right|\\ 2\end{array}\right)}-\frac{\sum_{i=1}^{\left|{\pi }_{\mathcal{X},:}^{*}\right|}\left(\begin{array}{c}\left|{\pi }_{\mathcal{X},i}^{*}\right|\\ 2\end{array}\right)\times \sum_{i=1}^{\left|{\pi }_{\mathcal{X},:}^{+}\right|}\left(\begin{array}{c}\left|{\pi }_{\mathcal{X},i}^{+}\right|\\ 2\end{array}\right)}{\left(\begin{array}{c}\left|{\mathcal{X}}_{:,1}\right|\\ 2\end{array}\right)}}$$
(21)

where \(\left| {\pi_{{{\mathbf{\mathcal{X}}},i}}^{*} \cap \pi_{{{\mathbf{\mathcal{X}}},j}}^{ + } } \right|\) is the number of data points shared between the \(i\) th cluster of consensus partition \(\pi_{{\mathbf{\mathcal{X}}}}^{*}\) and the \(j\) th cluster of target partition \(\pi_{{\mathbf{\mathcal{X}}}}^{ + }\). The binomial function \(\left( {\begin{array}{*{20}c} x \\ 2 \\ \end{array} } \right)\) is obtained as

$$ \left( {\begin{array}{*{20}c} x \\ 2 \\ \end{array} } \right) = \frac{x!}{{\left( {x - 2} \right)!2!}} = \frac{{x \times \left( {x - 1} \right)}}{2} $$
(22)

Given the ground-truth partition \(\pi_{{\mathbf{\mathcal{X}}}}^{ + }\), the normalized mutual information for a resultant partition \(\pi_{{\mathbf{\mathcal{X}}}}^{*}\) is achieved by

$$ NMI\left( {\pi_{{\mathbf{\mathcal{X}}}}^{*} ,\pi_{{\mathbf{\mathcal{X}}}}^{ + } } \right) = \frac{{\mathop \sum \nolimits_{i = 1}^{{\left| {\pi_{{{\mathbf{\mathcal{X}}},:}}^{*} } \right|}} \mathop \sum \nolimits_{j = 1}^{{\left| {\pi_{{{\mathbf{\mathcal{X}}},:}}^{ + } } \right|}} \left| {\pi_{{{\mathbf{\mathcal{X}}},i}}^{*} \cap \pi_{{{\mathbf{\mathcal{X}}},j}}^{ + } } \right|\log_{2} \left( {\frac{{\left| {{\mathcal{X}}_{:,1} } \right| \times \left| {\pi_{{{\mathbf{\mathcal{X}}},i}}^{*} \cap \pi_{{{\mathbf{\mathcal{X}}},j}}^{ + } } \right|}}{{\left| {\pi_{{{\mathbf{\mathcal{X}}},i}}^{*} } \right| \times \left| {\pi_{{{\mathbf{\mathcal{X}}},j}}^{ + } } \right|}}} \right)}}{{\sqrt {\mathop \sum \nolimits_{i = 1}^{{c_{*} }} \left( {\left| {\pi_{{{\mathbf{\mathcal{X}}},i}}^{*} } \right| \times \log_{2} \left( {\frac{{\left| {\pi_{{{\mathbf{\mathcal{X}}},i}}^{*} } \right|}}{{\left| {{\mathcal{X}}_{:,1} } \right|}}} \right)} \right) \times \mathop \sum \nolimits_{i = 1}^{c} \left( {\left| {\pi_{{{\mathbf{\mathcal{X}}},j}}^{ + } } \right| \times \log_{2} \left( {\frac{{\left| {\pi_{{{\mathbf{\mathcal{X}}},j}}^{ + } } \right|}}{{\left| {{\mathcal{X}}_{:,1} } \right|}}} \right)} \right)} }} $$
(23)

Also, accuracy of \(\pi_{*}\) is computed by

$$ ACC\left( {\pi_{{\mathbf{\mathcal{X}}}}^{*} ,\pi_{{\mathbf{\mathcal{X}}}}^{ + } } \right) = \mathop {\max }\limits_{\sigma } \mathop \sum \limits_{j = 1}^{{\left| {\pi_{{{\mathbf{\mathcal{X}}},:}}^{ + } } \right|}} \frac{{\left| {\pi_{{{\mathbf{\mathcal{X}}},\sigma_{j} }}^{*} \cap \pi_{{{\mathbf{\mathcal{X}}},j}}^{ + } } \right|}}{{\left| {{\mathcal{X}}_{:,1} } \right|}} $$
(24)

where the relabeling task \(\sigma\) is a permutation of \(\left\{ {1,2, \ldots ,\left| {\pi_{{{\mathbf{\mathcal{X}}},:}}^{*} } \right|} \right\}\) so that \(\sigma_{j} \in \left\{ {1,2, \ldots ,\left| {\pi_{{{\mathbf{\mathcal{X}}},:}}^{*} } \right|} \right\}\), \(\forall i \in \left\{ {1,2, \ldots ,\left| {\pi_{{{\mathbf{\mathcal{X}}},:}}^{*} } \right|} \right\}\) and \(\forall i,j \in \left\{ {1,2, \ldots ,\left| {\pi_{{{\mathbf{\mathcal{X}}},:}}^{*} } \right|} \right\}:\left( {i \ne j} \right) \to \left( {\sigma_{i} \ne \sigma_{j} } \right)\).

Finally, for a given target partition \(\pi_{{{\mathbf{\mathcal{X}}},:}}^{ + }\), F-measure of a resultant partition \({\pi }_{\mathcal{X},:}^{*}\) is acquired by

$$ FM\left( {\pi_{{\mathbf{\mathcal{X}}}}^{*} ,\pi_{{\mathbf{\mathcal{X}}}}^{ + } } \right) = \mathop {\max }\limits_{\sigma } \mathop \sum \limits_{j = 1}^{{\left| {\pi_{{{\mathbf{\mathcal{X}}},:}}^{ + } } \right|}} \frac{{2 \times \left| {\pi_{{{\mathbf{\mathcal{X}}},\sigma_{j} }}^{*} } \right| \times \frac{{\left| {\pi_{{{\mathbf{\mathcal{X}}},\sigma_{j} }}^{*} \cap \pi_{{{\mathbf{\mathcal{X}}},j}}^{ + } } \right|}}{{\left| {\pi_{{{\mathbf{\mathcal{X}}},j}}^{ + } } \right|}} \times \frac{{\left| {\pi_{{{\mathbf{\mathcal{X}}},\sigma_{j} }}^{*} \cap \pi_{{{\mathbf{\mathcal{X}}},j}}^{ + } } \right|}}{{\left| {\pi_{{{\mathbf{\mathcal{X}}},\sigma_{j} }}^{*} } \right|}}}}{{\left| {{\mathcal{X}}_{:,1} } \right| \times \left( {\frac{{\left| {\pi_{{{\mathbf{\mathcal{X}}},\sigma_{j} }}^{*} \cap \pi_{{{\mathbf{\mathcal{X}}},j}}^{ + } } \right|}}{{\left| {\pi_{{{\mathbf{\mathcal{X}}},j}}^{ + } } \right|}} + \frac{{\left| {\pi_{{{\mathbf{\mathcal{X}}},\sigma_{j} }}^{*} \cap \pi_{{{\mathbf{\mathcal{X}}},j}}^{ + } } \right|}}{{\left| {\pi_{{{\mathbf{\mathcal{X}}},\sigma_{j} }}^{*} } \right|}}} \right)}}. $$
(25)

The mentioned measures vary in the range of \(\left[ {0,1} \right]\). For any of them, the greater values indicate better quality of resultant partition \(\pi_{{\mathbf{\mathcal{X}}}}^{*}\). ACC and FM measures are asymmetric, but ARI and NMI are symmetric measures.

5.4 Numerical empirical analysis

The analysis of parameter \(r\) in our method, i.e. MLCC, is presented in Fig. 8. Figure 8 depicts performance of MLCC for different values of parameter \(r\) in terms of NMI. The results indicate that the best result is acquired at \(r = 20\). Indeed, after \(r \ge 10\), the results are acceptable and consistent. Therefore, we set \(r = 15\) from now on.

Fig. 8
figure 8

Effect of parameter r on the performance of the MLCC method in terms of normalized mutual information

Full size image

MLCC algorithm is compared in Fig. 9 with the state-of-the-art baseline methods mentioned in Sect. 5.2 in terms of NMI on several of benchmark data sets. Table 1 has provided the results of Fig. 9 in summary where the triple w-t-l contains integer numbers w, t and l which, respectively, indicate the number of data sets which the proposed method is the superior method on them, the number of data sets that the proposed method is the loser on them and the number of data sets that the proposed method is neither the loser nor the winner on them. Paired t-test has been used to accomplish all the tests. Superiority of the proposed method to all state-of-the-art baseline methods could be concluded from Table 1.

Fig. 9
figure 9

Comparison of the MLCC method with the state-of-the-art baseline methods on different data sets in terms of normalized mutual information

Full size image
Table 1 Summary of the presented results in Fig. 9
Full size table

Figures 10, 11 and 12 represent the comparison of the MLCC method with the state-of-the-art baseline methods on all of our data sets, respectively, in terms of adjacent rand index, accuracy and f-measure.

Fig. 10
figure 10

Comparison of the MLCC method with the state-of-the-art baseline methods on different data sets in terms of adjacent rand index

Full size image
Fig. 11
figure 11

Comparison of the MLCC method with the state-of-the-art baseline methods on different data sets in terms of accuracy

Full size image
Fig. 12
figure 12

Comparison of the MLCC method with the state-of-the-art baseline methods on different data sets in terms of f-measure

Full size image

According to Figs. 10, 11 and 12, the following conclusions could be drawn. First, the MLCC algorithm outperforms the state-of-the-art baseline methods in most of the used benchmark data sets. Second, although the state-of-the-art baseline methods outperform the MLCC algorithm in some of the used benchmark data sets, it is always among the top three best methods. All of the results presented in Figs. 9, 10, 11 and 12 have been validated by Friedman ANOVA test. The Friedman ANOVA test shows that there is always significant difference. For further analysis, the detailed results of Figs. 10, 11, 12 and 13 are presented in Table 2. In Table 2, the results of different clustering ensembles in terms of our four metrics have been presented.

Fig. 13
figure 13

Performances of different methods in the presence of different levels of noise in terms of normalized mutual information for (a) Iris data set and (b) Wine data set

Full size image
Table 2 The performance of the proposed method and the other methods in terms of NMI|ARI|Accuracy|FM
Full size table

We can also prove that the MLCC method has the time complexity of \(O\left( {r \times \left| {{\varvec{\pi}}_{{{\mathcal{X}},:}} } \right|^{3} } \right)\) or \(O\left( {r\left| {{\varvec{\pi}}_{{{\mathcal{X}},:}} } \right|^{3} \left| {{\varvec{\pi}}_{{\mathcal{X}}} } \right|^{3} } \right)\) in its worst case.

5.5 Noise-resistance analysis

We have examined the noise effect by adding Gaussian noise with different energy levels and analyzing robustness of the MLCC, \(ECSEAC\) and \(CSEAC\) as three best methods achieved by Table 1. The \(i\) th cluster of the data set is assumed to have the covariance of \(\Sigma_{i}\), while \(\aleph_{i}\) is considered to be a temporary noise data which has the same size as the cluster of data set mentioned for a noise ratio of \(\varsigma\). Data samples of \(\aleph_{i}\) are with the covariance matrix of \(\varsigma \times \Sigma_{i}\). The data samples of that temporary noise data are here added to the \(i\) th cluster's data samples. For all clusters in data set, the data samples of that temporary noise data with the covariance matrix \(\varsigma \times \Sigma_{i}\) are added to the data samples of the \(i\) th cluster to obtain a new noisy data set with noise ratio \(\varsigma \times 100\)%. We can easily observe that there is no noise when \(\varsigma = 0\). Figure 13 includes the results of the Iris and Wine data sets where NMI value is shown on the vertical axis and amount of the noise ratio \(\varsigma\) is shown on the horizontal axis. Apparently, by adding noise level, the gap between MLCC and other methods will be larger. It means MLCC is more robust against noise.

5.6 News clustering application

A widely used labelled Persian text benchmark was introduced as Hamshahri data set in AleAhmad et al. (2009) which includes 9 classes and 36 subclasses.

We have sampled a subset of Hamshahri data set containing sport, economic, rural, adventure, and foreign classes each of which has 200 texts (1000 texts totally). Efficacy of the k-means clusterer algorithm after obtaining the data set like Shahriari et al. (2015) without using a thesaurus is 60.32% in terms of the f-measure, while efficacy of the MLCC, \(CSEAC\) and \(ECSEAC\) algorithms are, respectively, 64.11%, 62.13% and 62.97%. Since \(CSEAC\), \(ECSEAC\), and MLCC are the best methods according to Table 2, this experiment is carried out using these methods and the results have been summarized in Fig. 14.

Fig. 14
figure 14

Performances of different methods on Hamshahri text data set

Full size image

6 Conclusions and future work

This work proposes a new consensus function in clustering ensemble named multi-level consensus clustering (MLCC). Since we use a multi-level clustering instead of direct object clustering, MLCC is a really efficient clusterer algorithm. An innovative similarity metric for measuring similarity between clusters is proposed. After obtaining an ensemble, a cluster–cluster similarity matrix using the mentioned metric is generated. The mentioned cluster–cluster similarity matrix is used to make an object–object or point–point similarity matrix. Then, we apply an average hierarchical clusterer algorithm on the point–point similarity matrix to make consensus partition. While MLCC is better than traditional clustering ensembles and simple version of clustering ensembles on traditional cluster–cluster similarity matrix, but its computational cost is not very bad. Accuracy and robustness of the proposed method are compared with the art clustering algorithms through the experimental tests. Also, time analysis is presented in the experimental results. Comparison of the proposed method with the state-of-the-art clustering ensemble methods in terms of 4 different metrics on numerous real-world and synthetic data sets reveals that the proposed method is the superior method which did not need relabeling mechanism.