Unsteady Mixed Bioconvection Flow of Eyring–Powell Nanofluid with Motile Gyrotactic Microorganisms Past Stretching Surface

Abstract

The provided mathematical analysis aims to scrutinize the behavior of gyrotactic microorganisms to depict their role in heat and mass transfer in an unsteady mixed convection stretched flow of special Eyring–Powell nanofluid loaded by nanoparticles and gyrotactic microorganisms with simultaneous impact of Lorentz forces and zero nanoparticle flux condition at boundary. A two-phase type is presented for modeling the nanofluid. Thought of microorganisms is adopted just to stabilize the pendant nanoparticles due to bioconvection which has been promoted by combined impacts of both buoyancy and magnetic field forces. The controlling highly nonlinear partial differential equations with the auxiliary conditions have been mutated into ordinary differential equations via a convenient similarity approach. Governing mutated equations have been solved computationally by means of fifth-order Runge–Kutta–Fehlberg scheme with 10⁻⁶ tolerance level, the numerical calculations were presented. Further, our computations illustrate that a significant impact of unsteady parameter by examining the factor values of skin friction and the local density numbers. While A parameter leads to weaken skin friction, it boosts the local density number. The coefficient of heat and motile microorganism transfer rates strengthen, when mixed convection parameter λ improves. While base fluid parameter ϵ weakens the rate of heat transfer, it enhances the local density number. In addition, comparison was provided between Newtonian and non-Newtonian Powell–Eyring fluid on velocity and temperature distributions to confirm the methodology. Comparison with given results for special conditions is presented and seen to be highly satisfactory.

1 Introduction

Flow of non-Newtonian liquids about either a stretching surfaces or circular cylinder have massive applications in both sciences and engineering. Extensively notable attention has been devoted to investigate miscellaneous patterns of non-Newtonian fluids. Among of these is Eyring–Powell liquid pattern which is more complex. A full mathematical model for Eyring–Powell fluid has suggested by Powell and Eyring [1]. This mathematical model characterizes properties of shear thinning fluids. Examples of such non-Newtonian liquids are ketchup, human blood, toothpaste, etc. This type of liquids has some features over the other patterns of non-Newtonian fluids. One of these advantages Eyring–Powell pattern correctly tends to Newtonian fluid behavior for low and high shear rates; also, this model is deduced from the kinetic theory rather than the experimental relationships.

Till now, a few contributions have been provided for the 2-dimensional Eyring–Powell fluid flow. Malik et al. [2] analyzed heat transfer of non-Newtonian Eyring–Powell liquid due to a stretching cylinder analytically. The authors debated two types of variable viscosity known as Reynolds and Vogels. Akbar et al. [3] examined the impact of MHD on incompressible, 2-dimensional flow of non-Newtonian Eyring–Powell fluid due to a linear stretching sheet. The impacts of fluid parameters on the non-dimensional velocity and shear stress have been addressed. The boundary layer flow and heat transfer of Eyring–Powell fluid along a moving stretching/shrinking sheet has been exhibited by Rosca and Pop [4]. Hayat et al. [5] analyzed steady-state flow of a non-Newtonian Eyring–Powell fluid due to a moving surface with convective boundary conditions. Numerical analysis of MHD viscous dissipation impact on natural convection heat and mass transfer of non-Newtonian Eyring–Powell fluid flow through porous media has been presented by Nabil et al. [6]. Via asymptotic boundary conditions procedure, Patel and Timol [7] explored the idea of Eyring–Powell fluid flow. Various contributions have been published for non-Newtonian Eyring–Powell fluids [8,9,10,11,12,13,14,15].

Recently, the investigation of flow and thermophysical properties of nanofluids has attracted construable interest according to its wide potential for the use of such liquids as efficient heat transfer liquids, and in several biomedical applications. The nanofluid word points out nanoparticles in a pure fluid, where the basic of a nanofluid was suggested by Choi [16] firstly. The researcher illustrated that by suspending a tiny quantity of nanoparticles to conventional heat transfer liquids, the thermal conductivity of the liquid enhanced by approximately a double factor. Buongiorno [17] presented seven slip mechanisms among nanoparticles and pure fluid. The particle Brownian motion and thermophoresis have been taken into account, and he illustrated that both Brownian motion and thermophoresis have major impact on forced convection in nanofluids. The shooting method has been applied by Rohni et al. [18] to obtain a numerical solution of the equations for a time-dependent shrinking surface with wall mass suction utilizing the nanofluid paradigm suggested by Buongiorno [17]. Also, Zaimi et al. [19] considered the Buongiorno model to examine unsteady flow along a contracting cylinder. Some of published contributions restricted on nanofluid model [20,21,22,23,24,25,26].

Bacteria and microalgae represent types of the microorganisms possess high density rather than water; thus, these microorganisms swim in upward direction against the gravity. Top layer of suspension is very dense than the lower ones because of gathering of microorganisms which cause unstable density distribution. So, convective instability takes place as a result and may lead to manners of convection. These arbitrary and involuntary movement manners of microorganisms in the suspension are known as bioconvection. Although solutions to solve these cases in real world are very significant, the wide modeling and mathematical simulations has lead to bioconvection nanofluid as unprecedented achievement. Bioconvection flow of microorganisms as a result in gyrotactic stimuli and water regular nanofluids including heat and mass transfer has been investigated by Siddiqa et al. [27]. Bhatti et al. [28] modeled mathematically chemical reaction impacts for MHD nanofluid flow with gyrotactic microorganisms to interpret the impact of thermal radiation. Mahdy [29] obtained a similarity solution for Darcy natural convection flow due to a vertical circular cone in a nanofluid including gyrotactic microorganisms. Lately, investigations concentrated on heat transfer that cause in bioconvection have widely utilized gyrotactic microorganisms [30,31,32,33,34,35,36].

Literature review illustrated that the flow of non-Newtonian Eyring–Powell nanofluid involving nanoparticles and gyrotactic microorganisms has not been gained much attention so far. The current contribution determinations is to accomplish this gap in the existing literature. Hence, a theoretical analysis has been presented to address the problem of an unsteady mixed bioconvection flow of a non-Newtonian Eryning–Powell nanofluid due to stretching sheet. At the end of the paper, impact of emerging physical factors on the velocity, temperature, concentration, motile microorganisms, drag force, heat, and mass transfer are elucidated through graphs and tables. As observed, the unsteadiness parameter and Eyring–Powell fluid parameter lead to boost the coefficient of drag force, while motile microorganism density number weakens. This case has not been treated before, so the outcomes are original and new. In the future, this contribution can be extended to recognize case of an inclined magnetic field or Eyring–Powell hybrid nanofluid.

2 Mathematical Equations

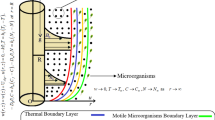
We scrutinize the unsteady state, two-dimensional MHD mixed bioconvection boundary layer flow of an incompressible non-Newtonian Eyring–Powell nanofluid with heat transfer and gyrotactic microorganisms due to a stretching sheet. The flow field model is described in the presence of a transverse magnetic field with uniform intensity B₀ imposed normal to the sheet. Additionally, with absence of voltage application, the Reynolds number becomes small. Therefore, the generated magnetic field has measly impact. Furthermore, we presume that nanoparticles have no any aspect on both the swimming velocity and microorganisms’ swimming direction. We depict the Cartesian coordinate system where x- and y-axes are plotted to be along and normal to the stretching sheet (Fig. 1). Let ${U}_w=\frac{ax}{\left(1-\gamma t\right)}$ represent the stretching velocity toward the x-direction. Eyring–Powell fluid stress tensor [12] is stated as

$$ S=- pI+{\tau}_{ij} $$

(1)

such that extra Cauchy stress tensors in an Eyring–Powell model τ_ij is expressed as [37]

$$ {\tau}_{ij}=\mu \frac{\partial {u}_i}{\partial {x}_j}+\frac{1}{\beta^{\ast }}{\sinh}^{-1}\left(\frac{1}{c}\frac{\partial {u}_i}{\partial {x}_j}\right) $$

(2)

Fig. 1

Nano-bioconvection non-Newtonian Eyring–Powell nanofluid flow model

Here, μ points out the dynamic viscosity, β^* and c represent non-Newtonian Eyring–Powell fluid material parameters. Let us use the second-order approximation of the function as:

$$ {\sinh}^{-1}\left(\frac{1}{c}\frac{\partial {u}_i}{\partial {x}_j}\right)\cong \frac{1}{c}\frac{\partial {u}_i}{\partial {x}_j}-\frac{1}{6}{\left(\frac{1}{c}\frac{\partial {u}_i}{\partial {x}_j}\right)}^3,\kern4em \left|\frac{1}{c}\frac{\partial {u}_i}{\partial {x}_j}\right|\ll 1 $$

The temperature T, nanoparticle volume fraction C and density of motile microorganisms χ at the sheet are taken to be ${T}_w(x)={T}_{\infty }+\frac{T_0x}{{\left(1-\gamma t\right)}^2}$, ${C}_0(x)=\frac{C_{\infty }x}{{\left(1-\gamma t\right)}^2}$, and ${\chi}_w(x)={\chi}_{\infty }+\frac{\chi_0x}{{\left(1-\gamma t\right)}^2}$, receptively, whereas the ambient of these quantities are T_∞, C_∞, and χ_∞. Noticing that a and γ stand for constants (where a > 0 and γ ⩽ 0, with γt < 1), and T₀ represents a constant, values T₀ < 0 and T₀ > 0 pointing out the opposing and assisting flows, respectively, while as T₀ = 0 yields forced convection limit (buoyancy force isn’t involving). Again, χ₀ is a constant. Further, for granted we presume that stability of Eyring–Powell nanofluid suspension is maintained and it is dilute (nanoparticles volume fraction less than 1%) to boost the gyrotactic microorganisms bioconvection in optimum way. Axiomatically high viscosity of pure fluid do not have positive impact on bioconvection; it is compulsory to dilute the suspension involving nanoparticles (Kuznetsov [20], Mosayebidorcheh et al. [22]). For an incompressible nanofluid following non-Newtonian Eyring–Powell model, the bioconvcetion flow governing equations can be stated via the Boussinesq approximations as Mutuku and Makinde [38] and Naseem et al. [35].

$$ \frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0 $$

(3)

$$ {\displaystyle \begin{array}{l}\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=\left({\nu}_f+\frac{1}{\rho_f{\beta}^{\ast }c}-\frac{1}{2{\rho}_f{\beta}^{\ast }{c}^3}{\left(\frac{\partial u}{\partial y}\right)}^2\right)\frac{\partial^2u}{\partial {y}^2}-\frac{\sigma {B}_0^2}{\rho_f}u\\ {}+\frac{g}{\rho_f}\left(\left(1-{C}_{\infty}\right){\rho}_{f\infty}\beta \left(T-{T}_{\infty}\right)-\left({\rho}_p-{\rho}_{f\infty}\right)\left(C-{C}_{\infty}\right)-\overset{\sim }{\gamma}\left({\rho}_m-{\rho}_{f\infty}\right)\left(\chi -{\chi}_{\infty}\right)\right)\end{array}} $$

(4)

(5)

$$ \frac{\partial C}{\partial t}+u\frac{\partial C}{\partial x}+v\frac{\partial C}{\partial y}={D}_B\frac{\partial^2C}{{\partial y}^2}+\frac{D_T}{T_{\infty }}\frac{\partial^2T}{{\partial y}^2} $$

(6)

$$ \frac{\partial \chi }{\partial t}+u\frac{\partial \chi }{\partial x}+v\frac{\partial \chi }{\partial y}+\frac{b{W}_c}{C_0}\frac{\partial }{\partial y}\left(\chi \frac{\partial C}{\partial y}\right)={D}_m\frac{\partial^2\chi }{\partial {y}^2} $$

(7)

subject to an appropriate initial and boundary conditions:

$$ {\displaystyle \begin{array}{l}t<0:\kern2em u\left(x,y\right)=v\left(x,y\right)=0,\kern2em T\left(x,y\right)={T}_{\infty },\kern1em C\left(x,y\right)={C}_{\infty },\kern1em \chi \left(x,y\right)={\chi}_{\infty}\\ {}t\geqslant 0:\kern1em u={U}_w,\kern1em v=0,\kern1em T={T}_w,\kern1em {D}_B\frac{\partial C}{\partial y}+\frac{D_T}{T_{\infty }}\frac{\partial T}{\partial y}=0,\kern1em \chi \left(x,0\right)={\chi}_w\kern2em \mathrm{at}\left(x,0\right)\\ {}u\left(x,\infty \right)\to 0,\kern1em T\left(x,\infty \right)\to {T}_{\infty },\kern1em C\left(x,\infty \right)\to {C}_{\infty },\kern1em \chi \left(x,\infty \right)\to {\chi}_{\infty },\end{array}} $$

(8)

Noticing that microorganism, nanoparticle concentration, and fluid densities are symbolized by ρ_m, ρ_p and ρ_f, respectively. ν_f stands for kinematic density, whereas the electrical conductivity be σ, the gravity vector is given by g, the fluid volume expansion factor is indicated by β, thermal diffusivity of regular fluid is represented by α_f, the ratio of effective heat capacitance of the nanoparticles is symbolized as ȷ, and symbols D_B, D_T, and D_m are used to indicate Brownian diffusion, thermophoretic diffusion, and diffusivity of microorganisms coefficients, respectively. The average volume of microorganisms is indicated by $\overset{\sim }{\gamma }$, and the maximum cell swimming speed and constant of chemotaxis are indicated by W_c and b, respectively. u and v symbolize non-Newtonian Eyring–Powell flow velocity components in the x and y axes, respectively.

With ψ(x, y) points out the stream function such that $u=\frac{\partial \psi }{\partial y}$ and $v=-\frac{\partial \psi }{\partial x}$, one notices that the continuity equation is satisfied. Upon the following similarity transformations,

$$ {\displaystyle \begin{array}{l}\eta ={\left(\frac{a}{\nu_f\left(1-\gamma t\right)}\right)}^{\frac{1}{2}}y,\kern1em \psi ={\left(\frac{a{\nu}_f}{1-\gamma t}\right)}^{\frac{1}{2}}f\left(\eta \right),\kern1em \theta \left(x,\eta \right)=\frac{T-{T}_{\infty }}{T_w-{T}_{\infty }},\\ {}\phi \left(x,\eta \right)=\frac{C-{C}_{\infty }}{C_0},\kern1em N\left(x,\eta \right)=\frac{\chi -{\chi}_{\infty }}{\chi_w-{\chi}_{\infty }},\end{array}} $$

(9)

So upon the previous transformation, Eq. (9), the dimensionless bio-convection non-Newtonian Eyring–Powell nanoflow governing equations and conditions are tended to:

$$ \left(1+\epsilon -\epsilon \delta {f}^{\prime \prime}\right){f}^{\prime \prime \prime }+f{f}^{\prime \prime }-f{\prime}^2-A\left({f}^{\prime }+\frac{1}{2}\eta {f}^{\prime \prime}\right)-{M}_g{f}^{\prime }+\lambda \left(\theta -{N}_r\phi -{R}_bN\right)=0 $$

(10)

$$ {\displaystyle \begin{array}{l}\mathrm{P}{\mathrm{r}}^{-1}\left({\theta}^{\prime \prime }+{N}_b\kern0.5em {\theta}^{\prime }{\phi}^{\prime }+{N}_t\kern0.5em \theta {\prime}^2\right)+f{\theta}^{\prime }-{f}^{\prime}\theta -A\left(2\theta +\frac{1}{2}\eta {\theta}^{\prime}\right)\\ {}\kern9em +{M}_gf{\prime}^2+{E}_c\left(\left(1+\epsilon \right){f}^{\prime }{\prime}^2-\frac{1}{3}\epsilon \delta {f}^{\prime }{\prime}^4\right)=0\end{array}} $$

(11)

$$ \phi^{\prime \prime }-{L}_e\left(A\left(2\phi +\frac{1}{2}\eta \phi^{\prime}\right)+f^{\prime}\phi - f\phi^{\prime}\right)+\frac{N_t}{N_b}\theta^{\prime \prime }=0 $$

(12)

$$ {N}^{\prime \prime }-{L}_b\left(A\left(2N+\frac{1}{2}\eta {N}^{\prime}\right)+{f}^{\prime }N-f{N}^{\prime}\right)\kern1em -{P}_e\left({\phi}^{\prime \prime}\left(N+\omega \right)+{N}^{\prime }{\phi}^{\prime}\right)=0 $$

(13)

The flow boundary conditions were restated as

$$ {\displaystyle \begin{array}{l}\mathrm{at}\kern1em \eta =0:\kern1em f={f}^{\prime }-1=0,\kern0.5em \theta =1,\kern0.5em {N}_b\kern0.1em {\phi}^{\prime }+{N}_t\kern0.1em {\theta}^{\prime }=0,\kern0.5em N=1\\ {}\mathrm{as}\kern1em \eta \to \infty :\kern1em {f}^{\prime}\to 0,\kern1em \theta \to 0,\kern1em \phi \to 0,\kern1em N\to 0\end{array}} $$

(14)

With ϵ and δ symbolize material fluid parameters, M_g stands for Hartmann number, N_r gives Buoyancy ratio parameter, λ points out mixed convection parameter, R_b means the bioconvection Rayleigh number, Pr indicates the Prandtl number, N_b is Brownian motion parameter, N_t stands for thermophoresis parameter, E_c symbolizes the Eckert number, L_e means the traditional Lewis number, L_b presents the bioconvection Lewis number, P_e symbolizes the bioconvection Peclet number and ω gives microorganism concentration difference parameter where these parameters are given mathematically by

(15)

Quantities of skin friction factor, local Nusselt, and density of motile microorganism numbers are formulated as

$$ {C}_f=\frac{\tau_w}{\rho_f{U}_w^2},\kern2em Nu=\frac{x{q}_w}{k_f\left({T}_w-{T}_{\infty}\right)},\kern2em Nn=\frac{x{q}_n}{D_m\left({\chi}_w-{\chi}_{\infty}\right)} $$

(16)

Here, shear stress, surface heat, and motile surface microorganism fluxes are indicated by τ_w, q_w, and q_n which mathematically are given by

$$ {\displaystyle \begin{array}{c}{\tau}_w={\left.\left({\mu}_f+\frac{1}{\beta^{\ast }c}\right)\frac{\partial u}{\partial y}-\frac{1}{6{\beta}^{\ast }{c}^3}{\left(\frac{\partial u}{\partial y}\right)}^3\right|}_{y=0},\\ {}{q}_w=-{k}_f{\left.\frac{\partial T}{\partial y}\right|}_{y=0},\\ {}{q}_n=-{D}_m{\left.\frac{\partial \chi }{\partial y}\right|}_{y=0}\end{array}} $$

(17)

In accordance to Eq. (9), the resulting non-dimensional formulas of the skin friction factor C_f, the local Nusselt number Nu, and local density of motile microorganism number Nn are approached to

$$ {\displaystyle \begin{array}{c}R{e}^{\frac{1}{2}}\kern0.5em {C}_f=\left(1+\epsilon \right){F}^{\prime \prime }(0)-\frac{1}{3}\epsilon \delta {F^{\prime \prime}}^3(0)\\ {}R{e}^{-\frac{1}{2}}\kern0.5em Nu=-{\theta}^{\prime }(0)\\ {}R{e}^{-\frac{1}{2}}\kern0.5em Nn=-{N}^{\prime }(0)\end{array}} $$

(18)

in which $\mathit{\operatorname{Re}}=\frac{U_wx}{\nu_f}$ stands for the local Reynolds number.

3 Numerical Approach

Now, for solving the nonlinear ordinary differential equations (ODE) (10)-(13) associated with adequate boundary conditions (14), Runge–Kutta Fehlberg fifth-order approach has been employed. The present technique contains the numerical evaluation for ordinary differential equations and via a trial step at the middle point of an integral, lower order terms of error can be canceled. In the present technique first, nonlinear differential equations have to mutate into first-order linear equations. To arrive this aim, needed variables are:

$$ {\left(f,f\prime, f\prime \prime, \theta, \theta \prime, \phi, \phi \prime, N,N\prime \right)}^T={\left({y}_1,y{\prime}_1={y}_2,y{\prime}_2={y}_3,{y}_4,y{\prime}_4={y}_5,{y}_y,y{\prime}_6={y}_7,{y}_8,y{\prime}_8={y}_9\right)}^T $$

(19)

The eventual expression of the flow equations by implementing the above transformation and Runge–Kutta fifth-order can be obtained from Eqs. (10)–(13) where y′₃ = f ′  ′ ′, y′₅ = θ ′ ′, y′₇ = ϕ ′ ′ and y′₉ = N ′ ′.

Some prerequisite are required to solve equations by Runge–Kutta fifth-order technique, involving:

• 1. The step size assumed to be Δη = 0.001.

• 2. Criterion of convergence has been chosen to be 10⁻⁶.

• 3. The adequate value for (η → ∞) has been selected to be 8.

• 4. As (η → ∞), in the boundary condition y₃(0) is corresponding to (f ′ (η) → 0), y₅(0) is corresponding to (θ(η) → 0), y₇(0) is corresponding to (ϕ(η) → 0) and y₉(0) is corresponding to N(η) → 0

Furthermore, a number of the remarkable techniques for numerical solving the nonlinear ODE have been mentioned in [41, 42]. Additionally, the veracity of applied numerical approach is confirmed. To assure our outcomes, the computations of the illustrated approach have been compared to those of Alsaeidi et al. [40] and Malik et al. [39] as given in Table 1. The outcomes of the current paper and other investigation has an excellent assent to each other.

Table 1 Comparison for skin friction with absent microorganisms

4 Results and Discussion

In this part, the impact of variant parameters on the Eyring–Powell nanofluid velocity, thermal, nanoparticle concentration, microorganisms concentration variations has been addressed, as well as skin friction factor, local Nusselt number, and the motile microorganism density number. Table 2 presents numerical calculations for skin friction coefficient, Nusselt number, and density motile microorganism number with variation of emerging parameters M _g, A, ϵ, λ, and R_b. All of M _g, A, ϵ, and R_b strengthen skin friction coefficient while λ reduces it. In addition, both of A and λ enhance variations of Nusselt and density motile microorganism numbers, while M _g, ϵ and R_b reduce it.

Table 2 Computations showing skin friction, Nusselt and motile microorganism density numbers with variations of some emerging parameters

Figure 2 demonstrates the changes in material fluid parameter ϵ on the nanofluid axial, radial velocity, and temperature variations. The figure reveals that for higher values of ϵ, all f, f′, and θ profiles strengthen. Because of $\epsilon =\frac{1}{\mu_f{\beta}^{\ast }c}$ so by enhancing ϵ viscosity of fluid, i.e., μ_f reduces, which results in strengthen velocity. As well, fluid becomes less viscous for higher values of ϵ which improves fluid velocity. The efficacy of unsteadiness parameter A on Eyring–Powell nanofluid velocity, temperature, nanoparticle concentration, and motile microorganism concentration fluctuations is elucidated in Figs. 3 and 4. As given, the unsteadiness parameter leads to weaken all of f ′ (η), θ(η), ϕ(η), and N(η). It is noticed that an enhance in unsteadiness parameter results in a weaken in the thermal boundary layer thickness, relate to strengthen in the wall temperature gradient, and hence generates an improvement in the surface heat transfer rate. Moreover, A leads to weaken skin friction coefficient but strengthen the motile microorganism density number as revealed in Fig. 5.

Fig. 2

Velocity and temperature variations versus ϵ parameter

Fig. 3

Velocity and temperature variations versus A parameter

Fig. 4

Nanoparticle concentration and motile microorganism variations versus A parameter

Fig. 5

Skin friction and otile microorganisms density number variations versus A parameter

In addition, the efficacy of bioconvection Rayleigh number R_b (=0, 1, 2, and 3) on Eyring–Powell nanofluid velocity and microorganisms concentration profiles is highlighted in Fig. 6. It has been found that due to the forces of buoyancy which produce by bioconvection, a rise in bioconvection Rayleigh number tends to weaken velocity whereas strengthens microorganism concentration N profiles. The performance of the Eckert number E_c on temperature and Nusselt number variations is presented in Fig. 7. Both of kinetic energy and enthalpy are the main parameters that affect the Eckert number. Thus, an upgrade in the Eckert number and subsequently boosting the particle kinetics, the thermal variation faces an improvement, whilst the local Nusselt number weakens. Figures 8 and 9 illustrate the efficacy of magnetic field parameter M_g on Eyring–Powell nanofluid axial and radial velocity, thermal θ, nanoparticle concentration ϕ and microorganisms concentration N fluctuations. Of course, the magnetic field produces Lorentz force and hence it must be considered whilst illustrating the nanofluid velocity function according to resistive nature of this force. An upgrade in M_g strengthens the Lorentz force magnitude. Due to this theme, weakening the axial and radial velocity and resistance to fluid flow can be remarked. Besides, thermal, nanoparticle concentration, and microorganism concentration fluctuations strengthen.

Fig. 6

Velocity and motile microorganism variations versus R_b parameter

Fig. 7

Temperature and Nusselt number variations versus E_c parameter

Fig. 8

Velocity and temperature variations versus M_g parameter

Fig. 9

Nanoparticle concentration and motile microorganism variations versus M_g parameter

The performance of the thermophoresis parameter N_t on temperature and Nusselt number variations is portrayed in Fig. 10. In the thermophoresis phenomenon, a number of particles due to thermophoretic force move from the hot to the cold domains. It is evident that temperature profile boosts when the thermophoresis parameter is increased, whereas the Nusselt number reduces. Besides, heat is created by the interaction of nanoparticles and the regular fluid caused by Brownian motion and thermophoresis impacts. Hence, the thermal boundary layer be thicker and the aspect is so renowned that vigorous temperature overshoots are given in the vicinity of the surface for greater value of N_t. Moreover, the impact of thermophoresis and Brownian motion parameters on nanoparticle concentration are plotted in Fig. 11. The N_t and N_b parameters have an inverse effect on ϕ, i.e., N_t leads to boost nanoparticle concentration but N_b decreases it. This holds practically attributed to larger values of N_b the random motion and collision of the macroscopic particles of the fluid boost. This weakens the concentration of the fluid. In the Buongiorno pattern, the Brownian motion parameter N_b varies inversely to the size of solid nanoparticles (which are considered to be spherical and homogenously distributed in the regular fluid). The aspect of bioconvection Lewis and Peclet numbers on the rescaled density of motile microorganisms of Eyring–Powell nanofluid is elucidated in Fig. 12. It is revealed that the rescaled motile microorganism boundary layer thickness is smaller. For increasing values of L_b, the diffusivity of microorganism weakens consequently, the fluid density of motile microorganisms has lowered gradually. Unlike bioconvection Lewis number, an upgrade in bioconvection Peclet number helps in strengthening the boundary layer thickness. The rescaled motile microorganism weakens with boosting bioconvection Lewis number but accentuates for higher Peclet numbers.The deviation in Nusselt and motile microorganism density numbers for some values of mixed convection λ and buoyancy ratio N_r parameters is displayed in Figs. 13 and 14, respectively. It is demonstrated that the rate of heat transfer expressed in terms of Nusselt number and motile microorganism density number enhance with mixed convection parameter, but they weaken with buoyancy ratio parameter. Figure 15 reveals the impact of the local non-Newtonian parameter, δ on the nondimensional skin friction coefficient and the motile microorganism density number. The skin friction is accentuated with increasing δ, for large values of ϵ. The rate of motile microorganism density is weakened with increasing δ parameter. Physically, it is valid due to viscosity of the fluid enhances by an increment the value of δ, which leads to weaken in the velocity of fluid and improving skin friction coefficient.

Fig. 10

Temperature and Nusselt number variations versus N_t parameter

Fig. 11

Nanoparticle concentration variations versus N_b and N_t parameter

Fig. 12

Motile microorganism variations versus L_b and P_e parameter

Fig. 13

Nusselt and motile microorganism density numbers versus λ parameter

Fig. 14

Nusselt and motile microorganism density numbers versus N_r parameter

Fig. 15

Nusselt and motile microorganism density numbers versus δ parameter

5 Conclusions

Boundary layer flow of unsteady mixed bioconvection of Eyring–Powell nanofluid with motile gyrotactic microorganisms over a stretching plate is addressed. The normalized governing flow equations are solved numerically via fifth-order Runge–Kutta method with shooting approach. The current research leads to the following delicate conclusions.

• 1. Higher values of magnetic filed M_g, bioconvection Rayleigh number R_b unsteadiness parameter A and Eyring–Powell fluid parameter ϵ lead to weaken velocity variation.

• 2. Heat transfer strengthens with N_t, Eyring–Powell fluid parameter ϵ, Eckert number E_c, and magnetic field M_g.

• 3. Nanoparticle concentration variation weakens for higher values of Brownian motion parameter N_b and unsteadiness parameter A.

• 4. The coefficient of drag force boosts with unsteadiness parameter A but motile microorganism density number decreases.

• 5. Buoyancy ratio parameter N_r weakens both rate of heat transfer and motile microorganism density.

• 6. Eyring–Powell fluid parameter δ strengthens skin friction factor and weakens motile microorganism density number.