A mathematical model of magneto hydrodynamics unsteady nanofluid flow containing gyrotactic micro-organism through a bidirectional stretching sheet

Abstract

The phenomenon of motile microorganisms enhances the stability of nanoparticles as well as improves heat transfer. The microorganism concept is accepted only for the stabilization of suspended nanomaterials due to bioconvection, which is facilitated by combined impacts of a magnetic field and buoyancy forces. The activity of gyrotactic microorganisms contained in time-dependent MHD nanofluid through a bidirectional extending surface with thermal radiation is viewed as in this ongoing article. Thermophoresis with diffusive Brownian movement is additionally noticed. The governing equations have been converted into a system of nonlinear ordinary differential equations (ODEs) by applying suitable similarity transformation. This framework then has been tackled mathematically by utilizing the spectral quasilinearization method (SQLM). The efficiency of this method has been presented and compared with previous data by showing in a table. The graphical portrayal of significant fluid parameters is evaluated by MATLAB programming. For physical interest skin friction, the Nusselt number, Sherwood number and microorganisms’ density number are determined numerically. We found that the unsteady parameter decreases the velocity and concentration boundary layer of microbes. Bioconvection Peclet numbers also decline the microorganisms’ concentration.

1 Introduction

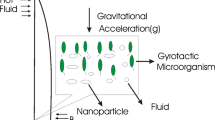
Nanofluid is a special kind of fluid where nanosized particles like metal or metallic oxide or polymer are mixed with some base fluid like water, oil, or ethylene, in such a way that no sedimentation happens (Fig. 1). This extraordinary sort of liquid has an incredible and significant industrial and biomedical application in heat and mass exchange; these days, it has been seen that nanofluids are more successful and proficient contrasted with a conventional ordinary fluid. These fluids are basically utilized for their huge properties in different locales like high heat conductivity, solidity, cooling and heat interchanger. There is a finer heat regulation in electronic gadgets like coolers, freezers, air-conditioners, generators and power improvement of various motor pumps. Nanofluids are good heat conductor also. Besides, the financial state to work nanofluid is likewise reasonable as it costs low. These days, its utilization in different medical analyses and drug delivery in human bodies is profoundly thought of, and overall effects of nanofluid are very much remarkable.

Fig. 1

Processing of nanofluid

The behaviour of microorganisms in nanofluid flow is taking interest nowadays. Taxes and kinetics are two kinds of processes by which microbes can move. They respond to the stimulus by many sources, like light, chemical reactions and temperature. The movement of microorganisms can be directional or random while responding to stimuli. The directional movement is called taxis and the random movement is called kinesis. The movement of microbes towards the light is called phototactic. Positive and negative taxes are defined by their movements in some certain direction. Microorganisms like Euglena attract light sources (see Fig. 2). Moreover, houseflies move towards the source of the light, called positive taxis, while mosquitoes move opposite to it, which is known as negative taxis. Kinesis is the random un-directional movement of the microbes. Oftentimes, microbes’ motility occurs due to the concentration difference in the system. Houseflies are attracted by the light while Mosquitoes move away from light; this behaviour of insects are known as positive and negative taxes respectively.

Fig. 2

Phototaxis of Euglena (microorganism)

Typically, thermal radiation is an important parameter in microorganisms; in many research, it has been found that due to radiation, temperature profile increases. On the other hand, bioconvection affects microorganism significantly; it gives rise to the movement fluctuation when microbes interact with nanoparticles present in the nanofluid. Often, chemical reactions and oxygen concentration gradients also can be the cause of microorganism oftentimes.

Li et al. [1] addressed the effect of thermal radiation on microorganisms in nanofluid flow. They consider the velocity slip condition in the momentum boundary layer, where Bhatti et al. [2] investigated the impact of chemical reactions on the motility of microbes. Buongiorno’s nanofluid model including microbial equation was examined by Zaman and Gul [3]. They conclude that the concentration of microbes decreases with the increment of porous parameters. The magnetic field has a significant impact on momentum; in the presence of it, Lorentz force is produced, which acts opposite to the velocity, and due to this phenomena, fluid velocity deteriorates. Many researchers [4,5,6,7] examined the behaviour of magnetic fields in heat-mass transportation in nanofluid flow. Ali et al. [8] analyzed the Cattaneo–Christov nanofluid model considering microbes and thermal radiation. Waqas et al. [9, 10] studied the bioconvective flow containing gyrotactic microorganisms passing through the expanded lamina, whereas Khan et al. [11] investigated bioconvection including the activation energy. They used a shooting method to solve the non-dimensionalized ruling equations; the local density number along with the Nusselt number and Sherwood number also has been calculated. Al-Khaled et al. [12] examined the microbe’s profile when chemical reactions were present. Chu et al. [13] investigated the couple-directional moving sheet including internal heat generation. The effect of activation energy and bioconvective nanofluid flow is being addressed by many scholars [14,15,16,17,18,19]. Ahmad et al. [20] did their research on free-forced convection on bidirectional expanding porous surfaces with the presence of chemical reactions. They found that porosity enhanced the velocity profile, whereas Kiyani et al. [21] investigated the Williamson nanofluid in a Darcy porous medium. Khan et al. [22] and Mabood et al. [23] studied the time-dependent convective boundary layer nanofluid flow. Spectral methods to solve non-linear ODEs are useful at present; many researchers [24,25,26,27,28] analyzed the viscous dissipation in time-dependent nanofluid flow by using the spectral method.

The Brownian diffusion effect with thermophoresis in nanofluid flow has been studied by Ahmad et al. [29,30,31]. Ramzan et al. [32] investigated the carbon nanotube nanofluid flow with non-constant thermal radiation. They noticed that the radial velocity and temperature enhanced with the continuous increment of nanoparticle volume fraction and also found the temperature profile enhanced due to thermal relaxation parameters. Hybrid nanofluid is an amalgam of two or more nanoparticles suspended in a suitable base fluid. This kind of fluid has considerable heat and mass transfer capacity compared to ordinary fluid. Chu et al. [33] studied the hybrid nanofluid flow between two collateral plates. Ahmad et al. [34, 35] investigated the microbe’s profile in a Darcy medium in the appearance of bioconvection. Gangadhar et al. [36] examined the entropy in microorganism, whereas Waqas et al. [37] and many other researchers [38,39,40,41,42,43,44,45,46] noticed the bioconvection effect in nanofluid flow. Some of them noticed microorganism effects in blood flow, and the slip velocity condition also has been considered many times. Mondal et al. [47] investigated the effect of the mixed convection flow on power law fluid. Aldabesh and Tlili [48] experimented with the enhancement of heat transfer in viscoelastic nanofluid flow. Moreover, Le et al. [49] did noble work by using wastewater to erase the metal with the help of polymer. Their experiment is highly recommended for industrial aspects. Sajjad et al. [50] investigated the compactional fluid dynamics analysis to re-use the waste heat produced in an extended heat exchanger. On the other hand, a review of the optical fibres has been done by Hussain et al. [51]. Le et al. [52] studied the pH-dependent anticancer drug distribution through a microchannel. Their invention can be a significant path for medical science. Li and Tlili [53] investigated the solar power system utilizing LAMMPS software. Tlili et al. [54] scrutinized the non-Newtonian nanofluid flow through a bidirectional stretching sheet by considering the non-linear thermal radiation and external heat generation. Additionally, the behaviour of tri-hybrid nanofluid through sinusoidal heated cylinder with the appearance of radiation has been examined by Smida et al. [55].

The primary point of this current examination is to construct a mathematical system for the 3D magnetohydrodynamics (MHD) time-dependent nanofluid flow with motile microorganisms through a bidirectional stretching sheet. As microbes’ movement is significantly dependent on time and is responsible for heat and mass transfer, we re-investigated our previously published paper [47] by considering the unsteady conditions. Here, we consider all the fluid properties as velocity, temperature and concentration which are dependent on time. The inter heat generation and applied magnetic field are also considered unsteady. Moreover, this experiment can be viewed as a comparison between two numerical methods for approximating unknown functions. With the view of previously published work, this kind of mathematical model has not been studied yet to the best of our knowledge. Hopefully, the output of this current paper is effective for engineering use.

2 Mathematical Formulation

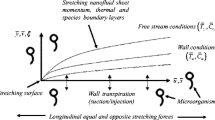
Microbes can only survive through water, so we choose water as the base fluid. We formed nanofluid by adding nanoparticles (concentration $<1\%$ in the water) in such a way that it maintains its stability, and no cluster takes place in the water. It is also noticed carefully that it does not affect the movement (swimming) of the microorganism. Microbes consume oxygen from the environment and swim faster due to the oxygen gradient; due to this phenomenon, the diffusion rate of microorganisms is more than that of the diffusion rate of nanoparticle molecules. Here, we have considered a three-dimensional magneto hydrodynamics nanofluid flow on a bi-directional time dependent expanding sheet. The velocity is bifacial; along the $x-{\text{axis}}$, the flow component is ${u}_{{\text{w}}}(x,t)=\frac{ax}{1-{\text{et}}}$; and the y-axis is ${v}_{{\text{w}}}(x,t)=\frac{by}{1-{\text{et}}}$, with $a>0$ and $b\ge 0$ (see Fig. 3). For balancing the expanding rate, we consider $1>{\text{et}}$. A non-constant magnetic field $B\left(t\right)=\frac{{B}_{0}}{1-{\text{et}}}$ acts normally to the extended sheet, e.g. $(z=0).$ Taking negligible magnetic Reynolds number to avoid magnetic induction, the Buongiorno nanofluid model is considered here. Thermal radiation is non-linear; unsteady heat generation/absorption $Q\left(x,t\right)=\frac{{ Q}^{*}}{1-{\text{et}}}$ is also included. $u {\text{and}} v$ are the velocity component along $x-{\text{axis}}$ and $y-{\text{axis}}$, respectively.

Fig. 3

Co-ordinate system of mathematical model

$$u=\frac{ax}{1-et},v=\frac{by}{1-et},-{k}_{f}\frac{\partial T}{\partial z}={h}_{f}\left({T}_{w}-T\right),-{D}_{B}\frac{\partial T}{\partial z}={h}_{m}\left({C}_{w}-C\right),w=0,n={n}_{w}$$

The unsteady form of temperature and fluid concentration are as follows:

${T}_{{\text{w}}}={T}_{\infty }+A\frac{{x}^{{\text{r}}}{y}^{{\text{s}}}}{1-{\text{et}}}$ and ${C}_{{\text{w}}}={C}_{\infty }+B\frac{{x}^{{\text{r}}}{y}^{{\text{s}}}}{1-{\text{et}}}$, where $A$ and $B$ are dimensional constants, $r {\text{and}} s$ are the non-dimensional power index which are used to balance the thermal as well as the concentration profile and ${T}_{\infty }$ and ${C}_{\infty }$ are the ambient temperature and concentration, respectively.

2.1 Constructing Mathematical Model

The governing equations of fluid flow for this present model are defined as follows [56]$:$

$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}=0$$

(1)

$$\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}+w\frac{\partial u}{\partial z}={\nu }_{f}\frac{{\partial }^{2}u}{\partial {z}^{2}}-\frac{{\sigma }_{f}{B}^{2}}{{\rho }_{f}}u$$

(2)

$$\frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}+w\frac{\partial v}{\partial z}={\nu }_{f}\frac{{\partial }^{2}u}{\partial {z}^{2}}-\frac{{\sigma }_{f}{B}^{2}}{{\rho }_{f}}v$$

(3)

$$\frac{\partial T}{\partial t}+u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}+w\frac{\partial T}{\partial z}={\alpha }_{f}\frac{{\partial }^{2}T}{\partial {z}^{2}}-\frac{1}{{\left(\rho {C}_{p}\right)}_{f}}\frac{\partial {q}_{r}}{\partial z}+\frac{Q}{{\left(\rho {C}_{p}\right)}_{f}}\left(T-{T}_{\infty }\right)+\tau \left[\frac{{D}_{B}}{\Delta C}\frac{\partial T}{\partial z}\frac{\partial C}{\partial z}+\frac{{D}_{T}}{{T}_{\infty }}{\left(\frac{\partial T}{\partial z}\right)}^{2}\right]$$

(4)

$$\frac{\partial C}{\partial t}+u\frac{\partial C}{\partial x}+v\frac{\partial C}{\partial y}+w\frac{\partial C}{\partial z}={D}_{B}\frac{{\partial }^{2}C}{\partial {z}^{2}}+\frac{{D}_{T}\Delta C}{{T}_{\infty }}\frac{{\partial }^{2}T}{\partial {z}^{2}}+R\left(C-{C}_{\infty }\right)$$

(5)

$$\frac{\partial n}{\partial t}+u\frac{\partial n}{\partial x}+v\frac{\partial n}{\partial y}+w\frac{\partial n}{\partial z}+\frac{b{W}_{c}}{\Delta C}\frac{\partial }{\partial z}\left(n\frac{\partial C}{\partial z}\right)={D}_{n}\frac{{\partial }^{2}n}{\partial {z}^{2}}+\frac{{D}_{T}}{{T}_{\infty }}\frac{{\partial }^{2}T}{\partial {z}^{2}}$$

(6)

In Eqs. (1) and (2) where they represent the momentum along $x-{\text{axis}}$ and $y-{\text{axis}}$, respectively, ${\nu }_{{\text{f}}},{\sigma }_{{\text{f}}}$ and ${\rho }_{{\text{f}}}$ were defined as the kinematic viscosity, electrical conductivity and density of the fluid, respectively. In the energy equation (Eq. (4)), ${\alpha }_{{\text{f}}}$ denotes thermal diffusivity; $Q$ signifies the internal heat source/sink. $Q>0$ indicates heat generation while $Q<0$ is heat absorption. $T$ and ${T}_{\infty }$ are the fluid temperature and ambient temperature, respectively, $C$ and ${C}_{\infty }$ are the fluid concentration and ambient concentration, ${C}_{{\text{p}}}$ is the specific heat, $\tau$ is the ratio of nanoparticle heat capacity over the base fluid heat capacity, ${D}_{{\text{B}}}$ denotes the Brownian diffusion coefficient, ${D}_{{\text{T}}}$ denotes the thermophoretic diffusion coefficient, ${D}_{{\text{n}}}$ denotes the Brownian diffusion coefficient of microorganism, $b$ is a chemotaxis constant and ${w}_{c}$ is the maximum speed of cell swimming.

For bulky medium, the Rosseland approximation is given as follows:

$${q}_{{\text{r}}}=-\frac{4{\sigma }^{*}}{3{K}^{*}}\frac{ \partial \left({T}^{4}\right)}{\partial y}, {\text{where}} {T}^{4}\cong 4{{T}_{\infty }}^{3}T-3{{T}_{\infty }}^{4}$$

(7)

considering temperature difference is very low within the flow, where ${q}_{{\text{r}}}$ is the radiative heat flux along y-axis, ${\sigma }^{*}$ is called Stefan–Boltzman constant, ${K}^{*}$ is the mean absorption coefficient and ${q}_{r}$ is acting along the $y-{\text{axis}}$ but ignored along the $x-{\text{axis}}$.

2.2 Boundary Conditions

The suitable boundary conditions satisfy Eqs. (1)-(6) and are considered as follows [56, 57]:

$$u=\frac{ax}{1-et},v=\frac{by}{1-et},-{k}_{f}\frac{\partial T}{\partial z}={h}_{f}\left({T}_{w}-T\right),-{D}_{B}\frac{\partial T}{\partial z}={h}_{m}\left({C}_{w}-C\right),w=0,n={n}_{w} {\text{at}}z=0 u=0,v=0,T\to {T}_{\infty },C\to {C}_{\infty },n\to {n}_{\infty } \mathrm{at }z\to \infty .$$

(8)

2.3 Equation Transformation

To convert the partial differential Eqs. (1) to (6) and (8) into non-linear ODEs, here, we use the following similarity transformation [57]$:$

$$u=\frac{ax}{1-et}{f}{\prime}\left(\eta \right),v=\frac{ay}{1-et}{g}{\prime}\left(\eta \right),w=-\sqrt{\frac{a{\nu }_{f}}{1-et} } \left(f\left(\eta \right)+g\left(\eta \right)\right),\theta \left(\eta \right)=\frac{T-{T}_{\infty }}{{T}_{w}-{T}_{\infty }}, \varphi \left(\eta \right)=\frac{C-{C}_{\infty }}{{C}_{w}-{C}_{\infty }},\chi \left(\eta \right)=\frac{n-{n}_{\infty }}{{n}_{w}-{n}_{\infty }},\eta =\sqrt{\frac{a}{{\nu }_{f}\left(1-et\right)}}z.$$

(9)

2.4 Transformed System of Ordinary Differential Equations

By using the above transformation (9) in Eqs. (2)-(6) and (8) we get

$${f}^{{\prime}{\prime}{\prime}}+\left(f+g\right){f}^{{\prime}{\prime}}-{{f}{\prime}}^{2}-\Omega \left({f}{\prime}+\frac{\eta }{2}{f}^{{\prime}{\prime}}\right)-M{f}{\prime}=0$$

(10)

$${g}^{\mathrm{^{\prime}}\mathrm{^{\prime}}\mathrm{^{\prime}}}+\left(f+g\right){g}^{\mathrm{^{\prime}}\mathrm{^{\prime}}}-{{g}^{\mathrm{^{\prime}}}}^{2}-\Omega \left({g}^{\mathrm{^{\prime}}}+\frac{\eta }{2}{g}^{\mathrm{^{\prime}}\mathrm{^{\prime}}}\right)-M{g}^{\mathrm{^{\prime}}}=0$$

(11)

$$\frac{1}{Pr}\left(1+Rd\right){\theta }^{{\prime}{\prime}}+\frac{Rd}{Pr}\left[{\left(\pi -1\right)}^{3}\left\{{\theta }^{3}{\theta }^{{\prime}{\prime}}+3{\theta }^{2}{{\theta }{\prime}}^{2}\right\}+3{\left(\pi -1\right)}^{2}\left\{{\theta }^{2}{\theta }^{{\prime}{\prime}}+2\theta {{\theta }{\prime}}^{2}\right\}+3\left(\pi -1\right)\left\{\theta {\theta }^{{\prime}{\prime}}+{{\theta }{\prime}}^{2}\right\} \right]+\left(f+g\right){\theta }{\prime}-\left(r{f}{\prime}-s{g}{\prime}\right)\theta -\Omega \left(\theta +\frac{\eta }{2}{\theta }{\prime}\right)+Nb{\theta }{\prime}{\varphi }{\prime}+Nt{{\theta }{\prime}}^{2}+Hg=0$$

(12)

$${\varphi }^{\mathrm{^{\prime}}\mathrm{^{\prime}}}+Sc\left[\left(f+g\right){\mathrm{\varnothing }}^{\mathrm{^{\prime}}}-\left(r{f}^{\mathrm{^{\prime}}}-s{g}^{\mathrm{^{\prime}}}\right)\varphi -\Omega \left(\varphi +\frac{\eta }{2}{\varphi }^{\mathrm{^{\prime}}}\right)\right]+\frac{Nt}{Nb}{\theta }^{\mathrm{^{\prime}}\mathrm{^{\prime}}}+{R}^{*}\varphi =0$$

(13)

$${\chi }^{{\prime}{\prime}}+Sb\left[\left(f+g\right){\chi }{\prime}-\left(r{f}{\prime}-s{g}{\prime}\right)\chi -\Omega \left(\chi +\frac{\eta }{2}{\chi }{\prime}\right)\right]-Pb\left[{\chi }{\prime}{\varphi }{\prime}+\left({\tau }_{0}+\chi \right){\varphi }^{{\prime}{\prime}}\right]+\frac{Nt}{Nn}{\theta }^{{\prime}{\prime}}=0$$

(14)

Boundary conditions (Eq. (8)) also have the non-dimensional form as follows:

$${f}{\prime}\left(0\right)=1,f\left(0\right)=0,{ g}{\prime}\left(0\right)=\alpha ,g\left(0\right)=0,$$

$$\begin{array}{cc}{\theta }{\prime}\left(0\right)=-{Bi}_{T}\left(1-\uptheta \left(0\right)\right),{\varphi }{\prime}\left(0\right)=-{Bi}_{C}\left(1-\mathrm{\varphi }\left(0\right)\right),\chi \left(0\right)=1& {\text{when}} \end{array}\eta \to 0.$$

and

$$\begin{array}{cc}{f}{\prime}\left(\infty \right)=0,{g}{\prime}\left(\infty \right)=0,\theta \left(\infty \right)=0,\varphi \left(\infty \right)=0,\chi \left(\infty \right)=0& {\text{when}} \end{array}\eta \to \infty .$$

(15)

Here, the parameters which are involved in transformed Eqs. (10)-(14) along with the transformed boundary conditions (15) are given as follows [15, 57]:

$\Omega =\frac{e}{a}$ is the unsteady parameter, $M=\frac{\sigma {B}_{0}^{2}}{a{\rho }_{{\text{f}}}}$ is the magnetic field parameter, ${{\text{Re}}}_{{\text{x}}}=\frac{{{\text{xu}}}_{{\text{w}}}}{{v}_{{\text{f}}}}$ is the Reynold number along $x-{\text{axis}}$, ${{\text{Re}}}_{{\text{y}}}={\left(\frac{b}{a}\right)}^{3}\frac{{{\text{yv}}}_{{\text{w}}}}{{v}_{{\text{f}}}}$ is the Reynolds number along y-axis, ${\text{Pr}}=\frac{{\nu }_{{\text{f}}}}{{\alpha }_{{\text{f}}}}$ is the Prandtl number, ${\text{Hg}}=\frac{{Q}^{*}}{a{\left(\uprho {{\text{C}}}_{{\text{p}}}\right)}_{{\text{f}}}}$ is the heat source/sink parameter, $\alpha =\frac{b}{a}$ is the bifacial stretching ratio,${\text{Nb}}=\frac{\uptau {D}_{{\text{B}}}\left({C}_{{\text{w}}}-{C}_{\infty }\right)}{\Delta C {\vartheta }_{{\text{f}}}}$ is the Brownian motion parameter, ${\text{Nt}}=\frac{\tau {D}_{{\text{T}}}\Delta T}{{\nu }_{{\text{f}}}{T}_{\infty }}$ is the thermophoresis parameter, $\pi =\frac{{T}_{{\text{f}}}}{{T}_{\infty }}$ is the temperature ratio parameter, ${\text{Sc}}=\frac{{\nu }_{{\text{f}}}}{{D}_{{\text{B}}}}$ is the Schmidt number, ${R}^{*}=\frac{R}{a}\left(1-{\text{et}}\right)$ is the chemical reaction rate, ${\text{Sb}}=\frac{{\nu }_{{\text{f}}}}{{D}_{{\text{n}}}}$ denotes as Schmidt number (bioconvection), ${\text{Pb}}=\frac{\upgamma {{\text{W}}}_{{\text{c}}}}{{D}_{{\text{n}}}}$ is the Peclet number (bioconvection), ${\tau }_{0}=\frac{{n}_{\infty }}{\Delta n}$ is the difference parameter of microbes concentration, ${\text{Nn}}=\frac{\tau {D}_{{\text{n}}}\Delta n}{{\nu }_{{\text{f}}}}$ denotes the Brownian motion parameter for bioconvection, ${\text{Rd}}=\frac{4{\sigma }^{*}{T}_{\infty }^{3}}{3{k}^{*}{K}_{{\text{f}}}}$ is the thermal radiation parameter, ${{\text{Bi}}}_{{\text{T}}}=\frac{{h}_{{\text{f}}}}{{k}_{{\text{f}}}}\sqrt{\frac{{\nu }_{{\text{f}}}\left(1-{\text{et}}\right)}{a}}$ is the Biot number for temperature, ${k}_{{\text{f}}}$ is the thermal conductivity, ${{\text{Bi}}}_{{\text{C}}}=\frac{{h}_{{\text{m}}}}{{D}_{{\text{m}}}}\sqrt{\frac{{\nu }_{{\text{f}}}\left(1-{\text{et}}\right)}{a}}$ is the Biot number for concentration, where ${h}_{{\text{f}}}$ denotes the convective heat transfer coefficient, and ${h}_{{\text{m}}}$ is the film mass transfer coefficient.

2.5 Quantities for Physical Interest

To obtain some physical attention which will be considerable for both technical and biomedical aspects, we found the bi-facial drag force, Nusselt number, Sherwood number and also the density number for microbes’ concentration. According to this present model, the above factors have been derived as follows:

The bi-directional drag forces are defined as.

$${Cf}_{rx}=\sqrt{Re} {Cf}_{x}= {2 f}^{\mathrm{^{\prime}}\mathrm{^{\prime}}}\left(0\right),$$

where

$${Cf}_{x}=\frac{{\tau }_{zx}}{{\frac{1}{2}\rho }_{f}{{u}_{w}}^{2}}.$$

(16)

$${Cf}_{ry}=\sqrt{Re} {Cf}_{y}= {2 g}^{\mathrm{^{\prime}}\mathrm{^{\prime}}}\left(0\right),$$

where

$${Cf}_{y}=\frac{{\tau }_{zy}}{{\frac{1}{2}\rho }_{f}{{v}_{w}}^{2}}$$

(17)

The local Nusselt number is defined as.

$${Nu}_{r}=\sqrt{Re}{N}_{{u}_{x}}=-\left(1+Rd\left\{1+\theta \left(0\right){\left(\Pi -1\right)}^{3}\right\}\right) {\theta }^{\mathrm{^{\prime}}}\left(0\right),$$

where

$${N}_{{u}_{x}}=\frac{x{q}_{w}}{{k}_{f}\left({T}_{w}-{T}_{\infty }\right)}.$$

(18)

The local Sherwood number is defined as

$$\begin{array}{cc}{Sh}_{r}=\frac{{Sh}_{x}}{\sqrt{Re}}=- {\varphi }{\prime}\left(0\right),& {\text{where}} {Sh}_{x}=\frac{x{q}_{m}}{{D}_{B}({C}_{w}-{C}_{\infty })}.\end{array}$$

(19)

The local density number of microbes is defined as

$$\begin{array}{cc}{Nm}_{r}=\frac{{Nm}_{x}}{\sqrt{Re}}=- {\chi }{\prime}(0),& {\text{where}} {Nm}_{x}=\frac{x{q}_{c}}{{D}_{n}\left({n}_{w}-{n}_{\infty }\right)}.\end{array}$$

(20)

$$\mathrm{with }{\tau }_{zx}={-{\mu }_{f}\left(\frac{\partial u}{\partial z}\right)}_{z=0},{\tau }_{zy}={-{\mu }_{f}\left(\frac{\partial v}{\partial z}\right)}_{z=0},{q}_{w}=-{k}_{f}{\left(\frac{\partial T}{\partial z}\right)}_{z=0}+{\left({q}_{r}\right)}_{z=0},{q}_{m}=-{D}_{B}{\left(\frac{\partial C}{\partial y}\right)}_{z=0}\mathrm{and }{q}_{c}=-{D}_{n}{\left(\frac{\partial n}{\partial z}\right)}_{z=0}.$$

(21)

3 Numerical Solution (SQLM)

To solve the system of nonlinear ordinary differential Eqs. (10)-(14) along with the boundary conditions Eq. (15), we have considered the spectral quasilinearization method [47, 57, 59]. This method has a high rate of convergence with few grid points; this is a considerable advantage compared to the other standard methods such as HAM (homotopy analysis method), finite difference technique or finite method. Homotopy has a low rate of convergence and accuracy valid at small-scaled regions. The finite method failed to solve non-linear systems; whether the finite difference technique is valid for a large number of grid points, SQLM overcomes most of these disadvantages. This characteristic is beneficial to save time and computational resources.

For computing the Spectral Chebyshev matrix, the physical domain $[0,\infty )$ of the problem truncated to the characteristic domain $[0, {L}_{{\text{x}}}]$ and then transformed to the standard interval $[-\mathrm{1,1}]$ by considering the linear transformation.

$$\eta = {L}_{{\text{x}}}(x+1)/2$$

${L}_{{\text{x}}}$ (finite) is known as a scaling parameter that defines the nature of flow beyond the boundary layer. The approximate solution in the form of a series solution can be evaluated in many ways, such as Bernoulli’s polynomials, the Chebyshev polynomials and the Legendre polynomial, but here, we considered the Lagrange polynomials formula:

$$u\left(x\right)=\sum_{i=0}^{{N}_{x}}u\left({x}_{i}\right){L}_{i}\left(x\right).$$

(22)

where

$${L}_{{\text{i}}}\left(x\right)=\prod_{i=0, i\ne j}^{{N}_{{\text{x}}}}\frac{x-{x}_{{\text{i}}}}{{x}_{{\text{k}}}-{x}_{{\text{i}}}}$$

(23)

Here, the unknown $u\left(x\right)$ is interpolated at the chosen Gauss–Lobatto grid points (collocation point):

$${x}_{i}=cos\left(\frac{\pi i}{N}\right), i=\mathrm{0,1}\dots .N$$

(24)

The interval $[-\mathrm{1,1}]$ discretize by using the above $N+1$ collocation points. $\left[-\mathrm{1,1}\right]$ is called the computational domain (CD).

We derived the following linear system of ordinary equations by applying the SQLM method:

$$\left\{\begin{array}{c}F={f}^{{\prime}{\prime}{\prime}}+\left(f+g\right){f}^{{\prime}{\prime}}-{{f}{\prime}}^{2}-\Omega \left({f}{\prime}+\frac{\eta }{2}{f}^{{\prime}{\prime}}\right)-M{f}{\prime}\\ {G=g}^{{\prime}{\prime}}+\left(f+g\right){g}^{{\prime}{\prime}}-{{g}{\prime}}^{2}-\Omega \left({g}{\prime}+\frac{\eta }{2}{g}^{{\prime}{\prime}}\right)-M{g}{\prime} \\ \Theta =\frac{1}{Pr}\left(1+Rd\right){\theta }^{{\prime}{\prime}}+\frac{Rd}{Pr}\left[{\left(\pi -1\right)}^{3}\left\{{\theta }^{3}{\theta }^{{\prime}{\prime}}+3{\theta }^{2}{{\theta }{\prime}}^{2}\right\}+3{\left(\pi -1\right)}^{2}\left\{{\theta }^{2}{\theta }^{{\prime}{\prime}}+2\theta {{\theta }{\prime}}^{2}\right\}+3\left(\pi -1\right)\left\{\theta {\theta }^{{\prime}{\prime}}+{{\theta }{\prime}}^{2}\right\} \right]\\ +\left(f+g\right){\theta }{\prime}-\left(r{f}{\prime}-s{g}{\prime}\right)\theta -\Omega \left(\theta +\frac{\eta }{2}{\theta }{\prime}\right)+Nb{\theta }{\prime}{\varphi }{\prime}+Nt{{\theta }{\prime}}^{2}+Hg\\ \overline{\varphi }={\varphi }^{{\prime}{\prime}}+Sc\left[\left(f+g\right){\varphi }{\prime}-\left(r{f}{\prime}-s{g}{\prime}\right)\varphi -\Omega \left(\varphi +\frac{\eta }{2}{\varphi }{\prime}\right)\right]+\frac{Nt}{Nb}{\theta }^{{\prime}{\prime}}+{R}^{*}\varphi \\ \overline{\chi }={\chi }^{{\prime}{\prime}}+Sb\left[\left(f+g\right){\chi }{\prime}-\left(r{f}{\prime}-s{g}{\prime}\right)\chi -\Omega \left(\chi +\frac{\eta }{2}{\chi }{\prime}\right)\right]-Pb\left[{\chi }{\prime}{\varphi }{\prime}+\left({\tau }_{0}+\chi \right){\varphi }^{{\prime}{\prime}}\right]+\frac{Nt}{Nn}{\theta }^{{\prime}{\prime}}\end{array}\right.$$

(25)

We make the iterative process as

$$\left\{\begin{array}{c}{a}_{0,r} {f}_{r+1}^{{\prime}{\prime}{\prime}}+{a}_{1,r }{{f}_{r+1}^{{\prime}{\prime}}+ a}_{2,r}{f}_{r+1}{\prime}+{a}_{3,r}{f}_{r+1}+{a}_{4,r}{g}_{r+1}-F={R}_{F}\\ {b}_{0,r} {g}_{r+1}^{{\prime}{\prime}{\prime}}+{b}_{1,r }{{g}_{r+1}^{{\prime}{\prime}}+ b}_{2,r}{g}_{r+1}{\prime}+{b}_{3,r}{g}_{r+1}+{b}_{4,r}{f}_{r+1}-G={R}_{G}\\ {c}_{0,r} {\theta }_{r+1}^{^{\prime\prime} }+{c}_{1,r} {\theta }_{r+1}{\prime}+{c}_{2,r}{\theta }_{r+1}+{c}_{3,r}{{f}{\prime}}_{r+1}+{c}_{4,r}{g}_{r+1}{\prime}\\ +{c}_{5,r}{{\varphi }{\prime}}_{r+1}+{c}_{6,r}{f}_{r+1}+{c}_{7,r}{g}_{r+1}-\Theta ={R}_{\Theta }\\ {d}_{0,r}{\varphi }_{r+1}^{{\prime}{\prime}}+{d}_{1,r}{\varphi }_{r+1}{\prime}+{d}_{2,r}{\varphi }_{r+1}+{d}_{3,r}{f}_{r+1}{\prime}+{d}_{4,r}{g}_{r+1}{\prime}\\ +{d}_{5,r}{f}_{r+1}+{d}_{6,r}{g}_{r+1}+{d}_{7,r}{\theta }_{r+1}^{{\prime}{\prime}}-\overline{\varphi }={R}_{\overline{\varphi }}\\ {e }_{0,r} {\chi }_{r+1}^{{\prime}{\prime}}+{e}_{1,r} {\chi }_{r+1}{\prime}+{e}_{2,r}{\chi }_{r+1}+{e}_{3,r}{{f}{\prime}}_{r+1}+{e}_{4,r}{{g}{\prime}}_{r+1}+{e}_{5,r}{f}_{r+1}\\ +{e}_{6,r}{g}_{r+1}+{e}_{7,r}{\varphi }_{r+1}^{{\prime}{\prime}}+{e}_{8,r}{\varphi }_{r+1}{\prime}+{e}_{9,r}{\theta }_{r+1}^{{\prime}{\prime}}-\overline{\chi }={R}_{\chi }\end{array}\right.$$

(26)

and the iteration scheme for boundary conditions $(12)$ is given by

$$\left\{\begin{array}{c}{f}_{r+1}{\prime}\left(0\right)=1 \\ {f}_{r+1}{\prime}\left(\infty \right)=0\\ {f}_{r+1}\left(0\right)=0\\ {g}_{r+1}{\prime}\left(0\right)= \Omega \\ {g}_{r+1}{\prime}\left(\infty \right)=0\\ {g}_{r+1}\left(0\right)=0\end{array}\mathrm{ and }\left\{\begin{array}{c}{\theta }_{r+1}{\prime}\left(0\right)=-{Bi}_{T}\left(1-{\theta }_{r+1}\left(0\right)\right)\\ {\theta }_{r+1}\left(\infty \right)=0\\ {\varphi }_{r+1}{\prime}\left(0\right)=-{Bi}_{C}\left(1-{\varphi }_{r+1}\left(0\right)\right)\\ {\theta }_{r+1}\left(\infty \right)=0\\ {\chi }_{r+1}\left(0\right)=1\\ {\chi }_{r+1}\left(\infty \right)=0\end{array}\right.\right.$$

(27)

The coefficients of Eq. (26) are as follows:

$$\left\{\begin{array}{c}{a}_{0,{\text{r}}}=1, \\ {a}_{1,{\text{r}}}=\left({f}_{{\text{r}}}+{g}_{{\text{r}}}\right)-\Omega \left(\frac{\eta }{2}\right)\\ {a}_{2,{\text{r}}}=-2{f}_{{\text{r}}}{\prime}-M-\Omega \\ {a}_{3,{\text{r}}}={f}_{{\text{r}}}^{^{\prime\prime} }\\ {a}_{4,{\text{r}}}={f}_{{\text{r}}}^{^{\prime\prime} }\end{array}\right.$$

(28)

$$\left\{\begin{array}{c}{b}_{0,{\text{r}}}=1\\ {b}_{1,{\text{r}}}=\left({f}_{{\text{r}}}+{g}_{{\text{r}}}\right)-\Omega \left(\frac{\eta }{2}\right)\\ {b}_{2,{\text{r}}}=-2{g}_{{\text{r}}}^{\mathrm{^{\prime}}}-M-\Omega \\ {b}_{3,{\text{r}}}={g}_{{\text{r}}}^{^{\prime\prime} }\\ {b}_{4,{\text{r}}}={g}_{{\text{r}}}^{^{\prime\prime} }\end{array}\right.$$

(29)

$$\left\{\begin{array}{c}{c}_{0,{\text{r}}}=\frac{1}{{\text{Pr}}}\left(1+{\text{Rd}}\right)+\frac{{\text{Rd}}}{{\text{Pr}}}\left\{{\left(\pi -1\right)}^{3}{{\uptheta }_{{\text{r}}+1}}^{3}+3{\left(\pi -1\right)}^{2}{{\uptheta }_{{\text{r}}+1}}^{2}+\left(\pi -1\right){\uptheta }_{{\text{r}}+1}\right\}\\ {c}_{1,{\text{r}}}=\frac{{\text{Rd}}}{{\text{Pr}}}\left\{6{\left(\pi -1\right)}^{3}{{\uptheta }_{{\text{r}}+1}}^{2}{{\uptheta }_{{\text{r}}+1}}^{\mathrm{^{\prime}}}+12{\left(\pi -1\right)}^{2}{\uptheta }_{{\text{r}}+1}{{\uptheta }_{{\text{r}}+1}}^{\mathrm{^{\prime}}}+6\left(\pi -1\right){{\uptheta }_{{\text{r}}+1}}^{\mathrm{^{\prime}}}\right\}\\ +\left({f}_{{\text{r}}}+{g}_{{\text{r}}}\right)-\Omega \left(\frac{\eta }{2}\right)+Nb{{\mathrm{\varnothing }}_{{\text{r}}+1}}^{\mathrm{^{\prime}}}+2Nt{{\uptheta }_{{\text{r}}+1}}^{\mathrm{^{\prime}}}\\ { c}_{2,{\text{r}}}=\frac{{\text{Rd}}}{{\text{Pr}}}\left\{{\left(\pi -1\right)}^{3}\left(3{{ {{\uptheta }_{{\text{r}}+1}}^{2}\uptheta }_{{\text{r}}+1}}^{\mathrm{^{\prime}}\mathrm{^{\prime}}}+6{\uptheta }_{{\text{r}}+1}{{\uptheta }_{{\text{r}}+1}}^{2}\right)+3{\left(\pi -1\right)}^{2}+3\left(\pi -1\right){{\uptheta }_{{\text{r}}+1}}^{\mathrm{^{\prime}}\mathrm{^{\prime}}}\right\}\\ -\left(r{{f}_{{\text{r}}}}^{\mathrm{^{\prime}}}+s{{g}_{{\text{r}}}}{\prime}\right)-\Omega +Hg.\\ {{\text{c}}}_{3,{\text{r}}}=-r{\uptheta }_{{\text{r}}+1}\\ {{\text{c}}}_{4,{\text{r}}}=-s{\uptheta }_{{\text{r}}+1}\\ {{\text{c}}}_{5,{\text{r}}}=Nb {\uptheta }_{{\text{r}}+1}^{\mathrm{^{\prime}}}\\ {{\text{c}}}_{5,{\text{r}}}=Nb {\uptheta }_{{\text{r}}+1}^{\mathrm{^{\prime}}}\end{array}\right.$$

(30)

$$\left\{\begin{array}{c}{d}_{0,{\text{r}}}=1\\ {d}_{1,{\text{r}}}=Sc\left(\left({f}_{{\text{r}}}+{g}_{{\text{r}}}\right)-\Omega \left(\frac{\eta }{2}\right)\right)\\ {d}_{2,{\text{r}}}=Sc\left[-\left(r{{f}_{{\text{r}}}}^{\mathrm{^{\prime}}}+s{{g}_{{\text{r}}}}^{\mathrm{^{\prime}}}\right)-\Omega +{R}^{*}\right]\\ {d}_{3,{\text{r}}}=-r Sc {\mathrm{\varphi }}_{{\text{r}}+1}\\ {d}_{4,{\text{r}}}=-s Sc {\mathrm{\varphi }}_{{\text{r}}+1}\\ {d}_{5,{\text{r}}}=Sc {\varphi }_{{\text{r}}+1}^{\mathrm{^{\prime}}}\\ {d}_{5,{\text{r}}}=Sc{ \varphi }_{r+1}^{\mathrm{^{\prime}}}\\ {d}_{6,{\text{r}}}=Sc{ \varphi }_{r+1}^{\mathrm{^{\prime}}}\\ {d}_{7,{\text{r}}}=\frac{{\text{Nt}}}{{\text{Nb}}}\end{array}\right.$$

(31)

$$\left\{\begin{array}{c}{e}_{0,{\text{r}}}=1,\\ {e}_{1,{\text{r}}}=Sb\left({f}_{{\text{r}}}+{g}_{{\text{r}}}\right)-\Omega \left(\frac{\eta }{2}\right)-Pb{\mathrm{\varphi }}_{{\text{r}}}^{\mathrm{^{\prime}}},\\ {e}_{2,{\text{r}}}=-Sb\left(r{{f}_{{\text{r}}}}{\prime}+s{{g}_{{\text{r}}}}{\prime}\right)-\Omega ,\\ {e}_{3,{\text{r}}}=-rSb{\upchi }_{\mathbf{r}+1},\\ {e}_{4,{\text{r}}}=-{\mathrm{s\chi }}_{{\text{r}}}Sb,\\ {e}_{5,{\text{r}}}=Sb{\upchi }_{{\text{r}}}^{\mathrm{^{\prime}}}\\ {e}_{6,{\text{r}}}=Sb{\upchi }_{{\text{r}}}^{\mathrm{^{\prime}}}\\ {e}_{7,{\text{r}}}=-Pb\left({\tau }_{0}+\chi \right)\\ {e}_{8,{\text{r}}}=-Pb{\upchi }_{{\text{r}}}^{\mathrm{^{\prime}}}\\ {e}_{9,{\text{r}}}=\frac{{\text{Nt}}}{{\text{Nn}}}\end{array}\right.$$

(32)

For convergency, choosing the suitable initial conditions is very important step whenever applying SQLM. Improper initial conditions may not be acquired to the accuracy and validity of this method. For this current model, we took the initial guess in the following way:

$$\left\{\begin{array}{c}{f}_{0}\left(\eta \right)=1-{e}^{-\eta }\\ {g}_{0}\left(\eta \right)=\alpha \left(1-{e}^{-\eta } \right)\\ {\theta }_{0}\left(\eta \right)=\left(\frac{{{\text{Bi}}}_{{\text{T}}}}{1+{{\text{Bi}}}_{{\text{T}}}}\right){e}^{-\eta }\\ {\varphi }_{0}\left(\eta \right)={\left(\frac{{{\text{Bi}}}_{{\text{C}}}}{1+{{\text{Bi}}}_{{\text{C}}}}\right)e}^{-\eta }\\ {\chi }_{0}\left(\eta \right)={e}^{-\eta }\end{array}\right.$$

(33)

4 Solution Convergence

A comparison of solution convergence between two numerical techniques is demonstrated in Table 1. It can be observed that the spectral quasilinearization method (SQLM) is a more recent and efficient numerical technique to solve the highly non-linear ordinary differential equations. This table shows that the convergency of the solutions can occur by applying SQLM with a few grid points (no. of grid points is $100$) and a limited number of iterations (no. of iterations is $10$).

Table 1 Comparison of the Keller Box method and SQLM technique for $\alpha =0.3, r=1.0, S=2.0,\Omega =0.6, \pi =1.4, {\text{Hg}}=0.2, {{\text{Bi}}}_{{\text{T}}}=0.5, {\mathrm{ Bi}}_{{\text{C}}}=0.3, {\text{Nt}}=0.4, {\text{Nb}}=0.5, {\text{Rd}}=0.8, M=0.7, {\text{Sb}}=0, {\text{Pb}}=0, {\text{Nn}}=0, {\text{tz}}=0$

4.1 Code Validation

This part provides assurance of current scrutiny in conjunction with previously released reports. We computed the results of $f\left(\infty \right)$, $g\left(\infty \right)$, ${f}^{^{\prime\prime} }\left(0\right)$ and ${g}^{^{\prime\prime} }\left(0\right)$ for a different choice of $\alpha$ and then compared the acquired results to Faisal et al. [56], Liu and Andersson [60] and Wang [61] published reports. Table 2 shows the results, and a solid scientific correlation with earlier findings has been demonstrated.

Table 2 Scientific connection with previous reports via numerical comparison

5 Results and Discussion

This segment contains the significant outcome of the entire research. We discussed the result graphically along with the physical satisfaction phenomena. Individual graphs for velocity, temperature, concentration, and microbes’ concentration for key parameters are presented here.

5.1 Impact of Magnetic Field $(M)$

Figure 4 provides the magnetic field effects on the Bi-directional velocity profile, thermal, concentration and also on the microbes’ concentration profile. Physically, the magnetic field produces the flow resisting Lorentz force; this force reduces the velocity profiles (see Fig. 4a and b), but the opposite behaviour can be shown for the temperature and nanofluid’s concentration. Also, we examined the effect of the magnetic field for two different values of the Prandtl number (see Fig. 4c and d). In both cases, each boundary layer increases [62]. On the other hand, the microbes’ concentration profile diminishes with the increment of magnetic parameters (Fig. 4e).

Fig. 4

Impact of $M$ on velocities (a) and (b), temperature (c), concentration (d) and microbes’ concentration (e)

5.2 Impact of Thermal Radiation $(Rd)$

Figure 5a and b show the impacts of thermal radiation on fluid temperature and concentration, respectively. According to the following figure, it is clear that the increment in thermal radiation temperature profile also increases [56] for comparative values of the Prandtl number ${\text{Pr}}$. The body temperature increases at a non-linear rate with radiation enhancement. The opposite nature of microbes’ concentration can be shown. For ${\text{Pr}}=3$, microbes’ profile exhibits a decrease in nature near to the wall, but as far it goes, this profile increases. But for ${\text{Pr}}=0.5$, it continuously decreases. We observed that the nanofluid concentration has a similar behaviour as microbes’ concentration. For the larger value of ${\text{Pr}}$, the concentration is enhanced.

Fig. 5

Effect of radiation ${\text{Rd}}$ on temperature (a) and nanofluid concentration (b)

5.3 Impact of Bioconvection Peclet Number $(Pb)$

The bioconvection Peclet number is a significant parameter when investigating the microbes’ behaviour in nanofluid flow. ${\text{Pb}}$ is directly related to the microbes’ cell swimming; with the enhancement of ${\text{Pb}}$, the speed of cell swimming also increases and leads to a deduction in microbes’ concentration. Figure 6 shows the effect of ${\text{Pb}}$ on microbes’ density profile.

Fig. 6

Effect of bioconvection Peclet number on microbes’ concentration

5.4 Impact of Microbes’ Brownian Motion Parameter $(Nn)$

An increment of the Brownian motion parameter reduces the concentration of microorganism (see Fig. 7). Due to the random motion of the microorganism contained in nanofluid, the concentration starts to decrease from the boundary wall to the ambient region.

Fig. 7

Effect of microbes’ Brownian motion parameter on microbes’ concentration

5.5 Impact of Thermophoretic Parameter $(Nt)$

In Fig. 8, the impact of thermophoresis on temperature, nanofluid concentration and microbes’ concentration is presented. In Fig. 8a, it is very clear that with the increment of thermophoresis, the gyrotactic microorganism concentration is enhanced. A similar behaviour can be seen for the thermal boundary layer also (see Fig. 8b, [56]).

Fig. 8

Effect of thermophoresis on microbes’ concentration (a), temperature (b)

5.6 Impact of Schmidt Number $(Sc)$

Physically, the Schmidt number is the ratio of momentum diffusivity to mass diffusivity. Body temperature increases with the increment of the Schmidt number for different values of heat source/sink parameter (see Fig. 9a$)$, but because the reduction of mass diffusivity opposite behaviour can be shown for microorganism concentration, it diminishes for larger values of the Schmidt number (see Fig. 9b).

Fig. 9

Effect of Schmidt number on temperature (a) and microbes’ concentration (b)

5.7 Impact of Unsteady Parameter $(\Omega )$

The effect of unsteady parameters on various boundary layers is shown in Fig. 10; each effect is described very transparently. It has been observed that this is a key parameter for the current research. The bi-directional velocities reduce due to the increment of $\Omega$ (see Fig. 10a and b); a similar nature can be seen for temperature (see Fig. 10c) and the microbe and nanofluid concentration (see Fig. 10d and e, respectively$)$. The results are benchmarked with the previously published work [63].

Fig. 10

Effect of unsteady parameter on bidirectional velocities (a) and (b) and temperature (c)

5.8 Temperature Ratio Parameter $(\pi )$

Temperature ratio parameter is a key parameter for this current research. Figure 11a exhibits the impact of $\pi$ on temperature profile. For ${\text{Pr}}=6.2$ and ${\text{Pr}}=0.5$, in both cases, the temperature profile decreases without any resistance. On the other hand, Fig. 11b demonstrates that the nanofluid concentration profile is decreasing at the wall $({\text{approx}}0<\pi <0.56)$ and then starts to increase for ${\text{Pr}}=0.5$; the identical behaviour can be shown for $\mathrm{Pr }=6.2$.

Fig. 11

Effect of temperature ratio parameter on temperature (a) and nanofluid concentration(b)

5.9 Bi-directional Stretching Ratio Parameter $(\alpha )$

Figure 12 represents the impact of stretching ratio parameter on various boundary layer profiles. It is a very interesting fact that $\alpha$ decreases the $x-$ directional velocity profile (Fig. 12a)while $y-$ directional velocity (Fig. 12b) increases with the enhancement of stretching ratio parameter$\alpha$. But the microbial concentration profile deteriorates far from the boundary wall (Fig. 12c). These results strongly agreed with [56].

Fig. 12

Effect of bi-directional stretching ratio parameter on bi-directional velocities (a) and (b) and microbial concentration (c)

It can be observed from Table 3 that microbes’ mass transfer rate decreases by about $3.84219\%$ when the bioconvection Peclet number increases from $0.1$ to $2.5.$ Opposingly, it increases about $32.36\%$ when microbes’ Brownian motion parameter increases from $0.5$ to $1.9.$ In the case of the enhancement of the bioconvection Schmidt number from $0.3$ to $0.7$, the microbes’ density number increases by about $84.1967\%.$ Additionally, the unsteady parameter also affects in the mass transfer of microbes significantly, whether it increases from $0.1$ to 0.7 microbes’ mass transfer increases by about $22.0927\%$.

Table 3 Microbes’ mass transfer (${{\text{Nm}}}_{{\text{r}}})$ analysis for different values of ${\text{Pb}}, M,\mathrm{ Nn } {\text{and}} \Omega$

From Table 4, it can be seen that when ${\text{Rd}}$ increases from $0.1$ to $1.2$, the Nusselt number increases by about $56.8089\%$; opposingly, in the case of magnetic increases from $0.1$ to $1.7$ field, it decreases about $21.8607\%$. But there is no such significant change in the Nusselt number for the enhancement of thermophoresis parameter. It just decreases by $0.625587\%$. A similar effect can be seen for the Brownian motion parameter; the Nusselt number decreases by $0.0300458\%$ when the Brownian motion parameter increases from $0.2$ to $0.8$.

Table 4 Heat mass transfer (${{\text{Nu}}}_{{\text{r}}}$) analysis table for different values of ${\text{Rd}}, M, {\text{Nt}}$ and ${\text{Nb}}$

Table 5 shows the changes in Sherwood number for the incrementation of different parameters. Firstly, for the incrementation of the magnetic parameter from $0.1$ to $1.2$, the skin friction along $x-{\text{axis}}$ decreases by about $28.2103\%,$ whereas skin friction along $y-{\text{axis}}$ decreases by about $34.3216\%$. In the case of the unsteady parameter, both the skin friction along $x-{\text{axis}}$ and $y-{\text{axis}}$ decrease by about $38.8717\%$ and $56.2968\%$, respectively. The stretching parameter has a significant effect on skin friction. It is observed that when it increases from $0.3$ to $1.0,$ the skin friction along $x-axis$ decreases by about $7.05338\%,$ but along $y-axis$, it increases by about $323.151\%,$ which result can be an important outcome for this current research.

Table 5 Skin friction ${{\text{Cf}}}_{{\text{rx}}}$ and ${{\text{Cf}}}_{{\text{ry}}}$ analysis table for different values of $M, \Omega {\text{and}} \alpha$

6 Conclusions

Previously we experimented on the behaviour of microorganism in nanofluid flow [47]. However, by reviewing previous literature, we found the unsteady movement of microorganism has a significant influence on heat and mass transportation. Here, we tried to develop a mathematical model of unsteady gyrotactic microorganism contained in nanofluid through a bidirectional stretching sheet with the internal heat generation/absorption and chemical reaction. The behaviour of bioconvection microbes’ Brownian motion parameter and Peclet number with microbial activity have not been deliberated to date to the best of our knowledge. Some of the leading findings are listed below:

• The unsteady magnetic field has a crucial impact on the microbe’s nature. The magnetic parameter decreases the microbial concentration, but increases the temperature. We examined it by taking several values of Prandtl number and made this significant conclusion.

• Bioconvection Peclet number diminishes the microbial concentration.

• Microbes’ concentration decreases with the increment of microbes’ Brownian motion parameter.

• Bi-directional stretching parameter enhances the velocity along $y-{\text{axis}}$ whether velocity diminishes along $x-{\text{axis}}$.

• The SQLM method can be viewed as an efficient method to approximate an unknown function.