Memristor-Based Volistor Gates Compute Logic with Low Power Consumption

Abstract

We introduce a novel volistor logic gate which uses voltage as input and resistance as output. Volistors rely on the diode-like behavior of rectifying memristors. We show how to realize the first logic level, counted from the input, of any Boolean function with volistor gates in a memristive crossbar network. Unlike stateful logic, there is no need to store the inputs as resistances, and computation is performed directly. The fan-in and fan-out of volistor gates are large and different from traditional memristor circuits. Compared to solely memristive stateful logic, a combination of volistors and stateful inhibition gates can significantly reduce the number of operations required to calculate arbitrary multi-output Boolean functions. The power consumption of volistor logic is computed and compared with the power consumption of stateful logic using the simulation results obtained by LTspice—when implemented in a 1 × 8 or an 8 × 1 crosspoint array, volistors consume significantly less power.

1 Introduction

Stateful logic computation with memristors is an area of active research. Borghetti et al. [1] proposed realizing stateful logic via material implication (IMP). In classical stateful memristive circuits, logic signals utilize resistances on inputs and outputs, meaning, the previous resistance state of the memristor affects the operations. In contrast, volistors do not use the previous resistance state in calculations. Other stateful logic gates have been proposed as well, e.g., inhibition (INH) [2] or AND [3]. INH gate implements Boolean function $a\overline{b}$ where a and b are positive and negative inputs, respectively. In stateful logic, the logic values are encoded by the resistance states of memristors. Stateful logic is usually performed in a generic structure called a crossbar array. Leakage pathways due to the half-select of memristors in a crossbar row or column can be suppressed by using rectifying memristors [4]. One key disadvantage of stateful logic is that a long sequence of operations is required to implement an arbitrary Boolean function.

Memristor ratioed logic (MRL) [5] is another approach to logic computation and is based on the resistive ratio of non-rectifying memristors. In MRL, logic values are voltage-based pulses and circuit structures are dependent entirely on the Boolean function being implemented. The output voltage depends only on input voltages regardless of the resistance of the memristors; however, the resistances affect the propagation delay of the gate. MRL gates consume both dynamic and static power. Further, as it lacks the inversion function, MRL is not logically complete without CMOS inverters.

In this paper, we introduce a new concept in memristor logic. We call it volistor gate (voltage-resistor gate) which has voltage-based inputs and resistance-based outputs. Therefore, volistor gates can only be used in the first level of logic implementation. This level can be composed of various types of gates and be complex. Logic synthesis methods with volistors are therefore different from classical logic synthesis. Volistors are implemented in generic crossbar arrays of rectifying memristors [6]. Unlike stateful logic, voltage pulses are the actual inputs to the volistor gates. It is always assumed that complemented input variables are available as voltage signals at no additional cost. Sometimes input signals are required in both positive and negative forms, e.g., x and $\overline{x}$. In addition, there is no propagation penalty as it exists in MRL. In a 1 × 8 crosspoint array, the propagation delay in volistors is shorter than in stateful INH. In a 1 × 8 crosspoint array, multi-input multi-output volistor gates consume less power than the corresponding stateful logic. The outputs of volistors are stored as the resistances of the target memristors. To provide the correct functionality, target memristors need to be initially closed, i.e., target memristors must be set to the low resistance state. With different coding schemes, either a volistor OR and NAND logic set or a volistor NOR and AND logic set can be realized in the same crossbar array. For instance, if the closed state of a memristor encodes logic “0” and the open state of a memristor encodes logic “1,” the set of OR and NAND operations is implemented. The reverse encoding scheme implements the NOR and AND logic set. With volistor logic, crossbar drivers need to supply only three voltage levels: V⁺, V⁻, or 0 V. In addition, the control circuitry must be capable of setting arbitrary nanowires in the crossbar to either high impedance (HZ) or grounding these nanowires through load resistors R_G. Obviously, the volistor network layer cannot implement every Boolean function such as Sum of Products. However, a combination of a volistor NOR and AND with stateful INH, or their dual logic of volistor OR and NAND with stateful IMP, can both be used to realize arbitrary multi-output Boolean functions. As will be presented, this hybrid realization is faster than an equivalent circuit realized with only stateful gates. The speed comparison of hybrid and stateful logic circuits will be presented in Section 4.

In Section 2, the hysteresis behavior of rectifying memristors is reviewed. In Section 3, volistor gates are described. In Section 4, the synthesis of arbitrary Boolean functions is discussed. In Section 5, the power consumption of volistor gates is computed and compared with stateful logic. In section 6, volistors in memory application are discussed. Section 7 is a summary of the work.

2 Rectifying Memristors

We used a rectifying memristor [4, 6] as a linear bistable device [7]. The behavior of a rectifying memristor is defined in (1), following [7]. Equation (1) describes a simplified model of diode-like memristor M demonstrated practically in [4]. R _M denotes resistance of memristor M; s is the state variable of M normalized to a real number in the range 0 through 1, s ϵ [0, 1], and therefore R _CLOSED  ≤ R _M  ≤ R _OPEN ; v is the voltage applied across M.

$$ {R}_M=\left\{\begin{array}{c}\hfill {R}_{OPEN}{\left(\frac{\kern0.24em {R}_{CLOSED}}{R_{OPEN}}\ \right)}^s\ v\ge 0\hfill \\ {}\hfill {R}_{OPEN}\kern3.13em v<0\hfill \end{array}\right. $$

(1)

R _OPEN denotes high resistance state of memristor M; R _CLOSED is low resistance state of memristor M. It is assumed that R _OPEN  = 500MΩ and R _CLOSED  = 500KΩ which are consistent with empirical results reported in [4]. The dynamic behavior of the state variable s is such that s changes in time as described in the linear differential Eq. (2). In Equation (2), v _CLOSE is a positive threshold voltage; v _OPEN is a negative threshold voltage. For simplicity, it is assumed that the threshold voltages v _CLOSE and v _OPEN are symmetric v _CLOSE  = − v _OPEN  ) and v _CLOSE= 1V; α is a positive constant associated with the switching rate of the memristor. Here, α is assumed to be 125 × 10⁷ (V. s)^− 1, following [7].

$$ \frac{ds}{dt}=\left\{\begin{array}{c}\hfill \alpha \left(v-{v}_{CLOSE}\right)\kern1.21em v>{v}_{CLOSE}\hfill \\ {}\hfill \alpha \left(v-{v}_{OPEN}\right)\kern1.21em v<{v}_{OPEN}\hfill \\ {}\hfill\ 0\kern4.09em elsewhere\hfill \end{array}\right. $$

(2)

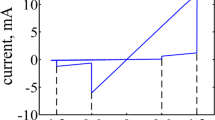
Figure 1a shows the i − v characteristic of rectifying memristor M described in (1) and (2). In this work, the positive programming voltage is defined v = 1.2V and denoted by V_SET; the application of V_SET will close switch M when it is open. Also, the negative programming voltage is defined v = − 1.2V and denoted by V_CLEAR; the application of V_CLEAR will open switch M when it is closed. Substituting all related values in Eq. (2) results in

Fig. 1

a The i − v characteristic of rectifying memristor M described in (1) and (2). A sinusoidal input voltage with frequency 25 MHz and amplitude 1.2 V is applied to memristor M. The inset shows the symbolic diagram of a rectifying memristor. b The i − v characteristics of 10 different rectifying memristors in the crossbar array. The inset shows the i − v characteristics plotted in log scale demonstrating current suppression at negative bias in the on-state [4]. c Threshold voltage distribution of 256 cells in the fabricated crossbar array. The threshold voltage is defined as the voltage at which the measured current is above 10^− 6 A [4]

$$ \frac{ds}{dt}=\left\{\begin{array}{c}\hfill 0.2\alpha \kern1.09em v=1.2\hfill \\ {}\hfill -0.2\alpha \kern0.97em v=-1.2\hfill \\ {}\hfill 0\kern1.09em elsewhere\hfill \end{array}\right. $$

The straightforward analytical solution of this differential equation is

$$ s\left(t+1\right)=\left\{\begin{array}{c}\hfill 0.2\alpha {T}^{+}\kern0.73em v=1.2\hfill \\ {}\hfill -0.2\alpha {T}^{-}\kern0.73em v=-1.2\hfill \\ {}\hfill\ s(t)\kern1.81em elsewhere\hfill \end{array}\right. $$

Since s is normalized to interval [0, 1], for the given values of α and v, the assumption of s(t + 1) = 1 results in the switching delay of T ⁺ = 4ns. The desired solution for (2) is

$$ s\left(t+1\right)=\left\{\begin{array}{c}\hfill 1\kern1.57em v=1.2\hfill \\ {}\hfill\ 0\kern1.45em v=-1.2\hfill \\ {}\hfill\ s(t)\kern0.85em -1\le v\le 1\hfill \end{array}\right. $$

Note that s(t) and s(t + 1) denote the current state and the next state of memristor M, respectively; for − 1 ≤ v ≤ 1, the resistance state of memristor remains unchanged, i.e., s(t + 1) = s(t). Obviously, a larger V_SET results in a smaller switching delay T ⁺, as suggested by Eq. (2).

This simplified model does not accurately describe the behavior of rectifying memristor M. For instance, the threshold voltages v _CLOSE and v _OPEN are assumed to be constant, and/or the programming rate $\frac{ds}{dt}$ and the applied voltage v are assumed to be piecewise linearly related. The behavior of rectifying memristors described in (1) and (2) is compared with the actual behavior of memristors reported in [4, 6] for applied voltage v below.

• 1)
  $$ v<0\mathrm{V} $$

The actual behavior of rectifying memristors shows that I ⁻ < 10^− 13 A and $\frac{I^{-}}{I^{+}}<{10}^{-6}$, where I ⁻ is the reverse biased current and I ⁺ is the forward biased current, and the $\frac{R_{\mathrm{OPEN}}}{R_{\mathrm{CLOSED}}}$ ratio is from three to six orders of magnitude (10³ − 10⁶). In our model, the $\frac{R_{\mathrm{OPEN}}}{R_{\mathrm{CLOSED}}}$ ratio is 10³ , which is consistent with the empirical results. However, the $\frac{I^{-}}{I^{+}}$ ratio is 10⁻³ which is much larger than the empirical results. Thus, using a precise memristor model would show even less power consumption in a crossbar array than our used model.

• 2)
  $$ 0\mathrm{V}<v<{v}_{\mathrm{CLOSE}} $$

Figure 1b shows the i − v characteristics of ten rectifying memristors in a 16 × 16 crossbar array overlaid on top of each other. The memristors show approximately the same piecewise linear relationship between i and v in the interval [0, v _CLOSE]. In other words, for applied voltage v, almost the same amount of current flows through all ten memristors. Therefore, Eqs. (1) and (2) with a fixed v can be applied uniformly to describe the behaviors exhibited by all memristors in the given interval. The linear behavior observed in Fig. 1a is the result of applying (1) and (2) which is uniform throughout all the memristors (Fig. 2).

• 3)
  $$ v>{v}_{\mathrm{CLOSE}} $$

The threshold voltage distribution of the rectifying memristors in the crossbar array is shown in Fig. 1c [4]. The difference in the threshold voltages results in a difference in the programming rates. Since the difference in the threshold voltages is not significant, i.e., v _CLOSE ∈ [2.1V, 2.5V], the difference in the programming rates is not significant either. A small increase in the pulse width driving the crossbar array ensures a complete state transition in the memristors. In our model, the programming rate is assumed to be constant and in accordance with the empirical results reported in [8, 9]. Although the description of the behavior of the rectifying memristors modeled by (1) and (2) is imprecise, they still can be used in estimating the power consumption in CMOS-memristive circuits.

3 Volistor Logic

In this section, volistor logic is introduced. The key idea behind volistor logic is that inputs are voltages and outputs are resistances. This is a significant change from the way the voltage drivers are used in stateful logic; however, the target memristor is still used as a memory element where the output is stored. The basic volistor logic gates are inverter, k-input NOR and k-input AND, and their duals: k-input OR and k-input NAND. In the following subsections, we define the basic architecture required for logic computations and describe the basic logic gates.

3.1 Crosspoint Architecture

The basic circuit structures for volistor logic computations are the 1 × 2 crosspoint array and 2 × 1 crosspoint array depicted in Fig. 2. The crosspoint array is a horizontal or a vertical vector of memristors, i.e., a one-dimensional array. Figure 2a shows a generic structure for logic operations. The circuit is comprised of two rectifying memristors, labeled S and T, electrically connected through the common horizontal nanowire HL. Just as in stateful IMP, S denotes the source memristor and T the target memristor. The vertical nanowire VL1 connected to source memristor S conveys input signal V _in . Let V⁺ = 0.6V and V⁻ = − 0.6V. The logical coding scheme for V _in is defined as follows: V⁺ encodes logic “1,” denoted vin = 1; 0 V encodes logic “0,” denoted vin = 0. The vertical nanowire VL2 connected to target memristor T carries a bias voltage, V _bias  = V⁻. Memristor T acts as a switch whose resistivity state t represents the output of the crosspoint array. When T is open, its high-resistivity state encodes logic “0,” i.e., t = 0. When T is closed, its low-resistivity state encodes logic “1,” t = 1. This interpretation of the resistivity state of T is used for performing NOR/AND logic set; another interpretation will be discussed in Section 3.5. Prior to logic computation, both memristors S and T must be closed. To unconditionally close a memristor, it must be forward biased by V_SET. Unlike the target memristor, the source memristor S acts as a diode. The 1 × 2 crosspoint array must satisfy (3).

Fig. 2

a A 1 × 2 crosspoint array; b a 2 × 1 crosspoint array

$$ \left\{\begin{array}{c}\hfill {V}_{OPEN}<{V}_{bias}<0V\hfill \\ {}\hfill {V}_{bias}-{V}_{in}={V}_{CLEAR}\hfill \end{array}\right. $$

(3)

Each nanowire must be either driven by one of the voltages V _in , V _bias , and 0 V or terminated with high impedance HZ or grounded by load resistor R_G as shown in Fig. 3. All these connections are realized with CMOS switches shown symbolically in Fig. 3. R_G is defined as geometric mean of R_OPEN and R_CLOSED, $\sqrt{{\mathrm{R}}_{\mathrm{OPEN}}\cdot {\mathrm{R}}_{\mathrm{CLOSED}}}=15\mathrm{M}\Omega$. The crosspoint array operates by the simultaneous application of V _in and V _bias to S and T, respectively. Since V _in  > V _bias , Ohm’s Law requires a flow of current through the array. However, given the structure of the array, the application of these voltages forward biases S and reverse biases T thus suppressing the flow of current. This means that V _HL  ≈ V _in where V_HL is the voltage on HL. If (3) is satisfied, the voltage across T will toggle that memristor, i.e., the new state of target memristor becomes t = 0.

Fig. 3

The symbolic illustration of driver circuitry connected to each nanowire

$$ \left\{\begin{array}{c}\hfill 0V < {V}_{bias} < {V}_{CLOSED}\hfill \\ {}\hfill {V}_{in}-{V}_{bias}={V}_{CLEAR}\hfill \end{array}\right. $$

(4)

The crosspoint arrays shown in Fig. 2 can be scaled to 1 × n and n × 1 arrays, allowing for multi-input multi-output volistor logic functions. The 1 × n and n × 1 crosspoint arrays must satisfy (3) and (4), respectively. In these arrays, logic computation is achieved by implementing the wired OR function, i.e., V_HL or V_VL denotes the logical OR of inputs vin ₁, …, vin _k where V_VL is the voltage on vertical nanowire VL and 1 ≤ k < n.

3.2 Volistor NOT Gate in a Crosspoint Array

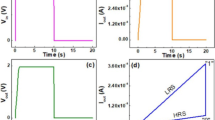
An inverter is the simplest gate to realize in volistor logic; the symbolic diagram is shown in Fig. 4a. Take, for example, the case where (vin, t ) = (1, 1) i.e., vin = 1 and t = 1. Both source and target memristors are initially closed. Single-output volistor NOT can be realized in either a 1 × 2 or a 2 × 1 crosspoint array. When realized in a 1 × 2 array, V _bias must be a negative voltage, V _in must be greater than or equal to 0 V, per (3), and horizontal nanowire HL must be connected to a high impedance, HZ. Connecting HL to HZ allows V _in to manifest on HL. Based on Ohm’s Law, current should flow through the array, since V _in  − V _bias  > 0V. However, memristor T is reverse biased and thus suppresses the flow of current. In this case, the voltage drop across memristor S is 1.198 mV, i.e., the voltage on HL equals 598.801 mV. The voltage drop across T is 1.198 V which is sufficient to open memristor T. This is the desired behavior of the inverter function that it results in (vin, t ) = (1, 0). Given the parameters introduced in Section 2, the propagation delay of single-output volistor NOT is 4.044 ns as shown in Fig. 5b.

Fig. 4

Symbolic notation for volistor single-input and two-input logic gates. a Volistor inverter; b two-input volistor NOR gate; c two-input volistor AND gate; d mixed-input NOR gate. Inside the gates, symbols V and R denote whether a signal is a voltage-based or resistance-based, respectively

Fig. 5

Volistor NOT behavior. a A 1 × 8 crossbar array implementing a four-output NOT and showing arbitrary nature of the locations of S and T. The contribution of each memristor is determined by the voltage driver to which it is connected. The horizontal nanowire is connected to HZ. b The operation of a one output NOT in a 1 × 2 array. V(hl) stabilizes at ≈ 600 mV indicating vin = “1” manifesting on HL. In addition V(t), which is the SPICE model’s representation of t, toggles to 0 V (t = “0”). c The operation of a 63 output NOT in a 1 × 64 array. V(hl) stabilizes and V(t) toggles as in b. d The operation of a one output NOT in a 1 × 2 array. V(hl) stabilizes at ≈−600 mV indicating vin = “0” manifesting on HL. As a result, V(t) remains 1 V (t = “1”). e V(hl) stabilizes as in d

Single-output volistor NOT can be extended to an arbitrary fan-out which corresponds to a multi-output gate realized in arrays of types 1 × n or n × 1. The multi-output NOT gate stores $\overline{vin}$ in up to n-1 target memristors in any arbitrary location in the array. The role of each memristor is determined by its driver, i.e., source memristors are driven by V _in and target memristors by V _bias . Interestingly, this means that a memristor’s function is independent of its position in the crosspoint array. Figure 5a shows a four-output volistor NOT gate implemented in a 1 × 8 array. Source memristor S is driven by V _in and target memristors T₁ ⋯ T₄ are driven by V _bias . Memristors X₁, X₂ and X₃ are terminated to HZ and do not take part in the circuit’s operation. The proper operation of a 63-output NOT gate with vin = 1 implemented in a 1 × 64 array and simulated in LTspice is depicted in Fig. 5c. V_HL is 528.881 mV and all 63 target memristors are switched off successfully in 6.223 ns. Figure 5d shows the desired behavior of volistor NOT implemented in a 1 × 2 array when vin = 0. V_HL is − 599.4μ V and the target switch remains closed. Figure 5e shows the behavior of a sixty three-output volistor NOT implemented in a 1 × 64 array where vin = 0. This results in V_HL = −35.559 mV and all target switches remaining closed.

Table 1 summarizes these configurations and their effects on V_HL. A NOT with an arbitrary fan-out can be realized in one pulse. We discuss this gate for completeness; in practice, it is not required since the logical negation can be created by appropriately selecting the vin values. In this paper, all volistor gates can appear only at the input layer.

Table 1 Implementation of multi-output volistor NOT gate

3.3 Volistor NOR Gate in a Crosspoint Array

The second basic gate in volistor logic is NOR. Figure 4b shows the symbolic diagram of a two-input volistor NOR gate. Since 1 × n arrays have been previously discussed, in this subsection, n × 1 arrays are considered. Take, for example, a two-input NOR gate where (vin ₁, vin ₂, t) = (1, 0, 1). This requires the application of input data to S₁ and S₂ and V _bias to T, as shown in Fig. 6. Since the function is realized in a 3 × 1 crosspoint array, Eq. (4) requires V _bias  > 0V and V _in  ≤ 0V. Based on Ohm’s Law, since V _bias  − V _in  > 0, a current should flow through the crosspoint array.

Fig. 6

A 3 × 1 crosspoint array used to perform two-input volistor NOR

However, S₂ and T are both reverse biased and thus they suppress the flow of current. The voltage drop across S₁ is 1.796 mV, i.e., V_VL = -598.203 mV. The voltage drop across T is −1.198 V which is sufficient to open T. Recall that all memristors are initially closed. The gate is realized by implementing wired-OR, i.e., the voltage on VL is the logical OR of vin ₁ and vin ₂. As before, V _in causes memristors S₁ and S₂ to behave as diodes and V _bias causes memristor T to behave as a switch. The output of the gate is the new state of the target switch T, either open or closed. Table 2 shows V_VL and t_d for various combinations of input values of a two-input, single-output volistor NOR gate implemented in a 3 × 1, and a sixty three-input, single-output volistor NOR gate implemented in a 64 × 1 crosspoint array. Note that with more logic “1” inputs, the value of V_VL approaches V _in and the propagation delay t_d gets shorter. Volistor logic allows a multi-input NOR gate to be realized in only one pulse.

Table 2 Implementation of multi-input single-output volistor NOR gate

3.4 Volistor AND Gate in a Crosspoint Array

The third basic gate in volistor logic is AND. This gate is realized as NOR with negated literals of the desired product applied to the crosspoint array. For example, the desired product $\overline{a}b\overline{c}$ is realized by applying (vin ₁, vin ₂, vin ₃) = (1, 0, 1) to the memristors. As a result, the voltage across T is sufficient to toggle t to “0” where $t=\overline{a+\overline{b}+c}$ and according to De Morgan’s Law $\overline{a+\overline{b}+c}=\overline{a}b\overline{c}$ which is the desired result. The AND gate can be scaled to perform multi-input multi-output operations. The details are the same as described for volistor NOR. In this work, it is assumed that negated inputs are always available at the same cost as the non-negated inputs. Volistor logic allows a multi-input AND to be realized in only one pulse.

3.5 Volistor OR and NAND Gates in a Crosspoint Array

In all volistor logic gates discussed above, the logical coding scheme of memristive switch T is defined as follows: an open switch encodes logic “0” and a closed switch encodes logic “1.” This scheme allows direct implementation of volistor NOR/AND; however, it does not allow for direct implementation of volistor OR/NAND. Therefore, executing a circuit with a volistor OR/NAND gate would require two consecutive pulses.

However, if the logical coding scheme of the memristor switch T is reversed, i.e., the open switch encodes logic “1” and the closed switch encodes logic “0,” then the OR/NAND gate can be realized in one pulse. This scheme allows a direct realization of volistor OR in the same manner as volistor NOR described in Section 3.3. Likewise, volistor NAND is realized by applying negated input logic values to the crosspoint array in the same manner as the volistor AND described in Section 3.4. The designer could use one of the two encoding schemes for the entire system or use both encoding schemes in a partitioned system. In each separate partition, one encoding scheme is utilized and partitions with different schemes communicate through inverters.

3.6 Mixed-Input Logic Gates in a Crosspoint Array

Inputs on standard volistor gates are voltages; however, as shown in Fig. 4d, implementing gates with mixed-inputs is possible using a hybrid of stateful and volistor logic where some inputs are represented by resistances and some by voltages. Figure 7 depicts a three-input NOR gate implemented in a 1 × 4 crosspoint array where (s, vin ₁, vin ₂, t) = (0, 0, 1, 1). In (s, vin ₁, vin ₂, t), s and t are resistive logic values of S₁ and T, and vin ₁ and vin ₂ are logic input voltages applied to S₂ and S₃, see Fig. 7. Specifically, s is the resistive logic value stored in S₁ and it is to be interpreted as logic “0.” Assume s has been set in a previous operation and that all memristors with voltage inputs have already been set to R_CLOSED. As in stateful logic, HL is grounded through R_G and V⁺ is applied to S₁. As in volistor logic input data are applied to memristors S₂ and S₃, and bias voltage V⁻ is applied to memristor T. Equation (3), discussed in Section 3.1, requires V _bias  = V⁻ and V _in  ≥ 0V. With this configuration, the resistive value of logic s manifests as a voltage on HL and the circuit operates in the same manner as a volistor NOR. Translation between logical encoding schemes is accomplished in the same manner as described in Section 3.5. Mixed volistor AND gate is realized with one extra step; since all input resistances need to be negated, one additional pulse is required.

Fig. 7

Mixed-input NOR. The implementation of three-input one-output NOR gate. The resistive input is stored in S₁ and the voltage inputs are applied to S₂ and S₃. The output is stored in memristor T

4 Hybrid Approach to Synthesize Boolean Functions in Crossbar Networks

In theory [10, 11], every single-output Boolean function of n variables can be realized in a crosspoint array with n source memristors and two additional working memristors. These working memristors can act as both source and target memristors. However, this realization leads to long sequences of pulses. These long sequences can be avoided by the use of crossbar arrays to realize arbitrary multi-output Boolean functions. Crosspoint arrays are the building blocks of crossbar arrays.

In this section, we first discuss hybrid computation in a crosspoint array and then we show how to implement arbitrary Boolean functions in a network of crossbar arrays. This network uses a combination of stateful, volistor, and mixed-input gates. These generic network structures can be used to implement logic functions in several forms such as SOP (Sum of Product), POS (Product of Sum), and TANT (Tree level AND NOT Network) [12]. TANT architecture requires non-inverted inputs, but we consider a generalized TANT with no restriction on input polarity. In this paper, stateful operations are realized solely with NOR and NOT. Note that the NOT gate can be obtained from INH by setting the non-inverted input to constant 1. Also, the NOR gate can be created by cascading stateful INH gates and setting the non-inverted input of the first gate of the cascade to constant 1, e.g., $\overline{a+b}=\left(1\cdot \overline{a}\right)\cdot \overline{b}$.

4.1 Hybrid Computation in a Crosspoint Array

The simplest structure to perform memristive logic computation is a crosspoint array. In this structure, computations can be performed by two approaches: (1) solely stateful logic [1], (2) a combination of mixed-input, stateful and volistor logic. We call the second approach the hybrid approach. The first approach is potentially slow since a long sequence of operations needs to be implemented. However, the second approach has the potential to reduce the number of required operations. We assume a SOP with M single literal degenerate products and N products with more than one literal, thus the SOP is the OR of M + N inputs. Realization of this SOP function requires a four-step process to be computed with the second approach:

• (1) CLEAR: Set all memristors to the closed state. In a 1 × n array, this requires driving all vertical nanowires to V⁺ and the horizontal nanowire to V⁻; for an n × 1 array, the driving voltages should be swapped. This step is realized in one pulse.

• (2) AND: Sequentially perform N volistor AND gates, each in one pulse. This step requires a total of N pulses.

• (3) NOR: Perform a NOR operation on N + M arguments. This includes the M single literal variables, which are supplied as voltages, and the N products from the previous step, which are stored as resistances. This step requires one pulse.

• (4) NOT: Negate the result of the previous step. This step requires one pulse.

Example 1

The following example describes the hybrid approach in a crosspoint array for the Boolean function $f= ab+\overline{a}\overline{b}+c$. This function can be realized in a 1 × 4 crosspoint array in five consecutive operations, one for CLEAR, two for AND, one for NOR, and one for NOT, as shown in Fig. 8.

Fig. 8

Example of hybrid computation in a crosspoint array. a A 1 × 4 crosspoint array used to implement SOP function f. b The circuit configuration to implement each step. The total number of consecutive operations (pulses) to realize f is 5

Figure 8a shows a 1 × 4 crosspoint array driven by V _i , and Fig. 8b shows the circuit configuration in each step. The first step is implemented by setting all V _i to V⁺ and HL to V⁻. This step will set the memristors M _i closed, i.e., encoding logic “1.” The second step is to compute the product ab. This step is implemented by setting V₁ and V₂ to V _ā and ${\mathrm{V}}_{\overline{b}}$ where V _ā and ${\mathrm{V}}_{\overline{b}}$ are voltage signals encoding literals ā and $\overline{b}$, respectively. The result of this computation is stored in M₄. Similarly, the second product, $\overline{a}\overline{b}$, is computed by setting V₁ and V₂ to V_a and V_b where V_a and V_b are voltage signals encoding literals a and b, respectively. The computed result is stored in M₃. The third step is realized with a mixed-input NOR gate, i.e., NOR $\left( ab,\ \overline{a}\overline{b},\ c\right)$. Note that variable c in SOP function f is a voltage signal, whereas ab and $\overline{a}\overline{b}$ are resistive signals. This step is implemented by connecting HL to the ground through R_G and driving V₁, V₂, V₃, and V₄ to V_c, V⁻, V⁺, and V⁺, respectively. The result of the NOR gate is stored in M₂. Currently, the logic value of M₂ is $\overline{f}$, thus the last step is to invert this logic value to obtain f. This step is implemented by connecting HL to ground through R_G and driving V₁ and V₂ to V⁻ and V⁺, respectively. Since M₃ and M₄ do not take part in the last computation, V₃ and V₄ are terminated to HZ.

As illustrated in Example 1, every SOP can be realized in N + 3 operations, requiring at least N + 1 + M memristors in the crosspoint array. In Example 1, M = 1, so we used four memristors. As a matter of proper operation, all target memristors T _i must be initially closed. Further, if any of the inputs are logic “1,” then at least one of those logic “1” inputs must be driving a closed source memristor S _i . If all such memristors S _i were open, the electrical characteristics of the memristors might prevent proper manifestation of the input voltage on the common nanowire. Therefore, all memristors should be initially closed. The closed state of a memristor will only change to open when driven by V _bias and the voltage drop across the memristor is V_OPEN. Therefore, a target memristor T can be used as a source memristor, i.e., driven by V _in in subsequent operations with no risk of changing its state. This reuse allows for compact logic implementations. However, this approach potentially results in all source memristors being open, so any subsequent logic “1” inputs have no closed memristor to drive. Therefore, the number of memristors in the array should be more than the number of products, i.e., extra memristors should be provided as dedicated targets. So, realizing volistor gates with many inputs is possible neglecting the resistance of the common nanowire. This allows implementing structures such as SOP with many products. However, in a crosspoint array, each nanowire is driven by an individual CMOS driver with control circuitry, as shown in Fig. 2. This requirement imposes a large area penalty potentially restricting the number of inputs to the gates. Extending a crosspoint array to a crossbar array overcomes this potential limitation and increases the overall memristive density.

4.2 Hybrid Computation in a Crossbar Array

The crosspoint array can be scaled into a two-dimensional crossbar array of size m × n. Each of the m rows in the crossbar array can be thought of as a 1 × n crosspoint array and each of the n columns can be thought of as an m × 1 crosspoint array. With this crossbar structure, in a single volistor operation, a product of literals can be created and copied to an arbitrary column memristor or row memristor in the crossbar simultaneously. The multi-output capability of crosspoint arrays discussed earlier allows an arbitrary number of copy operations to be performed in any of the two dimensions of the crossbar array. Figure 9a depicts target memristors as multi-input volistor gates whose outputs are the states of the corresponding memristors. Using the multi-output property, any combination of NOR/AND gates can be copied to any number of arbitrary locations in a single column. One operation is required for each gate type. In the worst case, the entire crossbar array can be populated with an arbitrary combination of gates in 2n operations. Populating the crossbar array in this manner is the first step (after initialization) to map a Boolean function to a generic crossbar fabric. This fabric may, in general, combine the use of volistor logic, mixed-input logic, and stateful logic in the same crossbar array to produce logic computations.

Fig. 9

The crossbar array. a A crossbar array divided into three blocks; the populated gates in the block labeled 1 are realized by volistors, but the blocks labeled 2 and 3 are realized with stateful NOR. b The symbolic two-level circuit is realized with the stateful approach. c The symbolic three-level circuit is realized with the hybrid approach. The first level of the circuit, L1, is realized with volistor logic, whereas the next levels, L2 and L3, are realized with the stateful approach

Example 2

As a means of discussing this hybrid approach, take for example, the implementation of function $f=\overline{\overline{a\overline{b}+\overline{c}\overline{d}}+\overline{A}}=\overline{\overline{B}+\overline{A}}= AB$. This implementation requires the same four-step process described in Section 4.1 and is illustrated in Fig. 10. The entries of the symbolic matrices represent the logic values stored in each memristor of the crossbar. Voltages applied to the horizontal and vertical nanowires are indicated by the values shown to the left of and on top of the matrices. The labels on top of the arrows between matrices indicate the number of operations required to move to the next matrix. Figure 10a shows the crossbar after initialization; the voltages to achieve this state are not shown. Figure 10b shows the result of computing the first product with volistor AND. Figure 10c shows the computation of the other product which is also realized with volistor AND. Figure 10d shows stateful logic being used to compute $\overline{B}=\overline{a\overline{b}+\overline{c}\overline{d}}$. In this step, V⁺ and V⁻ are equal to V_COND and V_SET, and R_G is the load resistor in stateful INH [2]. Figure 10e shows the implementation of a mixed NOR gate with resistance-based signal $\overline{B}$ and voltage-based signal Ā producing the desired function f.

Fig. 10

The symbolic matrices illustrate the steps of logic computations based on the hybrid approach for computing $f=\overline{\overline{a\overline{b}+\overline{c}\overline{d}}+\overline{A}}$. a Initialization step. b Computing $a\overline{b}$ with a volistor AND. c Computing $\overline{c}\overline{d}$ with a volistor AND. d Computing $\overline{a\overline{b}+\overline{c}\overline{d}}$ with a stateful NOR. e Computing f with a mixed-gate NOR

Fig. 11

Implementation of different forms of Boolean functions with the hybrid approach. a An example of a SOP function. b An example of a POS function. c An example of a three-level sum of products of sums. d An example of an EXOR of two products. e An example of a NAND-AND-EXOR logic function. f An example of an AND-EXOR-OR logic function. P stands for pulse (operation), e.g., 1P indicates that a related logic level requires one pulse to be implemented. VL and SL stand for volistor and stateful operations. In all circuits, only the first logic level is implemented with volistor logic

With the hybrid approach, the use of stateful IMP can be avoided. This simplifies the driver circuitry, removes the need for a keeper circuit [13], and simplifies crossbar initialization since all memristors are initialized as closed. The stateful approach also requires a step to store the inputs in the crossbar. However, since the hybrid approach uses voltages as inputs, no storage step is required. The main advantage of the hybrid approach over the stateful approach is that, for the same number of operations and memristors, one additional logic level can be realized. The hybrid approach uses the efficiency of volistors to implement the first level of logic which is usually most complex. Figure 9a depicts a crossbar array divided into three blocks. In stateful logic, the memristors in block 1 store inputs; the memristors in block 2 store the first-level logic outputs, and the memristor in block 3 stores the output of the second-level logic. In the hybrid approach, since inputs are voltages, the memristors in block 1 store the outputs of the first-level logic; the memristors in block 2 store the outputs of the second-level logic, and the memristor in block 3 stores the output of the third-level logic. With the same number of operations and the same number of memristors, the stateful approach produces only two-level logic (Fig. 9b) whereas the hybrid approach produces three-level logic as shown in Fig. 9c. However, since in volistor logic the inputs are voltages, there can be only one set of inputs applied to the crossbar at any given moment and therefore only one output can be computed at a time. In stateful logic, inputs are stored as resistances. Therefore, each row or column can be thought of as a distinct set of inputs capable of simultaneously producing distinct outputs, with the restriction that all outputs implement the same type of stateful gate [2], e.g., all the four NOR gates as shown in block 2 of Fig. 9a. In Section 4.3, we use the hybrid approach in a crossbar network to achieve different outputs in parallel.

4.3 Hybrid Computation in a Crossbar Network

In a data path of a larger memristor architecture, there are usually several combinational blocks as well as memories each of which is realized in one or more crossbars. A question arises as to how one can implement information transfer between these crossbars. Let us consider transfer of data from source memory to target combinational logic. The memories can store information as either voltage (e.g., CMOS memory) or as resistance. If data are stored as voltage, the first level of the target logic can be implemented with volistors. However, when data in memories are stored as resistances, the first logic level in combinational logic is realized with stateful NOR/NOT. Another problem is how to partition large combinational blocks to improve processing time by increasing parallelism. In a single crossbar array using volistor logic, identical gates with identical inputs can be produced in a single step. This is a limited form of parallelism that replaces fan-out. This limitation can be resolved using a network of many individual crossbars. Each individual crossbar can have as many copies as necessary of a single gate with identical inputs. This structure allows two or more separate crossbars to simultaneously calculate the first logic level of an arbitrary Boolean function. Additional logic levels can be achieved with stateful operations, mixed-input gates, or both. Table 3 shows different structures to realize Boolean functions that are well suited to this hybrid approach. Next, we present detailed examples for cases 2 and 5 from Table 3.

Table 3 Different forms of logic functions and their De Morgan’s equivalents

Example 3

POS implementation. The three variable EXOR expression f = a ⊕ b ⊕ c can be implemented as the POS expression $\left(a+b+c\right)\left(a+\overline{b}+\overline{c}\right)\left(\overline{a}+\overline{b}+c\right)\left(\overline{a}+b+\overline{c}\right)$. The De Morgan equivalent expression is $f=\overline{\overline{\left(a+b+c\right)}+\overline{\left(a+\overline{b}+\overline{c}\right)}+\overline{\left(\overline{a}+\overline{b}+c\right)}+\overline{\left(\overline{a}+b+\overline{c}\right)}}=\overline{w+x+y+z}$. The function is synthesized in four crossbar arrays each of which is 4 × 4. In this crossbar column, adjacent crossbars communicate through vertical switches capable of connecting and disconnecting the crossbars as illustrated in Fig. 12a. Figure 12b shows the crossbar column with closed vertical switches between all adjacent crossbars creating a 16 × 4 crossbar array. These switches are not further discussed in this work. Executing f is a three-step procedure.

Fig. 12

Implementation of POS function f in a crossbar network comprised of four crossbar arrays of size 4 × 4. The function is realized in a two-step procedure. a Realization of the first logic level of POS function f in separate crossbars. The network configuration shows the voltage drivers applied to each nanowire. This step produces four NOR gates. b The switches between the 4 × 4 arrays are closed to create a 16 × 4 crossbar array. The results w, x, y, and z of the first step are NORed to create the output of the POS function f

• (1) Initialize all crossbar arrays by driving all vertical nanowires with V⁺ and all horizontal nanowires with V⁻.

• (2) Simultaneously compute volistor NOR of each maxterm in a separate crossbar column as described in Section 3 3.3. In Fig. 12a, individual crossbar arrays A, B, C, and D compute $w=\overline{a+b+c}$, $x=\overline{a+\overline{b}+\overline{c}}$, $y=\overline{\overline{a}+\overline{b}+c}$, and $z=\overline{\overline{a}+b+\overline{c}}$ in parallel.

• (3) Connect the vertical switches between adjacent crossbars to form a 16 × 4 crossbar array. Perform a stateful NOR on the logic values computed in step 2 as illustrated in Fig. 12b.

Executing f with a solely stateful approach would require two steps plus the overhead of setting up each input [2]. This input overhead is directly proportional to the number of inputs in the largest sum. Volistor logic has no such input overhead; a multi-input gate and a single-input gate are both produced in the same number of steps. However, the solely stateful approach can be executed in two steps in a single crossbar whereas the hybrid approach would require more steps if performed in a single crossbar.

Example 4

NAND-AND-EXOR implementation. Consider the expression $f=e\cdot \overline{\overline{a}b}\cdot \overline{\overline{c}d}\oplus \overline{\overline{c}d}\cdot \overline{a}\overline{e}\cdot b$. The De Morgan equivalent expression is $f=\overline{\overline{\overline{e}+\overline{a}b+\overline{c}d+ae+\overline{b}}+\overline{\overline{\overline{e}+\overline{a}e+\overline{c}d}+\overline{\overline{c}d+ae+\overline{b}}}}=\overline{\overline{\overline{e}+x+y+z+\overline{b}}+\overline{\overline{\overline{e}+x+y}+\overline{y+z+\overline{b}}}}=\overline{\overline{\overline{w1}+\overline{w2}}+\overline{w1+w2}}=\overline{o1+o2}$. Executing f is the six-step procedure depicted in Fig. 13 and described as follows. In each step, all outputs are computed simultaneously.

Fig. 13

Realization of the De Morgan equivalent for the NAND-AND-EXOR expression f. The crossbar network is comprised of four crossbar arrays each of size 4 × 4. The function is realized in a six-step procedure. a The first logic level of f is realized with volistors, b the second logic level of f is realized with mixed-input gates, and c–e the rest of the logic levels are realized with stateful logic. Crossbar drivers are indicated by 0 V, V⁺, V⁻, R_G, and HZ. In each step, the performed operation is depicted by logic gates and the results of the operations are shown as outputs of the gates

• (1) Perform the initialization as in example 3.

• (2) Compute the products x, y, and z in parallel. Value y is computed twice to enable simultaneous computation in step 3 as in Fig. 13a. This realizes the four AND gates using volistors.

• (3) Using mixed-input gates, as described in Section 3.6, compute w1 and w2 where V _ē and ${\mathrm{V}}_{\overline{b}}$ are input voltages and x, y, and z are input resistances, as in Fig. 13b. This realizes the NOR logic level.

• (4) Produce $\overline{w1}$ and $\overline{w2}$ in parallel, as in Fig. 13c. This performs two stateful NOT operations in the third logic level.

• (5) Produce o2 and o1 in the fourth logic level, NOR, using the outputs calculated in steps 3 and 4, as in Fig. 13d.

• (6) Produce f from o2 and o1, as in Fig. 13e. This produces the fifth level of logic, NOR. Executing f with a solely stateful approach would require six steps plus the input setup overhead. Note that NAND-AND-EXOR circuits are a new concept in logic synthesis. These circuits are a generalization of the PSE circuits introduced in [14] in which only one argument of the AND layer is a NAND and others are literals.

5 Comparison of Power Consumption and Speed Between Stateful and Volistor Circuit Models

In this work, power measurements are made using the same model mentioned in Section 2 in the LTspice IV simulation environment. The average power P_avg consumed in a crosspoint array is computed using the equation P_avg = ∑V_RMS ⋅ I_RMS where V_RMS and I_RMS are the root mean squares of the voltage across and the current through each memristor. The average power consumption of each individual element of a 1 × n crosspoint array where n ≤ 64 is computed over a 10 ns interval beginning with the application of the driver voltages V⁺ = 0.6V, V⁻ = − 0.6V and 0 V which are applied for 8 ns. Let the power consumed in a source memristor set to logic “1” be denoted P_S1, the power consumed in a source memristor set to logic “0” be denoted P_S0, the power consumed in a target memristor be denoted P_T, and the power consumed in load resistor R_G be denoted P_RG. Let P_S denotes the total power consumption in all source memristors. The superscripts SL and VL are used to indicate power consumptions during stateful logic and volistor logic, respectively. For example, P ^SL_S0 is the power consumed by a source memristor set to logic “0” when SL is performed and P ^VL_S is the power consumed in all source memristors when volistor logic is performed. Table 4 describes the power consumption in each crosspoint element where V_HL and ${\hat{\mathrm{V}}}_{\mathrm{HL}}$ are the voltages on the horizontal nanowire during VL and SL operations, respectively. Table 4 is derived based on the average power equation P_avg and Ohm’s Law; the circuit elements considered in power computation are the resistance values of the memristors, either R_CLOSED or R_OPEN, load resistance R_G, and the driver voltages. The power required to connect the nanowires to V⁺, V⁻, 0V, R_G, and HZ is the same in both VL and SL operations and is not considered in this work. The resistance of the horizontal nanowire HL is negligible when compared with load resistance R_G. Jo et al. [15] reported that the resistive value of a relatively large width nanowire of diameter 120 nm used in a 1-kb crossbar array is at most 30 KΩ when implemented with relatively high resistance p-doped Si. This upper bound is much smaller than R_G = 15 MΩ chosen in this work. Recall, ${\mathrm{R}}_{\mathrm{G}}=\sqrt{{\mathrm{R}}_{\mathrm{OPEN}}\times {\mathrm{R}}_{\mathrm{CLOSED}}}$ and $\frac{{\ \mathrm{R}}_{\mathrm{OPEN}}}{{\mathrm{R}}_{\mathrm{CLOSED}}}={10}^3$ as mentioned in Section 2 and Section 3. The power consumed by volistor logic in a crosspoint array is entirely due to the leakage through the reverse biased rectifying memristors as there is no direct path to ground. However, when volistor logic is performed in a crossbar array, there is an additional power consumption in memristors not taking part in the operations. This is true for stateful logic as well. Since the power consumption in both cases is the same and we are only interested in comparing SL and VL, this additional power is not discussed. In this section, the power consumption in a crosspoint array for S ₁ > 0 and S ₁ = 0 is analyzed separately. For ease of reference, let S ₁ and S ₀ denote the numbers of source memristors set to vin = 1 and vin = 0, respectively; T denotes the number of target memristors; P_SL and P_VL denote the total power consumption in memristors and in load resistor R_G during SL and VL operations, respectively; and t_d denotes the switching delay—the time required to completely switch from the close state of a target memristor T to the open state.

Table 4 Power consumption in each crosspoint array element

5.1 Analysis of Power Consumption and Switching Delays in a 1 × 8 Crosspoint Array for S ₁ > 0

Table 5 compares the switching delay, t_d, and the overall power consumption in memristors and in load resistor R_G during SL and VL operations for various compositions of S ₁, S ₀ and $T,\frac{{\mathrm{P}}_{\mathrm{SL}}}{{\mathrm{P}}_{\mathrm{VL}}}$. From the simulation results shown in Table 5, the following is observed.

Table 5 Circuit element power consumption, switching delay and power ratio in a 1 × 8 crosspoint array

• (1) In SL and VL, P_T is approximately 2nW, i.e., the changes to the number and the high/low composition of input values slightly affect the power consumed by any individual target memristor T. This is expected given the characteristics of the rectifying memristors and considering that V_HL ≈ V_in.

• (2) The major contributor to the power consumption in SL is R_G—it consumes approximately eight times more power than each target memristor. In VL, P_RG = 0.

• (3) The minor contributors to the power consumption in SL is S₀ × P ^SL_S0 .

• (4) The major contributors to the power consumption in VL are determined based on S ₀ and T.

• (5) For any combination of S ₁, S ₀, and T, $\frac{{\mathrm{P}}_{\mathrm{SL}}}{{\mathrm{P}}_{\mathrm{VL}}}>2$. The lower bound of $\frac{{\mathrm{P}}_{\mathrm{SL}}}{{\mathrm{P}}_{\mathrm{VL}}}$ obtained for the composition of (S ₁, S ₀, T) = (1, 0, 7) is 2.129. 

• (6) For any combination of S ₁, S ₀, and T, t_d is always lower for VL.

As a summary, we observed that in a 1 × 8 crosspoint array VL circuit is faster than SL and consumes at most half the power of its SL technology equivalent.

In a 1 × 8 crosspoint array, for any composition of S ₁, S ₀, and T where S ₁ > 0, the power ratio can be approximated based on the following power properties, Property 1–Property 4.

Property 1

When S ₁ > 0, the power consumption in a target memristor during VL operation can be approximated as shown in (5).

$$ {\mathrm{P}}_{\mathrm{T}}^{\mathrm{VL}}\approx 4\times {\mathrm{P}}_{\mathrm{S}0}^{\mathrm{VL}} $$

(5)

Proof

The power consumption in a target memristor during VL operation is ${\mathrm{P}}_{\mathrm{T}}^{\mathrm{V}\mathrm{L}}=\frac{{\left({\mathrm{V}}_{\mathrm{HL}}-{\mathrm{V}}^{-}\right)}^2}{{\mathrm{R}}_{\mathrm{OPEN}}}=\frac{{\left({\mathrm{V}}_{\mathrm{HL}}+{\mathrm{V}}^{+}\right)}^2}{{\mathrm{R}}_{\mathrm{OPEN}}}$ and the power consumption in a source memristor set to logic “0” during VL operation is ${\mathrm{P}}_{\mathrm{S}0}^{\mathrm{V}\mathrm{L}}=\frac{{{\mathrm{V}}_{\mathrm{HL}}}^2}{{\mathrm{R}}_{\mathrm{OPEN}}}$. So, $\frac{{\mathrm{P}}_{\mathrm{T}}^{\mathrm{V}\mathrm{L}}}{{\mathrm{P}}_{\mathrm{S}0}^{\mathrm{V}\mathrm{L}}}=\frac{{\left({\mathrm{V}}_{\mathrm{HL}}+{\mathrm{V}}^{+}\right)}^2}{{{\mathrm{V}}_{\mathrm{HL}}}^2}$. Let V⁺ = V_HL + ε. As a result, $\frac{{\mathrm{P}}_{\mathrm{T}}^{\mathrm{V}\mathrm{L}}}{{\mathrm{P}}_{\mathrm{S}0}^{\mathrm{V}\mathrm{L}}}={\left[\frac{2{\mathrm{V}}_{\mathrm{HL}}+\upvarepsilon}{{\mathrm{V}}_{\mathrm{HL}}}\right]}^2={\left[2+\frac{\upvarepsilon}{{\mathrm{V}}_{\mathrm{HL}}}\right]}^2$. The upper and lower bounds of $\frac{{\mathrm{P}}_{\mathrm{T}}^{\mathrm{VL}}}{{\mathrm{P}}_{\mathrm{S}0}^{\mathrm{VL}}}$, obtained for the upper and lower bounds of $\frac{\upvarepsilon}{{\mathrm{V}}_{\mathrm{HL}}}$, are calculated for (S ₁, S ₀, T) = (1, 1 , 6 ) and (S ₁, S ₀, T) = (6, 1, 1), respectively. These compositions were simulated using LTspice obtaining $4.002\le \frac{{\mathrm{P}}_{\mathrm{T}}^{\mathrm{VL}}}{{\mathrm{P}}_{\mathrm{S}0}^{\mathrm{VL}}}\le \kern0.37em 4.052$. Therefore, for any combination of S ₁, S ₀, and T where S ₁ > 0 we can assume P ^VL_T  ≈ 4 × P ^VL_S0 .

Property 2

When S ₁ > 0, the power consumption in the load resistor can be approximated as shown in (6).

$$ {\mathrm{P}}_{\mathrm{RG}}\approx 8\times {\mathrm{P}}_{\mathrm{T}}^{\mathrm{SL}} $$

(6)

Proof

The power consumption in the load resistor is ${\mathrm{P}}_{\mathrm{R}\mathrm{G}}=\frac{{{\widehat{\mathrm{V}}}_{\mathrm{HL}}}^2}{{\mathrm{R}}_{\mathrm{G}}}$ and the power consumption in a target memristor during SL operation is ${\mathrm{P}}_{\mathrm{T}}^{\mathrm{SL}}=\frac{{\left({\widehat{\mathrm{V}}}_{\mathrm{HL}}-{\mathrm{V}}^{-}\right)}^2}{{\mathrm{R}}_{\mathrm{OPEN}}}=\frac{{\left({\widehat{\mathrm{V}}}_{\mathrm{HL}}+{\mathrm{V}}^{+}\right)}^2}{{\mathrm{R}}_{\mathrm{OPEN}}}$. So, $\frac{{\mathrm{P}}_{\mathrm{R}\mathrm{G}}}{{\mathrm{P}}_{\mathrm{T}}^{\mathrm{SL}}}=\frac{{{\widehat{\mathrm{V}}}_{\mathrm{HL}}}^2}{{\mathrm{R}}_{\mathrm{G}}}\times \frac{{\mathrm{R}}_{\mathrm{OPEN}}}{{\left({\widehat{\mathrm{V}}}_{\mathrm{HL}}+{\mathrm{V}}^{+}\right)}^2}=\frac{{\mathrm{R}}_{\mathrm{OPEN}}}{{\mathrm{R}}_{\mathrm{G}}}\times \frac{1}{{\left[\frac{{\widehat{\mathrm{V}}}_{\mathrm{HL}}+{\mathrm{V}}^{+}}{{\widehat{\mathrm{V}}}_{\mathrm{HL}}}\right]}^2}$. Let ${\mathrm{V}}^{+}={\widehat{\mathrm{V}}}_{\mathrm{HL}}+\widehat{\upvarepsilon}$. As a result, $\frac{{\mathrm{P}}_{\mathrm{R}\mathrm{G}}}{{\mathrm{P}}_{\mathrm{T}}^{\mathrm{SL}}}=\frac{{\mathrm{R}}_{\mathrm{OPEN}}}{{\mathrm{R}}_{\mathrm{G}}}\times \frac{1}{{\left[\frac{2{\widehat{\mathrm{V}}}_{\mathrm{HL}}+\widehat{\upvarepsilon}}{{\widehat{\mathrm{V}}}_{\mathrm{HL}}}\right]}^2}=\frac{{\mathrm{R}}_{\mathrm{OPEN}}}{{\mathrm{R}}_{\mathrm{G}}}\times \frac{1}{{\left[2+\frac{\widehat{\upvarepsilon}}{{\widehat{\mathrm{V}}}_{\mathrm{HL}}}\right]}^2}$. Computing the upper bound of $\frac{{\mathrm{P}}_{\mathrm{RG}}}{{\mathrm{P}}_{\mathrm{T}}^{\mathrm{SL}}}$ requires computing the lower bound of voltage ratio $\frac{\widehat{\upvarepsilon}}{{\widehat{\mathrm{V}}}_{\mathrm{HL}}}$. The upper and lower bounds of $\frac{{\mathrm{P}}_{\mathrm{RG}}}{{\mathrm{P}}_{\mathrm{T}}^{\mathrm{SL}}}$ or the lower and upper bounds of $\frac{\widehat{\upvarepsilon}}{{\widehat{\mathrm{V}}}_{\mathrm{HL}}}$ are calculated for the compositions of (S ₁, S ₀, T) = (7, 0, 1) and (S ₁, S ₀, T) = (1, 0, 7), respectively. These compositions were simulated using LTspice obtaining $7.542\le \frac{{\mathrm{P}}_{\mathrm{RG}}}{{\mathrm{P}}_{\mathrm{T}}^{\mathrm{SL}}}\le\ 7.866$. Therefore, for any combination of S ₁, S ₀, and T where S ₁ > 0 we can assume P_RG ≈ 8 × P ^SL_T .

Since P ^VL_T and P ^SL_T for any combination of S ₁, S ₀, and T where S ₁ > 0 are approximately 2nW, they can be replaced with P_T in (5) and (6).

Property 3

When S ₁ > 0, the power consumption in source memristors during SL operation is considerably smaller than the overall power consumption in target memristors and load resistor R_G as shown in (7).

$$ \frac{{\mathrm{P}}_{\mathrm{S}}^{\mathrm{S}\mathrm{L}}}{{\mathrm{P}}_{\mathrm{S}\mathrm{L}}-{\mathrm{P}}_{\mathrm{S}}^{\mathrm{S}\mathrm{L}}}\ll 1 $$

(7)

Proof

The simulation results show that the power consumption in source memristors during SL operation, P ^SL_S , is negligible when compared to the overall power consumption in target memristors and load resistor R_G. The power consumption in source memristors set to logic "1" is much larger than the power consumption in source memristors set to logic "0", as can be seen in follows: $\frac{{\mathrm{P}}_{\mathrm{S}1}^{\mathrm{S}\mathrm{L}}}{{\mathrm{P}}_{\mathrm{S}0}^{\mathrm{S}\mathrm{L}}}=\frac{{\left({\mathrm{V}}^{+}-{\widehat{\mathrm{V}}}_{\mathrm{HL}}\right)}^2}{{\mathrm{R}}_{\mathrm{CLOSED}}}\times \frac{{\mathrm{R}}_{\mathrm{OPEN}}}{{\left({\mathrm{V}}^{+}-{\widehat{\mathrm{V}}}_{\mathrm{HL}}\right)}^2}={10}^3$. Substituting P ^SL_S1  = 10³ × P ^SL_S0 in $\frac{{\mathrm{P}}_{\mathrm{S}}^{\mathrm{S}\mathrm{L}}}{{\mathrm{P}}_{\mathrm{S}\mathrm{L}}-{\mathrm{P}}_{\mathrm{S}}^{\mathrm{S}\mathrm{L}}}$ results in $\frac{\left({S}_1\times {10}^3+{S}_0\right)\times {\mathrm{P}}_{\mathrm{S}0}^{\mathrm{S}\mathrm{L}}}{{\mathrm{P}}_{\mathrm{S}\mathrm{L}}-{\mathrm{P}}_{\mathrm{S}}^{\mathrm{S}\mathrm{L}}}$. Substituting P_SL − P ^SL_S with T × P_T + P_RG or its equivalent (T + 8) × P_T in $\frac{\left({S}_1\times {10}^3+{S}_0\right)\times {\mathrm{P}}_{\mathrm{S}0}^{\mathrm{S}\mathrm{L}}}{{\mathrm{P}}_{\mathrm{S}\mathrm{L}}-{\mathrm{P}}_{\mathrm{S}}^{\mathrm{S}\mathrm{L}}}$ results in $\frac{\left({S}_1\times {10}^3+{S}_0\right)}{\left(T+8\right)\times \frac{{\mathrm{P}}_{\mathrm{T}}}{{\mathrm{P}}_{\mathrm{S}0}^{\mathrm{S}\mathrm{L}}}}$. It is required to compute the lower bound of $\frac{{\mathrm{P}}_{\mathrm{T}}}{{\mathrm{P}}_{\mathrm{S}0}^{\mathrm{S}\mathrm{L}}}$ to verify $\frac{\left({S}_1\times {10}^3+{S}_0\right)}{\left(T+8\right)\times \frac{{\mathrm{P}}_{\mathrm{T}}}{{\mathrm{P}}_{\mathrm{S}0}^{\mathrm{S}\mathrm{L}}}} \ll 1$. This power ratio, $\frac{{\mathrm{P}}_{\mathrm{T}}}{{\mathrm{P}}_{\mathrm{S}0}^{\mathrm{S}\mathrm{L}}}$, is equal to $\frac{{\left({\widehat{\mathrm{V}}}_{\mathrm{HL}}-{\mathrm{V}}^{-}\right)}^2}{{\mathrm{R}}_{\mathrm{OPEN}}}\times \frac{{\mathrm{R}}_{\mathrm{OPEN}}}{{\left({\mathrm{V}}^{+}-{\widehat{\mathrm{V}}}_{\mathrm{HL}}\right)}^2}$ or ${\left(\frac{2{\widehat{\mathrm{V}}}_{\mathrm{HL}}}{\widehat{\upvarepsilon}}+1\right)}^2$ considering  ${\mathrm{V}}^{+}={\widehat{\mathrm{V}}}_{\mathrm{HL}}+\widehat{\upvarepsilon}$. The lower bound of $\frac{{\mathrm{P}}_{\mathrm{T}}}{{\mathrm{P}}_{\mathrm{S}0}^{\mathrm{S}\mathrm{L}}}$obtained for the lower bound of $\frac{{\widehat{\mathrm{V}}}_{\mathrm{HL}}}{\widehat{\upvarepsilon}}$is calculated for (S ₁, S ₀, T) = (1, 1, 6). This composition results in $\frac{{\widehat{\mathrm{V}}}_{\mathrm{HL}}}{\widehat{\upvarepsilon}}=\kern0.37em 21.949$ and therefore $\frac{\left({S}_1\times {10}^3+{S}_0\right)}{\left(T+8\right)\times \frac{P_T}{P_{S0}^{SL}}}=$ 0.036 which is considerably smaller than 1 and thus proves (7). The immediate consequence of (7) for any combination of S ₁, S ₀ and T where S ₁ > 0 is P_SL − P ^SL_S  ≈ P_SL used in deriving (9).

Property 4

The power consumption in source memristors driven by logic “1” during VL operation is considerably smaller than the overall power consumption in source memristors driven by logic “0” and target memristors as in (8).

$$ \frac{S_1\times {\mathrm{P}}_{\mathrm{S}1}^{\mathrm{VL}}}{{\mathrm{P}}_{\mathrm{VL}}-{S}_1\times {\mathrm{P}}_{\mathrm{S}1}^{\mathrm{VL}}}\ll 1 $$

(8)

Proof

The simulation results show that the power consumption in source memristors driven by logic “1” during VL operation is negligible when compared to the overall power consumption in memristors. Using the results of simulations, inequality (8) can be proved as follows. $\frac{{\mathrm{S}}_1\times {\mathrm{P}}_{\mathrm{S}1}^{\mathrm{VL}}}{{\mathrm{P}}_{\mathrm{VL}}-{\mathrm{S}}_1\times {\mathrm{P}}_{\mathrm{S}1}^{\mathrm{VL}}}=\frac{{\mathrm{S}}_1\times {\mathrm{P}}_{\mathrm{S}1}^{\mathrm{VL}}}{{\mathrm{S}}_0\times {\mathrm{P}}_{\mathrm{S}0}^{\mathrm{VL}}+\mathrm{T}\times {\mathrm{P}}_{\mathrm{T}}}$. Using (6), $\frac{{\mathrm{S}}_1\times {\mathrm{P}}_{\mathrm{S}1}^{\mathrm{VL}}}{{\mathrm{S}}_0\times {\mathrm{P}}_{\mathrm{S}0}^{\mathrm{VL}}+\mathrm{T}\times {\mathrm{P}}_{\mathrm{T}}}\approx \frac{{\mathrm{S}}_1\times {\mathrm{P}}_{\mathrm{S}1}^{\mathrm{VL}}}{{\mathrm{S}}_0\times \frac{{\mathrm{P}}_{\mathrm{T}}}{4}+\mathrm{T}\times {\mathrm{P}}_{\mathrm{T}}}=\frac{{\mathrm{S}}_1}{\frac{{\mathrm{P}}_{\mathrm{T}}}{{\mathrm{P}}_{\mathrm{S}1}^{\mathrm{VL}}}\left(\frac{{\mathrm{S}}_0}{4}+\mathrm{T}\right)}$. The lower bound of $\frac{{\mathrm{P}}_{\mathrm{T}}}{{\mathrm{P}}_{\mathrm{S}1}^{\mathrm{VL}}}$ is required to verify $\frac{{\mathrm{S}}_1\times {\mathrm{P}}_{\mathrm{S}1}^{\mathrm{VL}}}{{\mathrm{P}}_{\mathrm{VL}}-{\mathrm{S}}_1\times {\mathrm{P}}_{\mathrm{S}1}^{\mathrm{VL}}}\ll 1$ and is obtained for the composition of (S₁, S₀, T) = (1, 0, 7). Note that $\frac{{\mathrm{P}}_{\mathrm{T}}}{{\mathrm{P}}_{\mathrm{S}1}^{\mathrm{V}\mathrm{L}}}=\frac{{\left(2{\mathrm{V}}_{\mathrm{HL}}+\upvarepsilon \right)}^2}{{\mathrm{R}}_{\mathrm{OPEN}}}\times \frac{{\mathrm{R}}_{\mathrm{CLOSED}}}{{\left({\mathrm{V}}^{+}-{\mathrm{V}}_{\mathrm{HL}}\right)}^2}={10}^{-3}\times {\left(\frac{2{\mathrm{V}}_{\mathrm{HL}}}{\upvarepsilon}+1\right)}^2$ where ε = V⁺ − V_HL. Using LTspice simulator, the lower bound of $\frac{{\mathrm{V}}_{\mathrm{HL}}}{\upvarepsilon}$ for the given combination is 70.929 and consequently $\frac{{\mathrm{P}}_{\mathrm{T}}}{{\mathrm{P}}_{\mathrm{S}1}^{\mathrm{VL}}} = 20.409$. Therefore, $\frac{{\mathrm{S}}_1\times {\mathrm{P}}_{\mathrm{S}1}^{\mathrm{VL}}}{{\mathrm{P}}_{\mathrm{VL}}-{\mathrm{S}}_1\times {\mathrm{P}}_{\mathrm{S}1}^{\mathrm{VL}}}\approx \kern0.37em 0.007$ is significantly smaller than 1 and thus proves (8). The immediate consequence of (8) for any combination of S₁, S₀, and T where S₁ > 0 is P_VL − S₁ × P ^VL_S1  ≈ P_VL used in deriving (9).

According to (7) and (8), $\frac{{\mathrm{P}}_{\mathrm{S}\mathrm{L}}}{{\mathrm{P}}_{\mathrm{VL}}}\approx \frac{T\times {\mathrm{P}}_{\mathrm{T}}+{\mathrm{P}}_{\mathrm{RG}}}{S_0\times {\mathrm{P}}_{\mathrm{S}0}^{\mathrm{VL}}+T\times {\mathrm{P}}_{\mathrm{T}}}$, and according to (5) and (6), $\frac{T\times {\mathrm{P}}_{\mathrm{T}}+{\mathrm{P}}_{\mathrm{RG}}}{S_0\times {\mathrm{P}}_{\mathrm{S}0}^{\mathrm{VL}}+T\times {\mathrm{P}}_{\mathrm{T}}}\approx \frac{T\times {\mathrm{P}}_{\mathrm{T}}+8\times {\mathrm{P}}_{\mathrm{T}}}{S_0\times \frac{{\mathrm{P}}_{\mathrm{T}}}{4}+T\times {\mathrm{P}}_{\mathrm{T}}}$. Therefore, for any combination of S ₁, S ₀, and T where S ₁ > 0, we can assume:

$$ \frac{{\mathrm{P}}_{\mathrm{SL}}}{{\mathrm{P}}_{\mathrm{VL}}}\approx \frac{T+8}{T+\frac{S_0}{4}} $$

(9)

The lower bound of (9) is larger than 2. Simplifying the inequality $\frac{T+8}{T+\frac{S_0}{4}}>2$ results in $T+\frac{S_0}{2}<8$. In a 1 × 8 crosspoint array for any composition of S ₁, S ₀, T where S ₁ > 0, the inequality $T+\frac{S_0}{2}<8$ holds and so $\frac{{\mathrm{P}}_{\mathrm{SL}}}{{\mathrm{P}}_{\mathrm{VL}}}>2$.

In terms of switching delay, volistor gates perform faster than stateful gates. The switching delay in both SL and VL operations corresponds to the voltage drop across the target memristors, or equivalently the voltage of the common nanowire during the operations. The lowest voltage drop across the target memristors is obtained for the composition of (S ₁, S ₀, T) = (1, 0, 7), for which t_d is 4.136 and 4.477 ns for VL and SL, respectively. The highest voltage drop across the target memristors is obtained for the composition of (S ₁, S ₀, T) = (7, 0, 1) for which t_d is 4.030 and 4.089 ns for VL and SL, respectively. Note that the increase of S ₁ reduces the switching delay in both SL and VL operations.

5.2 Analysis of Power Consumption in a 1 × n Crosspoint Array for S ₁ = 0

In a 1 × 8 crosspoint array, for S ₁ = 0 and any combination of S ₀ and T, our simulation results show that $\frac{{\mathrm{P}}_{\mathrm{SL}}}{{\mathrm{P}}_{\mathrm{VL}}}>1$. Table 6 compares the power consumption in memristors and load resistor R_G for S ₁ = 0 and various compositions of S ₀ and T during VL and SL operations. In all compositions, T is kept constant at 1 and S ₀ is varied between 1 and 7. Table 6 shows that the increase of S ₀ has almost no effect on P _VL , i.e. for all given compositions the power consumption in memristors during VL operation is almost equal to the power consumption in only target memristors.

Table 6 Comparison of power ratio $\frac{{\mathrm{P}}_{\mathrm{SL}}}{{\mathrm{P}}_{\mathrm{VL}}}$ of a multi-input NOR realized in a 1 × 8 cross point array with S ₁ = 0 and various values of S ₀

Property 5

When S ₁ = 0, the power consumption in source memristors driven by logic “0” during VL operation is considerably smaller than the overall power consumption in target memristors as in (10).

$$ \frac{\ {S}_0\times {\mathrm{P}}_{\mathrm{S}0}^{\mathrm{VL}}}{T\times {\mathrm{P}}_{\mathrm{T}}^{\mathrm{VL}}}\ll 1 $$

(10)

Proof

Our simulation results show that the overall power consumption in memristors during VL operation is almost equal to the power consumption in only target memristors when S ₁ = 0. The power ratio $\frac{\ {S}_0\times {\mathrm{P}}_{\mathrm{S}0}^{\mathrm{VL}}}{T\times {\mathrm{P}}_{\mathrm{T}}^{\mathrm{VL}}}$ is equal to $\frac{\ {S}_0}{T} \times \frac{{{\mathrm{V}}_{\mathrm{HL}}}^2}{{\mathrm{R}}_{\mathrm{CLOSED}}}\times \frac{{\mathrm{R}}_{\mathrm{OPEN}}}{{\left(\ {\mathrm{V}}_{\mathrm{HL}}+{\mathrm{V}}^{+}\right)}^2}={10}^3\left(\ \frac{S_0}{T}\right)\times \frac{1}{{\left(1+\frac{{\mathrm{V}}^{+}}{{\ \mathrm{V}}_{\mathrm{HL}}}\right)}^2}$. The upper bound of $\frac{{\mathrm{P}}_{\mathrm{S}0}^{\mathrm{VL}}}{{\mathrm{P}}_{\mathrm{T}}^{\mathrm{VL}}}$ is obtained for the composition of (S ₀, T) = (7, 1) which produces maximum V_HL. For this composition, V_HL = − 75.417µV and thus $\frac{{\mathrm{P}}_{\mathrm{S}0}^{\mathrm{VL}}}{{\mathrm{P}}_{\mathrm{T}}^{\mathrm{VL}}} = 1.106\times {10}^{-4}$ which is considerably smaller than 1 and proves (10). Note that for a larger crosspoint array equation (10) is also valid, e.g., in a 1 × 64 crosspoint array the upper bound of $\frac{{\mathrm{P}}_{\mathrm{S}0}^{\mathrm{VL}}}{{\mathrm{P}}_{\mathrm{T}}^{\mathrm{VL}}}$ is calculated for (S ₀, T) = (63, 1). For this composition, V_HL = − 8.3807µV, P_VL = 0.558nW, and consequently $\frac{{\mathrm{P}}_{\mathrm{S}0}^{\mathrm{VL}}}{{\mathrm{P}}_{\mathrm{T}}^{\mathrm{VL}}}=1.229\times {10}^{-5}\gg 1$. The consequence of (10) for any combination of S₀ and T is P_VL ≈ P_VL − S₀ × P ^VL_S0 . Note that for S ₁ = 0, P ^SL_T  ≠ P ^VL_T and the increase of S ₀ increases $\frac{{\mathrm{P}}_{\mathrm{SL}}}{{\mathrm{P}}_{\mathrm{VL}}}$ as shown in Table 6.

Table 7 compares $\frac{{\mathrm{P}}_{\mathrm{SL}}}{{\mathrm{P}}_{\mathrm{VL}}}$ for various compositions of S ₀ and T. In a 1 × n crosspoint array, for S ₁ = 0, the power consumption during SL operation is the same for both combinations (S ₀, T) = (n − k, k) and (S ₀, T) = (k, n − k) where 1 ≤ k < n. In other words, if the voltage on the common nanowire of the crosspoint array for (S ₀, T) = ( n − k, k) is ${\widehat{\mathrm{V}}}_{\mathrm{HL}}$, this voltage for (S ₀, T) = (k, n − k) would become $-{\widehat{\mathrm{V}}}_{\mathrm{HL}}$. For example, for (S ₀, T) = (2, 6) ${\widehat{\mathrm{V}}}_{\mathrm{HL}} = -51.096\mathrm{mV}$, but for (S ₀, T) = (6, 2) ${\widehat{\mathrm{V}}}_{\mathrm{HL}} = 51.096\mathrm{mV}$. In both compositions, P_SL = 4.246nW, as shown in Table 7. This circuit behavior causes $\frac{{\mathrm{P}}_{\mathrm{SL}}}{{\mathrm{P}}_{\mathrm{VL}}}$ to increase as S ₀ approaches n. As S ₀ increases, the voltage drop across the target memristors during SL operation becomes larger than the voltage drop across the target memristors during VL operation. Since all target memristors show the same resistance when reverse biased, $\frac{{\mathrm{P}}_{\mathrm{SL}}}{{\mathrm{P}}_{\mathrm{VL}}}>1$. Recall that in SL operation, all source memristors are connected to V⁺, whereas in VL operation, under the assumption of S ₁ = 0, all source memristors are only set to 0 V. Moreover, the power consumption in source memristors during VL operation is negligible as shown in (10); therefore, the increase of S ₀ slightly affects P_VL. However, the power consumption in source memristors and in load resistor R_G during SL operation can significantly increase the $\frac{{\mathrm{P}}_{\mathrm{SL}}}{{\mathrm{P}}_{\mathrm{VL}}}$ ratio. When S ₀ = T, during SL operation $\left|{\mathrm{V}}^{+}-{\widehat{\mathrm{V}}}_{\mathrm{HL}}\right|=\left|{\mathrm{V}}^{-}-{\widehat{\mathrm{V}}}_{\mathrm{HL}}\right|$, and thus ${\widehat{\mathrm{V}}}_{\mathrm{HL}}=0\mathrm{V}$ and P_RG = 0V. In other words, P ^SL_T  = P ^SL_S0 . In this case, $\frac{{\mathrm{P}}_{\mathrm{SL}}}{{\mathrm{P}}_{\mathrm{VL}}}\approx \kern0.37em 2$. For example, in a 1 × 8 crosspoint array for $\left({S}_{\mathsf{0}},\;T\right)=\left(4,\;4\right)$ $\frac{{\mathrm{P}}_{\mathrm{SL}}}{{\mathrm{P}}_{\mathrm{VL}}} = 2.113$, or in a 1 × 64 crosspoint array for (S₀, T) = (32, 32) $\frac{{\mathrm{P}}_{\mathrm{SL}}}{{\mathrm{P}}_{\mathrm{VL}}}=2.005$.

Table 7 Comparison of power ratio $\frac{{\mathrm{P}}_{\mathrm{SL}}}{{\mathrm{P}}_{\mathrm{VL}}}$ of a multi-input multi-output NOR realized in a 1 × 8 cross point array with S ₁ = 0 and various values of S ₀ and T

In a 1 × 8 crosspoint array, for any composition of S ₀ and T,  $\frac{{\mathrm{P}}_{\mathrm{SL}}}{{\mathrm{P}}_{\mathrm{VL}}}>1$, i.e., the lower bound of $\frac{{\mathrm{P}}_{\mathrm{SL}}}{{\mathrm{P}}_{\mathrm{VL}}}$ is 1.025, computed for (S ₀, T) = (1, 7). This composition maximizes P_VL, while minimizing P_SL as shown in Table 7. However, in a 1 × n crosspoint array where n > 8, the decrease of k in (S ₀, T) = (k, n − k) can bring $\frac{{\mathrm{P}}_{\mathrm{SL}}}{{\mathrm{P}}_{\mathrm{VL}}}$ to less than 1, as shown in Table 8. Table 8 shows various compositions of S ₀ and T for which $\frac{{\mathrm{P}}_{\mathrm{SL}}}{{\mathrm{P}}_{\mathrm{VL}}}<1$. In each composition, for a given S ₀, only the lower bound of T for which $\frac{{\mathrm{P}}_{\mathrm{SL}}}{{\mathrm{P}}_{\mathrm{VL}}}<1$ is presented, i.e., a larger T leads to a smaller $\frac{{\mathrm{P}}_{\mathrm{SL}}}{{\mathrm{P}}_{\mathrm{VL}}}$.

Table 8 A multi-input multi-output NOR with power ratio $\frac{{\mathrm{p}}_{\mathrm{sl}}}{{\mathrm{P}}_{\mathrm{vl}}}<1$ for some combinations of S ₀ and T with S ₁ = 0 realized in a 1 × n cross point array

5.3 Analysis of Power Consumption and Switching Delays in a 1 × 64 Crosspoint Arrays for S ₁ > 0

Tables 9, 10, 11, and 12 compare the switching delay and the overall power consumption in a 1 × 64 crosspoint array during SL and VL for various compositions of S ₁, S ₀, and T, where S ₁ > 0. The simulation results, shown in Tables 9, 10, 11, and 12, are consistent with the first four observations stated for a 1 × 8 crosspoint array in Section 5.1. However, unlike the last two observations stated for a 1 × 8 crosspoint array, the following is observed.

Table 9 Comparison of delay t_d and power ratio $\frac{{\mathrm{p}}_{\mathrm{sl}}}{{\mathrm{p}}_{\mathrm{vl}}}$ of a multi-input NOR realized in a 1 × 64 crosspoint array with S ₀ ≥ 33 and varied S ₁

Table 10 Comparison of delay t_d and power ratio $\frac{{\mathrm{p}}_{\mathrm{sl}}}{{\mathrm{p}}_{\mathrm{vl}}}$ of a multi-input NOR realized in a 1 × 64 crosspoint array with constant input values S ₀ and S ₁, and varied

Table 11 Comparison of delay t_d and power ratio $\frac{{\mathrm{p}}_{\mathrm{sl}}}{{\mathrm{p}}_{\mathrm{vl}}}$ of a multi-input NOR realized in a 1 × 64 crosspoint array with constant number of inputs and varied outputs

Table 12 Comparison of delays t_d and power ratio $\frac{{\mathrm{p}}_{\mathrm{sl}}}{{\mathrm{p}}_{\mathrm{vl}}}$ of a multi-input NOR realized in a 1 × 64 crosspoint array with varying S ₁ and S ₀ > 33

• (1) The main contributors to the power ratio $\frac{{\mathrm{P}}_{\mathrm{SL}}}{{\mathrm{P}}_{\mathrm{VL}}}$ are S ₀, T, and P_RG. For example, holding T constant while increasing S ₀, as shown in Table 9, decreases the power ratio $\frac{{\mathrm{P}}_{\mathrm{SL}}}{{\mathrm{P}}_{\mathrm{VL}}}$. In contrast, holding S ₀ constant while increasing T, as shown in Table 10, brings $\frac{{\mathrm{P}}_{\mathrm{SL}}}{{\mathrm{P}}_{\mathrm{VL}}}$ close to 1.

• (2) The switching delay t_d in VL is shorter than in SL if $\frac{{\mathrm{P}}_{\mathrm{S}1}^{\mathrm{S}\mathrm{L}}}{{\mathrm{P}}_{\mathrm{S}1}^{\mathrm{VL}}}>1$ and is equal or longer than in SL if $\frac{{\mathrm{P}}_{\mathrm{S}1}^{\mathrm{S}\mathrm{L}}}{{\mathrm{P}}_{\mathrm{S}1}^{\mathrm{VL}}}\le 1$.

In a 1 × 64 crosspoint array, for any composition of S ₁, S ₀, and T where S ₁ > 0 Eqs. (5), (7), and (8) hold and since $7.078\le \frac{{\mathrm{P}}_{\mathrm{RG}}}{{\mathrm{P}}_{\mathrm{T}}^{\mathrm{SL}}}\le \kern0.37em 8.328$ Eq. (6) can still approximate the relation between P_RG and P ^SL_T during SL operation. As a result, $\frac{{\mathrm{P}}_{\mathrm{SL}}}{{\mathrm{P}}_{\mathrm{VL}}}$ can still be approximated by (9). All derivations are in the same manner as shown in Section 5.1.

Table 9 shows that VL consumes more power than SL when S ₀ > 33. In this case, an increase of T brings the $\frac{{\mathrm{P}}_{\mathrm{SL}}}{{\mathrm{P}}_{\mathrm{VL}}}$ ratio close to 1 as predicted by (9). This prediction is varified in Table 10. The converse is also true, when S ₀ < 33, VL consumes less power than SL and the increase of T brings the $\frac{{\mathrm{P}}_{\mathrm{SL}}}{{\mathrm{P}}_{\mathrm{VL}}}$ ratio close to 1, as shown in Table 11. Note that the increase of S ₁ slightly affects the $\frac{{\mathrm{P}}_{\mathrm{SL}}}{{\mathrm{P}}_{\mathrm{VL}}}$ ratio as shown in Table 12.

In terms of switching delay, volistor gates perform faster than stateful gates when $\frac{{\mathrm{P}}_{\mathrm{S}1}^{\mathrm{S}\mathrm{L}}}{{\mathrm{P}}_{\mathrm{S}1}^{\mathrm{VL}}}>1$. When $\frac{{\mathrm{P}}_{\mathrm{S}1}^{\mathrm{S}\mathrm{L}}}{{\mathrm{P}}_{\mathrm{S}1}^{\mathrm{VL}}}\approx 1$, the propagation delay in both operations is almost the same; when $\frac{{\mathrm{P}}_{\mathrm{S}1}^{\mathrm{S}\mathrm{L}}}{{\mathrm{P}}_{\mathrm{S}1}^{\mathrm{VL}}}<1$, stateful gates perform faster than volistors. In other words, the switching delay changes with the voltage on the common nanowire of a crosspoint array or equivalently the voltage drop across the target memristors. A logic gate operates faster if the voltage drop across its target memristors is larger. The increase of S₀ versus the decrease of S₁ results in faster stateful gates and vice versa as shown in Table 9. In addition, the increase of T versus the decrease of S₁ results in faster volistor gates. Table 11 shows the increase of t_d in SL versus VL for constant S₀ with T varied from 1 to 57.

Table 9 shows $\frac{{\mathrm{P}}_{\mathrm{SL}}}{{\mathrm{P}}_{\mathrm{VL}}} < 1$ when S ₀ > 33, regardless of value S ₁. Table 12 reinforces our conclusion that S ₁ has almost no effect on the power ratio, $\frac{{\mathrm{P}}_{\mathrm{SL}}}{{\mathrm{P}}_{\mathrm{VL}}}$. The increase of S ₀ and the decrease of S ₁ result in P ^VL_S1  > P ^SL_S1 and thus a longer switching delay t_d for VL.

Table 10 shows how the increase of T affects $\frac{{\mathrm{P}}_{\mathrm{SL}}}{{\mathrm{P}}_{\mathrm{VL}}}$ when S ₀ > 33. The increase of T brings $\frac{{\mathrm{P}}_{\mathrm{SL}}}{{\mathrm{P}}_{\mathrm{VL}}}$ close to 1. For all compositions, t_d is longer for VL. This long switching delay is related to the increase of T and the large S ₀.

Table 11 shows how the increase of T affects $\frac{{\mathrm{P}}_{\mathrm{SL}}}{{\mathrm{P}}_{\mathrm{VL}}}$ when S ₁ and S ₀ are fixed at at 1 and 6, respectively. For all compositions, shown in Table 11, $\frac{{\mathrm{P}}_{\mathrm{RG}}}{S_0\times {\mathrm{P}}_{\mathrm{S}0}^{\mathrm{VL}}} \approx 5.2$; however, the increase of T brings $\frac{{\mathrm{P}}_{\mathrm{SL}}}{{\mathrm{P}}_{\mathrm{VL}}}$ close to 1, reducing the effect of $\frac{{\mathrm{P}}_{\mathrm{RG}}}{S_0\times {\mathrm{P}}_{\mathrm{S}0}^{\mathrm{VL}}}$ in $\frac{{\mathrm{P}}_{\mathrm{SL}}}{{\mathrm{P}}_{\mathrm{VL}}}$ significantly as predicted by (9). As a result, executing a multi-input multi-output gate in a small crosspoint array, e.g., 1 × 8, with VL is more power efficient than with SL. This conclusion is consistent with (9) and with the simulation results shown in Table 5. The increase of T results in P ^SL_S1  > P ^VL_S1 and thus longer t_d for SL.

Table 12 shows how the increase of S ₁ affects $\frac{{\mathrm{P}}_{\mathrm{SL}}}{{\mathrm{P}}_{\mathrm{VL}}}$ when S ₀ (> 33) and T are fixed at 40 and 1, respectively. The increase of S ₁ has almost no effect on $\frac{{\mathrm{P}}_{\mathrm{SL}}}{{\mathrm{P}}_{\mathrm{VL}}}$, i.e., all compositions result in almost the same power ratio of 0.856. Although the increase of S ₁ has almost no effect on $\frac{{\mathrm{P}}_{\mathrm{SL}}}{{\mathrm{P}}_{\mathrm{VL}}}$, it does decrease the switching delay in both SL and VL operations.

As a summary, in a 1 × 8 crosspoint array, the power consumption in SL is higher than in VL and volistors operate faster than stateful gates. In a 1 × 64 crosspoint array, when S ₁ > 0, the majority of the power consumption in VL is S ₀ × P ^VL_S0  + T × P_T, and in SL is P_RG + T × P_T as described in (5), (6), (7), and (8). In this case, $\frac{{\mathrm{P}}_{\mathrm{SL}}}{{\mathrm{P}}_{\mathrm{VL}}}$ can be approximated with (9). In a 1 × 64 crosspoint array, a multi-input volistor gate consumes less power than a multi-input stateful gate, unless the majority of inputs are logic “0.” When S ₁ = 0, a multi-input volistor gate consumes less power than a multi-input stateful gate. In a 1 × 64 crosspoint array, for S ₁ > 0, a logic gate with a large fan-out consumes the same power when realized with SL and VL. When S ₁ = 0, the majority of the power consumption in VL is T × P ^VL_T as shown in (10). However, in SL operation, the power consumption in each circuit element depends on the combination of S ₀ and T.

6 Memory Application

Memristors are nanoscale nonvolatile devices used primarily as resistive memory. The generic structure for memristive memory is a crossbar array. The crossbar arrays can be vertically stacked creating a 3D crossbar memory [16]. The potential problem of the crossbar structure is the leakage pathways from surrounding memory cells. In a recent work, Vourkas et al. [17] proposed memories comprised of parallel/serial complementary memristive switches. In order to have states that are distinguishable, they introduced insulating junctions within a crossbar array to restrain leakage pathways [18].

In another approach, Kim et al. [4] fabricated a crossbar array utilizing rectifying memristors rather than standard memristors. The use of rectifying memristors eliminates the leakage pathways due to the diode-like behavior of memristors, as discussed in Section 2. Furthermore, the large $\frac{R_{OPEN}}{R_{CLOSED}}$ ratio of the rectifying memristors allows for multi-level memory as demonstrated in [4]. This memory array can be programmed exploiting volistor gates. As demonstrated in Section 5, volistor gates are more efficient than stateful gates in terms of power consumption. In the process of programming the memory array, first, all memristors are initialized to low resistance state. This initialization step can be implemented in one clock cycle. Second, every cell of the memory array is programmed sequentially. The latter approach for memory realization is more efficient than the former approach in terms of simplicity, power consumption, reliability, and robustness, e.g., the second approach allows for multi-level memory realization. Furthermore, realization of memory array with rectifying memristors allows for programming the memory cells to exploit volistors, which is a more power-efficient approach than the conventional stateful approach. This distinction between memories is originated from the property of rectifying memristors over standard memristors.

Volistors can be used to create memory-like digital sensor integrating devices. These devices read voltages from many sensors in parallel/serial mode and convert them to words of stored resistive information. The stored information can be next processed by combinational stateful memristive circuits.

7 Conclusion

Volistors capitalize on the characteristics of rectifying memristors to allow voltages to be used directly as inputs. There is no need to store inputs as resistances in memristors before logic can be performed. This eliminates the use of R_G to read out the inputs in the first logic level and thus eliminates the most power-hungry circuit element in stateful logic. There is no static power in our circuits. The switching power consumed by volistor logic in a crosspoint array is entirely due to the leakage through the reverse biased rectifying memristor as there is no direct path to the ground. Using volistors at the first level provides NOR and AND directly which provides a flexibility sufficient to remove the need for IMP gates in stateful logic and to realize all subsequent levels with only NOR/NOT. Realizing all stateful logic levels with NOR/NOT simplifies the driver circuitry and removes the need for keeper circuits. An additional advantage is that the first-level volistor logic can have as many inputs as the number of available memristors in the crosspoint array within a single operation. However, inputs set to 0V incur a higher power penalty than the inputs set to V⁺ or V⁻. The two-dimensional, multi-output property of volistors provides for both a large fan-out (at the cost of increased power consumption) and for a great flexibility in the placement of calculation results. Using multiple crossbars in a network provides parallelization which leads to pipelined and SIMD architectures in the data path. Several different first-level volistor operations can be computed in separate crossbars at the same time, greatly speeding up what is typically the most complex level of Boolean function implementations. Subsequent logic levels can be accomplished in connected crossbars in an approach that uses mixed-input gates and stateful NOR. This hybrid approach with volistors and stateful NOR can be used to compute logic faster, with less power and with simpler external control circuitry than a solely stateful approach.