1 Introduction

Electricity is a commodity that must be produced and consumed simultaneously. Therefore, there is a need for flexible production resources that can be adjusted according to fluctuating and unpredictable real-time demand. As the supply side of most power markets has become a mix of traditional and new renewable assets, an increased amount of short-term uncertainty comes from the supply side. It is expected that the power markets’ dispatchable capacities will experience a greater demand for regulating reserves as the share of intermittent production grows [2]. Traditional power-producing assets are characterised by (some) flexibility and by time couplings in production, whereas the new renewables are characterised by nondispatchable production that is hard to plan and predict.

Growth of intermittent production has increased the mere number of energy markets with a shorter time horizon and the liquidity in those markets, catering to needs of inflexible producers and of the transmission system operator (TSO). Such markets can be either multilateral or organised by the transmission system operator. In addition, system services from spinning capacities are often traded in markets organised by the TSO. The shorter-term markets are tools to maintain the demand-supply balance and system security. Owners of dispatchable production assets can get higher value for their flexibility by trading wisely in the reserve markets. However, participating in multiple markets also makes the bidding and production planning processes more complex. This article contributes to quantify the effect of an ideal bidding process in multiple subsequent energy and reserve markets, and thereby contributes to understanding the trade-off between operational feasibility and optimal bidding theory.

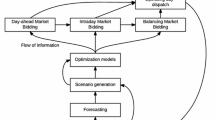
This article focuses on a set-up where the day-ahead electricity market is cleared first, and the reserve markets are cleared subsequently. In most electricity markets of today, the largest amount of electricity is traded in the day-ahead market [27], and therefore the day-ahead bid is one of the most important decisions. Does it pay to consider trading opportunities in subsequent markets when formulating the day-ahead market bid? Referring to Fig. 1, a framework where opportunities in the reserve markets are considered at the time of producing the day-ahead market bid will be referred to as “coordinated bidding”. An approach where subsequent markets are considered only after bidding into the previous market will be denominated “sequential bidding”. In technical terms, coordinated bids take all subsequent market scenarios into account, while sequential bids consider only scenarios in the upcoming market. A priori, coordinated bidding will yield higher profit than sequential bidding does, but to what degree? How does portfolio size influence these results?

Fig. 1
figure 1

Illustration of scenario trees used to create bids for each market with coordinated bidding (left) and sequential bidding (right)

Full size image

This paper contributes to the current research on electricity market bidding in several respects. First, we perform an extensive empirical comparison of the profit from sequential bidding with the profit from coordinated bidding, and evaluate them with respect to realised prices and volumes. Second, we acknowledge that the value from coordinated bidding is very dependent on the quality of the scenarios in terms of predictive ability and inter-market and inter-temporal relationships. Our scenario-generation methodology combines hourly probabilistic forecasts derived from quantile regression with a copula-based heuristic to create scenarios. This approach accurately models the price level and price profile uncertainty in the day-ahead market, while maintaining the relationship to the reserve market. To our knowledge, this approach has not been previously applied and it provides a better probabilistic description of day-ahead market prices than provided by previous studies. Third, although the value of the coordinated bidding approach for a flexible producer has been empirically studied previously [22, 24], no author has discussed the effect of portfolio size on the gains from coordinated bidding. This article gives both a qualitative discussion and an empirical quantification of the matter.

We derive our conclusions from a case study of a hydropower producer situated in the price zone NO3 in Norway. Bidding and the operation of production capacity are modelled using stochastic programming (SP). Section 2 addresses the existing literature on coordinated multimarket optimisation models, and how this paper contributes to it. We then provide an introduction to the energy markets treated in this paper in Sect. 3. In Sect. 4 we propose an SP model that produces bid curves for the Nord Pool day-ahead market, while taking into account the opportunities in subsequently cleared reserve markets. The scenario-generation approach for the stochastic problem is described in Sect. 5. In Sect. 6 we explain the scope of the computational case study. The results are presented and discussed in Sect. 7. Finally, Sect. 8 concludes the paper.

2 Coordinated bidding in the literature

Since 2005, deregulation has fostered a rich literature on bidding in electricity markets; consult [16, 17] for recent surveys. In contrast, the studies on multimarket optimisation are scarce and anecdotal. The earliest contributions focus on problem formulation and solution techniques, such as [5, 18, 21, 22]. Of these, only the last focuses on coordinated bidding.

More recently, the research has branched out to consider multimarket bidding in the context of hydro and wind [28], demand-side participation [23], and market power issues [29].

There are some efforts in the literature to quantify the value of coordinating bids between electricity markets (see [22, 24, 31]). Boomsma et al. [24] offer the most theoretical approach to the coordinated bidding problem. They derive bounds on the gains from coordinated bidding between the day-ahead market and the balancing market in the Nordic region. They also perform an empirical study reporting coordinated bidding gains of up to 25% for a price taker and of up to 5% for a market where there is a price response. We find that the gains from coordinated bidding suggested by [24] are too optimistic, because it builds on the assumption of unlimited sales potential in the balancing market. In our study, we limit the turnover in the balancing market. This approach is more in line with the effect of the price-taker as sketched by [24], since both modelling choices imply that the producer cannot sell an unlimited volume to the balancing market.

Given a proper description of uncertainty, the gains from coordinated bidding will always be zero or more. In evaluating the gains from coordinated bidding, the risk included in inaccurate scenario generation should be considered. Some authors use expected profits with respect to a scenario tree to arrive at conclusions about the gains associated with coordinating bids (see for instance [25]). This approach has the unfortunate consequence that value from coordination is always positive. Scenarios are supposed to represent the possible outcomes of the markets, but scenarios do not always do so in practice, especially for unpredictable reserve markets. The performance of bidding decisions should rather be evaluated using sample scenarios or actual realisations of prices and volumes, thus taking into account the uncertainty in the generated scenarios as well.

In addition, most research considers planning and bidding for a small portfolio of production resources, without regard to how portfolio size alters the gain. Most producers must plan for large portfolios. Portfolio size determines the recourse options of the producer and may affect possible gains from coordinated bidding. With a larger portfolio, the producer may have more flexibility to seize subsequent trade opportunities not accounted for in the initial day-ahead bidding. This may dilute the gains from coordination for very large portfolios. On the other hand, reserve markets are inherently unpredictable, so when coordinating planning fails because of forecasting errors, additional costs can be mitigated more effectively. A larger portfolio may allow the producer to make even more extreme bids in a coordinated framework. Aiming to quantify this effect, we conduct a case study with portfolio size as one of the control variables.

3 Energy markets

In this section we begin by briefly presenting the Nord Pool day-ahead market. It is the main arena for trading power in the Nordic region. In contrast to many other European electricity markets, the most important reserve markets are cleared after the clearing of the day-ahead market. The reserve markets we consider are the Nordic primary reserve and tertiary reserve markets. These markets are presented in Sects. 3.2 and 3.3, respectively.

3.1 Day-ahead market

The day-ahead market is the main arena for trading power. Producers can make a variety of bids. This paper considers only single hourly bids. The seller must decide how much he wants to deliver at what price, hour by hour. A buyer must assess how much power he needs to meet demand the following day, and how much to pay for this volume. Nord Pool aggregates both supply and demand curves and calculates the price that balances the two, referred to as the spot price.

The deadline is 12:00 CET for submitting bids for power which will be delivered the following day. Hourly prices are typically announced at 12:42 CET or later. An hourly price corresponds to a volume commitment for producers and buyers. From 00:00 CET the next day, power contracts are physically delivered (meaning that the power is provided to the buyer) hour by hour according to the contracts agreed. If a producer should fail to deliver the committed volume, the TSO will buy tertiary reserves on his behalf and bill him afterwards [12]. However, if the TSO suspects that the producer abuses the tertiary reserve regime, by repeatedly and systematically failing to meet his obligation from the day-ahead market, the TSO may withdraw the producer’s license to operate.

3.2 Primary reserve market

When either production or consumption changes, so does the frequency in the grid. A change in frequency of \(+/-\) 0.1 Hz activates primary reserves. The regulation of these reserves is completely automated within the respective plants, with the generator droop setting controlled by the producer restricting the degree of possible regulation. The market comprises both normal operation reserves (FCR-N) and disturbed operation reserves (FCR-D). In this paper, we model only the FCR-N day market, where commitments occur once a day, hour by hour.

Only an operating plant can deliver primary reserves. The producer is paid for the reservation of a power band, not for an actual delivery of energy. The width of the power band is determined by the droop setting on the generator. The supplier is remunerated for the half-width of the band (in MW).

To secure good distribution of primary reserves, producers are obliged to set their plants’ droop setting equal to or below 12 per cent. It is up to the TSO to decide which quantities of primary reserves to provide. The final committed bid sets the price for all participants, and the market is thus a marginal pricing market [13]. Bids are committed before 18:00 CET on the day before delivery, and final commitments are given by the TSO at 19:00.

3.3 Tertiary reserve market

The tertiary reserves market will be referred to as the “balancing market” (BM) in this paper. Tertiary reserves are used to reduce larger imbalances unforeseen at the time of day-ahead settlement, and are activated to relieve primary reserves, such that these more reactive reserves are ready for the next sudden imbalance. Tertiary reserves are also activated when regional bottlenecks are present.

A producer tentatively places an increasing bid curve for the market by 21:30 on the evening before the day of dispatch. However, bids can be changed until 45 min before the hour of schedule, and bids the evening ahead are merely for guiding the TSO.

The activation happens after a call from the TSO to the producer, and the producer must be able to fully activate the volume agreed upon within 15 min. Both production and consumption capacities can be offered in the market. In the case of tertiary reserves, the producer is paid for actual energy delivery. The TSO, at all times, has a list of offered reserves, and starts by activating the cheapest (upper) alternative whenever needed. The final activated bid sets the price for all market participants. In the case of upward regulation, the balancing price is by market rules equal to or higher than the day-ahead market price, and in the down-regulation case, the price is equal to or lower than the day-ahead market price. The absolute values of these differences (between balancing market and day-ahead market price) are referred to as “balancing market premiums” [14].

Fig. 2
figure 2

Sequential clearing of relevant markets

Full size image

Figure 2 shows the time line of bidding and clearing for all three markets (Table 1).

Table 1 Market characteristics
Full size table

4 Problem formulation

In this section, a stochastic mixed-integer programming model (SMIP) is developed for constructing bid curves for the day-ahead market, taking into account the bidding alternatives in the primary reserve and tertiary reserves markets. We also state the corresponding sequential planning model towards the end of the section. The models have a daily planning horizon, and water values from a long-term model are used as boundary conditions. The producer is modelled as a risk-neutral price taker.

The flow of information during the bidding process is stage-wise. When day-ahead prices clear, the producer obtains information about production obligations, and may then allocate these obligations to available production capacity. In addition, the producer submits bids for the primary reserve market. In the next stage, primary reserve prices and obligations are revealed. For the balancing market, final bids are placed at latest 45 min before the operating hour. The balancing market is then operated in real time, and the producer may or may not be dispatched during an operating hour. Hence, the problem consists of 27 stages, counting initial bid submission to the day-ahead market.

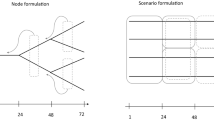
For computational tractability, we consider a simplified structure. This structure consists of three stages, and is illustrated in Fig. 3. In the first stage, the producer places day-ahead bids. In the second stage, day-ahead obligations are calculated according to the realised price. In addition, the producer receives information about the primary reserve price, and may decide on a commitment to this market. In the final stage, balancing market prices are revealed for the entire day and commitments are decided upon. This structure may seem like a violation of natural non-anticipativity. However, considering marginal pricing and the price taker assumption, the producer has an incentive to bid until marginal cost. Only prices above marginal cost are attractive to the producer, which would be reflected in a bid curve. Therefore, only inter-hour coordination and predictability in the trade-off between reserve markets are overestimated using this structure. In addition, day-ahead commitments are much more important for inter-hour coordination than reserves are because these commitments usually determine whether a generator is on or off. The calculated value from reserve markets should nevertheless be regarded as an upper bound.

Fig. 3
figure 3

Simplified structure decision tree (squares denote decisions, circles denote new information)

Full size image

Uncertainty is inevitable considering the problem at hand. The model contains parameters that are inherently stochastic: clearing prices in the three markets as well as the volumes traded in the balancing market. The producer has a set of scenarios, \(\mathcal {S}\), when constructing day-ahead bid curves. The scenarios contain day-ahead and primary reserve prices. For each \(s \in \mathcal {S}\), a set of scenarios \(\Omega ^s\) for prices and volumes in the balancing market is given.

The remainder of this section consists of three parts. In section 4.1 we introduce notation and define the mathematical model for the markets. Section 4.2 addresses modelling of production. Finally, in Sect. 4.3 we formulate the corresponding sequential bidding problem.

4.1 Modelling bidding and commitments

Throughout this section we use the following nomenclature: decision variables are represented by lower-case latin letters, parameters are represented by upper-case latin letter, while exogenous stochastic parameters are represented by lower-case greek letters. Sets are denoted by calligraphic letters. We seek to model four markets: day-ahead, primary reserve, upward balancing, and downward balancing. Let the set \(m \in \mathcal {M}\) denote the different markets

$$\begin{aligned} m \in \mathcal {M} = {\left\{ \begin{array}{ll} 1 &{}\quad \text {Day-ahead} \\ 2 &{}\quad \text {Primary reserve} \\ 3 &{} \quad \text {BM Up} \\ 4 &{}\quad \text {BM Down} \end{array}\right. } \end{aligned}$$
Fig. 4
figure 4

Example bid curve showing the relation between market price and producer commitment: Any clearing price within the interval in the figure will result in the specified commitment

Full size image

The here-and-now decision of the producer is to decide what bid curve to submit for the day-ahead market. Therefore, this is the only bid curve modelled explicitly. The bid curve consists of a set of non-decreasing price-volume pairs, see Fig. 4. The bid curve can be interpreted as an approximation of the supply function of the producer, i.e. the quantity it produces parameterized by market price \(x_{1ts}(\rho _{1ts})\), where \(\rho _{1ts}\) denotes the day-ahead price and \(x_{1ts}\) denotes the committed quantity. This function may be nonlinear and discontinuous due to nonlinearity of production cost and unit commitment decisions. To preserve the linearity of the model, we discretize the price axis by assigning fixed bid points and then optimise the corresponding volume. A similar approach was implemented by [4]. Bid points are assigned such that an equal number of price scenarios are distributed between each point. Let \(p \in \mathcal {P}\) denote the set of bid points, \(P_{p}\) the price of the bid point, and \(z_{pt}\) the bid volume of bid point \(p\) at time \(t\). Now, when a price clears between two bid points, a commitment will be determined by linear interpolation (1):

$$\begin{aligned} x_{1ts}=z_{pt}+(z_{p+1t}-z_{pt})\frac{\rho _{1ts}-P_p}{P_{p+1}-P_p} \end{aligned}$$
$$\begin{aligned} \text {if} \quad P_{p} \le \rho _{1ts} \le P_{(p+1)},\quad p \in \mathcal {P} {\setminus } |\mathcal {P}|,\quad s \in \mathcal {S},\quad t \in \mathcal {T} \end{aligned}$$
(1)
$$\begin{aligned} z_{(p+1)t} \ge z_{pt} \quad p \in \mathcal {P} {\setminus } |\mathcal {P}|,\quad t \in \mathcal {T} \end{aligned}$$
(2)

Next, for each price realisation in \(\mathcal {S}\), it must be decided what reservation of primary reserve to offer in each hour \(t \in \mathcal {T}\) for the day of planning. This reservation is allocated to the decision variable \(x_{2ts}\). Non-anticipativity is handled by

$$\begin{aligned} x_{mts} = x_{mts\omega } \quad m \in \{1,2\},\quad s \in \mathcal {S},\quad t \in \mathcal {T},\quad \omega \in \Omega ^s \end{aligned}$$
(3)

For the day-ahead and primary reserve markets, we assume that any volume can be delivered as long as these volumes are placed below market price and do not exceed production capacity. This is a reasonable approximation because possible delivery in these markets is small compared to total market demand. On the other hand, balancing market commitments are limited by the real-time demand for balancing power. Balancing demand may be zero in some hours, or small in other hours such that a producer might possibly deliver the entire demand. To prevent the producer from delivering the entire balancing demand at the exogenous price, we choose market-share modelling, an option pointed out by Klæboe and Fosso [27].

Therefore, we must model an explicit volume allowance in the balancing market. For example, (4) restricts balancing commitments by an estimated market share \(Y^{share}\) multiplied by the forecast demand in NO3 \(\nu _{mts\omega }\). Naturally, upward and downward balancing cannot be delivered simultaneously. A non-zero value in \(\nu _{3ts\omega }\) excludes a non-zero value in \(\nu _{4ts\omega }\) and vice versa.

$$\begin{aligned} x_{mts\omega } \le Y^{share} \nu _{mts\omega } \quad m \in \{3,4\},\quad s \in \mathcal {S},\quad t \in \mathcal {T}, \quad \omega \in \Omega ^s \end{aligned}$$
(4)

4.2 Modelling production

Next, we seek to model the connection between commitments and production. The committed volumes in each market must be allocated between the available generators. Let \(q_{1its\omega }\), \(q_{2its\omega }\), and \(q_{mits\omega }\) when \(m \in \{3,4\}\), denote the volume or reservation allocated to generator \(i\) at time \(t\) in scenario \(s\) for the day-ahead, primary reserve, and balancing market, respectively. Then it follows that

$$\begin{aligned} \sum _{i \in \mathcal {I}} q_{mits\omega }= x_{mts\omega }, \quad m \in \mathcal {M},\quad s \in \mathcal {S},\quad t \in \mathcal {T},\quad \omega \in \Omega ^s \end{aligned}$$
(5)

The primary reserve reservation on a running generator must lie within an interval, whose lower and upper bounds are functions of \(G^{max}_{i}\) and \(G^{min}_{i}\), the generator’s maximum and minimum droop settings. Generators \(\mathcal {I}\) can be turned on and off during the planning horizon by the binary variable \(u_{ihs\omega }\). This decision can be made for sub-periods \(h \in \mathcal {H}\) of the planning horizon, with corresponding operating hours \(\mathcal {T}^h\). Primary reserves can be offered only on operating generators, and we have the following relations for capacity reservations

$$\begin{aligned} u_{ihs\omega }\frac{0.2N_i}{G_{i}^{max}} \le q_{2its\omega } \le u_{ihs\omega }\frac{0.2N_i}{G_{i}^{min}} \quad h \in \mathcal {H},\quad i \in \mathcal {I},\quad s \in \mathcal {S},\quad t \in \mathcal {T}^h,\quad \omega \in \Omega ^s \end{aligned}$$
(6)

where \(N_i\) denotes nominal production.

Similarly, to ascertain that generators produce within the possible power range, the following two restrictions are required:

$$\begin{aligned} u_{ihs\omega }N^{max}_{i} \ge q_{1its\omega }+q_{2its\omega }+q_{3its\omega }-q_{4its\omega }, \quad h \in \mathcal {H},\quad i \in \mathcal {I},\quad s \in \mathcal {S}, \end{aligned}$$
$$\begin{aligned} t \in \mathcal {T}^h,\quad \omega \in \Omega ^s \end{aligned}$$
(7)
$$\begin{aligned} u_{ihs\omega }N^{min}_{i} \le q_{1its\omega }-q_{2its\omega }+q_{3its\omega }-q_{4its\omega }, \quad h \in \mathcal {H},\quad i \in \mathcal {I},\quad s \in \mathcal {S}, \end{aligned}$$
$$\begin{aligned} t \in \mathcal {T}^h,\quad \omega \in \Omega ^s \end{aligned}$$
(8)

where \(N_i^{max}\) and \(N_i^{min}\) denote upper and lower bounds on production, respectively. The primary reserve reservation must be included in both directions; hence, the change in sign of \(q_{2its\omega }\).

Start-up costs accrue whenever generators start operating after a period of standstill. Start-up costs are accounted for in the following formulation:

$$\begin{aligned} c_{ihs\omega } \ge C_{i}(u_{ihs\omega }-u_{i(h-1)s\omega }) \quad h \in \mathcal {H},\quad i \in \mathcal {I},\quad s \in \mathcal {S},\quad \omega \in \Omega ^s \end{aligned}$$
(9)

where \(C_i\) denotes the cost of a start-up.

The quantity of power produced depends on the volume discharged through the turbine system, the efficiency of the turbine, and the effective head according to the physical relation

$$\begin{aligned} q = \eta (d,h_{eff})\varrho gd h_{eff} \end{aligned}$$

where \(q\) is the power produced in watts, \(\eta (d,h_{eff})\) is the system efficiency at the given discharge and head, \(\varrho \) is the density of water in kg/m\(^3\), g is the gravitational constant, \(h_{eff}\) is the effective head in meters, and \(d\) is the discharge in m\(^3\)/s. The dependence on \(d\) is stressed to reveal the non-linear relationship between discharge and production. To preserve the linearity of the model and hence use linear programming tools, a set of cuts \(f \in \mathcal {F}\) is introduced. \(h_{eff} \) can for well-regulated reservoirs (i.e., those having a negligible change in the height of the water surface) be treated as constant throughout a day of planning. Approximation of the concave production curve is thus done, forcing

$$\begin{aligned} q_{1its\omega }+q_{3its\omega }-q_{4its\omega } \le A_{if}u_{ihs\omega }+B_{if}d_{its\omega } \quad h \in \mathcal {H},\quad i \in \mathcal {I},\quad f \in \mathcal {F},\quad s \in \mathcal {S}, \end{aligned}$$
$$\begin{aligned} t \in \mathcal {T}^h,\quad \omega \in \Omega ^s \end{aligned}$$
(10)

where primary reserve capacity is not included, because there is no net water usage in this market. There may be restrictions governing the minimum or maximum discharge of a generator (e.g., considering wildlife in a watercourse). For the same reasons, there may be restrictions on minimum and maximum volume \(v_{jts\omega }\) in a reservoir. Therefore, we introduce lower and upper bounds on discharge and reservoir volume

$$\begin{aligned} D^{min}_{i} \le d_{its\omega } \le D^{max}_{i} \quad i \in \mathcal {I},\quad s \in \mathcal {S}, \quad t \in \mathcal {T},\quad \omega \in \Omega ^s \end{aligned}$$
(11)
$$\begin{aligned} V^{min}_{j} \le v_{jts\omega } \le V^{max}_{j} \quad j \in \mathcal {J}, \quad s \in \mathcal {S},\quad t \in \mathcal {T},\quad \omega \in \Omega ^s \end{aligned}$$
(12)

where \(\mathcal {J}\) is the set of reservoirs. Furthermore, one must model how the reservoir levels respond to production, and to the interconnected flow between reservoirs. Since most watercourses consist of several reservoirs, production in one part of the watercourse will increase reservoir levels downstream. Let \(I_{jt}\) denote inflow, \(\Gamma _{ij}\) and \(\Lambda _{j'j}\) indicators for discharge at \(i\) and spill at \(j'\) ending up at \(j\), and \(o_{j'ts\omega }\) the spill at \(j'\) at time \(t\). Now we get

$$\begin{aligned} v_{jts\omega }-v_{j(t-1)s\omega } = I_{jt}+\sum _{i \in \mathcal {I}}\Gamma _{ij}d_{its\omega }+\sum _{j' \in \mathcal {J}}\Lambda _{j'j}o_{j'ts\omega }, \quad j \in \mathcal {J},\quad s \in \mathcal {S},\quad t \in \mathcal {T}, \end{aligned}$$
$$\begin{aligned} \omega \in \Omega ^s \end{aligned}$$
(13)
$$\begin{aligned} v_{j1s\omega }-V^{0}_{j} = I_{j1}+\sum _{i \in \mathcal {I}}\Gamma _{ij}d_{i1s\omega }+\sum _{j' \in \mathcal {J}}\Lambda _{j'j}o_{j'1s\omega }, \quad j \in \mathcal {J},\quad s \in \mathcal {S},\quad \omega \in \Omega ^s \end{aligned}$$
(14)

where \(V^{0}_{j}\) denotes the initial volume.

Next, we model the value of water in the reservoirs. In addition to depending on the outlook on prices, the marginal water value depends on the level of the reservoirs. It is high at low levels, and tends to zero at full reservoirs. Hence, the water value curve is concave and can be modelled by linear cuts to gain linearity [30].

We introduce a set of cuts \(l \in \mathcal {L}\) reflecting the different levels. Let \(w_{ks}\) denote the future income of watercourse \(k\) at the end of the period, \(E_{lk}\) the reference level of future income, \(W_{jk}\) the marginal water value at the reference level, \(V_{jl}\) the reference level, and \(\mathcal {J}^{k}\) the set of reservoirs in the watercourse. Then for all cuts, it must hold that

$$\begin{aligned} w_{ks\omega } \le E_{lk}+\sum _{j \in \mathcal {J}^k}W_{jk}(v_{j|T|s\omega }-V_{jl})\quad k \in \mathcal {K},\quad l \in \mathcal {L},\quad s \in \mathcal {S},\quad \omega \in \Omega ^s \quad \end{aligned}$$
(15)

Finally, the objective function is

$$\begin{aligned} \underset{x,z,q,u,c,d,v,o,w}{\text {maximise}} \sum _{s \in \mathcal {S}}\sum _{\omega \in \Omega ^s}\pi _{s\omega } \left( \sum _{m \in \mathcal {M}} \sum _{t \in \mathcal {T}} (\rho _{mts\omega }+\iota _{m} \rho _{1ts\omega })x_{mts\omega } + \sum _{k \in \mathcal {K}} w_{ks\omega } - \sum _{i \in \mathcal {I}} \sum _{h \in \mathcal {H}} c_{ihs\omega } \right) ,\nonumber \\ \end{aligned}$$
(16)

where \(\pi _{s\omega }\) denotes the probability of a scenario and \(\rho _{3ts\omega }\) and \(\rho _{4ts\omega }\) are upward- and downward-balancing premiums, respectively. For a more compact formulation, the day-ahead and primary reserve prices are written with double scenario indices, but \(\rho _{mts\omega }\)=\(\rho _{mts}\) for \(m=\{1,2\}\) for all \(\omega \in \Omega ^s\). \(\iota _m\) is a dummy. In accordance with the market mechanisms, we define \(\iota _{1}=0\), \(\iota _{2}=0\), \(\iota _{3}=1\), and \(\iota _{4}=-1\). The coordinated bidding problem is obtained by maximizing (16) subject to (1)–(15). The model can, given a reasonable instance size, be solved by direct implementation in off-the-shelf mixed integer linear programming solvers.

4.3 Sequential model

The sequential model formulation is very similar to the coordinated model. However, in this formulation we consider only a set \(\mathcal {S}\) of day-ahead scenarios. No reserve markets scenarios are used when optimising the bid curve, which produces a somewhat simplified two-stage planning problem. All other assumptions stated in the previous part of this section continue to hold for the sequential formulation as well. We simply state the model in full in the following:

$$\begin{aligned} \underset{x,z,q,u,c,d,v,o,w}{\text {maximise}} \sum _{s \in \mathcal {S}}\pi _{s} \left( \sum _{t \in \mathcal {T}} \rho _{1ts}x_{1ts} + \sum _{k \in \mathcal {K}} w_{ks} - \sum _{i \in \mathcal {I}} \sum _{h \in \mathcal {H}} c_{ihs} \right) , \end{aligned}$$
(17)

subject to

$$\begin{aligned} x_{1ts}=z_{pt}+(z_{p+1t}-z_{pt})\frac{\rho _{1ts}-P_p}{P_{p+1}-P_p} \end{aligned}$$
$$\begin{aligned} \text {if} \quad P_{p} \le \rho _{1ts} \le P_{(p+1)}, p \in \mathcal {P} {\setminus } |\mathcal {P}|,\quad s \in \mathcal {S},\quad t \in \mathcal {T} \end{aligned}$$
(18)
$$\begin{aligned} z_{(p+1)t} \ge z_{pt} \quad p \in \mathcal {P} {\setminus } |\mathcal {P}|,\quad t \in \mathcal {T} \end{aligned}$$
(19)
$$\begin{aligned} \sum _{i \in \mathcal {I}} q_{1its}= x_{1ts}, \quad s \in \mathcal {S},\quad t \in \mathcal {T} \end{aligned}$$
(20)
$$\begin{aligned} u_{ihs}N^{min}_{i} \le q_{1its} \le u_{ihs}N^{max}_{i}, \quad h \in \mathcal {H},\quad i \in \mathcal {I},\quad s \in \mathcal {S},\quad t \in \mathcal {T}^h \end{aligned}$$
(21)
$$\begin{aligned} c_{ihs} \ge C_{i}(u_{ihs}-u_{i(h-1)s}) \quad h \in \mathcal {H}, i \in \mathcal {I},\quad s \in \mathcal {S} \end{aligned}$$
(22)
$$\begin{aligned} q_{1its}\le A_{if}u_{ihs}+B_{if}d_{its} \quad h \in \mathcal {H},\quad i \in \mathcal {I},\quad f \in \mathcal {F}, \quad s \in \mathcal {S},\quad t \in \mathcal {T}^h \end{aligned}$$
(23)
$$\begin{aligned} D^{min}_{i} \le d_{its} \le D^{max}_{i} \quad i \in \mathcal {I},\quad s \in \mathcal {S},\quad t \in \mathcal {T} \end{aligned}$$
(24)
$$\begin{aligned} V^{min}_{j} \le v_{jts} \le V^{max}_{j} \quad j \in \mathcal {J},\quad s \in \mathcal {S},\quad t \in \mathcal {T} \end{aligned}$$
(25)
$$\begin{aligned} v_{jts}-v_{j(t-1)s} = I_{jt}+\sum _{i \in \mathcal {I}}\Gamma _{ij}d_{its}+\sum _{j' \in \mathcal {J}}\Lambda _{j'j}o_{j'ts}, \quad j \in \mathcal {J}, \quad s \in \mathcal {S},\quad t \in \mathcal {T}\qquad \end{aligned}$$
(26)
$$\begin{aligned} v_{j1s}-V^{0}_{j} = I_{j1}+\sum _{i \in \mathcal {I}}\Gamma _{ij}d_{i1s}+\sum _{j' \in \mathcal {J}}\Lambda _{j'j}o_{j'1s}, \quad j \in \mathcal {J},\quad s \in \mathcal {S} \end{aligned}$$
(27)
$$\begin{aligned} w_{ks} \le E_{lk}+\sum _{j \in \mathcal {J}^k}W_{jk}(v_{j|T|s}-V_{jl})\quad k \in \mathcal {K},\quad l \in \mathcal {L},\quad s \in \mathcal {S} \end{aligned}$$
(28)

5 Scenario generation

The stochastic parameters are the day-ahead price, the primary reserve price, the balancing premium, and the volume in both regulating directions (\(\rho _{mts}, m \in \{1,2\}\), \(\rho _{mts\omega }, m \in \{3,4\}\), \(\nu _{mts\omega }, m \in \{3,4\}\)). These parameters must be specified using an appropriate scenario-generation algorithm.

Scenario generation consists of three building blocks. First, we must construct reliable probabilistic forecasts for each of the hours and each of the markets. These forecasts enable us to make relevant scenarios for the day of planning, and to reflect uncertainty appropriately. Second, we must discretise the probabilistic forecast distributions into scenarios by taking into account the relationship (dependence) between hours and markets. Finally, we must construct a branching structure between the stages.

Fig. 5
figure 5

Plot for the day-ahead and primary reserve prices 2014–2016

Full size image

We propose and test a modified quantile autoregression (QAR) model for the day-ahead and primary reserve prices to obtain hourly probabilistic forecasts. This approach allows us to relate the scale, shape, and location of the conditional price to the price level, which is not possible using a constant-coefficient time series. We construct scenarios from these forecasts using the copula-based heuristic presented in [7]. Copulas are an effective way of modelling non-elliptical distributions for which correlations fail to capture dependencies.

The balancing market volumes and premiums can be interpreted as unequally spaced time series, and the resampling techniques in [8] are used. Thereafter AR/ARMA models are fitted and used to provide distribution-based probabilistic forecasts that in turn are combined with the copula heuristic to generate scenarios.

This section in structured as follows: Sect. 5.1 presents the market relationships that must be accounted for in the scenario generation. Sections 5.2 and 5.3 discuss modelling of the day-ahead/primary reserves and of the balancing market, respectively. Section 5.4 briefly describes the copula-based heuristic, and Sect. 5.5 connects the dots and outlines the final generation algorithm.

5.1 Relationships between the markets

We have performed an empirical study of the markets at hand in the period 2014–2016 in the Nord Pool price zone NO3. This study reveals certain relationships between the markets. Table 2 shows how we have chosen to model the relationships using the findings. Both reserve markets are related to the day-ahead price. Balancing market premiums are higher when the day-ahead price is high. In contrast, the primary reserve price declines when the day-ahead price increases, however in a non-linear fashion; see Fig. 5. Reserve markets are treated as independent of each other, solely conditional on the day-ahead price.

Table 2 Modelled relationships between the markets
Full size table

5.2 Probabilistic forecasts for day-ahead and primary reserve prices

Day-ahead and primary reserve prices are very similar in several respects. Both markets are cleared day-ahead and all 24 hourly prices are quoted simultanously. In addition, the individual hours in each market have different statistical properties (e.g., variance). Finally, prices in both markets are stationary and highly autocorrelated. We therefore aim to model day-ahead and primary reserve prices in the same manner.

Both day-ahead and primary reserve prices exhibit an autoregressive signature with slowly decaying positive ACF. We therefore turn our attention to autoregressive models. Autoregressive models are intended for stochastic processes in which the next observation depends on a combination of previous observations. However, day-ahead and primary reserve prices are quoted simultaneously for all hours in a day. The information set that market participants use is the same for all bidding hours. It is therefore unsound from a methodological perspective to model the sequence of day-ahead and primary reserve prices as a one-dimensional hourly time series. To see this, consider the transition between two consecutive days. The price at hour \(1\) on day \(y\) should not necessarily be strongly correlated with the price at hour \(24\) on day \(y-1\). In addition, day-ahead and primary reserve prices exhibit very different statistical characteristics of variance and mean reversion at each of the hours. One should therefore not model all hours with the same time-series coefficients. Rather, the prices should be modelled as a 24-dimensional cross-sectional panel, with discrete time increments of one day.

Electricity prices are often modelled using constant coefficient time series such as ARIMA. One problem with this approach is that the innovation term has constant variance independent of the forecast price level. Quantile autoregression, on the other hand, captures the systematic influence of previous prices on the conditional distribution of the price in terms of shape, scale, and location. It has been used for scenario generation before; see for example [10]. This approach is valuable because price variance can be related to the forecasted value (e.g., high forecasts might yield a higher variance of innovations). Processes with asymmetric dynamics can also be modelled efficiently with QAR [9]. In terms of the notation in this paper, a QAR process of order \(r\) can be written

$$\begin{aligned}&Q_{{\rho }_{mt}(y)}\big (\tau |\rho _{mt}(y-1),\ldots ,\rho _{mt}(y-r)\big )\nonumber \\&\quad =\phi _{mt0}(\tau )+\phi _{mt1}(\tau )\rho _{mt}(y-1)+\cdots +\phi _{mtr}(\tau )\rho _{mt}(y-r) \end{aligned}$$
(29)

where \(\tau \) denotes the quantile and \(\varvec{\phi }_{mt}(\tau )\) are coefficients. For some discretisation \(\tau \in (0,1)\), we obtain an approximation of the conditional density.

The partial autocorrelation function of the series and the Bayesian information criterion are used to identify the order of the process. Approximately all hours in both markets are of order 3. To be able to compare coefficients between hours directly, our choice is to model all hours as the same order. In addition, there are weekly seasonal effects, so a seasonal term with coefficient \(\Phi _{mt7}(\tau )\) is added.

$$\begin{aligned} Q_{{\rho }_{mt}(y)}(\tau |\cdot )= & {} \phi _{mt1}(\tau )\rho _{mt}(y-1)+\phi _{mt2}(\tau )\rho _{mt}(y-2)+\phi _{mt3}(\tau )\rho _{mt}(y-3)\nonumber \\&+\, \Phi _{mt7}(\tau )\rho _{mt}(y-7)+\phi _{mt0}(\tau ),\quad \tau \in (0,1) \end{aligned}$$
(30)

Extensions to the basic model The hourly prices may be interpreted as a cross-sectional panel, and are correlated across hours. One should therefore include price information at other hours on previous days to forecast hour \(t\) on day \(y\). A principal-component analysis reveals that the daily mean price accounts for approximately 83% and 71% of the variance in hourly prices across the panel in the day-ahead and primary reserve markets, respectively. Yesterday’s mean price can therefore be inserted into the model (30) as a proxy for the overall price across all hours. We arrive at the following model for the conditional price density at hour \(t\):

$$\begin{aligned} Q_{{\rho }_{mt}(y)}(\tau |\cdot )= & {} \phi _{mt1}(\tau )\rho _{mt}(y-1)+\phi _{mt2}(\tau )\rho _{mt}(y-2)+\phi _{mt3}(\tau )\rho _{mt}(y-3)\nonumber \\&+\, \Phi _{mt7}(\tau )\rho _{mt}(y-7)+\psi _{mt}(\tau )\mu _{\rho _{m}}(y-1)+\phi _{mt0}(\tau ),\quad \tau \in (0,1)\nonumber \\ \end{aligned}$$
(31)

where \(\mu _{\rho _{m}}(y-1)\) is yesterday’s mean price in the market. The model is estimated using regular quantile regression for each hour separately because of the different characteristics between hours. The conditional distribution is obtained by performing cubic interpolationFootnote 1 between the conditional quantiles found at 5% increments between the 5% and 95% quantiles. Due to tail uncertainty, tails below 5% and above 95% are estimated using empirical tails of the error distribution associated with the median of the conditional price (\(\tau =0.5\)).

The model has been tested in terms of Christoffersen’s test for interval forecasts [11] for both unconditional and conditional coverage for the first 50 days in 2016. The results are generally very good; almost all hours pass the test at the 1% significance level. We are thus confident that the model provides forecasts with good calibration.

5.3 Modelling the balancing market

The balancing market is essentially modelled the same way as the best performing model from [3] is, with some adjustments.

Balancing states An hour-specific Markov matrix is used to model the transitions between balancing states. Should there be regulation, the balancing volume in that direction is strictly positive. Let \(\vartheta _t\) denote the balancing state of the system at time \(t\)

$$\begin{aligned} \vartheta _{t} = \left\{ \begin{array}{ll} -1 &{}\quad \text {if down regulation, i.e.,}\quad \nu _{4t}>0 \\ 0 &{}\quad \text {if no regulation, i.e.,}\quad \nu _{mt}=0 \qquad m \in \{3,4\}\\ 1 &{}\quad \text {if up regulation, i.e.,}\quad \nu _{3t}>0 \end{array}\right. \end{aligned}$$
(32)

An hour-specific Markov model has a transition probability matrix

$$\begin{aligned} \xi _t= \begin{bmatrix} \xi _{11t}&\dots&\xi _{1nt} \\ \vdots&\ddots&\vdots \\ \xi _{m1t}&\dots&\xi _{mnt} \end{bmatrix} \end{aligned}$$
(33)

where \(\xi _{ijt}\) denotes the probability of the balancing state switching from state i to state j from hour t to hour \(t+1\). In our case, \(\xi _{t}\) is a \(3\times 3\) matrix reflecting the possible outcomes of \(\vartheta _{t}\). Estimators for \(\xi _{ijt}\) are calculated according to

$$\begin{aligned} \xi _{ijt}=\frac{|\vartheta _{t}=i \cap \vartheta _{t+1}=j|}{|\vartheta _{t}=i|} \end{aligned}$$
(34)

using historical data, where \(|\cdot |\) denotes the number of entries in a set. These can be used to simulate outcomes for the regulating state throughout the day of planning.

Balancing volumes We can think of the balancing volume (and premiums) as unequally spaced or irregularly sampled time series. That is, hours with zero volume in the historical data are simply regarded as hours in which no information about the volume or price process is available. If we had included such zero hours in the analysis, results would have been biased. On the other hand, if we had excluded zero values and artificially compressed the time series, hours that are far apart in time would have contributed to the calculation as if they were consecutive. Other options include linear interpolation in the data and mean value substitution, but as [8] points out, this smoothens the data and causes bias. Erdogan et al. [8] present a statistical model for unequally spaced time series. The core idea is to use an autoregressive process of order 1 to resample the missing values. Ordinary time series techniques can be applied after resampling. We use this methodology to resample balancing volumes.

We now consider probabilistic forecasting of the balancing volumes. After the resampling process, AR(1) models are fitted to the resampled series for a training period of 80 days. The estimated Gaussian distribution from the AR(1) model can be used to provide probabilistic forecasts for the forecasting horizon of 12–36 h.

Balancing premiums The regulating premiums are obviously dependent on the regulating state. Premiums are also dependent to a varying degree on the day-ahead price and balancing volumes. Two of the best models from [3] use the day-ahead price and/or volume as exogenous variables. Because of the correlation between these quantities in NO3, we include those same exogenous parameters in this model.

Since there is no volume in hours without regulation, the premium is not of any relevance to the decision model at these hours. We follow the resampling procedure in [8] for premiums as well, because our testing shows that this approach provides the best results. The resampled time series is of order 2 even after resampling. An ARMA(2,0,1) model eliminates all autocorrelation in the residuals, and is fitted to the resampled data with resampled volumes and the day-ahead price as exogenous variables. Predictive densities can be obtained by simulating pairs of volumes and premiums conditional on each day-ahead price scenario \(s \in \mathcal {S}\). By simulating conditional on the spot price, we can construct a branching from the second to the third stage, including the effect of knowing the day-ahead price on premiums.

5.4 Modelling dependence between hours and across markets

Dependence between random variables should not always be modelled linearly using correlations. For instance, in morning hours there is some threshold day-ahead price, at which the primary reserve price is expected to be low, typically in the range of 15–25 NOK/MWh. If the day-ahead price is reduced from this threshold by only a few per cent, the primary reserve price can be expected to increase sharply. On the other hand, if the day-ahead price is increased from the threshold value by a few per cent, very little is expected to happen to the primary reserve price. Dependence in downturns differs from dependence in upturns. Correlations are not sufficient to model such dynamics.

The models proposed in Sects. 5.2 and 5.3 provide hourly predictive densities for prices and volumes. Constructing daily paths from these densities with correct dependence properties between hours and markets is our next goal. Nowotarski et al. [26] state that two main solutions exist in the literature in the context of probabilistic electricity price forecasting. The first one is to use the correlation between the marginal distributions. This solution has a major drawback; it describes only linear relationships. The second solution (only for hourly dependence) is to simulate daily paths. This solution has an obvious drawback in that a large number of simulations are needed to reduce sampling error, and raises a need for scenario reduction.

Dependence across hours and across markets (day-ahead, primary reserve and balancing volume premium) will be modelled with the copula-based approach in [7]. In this section, we explain only briefly what a copula is, and the goal of generating scenarios from a copula. For a more extensive introduction to copula theory and to copula-based scenario generation, the reader is referred to the original work by Kaut.

Copula-based scenario generation A copula is the joint cumulative distribution function of any n-dimensional random vector with standard uniform margins, that is, a function \(K\) : \([0, 1]^{n} \rightarrow [0, 1]\). Sklars theorem [32] states that for any n-dimensional cumulative distribution function \(F\) with marginal distribution functions \(F_{1}, \ldots , F_{n}\), a copula \(K\) exists such that

$$\begin{aligned} F(\alpha _{1},\ldots ,\alpha _{n})=K\bigl (F_{1}(\alpha _{1}),\ldots ,F_{n}(\alpha _{n})\bigr ) \end{aligned}$$
(35)

If all the marginal cumulative distribution functions \(F_{i}\) are continuous, then there exists only one unique \(K\). A consequence of the theorem is that for every \(\gamma = (\gamma _{1}, \ldots , \gamma _{n}) \in [0, 1]^{n}\) we have

$$\begin{aligned} K(\gamma _{1},\ldots ,\gamma _{n})=F\left( F_{1}^{-1}(\gamma _{1}),\ldots ,F_{n}^{-1}(\gamma _{n})\right) , \end{aligned}$$
(36)

where \(F_{i}^{-1} \) is the generalized inverse of \(F_{i}\), meaning that knowing the marginal cdfs and the copula is the same as fully knowing the multivariate cdf. The copula approach contrasts with correlations that assume a linear dependence. Furthermore, copulas, unlike correlations, are independent from the marginal distributions. Therefore we can model the two independently. A copula models only the interdependence of two or more distributions; the information about the distributions themselves has been removed.

Obtaining the copula for a multivariate distribution is a non-trivial task. Instead we construct an empirical copula, \(K_{T}\), from historical samples, each historical sample containing one sample price/volume from each of the markets modelled.

The method takes the number of scenarios to generate, \(S\), as input. The goal of the method is now to generate the copula scenarios for each margin \(\tilde{\gamma }_{sg}, s \in \{1\ldots S\}, g \in \{1\ldots n\}\), that in aggregate deviate as little as possible from the target copula. According to the definition of a copula, the scenarios \(\tilde{\gamma }_{sg}\) should be placed approximately uniformly between 0 and 1. In addition, for all \(s \in \{1\ldots S\}\), \(\tilde{\gamma }_{sg}\) must be connected across the \(n\) distributions (hours and markets), such that the dependence between distributions resembles the one of the target copula. This dependence is achieved by solving an assignment problem heuristically. The problem minimises the deviation between the target copula and the copula defined by the scenarios.

After obtaining \(\tilde{\gamma }_{sg}\), we can make the transformation back to target variables. We calculate the actual price scenarios using \(F_g^{-1}(\tilde{\gamma }_{sg})\). These scenarios will be correctly distributed across each margin and will also have correct dependence properties between hours and markets.

5.5 Scenario generation algorithm and evaluation

Figure 6 shows a rough sketch of the scenario-generation methodology. The reader is reminded of the problem structure in Fig. 3, consisting of three stages. The here-and-now decision is to decide on the bid curve to submit in the day-ahead market. No decision is made between the day-ahead price realisation and the primary reserve price realisation. Hence, there is no need to create additional branching between these events. We instead model pairs of day-ahead and primary reserve prices in the same scenario set \(s \in \mathcal {S}\). The copula-based heuristic is used to model dependence in the scenarios. In the second stage, a primary reserve commitment is decided upon with the opportunity cost of lost balancing market opportunities. Hence, for each \(s\) there must be a set of possible balancing market realisations \(\omega \in \Omega ^s\). The balancing market premiums are dependent on the day-ahead price, and are therefore generated conditional on each day-ahead price scenario. Dependence between balancing market volumes and premiums is also modelled using the copula-based heuristic.

Fig. 6
figure 6

Final model overview

Full size image

The scenario-generation algorithm is implemented partly in Matlab and partly in C++. In the following, we outline a high-level pseudocode for the algorithm. Our goal is to clarify how the different building blocks from this section fit into the procedure.

  1. 1.

    Hourly probabilistic forecasts are created using quantile regression on an hourly basis for day-ahead and primary reserve prices.

  2. 2.

    The copula heuristic is used to create the desired number of day-ahead and primary reserve scenarios, with respect to the connection between hours and the connection between markets. We use the empirical copula of the training period directly as the target to model dependence.

  3. 3.

    Balancing market data are resampled.

  4. 4.

    Balancing market dependence is modelled using its empirical copula, and copula scenarios are generated before simulation.

  5. 5.

    Appropriate AR/ARMA models are fitted to the balancing market volumes and premiums and used to simulate a large number \(N\) times. Premiums have day-ahead price scenarios as the explanatory variable, and thereby the linear dependence between the day-ahead price and premiums is respected. Using the simulations, we approximate the predictive density for volumes and premiums on an hourly basis for the 12–36-h forecasting horizon.

  6. 6.

    Cumulative distributions for the balancing market are matched with copula scenarios to yield scenarios of target variables.

  7. 7.

    The balancing state is simulated using the hour-specific Markov model in each branch. Volumes and premiums at hours where \(\vartheta _{ts\omega }=0\) are set to zero.

Fig. 7
figure 7

Example of 10 generated day-ahead price scenarios along with the realised price. Note that the variance in the scenarios is higher at the more volatile hours

Full size image

An example of 10 generated scenarios for the day-ahead price can be found in Fig. 7. Scenarios are evaluated in terms of in-sample and out-of-sample stability as defined in [6]. Stable scenario trees are produced for 40 day-ahead/primary reserve scenarios, with four balancing scenarios per branch.

6 Case description

The gains from coordinated bidding are quantified by comparing the profits from a coordinated bidding approach to the profits from a purely sequential approach. The test set-up is outlined in Fig. 1, where coordinated bidding relies on decisions informed by the full scenario tree, whereas sequential bidding relies on information about only the next market at hand. All results are from the first 250 days of 2016.

Aggregating time steps into sub-periods Unit commitment is an important part of the decision problem, especially concerning the delivery of primary reserves that require spinning units. The problem is thus a SMIP problem with binary variables in the second stage, which makes it challenging to solve. The problem can be solved for hourly granularity only with small portfolios, typically one watercourse. To mitigate this problem, we allow for partitioning of the planning horizon into sub-periods, \(h \in \mathcal {H}\), with corresponding operating hours \(t \in \mathcal {T}^h\). The generator on/off decision variable, \(u_{ighs\omega }\), requires that a generator in a given scenario be either on or off during the entire sub-period. We use the three sub-periods \(\mathcal {T}^{1}=\{1\ldots 7\}\), \(\mathcal {T}^{2}=\{8\ldots 19\}\), and \(\mathcal {T}^{3}=\{20\ldots 24\}\) when constructing the day-ahead bid curve in both approaches. Production is planned in sub-periods. However, realised production may be very different. Sub-periods are used only in the day-ahead planning phase. When the real prices are revealed, any commitment is possible, and the next decisions are made hour by hour according to the commitment, without regard to sub-periods. Comparing Table 3 and 4 reveals that the results from using hourly granularity and three sub-periods are quite similar, and the reported gains from coordinated bidding are quite close in the two models.

Table 3 Accumulated profit for one watercourse with hourly planning (NOK)
Full size table

Balancing market volume restriction In the balancing market, demand is inherently unpredictable, clustered, and of varying size. Because of the small volumes demanded, one producer could very well sell the entire volume. In this case, the producer would act as price maker. When volumes are larger, several producers likely contribute to delivering such volumes. \(\nu _{mts}\) forecasts the entire demand in hour \(t\) in scenario \(s\) in NO3. It is therefore unsound to let one producer deliver the entire volume. To do so would imply that no other producers placed bids beneath the market price, and would violate the price-taker assumption. Our approach is simply to restrict the balancing volume sold by the decision model to a market share multiplied by the total volume traded in a balancing hour. The market share used corresponds to the producer’s share of the total day-ahead delivery in 2016, 15%.

Bid points Bid points are fixed before the problem is solved. We update the bid points for every planning day of the test period. Fixing bid point is done by placing \(|P|\) bid points such that price scenarios are distributed approximately uniformly between the bins defined by neighbouring bid points. We choose \(|P|=\frac{|S|-2}{2}\), which gives the highest number of bid points, and whereby non-anticipativity of the bid curve with respect to the scenarios is still ensured [15]. If interpolation (with a realisation) causes infeasible production, the commitment is set to the nearest feasible point.

Watercourses All involved watercourses are physically disconnected from each other and contain only one reservoir and one generator each. All generators have production capacities in the range of 35–55 MW, and are considered small compared to associated reservoirs. Hence, reservoir volumes and heads change negligibly over 24 hours, and one water-value cut is regarded as sufficient.

Table 4 Accumulated profit for one watercourse with sub-periods planning (NOK)
Full size table

7 The effect of portfolio size on gains from coordinated bidding

Theoretically, coordinated planning always outperforms sequential planning, and the magnitude of the gain is expected to increase when reserve opportunities are predictable and there is limited flexibility to respond to reserve opportunities not accounted for in the first-stage decision. Obviously, predictability of reserve opportunities is not a function of portfolio size. However, when more production resources are added, it is cheaper and easier to reallocate committed production. For example, the load on multiple running units can be increased to allow one unit to turn off in order to seize a favourable downward balancing price, whereas this approach will be impossible with a single unit.

However, some reserve-market opportunities cannot be seized after the closing of the day-ahead market bidding, regardless of portfolio size. When day-ahead market prices are low, typically in the late night/early morning, day-ahead market price expectations may not be sufficient to make a commitment for the day-ahead market income alone. If income from the primary reserve capacity is included, as well as possibilities for downward balancing, the total income may be enough to justify unit commitment. Such opportunities require running generators, and cannot be seized if no generators are running, no matter how many generators there are.

The results from running with a one-watercourse portfolio are presented in Table 4. Profits equal income minus the net value of water usage associated with the trades (primary reserves do not use water, balancing down saves water, while the other trades use water). We first note that there is additional value from participating in the reserve markets; both planning approaches yield a positive profit in all reserve markets. The gain from coordinated bidding, however, is approximately one per cent. We observe a modest reduction in profit from the day-ahead market compared to the profit from the sequential planning approach. On the other hand, profits from all reserve markets increase significantly. There is, in other words, not only a modest increase in profits, but also a shift towards reserve markets. Total start-up costs also increase marginally.

Next, we add a second and then a third watercourse to the portfolio. Once again, we run the testing approaches for all 250 days. The results can be found in Table 5. When planning for two watercourses simultaneously, the gain from coordinated bidding decreases to about 0.5%. In addition, we observe that the profits in each market differ less between coordinated and sequential planning with a larger portfolio. Day-ahead profits are more similar between the two planning regimes, and so are reserve market profits.

Moving on to three watercourses, the trend continues to some degree, but the decline in gain from the two-watercourse case is almost negligible. The gains from coordinated bidding seem to converge to a stable level just below 0.5%.

Table 5 Gains from coordination by portfolio size (%)
Full size table

The decline in gain when moving from a one-watercourse to a two-watercourse portfolio may be explained by the increased flexibility. Increased flexibility allows the sequential planner to seize reserve-market opportunities that are not feasible with only one watercourse at the planner’s disposal. In this sense it is less valuable to plan for such opportunities; they will occur anyway. Moving to three watercourses, we again see a light decline in the gain from coordinated bidding. However, this decline is extremely small. The profit contribution from each market converges even more for the two planning regimes. This convergence may have a natural interpretation. In addition to increased flexibility, the convergence may stem from the limited balancing demand. Even though we add more production capacity, the balancing demand is identical. Thereby, the sequential approaches may catch up with coordinated bidding’s performance simply because there is no more balancing demand that coordinated planning can use. However, for the primary reserve markets there are no limits to demand, so saturation of market demand can explain only parts of the decline. Future research should nevertheless look into the sensitivity in gains with respect to the market share, as well as with respect to scenarios with larger balancing demand.

When moving from one to two watercourses, gains decline. Some of this decline may be explained by the binary nature of decisions about production resources. Generators are either on or off, and if primary reserves are offered, the producer cannot turn the generator off. When moving from two to three watercourses, gains decrease only marginally. It might very well be the case that coordinated bidding has some value even for very large portfolios. For instance, downward balancing and offering primary reserves require operating generators. Hence, it does not matter how many generators are in the portfolio if none are running. Such opportunities can never be exploited, and sequential planning will fail to capture this phenomenon.

8 Conclusions

We have developed a SMIP for constructing bid curves for the day-ahead market, taking subsequent market opportunities into account. For different portfolio sizes, we have compared the performance of coordinated planning to that of purely sequential planning.

Coordinated bidding seems to have a very moderate potential for increasing profits, given the current Nordic reserve market prices and volumes. When planning for only one watercourse, gains of about 1% can be expected. When planning for more watercourses simultaneously, the value of coordinated bidding decreases to about 0.5%. Having more generators increases recourse options, and it is likely that having more generators dilutes the value of coordinated planning. The producer can simply reallocate production to respond to reserve market opportunities.

We thus conclude that gains decline when increasing the portfolio size, but that there is also a tendency towards stabilisation. The value of coordination seems to be diluted by production flexibility when planning for increasingly larger portfolios. However, committing units for later delivery of primary reserves and downward balancing services is an opportunity that a sequential planner will never see, no matter how flexible his portfolio.

The insights in how the portfolio size influences the gains from coordinated bidding are likely transferrable to other types of dispatchable production, such as thermal generators. However, reserve markets are generally small compared to day-ahead markets and are of an unpredictable nature. This unpredictability makes any kind of coordination strategy between the markets unreliable and the upside potential is limited because of market size.